MetaTrader 5 / Examples
Русский
preview
Brain Storm Optimization algorithm (Part II): Multimodality

Brain Storm Optimization algorithm (Part II): Multimodality

MetaTrader 5 — Examples | 30 August 2024, 14:49
232 4
Andrey Dik
Andrey Dik

Contents

1. Introduction
2. Algorithm implementation
3. Test results


1. Introduction

In the first part of the article , we delved into the world of optimization with the Brain Storm Optimization (BSO) algorithm revealing the basic principles of this innovative brainstorming-inspired method. Along with studying its logical structure, we also delved into a discussion of clustering methods - K-Means and K-Means++. Brain Storm Optimization (BSO) is an optimization method that incorporates idea generation and evaluation phases in group activities. This algorithm contributed to the field of optimization in conjunction with clustering methods. Clustering allows us to identify groups of similar data elements, which helps BSO find optimal solutions. The use of the mutation method allows the algorithm to bypass obstacles in the solution search space and search for more efficient paths to the optimum.

Now it is time to move on to real action! In the second part, we will dive into the practical implementation of the algorithm, talk about multimodality, test the algorithm and summarize the results.


2. Algorithm implementation

Let's briefly outline the key points in the BSO algorithm logic:

  1. Clustering.
  2. Cluster shift.
  3. Selecting ideas from clusters: cluster centroids or ideas from clusters.
  4. Merging selected ideas.
  5. Mutation of ideas obtained at previous stages.
  6. Selection of ideas for stages 2, 3 and 4. Placing new ideas into the parent population and sorting them.

We move on to the description of the BSO algorithm code.

Let's implement the structure of the S_BSO_Agent agent algorithm. The structure is used to describe each agent in the BSO algorithm.

1. The structure contains the following fields:

  • c[] - array for storing agent coordinates.
  • f - variable for storing the agent score (fitness).
  • label - variable for storing the cluster membership label.

2. Init - S_BSO_Agent structure method, which initializes the structure fields. It takes the "coords" integer argument used to resize the "c" coordinate array using the ArrayResize function.
3. f = -DBL_MAX - sets the initial value of the "f" variable equal to the minimum possible value of a double number.
4. label = -1 - sets the initial value of the "label" variable equal to -1, which means that the agent does not belong to any cluster.

This code represents the basic data structure for agents in the BSO optimization algorithm and initializes their fields when a new agent is created.

//——————————————————————————————————————————————————————————————————————————————
struct S_BSO_Agent
{
    double c     []; //coordinates
    double f;        //fitness
    int    label;    //cluster membership label

    void Init (int coords)
    {
      ArrayResize (c,     coords);
      f     = -DBL_MAX;
      label = -1;
    }
};
//——————————————————————————————————————————————————————————————————————————————

We have already discussed the K-Means and K-Means++ clustering algorithms in detail in the previous article, so we will not dwell on them here.

Let's move on to the description of the C_AO_BSO class code, which is an inheritor of the base class of C_AO population algorithms and contains the following fields and methods:

1. Public fields:

  • ao_name - optimization algorithm name.
  • ao_desc - optimization algorithm description.
  • ao_link - link to the article about the optimization algorithm.
  • popSize - population size.
  • parentPopSize - parent population size.
  • clustersNumb - number of clusters.
  • p_Replace - replacement probability.
  • p_One - single choice probability.
  • p_One_center - probability of selecting one center or individual in the selected cluster.
  • p_Two_center - probability of selecting two centers or two individuals in the selected cluster.
  • k_Mutation - mutation ratio.
  • distribCoeff - distribution ratio.
  • agent - agent array.
  • parents - array of parents.
  • clusters - array of clusters.
  • km - KMeans class object.

2. The options available are:

  • SetParams - method for setting algorithm parameters.
  • Init - method for initializing the algorithm. The method accepts minimum and maximum search ranges, search step and number of epochs.
  • Moving - method for moving agents.
  • Revision - method for revising agents.

3. Private fields:

  • parentsTemp - temporary array of parents.
  • epochs - maximum number of epochs.
  • epochsNow - current epoch.
//——————————————————————————————————————————————————————————————————————————————
class C_AO_BSO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BSO () { }
  C_AO_BSO ()
  {
    ao_name = "BSO";
    ao_desc = "Brain Storm Optimization";
    ao_link = "https://www.mql5.com/en/articles/14622";

    popSize        = 25;   //population size

    parentPopSize  = 50;   //parent population size;
    clustersNumb   = 5;    //number of clusters
    p_Replace      = 0.1;  //replace probability
    p_One          = 0.5;  //probability of choosing one
    p_One_center   = 0.3;  //probability of choosing one center
    p_Two_center   = 0.2;  //probability of choosing two centers
    k_Mutation     = 20.0; //mutation coefficient
    distribCoeff   = 1.0;  //distribution coefficient

    ArrayResize (params, 9);

    params [0].name = "popSize";       params [0].val  = popSize;

    params [1].name = "parentPopSize"; params [1].val  = parentPopSize;
    params [2].name = "clustersNumb";  params [2].val  = clustersNumb;
    params [3].name = "p_Replace";     params [3].val  = p_Replace;
    params [4].name = "p_One";         params [4].val  = p_One;
    params [5].name = "p_One_center";  params [5].val  = p_One_center;
    params [6].name = "p_Two_center";  params [6].val  = p_Two_center;
    params [7].name = "k_Mutation";    params [7].val  = k_Mutation;
    params [8].name = "distribCoeff";  params [8].val  = distribCoeff;
  }

  void SetParams ()
  {
    popSize       = (int)params [0].val;

    parentPopSize = (int)params [1].val;
    clustersNumb  = (int)params [2].val;
    p_Replace     = params      [3].val;
    p_One         = params      [4].val;
    p_One_center  = params      [5].val;
    p_Two_center  = params      [6].val;
    k_Mutation    = params      [7].val;
    distribCoeff  = params      [8].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving    ();
  void Revision  ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  int    parentPopSize; //parent population size;
  int    clustersNumb;  //number of clusters
  double p_Replace;     //replace probability
  double p_One;         //probability of choosing one
  double p_One_center;  //probability of choosing one center
  double p_Two_center;  //probability of choosing two centers
  double k_Mutation;    //mutation coefficient
  double distribCoeff;  //distribution coefficient

  S_BSO_Agent  agent   [];
  S_BSO_Agent  parents [];

  S_Clusters   clusters [];
  S_BSO_KMeans km;

  private: //-------------------------------------------------------------------
  S_BSO_Agent  parentsTemp [];
  int          epochs;
  int          epochsNow;
};
//——————————————————————————————————————————————————————————————————————————————

The Init method of the C_AO_BSO class performs the following actions to initialize the optimization algorithm:

  • Checking initialization. First, the StandardInit method is called with the search range and step parameters. If StandardInit returns 'false', the initialization is aborted and the Init method reutrns 'false'.
  • Agent initialization. The "agent" array is resized to "popSize". The Init method is called for each agent with the "coords" parameter defining the number of coordinates.
  • Cluster initialization. The "clusters" array is resized to "clustersNumb" (the maximum number of clusters), and the Init method is called for each cluster.
  • Parent initialization. The "parents" and "parentsTemp" arrays are resized to "parentPopSize + popSize" and the Init method is called for each parent. The arrays should be of such a size that they can accommodate both the parent and child populations for subsequent sorting.
  • Setting the epochs. The "epochs" and "epochsNow" values are set according to the passed parameter "epochsP" and "0" respectively.

The method returns "true" if all initialization steps are completed successfully. This prepares the algorithm to perform the optimization for a given number of epochs.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BSO::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  ArrayResize (clusters, clustersNumb);
  for (int i = 0; i < clustersNumb; i++) clusters [i].Init (coords);

  ArrayResize (parents,     parentPopSize + popSize);
  ArrayResize (parentsTemp, parentPopSize + popSize);

  for (int i = 0; i < parentPopSize + popSize; i++)
  {
    parents     [i].Init (coords);
    parentsTemp [i].Init (coords);
  }

  epochs    = epochsP;
  epochsNow = 0;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

The Moving method of the C_AO_BSO class is used to move agents during optimization. The method does the following:

  1. The value of the current epoch ("epochsNow++") is increased.
  2. If "revision" is 'false', the agents' coordinates are initialized using random values in the specified ranges. The method then terminates.
  3. If "revision" is not 'false', then new coordinates are calculated for each agent using equations and probabilities.
  4. Various mathematical calculations, random numbers and probabilities are used to determine the new coordinates of the agents.
  5. New coordinates are calculated according to the conditions and probabilities.
  6. The new coordinates are set using the SeInDiSp method to adjust the values according to the search ranges and steps.
  7. A new idea is generated that replaces the selected cluster center (cluster center offset) if the condition "u.RNDprobab () < p_Replace" is met.
  8. An idea from one cluster is selected if the "u.RNDprobab () < p_One" condition is met.
  9. Ideas from two clusters are selected if the "u.RNDprobab () < p_One" condition is not met.
  10. Mutation of agent coordinates occurs.
  11. New coordinates of agents are saved.

This method is responsible for updating the coordinates of agents in the BSO optimization algorithm according to the current epoch and probabilities. Let's highlight in color the corresponding sections of code that describe different models of agent behavior:

  • Generating a new idea. With each new epoch, agents more thoroughly explore the neighborhoods of the found global solution according to the "p_Replace" ratio trying to get closer to the global optimum and shifting the centroids.
  • Exploring the neighborhood of a single cluster. Considering the "p_One" ratio, agents explore the neighborhoods of one randomly selected cluster. Thus, the exploration of all areas where agents are located in the population continues.
  • Selecting ideas from two clusters. If the "u.RNDprobab () < p_One" condition is not met, ideas from two randomly selected clusters are selected.
  • Mutation. The agent coordinates are subject to mutation, which ensures population diversity and helps to avoid premature convergence to local optima.
  • Saving agents. After all operations, the new agent coordinates are saved for the next iteration.
//——————————————————————————————————————————————————————————————————————————————
void C_AO_BSO::Moving ()
{
  epochsNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

        agent [i].c [c] = a [i].c [c];
      }
    }

    return;
  }

  //----------------------------------------------------------------------------
  //----------------------------------------------------------------------------
  int    cIndx_1    = 0;  //index in the list of non-empty clusters
  int    iIndx_1    = 0;  //index in the list of ideas in the cluster
  int    cIndx_2    = 0;  //index in the list of non-empty clusters
  int    iIndx_2    = 0;  //index in the list of ideas in the cluster
  double min        = 0.0;
  double max        = 0.0;
  double dist       = 0.0;
  double val        = 0.0;
  double X1         = 0.0;
  double X2         = 0.0;
  int    clListSize = 0;
  int    clustList [];
  ArrayResize (clustList, 0, clustersNumb);

  //----------------------------------------------------------------------------
  //let's make a list of non-empty clusters
  for (int cl = 0; cl < clustersNumb; cl++)
  {
    if (clusters [cl].count > 0)
    {
      clListSize++;
      ArrayResize (clustList, clListSize);
      clustList [clListSize - 1] = cl;
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    //==========================================================================
    //generating a new idea that replaces the selected cluster center (cluster center offset)
    if (u.RNDprobab () < p_Replace)
    {
      cIndx_1 = u.RNDminusOne (clListSize);

      for (int c = 0; c < coords; c++)
      {
        val = clusters [clustList [cIndx_1]].centroid [c];

        dist = (rangeMax [c] - rangeMin [c]) * 0.8;

        min = val - dist; if (min < rangeMin [c]) min = rangeMin [c];
        max = val + dist; if (max > rangeMax [c]) max = rangeMax [c];

        val = u.GaussDistribution (val, min, max, 3);
        val = u.SeInDiSp  (val, rangeMin [c], rangeMax [c], rangeStep [c]);

        clusters [clustList [cIndx_1]].centroid [c] = val;
      }
    }

    //==========================================================================
    //an idea from one cluster is selected
    if (u.RNDprobab () < p_One)
    {
      cIndx_1 = u.RNDminusOne (clListSize);

      //------------------------------------------------------------------------
      if (u.RNDprobab () < p_One_center) //select cluster center
      {
        for (int c = 0; c < coords; c++)
        {
          a [i].c [c] = clusters [clustList [cIndx_1]].centroid [c];
        }
      }
      //------------------------------------------------------------------------
      else                               //random idea from the cluster
      {
        iIndx_1 = u.RNDminusOne (clusters [clustList [cIndx_1]].count);

        for (int c = 0; c < coords; c++)
        {
          a [i].c [c] = parents [clusters [clustList [cIndx_1]].ideasList [iIndx_1]].c [c];
        }
      }
    }
    //==========================================================================
    //select ideas from two clusters
    else
    {
      if (clListSize == 1)
      {
        cIndx_1 = 0;
        cIndx_2 = 0;
      }
      else
      {
        if (clListSize == 2)
        {
          cIndx_1 = 0;
          cIndx_2 = 1;
        }
        else
        {
          cIndx_1 = u.RNDminusOne (clListSize);

          do
          {
            cIndx_2 = u.RNDminusOne (clListSize);
          }
          while (cIndx_1 == cIndx_2);
        }
      }

      //------------------------------------------------------------------------
      if (u.RNDprobab () < p_Two_center) //two cluster centers selected
      {
        for (int c = 0; c < coords; c++)
        {
          X1 = clusters [clustList [cIndx_1]].centroid [c];
          X2 = clusters [clustList [cIndx_2]].centroid [c];

          a [i].c [c] = u.RNDfromCI (X1, X2);
        }
      }
      //------------------------------------------------------------------------
      else //two ideas from two selected clusters
      {
        iIndx_1 = u.RNDminusOne (clusters [clustList [cIndx_1]].count);
        iIndx_2 = u.RNDminusOne (clusters [clustList [cIndx_2]].count);

        for (int c = 0; c < coords; c++)
        {
          X1 = parents [clusters [clustList [cIndx_1]].ideasList [iIndx_1]].c [c];
          X2 = parents [clusters [clustList [cIndx_2]].ideasList [iIndx_2]].c [c];

          a [i].c [c] = u.RNDfromCI (X1, X2);
        }
      }
    }

    //==========================================================================
    //Mutation
    for (int c = 0; c < coords; c++)
    {
      int x = (int)u.Scale (epochsNow, 1, epochs, 1, 200);

      double ξ = (1.0 / (1.0 + exp (-((100 - x) / k_Mutation))));// * u.RNDprobab ();

      double dist = (rangeMax [c] - rangeMin [c]) * distribCoeff * ξ;
      double min = a [i].c [c] - dist; if (min < rangeMin [c]) min = rangeMin [c];
      double max = a [i].c [c] + dist; if (max > rangeMax [c]) max = rangeMax [c];

      val = a [i].c [c];

      a [i].c [c] = u.GaussDistribution (val, min, max, 8);
    }

    //Save the agent-----------------------------------------------------------
    for (int c = 0; c < coords; c++)
    {
      val = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      a     [i].c [c] = val;
      agent [i].c [c] = val;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

The main task of the Revision method of the C_AO_BSO class is to update the global solution and build solution clusters. The method does the following:

  1. Getting fitness. A fitness value is extracted for each agent in the population and saved in the corresponding field of the agent structure.
  2. Transferring new ideas to the population. New ideas (agents) generated during the optimization process are added to the parent population.
  3. Sorting the parent population. The parent population is sorted by fitness. This allows only the best solutions to participate in the creation of new ideas on the next epoch.
  4. Checking for the best solution. If the fitness of the best agent in the parent population exceeds the current best solution, then the best solution and its coordinates are updated.
  5. Performing clustering. If this is the first iteration, the k-means algorithm is initialized with the parent population and clusters. The k-means algorithm is then launched for clustering the parent population.
  6. Assigning the best cluster solution as the cluster center. For each cluster, it is checked whether it has agents (clusters may be empty). If it has, then we check if each agent in the parent population belongs to the cluster. If the agent fitness exceeds the current cluster fitness, then the cluster fitness and its centroid are updated (the centroid participates in the creation of new ideas).
//——————————————————————————————————————————————————————————————————————————————
void C_AO_BSO::Revision ()
{
  //get fitness--------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    agent [i].f = a [i].f;
  }

  //pass new ideas to the population--------------------------------------------
  for (int i = parentPopSize; i < parentPopSize + popSize; i++)
  {
    parents [i] = agent [i - parentPopSize];
  }

  //sort out the parent population----------------------------------------
  u.Sorting (parents, parentsTemp, parentPopSize + popSize);

  if (parents [0].f > fB)
  {
    fB = parents [0].f;
    ArrayCopy (cB, parents [0].c, 0, 0, WHOLE_ARRAY);
  }

  //perform clustering-----------------------------------------------------
  if (!revision)
  {
    km.KMeansInit (parents, parentPopSize, clusters);
    revision = true;
  }

  km.KMeansInit (parents, parentPopSize, clusters);
  km.KMeans     (parents, parentPopSize, clusters);

  //Assign the best cluster solution as the cluster center--------------------------
  for (int cl = 0; cl < clustersNumb; cl++)
  {
    clusters [cl].f = -DBL_MAX;

    if (clusters [cl].count > 0)
    {
      for (int p = 0; p < parentPopSize; p++)
      {
        if (parents [p].label == cl)
        {
          if (parents [p].f > clusters [cl].f)
          {
            clusters [cl].f = parents [p].f;
            ArrayCopy (clusters [cl].centroid, parents [p].c, 0, 0, WHOLE_ARRAY);
          }
        }
      }
    }
  }
}//——————————————————————————————————————————————————————————————————————————————

As for the multimodality, the BSO algorithm was originally introduced as an optimization method for solving multimodal problems. However, the test results showed that significant local extremes are not sufficiently explored by this algorithm, and many of them remain unnoticed. My current implementation may not be the most optimal one. Therefore, I decided to pay more attention to the adaptivity of agents in the context of K-Means clustering. This required some changes to the clustering algorithm.

As you might remember, in the framework of optimization algorithms, multimodality means that the function to be optimized has several optimal points or peaks. Such functions may contain several local optima, which may be either close to the global optimum in terms of the fitness function value or significant within the framework of the problem being solved. Clustering can help to highlight different regions in the search space where the feature has different modalities.

So, let's try to enhance the influence of agent fitness on clustering. Let's wrap the function of calculating distances between agents in the new FitnessDistance function. It will have an additional parameter "alpha", which acts as a ratio of significance balance between distance and fitness.

The FitnessDistance function calculates the distance between an agent and a cluster centroid, taking into account both the distance and the difference in the fitness function between them. This is done by calculating a weighted sum of the distance and the absolute value of the difference between the agent fitness function and the centroid. The "alpha" weight determines the relative importance of the distance compared to the difference in the fitness function.

//——————————————————————————————————————————————————————————————————————————————
double FitnessDistance (S_BSO_Agent &data, S_Cluster &clust, double alpha)
{
  double distance = VectorDistance (data.c, clust.centroid);
  double fitness_diff = fabs (data.f - clust.f);
  return alpha * distance + (1 - alpha) * fitness_diff;
}
//——————————————————————————————————————————————————————————————————————————————

The KMeans method is supplemented with the "alpha" parameter: 

void KMeans (S_BSO_Agent &data [], int dataSizeClust, S_Cluster &clust [], double alpha)

Let's change the code section of the KMeans method responsible for updating the centroids, so that each cluster has the maximum fitness value for an individual, which is part of the cluster.

// Update the centroids
double sum_c [];
ArrayResize (sum_c, ArraySize (data [0].c));
double sum_f = 0.0;

for (int cl = 0; cl < nClusters; cl++)
{
  ArrayInitialize (sum_c, 0.0);

  clust [cl].count = 0;
  ArrayResize (clust [cl].ideasList, 0);
  sum_f = -DBL_MAX;

  for (int d = 0; d < dataSizeClust; d++)
  {
    if (data [d].label == cl)
    {
      for (int k = 0; k < ArraySize (data [d].c); k++)
      {
        sum_c [k] += data [d].c [k];
      }

      if (data [d].f > sum_f) sum_f = data [d].f;

      clust [cl].count++;
      ArrayResize (clust [cl].ideasList, clust [cl].count);
      clust [cl].ideasList [clust [cl].count - 1] = d;
    }
  }

  if (clust [cl].count > 0)
  {
    for (int k = 0; k < ArraySize (sum_c); k++)
    {
      clust [cl].centroid [k] = sum_c [k] / clust [cl].count;
    }
  }
}

The changes made allow the fitness function to be taken into account during clustering, but they did not lead to a noticeable improvement in the allocation of individual modes in the fitness function and did not affect the results. This may be due to the fact that using a fitness function in the clustering process is not always efficient, at least in this implementation of BSO.

If K-Means and K-Means++ do not provide the desired results, we can try other clustering methods:

1. Density-based spatial clustering for noisy applications (DBSCAN) - the clustering method is based on density rather than distance. It groups together points that are close to each other in the feature space and have a sufficient number of neighbors. DBSCAN is one of the most commonly used clustering algorithms.

2. Hierarchical Clustering builds a hierarchy of clusters, where each cluster is linked to its two closest clusters. Hierarchical clustering can be agglomerative (bottom-up) or divisional (top-down).

3. Gaussian mixture model (GMM) - this statistical model assumes that all observed data are generated from a mixture of several Gaussian distributions whose parameters are unknown. Each cluster corresponds to one of these distributions.

4. Spectral clustering uses the eigenvectors of the similarity matrix to reduce the dimensionality of the data before clustering in a low-dimensional space.

There are quite a lot of clustering methods to try and conduct further research in this area. If you are willing to experiment, the K-Means method can be replaced with any other in the attached code.


3. Test results

BSO algorithm results:

BSO|Brain Storm Optimization|25.0|50.0|5.0|0.1|0.5|0.3|0.2|20.0|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9301770731803266
25 Hilly's; Func runs: 10000; result: 0.5801719580773876
500 Hilly's; Func runs: 10000; result: 0.30916005647304245
=============================
5 Forest's; Func runs: 10000; result: 0.929981802038364
25 Forest's; Func runs: 10000; result: 0.5907047167619348
500 Forest's; Func runs: 10000; result: 0.2477599978259004
=============================
5 Megacity's; Func runs: 10000; result: 0.5246153846153847
25 Megacity's; Func runs: 10000; result: 0.2784615384615384
500 Megacity's; Func runs: 10000; result: 0.1253384615384627
=============================
All score: 4.51637 (50.18%)

The results of testing the algorithm on test functions (All score of 4.51637 corresponds to 50.18% of the maximum possible value) show that using the parameters specified in the first line of the prints yields quite good results. The values of the function results are in the range from 0.125 for 1000 optimized parameters and up to 0.93 for 10, respectively, which indicates that the algorithm is quite successful in finding optimal solutions.

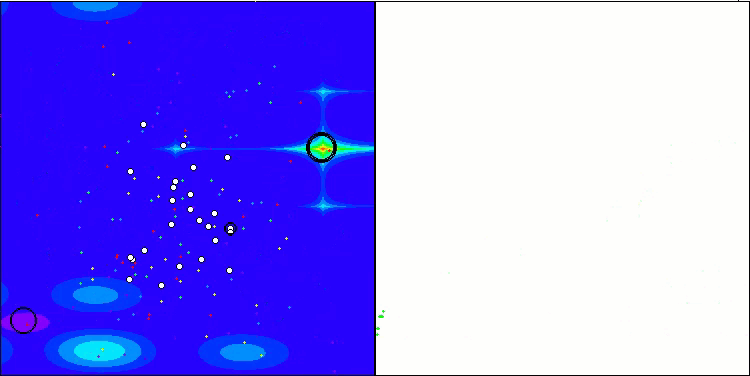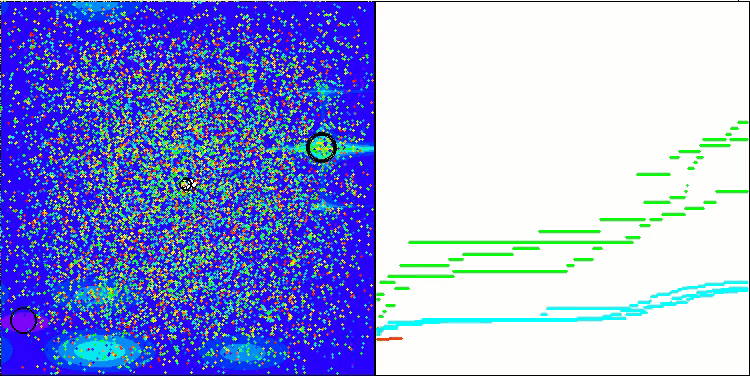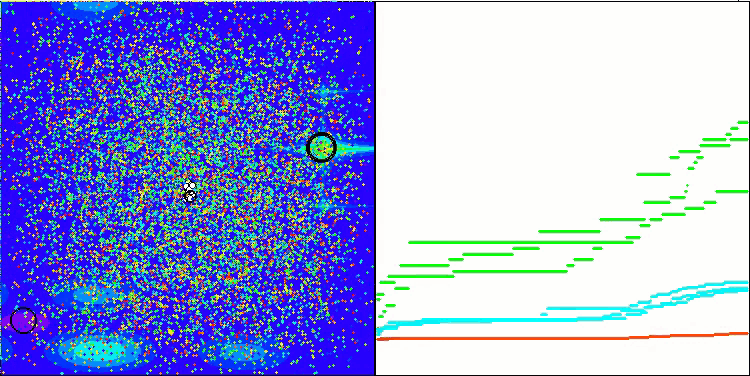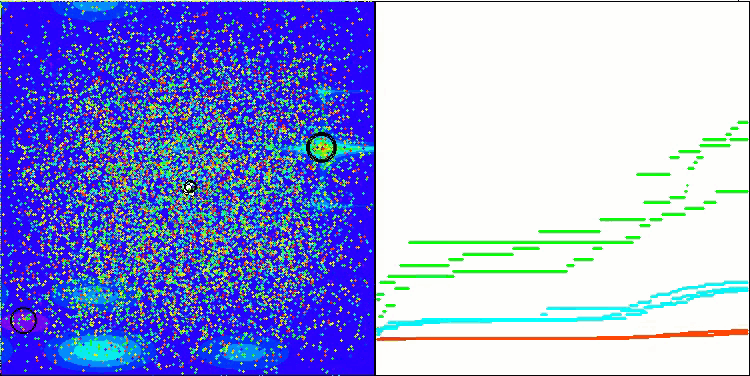
I would like to separately note how the clustering of solutions looks on the visualization. This process is especially noticeable on functions with the maximum number of parameters, as from the initial chaos, with each completed iteration, the characteristic sections of the clusters begin to stand out more and more clearly.

Hilly

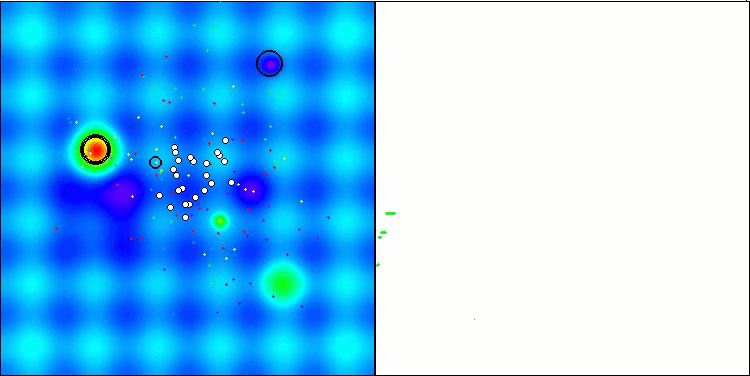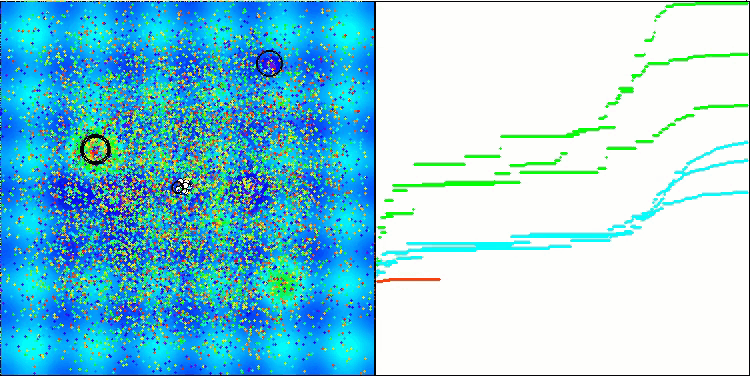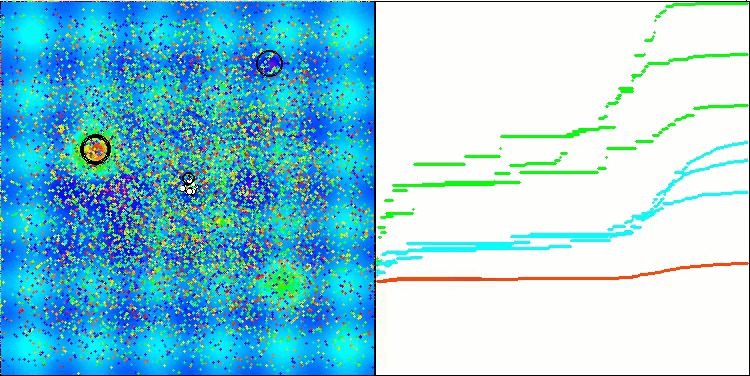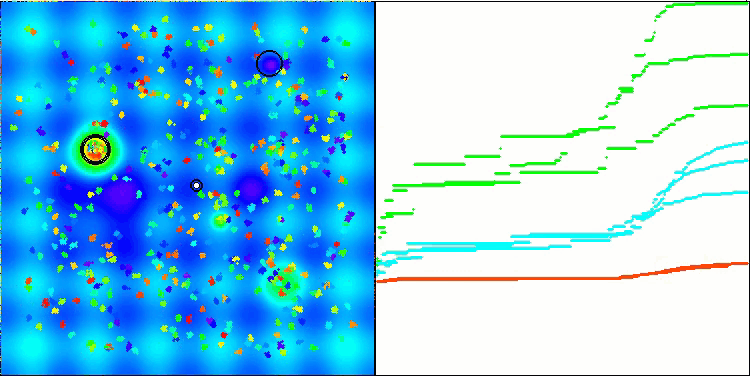
  BSO on the Hilly test function.

Forest

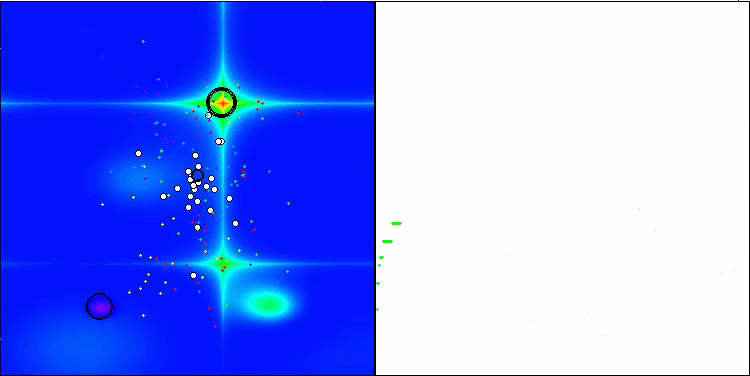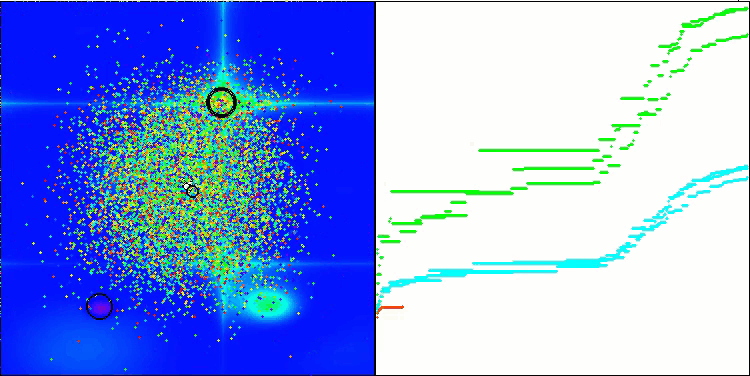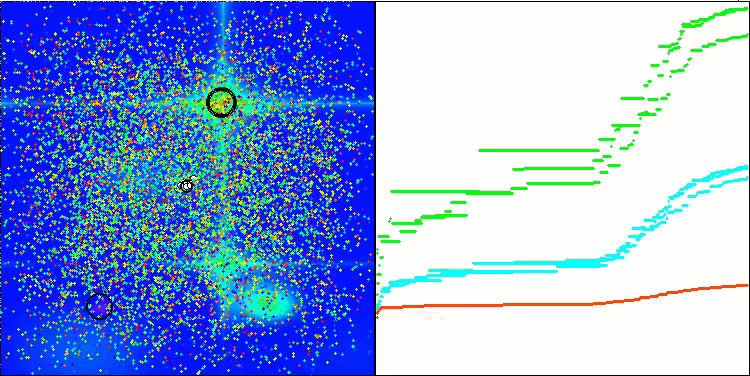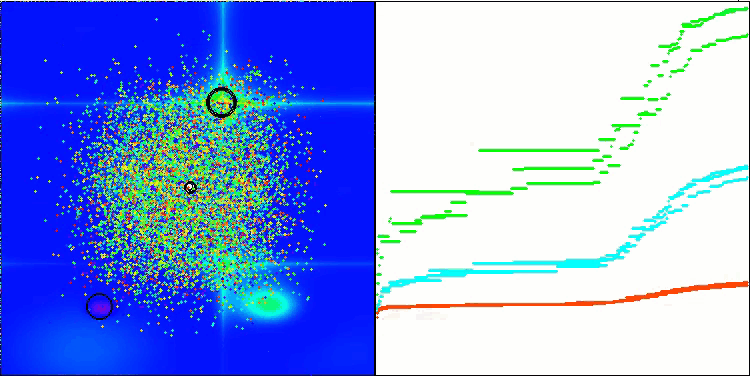
  BSO on the Forest test function.

Megacity

  BSO on the Megacity test function.

I had high expectations for this algorithm and hoped to see it at the top of the ranking table. After all, this is the first time that I used the clustering method in combination with the mutation method, which were supposed to show unique results. I was a bit disappointed to see that the algorithm only ranked at the top of the ranking table, but not among the leaders. BSO demonstrates excellent results on the Forest and Megacity functions with 1000 parameters, which are quite worthy of the table leaders.

However, while BSO performed well overall and placed well in the rankings, it requires careful parameter tuning to achieve maximum efficiency. Numerous tunable parameters include convergence rate, population size, mutation methods, and idea evaluation, which affect the algorithm performance.

#
AO
Description
Hilly
Hilly final
Forest
Forest final
Megacity (discrete)
Megacity final
Final result
% of MAX
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 BGA binary genetic algorithm 0.99992 0.99484 0.50483 2.49959 1.00000 0.99975 0.32054 2.32029 0.90667 0.96400 0.23035 2.10102 6.921 76.90
2 (P+O)ES (P+O) evolution strategies 0.99934 0.91895 0.56297 2.48127 1.00000 0.93522 0.39179 2.32701 0.83167 0.64433 0.21155 1.68755 6.496 72.18
3 SDSm stochastic diffusion search M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
4 ESG evolution of social groups 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
5 SIA simulated isotropic annealing 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
6 DE differential evolution 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
7 BSA bird swarm algorithm 0.90857 0.73661 0.25767 1.90285 0.90437 0.81619 0.16401 1.88457 0.61692 0.54154 0.10951 1.26797 5.055 56.17
8 HS harmony search 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
9 SSG saplings sowing and growing 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
10 (PO)ES (PO) evolution strategies 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
11 BSO brain storm optimization 0.91301 0.56222 0.30047 1.77570 0.97162 0.57162 0.23449 1,77772 0.60462 0.27138 0.12011 0.99611 4.550 50.55
12 WOAm wale optimization algorithm M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
13 ACOm ant colony optimization M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
14 BFO-GA bacterial foraging optimization - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
15 MEC mind evolutionary computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
16 IWO invasive weed optimization 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
17 Micro-AIS micro artificial immune system 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
18 COAm cuckoo optimization algorithm M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
19 SDOm spiral dynamics optimization M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
20 NMm Nelder-Mead method M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
21 FAm firefly algorithm M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
22 GSA gravitational search algorithm 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
23 BFO bacterial foraging optimization 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
24 ABC artificial bee colony 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
25 BA bat algorithm 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
26 SA simulated annealing 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
27 IWDm intelligent water drops M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
28 PSO particle swarm optimisation 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
29 Boids boids algorithm 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
30 MA monkey algorithm 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
31 SFL shuffled frog-leaping 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
32 FSS fish school search 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
33 RND random 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
34 GWO grey wolf optimizer 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
35 CSS charged system search 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
36 EM electroMagnetism-like algorithm 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


Summary

The BSO algorithm has several advantages, including flexibility, exploration-exploitation balance, and adaptability to various optimization problems.

However, the efficiency of the algorithm is highly dependent on the settings of external parameters (the number of external parameters is the main drawback of BSO), so it is necessary to conduct careful research and experiments to determine the optimal settings for each specific task.

I encourage all optimization enthusiasts to join the experiments and jointly explore the capabilities of the algorithm in solving practical problems. If anyone finds more interesting results and better external parameters, please share them in the comments to the article.

Tab

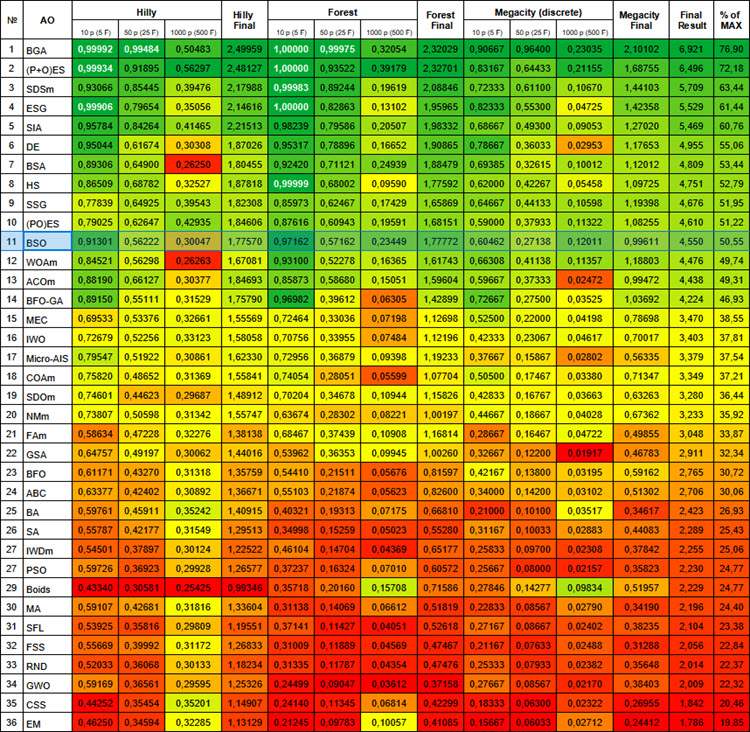
Figure 1. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white

chart

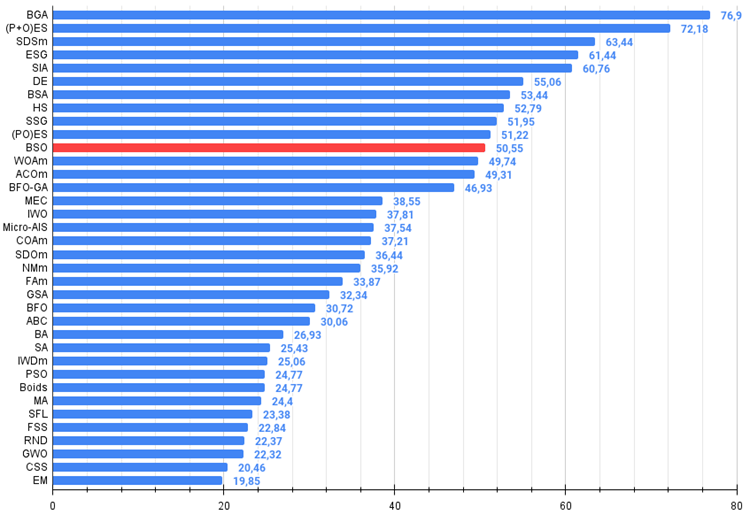
Figure 2. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,

where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)

BSO pros and cons:

Advantages:

  1. Good results on the sharp Forest function and discrete Megacity of large dimension.

Disadvantages:

  1. A very large number of external parameters.
  2. Complex architecture and implementation.
  3. High load on computing resources.

The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.

Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/14622

Attached files |
Download ZIP
BSO.zip (28.18 KB)
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.

Other articles by this author

Last comments | Go to discussion (4)
fxsaber
fxsaber | 19 Apr 2024 at 09:23
If multimodality works, it should show a lot of sine vertices.
fxsaber
fxsaber | 19 Apr 2024 at 10:02
An example of when a monomodal AO fails.

Forum on trading, automated trading systems and testing trading strategies

Discussion of the article "The role of random number generator quality in the efficiency of optimisation algorithms"

fxsaber, 2024.04.01 19:17

Took a function like this. 
input double X = 0;

double OnTester() { return(MathTan(X)); }

Some obscure result. If you implement iterative poking, I suppose you can find a lot of "rocks".

Tangent is an unsuccessful FF, TS-FF is much easier to poke out.

Andrey Dik
Andrey Dik | 19 Apr 2024 at 10:09
fxsaber #:
If multimodality works, it should show a lot of sine vertices.
I must say that I am not satisfied with the performance of the algorithm as far as multimodality is concerned. In the article I encourage readers to join the research of the algorithm, I think there is a potential for its improvement. Perhaps it is necessary to keep a separate "reference" modal map, so that it could be periodically updated and replenished in the process of optimisation.
Andrey Dik
Andrey Dik | 19 Apr 2024 at 17:15
In my opinion, ESG is much better at modding than ESG, if we go purely visual. I would like to add the possibility for social groups to participate in clustering. Thoughts out loud.
Features of Custom Indicators Creation Features of Custom Indicators Creation
Creation of Custom Indicators in the MetaTrader trading system has a number of features.
Neural Networks Made Easy (Part 83): The "Conformer" Spatio-Temporal Continuous Attention Transformer Algorithm Neural Networks Made Easy (Part 83): The "Conformer" Spatio-Temporal Continuous Attention Transformer Algorithm
This article introduces the Conformer algorithm originally developed for the purpose of weather forecasting, which in terms of variability and capriciousness can be compared to financial markets. Conformer is a complex method. It combines the advantages of attention models and ordinary differential equations.
Features of Experts Advisors Features of Experts Advisors
Creation of expert advisors in the MetaTrader trading system has a number of features.
Building A Candlestick Trend Constraint Model (Part 8): Expert Advisor Development (II) Building A Candlestick Trend Constraint Model (Part 8): Expert Advisor Development (II)
Think about an independent Expert Advisor. Previously, we discussed an indicator-based Expert Advisor that also partnered with an independent script for drawing risk and reward geometry. Today, we will discuss the architecture of an MQL5 Expert Advisor, that integrates, all the features in one program.