构建一个用于实现带约束条件的自定义最大值的通用优化公式（GOF）

介绍 — 优化问题的基本概念

优化问题包含两个阶段：1) 问题表述（或定义），2) 问题求解。在第一阶段，主要有三个组成部分：输入变量、目标函数和约束函数。在第二阶段，利用优化算法对问题进行数值求解。

变量 (用x_1 , x_2 , x_3 , …, x_n表示)：变量是我们用来调整以实现最大化目标函数的“旋钮”。变量有很多类型：integer（整型）, real（实数型）, 和 Boolean（布尔型）。在EA中，我们可以使用诸如移动平均周期、入场时的盈利目标（Take Profit, TP）与止损（Stop Loss, SL）比例、止损点数（以点差pips为单位）等变量。

目标函数（用 f_i (x)表示）： 如果存在多个目标函数，该问题就被称为多目标优化问题。MetaTrader 5的优化算法仅期望一个目标函数，因此，为了考虑多个目标，我们需要将它们组合成一个。将目标函数组合起来的最简单方法是创建它们的加权和。一些开发者建议使用乘法运算来组合它们，这在某些情况下可能有效，但我们更倾向于使用求和作为更好的方法。在本文中，我们将使用“有针对性且加权”的目标求和法，如下文所述。目标函数的示例包括：账户余额、盈利目标、胜率、年化收益率、净利润等。

约束函数（用g_i (x)表示）： 这些函数用于生成一个用户期望的界限值。这个界限可以是上界，就像在 g_i(x) ≤ U_i 中一样，其中 g_i(x) 是第 i 个约束条件，U_i 是上界。同样地，下界约束就像 g_i(x) ≥ L_i 一样，其中 L_i 是下界。

MetaTrader 5 优化算法仅接受对输入变量（也称为侧面约束）施加的约束，例如，3 <= x_1 <= 4，但不能使用其他类型的约束。因此，我们需要将任何额外的约束 g_i(x) 纳入最终且唯一的目标函数F(x) 中，如下所示。约束函数 g_i(x) 的例子包括：限制连续亏损的次数、夏普比率、胜率等。

优化算法

一般而言，优化算法主要有两种类型。第一种类型更为经典，基于优化问题中所有函数的梯度计算（这种方法可以追溯到艾萨克·牛顿的时代）。第二种类型则较为新近（自20世纪70年代左右起），完全不使用梯度信息。介于这两者之间，可能还有一些结合上述两种方法的算法，但我们在这里无需讨论它们。MetaTrader 5设置选项卡中的“基于快速遗传的算法”属于第二种类型。这使我们能够无需计算目标函数和约束函数的梯度。更进一步的是，由于MetaTrader 5的算法无需考虑梯度，因此我们能够考虑那些不适用于梯度算法的约束函数。关于这一点，下面将进行更详细的讨论。

重要的一点是，MetaTrader 5中的“慢速完整算法”实际上并不是一种优化算法，而是一种暴力求解法，即在侧约束条件下，对所有输入变量所有可能值的组合进行穷举评估。

由多个目标函数f_i(x)构建而成的目标函数F(x)

在本节中，我们将讨论如何将多个目标函数组合成一个单一的目标函数F。

如引言部分所述，我们使用求和的方式来组合多个目标函数。如果读者希望使用乘积组合的方式，可以自行修改源代码。求和组合公式为：

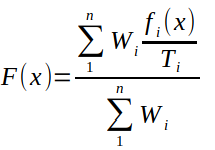
其中 

• x是包含n个输入变量的向量
• f_i(x) i是第i个目标函数
• W_i是第i个权重
• T_i是第i个目标函数的第i个目标值

目标值的作用是对给定的目标进行归一化（除法运算），使得在求和过程中，该目标能够与其他目标进行比较。换句话说，加权和是针对“归一化”后的目标函数计算的。权重W_i作为乘数，与归一化后的目标（f_i(x)/T_i）相乘，从而使用户能够识别哪个归一化后的目标比其他目标更重要。通过将W_i*f_i(x)/T_i的和除以W_i的和，可以使权重W_i凸化。

W_i的选择：权重的凸化使用户能够关注它们的相对值，而不是绝对值。</i0例如，假设有三个目标：年回报率、回收率和盈利因子。权重W_1=10, W_2=5, W_3=1与W_1=100, W_2=50, W_3=10具有相同的效果，即归一化后的目标1（年回报率/T_1）被认为是归一化后的目标2（回收率/T_2）的两倍重要，并且是归一化后的目标3（盈利因子/T_3）的十倍重要。只要权重是正数，并且能够根据用户的标准表达相对重要性，就没有对错之分。

T_i的选择： 在进行全面优化之前，需要谨慎选择目标值T_i，最好多进行几次模拟。这样做是为了估计每个目标函数的范围，并设置T_i值，使得归一化后的函数（f_i(x)/T_i）具有可比的数量级。例如，假设你的账户初始余额为10,000；在优化之前，你的EA使最终余额约为20,000；盈利因子为0.9。如果你设置优化问题有两个目标：f_1 = 余额，f_2 = 盈利因子，那么目标值的一个好选择是：T_1 = 30,000，T_2 = 2，这将使两个归一化后的函数具有相同的数量级（可比值）。在全面运行优化后，你可能会发现EA给出了非常大的最终余额和相似的盈利因子。在这一点上，如果归一化后的函数具有不同的数量级，你可以调整T_i值。目标值也必须是正实数。请自行判断。当我们讨论GOF代码的输出时，将更详细地讨论这个话题。

添加约束条件 

将目标函数定义为各个单个目标的加权和是非常标准的做法。现在，我们引入一种简单的方法，将约束函数纳入优化问题中，同时确保MetaTrader 5的快速遗传算法仍然有效。我们将使用拉格朗日方法的一种改进版本，该方法通过从单个优化目标中减去一个惩罚项来实现。为此，我们将定义新的惩罚函数，以衡量每个约束条件被违反的程度：

如你所见，当g_i(x)被违反时，P_i(x)为正，否则为零。如果U_i或L_i为零，我们将其替换为1，以避免除以零的情况。

在拉格朗日乘法中，每个约束条件都有一个乘数，其值是方程组的解。在我们的改进版本中，我们假设所有乘数都是相同的，并具有一个常数值k_p（见下方公式）。这种简化在这里是可行的，因为优化算法不需要计算优化问题中任何函数的梯度。

最终的单一目标函数F(x)是：

注：符号“:=”表示赋值，而不是数学定义。 

乘数k_p扮演着拉格朗日乘数因子的角色，用于迫使不可行设计（即违反至少一个约束的设计）具有非常低的目标值。这种目标值的降低将使MetaTrader 5中的遗传算法将该设计的排名降得很低，从而使其不太可能被用于下一代设计的繁殖。

乘数k_o不是拉格朗日乘子方法的一部分。它用于增加可行设计的目标函数值，以便在MetaTrader 5终端的优化图中扩展Y轴的正面区域。 

用户可以在输入参数的其他参数部分中更改k_o和k_p的值。我们建议k_o和k_p的值取10的幂（例如，10、100、1000等）。

MetaTrader 5输入参数页的截图

在GOF中，有三个输入参数部分：目标函数、约束函数和其他杂项。

下面是目标函数部分。在问题表述中，可以从后面将要展示的18个可能函数中选择最多5个目标函数。按照代码逻辑，可以添加超过5个目标函数，但超过3个目标函数会使得权重和目标的选择变得更加困难。同样地，按照代码逻辑，也可以添加超过18个可能的函数。

下面是硬约束函数部分。在GOF中，可以从已实现的14个约束函数中选择最多10个约束添加到优化公式中。按照代码逻辑，可以添加超过10个约束条件。同样地，根据代码逻辑，也可以向这14个约束函数的列表中添加新的约束。

下面是其他优化参数部分。关于这一部分的更多内容将在接下来的段落中讨论。

在EA中使用GenericOptimizationFormulation.mqh

如果你没有耐心读整篇文章，我们首先为你提供在你的EA中使用此代码的步骤，这样你可以先尝试操作，然后再带着更深入的理解去阅读文章的其余部分。下面是GenericOptimizationFormulation.mqh文件中的初始注释内容：

/*
要在你的EA中使用此文件，你必须执行以下步骤：
-编辑你的EA .mq5文件
-在输入变量之后和OnInit() 函数之前插入以下两行代码：
ulong gof_magic= an_ulong_value;
#include <YOUR_INCLUDE_LOCATION\GenericOptimizationFormulation.mqh>
-保存并编译你的EA文件
-如果你遇到编译错误，请确保你做到了以下几点：
-用包含magic数值的变量或直接用magic数值替换 an_ulong_value
-用你的包含文件所在的文件夹名替换YOUR_INCLUDE_LOCATION
*/

希望上面的插入内容能够不言自明。稍后我们将使用MetaTrader 5的均线交易EA作为示例进行展示。现在让我们继续解释源代码。

源代码：GenericOptimizationFormulation.mqh

既然我们已经给出了目标函数和约束的公式，现在我们来讨论MQL5代码的实现，并展示一些代码片段。

 敬请读者注意：

• 据说，代码行数超过七行的软件存在bug的概率不为零。而GOF（可能是指我们的优化框架或库）拥有上千行代码，所以存在bug的概率肯定不为零。我们鼓励读者在评论区提供反馈，以便我们改进代码。
• 如果你发现更好的代码编写方式，我们非常期待看到你的优化代码，以便改进GOF。
• 你可以添加自己的目标函数和约束到代码中使程序更强大。也请在评论区分享它们。

包含的库

首先，我们需要包含一些用于统计和代数的库：

#include <Math\Stat\Lognormal.mqh>
#include <Math\Stat\Uniform.mqh>
#include <Math\Alglib\alglib.mqh>

从中选择目标函数：

enum gof_FunctionDefs {        // functions to build objective
   MAX_NONE=0,                 // 0] None
   MAX_AnnRetPct,              // 1] Annual Return %
   MAX_Balance,                // 2] Balance
   MAX_NetProfit,              // 3] Net Profit
   MAX_SharpeRatio,            // 4] Sharpe Ratio
   MAX_ExpPayOff,              // 5] Expected Payoff
   MAX_RecovFact,              // 6] Recovery Factor
   MAX_ProfFact,               // 7] Profit Factor
   MAX_LRcrr3,                 // 8] LRcrr^3
   MAX_NbrTradesPerWeek,       // 9] #Trades/week
   MAX_WinRatePct,             // 10] Win Rate %
   MAX_Rew2RiskRatio,          // 11] Reward/Risk(RRR=AvgWin/AvgLoss)
   MAX_OneOverLRstd,           // 12] 1/(LR std%)
   MAX_OneHoverWorstTradePct,  // 13] 100/(1+|WorstLoss/Init.Dep*100|)
   MAX_LR,                     // 14] LRslope*LRcorr/LRstd
   MAX_OneHoverEqtyMaxDDpct,   // 15] 100/(1+EqtyMaxDD%))
   MAX_StratEfficiency,        // 16] Seff=Profit/(TotalTrades*AvgLot)
   MAX_KellyCrit,              // 17] Kelly Criterion
   MAX_OneOverRoRApct          // 18] 1/Max(0.01,RoRA %)
};

有18个可能的目标函数，最多可以选择5个来构建优化问题。用户可以根据相同的实现模式在源代码中添加更多函数。从目标函数的名称上就能了解其意义，但以下提到的几个除外：

• LRcrr^3：线性回归相关系数的三次方。
• 1/(LR std%)：LR std是线性回归标准差。其倒数衡量了权益曲线与直线的紧密程度。
• 100/(1+|WorstLoss/Init.Dep*100|)：最大亏损除以初始保证金是衡量表现不佳的指标。其倒数则是衡量良好表现的指标。
• LRslope*LRcorr/LRstd：这是线性回归中三个函数（斜率、相关系数和标准差）的乘积目标。
• Seff=Profit/(TotalTrades*AvgLot)：是衡量策略效率的指标。我们更倾向于选择利润高、交易次数少且头寸规模小的策略。
• 1/Max(0.01,RoRA %)：RoRA是账户破产风险（Risk of Ruin Account）。这是通过我们稍后将讨论的蒙特卡洛模拟计算得出的。

从中选择硬约束条件：

enum gof_HardConstrains {
   hc_NONE=0,                     // 0] None
   hc_MaxAccountLoss_pct,         // 1] Account Loss % InitDep
   hc_maxAllowed_DDpct,           // 2] Equity DrawDown %
   hc_maxAllowednbrConLossTrades, // 3] Consecutive losing trades
   hc_minAllowedWin_pct,          // 4] Win Rate %
   hc_minAllowedNbrTradesPerWeek, // 5] # trades/week
   hc_minAllowedRecovFactor,      // 6] Recov Factor
   hc_minAllowedRRRFactor,        // 7] Reward/Risk ratio
   hc_minAllowedAnnualReturn_pct, // 8] Annual Return in %
   hc_minAllowedProfFactor,       // 9] Profit Factor
   hc_minAllowedSharpeFactor,     // 10] Sharpe Factor
   hc_minAllowedExpPayOff,        // 11] Expected PayOff
   hc_minAllowedMarginLevel,      // 12] Smallest Margin Level
   hc_maxAllowedTradeLoss,        // 13] Max Loss trade
   hc_maxAllowedRoRApct           // 14] Risk of Ruin(%)
};
enum gof_HardConstType {
   hc_GT=0, // >=     Greater or equal to
   hc_LT    // <=     Less or equal to
};

有14个可能的约束条件，最多可以选择10个来构建优化问题。用户可以根据相同的实现模式在源代码中添加更多约束。从约束函数的名称就能知道其代表什么。约束分为两种类型，hc_GT表示有下界的约束，ht_LT表示有上界的约束。当我们展示如何使用它们时会进一步说明这一点。

破产风险选项

enum gof_RoRaCapital {
   roraCustomPct=0,  // Custom % of Ini.Dep.
   roraCustomAmount, // Custom Capital amount
   roraIniDep        // Initial deposit
};

在计算破产风险时，“账户”资金有三种定义方式。第一种是将其定义为初始入金的百分比。第二种是账户货币中给定的固定资本金额。第三种是第一种情况的特例，即百分比为100%。关于破产风险的详细解释，稍后会结合代码给出。

目标函数的小数位数

如前所述，我们可以选择使用结果列中的两位小数来显示模拟的额外信息。以下是选项：

enum gof_objFuncDecimals {
   fr_winRate=0, // WinRate %
   fr_MCRoRA,    // MonteCarlo Sim Risk of Ruin Account %
   fr_LRcorr,    // LR correlation
   fr_ConLoss,   // Max # Consecutive losing Trades
   fr_NONE       // None
};

fr_winRate 是模拟中的胜率百分比。例如，如果胜率为 34%，则结果目标值为 0.39。如果胜率是100%，它将显示为0.99。

fr_MCRoRA 表示账户破产风险百分比。例如，如果账户破产风险为 11%，则结果目标值为 0.11。

fr_LRcorr 表示线性回归相关系数。例如，如果系数为 0.88，则结果目标值为 0.88。

fr_ConLoss 表示连续亏损交易的最大次数。例如，如果这个数字是 7，则结果目标值应为0.07。如果数字超过 99，则结果目标值将显示为 0.99。

fr_NONE 用于当你不想用小数表示任何信息时。

对象函数

代码中的下一部分是选择单个目标函数（最多 5 个）。下面只展示了第一个函数及其目标和权重的代码片段。

input group   "- Build Custom Objective to Maximize:"
sinput gof_FunctionDefs gof_Func1   = MAX_AnnRetPct;          // Select Objective Function to Maximize 1:
sinput double gof_Target1           = 200;                    // Target 1
sinput double gof_Weight1           = 1;                      // Weight 1

约束函数

input group   "- Hard Constraints:"
sinput bool   gof_IncludeHardConstraints     = true;//if false, all constraints are ignored

sinput gof_HardConstrains gof_HC_1=hc_minAllowedAnnualReturn_pct; // Select Constraint Function 1:
sinput gof_HardConstType gof_HCType_1=hc_GT; // Type 1
sinput double gof_HCBound_1=50; // Bound Value 1

可以通过设置 gof_IncludeHardConstraints=false 来关闭所有硬约束。接下来是选择第一个约束，它的类型，以及它的界限值。所有十个约束都使用相同的格式。

其他各类优化参数

input group   "------ Misc Optimization Params -----"
sinput gof_objFuncDecimals gof_fr                  = fr_winRate;     // Choose Result-column's decimals
sinput gof_RoRaCapital  gof_roraMaxCap             = roraCustomPct;  // Choose capital method for Risk of Ruin
sinput double           gof_RoraCustomValue        = 10;             // Custom Value for Risk of Ruin (if needed)
sinput bool             gof_drawSummary            = false;          // Draw summary on chart
sinput bool             gof_printSummary           = true;           // Print summary on journal
sinput bool             gof_discardLargestProfit   = false;          // Subtract Largest Profit from Netprofit
sinput bool             gof_discardLargestLoss     = false;          // Add Largest Loss to Net profit
sinput double           gof_PenaltyMultiplier      = 100;            // Multiplier for Penalties (k_p)
sinput double           gof_ObjMultiplier          = 100;            // Multiplier for Objectives (k_o)

在上面部分，我们选择：

• gof_fr：在结果列中，以小数形式显示的数值。 
• gof_roraMaxCap：计算RoRA的方法。
• gof_RoraCustomValue：RoRA的资本值或初始存款的百分比。这取决于您在上一行中的选择。
• gof_drawSummary：您可以选择在图表上绘制GOF报告摘要。
• gof_printSummary：您可以选择在“日志”选项卡上打印GOF报告摘要。
• gof_discardLargestProfit：您可以从净利润中减去最大利润，以抑制那些只追求单一大额收益的策略。
• gof_discardLargestLoss：您可以将最大损失加到净利润上，以抑制那些可能产生大额损失的策略。 
• gof_PenaltyMultiplier：目标函数定义中之前提到的乘数“K_p”。
• gof_ObjMultiplier：目标函数定义中之前提到的乘数“K_o”。

其他选项部分的默认参数就能够很好的运行程序了。

下面的代码行是用于定义变量，并从MetaTrader 5的TesterStatistics()函数中获取值。在此之后是GOF的主要代码段：

//------------ GOF ----------------------
// Printing and displaying results from the simulation
   GOFsummaryReport();

// calculate the single objective function
   double SingleObjective = calcObjFunc();

// calculate the total penalty from constraint violations
   if(gof_IncludeHardConstraints) gof_constraintTotalPenalty=calcContraintTotalPenalty(gof_displayContraintFlag);

// Compute customMaxCriterion
// gof_PenaltyMultiplier pushes infeasible designs to have low objective values
// gof_PenaltyMultiplier expand the positive side of the Y axis
   double customMaxCriterion=gof_constraintTotalPenalty>0?
                             SingleObjective-gof_PenaltyMultiplier*gof_constraintTotalPenalty:
                             gof_ObjMultiplier*SingleObjective;

// add additional simulation result as two decimal digits in the result column
   customMaxCriterion=AddDecimalsToCustomMax(customMaxCriterion);

// Printing and displaying more results from GOF
   FinishGOFsummaryReport(customMaxCriterion);

   return (NormalizeDouble(customMaxCriterion,2));

上面的代码表示： 

• GOFsummaryReport()用于准备GOF摘要报告，该报告将显示在“日志”选项卡和图表上。
• calcObjFunc()用于计算组合单一目标函数。
• calcContraintTotalPenalty()用于计算由于违反约束而产生的总惩罚。
• customMaxCriterion是根据引言中的说明，计算单一目标减去违反约束的总惩罚的总和。
• AddDecimalsToCustomMax()用于向customMaxCriterion的小数部分添加信息。
• FinishGOFsummaryReport() 用于完成并打印GOF摘要报告。

代码的其余部分直接实现了引言中给出的公式。唯一值得讨论的部分是破产风险的计算。

使用蒙特卡洛模拟计算破产风险

破产风险可以通过一个简单的公式，来计算，但我们选择使用蒙特卡洛模拟，因为简单的公式没有给出合理的结果。对于蒙特卡洛方法，我们需要知道平均盈利和亏损、这些盈利和亏损的标准差、胜率以及模拟中的交易数量。此外，我们还需要提供定义账户破产的资本金额。 

double MonteCarlo_RiskOfRuinAccount(double WinRatePct, double AvgWin, double AvgLoss, double limitLoss_money, int nTrades) {
// 10000 Montecarlo simulations, each with at least 100 trades.
// Ideally, if we had lots of trades in the history, we could use a Markov Chain transfer probability matrix
//  we are limiting the statistics to mean & stdev, without knowledge of a transfer probability information

   double posDealsMean,posDealsStd,negDealsMean,negDealsStd;
   CalcDealStatistics(gof_dealsEquity, posDealsMean,posDealsStd,negDealsMean,negDealsStd);

// seeding the random number generator
   MathSrand((int)TimeLocal()+1);

// ignore posDealsMean and negDealsMean. Use AvgWin and AvgLoss instead
   AvgLoss=MathAbs(AvgLoss);
   WinRatePct=MathMin(100,MathMax(0,WinRatePct));

// case when win rate is 100%:
   if((int)(WinRatePct*nTrades/100)>=nTrades) {
      WinRatePct=99;          // just to be a bit conservative if winrate=100%
      AvgLoss=AvgWin/2;       // a guessengineering value
      negDealsStd=posDealsStd;// a guessengineering value
   }

// Use log-normal distribution function. Mean and Std are estimated as:
   double win_lnMean =log(AvgWin*AvgWin/sqrt(AvgWin*AvgWin+posDealsStd*posDealsStd));
   double loss_lnMean=log(AvgLoss*AvgLoss/sqrt(AvgLoss*AvgLoss+negDealsStd*negDealsStd));
   double win_lnstd  =sqrt(log(1+(posDealsStd*posDealsStd)/(AvgWin*AvgWin)));
   double loss_lnstd =sqrt(log(1+(negDealsStd*negDealsStd)/(AvgLoss*AvgLoss)));

   double rand_Win[],rand_Loss[];
   double r[];

// limit amount of money that defines Ruin
   limitLoss_money=MathAbs(limitLoss_money);
   bool success;
   int ruinCount=0; // counter of ruins
   int successfulMCcounter=0;
   int nTradesPerSim=MathMax(100,nTrades);// at least 100 trades per sim
   int nMCsims=10000; // MC sims, each one with nTradesPerSim

   for(int iMC=0; iMC<nMCsims; iMC++) {
      success=MathRandomUniform(0,1,nTradesPerSim,r);

      // generate nTradesPerSim wins and losses for each simulation
      // use LogNormal distribution
      success&=MathQuantileLognormal(r,win_lnMean,win_lnstd,true,false,rand_Win);
      success&=MathQuantileLognormal(r,loss_lnMean,loss_lnstd,true,false,rand_Loss);
      if(!success)continue;
      successfulMCcounter++;
      //simulate nTradesPerSim
      double eqty=0; // start each simulation with zero equity
      for(int i=0; i<nTradesPerSim; i++) {

         // draw a random number in [0,1]
         double randNumber=(double)MathRand()/32767.;

         // select a win or a loss depending on the win rate and the random number
         // and add to the equity
         eqty+=randNumber*100 < WinRatePct?
               rand_Win[i]:
               -rand_Loss[i];

         // check if equity is below the limit (ruin)
         // count the number of times there is a ruin
         if(eqty<= -limitLoss_money) {
            ruinCount++;
            break;
         }
      }
   }
// compute risk of ruin as percentage
   double RiskOfRuinPct=(double)(ruinCount)/successfulMCcounter*100.;
   return(RiskOfRuinPct);
}

我们在上面的代码中插入了许多注释行，以便于理解。源代码中也包含了CalcDealStatistics()函数，该函数用于计算盈利和亏损的标准差。在破产风险计算中，主要假设是交易历史遵循对数正态分布（Log-Normal），以确保分布的样本分别为正数和负数，分别代表盈利和亏损。

理想情况下，如果我们有大量的历史交易，可以使用马尔可夫链转移概率矩阵，而不是假设交易历史具有“对数正态性”。然而，由于交易历史通常只有几百笔交易（最多），因此信息不足以准确构建马尔可夫链转移概率矩阵。 

解读蒙特卡洛破产风险

蒙特卡洛模拟结果应被解读为资本损失风险的概率，而非预测值。例如，如果蒙特卡洛模拟的返回值为1%，这意味着你的交易策略有1%的概率（可能性）会完全损失你所投入的全部资本。这并不意味着你会损失所投入资本的1%。

为自定义最大值添加小数位

这是一项棘手的任务。如果读者发现了更好的方法，请分享出来。一旦计算出小数位值（在代码中命名为dec），就会以下面的方式修改目标值（obj）：

  obj=obj>0?
       MathFloor(obj*gof_ObjPositiveScalefactor)+dec/100.:
       -(MathFloor(-obj*gof_ObjNegativeScalefactor)+dec/100.);

如您所见，如果obj是一个正值，它会乘以一个较大的数（gof_ObjPositiveScalefactor=1e6），然后取整，接着将dec的值除以100，并作为小数部分添加。当obj的值为负（意味着存在许多约束被违反）时，obj会乘以一个不同的数(gof_ObjPositiveScalefactor =1e3) ，以压缩负值的纵轴。

在MetaTrader 5的移动平均线EA中实现GOF

以下是一个示例，展示了如何在MetaTrader 5的Moving Averages.mq5（移动平均线EA）中实现GOF：

//+------------------------------------------------------------------+
//|                                              Moving Averages.mq5 |
//|                             Copyright 2000-2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2000-2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#include <Trade\Trade.mqh>

input double MaximumRisk        = 0.02;    // Maximum Risk in percentage
input double DecreaseFactor     = 3;       // Descrease factor
input int    MovingPeriod       = 12;      // Moving Average period
input int    MovingShift        = 6;       // Moving Average shift
//---
int    ExtHandle=0;
bool   ExtHedging=false;
CTrade ExtTrade;

#define MA_MAGIC 1234501

// changes needed to use the GenericOptimizationFormulation (GOF):
ulong gof_magic= MA_MAGIC;
#include <GenericOptimizationFormulation.mqh>
// end of changes

就是这些了！仅有两行代码需要添加到EA文件中。

使用GOF进行优化的例子

示例 1：单一目标，无约束条件 （就像在MetaTrader 5的设置选项卡中使用最大账户余额一样）：

输入参数选项卡如下。由于只有一个目标，因此目标和权重完全不相关。请注意，在硬约束部分，第一个布尔变量是如何关闭所有约束的：

其他选项部分的设置是：

结果显示如下：请注意，“结果”列显示的不是账户余额，而是经过修改的目标值，其中胜率以小数形式表示。

我们可以看到，变量的最佳组合（9,9,3）产生了939.81的利润和41%的胜率。

我们对表格中的最佳组合（第一行）进行了模拟。在“日志”选项卡中打印的GOF总结报告如下：

我们将在下一个例子中更详细的回顾GOF总结报告。

示例 2：3个目标和5个约束

设置选项卡与之前的相同。输入变量和范围也保持不变。GOF变量的输入选项卡如下所示。

目标：

• 年化回报，目标为50%，权重为100
• 恢复因子，目标为10，权重为10
• 胜率百分比，目标为100%，权重为10 

约束：

• 账户损失占初始存款的比例应小于或等于10%
• 净值回撤百分比应小于或等于10%
• 连续亏损交易次数应小于或等于5次
• 胜率应大于或等于35%
• 破产风险账户应小于或等于0.5%

用于计算破产风险的资本被设定为初始存款的10%，即账户货币的1000个单位，如上面“其他”参数设置部分所示。

优化表中的第一行显示，最佳设计方案是（10,6,6）。

请注意，优化器找到了一个与第一个示例相比利润较低（805.64对比839.81）的解决方案，但这个新的设计方案满足了所有五个约束条件，并最大限度地综合了三个目标。

GOF总结报告 

通过模拟上述优化表中的第一行，我们得到了下面的GOF总结报告：

GOF总结报告有三个部分。第一部分包含了许多来自“回溯测试”（BackTest）选项卡的数量指标。此外，还有一些在“回溯测试”选项卡中不存在的额外数量指标：年化利润、测试年数、盈亏比（RRR）、平均交易量和最大交易量、盈亏标准差，以及在模拟期间达到的最低保证金水平。

第二部分是关于目标函数的。这里每个目标都有四个值：目标值、目标设定值、权重和贡献百分比。贡献百分比是指该目标函数对总的单一目标的贡献度。在本例中，年化回报贡献了95.1%，恢复因子贡献了1.4%，胜率贡献了3.5%，总计为总单一目标的100%。目标和权重会影响这些贡献度。 

第三部分是关于约束条件的。每个约束条件都会打印出"pass" 或者 "Fail"的消息，并且还会显示约束条件的实际值与输入边界值的比较结果。

为了进行比较，我们按照示例2中的优化公式，对示例1中的第一个设计方案（9, 9, 3）进行了运行。以下是该模拟的总结。请注意，这里有一个约束条件被违反。连续亏损次数为6次，超过了优化公式中给定的边界值5次。因此，尽管最大余额设计方案（9,9,3）的利润高于多目标/受约束设计方案（10,6,6），但满足所有约束条件的是（10,6,6）设计方案。 

使用GenericOptimizationFormulation.mqh时的建议

在选择多个目标和多个约束时应谨慎行事，因为这意味着更大的自由度。以下是一些通用的建议：

1. 目标不要超过3个。虽然代码允许最多设置5个目标，但当目标数量超过3个时，选择影响最终结果的目标值和权重会变得更加困难。
2. 在选择上限（U_i）和下限（L_i）时，应根据自己的偏好设置约束，并且不要设置得太紧。如果边界设置得太紧，则无法得到任何可行的输入变量组合。
3. 如果不知道某个给定约束应设置什么边界值，可以将该约束移动到目标部分，并通过检查GOF总结报告来了解其行为（大小、符号等）。
4. 如果想要更好的图表，或者发现优化器没有产生预期的结果，可以调整k_o和k_p。
5. 请记住，最佳的设计方案（优化表中的第一行）并不一定是最盈利的设计，而是基于您选择的具体目标和约束，目标函数值最高的方案。
6. 我们建议优化完成后，按其他列（如利润、恢复因子、回撤、预期收益、利润因子等）对设计方案进行排序。每个排序的顶行都可能是您要考虑进行模拟以审查GOF总结报告的候选方案。
7. 示例#2较好的选择了目标和约束条件。请将它们作为您实验的起点。

当出问题时

您可能会设置一个优化公式，但它并未提供您预期的结果。以下是一些可能导致这种情况发生的原因：

1. 约束条件过于严格，导致MetaTrader 5的遗传优化算法需要经历许多代才能得到一个正的目标函数值，而在某些情况下，它可能根本无法达到。解决方案：放宽您的约束条件。
2. 约束条件之间存在冲突。解决方案：检查约束条件是否逻辑上一致。
3. 优化方案的图表在y轴上对负值存在偏差（即，负值占据的空间比正值多）。解决方案：增加K_o或减小K_p，或者两者都进行调整。
4. 您喜欢的一些设计方案在优化表中并未出现在顶部。请记住，目标和权重会影响优化目标，同时，任何一个约束条件的违反都可能导致目标在表中的排名下降。解决方案：通过调整目标、权重和约束条件来重新构建您的优化问题。

   

结论

我们希望这个通用优化公式（GOF）能对您有所帮助。现在，您有了更多的自由度来选择多个目标和多个约束条件，以便设置您喜欢的优化问题。