Механизмы гейтинга в ансамблевом обучении

MetaTrader 5 — Примеры | 14 июля 2025, 15:24

167

Методы пропускания динамически корректируют влияние отдельных моделей на основе контекстуальной информации с использованием gate-переменных. Эти переменные действуют как механизмы контроля, стратегически взвешивая выходные данные модели для достижения более высоких показателей прогнозирования по сравнению с любой другой моделью.

В отличие от традиционных ансамблевых методов, основанных на усреднении, голосовании или суммировании, гейтинг явно использует gate-переменные для комбинирования моделей. Этот подход особенно ценен в сценариях с подвижной эффективностью модели, таких как финансовое прогнозирование, где экономические тенденции влияют на точность прогнозирования. Благодаря адаптивному взвешиванию моделей в зависимости от контекста, гейтинг повышает точность и адаптивность в сложных условиях.

Методы пропускания обычно делятся на две категории: выбор одной модели на основе gate-переменных или объединение выходных данных из всех моделей с зависящими от контекста весами. Последний часто более надежен, поскольку использует преимущества множества моделей. В следующих разделах рассматриваются примеры обоих подходов: заранее определенной и приобретенной в процессе обучения специализации.

Заранее определенная специализация

Заранее определенная специализация представляет собой фундаментальную форму пропускания, при которой одна переменная выступает в качестве решающего фактора при выборе между двумя или большим количеством предварительно подготовленных экспертных моделей. Этот подход эффективно разделяет входное пространство, направляя экземпляры к наиболее подходящей модели на основе значения пропускающей переменной. Чтобы проиллюстрировать эту концепцию, рассмотрим задачу бинарной классификации, изображенную в двумерном пространстве признаков, с переменными A и B. В этом гипотетическом сценарии переменная В демонстрирует незначительную способность к различению между двумя классами, в то время как переменная А демонстрирует умеренную прогностическую способность, обеспечивая точную классификацию в одних случаях, но давая неоднозначные результаты в других.

Scatter plot of feature space

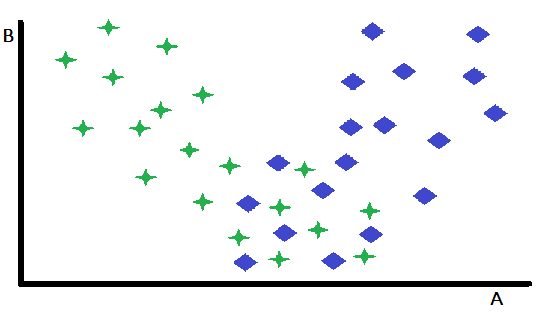
Тщательный анализ диаграммы рассеяния признаков показывает, что переменная B эффективно отличает случаи, для которых A служит надежным классификатором, от тех, где ее прогностическая способность снижена. В частности, экземпляры, характеризующиеся высокими значениями B, демонстрируют превосходную точность классификации при использовании A в качестве основного предиктора. Это наблюдение предполагает естественную стратегию секционирования: разделение набора данных на основе порогового значения B. Такое секционирование позволяет разработать две различные модели классификации: одна оптимизирована для случаев с высокими значениями B (где A является сильным предиктором), а другая - для случаев с низкими значениями B (где A может быть менее надежным). Х

отя этот упрощенный пример демонстрирует основной принцип, важно понимать, что преимущества такого секционирования могут быть ограничены, когда оставшееся подмножество экземпляров оказывается сложным для классификации. Ключевое преимущество этого подхода заключается в его способности выделять и эффективно устранять наиболее легко поддающиеся классификации экземпляры. Это упрощение также помогает в разработке более эффективных моделей для оставшегося, более сложного подмножества данных. Хотя только что описанный пример был сосредоточен на одной переменной для прояснения концепции, в практических приложениях выбор подходящей модели может зависеть от значений нескольких переменных, которые могут быть включены или не включены в основной набор предикторов, используемых отдельными моделями.

Специализация, приобретенная в ходе обучения

Приобретенная специализация представляет собой более сложный подход к гейтингу, при котором оптимальная переменная разделения и соответствующий ей порог не определяются априори, а извлекаются из самих данных. Хотя визуальный осмотр диаграмм рассеяния иногда может дать предварительное представление о потенциальных переменных разделения и их пороговых значениях, такие интуитивные подходы часто не работают при реальном применении.

На практике необходим более систематический подход, основанный на данных. Обычно это включает в себя тщательный процесс поиска, включающий изучение широкого спектра потенциальных переменных разделения и связанных с ними пороговых значений. Для каждой возможной переменной разделения и порогового значения набор данных разбивается на разделы, а отдельные модели обучаются и оцениваются на результирующих подмножествах. Этот итеративный процесс исследования, обучения и оценки может потребовать больших вычислительных затрат, особенно при работе с большими наборами данных или сложными моделями. Однако потенциальный выигрыш в эффективности модели часто оправдывает увеличение вычислительных затрат.

Кроме того, поиск оптимальных переменных для разделения не должен ограничиваться одним кандидатом. Вместо этого для определения наиболее эффективной стратегии гейтинга необходима всесторонняя оценка множества потенциальных переменных. Это требует систематического изучения пространства признаков для выявления переменных, обладающих высокой прогностической способностью при определении оптимальной модели для каждого подмножества данных. Поиск оптимальных gate-переменных может быть осуществлен с помощью нейронных сетей или других алгоритмов обучения для установления взаимосвязи между входными данными и компонентными моделями.

Приобретенная в ходе обучения специализация с использованием выходных данных модели в качестве пропускающих переменных

Вариант приобретенной в ходе обучения специализации использует уникальный подход к выбору модели, основанный на анализе прогнозов, сгенерированных всеми конкурирующими моделями. В отличие от методов пропускания, требующих заранее определенных переменных для выбора модели, в этом подходе в качестве факторов принятия решений используются собственные прогнозы моделей. По сути, эта форма приобретенной в ходе обучения специализации предполагает метауровневый анализ выходных данных модели. Все конкурирующие модели сначала запускаются для генерации прогнозов для заданных входных данных. Впоследствии эти прогнозы анализируются, чтобы определить наиболее надежную модель для данного конкретного экземпляра. Такой подход эффективно преобразует сами выходные данные модели в динамические "gate-переменные", определяющие процессом отбора.

Упрощенный пример можно проиллюстрировать в сценарии бинарной классификации с двумя конкурирующими моделями. Когда обе модели сходятся в названии класса, процесс выбора становится простым. Однако в случаях возникновения разногласий для разрешения конфликта требуется системный подход.

Один из иногда эффективных, но примитивных методов включает анализ обучающих данных для определения наиболее надежного правила принятия решений для разрешения противоречивых прогнозов. Этот анализ требует изучения данных об эффективности в выборке, чтобы определить, какая модель демонстрирует более высокую точность в конкретных конфликтных сценариях. Например, если модель стабильно превосходит вторую модель, когда обе модели расходятся во мнениях, то приоритет следует отдавать прогнозированию первой модели.

Такой основанный на данных подход позволяет разработать набор правил принятия решений, оптимизирующий комбинацию выходных данных модели на основе эмпирических данных.

Применение этого простого метода имеет очевидные ограничения. Если обучающие образцы не являются репрезентативными для большинства экземпляров вне выборки, которые будут встречаться при использовании в реальном мире, то результирующая модель ансамбля будет бесполезной. Более сложные методологии, такие как обсуждаемая в следующем разделе, обладают большей применимостью и, как правило, демонстрируют превосходную эффективность при практическом применении. Тем не менее, когда требуется эффективный с точки зрения вычислений и оперативный алгоритм, представленный здесь метод может оказаться адекватным. Кроме того, углубленный анализ этого упрощенного алгоритма обеспечивает ценную основу для понимания более сложных концепций.

Полный исходный код этого метода можно найти в файле oracle.mqh, прилагаемом в конце настоящей статьи. Следующий код является объявлением класса COracle.

//+------------------------------------------------------------------+
//| Tabulated combination of component model outputs                 |
//+------------------------------------------------------------------+
class COracle
  {
private:
   ulong             m_ncases;
   ulong             m_nin;
   ulong             m_ncats;
   uint              m_nmodels;
   matrix            m_thresh;
   ulong             m_tally[];
public:
                     COracle(void);
                    ~COracle(void);
   bool              fit(matrix &predictors, vector &targets, IModel* &models[],ulong ncats);
   double            predict(vector &inputs,IModel* &models[]);

  };

Класс определяет два ключевых контейнера: m_thresh и m_tally. В матрице m_thresh хранятся выходные пороговые значения, разбивающие обучающий набор на подмножества одинакового размера, в то время как массив m_tally определяет оптимальную модель для каждого из этих подмножеств. Вызов функции fit() создает модель на основе предоставленных обучающих данных. Ниже приведен начальный раздел этого метода.

//+------------------------------------------------------------------+
//| fit an oracle                                                    |
//+------------------------------------------------------------------+
bool COracle::fit(matrix &predictors,vector &targets,IModel *&models[],ulong ncats)
  {
   if(predictors.Rows()!=targets.Size())
     {
      Print(__FUNCTION__," ",__LINE__," invalid inputs ");
      return false;
     }

   m_ncases = predictors.Rows();
   m_nin = predictors.Cols();
   m_nmodels = models.Size();

   m_ncats = ncats;
   ulong nthresh = m_ncats - 1;
   ulong nbins = 1;

   nbins = (ulong)pow(m_ncats,m_nmodels);

   m_thresh = matrix::Zeros(m_nmodels,nthresh);

   ZeroMemory(m_tally);

   if(ArrayResize(m_tally,int(nbins))<0)
     {
      Print(__FUNCTION__," ", __LINE__," error ", GetLastError());
      return false;
     }

   matrix outputs(m_ncases,m_nmodels);
   matrix bins(nbins,m_nmodels);

   bins.Fill(0.0);

   vector inrow;
   for(ulong icase=0;icase<m_ncases; icase++)
     {
      inrow=predictors.Row(icase);
      for(uint imodel =0; imodel<m_nmodels; imodel++)
         outputs[icase][imodel] = models[imodel].forecast(inrow);
     }

   double frac;
   for(uint imodel =0; imodel<m_nmodels; imodel++)
     {
      inrow = outputs.Col(imodel);
      qsortd(0,long(m_ncases-1),inrow);
      for(ulong i = 0; i<nthresh; i++)
        {
         frac = double(i+1)/double(ncats);
         m_thresh[imodel][i] = inrow[ulong(frac*(m_ncases-1))];
        }
     }

Метод начинается со сбора прогнозов для каждой компонентной модели в матрице выходных данных. Матрица интервалов используется для подсчета количества раз, когда каждая модель оказывалась лучшей в своем интервале. Затем для каждого столбца в матрице выходных данных определяется количество пороговых значений путем нахождения записей с равным интервалом в отсортированном векторе столбцов inrow. Следующий раздел метода fit() выполняется следующим образом.

vector outrow;
   ulong ibin,index, klow, khigh, ibest, k;
   k = 0;
   double diff,best;
   for(ulong icase=0;icase<m_ncases; icase++)
     {
      inrow = predictors.Row(icase);
      outrow = outputs.Row(icase);
      ibin = 0;
      index = 1;
      for(uint imodel =0; imodel<m_nmodels; imodel++)
        {
         if(outrow[imodel] <= m_thresh[imodel][0])
            k = 0;
         else
            if(outrow[imodel] > m_thresh[imodel][nthresh-1])
               k = nthresh;
            else
              {
               klow = 0;
               khigh = nthresh-1;
               while(true)
                 {
                  k = (klow+khigh)/2;
                  if(k == klow)
                    {
                     k = khigh;
                     break;
                    }
                  if(outrow[imodel]<=m_thresh[imodel][k])
                     khigh = k;
                  else
                     klow = k;
                 }
              }
         ibin += k * index;
         index *= ncats;
        }
      best = DBL_MAX;

Для каждого образца в обучающем наборе данных определяется диапазон, соответствующий ее модельному прогнозу. Затем из набора прогнозов компонентной модели находится наиболее близкий к значению true прогноз. При обнаружении увеличивается комбинация соответствующей модели диапазона. Заключительный раздел метода fit() завершается следующим кодом.

for(uint imodel =0; imodel<m_nmodels; imodel++)
        {
         diff = fabs(outrow[imodel] - targets[icase]);
         if(diff<best)
           {
            best = diff;
            k = imodel;
           }
        }
      bins[ibin][k]+=1.0;
     }

   for(ibin =0; ibin<nbins; ibin++)
     {
      k = 0;
      ibest = 0;
      for(uint imodel = 0; imodel<m_nmodels; imodel++)
        {
         if(bins[ibin][imodel] > double(ibest))
           {
            ibest = ulong(bins[ibin][imodel]);
            k = ulong(imodel);
           }
        }
      m_tally[ibin] = k;
     }

   return true;
  }

Заключительные шаги включают в себя просмотр матрицы диапазонов, чтобы найти модель, которая чаще всего выбиралась для этого диапазона, а индексы этих моделей сохраняются в m_tally. Процесс биннинга, используемый в рамках этого анализа, использует матричную структуру для эффективной классификации обучающих выборок на основе их классификаций по нескольким моделям. Матрицу можно рассматривать как вектор, содержащий другие векторы, длина которых соответствует количеству рассматриваемых моделей. В каждом из них хранится частота, с которой каждая модель была определена как наиболее близкая к целевой для конкретной комбинации категорий, представленных в диапазоне.

Для иллюстрации рассмотрим сценарий с тремя моделями и четырьмя категориями. Визуализируем трехмерное пространство, где каждая ось представляет собой модель и разделена на четыре категории. В результате получается куб размером 4х4х4, каждая уникальная точка которого представляет собой определенную комбинацию назначений категорий в трех моделях.

В процессе объединения используется пара переменных индексации. Первый из этой пары непосредственно относится к определенному диапазону или ряду в матрице, соответствующему уникальной комбинации категорий для образца. Вторая индексирующая переменная действует как коэффициент масштабирования, обеспечивая корректную навигацию приращений в многомерном пространстве.

Такая схема индексации гарантирует, что каждое приращение индекса ряда корректно помещает образец в соответствующий диапазон матрицы, эффективно фиксируя общие назначения категорий для всех моделей.

Метод predict() исполняет все модели, чтобы найти диапазон, к которому относятся выходные данные. Затем проверяется массив m_tally, чтобы определить, какая модель с наибольшей вероятностью будет наиболее подходящей для применения с данным образцом.

//+------------------------------------------------------------------+
//| make a prediction                                                |
//+------------------------------------------------------------------+
double COracle::predict(vector &inputs,IModel* &models[])
  {
   ulong k, klow, khigh, ibin, index, nthresh ;
   nthresh = m_ncats -1;
   k = 0;
   ibin = 0;
   index = 1;
   vector otk(m_nmodels);

   for(uint imodel = 0; imodel<m_nmodels; imodel++)
     {
      otk[imodel] = models[imodel].forecast(inputs);

      if(otk[imodel]<m_thresh[imodel][0])
         k = 0;
      else
         if(otk[imodel]>m_thresh[imodel][nthresh-1])
            k = nthresh - 1;
         else
           {
            klow=0;
            khigh = nthresh -1 ;
            while(true)
              {
               k = (klow + khigh) / 2;
               if(k == klow)
                 {
                  k = khigh;
                  break;
                 }
               if(otk[imodel] <= m_thresh[imodel][k])
                  khigh = k;
               else
                  klow = k;
              }
           }
      ibin += k*index;
      index *= m_ncats;
     }

   return otk[ulong(m_tally[ibin])];
  }

Тестирование кода

Скрипт Oracle_Demo.mq5 тестирует функциональность класса COracle. Эта программа позволяет пользователю настраивать различные параметры моделирования, включая размер обучающего набора данных, количество диапазонов, количество моделей и уровень шума, определяющий сложность задачи прогнозирования. В приведенных ниже выходных данных скрипта представлены результаты, полученные в ряде сценариев с использованием трех моделей эквивалентной прогностической мощности.

Простая сложность прогнозирования, 2 диапазона и объем обучающих данных в 10 выборок.

PF      0       13:59:15.542    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10777835
MQ      0       13:59:15.542    Oracle_Demo (BTCUSD,D1) Oracle error = 0.10777835

Умеренная сложность прогнозирования, 2 диапазона и объем обучающих данных в 10 выборок.

FD      0       14:00:30.967    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.38588979
KG      0       14:00:30.967    Oracle_Demo (BTCUSD,D1) Oracle error = 0.38529990

Высокая сложность прогнозирования, 2 диапазона и объем обучающих данных в 10 выборок.

ES      0       14:01:11.874    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.16908710
ND      0       14:01:11.874    Oracle_Demo (BTCUSD,D1) Oracle error = 1.16824689

Простая сложность прогнозирования, 2 диапазона и объем обучающих данных в 100 выборок.

LQ      0       14:02:57.441    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10706090
NJ      0       14:02:57.441    Oracle_Demo (BTCUSD,D1) Oracle error = 0.10705483

Умеренная сложность прогнозирования, 2 диапазона и объем обучающих данных в 100 выборок.

LL      0       14:04:24.070    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.36310507
JO      0       14:04:24.070    Oracle_Demo (BTCUSD,D1) Oracle error = 0.36303485

Высокая сложность прогнозирования, 2 диапазона и объем обучающих данных в 100 выборок.

RJ      0       14:06:02.290    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.12115161
PM      0       14:06:02.290    Oracle_Demo (BTCUSD,D1) Oracle error = 1.12076456

Простая сложность прогнозирования, 4 диапазона и объем обучающих данных в 100 выборок.

FI      0       14:08:24.445    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10681953
FR      0       14:08:24.445    Oracle_Demo (BTCUSD,D1) Oracle error = 0.10681329

Умеренная сложность прогнозирования, 4 диапазона и объем обучающих данных в 100 выборок.

KG      0       14:10:29.012    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.36348921
LP      0       14:10:29.012    Oracle_Demo (BTCUSD,D1) Oracle error = 0.36363647

Высокая сложность прогнозирования, 4 диапазона и объем обучающих данных в 100 выборок.

MR      0       14:12:16.225    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.12231642
EE      0       14:12:16.225    Oracle_Demo (BTCUSD,D1) Oracle error = 1.12258202

Последующие эксперименты включали четвертую модель, предназначенную для получения случайных прогнозов, тем самым моделируя сценарий с неинформативной моделью. Представленные ниже результаты демонстрируют значительные изменения в поведении системы.

Простая сложность прогнозирования, 2 диапазона и объем обучающих данных в 10 выборок.

GH      0       14:13:47.886    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12971017
MS      0       14:13:47.886    Oracle_Demo (BTCUSD,D1) Oracle error = 0.14153652

Умеренная сложность прогнозирования, 2 диапазона и объем обучающих данных в 10 выборок.

JN      0       14:14:16.985    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.40381512
MI      0       14:14:16.985    Oracle_Demo (BTCUSD,D1) Oracle error = 0.40074764

Высокая сложность прогнозирования, 2 диапазона и объем обучающих данных в 10 выборок.

ND      0       14:14:54.040    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.16720001
OG      0       14:14:54.040    Oracle_Demo (BTCUSD,D1) Oracle error = 1.16304663

Простая сложность прогнозирования, 2 диапазона и объем обучающих данных в 100 выборок.

QJ      0       14:17:05.521    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12727773
HM      0       14:17:05.521    Oracle_Demo (BTCUSD,D1) Oracle error = 0.17687364

Умеренная сложность прогнозирования, 2 диапазона и объем обучающих данных в 100 выборок.

QP      0       14:18:26.976    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.38337835
CK      0       14:18:26.976    Oracle_Demo (BTCUSD,D1) Oracle error = 0.39318874

Высокая сложность прогнозирования, 2 диапазона и объем обучающих данных в 100 выборок.

IF      0       14:20:01.925    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.13780482
IQ      0       14:20:01.925    Oracle_Demo (BTCUSD,D1) Oracle error = 1.13878032

Простая сложность прогнозирования, 4 диапазона и объем обучающих данных в 100 выборок.

HL      0       14:23:03.090    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12709947
QO      0       14:23:03.090    Oracle_Demo (BTCUSD,D1) Oracle error = 0.11975572

Умеренная сложность прогнозирования, 4 диапазона и объем обучающих данных в 100 выборок.

CR      0       14:25:25.091    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.38314408
CE      0       14:25:25.091    Oracle_Demo (BTCUSD,D1) Oracle error = 0.37892436

Высокая сложность прогнозирования, 4 диапазона и объем обучающих данных в 100 выборок.

GH      0       14:27:50.024    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.13828093
CS      0       14:27:50.024    Oracle_Demo (BTCUSD,D1) Oracle error = 1.13422816

Анализ обоих наборов результатов показывает, что в сценариях с низким уровнем шума этот метод демонстрирует исключительную эффективность, что приводит к существенному снижению дисперсии ошибок. И наоборот, в сценариях с высоким уровнем шума этот метод не только не обеспечивает существенных улучшений, но и часто приводит к снижению эффективности по сравнению с использованием одной модели. Это явление наблюдается даже тогда, когда все составляющие модели обладают эквивалентной прогностической способностью, хотя различия в эффективности в таких случаях, по общему признанию, незначительны.

Тесты также показали, что использование четырех диапазонов вместо двух приводило к непоследовательной и незначительной разнице в эффективности. Этот результат неудивителен, учитывая, что либо все модели обладают сопоставимой прогностической способностью, либо одна модель постоянно выдает бесполезные прогнозы. Основная функция этого алгоритма в данном контексте заключается в выявлении и отбрасывании неинформативных моделей в случае их присутствия. Однако вполне возможно, что существуют сценарии, в которых большее число категорий оказалось бы полезным.

Ансамбли управляемой общие регрессиии

В данном разделе представлен широко применимый метод комбинирования моделей, использующий пропускающие переменные. Данный метод основан на концепциях нейронных сетей общей регрессии (General Regression Neural Networks, GRNN) и позволяет одной или нескольким переменным служить динамическими воротами, модулирующими влияние каждой из составляющих модели. В отличие от более ранних методов гейтинга, требующих выбора одной модели для получения конечного результата, гейтинг общей регрессии объединяет результаты всех составляющих моделей путем оптимального взвешивания каждой из них на основе gate-переменных. Эти пропускающие переменные могут включать в себя внешние измеренные значения, а также выходные данные отдельных моделей. Данный подход называется методом управляемой общие регрессиии.

Реализация этого метода требует, по крайней мере, двух обученных моделей компонентов и отдельного набора данных для обучения ансамбля, основанного на GRNN. Обучающий набор данных должен содержать одну или несколько gate-переменных, прогнозы из моделей компонентов, а также соответствующие целевые значения. Примечательно, что некоторые выходные данные моделей компонентов также можно обозначить как gate-переменные, что еще больше повышает гибкость подхода.

Нейронная сеть общей регрессии (GRNN) это тип искусственной нейронной сети, предназначенной для регрессионных задач, включающих в себя прогнозирование непрерывных выходных данных. GRNN работает на основе принципов ядерной оценки плотности и опирается на основанный на памяти подход к обучению. Он состоит из четырех уровней: входного, шаблонного, суммирующего и выходного.

Входной уровень получает переменные-предикторы, которые передаются на уровень шаблонов, где каждый нейрон представляет обучающий образец и вычисляет сходство между входными данными и обучающими данными, используя радиальную базисную функцию. Уровень суммирования объединяет взвешенные выходные данные уровня шаблона, а уровень вывода выдает окончательный прогноз путем нормализации суммы весов.

GRNN особенно удобен для моделирования нелинейных зависимостей, требует минимального времени на обучение и автоматически адаптируется к базовому распределению данных. В

этом контексте взвешенное евклидово расстояние между тестовой и обучающей выборками определяется gate-переменными. В частности, при оценке тестовой выборки GRNN-гейт определяет приоритет обучающих выборок, gate-переменные которых очень похожи на переменные тестовой выборки. При использовании GRNN для прогнозирования квадратичной погрешности модели прогнозируемая квадратичная погрешность для компонентной модели рассчитывается с использованием приведенного ниже уравнения.

Error estimate equation

Хотя существует бесконечно много способов комбинирования компонентных моделей для получения совместного прогноза, самый простой подход предполагает выражение окончательного прогноза в виде линейной комбинации выходных данных моделей. Если компонентные модели обладают желаемым свойством непредвзятых прогнозов, то это свойство сохраняется только при условии, что весовые коэффициенты в сумме равны единице. Даже если прогнозы не являются строго объективными, это условие остается выгодным в большинстве сценариев. Для линейной комбинации несмещенных оценщиков с минимальной среднеквадратичной ошибкой оптимальные веса пропорциональны обратной величине дисперсии каждого оценщика. Заменив дисперсию прогнозируемой квадратичной ошибкой, веса можно рассчитать по следующей формуле.

Weights Equation

Чтобы сгенерировать прогноз, пропущенный через GRNN, с учетом соответствующих значений сигма-весов, мы начинаем с оценки ошибки прогнозирования для каждой модели на данной тестовой выборке. Затем вычисляются веса, а компонентные модели оцениваются на тестовом образце. Наконец, отдельные прогнозы из компонентных моделей объединяются в итоговую оценку с использованием рассчитанных весов.

Определение оптимальных значений для сигма-весов является непростой задачей, поскольку требует оценки с использованием обучающих данных. Наиболее эффективным методом оценки качества сигма-вектора-кандидата является перекрестная проверка. Она включает в себя удаление образца из обучающего набора, который будет использоваться в качестве тестового примера, генерируя пропускаемый через GRNN прогноз для этого образца с использованием указанного сигма-вектора и сравнивая прогнозируемое значение со значением true. Затем образец возвращается в обучающий набор и процесс повторяется для всех образцов в наборе данных. Среднеквадратичная ошибка на этих повторениях служит мерой качества сигма-вектора-кандидата.

Любой алгоритм оптимизации без использования производных можно использовать для определения набора сигма-весов, который минимизирует ошибку перекрестной проверки. Среди доступных опций дифференциальная эволюция известна своей надежностью и широким применением. Однако метод Пауэлла представляет собой эффективную с точки зрения вычислений альтернативу, демонстрирующую удовлетворительную эффективность в большинстве видов практических применений. Учитывая эффективность метода Пауэлла, он был использован для данного исследования, несмотря на случайное превосходство дифференциальной эволюции в редких случаях, связанных с множественными локальными экстремумами.

Файл gatedreg.mqh содержит исходный код класса CGatedReg, реализующий только что описанный основанный на GRNN управляемый ансамблевый метод. Объявление класса представлено ниже.

//+------------------------------------------------------------------+
//|  GRNN gating model combination                                   |
//+------------------------------------------------------------------+
class CGatedReg:public CPowellsMethod
  {
private:
   ulong             m_nsamples;
   ulong             m_ngates;
   ulong             m_nmodels;
   matrix            m_tset;
   vector            m_sigma;
   vector            m_errvals;
   vector            m_params;

   double            criter(vector &params);
   double            trial(vector &gates, vector &contenders,long i_exclude,long n_exclude);
   virtual double    func(vector &p) {  return criter(p); }
public:
                     CGatedReg(void);
                    ~CGatedReg(void);
   bool              fit(matrix &gates, matrix &contenders,vector &targets);
   double            predict(vector &gates, vector &contenders);
  };

Предполагается, что полученные на основе компонентных моделей прогнозы были предварительно вычислены и сохранены в виде матрицы. Каждая модель должна была пройти предварительное обучение, чтобы прогнозировать зависимую переменную. Gate-переменные (часто одна переменная) будут использоваться для дифференциального взвешивания вкладов этих компонентных моделей в окончательный прогноз. Метод fit() отвечает за копирование необходимых обучающих данных и определение оптимальных сигма-весов. Далее приведена реализация этого метода.

//+------------------------------------------------------------------+
//| fit a gated grnn model                                           |
//+------------------------------------------------------------------+
bool CGatedReg::fit(matrix &gates,matrix &contenders,vector &targets)
  {
   if(gates.Rows()!=contenders.Rows() || contenders.Rows()!=targets.Size()  || gates.Rows()!=targets.Size())
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid training data ");
      return false;
     }
   m_nsamples = gates.Rows();
   m_ngates = gates.Cols();
   m_nmodels = contenders.Cols();

   m_tset = matrix::Zeros(m_nsamples,m_ngates+m_nmodels+1);
   m_sigma = vector::Zeros(m_ngates);
   m_errvals = vector::Zeros(m_nmodels);

   for(ulong i = 0; i<m_nsamples; i++)
     {
      for(ulong j = 0; j<m_ngates; j++)
         m_tset[i][j] = gates[i][j];
      for(ulong k = 0; k<m_nmodels; k++)
         m_tset[i][m_ngates+k] = contenders[i][k];
      m_tset[i][m_ngates+m_nmodels] = targets[i];
     }

   m_params = vector::Zeros(m_ngates);

   double err =  criter(m_params);
   if(err > 0.0)
      Optimize(m_params);

   criter(m_params);

   return true;

  }

Обучающие данные, содержащие все входные данные для метода fit(), должны быть сохранены, поскольку последующие прогнозы требуют использования общей регрессии для промежуточного прогнозирования ошибок каждой модели. Кроме того, для каждого прогнозирования потребуется вектор m_errval. Метод оптимизации Пауэлла используется для определения оптимальных сигма-весов. Подлежащая минимизации целевая функция определяется как приватный метод criter().

//+------------------------------------------------------------------+
//|  function criterion                                              |
//+------------------------------------------------------------------+
double CGatedReg::criter(vector &params)
  {
   int i, ngates, nmodels, ncases;
   double  out, diff, error, penalty ;
   vector inputs1,inputs2,row;

   ngates = int(m_ngates); ;
   nmodels = int(m_nmodels) ;
   ncases = int(m_nsamples) ;

   penalty = 0.0 ;
   for(i=0 ; i<ngates ; i++)
     {
      if(params[i] > 8.0)
        {
         m_sigma[i] = exp(8.0) ;
         penalty += 10.0 * (params[i] - 8.0) ;
        }
      else
         if(params[i] < -8.0)
           {
            m_sigma[i] = exp(-8.0) ;
            penalty += 10.0 * (-params[i] - 8.0) ;
           }
         else
            m_sigma[i] = exp(params[i]) ;
     }

   error = 0.0 ;

   for(i=0 ; i<ncases ; i++)
     {
      row = m_tset.Row(i);
      inputs1 = np::sliceVector(row,0,m_ngates);
      inputs2 = np::sliceVector(row,ulong(ngates),ulong(ngates+nmodels));
      out = trial(inputs1, inputs2, long(i), 0) ;
      diff = row[ngates+nmodels] - out ;
      error += diff * diff ;
     }

   return error / double(ncases) + penalty ;

  }

Этот метод использует перекрестную проверку для оценки качества пробного сигма-вектора. Вместо прямой оптимизации каждой сигмы оптимизируется логарифм сигмы. Это линеаризует влияние изменений, что приводит к повышению стабильности. Для устранения проблем, связанных с поверхностью погрешности GRNN-гейта, проявляющего плоскостность при экстремальных значениях. Функция criterion изначально возводит параметр в степень, одновременно устанавливая ограниченный диапазон. Для поощрения сигма-значений, не являющихся экстремальными, вводится штрафной срок. Для каждого обучающего образца делается прогноз, и этот прогноз сравнивается со значением true. Квадратичная ошибка накапливается и служит критерием ошибки.

Элементы m_errvals инициализируются нулем, чтобы суммировать числитель уравнения ошибки. Знаменатель этого уравнения не требует явного вычисления, поскольку он аннулируется при рассмотрении коэффициента нормализации в знаменателе уравнения весов. Перед включением каждого члена в сумму проверяется последовательная близость тестового образца к обучающему образцу.

Этот метод может быть использован для прогнозирования, основанного как на членах обучающего набора, так и на совершенно неизвестных образцах. Передавая порядковый номер i_exclude каждого обучающего образца в процедуру trial(), можно реализовать перекрестную проверку. Также передается ограничение на расстояние, n_exclude. Как правило, это значение равно нулю, за исключением только одного случая.

Читатели, должны отметить, что алгоритм перекрестной проверки имеет серьезные ограничения, когда дело доходит до обработки обучающих наборов, демонстрирующих последовательную корреляцию. Это является общим для данных временного ряда. Это можно решить, исключив образцы, которые пространственно близки к тестируемому обучающему образцу.

//+------------------------------------------------------------------+
//| trial ( )                                                        |
//+------------------------------------------------------------------+
double CGatedReg::trial(vector &gates, vector &contenders, long i_exclude,long n_exclude)
  {
   int icase, ivar, idist, size, ncases;
   double psum, diff, dist, err, out ;

   m_errvals.Fill(0.0);
   int ngates = int(m_ngates);
   int nmodels = int(m_nmodels);
   size = ngates + nmodels + 1 ;
   ncases = int(m_nsamples);

   for(icase=0 ; icase<ncases ; icase++)
     {

      idist = (int)fabs(int(i_exclude) - icase) ;
      if(ncases - idist < idist)
         idist = ncases - idist ;

      if(idist <= int(n_exclude))
         continue ;

      dist = 0.0 ;

      for(ivar=0 ; ivar<ngates ; ivar++)
        {
         diff = gates[ivar] - m_tset[icase][ivar] ;
         diff /= m_sigma[ivar] ;
         dist += diff * diff ;
        }

      dist = exp(-dist) ;

      for(ivar=0 ; ivar<nmodels ; ivar++)
        {
         err = m_tset[icase][ngates+ivar] - m_tset[icase][ngates+nmodels] ;
         m_errvals[ivar] += dist * err * err ;
        }

     }

   psum = 0.0 ;
   for(ivar=0 ; ivar<nmodels ; ivar++)
     {
      if(m_errvals[ivar] > 1.e-30)
         m_errvals[ivar] = 1.0 / m_errvals[ivar] ;
      else
         m_errvals[ivar] = 1.e30 ;
      psum += m_errvals[ivar] ;
     }

   for(ivar=0 ; ivar<nmodels ; ivar++)
      m_errvals[ivar] /= psum ;

   out = 0.0 ;
   for(ivar=0 ; ivar<nmodels ; ivar++)
      out += m_errvals[ivar] * contenders[ivar] ;

   return out ;
  }

Если обучающий пример проходит тест на исключение перекрестной проверки, вычисляется взвешенное евклидово расстояние между двумя примерами. Это расстояние возводится в степень для использования при вычислении ошибки прогнозирования для каждой компонентной модели. Впоследствии для каждой модели определяется погрешность прогнозирования. Заключительный шаг включает в себя использование уравнения весов модели для объединения результатов каждой конкурирующей модели в единый прогноз. Это и есть возвращаемое функцией значение.

//+------------------------------------------------------------------+
//|  infer                                                           |
//+------------------------------------------------------------------+
double CGatedReg::predict(vector &gates,vector &contenders)
  {
   return trial(gates,contenders,-1,0);
  }

Тестирование управляемого ансамбля GRNN

Скрипт Gating_Demo.mqh предлагает всестороннее сравнение четырех различных стратегий гейтинга. Каждая стратегия служит своей уникальной цели, демонстрируя различные аспекты выбора и сочетания моделей. Вот краткий обзор четырёх стратегий:

Компонентные прогнозы как переменные гейтинга: Этот подход напрямую использует прогнозы отдельных компонентных моделей в качестве переменных гейтинга, что позволяет проводить прямое сравнение с базовым методом (класс COracle). Он проверяет эффект использования собственных выходных данных моделей в качестве факторов принятия решений при отборе модели.

Гейтинг оригинальных переменных: В этой стратегии исходные входные переменные (используемые компонентными моделями) служат в качестве пропускающих переменных. Учитывая, что эти переменные не предназначены для использования в качестве эффективных сигналов гейтинга, этот подход помогает продемонстрировать влияние плохих или нерелевантных пропускающих переменных на эффективность модели.

Случайный гейтинг: В этой стратегии применяются случайно сгенерированные числа в качестве пропускающих переменных, имитируя сценарий, в котором отсутствуют информативные пропускающие переменные. Она служит базовой линией, показывающей снижение эффективности при использовании полностью неинформативных сигналов.

Гейтинг на основе коэффициента: При таком подходе в качестве пропускающей переменной используется логарифм отношения между погрешностями прогнозирования первой и второй моделей. Хотя этот метод был бы нереалистичным в реальных условиях (поскольку истинная погрешность прогнозирования моделей, как правило, неизвестна), он служит идеализированным сценарием для двух моделей. Для нескольких моделей он предоставляет частичную, но по-прежнему ценную информацию о гейтинге.

Эти четыре стратегии предназначены для тестирования различных условий эффективности и дают представление о сильных и слабых сторонах различных методов гейтинга для ансамблевого обучения. Скрипт оценивает, как каждая стратегия гейтинга влияет на общую точность прогнозирования и дисперсию ошибок, что позволяет более четко понять эффективность механизма пропускания GRNN.

Три модели, 100 образцов и низкая сложность прогнозирования.

EK      0       14:36:33.869    Gating_Demo (BTCUSD,D1)  1000    replications completed.
GL      0       14:36:33.869    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10790466
JP      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Component error = 0.10790458
DF      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Original error = 0.10790458
HM      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Random error = 0.10790458
DJ      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Ratio error = 0.10790458

Три модели, 100 образцов и высокая сложность прогнозирования.

GF      0       14:40:57.600    Gating_Demo (BTCUSD,D1)  1000    replications completed.
LQ      0       14:40:57.600    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.12143040
FE      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Component error = 1.11991444
GQ      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Original error = 1.11991445
QI      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Random error = 1.11991443
EO      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Ratio error = 1.11991443

Четыре модели, 100 образцов и низкая сложность прогнозирования.

IO      0       14:42:58.751    Gating_Demo (BTCUSD,D1)  1000    replications completed.
LK      0       14:42:58.751    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12792841
RS      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Component error = 0.11516554
MK      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Original error = 0.11516373
GR      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Random error = 0.11516595
GE      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Ratio error = 0.11516595

Четыре модели, 100 образцов и высокая сложность прогнозирования.

QQ      0       14:45:15.030    Gating_Demo (BTCUSD,D1)  1000    replications completed.
HE      0       14:45:15.030    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.14025014
EI      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Component error = 1.13144872
GM      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Original error = 1.13144863
QD      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Random error = 1.13144883
NL      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Ratio error = 1.13144882

Удивительное повышение эффективности, достигнутое благодаря случайному пропусканию, можно объяснить тем, как работает алгоритм пропускания GRNN. В типичных сценариях можно было бы ожидать, что случайные пропускающие сигналы ухудшат эффективность модели, поскольку вносят шум и не предоставляют полезной информации для отбора модели. Однако механизм GRNN основан на взвешенных евклидовых расстояниях между обучающими образцами и корректирует свой прогноз в зависимости от того, насколько тестовый образец похож на обучающие образцы.

В случаях, когда пропускающий сигнал является случайным, алгоритм GRNN по-прежнему использует общую структуру данных и моделей для вычисления средневзвешенного значения прогнозов компонентной модели. Поскольку случайные значения пропускания не приводят к сильному смещению в сторону какой-либо конкретной модели, алгоритм может в большей степени полагаться на внутреннюю структуру данных и эффективность отдельных моделей, которые обучены хорошо прогнозировать. Общим результатом может стать более надежная комбинация моделей, при этом случайное пропускание фактически действует как нейтрализатор, гарантируя, что ни одна модель не будет доминировать в процессе принятия решений.

В случае, когда три модели демонстрируют высокую точность прогнозирования, а одна модель генерирует случайные прогнозы, подход со случайным гейтингом может непреднамеренно послужить методом отбрасывания случайной модели путем уменьшения ее влияния в ансамбле. Это приводит к ситуации, когда эффективность модели ансамбля значительно улучшается, поскольку влияние неинформативной случайной модели сводится к минимуму.

Таким образом, хотя случайное пропускание может показаться интуитивно проигрышным, процесс пропускания GRNN может использовать структуру набора данных и моделей таким образом, что это приводит к неожиданным улучшениям, особенно в "простых" задачах прогнозирования, когда модели уже обладают высокой точностью. Такое поведение подчеркивает мощь метода пропускания GRNN, который даже в неоптимальных ситуациях может использовать потенциал нескольких моделей для получения улучшенных прогнозов путем эффективного взвешивания вклада каждой модели.

Алгоритм эффективно оценивает погрешность прогнозирования каждой модели. При наличии модели с неизменно высокими погрешностями прогнозирования, как в случае модели случайного прогнозирования, погрешность прогнозирования будет последовательно генерировать большие оценки погрешности для этой модели. Это затем приводит к тому, что схема взвешивания ансамбля присваивает этой модели соответственно низкий вес в рамках взвешенной комбинации.

Это наблюдение подчеркивает ключевое преимущество GRNN-гейтинга. Он может эффективно выявлять и снижать вес моделей с низкой прогностической эффективностью, даже если сами пропускающие переменные не обладают присущей им прогностической способностью. Следовательно, даже в ситуациях, когда сигналы пропускания предоставляют ограниченную информацию или не содержат никакой релевантной информации, GRNN-гейтинг все равно может значительно повысить эффективность, особенно когда ансамбль включает модели с различным уровнем точности прогнозирования.

Заключение

Эти методы демонстрируют адаптивность пропускающих механизмов для повышения интерпретируемости и прогностической способности алгоритмов обучения. Выбор метода зависит от конкретного контекста, включая сложность задачи, характер данных и вычислительные ограничения. Часто комбинация методов, таких как методы оптимизации в сочетании с анализом предметной области, дает наиболее эффективные и поддающиеся интерпретации результаты. Весь код, на который мы ссылаемся в настоящей статье, прилагается в конце. В таблице ниже приведены описания всех прилагаемых исходных файлов.

Название файла	Описание
MQL5/include/gatedreg.mqh	Содержит определение класса CGatedReg, реализующего управляемый ансамбль GRNN
MQL5/include/imodel.mqh	Содержит определение интерфейсов, которые инкапсулируют обученную модель
MQL5/include/minimize.mqh	Содержит определение CPowellsMethod, реализующего минимизацию функций с использованием метода Пауэлла
MQL5/include/multilayerperceptron.mqh	Содержит определение класса CMlp, который является реализацией многослойного персептрона
MQL5/include/np.mqh	Набор универсальных вспомогательных функций для манипулирования векторами и матрицами
MQL5/include/oracle.mqh	Предоставляет определение класса COracle и позволяет выбирать модель из набора специализированных компонентных моделей
MQL5/include/qsort.mqh	Предоставляет простые функции для сортировки векторов
Mql5/scripts/Gating_Demo.mq5	Скрипт, демонстрирующий функциональность, предоставляемую классом CGatedReg
Mql5/scripts/Oracle_Demo.mq5	Ещё один скрипт, демонстрирующий использование класса COracle

Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/16995

Прикрепленные файлы |

Загрузить ZIP

gatedreg.mqh (6.47 KB)

imodel.mqh (1.47 KB)

minimize.mqh (17.22 KB)

multilayerperceptron.mqh (6.64 KB)

np.mqh (80.58 KB)

oracle.mqh (5.66 KB)

qsort.mqh (2.48 KB)

Gating_Demo.mq5 (13.27 KB)

Oracle_Demo.mq5 (9.57 KB)

Mql5.zip (25.86 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Нейросети в трейдинге: Сквозная многомерная модель прогнозирования временных рядов (GinAR)

Предлагаем познакомиться с инновационным подходом к прогнозированию временных рядов с пропущенными данными на базе фреймворка GinAR. В статье показана реализация ключевых компонентов на OpenCL, что обеспечивает высокую производительность. В следующей публикации мы подробно рассмотрим интеграцию этих решений в MQL5. Это позволит понять, как применять метод на практике в трейдинге.

Тестирование надежности торговых советников

При разработке стратегии необходимо учитывать множество сложных деталей, на многие из которых не обращают особого внимания начинающие трейдеры. В результате многим трейдерам, включая меня, пришлось усвоить эти уроки на собственном горьком опыте. Данная статья основана на моих наблюдениях за распространенными подводными камнями, с которыми сталкивается большинство начинающих трейдеров при разработке стратегий на MQL5. В ней представлен ряд советов, хитростей и примеров, которые помогут определить причину дисквалификации советника и протестировать надежность наших собственных советников простым в применении способом. Цель состоит в том, чтобы обучить читателей, помогая им избежать мошенничества в будущем при покупке советников, а также предотвратить ошибки при разработке собственной стратегии.

Экстремальная оптимизация — Extremal Optimization (EO)

В данной статье рассматривается алгоритм Extremal Optimization (EO) — метод оптимизации, вдохновленный моделью самоорганизованной критичности Бака-Снеппена, где эволюция происходит через устранение наихудших компонентов системы. Модифицированная популяционная версия алгоритма демонстрирует отход от теоретических принципов в пользу практической эффективности, что приводит к созданию мощных вычислительных инструментов.

Прогнозирование трендов с помощью LSTM для стратегий следования за трендом

Долгая кратковременная память (LSTM) - это тип рекуррентной нейронной сети (RNN), предназначенной для моделирования последовательных данных путем эффективного учета долгосрочных зависимостей и решения проблемы исчезающего градиента. В настоящей статье мы рассмотрим, как использовать LSTM для прогнозирования будущих тенденций, повышая эффективность стратегий следования за трендами. В статье будет рассказано о внедрении ключевых концепций и стоящей за разработкой мотивации, извлечении данных из MetaTrader 5, использовании этих данных для обучения модели на Python, интеграции модели машинного обучения в MQL5, а также о результатах и перспективах на будущее на основании статистического бэк-тестирования.