Знакомство с кривыми рабочих характеристик приемника (ROC-кривыми)

MetaTrader 5 — Примеры | 16 июля 2025, 08:42

302

Francis Dube

Введение

График рабочей характеристики приемника (Receiver Operating Characteristic, ROC) служит методом визуализации, организации и выбора классификаторов в зависимости от их производительности. Возникшие в теории обнаружения сигналов, графики ROC использовались для иллюстрации альтернативы между истинно положительными и ложноположительными показателями классификаторов. Помимо их общей полезности в качестве метода построения графиков, ROC-кривые демонстрируют свойства, придающие им особенную ценность в областях, характеризующихся неравномерными распределениями классов и разнородными затратами на ошибки классификации. Это особенно актуально для классификаторов, которые применяются к наборам данных финансовых временных рядов.

Хотя концептуальная основа ROC-графиков проста, практическое применение выявляет сложности, требующие тщательного рассмотрения. Более того, при их эмпирическом использовании имеются распространенные заблуждения и потенциальные ловушки. Целью данной статьи является базовое введение в тему ROC-кривых и послужить практическим руководством по их применению при оценке эффективности классификаторов.

Бинарная формулировка классификаций

Во многих практических приложениях решаются задачи бинарной классификации, в которых экземпляры относятся к одному из двух взаимоисключающих и совместно исчерпывающих классов. Распространенный пример такого сценария возникает при определении одного целевого класса, и каждый экземпляр классифицируют либо как член этого класса, либо как дополнение к нему. Рассмотрим, к примеру, классификацию радиолокационных сигналов, где обнаруженный контур на экране классифицируют либо как объект-танк (целевой класс), либо как объект, не являющийся танком. Сходным образом, сделку по кредитной карте можно классифицировать как мошенническую (целевой класс) или законную.

Целевой или нет?

Эта конкретная формулировка задачи бинарной классификации, которая характеризуется определением одного целевого класса, образует основу для последующего анализа. Вместо явного отнесения экземпляров к одному из двух различных классов, принятый здесь подход концентрируется на определении принадлежности экземпляра к обозначенному целевому классу. Хотя используемая терминология со ссылкой на «цель» и дополнение к ней заставляет думать о военном деле, такая концепция широко применяется. Целевой класс может представлять собой различные сущности, например злокачественную опухоль, успешную финансовую сделку или, как упоминалось выше, мошенническую сделку по кредитной карте. Важной характеристикой является двойственность класса, представляющего основной интерес, и всех прочих возможностей.

Матрица путаницы

Для данного классификатора, примененного к тестовому набору данных, возможны четыре различных результата. Если экземпляр, принадлежащий к положительному классу, классифицируется как положительный, он обозначается как истинно положительный, (TP). И наоборот, если он классифицируется как отрицательный, он обозначается как ложноотрицательный, (FN). Аналогично, если принадлежащий к отрицательному классу экземпляр классифицируется как отрицательный, он обозначается как истинно отрицательный, (TN); а если он классифицируется как положительный, он обозначается как ложноположительный, (FP). Эти четыре значения составляют матрицу путаницы размером два на два, которую также называют таблицей сопряженности признаков.

Матрица путаницы

Это матрица отражает распределение экземпляров по четырем указанным результатам и служит основой для многочисленных широко применяемых показателей эффективности, среди которых, например:

Коэффициент попадания (Hit Rate) или чувствительность (Sensitivity), или полнота (Recall): доля целевых экземпляров, правильно классифицированных как цели, рассчитывается как TP / (TP + FN).

Частота ложных срабатываний (False Alarm Rate) (частота ошибок первого рода): доля нецелевых экземпляров, неправильно классифицированных как цели, рассчитывается как FP / (TN + FP).

Частота пропусков (Miss Rate) (частота ошибок второго рода): доля целевых экземпляров, неправильно классифицированных как нецелевые, рассчитывается как FN / (TP + FN).

Специфичность (Specificity): доля нецелевых экземпляров, правильно классифицированных как нецелевые, рассчитывается как TN / (TN + FP).

В Википедии есть полезная графика, отображающая обширный список показателей эффективности, полученный из матрицы путаницы.

Таблица путаницы

ROC-кривые

Внутренние механизмы большинства бинарных классификационных моделей создают числовой прогноз, а затем сравнивают его с заданным пороговым значением. Если прогнозируемое число равно этому порогу или превосходит его, экземпляр классифицируется как целевой; иначе он классифицируется как нецелевой. Очевидно, что пороговое значение влияет на все ранее упомянутые показатели эффективности. Установка порогового значения на уровне или ниже минимально возможного прогнозируемого значения приводит к классификации всех экземпляров, классифицируемых как целевые, обеспечивая идеальную частоту попаданий, но соответственно и низкую частоту ложных срабатываний.

Механизм принятия решений

В свою очередь, при установке порога выше максимально возможного прогнозируемого значения все экземпляры классифицируются как нецелевые, что приводит к нулевой частоте попаданий и абсолютно нулевой частоте ложных срабатываний. Оптимальное пороговое значение находится между этими крайними значениями. При систематическом изменении порогового значения по всему диапазону и частота попаданий, и частота ложных срабатываний изменяются в своих соответствующих диапазонах от 0 до 1, причем один показатель улучшается за счет другого. Кривая, полученная построением графика зависимости этих частот друг от друга (при этом порог выступает в качестве скрытого параметра), называется кривой рабочей характеристики приемника (Receiver Operating Characteristic, ROC).

Традиционно ROC-кривую изображают, располагая частоту ложных срабатываний по горизонтальной оси, а частоту попаданий — по вертикальной. Рассмотрим модель классификации, выдающую случайные числовые прогнозы, не коррелирующие с истинным классом случая.

Случайная эффективность

При таком сценарии частота попаданий и частота ложных срабатываний в среднем будут одинаковыми по всем пороговым значениям, в результате чего получится ROC-кривая, которая приближается к диагонали, проходящей из нижнего левого в верхний правый угол графика. Например, если классификатор случайным образом относит экземпляр к положительному классу с вероятностью 50%, ожидается, что он правильно классифицирует 50% как положительных, так и отрицательных экземпляров, что приводит к точке с координатами (0.5, 0.5) в ROC-пространстве.

Аналогично, если классификатор относит экземпляр к положительному классу с вероятностью 90%, ожидается, что он правильно классифицирует 90% положительных экземпляров; но при этом доля ложноположительных результатов увеличится до 90%, выдавая точку с координатами (0.9, 0.9). Следовательно, случайный классификатор сгенерирует ROC-точку, проходящую по диагонали, причем ее положение определяется частотой, с которой он предсказывает положительный класс. Для достижения эффективности, превышающей эффективность случайного угадывания, на что указывает местоположение в пределах верхней треугольной области ROC-пространства, классификатор должен использовать информативные закономерности, присутствующие в данных.

Абсолютная эффективность

С другой стороны, идеальная модель, характеризующаяся существованием порога, который четко отделяет целевые значения (прогнозируемые значения, равные пороговому уровню или превышающие его) от нецелевых (прогнозируемые значения ниже порогового уровня), демонстрирует отчетливую ROC-кривую. При переходе параметрического порогового значения от минимального к оптимальному уровню частота ложных срабатываний снижается с 1 до 0, а частота попаданий неизменно остается на уровне 1. Последующие повышения параметрического порогового уровня вызывает снижение частоты попаданий с 1 до 0, при этом частота ложных срабатываний остается на уровне 0. Это приводит к получению ROC-кривой, образующей путь от верхнего правого в верхний левый угол, а затем в нижний левый угол.

Промежуточная эффективность

Модели промежуточной эффективности, демонстрирующие точность в промежутке между этими крайними вариантами, будут формировать ROC-кривые, расположенные между диагональю и верхним левым углом. Степень отклонения кривой от диагонали в направлении верхнего левого угла характеризует эффективность модели. В общем смысле точка на ROC-графике считается превосходящей другую, если у нее более высокая частота истинно положительных результатов, более низкая частота ложноположительных результатов или и то, и другое. Классификаторы, расположенные на левой стороне ROC-графика близко к оси абсцисс, могут характеризоваться как пессимистичные.

Эти классификаторы демонстрируют тенденцию выдавать положительные классификации только при наличии существенных доказательств, что приводит к низкому уровню ложноположительных результатов, но часто сопровождается снижением уровня истинно положительных результатов. И наоборот, классификаторы, расположенные вверху в правой части ROC-графика, характеризующиеся как менее консервативные, склонны выдавать положительные классификации даже при минимальных доказательствах, что приводит к высокому уровню истинно положительных результатов, но часто сопровождается повышенным уровнем ложноположительных результатов. В многочисленных сфера реальной жизни, где отрицательные экземпляры преобладают, эффективность классификаторов в области слева от ROC-графика становится все более релевантной.

Классификаторы, находящиеся в пределах нижней правой треугольной области ROC-пространства, демонстрируют эффективность, уступающую эффективности случайного угадывания. Следовательно, эта область, как правило, лишена точек данных на ROC-графиках. Отрицание классификатора, определяемое как разворот его классификационных решений по всем экземплярам, приводит к тому, что его истинно положительные классификации становятся ложноотрицательными ошибками, а ложноположительные классификации становятся истинными отрицательными классификациями. Таким образом, любой классификатор, выдающий точку внутри нижнего правого треугольника, можно преобразовать посредством отрицания для получения соответствующей точки внутри верхнего левого треугольника. Классификатор, располагающийся по диагонали, можно охарактеризовать как не обладающий конкретной информацией о принадлежности к какому-либо классу. И наоборот, классификатор, расположенный ниже диагонали, можно интерпретировать как имеющий информативные закономерности, хотя и применяющий их ошибочно.

Показатели эффективности ROC

Хотя визуальный осмотр графика ROC-кривой может предложить предварительные аналитические сведения, более полное понимание эффективности модели достигается посредством анализа соответствующих показателей. Перед подробным анализом необходимо прояснить конструкции данных, характеризующие ROC-кривую. Для лучшего понимания представлен наглядный пример.

В таблице ниже представлена гипотетическая выборка показателей эффективности ROC, полученных на основе классификационной модели. В этом примере используется набор данных iris, доступный в библиотеке Sklearn Python. В соответствии с парадигмой «целевой/нецелевой» задача классификации сводилась к идентификации единственного варианта iris. В частности, если в качестве целевого обозначен вариант setosa, все прочие варианты классифицируются как нецелевые. В соответствии с традиционными подходами к классификации модель была обучена генерировать результат 0 для нецелевых и 1 для целевых вариантов. Соответственно были преобразованы метки выборок. Следует отметить, что допустимы и альтернативные схемы маркировки.

Для каждого порогового значения в пределах дерева решений генерируется матрица путаницы для вычисления истинно положительных и ложноположительных результатов. В этих расчетах используется значение выходной вероятности или функции принятия решения, полученное с помощью обученной модели прогнозирования, а соответствующий порог определяет принадлежность к тому или иному классу. Представленная в этой работе таблица была сгенерирована с помощью скрипта OC_curves_table_demo.mq5.

KG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     TPR   FPR   FNR   TNR   PREC  NPREC  M_E   ACC   B_ACC THRESH
NF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.038 0.000 0.962 1.000 1.000 0.000 0.481 0.667 0.519 0.98195
DI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.077 0.000 0.923 1.000 1.000 0.000 0.462 0.680 0.538 0.97708
OI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.115 0.000 0.885 1.000 1.000 0.000 0.442 0.693 0.558 0.97556
GI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.154 0.000 0.846 1.000 1.000 0.000 0.423 0.707 0.577 0.97334
GH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.192 0.000 0.808 1.000 1.000 0.000 0.404 0.720 0.596 0.97221
RH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.231 0.000 0.769 1.000 1.000 0.000 0.385 0.733 0.615 0.97211
IK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.269 0.000 0.731 1.000 1.000 0.000 0.365 0.747 0.635 0.96935
CK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.308 0.000 0.692 1.000 1.000 0.000 0.346 0.760 0.654 0.96736
NK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.346 0.000 0.654 1.000 1.000 0.000 0.327 0.773 0.673 0.96715
EJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.385 0.000 0.615 1.000 1.000 0.000 0.308 0.787 0.692 0.96645
DJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.423 0.000 0.577 1.000 1.000 0.000 0.288 0.800 0.712 0.96552
HJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.462 0.000 0.538 1.000 1.000 0.000 0.269 0.813 0.731 0.96534
NM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.500 0.000 0.500 1.000 1.000 0.000 0.250 0.827 0.750 0.96417
GM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.538 0.000 0.462 1.000 1.000 0.000 0.231 0.840 0.769 0.96155
CL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.577 0.000 0.423 1.000 1.000 0.000 0.212 0.853 0.788 0.95943
LL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.615 0.000 0.385 1.000 1.000 0.000 0.192 0.867 0.808 0.95699
NL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.654 0.000 0.346 1.000 1.000 0.000 0.173 0.880 0.827 0.95593
KO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.692 0.000 0.308 1.000 1.000 0.000 0.154 0.893 0.846 0.95534
NO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.731 0.000 0.269 1.000 1.000 0.000 0.135 0.907 0.865 0.95258
NO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.769 0.000 0.231 1.000 1.000 0.000 0.115 0.920 0.885 0.94991
EN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.808 0.000 0.192 1.000 1.000 0.000 0.096 0.933 0.904 0.94660
CN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.846 0.000 0.154 1.000 1.000 0.000 0.077 0.947 0.923 0.94489
OQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.885 0.000 0.115 1.000 1.000 0.000 0.058 0.960 0.942 0.94420
NQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.923 0.000 0.077 1.000 1.000 0.000 0.038 0.973 0.962 0.93619
GQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.962 0.000 0.038 1.000 1.000 0.000 0.019 0.987 0.981 0.92375
PP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.000 0.000 1.000 1.000 0.000 0.000 1.000 1.000 0.92087
OP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.020 0.000 0.980 0.963 0.037 0.010 0.987 0.990 0.12257
RP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.041 0.000 0.959 0.929 0.071 0.020 0.973 0.980 0.07124
RS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.061 0.000 0.939 0.897 0.103 0.031 0.960 0.969 0.05349
KS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.082 0.000 0.918 0.867 0.133 0.041 0.947 0.959 0.04072
KR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.102 0.000 0.898 0.839 0.161 0.051 0.933 0.949 0.03502
KR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.122 0.000 0.878 0.812 0.188 0.061 0.920 0.939 0.02523
JR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.143 0.000 0.857 0.788 0.212 0.071 0.907 0.929 0.02147
HE      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.163 0.000 0.837 0.765 0.235 0.082 0.893 0.918 0.01841
QE      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.184 0.000 0.816 0.743 0.257 0.092 0.880 0.908 0.01488
DE      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.204 0.000 0.796 0.722 0.278 0.102 0.867 0.898 0.01332
PD      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.224 0.000 0.776 0.703 0.297 0.112 0.853 0.888 0.01195
PD      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.245 0.000 0.755 0.684 0.316 0.122 0.840 0.878 0.01058
MG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.265 0.000 0.735 0.667 0.333 0.133 0.827 0.867 0.00819
JG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.286 0.000 0.714 0.650 0.350 0.143 0.813 0.857 0.00744
EG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.306 0.000 0.694 0.634 0.366 0.153 0.800 0.847 0.00683
LF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.327 0.000 0.673 0.619 0.381 0.163 0.787 0.837 0.00635
CF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.347 0.000 0.653 0.605 0.395 0.173 0.773 0.827 0.00589
KF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.367 0.000 0.633 0.591 0.409 0.184 0.760 0.816 0.00578
JI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.388 0.000 0.612 0.578 0.422 0.194 0.747 0.806 0.00556
JI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.408 0.000 0.592 0.565 0.435 0.204 0.733 0.796 0.00494
NH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.429 0.000 0.571 0.553 0.447 0.214 0.720 0.786 0.00416
PH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.449 0.000 0.551 0.542 0.458 0.224 0.707 0.776 0.00347
LH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.469 0.000 0.531 0.531 0.469 0.235 0.693 0.765 0.00244
KK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.490 0.000 0.510 0.520 0.480 0.245 0.680 0.755 0.00238
HK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.510 0.000 0.490 0.510 0.490 0.255 0.667 0.745 0.00225
LK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.531 0.000 0.469 0.500 0.500 0.265 0.653 0.735 0.00213
PJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.551 0.000 0.449 0.491 0.509 0.276 0.640 0.724 0.00192
CJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.571 0.000 0.429 0.481 0.519 0.286 0.627 0.714 0.00189
EM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.592 0.000 0.408 0.473 0.527 0.296 0.613 0.704 0.00177
IM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.612 0.000 0.388 0.464 0.536 0.306 0.600 0.694 0.00157
HM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.633 0.000 0.367 0.456 0.544 0.316 0.587 0.684 0.00132
EL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.653 0.000 0.347 0.448 0.552 0.327 0.573 0.673 0.00127
DL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.673 0.000 0.327 0.441 0.559 0.337 0.560 0.663 0.00119
KL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.694 0.000 0.306 0.433 0.567 0.347 0.547 0.653 0.00104
DO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.714 0.000 0.286 0.426 0.574 0.357 0.533 0.643 0.00102
RO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.735 0.000 0.265 0.419 0.581 0.367 0.520 0.633 0.00085
DN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.755 0.000 0.245 0.413 0.587 0.378 0.507 0.622 0.00082
EN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.776 0.000 0.224 0.406 0.594 0.388 0.493 0.612 0.00069
HN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.796 0.000 0.204 0.400 0.600 0.398 0.480 0.602 0.00062
HQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.816 0.000 0.184 0.394 0.606 0.408 0.467 0.592 0.00052
DQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.837 0.000 0.163 0.388 0.612 0.418 0.453 0.582 0.00048
FQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.857 0.000 0.143 0.382 0.618 0.429 0.440 0.571 0.00044
MP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.878 0.000 0.122 0.377 0.623 0.439 0.427 0.561 0.00028
LP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.898 0.000 0.102 0.371 0.629 0.449 0.413 0.551 0.00026
NS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.918 0.000 0.082 0.366 0.634 0.459 0.400 0.541 0.00015
ES      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.939 0.000 0.061 0.361 0.639 0.469 0.387 0.531 0.00012
MS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.959 0.000 0.041 0.356 0.644 0.480 0.373 0.520 0.00007
QR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.980 0.000 0.020 0.351 0.649 0.490 0.360 0.510 0.00004
CR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 1.000 0.000 0.000 0.347 0.653 0.500 0.347 0.500 0.00002

Изучение табличных данных ROC-кривой выявило заметную тенденцию: как TPR, так и FPR демонстрируют снижение с 1 до 0 по мере увеличения порога принятия решения. Учитывая присущую модели прогностическую способность, FPR демонстрирует более быстрое снижение, чем TPR. Примечательно, что FPR достигает нуля, тогда как TPR сохраняет значение 1. Следовательно, если относительная стоимость ошибок первого и второго типа существенно не различается, ожидается, что оптимальный порог будет находиться в интервале, определяемом этими предельными значениями. Кроме того, важно отметить: в таблицу включена специфичность, что эквивалеyтно истинно отрицательному показателю (True Negative Rate, TNR) и дополняет собой значение FPR.

Во многих примерах определение оптимального порога можно получить путем непосредственного просмотра столбцов «Доля истинно положительных результатов» (True Positive Rate, TPR) и «Доля ложноположительных результатов» (False Positive Rate, FPR). Возможность интерпретировать этот процесс усиливается включением размеров целевых и нецелевых выборок. Если связанные с ошибками первого и второго типов затраты приблизительно равны, то средняя ошибка служит подходящим показателем скалярной эффективности. Этот показатель, обозначенный в таблице как M_E, рассчитывается как среднее арифметическое частоты ложных срабатываний и частоты пропусков.

Однако в сценариях, в которых стоимость ошибок этих типов существенно различается, показатель средней ошибки теряет свою значимость. Точность, в частности, является исключительно важным показателем эффективности в различных приложениях. Как правило, основной интерес представляет точность обнаружения цели. В определенных ситуациях точность выявления нецелевых значений может оказаться не менее значимой. Для точного обнаружения целей в столбце с меткой PREC содержится соответствующая информация. При этом столбец с меткой NPREC имеет значение для точной идентификации нецелевых объектов.

В таблице представлены дополнительные показатели эффективности, включая точность (ACC) и сбалансированную точность (B_ACC). Точность определяется как доля в общем наборе данных правильно классифицированных случаев, включающих в себя и истинно положительные и истинно отрицательные. Сбалансированная точность, рассчитанная как среднее арифметическое чувствительности и специфичности, используется для смягчения воздействия несбалансированности классов — состояния, характеризующегося значительными различиями в размерах выборок целевых и нецелевых классов. Перед обсуждением площади под ROC-кривой обеспечиваем рассмотрение вычислительных процедур, которые используются для создания вышеназванной таблицы показателей ROC. В частности, будет проанализирован код, который отвечает за расчет связанных с ROC показателей.

Соответствующий код инкапсулирован в заголовочном файле roc_curves.mqh, определяющем ряд функций и структуру данных conf_stats. Структура conf_stats служит контейнером для хранения различных параметров, полученных из матрицы путаницы.

//+------------------------------------------------------------------+
//|  confusion matrix stats                                          |
//+------------------------------------------------------------------+
struct conf_stats
  {
   double              tn;                //true negatives
   double              tp;                //true positives
   double              fn;                //false negatives
   double              fp;                //false positives
   double              num_targets;       //number of actual positive labels(target)
   double              num_non_targets;   //number of acutal negative labels(non targets)
   double            tp_rate;             //true positives rate - hit rate -  recall - sensitivity
   double            fp_rate;             //false positives rate - fall out - type 1 error
   double            fn_rate;             //false negatives rate - miss rate - type 2 error
   double            tn_rate;             //true negatives rate - specificity
   double            precision;           //precision - positive predictve value
   double            null_precision;      //null precision - false discovery rate
   double            prevalence;          //prevalence
   double            lr_plus;             //positive likelihood ratio
   double            lr_neg;              //negative likelihood ratio
   double            for_rate;            //false omission rate
   double            npv;                 //negative predictive value
   double            acc;                 //accuracy
   double            b_acc;               //balanced accuracy
   double            f1_score;            //f1 score
   double            mean_error;          //mean error
  };

Структура conf_stats функционирует как основной параметр в функции roc_stats(), облегчая хранение результатов оценки, полученных из матрицы путаницы. Оценка проводится на основе набора данных, включающего метки true, соответствующие прогнозы и заданный порог. Метки true предоставляются в виде вектора, обозначенного как целевые объекты, и служат вторым параметром. Третий аргумент (probas) представляет собой вектор прогнозируемых вероятностей или переменных принятия решений.

//+------------------------------------------------------------------+
//| defines                                                          |
//+------------------------------------------------------------------+
bool roc_stats(conf_stats &cmat, vector &targets, vector &probas, double threshold, long target_label = 1, long non_target_label= 0)
  {
   vector all_labels = np::unique(targets);

   if(all_labels.Size()!=2 || long(all_labels[all_labels.ArgMin()])!=non_target_label || long(all_labels[all_labels.ArgMax()])!=target_label || target_label<=non_target_label)
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid inputs ");
      return false;
     }
//---
   cmat.tp=cmat.fn=cmat.tn=cmat.fp = 0.0;
//---
   for(ulong i = 0; i<targets.Size(); i++)
     {
      if(probas[i]>=threshold && long(targets[i]) == target_label)
         cmat.tp++;
      else
         if(probas[i]>=threshold && long(targets[i]) == non_target_label)
            cmat.fp++;
         else
            if(probas[i]<threshold && long(targets[i]) == target_label)
               cmat.fn++;
            else
               cmat.tn++;
     }
//---
   cmat.num_targets = cmat.tp+cmat.fn;
   cmat.num_non_targets = cmat.fp+cmat.tn;
//---
   cmat.tp_rate = (cmat.tp+cmat.fn>0.0)?(cmat.tp/(cmat.tp+cmat.fn)):double("na");
   cmat.fp_rate = (cmat.tn+cmat.fp>0.0)?(cmat.fp/(cmat.tn+cmat.fp)):double("na");
   cmat.fn_rate = (cmat.tp+cmat.fn>0.0)?(cmat.fn/(cmat.tp+cmat.fn)):double("na");
   cmat.tn_rate = (cmat.tn+cmat.fp>0.0)?(cmat.tn/(cmat.tn+cmat.fp)):double("na");
   cmat.precision = (cmat.tp+cmat.fp>0.0)?(cmat.tp/(cmat.tp+cmat.fp)):double("na");
   cmat.null_precision = 1.0 - cmat.precision;
   cmat.for_rate = (cmat.tn+cmat.fn>0.0)?(cmat.fn/(cmat.tn+cmat.fn)):double("na");
   cmat.npv = 1.0 - cmat.for_rate;
   cmat.lr_plus = (cmat.fp_rate>0.0)?(cmat.tp_rate/cmat.fp_rate):double("na");
   cmat.lr_neg = (cmat.tn_rate>0.0)?(cmat.fn_rate/cmat.tn_rate):double("na");
   cmat.prevalence = (cmat.num_non_targets+cmat.num_targets>0.0)?(cmat.num_targets/(cmat.num_non_targets+cmat.num_targets)):double("na");
   cmat.acc = (cmat.num_non_targets+cmat.num_targets>0.0)?((cmat.tp+cmat.tn)/(cmat.num_non_targets+cmat.num_targets)):double("na");
   cmat.b_acc = ((cmat.tp_rate+cmat.tn_rate)/2.0);
   cmat.f1_score = (cmat.tp+cmat.fp+cmat.fn>0.0)?((2.0*cmat.tp)/(2.0*cmat.tp+cmat.fp+cmat.fn)):double("na");
   cmat.mean_error = ((cmat.fp_rate+cmat.fn_rate)/2.0);
//---
   return true;
//---
  }

Пороговый параметр определяет критическое значение, используемое для определения принадлежности к тому или иному классу. Последние два параметра позволяют явно указывать целевые и нецелевые метки соответственно. Функция возвращает логическое значение, обозначающее успешное выполнение как true, а возникновение ошибки — как false.

//+------------------------------------------------------------------+
//| roc table                                                        |
//+------------------------------------------------------------------+
matrix roc_table(vector &true_targets,matrix &probas,ulong target_probs_col = 1, long target_label = 1, long non_target_label= 0)
  {
   matrix roctable(probas.Rows(),10);

   conf_stats mts;

   vector probs = probas.Col(target_probs_col);

   if(!np::quickSort(probs,false,0,probs.Size()-1))
      return matrix::Zeros(1,1);

   for(ulong i = 0; i<roctable.Rows(); i++)
     {
      if(!roc_stats(mts,true_targets,probas.Col(target_probs_col),probs[i],target_label,non_target_label))
         return matrix::Zeros(1,1);
      roctable[i][0] = mts.tp_rate;
      roctable[i][1] = mts.fp_rate;
      roctable[i][2] = mts.fn_rate;
      roctable[i][3] = mts.tn_rate;
      roctable[i][4] = mts.precision;
      roctable[i][5] = mts.null_precision;
      roctable[i][6] = mts.mean_error;
      roctable[i][7] = mts.acc;
      roctable[i][8] = mts.b_acc;
      roctable[i][9] = probs[i];
     }
//---
   return roctable;
  }

Функция roc_table() генерирует матрицу, содержащую данные ROC-кривой. Входные параметры включают вектор меток класса true, матрицу прогнозируемых вероятностей или переменные принятия решений и беззнаковое длинное целое, указывающее индекс столбца для определения принадлежности к классу в многостолбцовых матрицах. Последние два параметра определяют целевые и нецелевые метки. В случае ошибки функция возвращает матрицу нулей размером 1x1. Необходимо отметить, что обе функции, roc_stats() и roc_table() специально разработаны для моделей двоичной классификации. Несоблюдение этого требования приведет к появлению сообщения об ошибке.

//+------------------------------------------------------------------+
//| roc curve table display                                          |
//+------------------------------------------------------------------+
string roc_table_display(matrix &out)
  {
   string output,temp;

   if(out.Rows()>=10)
     {
      output = "TPR   FPR   FNR   TNR   PREC  NPREC  M_E   ACC   B_ACC THRESH";
      for(ulong i = 0; i<out.Rows(); i++)
        {
         temp = StringFormat("\n%5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.5lf",
                             out[i][0],out[i][1],out[i][2],out[i][3],out[i][4],out[i][5],out[i][6],out[i][7],out[i][8],out[i][9]);
         StringAdd(output,temp);
        }
     }
   return output;
  }

Функция roc_table_display() принимает один параметр матрицы, лучше всего — вывод из предыдущего вызова функции roc_table(), и форматирует данные в таблично-строковое представление.

Площадь под ROC-кривой

Площадь под ROC-кривой (Area Under the ROC Curve, AUC) обеспечивает краткую и однозначную метрику производительности классификатора, устраняющую чрезмерную детализацию полной ROC-кривой. В то время как ROC-кривая визуально отображает противоречие между истинными и ложными положительными показателями, дает количественную характеристику общей способности модели различать классы. Непригодная модель, представленная диагональной линией на графике ROC, дает значение AUC, равное 0.5, указывая на производительность при случайном чтении и записи. Напротив, AUC в идеальной модели с огибающей верхний левый угол ROC-кривой достигает значения 1.0. Таким образом, большее значение AUC означает более высокую производительность модели. Расчет AUC включает в себя определение площади под ROC-кривой, а благодаря присущей тестовым наборам данных статистической вариативности для точной оценки достаточно простого суммирования, что исключает необходимость сложного численного интегрирования.

AUC располагает значимой статистической интерпретацией: она представляет собой вероятность присвоения классификатором более высокого ранга случайно выбранному положительному экземпляру, чем случайно выбранному отрицательному экземпляру. Эта характеристика устанавливает тождество между AUC и критерием суммы рангов Уилкоксона, известным также как U-критерий Манна-Уитни.

Критерий суммы рангов Уилкоксона — непараметрический статистический метод, оценивающий разницу между двумя независимыми группами, не предполагая нормальность. Он работает, ранжируя все наблюдения и сравнивая суммы рангов между группами, оценивая тем самым различия в медианах.

Кроме того, AUC неразрывно связана с коэффициентом Джини. В частности, коэффициент Джини выводится как удвоенная площадь между диагональной линией вероятности и ROC-кривой. Коэффициент Джини — мера неравенства распределения, количественно определяющая степень дисперсии в распределении, которая варьируется от 0 (полное равенство) до 1 (максимальное неравенство). С точки зрения распределения доходов, он отражает несогласованность уровней дохода. Графически коэффициент Джини определяется как соотношение площади между кривой Лоренца и линией полного равенства к площади под линией полного равенства.

Функция roc_auc(), определенная во включаемом файле roc_curves.mqh, вычисляет AUC для задачи двоичной классификации с возможностью ограничить вычисления определенным максимальным значением FPR. В качестве входных данных она принимает истинные метки классов и прогнозируемые вероятности, а также необязательную целевую метку и максимальное значение FPR. Если максимальное значение FPR равно 1.0, вычисляется стандартная AUC. В ином случае она вычисляет ROC-кривую, находит на кривой точку, соответствующую максимальному значению FPR с помощью searchsorted, интерполирует значение TPR в этой точке, а затем вычисляет часть AUC до этого максимального значения FPR с помощью метода трапеций. Наконец, она нормализует эту часть AUC до значения между 0.5 и 1.0, предоставляя таким образом эффективную меру оценки производительности классификатора в указанном диапазоне FPR.

//+------------------------------------------------------------------+
//|  area under the curve                                            |
//+------------------------------------------------------------------+
double roc_auc(vector &true_classes, matrix &predicted_probs,long target_label=1,double max_fpr=1.0)
  {
   vector all_labels = np::unique(true_classes);

   if(all_labels.Size()!=2|| max_fpr<=0.0 || max_fpr>1.0)
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid inputs ");
      return EMPTY_VALUE;
     }

   if(max_fpr == 1.0)
     {
      vector auc = true_classes.ClassificationScore(predicted_probs,CLASSIFICATION_ROC_AUC,AVERAGE_BINARY);
      return auc[0];
     }

   matrix tpr,fpr,threshs;

   if(!true_classes.ReceiverOperatingCharacteristic(predicted_probs,AVERAGE_BINARY,fpr,tpr,threshs))
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid inputs ");
      return EMPTY_VALUE;
     }

   vector xp(1);
   xp[0] = max_fpr;
   vector stop;

   if(!np::searchsorted(fpr.Row(0),xp,true,stop))
     {
      Print(__FUNCTION__, " ", __LINE__, " searchsorted failed ");
      return EMPTY_VALUE;
     }

   vector xpts(2);
   vector ypts(2);

   xpts[0] = fpr[0][long(stop[0])-1];
   xpts[1] = fpr[0][long(stop[0])];
   ypts[0] = tpr[0][long(stop[0])-1];
   ypts[1] = tpr[0][long(stop[0])];

   vector vtpr = tpr.Row(0);
   vtpr = np::sliceVector(vtpr,0,long(stop[0]));
   vector vfpr = fpr.Row(0);
   vfpr = np::sliceVector(vfpr,0,long(stop[0]));

   if(!vtpr.Resize(vtpr.Size()+1) || !vfpr.Resize(vfpr.Size()+1))
     {
      Print(__FUNCTION__, " ", __LINE__, " error  ", GetLastError());
      return EMPTY_VALUE;
     }

   vfpr[vfpr.Size()-1] = max_fpr;

   vector yint = np::interp(xp,xpts,ypts);


   vtpr[vtpr.Size()-1] = yint[0];

   double direction = 1.0;

   vector dx = np::diff(vfpr);

   if(dx[dx.ArgMin()]<0.0)
      direction = -1.0;

   double partial_auc = direction*np::trapezoid(vtpr,vfpr);

   if(partial_auc == EMPTY_VALUE)
     {
      Print(__FUNCTION__, " ", __LINE__, " trapz failed ");
      return EMPTY_VALUE;
     }

   double minarea = 0.5*(max_fpr*max_fpr);
   double maxarea = max_fpr;

   return 0.5*(1+(partial_auc-minarea)/(maxarea-minarea));
  }

Параметр max_fpr упрощает вычисление части площади под ROC-кривой (AUC), тем самым позволяя оценивать эффективность классификатора в заданном диапазоне значений FPR. Такая функциональность особенно значима в тех случаях, когда акцент делается на производительности при более низких пороговых значениях FPR. Кроме того, она оказывается полезной при анализе несбалансированных наборов данных, где на ROC-кривую может непропорционально сильно влиять значительное количество истинно отрицательных значений. Использование этого параметра позволяет целенаправленно оценивать соответствующую области кривой.

Хотя кривые рабочих характеристик приемника (ROC) обеспечивают полезную основу для оценки классификатора, их применение для определения окончательного превосходства классификатора гарантирует тщательное рассмотрение, особенно при учете стоимости некорректной классификации. Хотя AUC предлагает показатель для оценки качества классификатора, сравнительные оценки эффективности требуют более тонкого подхода. Для надлежащего рассмотрения вопросов затрат необходимо вернуться к базовой матрице путаницы.

Традиционные парадигмы классификации часто отдают приоритет достижению максимальной точности, безусловно предполагая одинаковые затраты на все ошибочные классификации. Напротив, чувствительная к затратам классификация учитывает различия в затратах, связанные с различными типами ошибок, стремясь свести к минимуму совокупную стоимость ошибок, а не просто оптимизировать точность. Например, в классификаторе, предназначенном для выявления перспективных инвестиционных акций, стоимость упущенной возможности (ложноотрицательный результат) можно считать менее весомой, чем стоимость ложноположительного результата. Распределение затрат по каждому типу ошибочной классификации дает матрицу затрат. Эта матрица определяет затраты, связанные с различными результатами прогнозирования, с указанием штрафов или потерь, понесенных из-за неверных прогнозов, такие как ложноположительные и ложноотрицательные результаты, а также с потенциальным включением затрат на корректные прогнозы. Ниже представлена гипотетическая матрица путаницы, сопровождаемая соответствующей ей матрицей затрат.

Матрица затрат

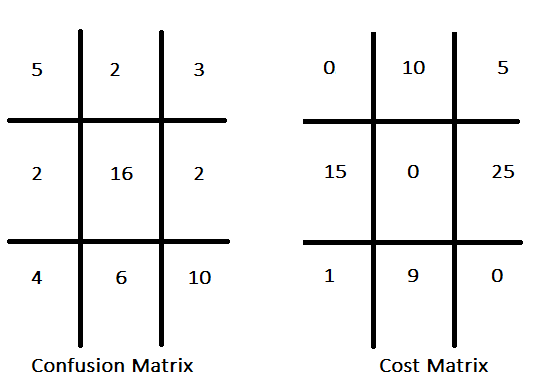
Обычно в матрице затрат по диагонали располагаются нулевые значения, что означает отсутствие затрат, связанных с корректными прогнозами. Это распространенный порядок действий, хотя и не обязательный. Учитывая заданную структуру затрат для всех типов некорректной классификации, содержащуюся в матрице путаницы информацию можно объединить в единый показатель эффективности. Примитивный подход заключается в умножении частоты каждого типа ошибочной классификации на соответствующие ей затраты и последующем суммировании этих произведений. Однако эффективность такой метрики зависит от точности отражения пропорциями классов в наборе данных тех, которые встречаются в реальных приложениях.

Более надежным показателем чувствительной к затратам эффективности является ожидаемая стоимость отдельного образца. Эта метрика выводится посредством нормализации количества выборок матрицы путаницы по соответствующим им суммам строк, давая условные вероятности отнесенных к различным категориям классов при наличии истинных классов. Затем эти вероятности умножаются на соответствующие им затраты из матрицы затрат, и эти произведения суммируются по каждой строке, в результате чего получается ожидаемая стоимость для члена каждого класса. Затем такие специфичные для каждого класса затраты взвешиваются по ожидаемым пропорциям образцов в каждом классе и суммируются, в результате чего получается общая ожидаемая стоимость для каждого образца. Оценка ожидаемых пропорций классов в реальных условиях требует комплексной оценки базового распределения данных в среде развертывания. Методологии этой оценки включают:

Анализ исторических данных, в ходе которого существующие записи изучаются для получения надежных оценок пропорций классов. Например, при медицинской диагностике истории болезни пациентов могут стать пояснением относительно распространенности заболеваний.

Консультации с экспертами в предметной области, чьи специальные знания могут уточнить или подтвердить оценки, полученные другими способами.

Внедрение методов репрезентативной выборки, когда возможен сбор новых данных, что гарантирует точное отражение выборкой реального распределения, особенно в несбалансированных наборах данных. Стратифицированная выборка может дополнительно гарантировать приемлемую репрезентативность всех классов, даже в случаях неравномерного распределения.

Ожидаемые пропорции образцов внутри класса формально эквивалентны априорным вероятностям. В конкретном контексте бинарной классификации пусть
q обозначает априорную вероятность принадлежности образца целевому классу. Далее определим p1 как вероятность ошибки типа I (ложноположительный результат), где c1 представляет собой соответствующие затраты, а p2 — как вероятность ошибки типа II (ложноотрицательный результат), где c2 представляет собой соответствующие затраты. Во многих приложениях q можно определить теоретическими либо эмпирическими методами, а затраты c1 и c2 известны либо точно, либо с достаточно точным приближением. Следовательно, эти три величины можно рассматривать как фиксированные параметры. Вероятности ошибок p1 и p2 определяются порогом классификации. Ожидаемая стоимость выражается следующим уравнением.

Результаты перестановок в этом уравнении.

Переработанная формула затрат

Демонстрация линейной зависимости между p1 и p2 для любой заданной ожидаемой стоимости. При графическом изображении этой линейной зависимости на ROC-кривой ее наклон определяется априорной вероятностью q и соотношением затрат c2/c1. Изменение ожидаемой стоимости порождает группу параллельных линий, при этом расположенные ниже и правее линии обозначают более высокие затраты. Пересечение этой линии с ROC-кривой в двух точках указывает на два пороговых значения, производящих эквивалентные, хоть и не оптимальные, затраты. Линии, полностью расположенные выше и левее ROC-кривой, отображают не достижимую для данной модели производительность. Касательная к ROC-кривой обозначает оптимальные достижимые затраты.

В этом анализе подчеркнуто, что AUC не обязательно обеспечивает окончательную оценку практической эффективности модели классификации. Хотя AUC представляет собой надежный общий показатель качества, польза от него уменьшается, если учитывать эксплуатационные расходы, поскольку он может приводить к ошибочным выводам в сферах применения, чувствительных к стоимости.

Задачи разрешимости с более чем двумя классами

Расширение структуры ROC-кривой на многоклассовую классификацию требует принятия определенных стратегий адаптации. В основном используются два методологических подхода: «Один против остальных» (One-vs-Rest, OvR), известный также как «Один против всех» (One-vs-All, OvA), и «Один против одного» (One-vs-One, OvO). Стратегия OvR преобразует многоклассовую задачу в несколько задач бинарной классификации, рассматривая каждый класс как положительный по отношению к объединенным остальным классам, что приводит к получению n ROC-кривых для n классов. Напротив, метод OvO строит задачи бинарной классификации для всех возможных пар классов, выдавая n(n-1)/2 ROC-кривых.

Для объединения показателей эффективности, полученных на основе таких бинарных классификаций, используются методы усреднения. Микроусреднение вычисляет глобальные значения TPR и FPR, учитывая все экземпляры по всем классам, присваивая таким образом каждому экземпляру одинаковый вес. Макроусреднение, с другой стороны, вычисляет TPR и FPR отдельно для каждого класса, а затем усредняет их, присваивая тем самым равный вес каждому классу. Особенно полезен этот метод, когда особое значение имеет специфичная для класса эффективность. Следовательно, интерпретация многоклассовых ROC-кривых зависит от выбранной стратегии разбиения (OvR или OvO) и метода усреднения (микро или макро), поскольку такие решения оказывают существенное влияние на результирующую оценку эффективности.

Встроенные функции MQL5 для ROC-кривых и AUC

В языке MQL5 расчет кривых рабочих характеристик приемника (ROC-кривых) и площади под кривой (AUC) упрощается благодаря специальным функциональным возможностям. Мобильный

Векторный метод ReceiverOperatingCharacteristic() используется для генерации необходимых значений в целях визуализации ROC-кривых. Этот метод работает на векторе, предоставляющем истинные метки классов. Первый аргумент — матрица вероятностей или порогов решений, структурированная столбцами, соответствующими номерам классов. Второй аргумент — переменная перечисления ENUM_AVERAGE_MODE, определяющая методологию усреднения. Примечательно, что эта функция поддерживает только AVERAGE_NONE, AVERAGE_BINARY и AVERAGE_MICRO. После успешного исполнения частоты ложноположительных (FPR) и истинно положительных (TPR) срабатываний, а также связанные с ними пороговые значения записываются в назначенные матрицы — последние три параметра. Метод возвращает логическое значение, указывающее на успешность исполнения.

Вычисление AUC выполняется с помощью векторного метода ClassificationScore(). Как и метод ROC, он применяется к вектору истинных меток классов и требует наличия матрицы спрогнозированных вероятностей или порогов решений. Второй параметр — переменная перечисления ENUM_CLASSIFICATION_METRIC, которая должна быть установлена на CLASSIFICATION_ROC_AUC для указания на расчет AUC. В отличие от метода ROC, эта функция учитывает все значения ENUM_AVERAGE_MODE. Метод возвращает вектор вычисленных областей, мощность которого зависит режима усреднения и количества классов, присутствующих в наборе данных.

Для иллюстрации влияния разных режимов усреднения был разработан скрипт ROC_Demo.mq5. Этот скрипт использует набор данных Iris и модель логистической регрессии для решения настраиваемых пользователем задач бинарной или многоклассовой классификации. Ниже представлен полный код скрипта.

//+------------------------------------------------------------------+
//|                                                     ROC_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<logistic.mqh>
#include<ErrorDescription.mqh>
#include<Generic/SortedSet.mqh>
//---
enum CLASSIFICATION_TYPE
  {
   BINARY_CLASS = 0,//binary classification problem
   MULITI_CLASS//multiclass classification problem
  };
//--- input parameters
input double   Train_Test_Split = 0.5;
input int      Random_Seed = 125;
input CLASSIFICATION_TYPE classification_problem = BINARY_CLASS;
input ENUM_AVERAGE_MODE av_mode = AVERAGE_BINARY;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndSeed(Random_Seed,Random_Seed+Random_Seed,rngstate.GetInnerObj());
//---
   matrix data = np::readcsv("iris.csv");
   data = np::sliceMatrixCols(data,1);
//---
   if(classification_problem == BINARY_CLASS)
      data = np::sliceMatrixRows(data,0,100);
//---
   ulong rindices[],trainset[],testset[];
   np::arange(rindices,int(data.Rows()));
//---
//---
   if(!np::shuffleArray(rindices,GetPointer(rngstate)) || ArrayCopy(trainset,rindices,0,0,int(ceil(Train_Test_Split*rindices.Size())))<0 || !ArraySort(trainset))
     {
      Print(__LINE__, "  error ", ErrorDescription(GetLastError()));
      return;
     }
//---
   CSortedSet<ulong> test_set(rindices);
//---
   test_set.ExceptWith(trainset);
//---
   test_set.CopyTo(testset);
//---
   matrix testdata = np::selectMatrixRows(data,testset);
   matrix test_predictors = np::sliceMatrixCols(testdata,0,4);
   vector test_targets = testdata.Col(4);
   matrix traindata = np::selectMatrixRows(data,trainset);
   matrix train_preditors = np::sliceMatrixCols(traindata,0,4);
   vector train_targets = traindata.Col(4);
//---
   logistic::Clogit logit;
//--
   if(!logit.fit(train_preditors,train_targets))
     {
      Print(" error training logistic model ");
      return;
     }
//---
   matrix y_probas = logit.probas(test_predictors);
   vector y_preds = logit.predict(test_predictors);
//---
   vector auc = test_targets.ClassificationScore(y_probas,CLASSIFICATION_ROC_AUC,av_mode);
//---
   if(auc.Size()>0)
      Print(" AUC ", auc);
   else
      Print(" AUC error ", ErrorDescription(GetLastError()));
//---
   matrix fpr,tpr,threshs;
   if(!test_targets.ReceiverOperatingCharacteristic(y_probas,av_mode,fpr,tpr,threshs))
     {
      Print(" ROC error ", ErrorDescription(GetLastError()));
      return;
     }
//---
   string legend;
   for(ulong i = 0; i<auc.Size(); i++)
     {
      string temp = (i!=int(auc.Size()-1))?StringFormat("%.3lf,",auc[i]):StringFormat("%.3lf",auc[i]);
      StringAdd(legend,temp);
     }

   CGraphic* roc = np::plotMatrices(fpr, tpr,"ROC",false,"FPR","TPR",legend,true,0,0,10,10,600,500);
   if(CheckPointer(roc)!=POINTER_INVALID)
     {
      Sleep(7000);
      roc.Destroy();
      delete roc;
      ChartRedraw();
     }
  }
//+------------------------------------------------------------------+

Первоначально исследуется задача бинарной классификации с режимом усреднения, установленным на AVERAGE_BINARY. В этом режиме расчет ROC-кривой и AUC происходит, исходя из предположения, что целевой класс обозначен как 1, что соответствует фундаментальной парадигме «целевой — нецелевой», присущей построению ROC-кривых. Результат выполнения скрипта с такими настройками показывает, что вектор значений AUC содержит один элемент. Более того, FPR, TPR и пороговые матрицы состоят каждый из одной строки.

Вывод демострационного скрипта ROC. Бинарная классификация

MK      0       12:45:28.930    ROC_Demo (Crash 1000 Index,M5)   AUC [1]

Для изучения ROC-кривой и связанной с ней AUC по целевым классам, за исключением метки 1, режим усреднения следует установить на AVERAGE_NONE. В этом режиме функции ReceiverOperatingCharacteristic() и ClassificationScore() оценивают каждый класс в отдельности как целевой, выдавая соответствующие результаты. Выполнение скрипта с AVERAGE_NONE и задачей бинарной классификации производит следующий результат. В этом случае ROC-график отображает две кривые, представляющие собой графики соответствующих строк в матрицах FPR и TPR. Также рассчитываются два значения AUC.

Демонстрационная бинарная классификация ROC - без усреднения

CK      0       16:42:43.249    ROC_Demo (Crash 1000 Index,M5)   AUC [1,1]

Результаты представлены в соответствии с порядком маркировки классов. Например, в задаче бинарной классификации, изображенной в вышеупомянутом скрипте, с метками 0 и 1 первые строки TPR, FPR и пороговых матриц представляют собой значения ROC-кривых, когда метка 0 считается целевым классом, а вторые строки воспринимают в качестве цели метку 1. Такой же условный порядок применяется к значениям AUC. Уместно отметить, что такой формат результата одинаков для всех статистических данных ROC, рассчитанных на основе многоклассовых наборов данных. В случаях бинарной классификации использование каких-либо параметров усреднения, кроме AVERAGE_NONE и AVERAGE_BINARY, подразумевает применение вычислительных методов, соответствующих обработке многоклассовых наборов данных. Напротив, при многоклассовой классификации AVERAGE_BINARY вызывает ошибку. Однако AVERAGE_MICRO, AVERAGE_MACRO и AVERAGE_WEIGHTED выдают единое, совокупное значение AUC.

Демонстрационный мультикласс ROC - без усреднения

LL      0       17:27:13.673    ROC_Demo (Crash 1000 Index,M5)   AUC [1,0.9965694682675815,0.9969135802469137]

Режим усреднения AVERAGE_MICRO глобально вычисляет ROC-кривые и AUC, обрабатывая каждый элемент матрицы истинного класса, полученной прямым кодированием, как отдельную метку. Этот подход преобразует многоклассовую задачу в задачу бинарной классификации посредством изначального прямого кодирования меток истинных классов, создавая матрицу, столбцы которых соответствуют количеству классов. Эта матрица, как и прогнозируемые пороги решений или матрица вероятностей, сводится затем к одностолбцовой структуре. Последующие расчеты ROC-кривых и AUC выполняются на таких одностолбцовых контейнерах. Эта методология позволяет получить комплексные показатели эффективности по всем классам, присваивая каждому экземпляру одинаковый вес. Она особенно выгодна в сценариях со значительным дисбалансом классов, смягчая перекос в сторону класса большинства. Эмпирические результаты из демонстрационного скрипта иллюстрируют такое поведение.

Демонстрационный мультикласс ROC - микроусреднение

RG      0       17:26:51.955    ROC_Demo (Crash 1000 Index,M5)   AUC [0.9984000000000001]

Режим усреднения AVERAGE_MACRO применяет отдельную стратегию для устранения дисбаланса классов. Оценка каждого класса осуществляется отдельно, при этом AUC рассчитывается на основе вероятностей соответствующего класса. Затем окончательное значение AUC выводится как среднее арифметическое этих отдельных значений AUC. Примечательно: в документации MQL5 указано, что AVERAGE_MACRO не поддерживается методом ReceiverOperatingCharacteristic(). Метод ClassificationScore() реализует принцип OvR для расчета AUC в многоклассовых наборах данных. Выполнение скрипта с AVERAGE_MACRO подтверждает успешный расчет AUC, тогда как сгенерировать ROC-кривых, как и ожидалось, не получается.

ER      0       17:26:09.341    ROC_Demo (Crash 1000 Index,M5)   AUC [0.997827682838166]
NF      0       17:26:09.341    ROC_Demo (Crash 1000 Index,M5)   ROC error Wrong parameter when calling the system function

Режим усреднения AVERAGE_WEIGHTED работает примерно так же, как AVERAGE_MACRO, за исключением этапа окончательного агрегирования. Вместо простого среднего арифметического вычисляется средневзвешенное значение, когда веса определяются распределением классов с метками истинных классов. Такой подход выдает окончательное значение AUC, которое учитывает доминирующие классы в наборе данных. Как и AVERAGE_MACRO, функция ReceiverOperatingCharacteristic() не поддерживает AVERAGE_WEIGHTED. Вывод скрипта иллюстрирует такое поведение.

IN      0       17:26:28.465    ROC_Demo (Crash 1000 Index,M5)   AUC [0.9978825995807129]
HO      0       17:26:28.465    ROC_Demo (Crash 1000 Index,M5)   ROC error Wrong parameter when calling the system function

Заключение

ROC-кривые — эффективный инструмент для визуализации и оценки классификаторов. Они обеспечивают более полную оценку эффективности классификации по сравнению с такими скалярными показателями, как точность, частота ошибок или цена ошибки. Разделяя производительность классификатора от перекоса классов и цены ошибки, они предлагают преимущества по сравнению с альтернативными методами оценки, включая кривые точности и кривые отклика модели. Однако, как с любым показателем оценки, обоснованное применение ROC-графиков требует глубокого понимания их внутренних характеристик и ограничений. Предполагается, что эта статья посодействует расширению общих знаний о ROC-кривых и будет способствовать выбору усовершенствованных методов оценки внутри сообщества.

Название файла	Описание файла
MQL5/Scripts/ROC_Demo.mq5	Используемый скрипт демонстрирует встроенные функции MQL5, связанные с ROC-кривыми.
MQL5/Scripts/ ROC_curves_table_demo.mq5	Скрипт, демонстрирующий создание различных показателей эффективности на основе ROC.
MQL5/Include/logisitc.mqh	Заголовочный файл, содержащий определение класса Clogit, реализующий логистическую регрессию.
MQL5/Include/roc_curves.mqh	Заголовок пользовательских функций, реализующий различные утилиты для оценки эффективности бинарных классификаций.
MQL5/Include/np.mqh	Заголовочный файл различных векторных и матричных служебных функций.
MQL5/Files/iris.csv	CSV-файл набора данных iris.

Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/17390

Прикрепленные файлы |

Загрузить ZIP

iris.csv (3.29 KB)

np.mqh (90.9 KB)

logistic.mqh (16.16 KB)

roc_curves.mqh (8.92 KB)

ROC_curves_table_demo.mq5 (2.81 KB)

ROC_Demo.mq5 (3.56 KB)

Mql5.zip (22.86 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Автоматизация торговых стратегий на MQL5 (Часть 6): Поиск ордер-блоков для торговли по концепции Smart Money

В настоящей статье мы автоматизируем обнаружение ордер-блоков на MQL5, используя чистый анализ движения цены. Мы определяем ордер-блоки , реализуем их обнаружение и интегрируем автоматическое исполнение сделок. Наконец, для оценки эффективности стратегии, мы проведём её бэк-тестирование.

Экстремальная оптимизация — Extremal Optimization (EO)

В данной статье рассматривается алгоритм Extremal Optimization (EO) — метод оптимизации, вдохновленный моделью самоорганизованной критичности Бака-Снеппена, где эволюция происходит через устранение наихудших компонентов системы. Модифицированная популяционная версия алгоритма демонстрирует отход от теоретических принципов в пользу практической эффективности, что приводит к созданию мощных вычислительных инструментов.

Пользовательские символы MQL5: Создаем символ 3D-баров

В данной статье представлено детальное руководство по созданию инновационного индикатора 3DBarCustomSymbol.mq5, который генерирует пользовательские символы в MetaTrader 5, объединяющие цену, время, объем и волатильность в единое трехмерное представление. Рассматриваются математические основы, архитектура системы, практические аспекты реализации и применения в торговых стратегиях.

Нейросети в трейдинге: Сквозная многомерная модель прогнозирования временных рядов (GinAR)

Предлагаем познакомиться с инновационным подходом к прогнозированию временных рядов с пропущенными данными на базе фреймворка GinAR. В статье показана реализация ключевых компонентов на OpenCL, что обеспечивает высокую производительность. В следующей публикации мы подробно рассмотрим интеграцию этих решений в MQL5. Это позволит понять, как применять метод на практике в трейдинге.