Нейросети в трейдинге: Сквозная многомерная модель прогнозирования временных рядов (GinAR)

Введение

Прогнозирование многомерных временных рядов (MTSF) стало неотъемлемой частью анализа в различных отраслях — от транспорта и экологии до, конечно же, финансовых рынков. В нашей сфере это означает умение прогнозировать поведение нескольких взаимосвязанных финансовых инструментов (акций, индексов, валют) на основе их исторической динамики. Такие модели позволяют принимать более взвешенные инвестиционные решения, управлять рисками и выявлять скрытые взаимосвязи между активами.

Формально многомерный временной ряд (MTS) можно представить как пространственно-временной граф, где каждая переменная (будь то курс валюты, объём торгов или ставка доходности) наблюдается во времени и соотносится с другими переменными через скрытые зависимости. Эти зависимости делятся на два ключевых типа: временные (причинно-следственные связи между событиями) и пространственные (взаимовлияние между активами или секторами рынка).

Для эффективного прогнозирования MTS жизненно важно уметь выявлять и использовать эти пространственно-временные зависимости. Особенно это критично в условиях высокой волатильности и рыночных шоков, когда традиционные модели просто не успевают адаптироваться. На помощь приходят графовые нейросети. Эти модели сочетают преимущества графовых сверточных сетей и рекуррентных моделей, позволяя строить более точные прогнозы на основе сложных зависимостей между переменными.

Но на практике всё не так гладко. Финансовые данные часто неполные. Часть метрик недоступна, либо наблюдается только часть временного интервала. Пропуски могут быть вызваны чем угодно: сбоями в поставке данных, изменениями в политике расчёта показателей, техническими ошибками брокеров. И если отсутствуют данные по ключевым активам, то точность прогноза резко падает. Графовые модели, как правило, в таких случаях теряют способность адекватно оценивать зависимости, что ведёт к лавинообразному накоплению ошибок и снижению качества прогнозов.

Некоторые попытки обойти эту проблему основаны на простом исключении недоступных переменных. Но это недальновидно — отсутствие данных по важному активу может разрушить всю логическую структуру модели и привести к ошибочным выводам. Более изощрённые подходы используют методы восстановления пропусков (импутации), комбинируя временной контекст и фиксированные пространственные связи (например, корреляции или сетевые структуры между активами). Однако такие методы часто дают сбои при высоком проценте пропущенных данных или в условиях, когда нет надёжных связей между наблюдаемыми и пропущенными переменными. И снова — ошибки накапливаются, прогноз становится недостоверным.

Что же делать? Решение лежит в построении моделей, способных использовать информацию о доступных переменных для восстановления недостающих данных прямо в процессе прогнозирования, не разделяя обучение на этапы «Восстановление → Прогноз». Именно так работает новый фреймворк Graph Interpolation Attention Recursive Network (GinAR), представленный в работе "GinAR: An End-To-End Multivariate Time Series Forecasting Model Suitable for Variable Missing". Это новая end-to-end архитектура, ориентированная на работу с пропущенными переменными в многомерных временных рядах.

В основе GinAR лежит простая рекурсивная сеть (SRU), в которую встроены два ключевых компонента:

1. Interpolation Attention (IA) — механизм, который восстанавливает недостающие переменные с помощью применения алгоритмов внимания к доступным данным. Это позволяет избежать ошибок, вызванных попытками копать в нулях и выбросах.
2. Adaptive Graph Convolution (AGCN) — адаптивная графовая свёртка, которая пересобирает структуру взаимосвязей между переменными уже после восстановления, позволяя учитывать как прямые, так и косвенные корреляции между активами.

Таким образом, GinAR одновременно прогнозирует и корректирует модель зависимостей, не давая ошибкам размножаться. И что особенно важно — она работает даже в экстремальных условиях. В тестах на реальных данных, проведенных авторами фреймворка, модель сохраняла высокую точность, даже когда до 90% переменных были недоступны. Представьте себе ситуацию, когда у вас есть только данные по нескольким активам из портфеля, а остальные молчат — GinAR всё равно делает прогноз по всей системе.

Вкратце, ключевые достижения GinAR:

• Это первая модель, ориентированная на MTSF с пропущенными переменными, которая работает без предварительного этапа восстановления.
• Новая архитектура (IA + AGCN) заменяет полносвязанные слои SRU, минимизируя искажения зависимостей.
• Согласно результатам экспериментов, представленным в авторской работе, GinAR обошла 11 других моделей на пяти различных наборах данных, показывая уверенные результаты даже при критически высоком уровне пропусков.

Для финансовых рынков это означает только одно: даже при частичном отсутствии данных можно прогнозировать системно и точно. А значит, адаптивные стратегии, стресс-тесты и управление рисками можно реализовать надёжно, не полагаясь на идеальные исходные данные. Ведь в реальности рынок никогда не бывает идеальным — и именно для использования в таких условиях GinAR был создан.

Алгоритм GinAR

Архитектура фреймворка GinAR строится по классической схеме Энкодер → Декодер. В качестве Энкодера используется стек слоёв GinAR, а Декодер реализован на базе многослойного перцептрона (MLP). Ключевым элементом системы является ячейка GinAR — модуль, построенный по принципу рекурсивного моделирования. При подаче на вход неполных данных, то есть временных рядов с пропущенными переменными, модель способна прогнозировать будущие значения всех переменных одновременно — даже тех, для которых отсутствует полная история.

Проектируя внутреннюю логику GinAR, авторы фреймворка предложили заменить все полносвязные слои (fully connected) в классической рекурсивной структуре SRU на два специализированных компонента — IA (Interpolation Attention) и AGCN (Adaptive Graph Convolution Network).

Первый компонент восстанавливает недостающие переменные, используя информацию от доступных соседей. В условиях финансовых рынков это особенно важно: если отсутствуют данные по ключевым активам, даже частично, модель может резко потерять точность. Механизм IA позволяет избежать этого, восстанавливая осмысленные представления недостающих временных рядов на основе имеющихся и минимизируя влияние шума.

Второй компонент — AGCN — отказывается от фиксированных графов зависимостей (например, заранее заданных связей между активами, индексами, секторами) и обучает адаптивную структуру графа прямо в процессе обучения. Это даёт возможность гибко захватывать пространственные связи между переменными, даже если они изменчивы или неочевидны.

ЭнкодерGinAR реализован через рекурсивную схему, в которой на каждом временном шаге на вход подаются признаки текущего момента и внутреннее состояние из предыдущего шага. Ячейка GinAR обрабатывает их, обновляет состояние и формирует скрытое представление текущего временного шага. Такой подход позволяет одновременно восстанавливать пропущенные данные, реконструировать граф зависимостей и извлекать динамические закономерности — всё в одном модуле. Благодаря остаточным соединениям (skip connections), модель может быть глубокой, не теряя стабильности обучения. Это особенно важно в задачах предсказания сложных рыночных сигналов, где важны как краткосрочные колебания, так и долгосрочные тренды.

Следующим этапом является прогнозирование. Для этого необходимо правильно агрегировать полученные скрытые представления. С одной стороны, каждое финальное скрытое состояние GinAR-ячейки содержит полную информацию о временной структуре исходных данных — это заслуга рекурсивного характера модели. С другой стороны, благодаря многослойности и наличию skip-соединений, каждое скрытое представление отражает разные уровни абстракции: от микродвижений до глобальных корреляций. Поэтому признаки всех слоёв объединяются в один тензор и подаются на вход Декодеру. В роли декодера выступает многослойный перцептрон, обученный по стратегии Direct Multi-Step Forecasting (DMSF) — прямого многопериодного прогноза. Такой подход позволяет сразу прогнозировать весь целевой горизонт (например, движение котировок на ближайшие 5–10 баров), не прибегая к пошаговому итеративному прогнозированию, которое склонно к накоплению ошибок.

В результате GinAR формирует устойчивую архитектуру, способную эффективно справляться с задачами прогнозирования в условиях пропущенных данных, динамических взаимосвязей и высокой корреляции между временными рядами. Модель объединяет в себе восстановление данных, обучение графа и прогноз — всё в одном end-to-end решении, способном адаптироваться к реальным условиям рыночной неопределённости.

Механизм Interpolation Attention (IA) предназначен для восстановления представлений переменных с полностью отсутствующими историческими данными. Для каждой пропущенной переменной требуется определить множество нормальных переменных, на основе которых будет выполняться восстановление, а также соответствующие веса влияния этих переменных. Этот процесс состоит из двух ключевых этапов: сначала формируются соответствия между пропущенными и доступными переменными, а затем применяется механизм внимания для агрегирования информации и восстановления.

На первом этапе строится матрица соответствий между переменными. Инициализируется диагональная матрица IN ∈ Rᴺ*ᴺ, а также два матричных эмбеддинга переменных: EIA1 ∈ Rᴺ*ᵈ и EIA2 ∈ Rᵈ*ᴺ. Эти эмбеддинги обучаются совместно с моделью. Корреляционная матрица между переменными вычисляется по формуле:

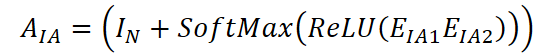
Элемент (i, j) матрицы AIA ∈ Rᴺ*ᴺ отражает степень связи между переменными i и j. Если значение положительно, это указывает на то, что нормальная переменная j может быть использована для восстановления пропущенной переменной i. Таким образом, для каждой пропущенной переменной i можно выделить множество связанных нормальных переменных N(i) ⊆ {1,…,N}.

После определения соответствий, выполняется восстановление представлений пропущенных переменных с помощью механизмов внимания. Для этого вычисляются коэффициенты внимания aij, отражающие важность нормальной переменной j при восстановлении переменной i:

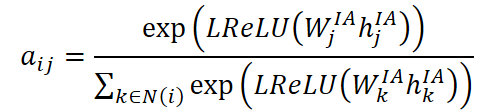
где hᴵᴬj — текущее скрытое представление переменной j, а Wᴵᴬj — обучаемая матрица весов. Активация выполняется через функцию LReLU, что позволяет избежать обнуления градиентов при слабых активациях.

Полученные коэффициенты используются для агрегации информации от нормальных переменных. Представление пропущенной переменной i восстанавливается по формуле:

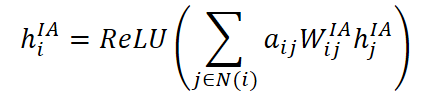
где Wᴵᴬij — индивидуальная обучаемая матрица весов для каждой пары переменных i и j, а итоговая агрегация нормализуется с помощью ReLU для повышения устойчивости к выбросам.

Этот процесс повторяется для всех пропущенных переменных до тех пор, пока не будут восстановлены представления для всех M недостающих компонентов. После этого получается новый тензор XᴵᴬM ∈ Rᴺ*ᴴ*ᶜ′, в котором все переменные (в том числе ранее недостающие) имеют полные скрытые представления. Следует отметить, что на практике для повышения эффективности восстановления шаги 2 и 3 реализуются с помощью матричного умножения и параллельных вычислений.

Таким образом, механизм Interpolation Attention позволяет гибко восстанавливать данные в многомерных временных рядах с отсутствующими переменными, без необходимости жёстко фиксировать структуру связей между переменными заранее. Это особенно важно для задач в области финансового прогнозирования, где структуры корреляций между активами могут быть изменчивыми, а исторические данные — неполными или шумными.

В задачах многомерного прогнозирования временных рядов часто используют заранее заданную структуру графа, чтобы отразить пространственные зависимости между переменными. Для этого определяется матрица смежности A, которая позволяет модели захватывать базовые взаимосвязи. Однако, в условиях значительного объёма пропущенных данных, особенно при отсутствии полной информации по ряду переменных, такая предопределённая структура графа может быть недостаточной. Чтобы преодолеть это ограничение, авторами фреймворка вводится адаптивная графовая свёртка, объединяющая заранее заданную структуру и граф, формируемый на основе данных.

В качестве основы предопределённой структуры графа используется либо информация о расстояниях (например, для транспортных сетей), либо коэффициент корреляции Пирсона между переменными, если данные не содержат информации о топологии. Матрица смежности для графовой свёртки в этом случае вычисляется следующим образом:

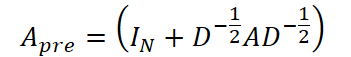
где IN ∈ Rᴺ*ᴺ — единичная диагональная матрица, D — матрица степеней вершин графа, а A — исходная матрица смежности. Такая нормализация позволяет стабилизировать масштаб весов при обучении.

Однако, когда часть переменных отсутствует, или их связи неизвестны, необходимо динамически выявлять пространственные зависимости. Для этого строится адаптивный граф, обучаемый на основе данных. Начинается этот процесс с инициализации единичной диагональной матрицы IN ∈ Rᴺ*ᴺ и случайной инициализации эмбеддингов переменных EA ∈ Rᴺ*ᵈ. Эти эмбеддинги обновляются в процессе обучения модели.

После восстановления переменных с помощью механизма IA, получаем тензор скрытых представлений XᴵᴬM ∈ Rᴺ*ᴴ*ᶜ′. Далее вычисляется обновлённое представление переменных En ∈ Rᴺ*ᵈ, объединяющее как эмбеддинги, так и временные представления:

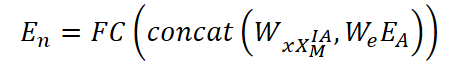
где Wx и We — обучаемые матрицы весов для временных признаков и эмбеддингов соответственно, а concat(⋅) — операция конкатенации вдоль последней оси. Это представление используется для построения адаптивной матрицы смежности:

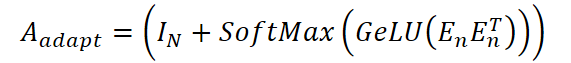
Финальным шагом является агрегация информации с обоих графов через адаптивную графовую свёртку, комбинирующую два канала: один использует предопределённую структуру, другой — адаптивную. Итоговое представление переменных рассчитывается по формуле:

Такая конструкция обеспечивает объединение статической и динамической пространственной информации, что особенно важно при прогнозировании многомерных временных рядов с частично отсутствующими переменными.

Благодаря комбинированию двух графов, модель получает устойчивую и адаптивную структуру, позволяющую точнее выявлять зависимости между переменными и, как следствие, улучшать точность краткосрочного и среднесрочного прогнозирования.

Основная идея архитектуры GinAR заключается в интеграции механизма интерполяционного внимания (IA) и адаптивной графовой свёртки (AGCN) в простую рекурсивную модель. Такая комбинация позволяет не только восстанавливать пропущенные переменные, но и эффективно учитывать пространственно-временные зависимости.

Подробно рассмотрим устройство ячейки GinAR и пошаговый процесс прогнозирования данных.

На уровне одного временного шага ячейка GinAR представляет собой базовый вычислительный блок. Она использует IA для восстановления недостающих исходных значений и AGCN для обработки пространственных связей между переменными. На вход поступает тензор xT, который сначала преобразуется с помощью механизма интерполяционного внимания:

Далее рассчитываются управляющие ворота забывания fT и сброса rT через агрегацию информации из предопределённого графа Apre и адаптивного графа Aadapt:

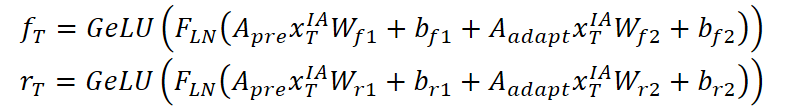
Новый статус cT формируется как комбинация текущего преобразованного входа и предыдущего состояния cT-1, взвешенных по воротам забывания:

Наконец, скрытое состояние hT вычисляется через нелинейное смешивание обновлённого состояния ячейки и входа:

Таким образом, каждая ячейка GinAR выполняет полный цикл обновления внутренних состояний, включая восстановление данных и агрегацию пространственной информации.

На глобальном уровне Энкодер GinAR состоит из нескольких слоёв GinAR. Каждый слой включает H последовательно соединённых ячеек. Исходные входные данные X∈ Rᴺ*ᴴ*ᶜ предварительно нормализуются и маскируются, формируя тензор XM ∈ Rᴺ*ᴴ*ᶜ, где значения M переменных обнуляются.

Далее XM передаётся на вход первого слоя GinAR, в котором каждая ячейка отвечает за обработку одного временного шага. Процесс начинается с инициализации состояния c₀, после чего x₁ и c₀ передаются в первую ячейку, формируя h¹₁ и c₁. Эти значения далее переходят в следующую ячейку вместе с x₂ и так далее. В результате получается последовательность скрытых состояний первого слоя h¹ = [h¹₁, h¹₂, …, h¹H].

Этот тензор становится входом для следующего слоя. Процесс повторяется до тех пор, пока не будут пройдены все n слоёв. Затем, из каждого слоя извлекается последнее скрытое состояние hHⁱ, и они объединяются в итоговый вектор halln.

Итоговое представление halln поступает в декодер на основе многослойного перцептрона (MLP), который генерирует прогнозные значения:

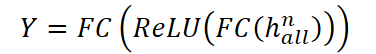
Таким образом, GinAR реализует полную end-to-end обработку временных рядов с пропущенными значениями, объединяя реконструкцию данных и моделирование пространственно-временных зависимостей в едином рекурсивно-свёрточном фреймворке.

Авторская визуализация фреймворка GinAR представлена ниже.

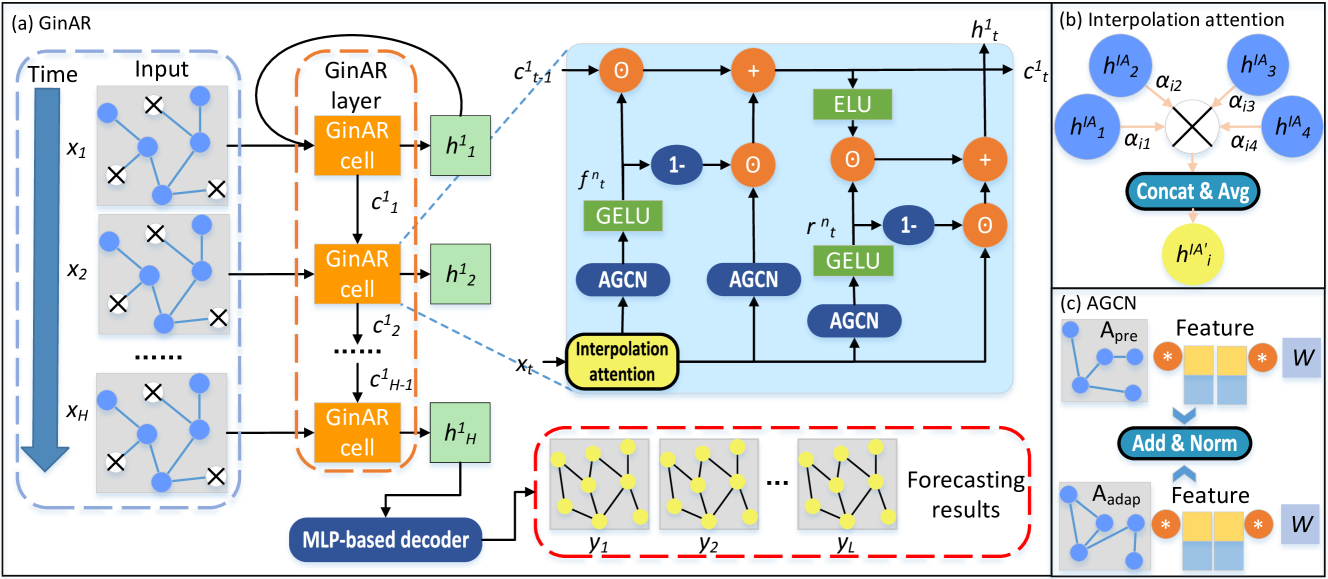
Реализация средствами MQL5

После рассмотрения теоретических аспектов фреймворка GinAR, мы переходим к практической части, где продемонстрируем один из вариантов реализации описанных подходов, предложенных авторами фреймворка, средствами MQL5.

Однако прежде, чем приступить к построению основного алгоритма, необходимо провести небольшую подготовительную работу. Как видно из вышеизложенного описания GinAR, в оригинальном алгоритме многократно применяется нормализация данных с использованием функции SoftMax. В связи с этим, мы приняли решение реализовать её как отдельную функцию на стороне OpenCL-программы, обеспечив тем самым гибкость и высокую производительность при работе с многомерными данными.

Подготовительная работа

Для лучшей организации мы разбили реализацию алгоритма на отдельные функциональные блоки. Начнем с первого: поиск максимального значения среди потоков рабочей группы. Эту задачу выполняет функция LocalMax.

Функция LocalMax принимает два параметра: значение, рассчитанное в текущем потоке, и номер измерения в пространстве задач (loc), по которому потоки объединяются в рабочие группы.

#define BarrierLoc      barrier(CLK_LOCAL_MEM_FENCE)
float LocalMax(const float value, const int loc)
  {
   const size_t id = get_local_id(loc);
   const size_t total = get_local_size(loc);
//---
   __local float Temp[LOCAL_ARRAY_SIZE];
   const uint ls = min((uint)total, (uint)LOCAL_ARRAY_SIZE); 

На первом этапе определяются идентификатор потока в локальной группе и общий размер рабочей группы. Далее создается массив Temp, размещённый в локальной памяти устройства, который будет использоваться для обмена промежуточными значениями между потоками одной рабочей группы.

Затем начинается перебор всех подгрупп, формируемых внутри рабочей группы, с целью найти локальные максимумы. Значения записываются в элементы массива Temp.

//--- Look Max
   for(int d = 0; d < total; d += ls)
     {
      if(id >= d && id < (d + ls) &&
         (d == 0 || Temp[id - d] < value))
         Temp[id - d] = IsNaNOrInf(value, MIN_VALUE);
      BarrierLoc;
     }

После этого запускается итеративный процесс редукции (схлопывания) массива Temp до одного значения — максимального среди всех элементов.

   int count = ls;
   do
     {
      count = (count + 1) / 2;
      if(id < count && (id + count) < ls && Temp[id] < Temp[id + count])
         Temp[id] = Temp[id + count];
      BarrierLoc;
     }
   while(count > 1);
//---
   return IsNaNOrInf(Temp[0], MIN_VALUE);
  }

Результат выполнения операций возвращаем вызывающей программе.

Аналогично предыдущей функции LocalMax, создаём ещё один базовый строительный блок — функцию суммирования элементов в пределах локальной рабочей группы. Эту задачу выполняет функция LocalSum, построенная по тому же принципу, что и LocalMax, но с операцией сложения вместо поиска максимума.

float LocalSum(const float value, const int loc)
  {
   const size_t id = get_local_id(loc);
   const size_t total = get_local_size(loc);
//---
   __local float Temp[LOCAL_ARRAY_SIZE];
   const uint ls = min((uint)total, (uint)LOCAL_ARRAY_SIZE);

На начальном этапе, как и прежде, определяются идентификатор потока и размер рабочей группы. Также создаётся локальный массив Temp, где будут храниться промежуточные суммы.

Далее — перебор всех потоков локальной группы с накоплением промежуточных значений. Обратите внимание на использование условия d == 0, которое позволяет корректно инициализировать массив Temp на первой итерации.

//--- Sum
   float result = IsNaNOrInf(value, 0);
   for(int d = 0; d < total; d += ls)
     {
      if(id >= d && id < (d + ls))
         Temp[id - d] = (d == 0 ? result : Temp[id - d] + result);
      BarrierLoc;
     }

После этого, реализуется знакомая нам редукция с двукратным делением числа элементов — здесь вместо сравнения происходит простое суммирование элементов массива Temp.

   int count = ls;
   do
     {
      count = (count + 1) / 2;
      if(id < count && (id + count) < ls)
         Temp[id] += Temp[id + count];
      BarrierLoc;
     }
   while(count > 1);
   result = IsNaNOrInf(Temp[0], 0);
//---
   return result;
  }

Финальное значение (сумма всех элементов в рабочей группе) возвращается вызывающей программе.

На завершающем этапе подготовительной работы мы объединим ранее реализованные вспомогательные функции LocalMax и LocalSum в единый алгоритм функции LocalSoftMax, которая выполняет численно устойчивую нормализацию значений внутри рабочей группы.

float LocalSoftMax(const float value, const int loc)
  {
//--- Look Max
   const float max = LocalMax(value, loc);
   BarrierLoc;

Внутри функции LocalSoftMax сначала вызывается LocalMax — она находит максимальное значение среди всех потоков рабочей группы. Это необходимо для стабилизации вычислений: вычитание максимума из каждого значения позволяет избежать переполнений и повысить числовую устойчивость экспоненциальных операций.

После этого, уже с учётом смещения, вычисляется экспонента от каждого значения. Результат этой операции временно сохраняется в переменную result, после чего мы вызываем функцию LocalSum для подсчёта общей суммы экспонент в пределах группы.

//--- SoftMax
   float result = IsNaNOrInf(exp(value - max), 0);
   const float sum = LocalSum(result, loc);
   result = IsNaNOrInf(result / (sum == 0 ? 1 : sum), 0);
//---
   return result;
  }

Далее осуществляется нормализация: значение result делится на сумму всех экспонент. При этом дополнительно предусмотрена защита от деления на ноль — если сумма равна нулю, в знаменателе используется единица. Заключительным шагом возвращаем нормализованное значение.

Такая структура позволяет использовать SoftMax как гибкий строительный блок для дальнейших OpenCL-ядер. Это делает код чище, упрощает отладку и улучшает читаемость всей архитектуры, особенно в контексте графовых моделей и механизмов внимания, применяемых в реализации GinAR средствами MQL5.

Однако, для обучения модели по-прежнему недостаточно только прямого прохода через SoftMax. Чтобы корректно обновлять веса в процессе обратного распространения ошибки, необходимо реализовать соответствующую функцию распределения градиента. Такая функция позволяет модели учитывать, как изменение входного значения повлияет на итоговую ошибку.

Данный функционал мы реализуем в функции LocalSoftMaxGrad, которая определит градиент функции SoftMax по отношению к входному значению. Входными параметрами являются: значение value, соответствующее выходу из SoftMax; градиент grad, переданный с более позднего слоя сети; индексное значение измерения пространства задач loc, по которому формируются рабочие группы.

float LocalSoftMaxGrad(const float value, const float grad, const int loc)
  {
   const size_t id = get_local_id(loc);
   const size_t total = get_local_size(loc);
//---
   __local float Temp[LOCAL_ARRAY_SIZE];
   const uint ls = min((uint)total, (uint)LOCAL_ARRAY_SIZE);

В начале функции определяем номер текущего потока и общее количество потоков в локальной группе. Создаём локальный массив Temp для хранения промежуточных значений, аналогично тому, как это делалось в LocalMax и LocalSum. Переменная val представляет собой защищённое от ошибок значение входа.

   float result = 0;
   float val = IsNaNOrInf(value, 0);
   for(uint d = 0; d < total; d += ls)
     {
      if(id >= d && id < (d + ls))
         Temp[id - d] = IsNaNOrInf(val * grad, 0);
      BarrierLoc;
      for(uint l = 0; l < min(ls, (uint)(total - d)); l++)
         result += Temp[l] * ((float)((d + l) == id) - val);
      BarrierLoc;
     }
//---
   return result;
  }

Далее запускаем итерацию по подгруппам в пределах всей рабочей группы. В каждом блоке мы заполняем временный буфер значениями произведения val * grad и, используя классическое выражение для производной SoftMax, накапливаем результат в переменной result. Само выражение использует логическую проверку (d + l) == id, которая обеспечивает корректную обработку диагональных и недиагональных элементов Якобиана.

Результатом работы функции является итоговое значение градиента, соответствующее данному элементу входа. Этот результат возвращается вызывающему ядру, обеспечивая корректную реализацию обратного прохода в архитектуре модели.

Таким образом, эта функция завершает реализацию полного цикла обработки SoftMax в рамках OpenCL-модуля — от прямого вычисления до корректного обратного распространения градиента.

Interpolation Attention

После завершения подготовительной работы, связанной с реализацией базовых операций, таких как SoftMax и распределения его градиента, мы переходим к построению механизма Interpolation Attention, который играет ключевую роль в архитектуре GinAR. На первом этапе наша цель — реализовать прямой проход этого алгоритма средствами OpenCL, обеспечив эффективную параллельную обработку на стороне графического ускорителя.

В качестве входных данных ядро InterpositionAttention принимает несколько массивов:

• матрицу входных признаков matrix_in,
• обучаемые параметры W и A,
• латентные представления GL, 
• матрицы смежности Adj,
• промежуточные представления H,
• значения внимания Atten,
• результирующую матрицу matrix_out.

Дополнительно передаётся размерность признакового пространства dimension.

__kernel void InterpositionAttention(__global const float* matrix_in,
                                     __global const float* W,
                                     __global const float* A,
                                     __global const float* GL,
                                     __global float* Adj,
                                     __global float* H,
                                     __global float* Atten,
                                     __global float* matrix_out,
                                     const int dimension
                                    )
  {
   const size_t i = get_global_id(0);
   const size_t j = get_local_id(1);
   const size_t total = get_global_size(0);
   const size_t total_loc = get_local_size(1);

В начале работы мы определяем глобальные и локальные индексы потоков i и j, которые будут использоваться для перебора элементов во входных и выходных массивах. Затем, рассчитываем соответствующие смещения, чтобы обеспечить корректный доступ к подмассивам внутри глобального буфера.

const int shift_i = i * dimension;
const int shift_j = j * dimension;
const int shift_adj = i * total_loc + j;

Первым шагом осуществляется расчёт весов смежности между двумя узлами i и j путём попарного умножения их латентных представлений из массива GL.

float adj = 0;
for(int d = 0; d < dimension; d++)
   adj += IsNaNOrInf(GL[shift_i + d] * GL[shift_j + d], 0);
adj = max(IsNaNOrInf(adj, 0), 0);
adj = LocalSoftMax(adj, 1);
Adj[shift_adj] = adj;
adj += (float)(i == j);

Результат аккумулируется в переменной adj, нормализуется с помощью функции LocalSoftMax и сохраняется в матрице смежности Adj. Затем к значению adj добавляется единица, если i совпадает с j, обеспечивая тем самым сохранение диагонального элемента.

Далее переходим к формированию промежуточного представления H. Для этого поэтапно перемножаются входные признаки текущего узла с обучаемой матрицей весов W. Каждое значение сохраняется в массиве H, а для синхронизации между потоками используется барьер BarrierLoc.

for(int id_h = 0; id_h < dimension; id_h += total_loc)
  {
   if(j >= (dimension - id_h))
      break;
   float h = 0;
   for(int w = 0; w < dimension; w++)
      h += IsNaNOrInf(matrix_in[shift_i + w] * W[(id_h + j) * dimension + w], 0);
   H[shift_i + id_h + j] = h;
   BarrierLoc;
  }

После того, как H сформировано, рассчитывается значение внимания e, определяющее важность взаимодействия между узлами i и j. Значение инициализируется как малая положительная величина, чтобы избежать деления на ноль. В случае положительной корреляции между элементами, происходит накопление взвешенных скалярных произведений между соответствующими строками H и обучаемым вектором A. Результат снова нормализуется функцией LocalSoftMax и сохраняется в массиве Atten.

float e = 1e-12f;
if(adj > 0)
  {
   e = 0;
   for(int a = 0; a < dimension; a++)
      e += IsNaNOrInf(H[shift_i + a] * A[a], 0) + IsNaNOrInf(H[shift_j + a] * A[dimension + a], 0);
  }
e = LocalSoftMax(e, 1);
Atten[shift_adj] = e;

Финальный этап — восстановление значения анализируемой переменной на основе информации, полученной от других, наблюдаемых переменных. Значение пропущенной (или восстанавливаемой) переменной i агрегируется путём взвешенного суммирования представлений переменных j, при этом сами представления умножаются на соответствующие значения коэффициентов внимания. Такая агрегация позволяет передать полезную информацию от соседей к целевой переменной.

 for(int d = 0; d < dimension; d += total_loc)
   {
    if(j >= (dimension - d))
       break;
    float out = 0;
    int shift_h = d + j;
    int shift_att = i * total_loc;
    int shift_out = i * dimension + shift_h;
    for(int n = 0; n < total_loc; n++)
       out += IsNaNOrInf(H[shift_h + n * dimension] * Atten[shift_att + n], 0);
    matrix_out[shift_out] = Activation(out, ActFunc_LReLU);
   }
}

Для повышения устойчивости к выбросам и смягчения влияния аномальных значений, полученный результат нормализуется с помощью функции активации LReLU. Это способствует более стабильному обучению модели, особенно в условиях нестабильной или зашумлённой выборки.

Этот шаг завершает прямой проход Interpolation Attention и формирует финальное представление переменной i, учитывающее как внутренние связи между переменными, так и обученные параметры корреляции.

Таким образом, описанное ядро OpenCL реализует прямой проход Interpolation Attention, эффективно используя параллелизм для обработки элементов графовой структуры. Оно обеспечивает построение адаптивной модели взаимодействия между элементами временного ряда на базе латентных признаков, что позволяет учитывать контекст и гибко адаптироваться к структуре данных.

Следующим этапом нашей работы является реализация алгоритма обратного прохода Interpolation Attention, который мы также оформим в виде OpenCL-ядра. В данной функции рассчитываются градиенты для всех участвующих в прямом проходе параметров и исходных данных.

Основная идея кода — для каждого элемента производим вычисление частных производных ошибки по отношению к промежуточным переменным: скрытым признакам H, коэффициентам внимания Atten, входным матрицам, весам и матрице признаков GL.

__kernel void InterpositionAttentionGrad(__global const float* matrix_in,
                                         __global float* matrix_in_gr,
                                         __global const float* W,
                                         __global float* W_gr,
                                         __global const float* A,
                                         __global float* A_gr,
                                         __global const float* GL,
                                         __global float* GL_gr,
                                         __global float* Adj,
                                         __global float* H,
                                         __global float* H_gr,
                                         __global float* Atten,
                                         __global float* matrix_out_gr,
                                         const int dimension
                                        )
  {
   const size_t i = get_global_id(0);
   const size_t j = get_local_id(1);
   const size_t total = get_global_size(0);
   const size_t total_loc = get_local_size(1);

Внутри кернела для каждого потока (идентифицируемого индексами i и j) происходит последовательный расчёт:

• Градиенты по скрытым признакам Hgrad вычисляются, исходя из градиентов по выходу и весов внимания, с учётом функции активации LeakyReLU.

   const int shift_i = i * dimension;
   const int shift_j = j * dimension;
   const int shift_adj = i * total_loc + j;
//--- H Gradient
   for(int d = 0; d < dimension; d += total_loc)
     {
      if(j >= (dimension - d))
         break;
      float h_grad = 0;
      int shift_h = shift_i + d + j;
      int shift_att = i;
      int shift_out = d + j;
      for(int n = 0; n < total_loc; n++)
        {
         float gr = matrix_out_gr[shift_out + n * dimension];
         h_grad += IsNaNOrInf(
                      Deactivation(gr, gr, ActFunc_LReLU) * Atten[shift_att + n * total_loc], 0);
        }
      H_gr[shift_h] = h_grad;
      BarrierLoc;
     }

• Затем рассчитывается градиент по коэффициентам внимания Attgrad, который проходит через функцию обратного SoftMax для корректного распространения ошибок в распределении внимания.

//--- Attention Gradient
   float att_grad = 0;
   for(int d = 0; d < dimension; d++)
     {
      float gr = matrix_out_gr[shift_i + d];
      gr = Deactivation(gr, gr, ActFunc_LReLU);
      att_grad += IsNaNOrInf(gr * H[shift_j + d], 0)
     }
   att_grad = LocalSoftMaxGrad(Atten[shift_adj], att_grad, 1);

• Этот градиент далее используется для обновления градиентов по скрытым признакам H с учётом весов матрицы A, а также для накопления градиентов по самой матрице A.

for(int d = 0; d < dimension; d++)
  {
   float h_grad = att_grad * A[d];
   h_grad = LocalSum(h_grad, 1);
   if(j == 0)
      H_gr[shift_i + d] += h_grad;
   h_grad = att_grad * A[dimension + d];
   h_grad = LocalSum(h_grad, 1);
   if(j == 0)
      H_gr[shift_j + d] += h_grad;
   float a_grad = att_grad * H[shift_i + d];
   a_grad = LocalSum(a_grad, 1);
   A_gr[d] += a_grad;
   a_grad = att_grad * H[shift_j + d];
   a_grad = LocalSum(a_grad, 1);
   A_gr[dimension + d] += a_grad;
  }

• Градиенты по входным признакам получают, используя градиенты скрытых признаков и весовые матрицы W, что позволяет корректно обновить входные данные в процессе обучения.

//--- Inputs' Gradient
   for(int d = 0; d < dimension; d += total_loc)
     {
      if(j >= (dimension - id_h))
         break;
      float grad = 0;
      for(int w = 0; w < dimension; w++)
         grad += IsNaNOrInf(H_gr[shift_i + w] * W[(id_h + j) + dimension * w], 0);
      matrix_in_gr[shift_i + d + j] = grad;
      BarrierLoc;
     }

• Наконец, градиенты по адаптивной матрице GL вычисляются через обратный SoftMax по смежности и аккумулируются для обеих переменных i и j.

//--- Adj Gradient
   float grad = LocalSoftMaxGrad(Adj[shift_adj], att_grad, 1);
   for(int d = 0; d < dimension; d++)
     {
      GL_gr[shift_i + d] += IsNaNOrInf(grad * GL[shift_j + d], 0);
      GL_gr[shift_j + d] += IsNaNOrInf(grad * GL[shift_i + d], 0);
     }
  }

Общая структура функции построена с использованием локальной синхронизации потоков (BarrierLoc), что обеспечивает корректность обмена данными между ними и предотвращает гонки.

Такой подход обеспечивает точное и стабильное обновление всех параметров модели во время обучения, позволяя эффективно корректировать веса и повышать качество восстановления пропущенных значений в многомерных временных рядах.

На этом этапе мы завершаем реализацию ключевых компонентов на стороне OpenCL-программы. Следующим логичным шагом станет организация всего процесса в основной программе — интеграция, управление вычислениями и обучение модели средствами MQL5. Однако объем материала уже значительно вырос, и, чтобы сохранить ясность и качество изложения, предлагаю сделать паузу.

Продолжим эту важную работу в следующей статье, где подробно разберем практическую реализацию алгоритма в MQL5, тонкости взаимодействия с OpenCL и оптимизацию производительности. Так мы сможем сосредоточиться на каждом этапе без спешки, сохраняя глубину и полноту раскрытия темы.

Заключение

В завершение можно подчеркнуть, что представленный фреймворк GinAR демонстрирует мощный подход к прогнозированию многомерных временных рядов с пропущенными значениями. Интеграция интерполяционного внимания и адаптивной графовой свёртки в рекурсивную архитектуру позволяет эффективно восстанавливать отсутствующие данные и учитывать сложные пространственно-временные зависимости.

Практическая реализация ключевых компонентов на языке OpenCL, представленная в статье, открывает широкие возможности для дальнейшей оптимизации и внедрения в реальные торговые системы.

Дальнейшая работа будет посвящена интеграции этих разработок в основную программу на MQL5, что позволит раскрыть весь потенциал предложенных методов. Приглашаю читателей продолжить знакомство с темой в следующей статье.

Ссылки

• GinAR: An End-To-End Multivariate Time Series Forecasting Model Suitable for Variable Missing
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Study.mq5	Советник	Советник офлайн обучения моделей
2	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
3	Test.mq5	Советник	Советник для тестирования модели
4	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
5	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
6	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы