
Стратегия орла — Eagle Strategy (ES)
Содержание
Введение
В мире программирования, особенно при разработке торговых советников, эффективная оптимизация играет критически важную роль. Узкоспециализированные задачи поиска оптимального решения среди огромного пространства возможных вариантов требуют применения продвинутых алгоритмов. Традиционные методы оптимизации зачастую оказываются неэффективными, застревая в локальных экстремумах не находят глобально лучшее решение.
В связи с этим, всё большее внимание обращается метаэвристическим алгоритмам, вдохновлённым самой природой, методам прошедшим естественную эволюцию. Эти алгоритмы способны находить хорошие, а зачастую и близкие к оптимальным решения, даже в задачах, где скорость вычислений имеет первостепенное значение.
В условиях постоянного стремления к решению всё более сложных и ресурсоёмких задач, сегодня мы рассмотрим ещё одну перспективную попытку — алгоритм Eagle Strategy (ES). Этот алгоритм, вдохновлённый охотничьим поведением орла, представляет собой новую метаэвристику, предназначенную для решения оптимизационных задач, путем имитации стратегии визуального поиска и динамичного преследования добычи.
Реализация алгоритма
Представьте себе золотого орла, парящего высоко в небе в поисках добычи. Его стратегия охоты удивительно эффективна и состоит из двух четких этапов: сначала он летает на большой высоте, осматривая огромную территорию хаотичными зигзагообразными движениями, а затем, заметив цель, стремительно пикирует вниз, концентрируя все усилия на конкретной жертве. Именно эта природная мудрость легла в основу алгоритма Eagle Strategy (Стратегия Орла), разработанного в 2010 году для решения сложных задач оптимизации.
На первом этапе алгоритм использует так называемые полеты Леви — математическую модель, описывающую движение в пространстве. В отличие от обычного случайного блуждания, где шаги примерно одинаковы, полет Леви включает множество маленьких шагов, перемежающихся редкими, но очень длинными прыжками.
Когда алгоритм находит перспективную область (как орел, заметивший добычу), включается второй этап — интенсивный локальный поиск с помощью алгоритма светлячков, мы уже рассматривали такой известный алгоритм в одной из статей. Несколько поисковых агентов, словно светлячки в ночи, притягиваются к более ярким (успешным) соседям. Яркость светлячка соответствует качеству найденного им решения, а притяжение ослабевает с расстоянием по экспоненциальному закону. Это создает баланс между исследованием окрестностей и движением к лучшему известному решению.
Ключевая инновация ES заключается в циклическом чередовании этих двух режимов. После интенсивного локального поиска, алгоритм снова переключается на глобальное исследование, совершая длинный прыжок в новую неизведанную область пространства поиска. Это предотвращает преждевременную сходимость и позволяет находить глобальный оптимум даже в очень сложных ландшафтах с множеством локальных экстремумов.
Параметры алгоритма интуитивно понятны и легко настраиваются. Размер популяции определяет количество одновременно исследующих агентов, параметр Леви контролирует соотношение между короткими и длинными прыжками, радиус гиперсферы задает область интенсивного локального поиска, а коэффициент рандомизации добавляет элемент случайности для выхода из тупиковых ситуаций. Эта гибкость позволяет адаптировать алгоритм под конкретную задачу без глубокого понимания математической теории.
Философия ES алгоритма проста и изящна: глобальное видение в сочетании с локальной точностью. Подобно тому, как орел сочетает обзорный полет с прицельной атакой, алгоритм балансирует между исследованием неизвестных областей и эксплуатацией найденных перспективных решений.
Ключевыми особенностями алгоритма являются: автоматическое переключение между фазами при улучшении решения, адаптивные параметры (λ уменьшается при стагнации, размер шага убывает со временем) и баланс между исследованием новых областей и эксплуатацией найденных решений.
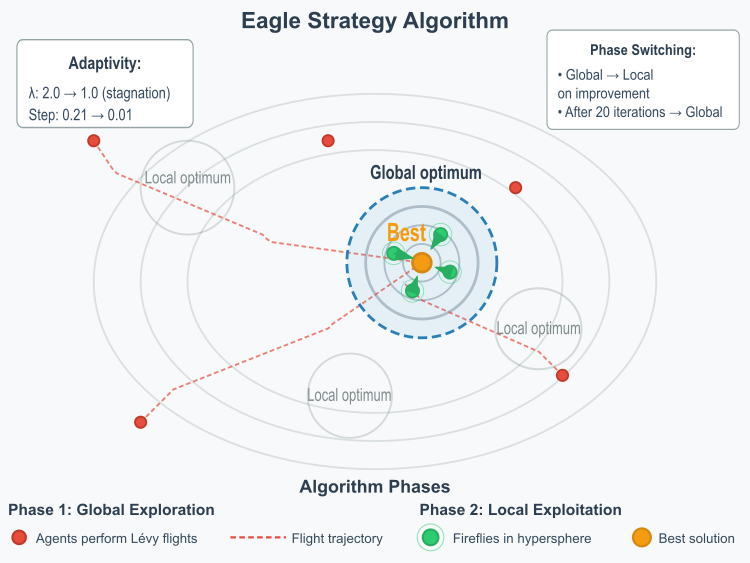
Рисунок 1. Иллюстрация работы алгоритма ES
Иллюстрация отображает две фазы работы алгоритма, траектории полетов Леви (красные пунктирные линии), гиперсферу локального поиска (голубой круг), движение светлячков внутри сферы (зеленые точки с ореолами), контурные линии функции оптимизации.
Переходим к написанию псевдокода алгоритма.
ИНИЦИАЛИЗАЦИЯ:
1. Создать популяцию агентов со случайными позициями
2. Установить флаг глобального поиска (фаза = глобальная)
3. Инициализировать счетчики стагнации и прогресса
ОСНОВНОЙ ЦИКЛ (пока не достигнут критерий остановки):
ЕСЛИ (фаза = глобальная):
ДЛЯ каждого агента:
- сгенерировать шаг Леви используя алгоритм Мантенья
- вычислить адаптивный масштаб шага (больше в начале, меньше в конце)
- обновить позицию: новая_позиция = текущая + шаг_Леви × масштаб
- применить граничные ограничения
ЕСЛИ (найдено улучшение глобального лучшего):
- Переключиться на локальную фазу
- Найти лучшего агента как центр локального поиска
- Сбросить счетчик стагнации
ИНАЧЕ:
- Увеличить счетчик стагнации
- ЕСЛИ (стагнация > 5 итераций):
- Уменьшить параметр λ для более агрессивных полетов
ИНАЧЕ (фаза = локальная):
С вероятностью 80%:
- определить агентов в гиперсфере радиуса 0.1 вокруг лучшего
- ЕСЛИ (агентов < 5):
- Взять 5 ближайших соседей или 30% популяции
ДЛЯ каждого агента в локальной группе:
ДЛЯ каждого другого агента в группе:
ЕСЛИ (другой агент лучше):
- вычислить привлекательность β = β₀ × exp(-γ × расстояние²)
- переместить агента: позиция += β × (лучший - текущий) + случайный_шум
С вероятностью 20%:
- Частично скопировать координаты глобального лучшего в случайных агентов
- Увеличить счетчик локальных итераций
- ЕСЛИ (выполнено 20 локальных итераций):
- Вернуться к глобальной фазе
- Восстановить исходный параметр λ
ОБНОВЛЕНИЕ:
ДЛЯ каждого агента:
- вычислить приспособленность
- обновить персональное лучшее
- обновить глобальное лучшее
В данной реализации алгоритма ES для генерации чисел с распределением Леви применим численный метод — алгоритм Мантенья, который был предложен R.N. Mantegna в 1994 году и стал стандартным способом симуляции полетов Леви в оптимизационных алгоритмах. Мантенья математически доказал, что отношение двух специально масштабированных гауссовских величин дает распределение, очень близкое к распределению Леви для диапазона значений, важных в практических приложениях. Суть его заключается в следующем:
// Вычисление сигмы для алгоритма Мантенья double numerator = Gamma(1.0 + lambda) * MathSin(M_PI * lambda / 2.0); double denominator = Gamma((1.0 + lambda) / 2.0) * lambda * MathPow(2.0, (lambda - 1.0) / 2.0); double sigma = MathPow(numerator / denominator, 1.0 / lambda); // Генерация u и v из нормальных распределений double u_val = GenerateGaussian() * sigma; double v_val = MathAbs(GenerateGaussian()); // Вычисление шага Леви levyStep[c] = u_val / MathPow(v_val, 1.0 / lambda);
Берем две случайные величины:
- u - из нормального распределения N(0, σ²)
- v - из нормального распределения N(0, 1)
σ = [Γ(1+λ) × sin(πλ/2) / (Γ((1+λ)/2) × λ × 2^((λ-1)/2))]^(1/λ)
где Γ — гамма-функция, λ - параметр распределения Леви (1 < λ ≤ 3).
Важно заметить, что при определении гамма-функции (для вычисления параметра σ в методе Мантенья) используется аппроксимация Ланцоша, это высокоточный численный метод для вычисления гамма-функции. Это один из самых эффективных способов вычисления Γ(z) и в коде реализовано отдельной функцией, которую разберем последней.
Основная формула выглядит следующим образом:
Γ(z+1) = √(2π) × ((z+g+0.5)^(z+0.5)) × e^(-(z+g+0.5)) × Ag(z)
где: g - параметр (обычно 7); Ag(z) - ряд с предварительно вычисленными коэффициентами, при g=7 и 9 коэффициентах дает точность примерно 15 значащих цифр.
Для z < 0.5 используется соотношение в формуле отражения, что позволяет вычислять гамма-функцию для всех действительных чисел:
Γ(z) × Γ(1-z) = π / sin(πz)
Без эффективного вычисления гамма-функции генерация полетов Леви была бы вычислительно затратной, что существенно замедлило бы весь алгоритм оптимизации.
Итоговый шаг Леви:
step = u / |v|^(1/λ) Алгоритм генерирует последовательность шагов с характерным для полетов Леви поведением: много маленьких шагов (локальное исследование), редкие, но очень большие прыжки (глобальное исследование) и степенной закон распределения длин шагов.
Преимущества данного метода сочетают в себе простоту решения, потому что требуется только генератор нормального распределения, и стабильность, численная устойчивость алгоритма. Именно это свойство делает полеты Леви эффективным для оптимизации — они обеспечивают оптимальный баланс между детальным изучением локальных областей и быстрым переходом в новые регионы пространства поиска.
После детального рассмотрения методов, применяемых в алгоритме ES, можем смело перейти к написанию класса "C_AO_ES", который представляет реализацию метода оптимизации, основанного на стратегии охоты орла и наследуется от базового класса "C_AO". Метод использует двухэтапный подход: сначала проводится глобальный поиск, чтобы определить потенциально перспективные области, затем — локальный поиск внутри выбранной части поиска для уточнения результата.
Размер популяции "popSize" задает количество "candidate" решений, участвующих в поиске. Параметр Леви "lambda" управляет распределением для случайных шагов. Радиус гиперсферы "sphereRadius" определяет область для локального поиска. Количество итераций локального поиска "localIterations" указывает, сколько раз производится уточнение решения внутри гиперсферы. Параметры рандомизации "alpha" и привлекательности "beta0" регулируют компоненты моделей поиска, такие как случайные движения и влияние "света" (в терминах метафоры).
Глобальная исследовательская фаза (GlobalExploration) ориентирована на поиск "promising" областей во всем поисковом пространстве, используя случайные шаги, сгенерированные по распределению Леви. Такой подход способствует взрывному поиску и масштабированию на большие пространства.
Локальная эксплуатационная фаза (LocalExploitation) проводит более тщательный поиск внутри гиперсферы вокруг выбранной точки. В этом случае используются более мелкие и точные шаги, соответствующие локальной оптимизации.
Генерация шагов Леви (GenerateLevyStep) создает случайные движения по методу распределения Леви, это обеспечивает как мелкие, так и крупные скачки в пространстве поиска для балансировки исследования и эксплуатации.
Класс содержит механизмы для отслеживания прогресса поиска, такие как запоминание лучшего найденного решения, счетчики стагнации (если решение не улучшается), а также циклы по эпохам, чтобы ограничить работу алгоритма по времени или итерациям, расчеты параметров распределений для случайных шагов, в частности, генерация гауссовых и распределений Леви и методы для управления фазами поиска, что обеспечивает переключение между глобальной и локальной стадией, а также контроль за их работой.
В общей сложности, метод представляет стратегию поиска, сочетающую широкие исследования пространства для выявления потенциальных областей с последующей тщательной локальной оптимизацией для достижения точных решений, используя параметры и механизмы, позволяющие адаптировать его поведение под конкретные задачи и условия.
//———————————————————————————————————————————————————————————————————— class C_AO_ES : public C_AO { public: //---------------------------------------------------------- ~C_AO_ES () { } C_AO_ES () { ao_name = "ES"; ao_desc = "Eagle Strategy"; ao_link = "https://www.mql5.com/ru/articles/18460"; popSize = 100; // размер популяции lambda = 1.0; // параметр распределения Леви (1 < λ ≤ 3) sphereRadius = 0.1; // радиус гиперсферы для локального поиска localIterations = 20; // количество итераций локального поиска alpha = 0.1; // параметр рандомизации для Firefly beta0 = 1.2; // начальная привлекательность ArrayResize (params, 6); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "lambda"; params [1].val = lambda; params [2].name = "sphereRadius"; params [2].val = sphereRadius; params [3].name = "localIterations"; params [3].val = localIterations; params [4].name = "alpha"; params [4].val = alpha; params [5].name = "beta0"; params [5].val = beta0; } void SetParams () { popSize = (int)params [0].val; lambda = params [1].val; sphereRadius = params [2].val; localIterations = (int)params [3].val; alpha = params [4].val; beta0 = params [5].val; } bool Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0); // количество эпох void Moving (); void Revision (); //------------------------------------------------------------------ double lambda; // параметр распределения Леви (1 < λ ≤ 3) double sphereRadius; // радиус гиперсферы для локального поиска int localIterations; // количество итераций локального поиска double alpha; // параметр рандомизации double beta0; // начальная привлекательность private: //--------------------------------------------------------- double gamma_es; // коэффициент поглощения света double levyStep []; // массив для шагов Леви // Отслеживание фаз bool inLocalSearchPhase; // флаг локального поиска int localSearchCenter; // центр локального поиска int localSearchCounter; // счетчик итераций локального поиска // Отслеживание сходимости double prevBestFitness; // предыдущее лучшее значение int stagnationCounter; // счетчик стагнации // Отслеживание эпох int epochCurrent; // текущая эпоха int epochMax; // максимальное количество эпох // Вспомогательные методы void GlobalExploration (); void LocalExploitation (); void GenerateLevyStep (); double GenerateGaussian (); double Gamma (double z); }; //————————————————————————————————————————————————————————————————————
Метод "Init" класса "C_AO_ES" выполняет инициализацию алгоритма оптимизации перед началом процесса поиска. Сначала вызывается метод "StandardInit", отвечающий за стандартную инициализацию алгоритма, он выполняет настройку общих параметров и структур данных, если "StandardInit" завершается неудачно, то и весь метод возвращает "false", сигнализируя о неудачной инициализации.
Далее выделяется память для массива "levyStep" размером, равным количеству координат "coords". Этот массив будет использоваться для хранения шагов, генерируемых в соответствии с распределением Леви. Флагу "inLocalSearchPhase" присваивается значение "false", алгоритм изначально находится в фазе глобального поиска. Переменные "localSearchCenter" и "localSearchCounter" устанавливаются в "0", чтобы подготовить счетчики для локального поиска.
Инициализация параметров сходимости:
- prevBestFitness устанавливается в минимальное возможное значение, чтобы первое найденное решение гарантированно считалось лучше предыдущего.
- stagnationCounter устанавливается в "0" для отслеживания количества итераций без улучшения наилучшего найденного решения.
Инициализация параметров эпох:
- epochMax присваивается значение входного параметра "epochsP", устанавливающего максимальное количество эпох (итераций) работы алгоритма.
- epochCurrent устанавливается в "0" для отслеживания текущей эпохи.
Установка фиксированного параметра: переменной "gamma_es" присваивается значение "1.0". Этот параметр используется в алгоритме "Firefly", который является частью общей стратегии.
Инициализируется начальная популяция решений "a". Для каждого решения в популяции:
- Каждая координата вектора решения (a[i].c[c]) инициализируется случайным значением, взятым из диапазона [rangeMin[c], rangeMax[c]].
- Значение каждой координаты "округляется" до ближайшего допустимого значения с учетом шага (rangeStep[c]), используя метод "u.SeInDiSp".
- Значение целевой функции (a[i].f и a[i].fB) для каждого решения устанавливается в "-DBL_MAX".
//———————————————————————————————————————————————————————————————————— bool C_AO_ES::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //------------------------------------------------------------------ // Инициализация массивов ArrayResize (levyStep, coords); // Инициализация отслеживания фаз inLocalSearchPhase = false; localSearchCenter = 0; localSearchCounter = 0; // Инициализация отслеживания сходимости prevBestFitness = -DBL_MAX; stagnationCounter = 0; // Инициализация отслеживания эпох epochMax = epochsP; epochCurrent = 0; // Фиксированный параметр Firefly gamma_es = 1.0; // Инициализация популяции случайным образом for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } a [i].f = -DBL_MAX; a [i].fB = -DBL_MAX; } return true; } //————————————————————————————————————————————————————————————————————
Метод "Moving" реализует основную логику итерационного процесса оптимизации, чередуя между глобальным поиском и локальной эксплуатацией. Каждый вызов метода увеличивает счетчик эпох, для отслеживания прогресса алгоритма.
Обработка фаз поиска:-
если текущая фаза — глобальный поиск, выполняется исследование пространства с помощью шагов, моделируемых по распределению Леви, осуществляется генерация новых решений в целом пространстве, чтобы искать новые области с потенциалом;
-
если после глобального поиска найдено улучшение — алгоритм переключается налокальную фазу. При этом выбирается наиболее перспективное решение (агент), вокруг которого будет проведен поиск с целью его уточнения;
-
если улучшений не происходит в течение нескольких итераций (накапливается стагнация), увеличивается активность для поиска новых решений за счет более агрессивных летательных шагов, уменьшая параметр "lambda" для более широкого исследованию пространства;
-
в случае, если алгоритм находится в фазе локального поиска, с вероятностью 80% выполняется локальная оптимизация с использованием метода, который моделирует алгоритм "Firefly". В этом случае производится уточнение выбранного решения, и счетчик локальных итераций увеличивается, после достижения заданного количества итераций локального поиска или по решению, происходит возврат к глобальному поиску.
Таким образом, метод реализует стратегию поэтапного и гибкого поиска, перетекания между глобальным исследованием пространства и целенаправленной локальной оптимизацией. Это позволяет балансировать между исследованием новых областей и улучшением существующих решений.
//———————————————————————————————————————————————————————————————————— void C_AO_ES::Moving () { epochCurrent++; // ПРИНЯТИЕ РЕШЕНИЯ О ФАЗЕ: Чередование между глобальным и локальным поиском if (!inLocalSearchPhase) { // ФАЗА 1: ГЛОБАЛЬНОЕ ИССЛЕДОВАНИЕ с использованием полетов Леви GlobalExploration (); // Проверка необходимости переключения на локальный поиск // Переключаемся, если нашли многообещающую область (улучшение лучшей приспособленности) if (fB > prevBestFitness) { inLocalSearchPhase = true; localSearchCounter = 0; prevBestFitness = fB; stagnationCounter = 0; // Поиск лучшего агента для центрирования локального поиска localSearchCenter = 0; double bestFit = -DBL_MAX; for (int i = 0; i < popSize; i++) { if (a [i].f > bestFit) { bestFit = a [i].f; localSearchCenter = i; } } } else { stagnationCounter++; // При стагнации увеличиваем исследование if (stagnationCounter > 5) { lambda = MathMax (1.0, lambda - 0.1); // Делаем полеты Леви более агрессивными } } } else { if (u.RNDprobab () < 0.8) { // ФАЗА 2: ЛОКАЛЬНАЯ ЭКСПЛУАТАЦИЯ с использованием алгоритма Firefly LocalExploitation (); localSearchCounter++; // Возврат к глобальному поиску после завершения локальных итераций if (localSearchCounter >= localIterations) { inLocalSearchPhase = false; lambda = params [1].val; // Сброс lambda к исходному значению } } else { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { if (u.RNDprobab () < 0.5) { a [i].c [c] = cB [c]; } } } } } } //————————————————————————————————————————————————————————————————————
Метод "Revision" предназначен для обновления информации о лучших решениях в процессе работы алгоритма. Метод проходит по всем элементам текущей популяции решений и для каждого решения сравнивает его текущую приспособленность (фитнес) с сохраненной в его персональном лучшем результате. Если текущее значение лучше, то обновляется персональный лучший результат и соответствующее решение (сохраняется лучшее решение текущей итерации).
Затем, метод сравнивает приспособленность каждого решения с текущим глобальным лучшим значением, найденным по всей популяции и если текущий результат самый лучший, то обновляется глобальный результат и сохраняется соответствующее решение. Таким образом, метод поддерживает актуальную информацию о локальных и глобальных оптимальных решениях в текущем состоянии алгоритма, обеспечивая сохранение лучших найденных решений на каждом шаге.
//———————————————————————————————————————————————————————————————————— void C_AO_ES::Revision () { for (int i = 0; i < popSize; i++) { // Обновление персонального лучшего if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } // Обновление глобального лучшего if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //————————————————————————————————————————————————————————————————————
Метод "GlobalExploration" реализует фазу глобального поиска, используя полеты Леви для исследования пространства решений. Для каждого решения в цикле по всей популяции генерируется случайный шаг с использованием распределения Леви, он определяет направление и длину перемещения в пространстве решений.
Распределение Леви характеризуется "тяжелыми хвостами", что позволяет делать небольшие уточняющие шаги, так и выполнять большие редкие скачки для исследования отдаленных областей. В цикле по каждой координате решения вычисляется:
- размах поиска (разница между максимальным и минимальным значением координаты),
- адаптивный масштабный коэффициент "stepScale". Он уменьшается по мере прогресса поиска (чем ближе к концу, тем шаги меньше), способствует сужению области поиска вокруг перспективных решений, тогда как в самом начале поиска шаги больше для более широкого исследования.
- применяется шаг Леви: координата текущего решения изменяется на величину, пропорциональную шагу Леви, размаху поиска и масштабному коэффициенту.
- коррекция границ: проверяется, не вышла ли новая координата за допустимые границы; если вышла, то значение корректируется, чтобы оставаться в пределах заданного диапазона.
//———————————————————————————————————————————————————————————————————— // ФАЗА 1: Глобальное исследование с использованием полетов Леви void C_AO_ES::GlobalExploration () { for (int i = 0; i < popSize; i++) { // Генерация шага Леви GenerateLevyStep (); // Обновление позиции с использованием полета Леви for (int c = 0; c < coords; c++) { double range = rangeMax [c] - rangeMin [c]; // Адаптивный размер шага в зависимости от прогресса поиска double progress = (epochMax > 0) ? (double)epochCurrent / (double)epochMax : 0.5; double stepScale = 0.01 + 0.2 * (1.0 - progress); // Начинаем с больших шагов // Применение шага Леви a [i].c [c] += levyStep [c] * range * stepScale; // Ограничения границ a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //————————————————————————————————————————————————————————————————————
Метод "LocalExploitation" реализует стадию локального улучшения решений с помощью алгоритма Светлячков (Firefly). На начальном этапе определяется агенты, находящихся внутри заданной гиперсферы вокруг лучшего решения. Для этого считается расстояние каждого агента до центра гиперсферы, и если оно меньше радиуса или агент является центром поиска, он включается в выбранную группу.
Если внутри гиперсферы оказалось слишком мало агентов, то выполняется расширение области поиска за счет ближайших соседей. Для этого для всех агентов рассчитывается расстояние до центра, и выбираются ближайшие — либо по числовому количеству (например, 5), либо по доле населения (например, 30%). Эти агенты добавляются в группу.
Область применения алгоритма Светлячков: на выбранных агентах происходит взаимодействие согласно правилам алгоритма:- Для каждого агента проверяется, есть ли в группе другой агент с лучшей приспособленностью.
- Если такой есть, текущий агент перемещается в сторону более привлекательного (лучшего) агента, при этом рассчитывается расстояние между ними.
- Чем привлекательнее другой агент, тем больше его "светимость" (зависит от расстояния и параметров алгоритма).
- Перемещение включает в себя аккуратное смешение — агент сдвигается в сторону более привлекательного агента с добавлением случайных колебаний для разнообразия поиска.
- После перемещений контролируются границы координат, чтобы решения остались в допустимом диапазоне.
В результате, метод позволяет локально улучшить решения вблизи лучших найденных точек, используя взаимодействие агентов по модели стратегии алгоритма Светлячков: лучшие решения притягивают к себе худшие, способствуя точечной оптимизации пространства решений.
//———————————————————————————————————————————————————————————————————— // ФАЗА 2: Локальная эксплуатация с использованием алгоритма Firefly void C_AO_ES::LocalExploitation () { // Идентификация агентов внутри гиперсферы вокруг лучшего решения double agents_in_sphere []; ArrayResize (agents_in_sphere, 0); for (int i = 0; i < popSize; i++) { double normalized_dist = 0.0; for (int c = 0; c < coords; c++) { double diff = (a [i].c [c] - a [localSearchCenter].c [c]) / (rangeMax [c] - rangeMin [c]); normalized_dist += diff * diff; } normalized_dist = MathSqrt (normalized_dist); // Включаем агентов внутри сферы или сам центр if (normalized_dist <= sphereRadius || i == localSearchCenter) { int size = ArraySize (agents_in_sphere); ArrayResize (agents_in_sphere, size + 1); agents_in_sphere [size] = i; } } // Если слишком мало агентов, расширяем до ближайших соседей if (ArraySize (agents_in_sphere) < 5) { ArrayResize (agents_in_sphere, 0); // Вычисляем расстояния для всех агентов double distances []; ArrayResize (distances, popSize); for (int i = 0; i < popSize; i++) { if (i == localSearchCenter) { distances [i] = 0.0; } else { double dist = 0.0; for (int c = 0; c < coords; c++) { double diff = (a [i].c [c] - a [localSearchCenter].c [c]) / (rangeMax [c] - rangeMin [c]); dist += diff * diff; } distances [i] = MathSqrt (dist); } } // Берем ближайших 5 агентов или 30% популяции int numAgents = MathMin (popSize, MathMax (5, popSize / 3)); ArrayResize (agents_in_sphere, numAgents); // Простой выбор ближайших агентов for (int k = 0; k < numAgents; k++) { double minDist = DBL_MAX; int minIdx = -1; for (int i = 0; i < popSize; i++) { bool already_selected = false; for (int j = 0; j < k; j++) { if (agents_in_sphere [j] == i) { already_selected = true; break; } } if (!already_selected && distances [i] < minDist) { minDist = distances [i]; minIdx = i; } } agents_in_sphere [k] = minIdx; } } // Выполнение алгоритма Firefly на выбранных агентах int numLocalAgents = ArraySize (agents_in_sphere); for (int i = 0; i < numLocalAgents; i++) { int idx_i = (int)agents_in_sphere [i]; for (int j = 0; j < numLocalAgents; j++) { if (i == j) continue; int idx_j = (int)agents_in_sphere [j]; // Если агент j лучше агента i, двигаем i к j if (a [idx_j].f > a [idx_i].f) { // Вычисление расстояния double r_squared = 0.0; for (int c = 0; c < coords; c++) { double diff = (a [idx_j].c [c] - a [idx_i].c [c]) / (rangeMax [c] - rangeMin [c]); r_squared += diff * diff; } // Вычисление привлекательности double beta = beta0 * MathExp (-gamma_es * r_squared); // Перемещение агента i к агенту j for (int c = 0; c < coords; c++) { double range = rangeMax [c] - rangeMin [c]; // Уравнение движения Firefly a [idx_i].c [c] += beta * (a [idx_j].c [c] - a [idx_i].c [c]) + alpha * (u.RNDfromCI (-0.5, 0.5)) * range * 0.1; // Применение границ a [idx_i].c [c] = u.SeInDiSp (a [idx_i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } } //————————————————————————————————————————————————————————————————————
Метод "GenerateLevyStep" отвечает за генерацию шага Леви, необходимого для реализациистратегии глобального исследования в алгоритме оптимизации. Метод использует алгоритм Мантенья для генерации этих шагов, об этом методе мы уже рассказали выше.
Вычисление сигмы:
Формула в коде вычисляет параметр "sigma". Этот параметр связан с масштабом распределения Леви и зависит от константы "lambda", характеризующей форму распределения Леви (определяет, насколько "тяжелыми" будут хвосты распределения). Gamma () — это гамма-функция, обобщение факториала на вещественные числа (код данного метода представлен ниже). Этот параметр необходим для генерации величин, подчиняющихся нормальному распределению, которые затем используются в алгоритме Мантенья.
Генерация шага Леви происходит независимо для каждой координаты (параметра) решения. Генерируются две случайные величины "u_val" и "v_val" из нормального (гауссовского) распределения, "v_val" берется по модулю. Рассчитывается шаг Леви "levyStep [c]" по формуле алгоритма Мантенья: u_val / Math.pow(v_val, 1.0 / lambda). Выполняется проверка на случай деления на ноль (если v_val очень мала). Шаг Леви ограничивается по абсолютной величине. Это делается для предотвращения слишком больших скачков.
В результате работы метода генерируется массив "levyStep", содержащий величины шагов Леви для каждой координаты. Эти шаги затем используются в методе "GlobalExploration", чтобы обновить положение каждого решения в пространстве поиска.
//———————————————————————————————————————————————————————————————————— // Генерация шага Леви с использованием алгоритма Мантенья void C_AO_ES::GenerateLevyStep () { // Вычисление сигмы для алгоритма Мантенья double numerator = Gamma (1.0 + lambda) * MathSin (M_PI * lambda / 2.0); double denominator = Gamma ((1.0 + lambda) / 2.0) * lambda * MathPow (2.0, (lambda - 1.0) / 2.0); double sigma = MathPow (numerator / denominator, 1.0 / lambda); for (int c = 0; c < coords; c++) { // Генерация u и v из нормальных распределений double u_val = GenerateGaussian () * sigma; double v_val = MathAbs (GenerateGaussian ()); // Вычисление шага Леви if (v_val > 1e-10) { levyStep [c] = u_val / MathPow (v_val, 1.0 / lambda); } else { levyStep [c] = 0.0; } // Ограничение экстремальных значений if (MathAbs (levyStep [c]) > 10.0) { levyStep [c] = 10.0 * (levyStep [c] > 0 ? 1.0 : -1.0); } } } //————————————————————————————————————————————————————————————————————
Метод "GenerateGaussian" реализует генерацию случайных чисел, подчиняющихся нормальному (гауссовскому) распределению со средним значением "0" и стандартным отклонением "1". Он использует преобразование Бокса-Мюллера, достаточно распространенный метод для этой задачи, мы уже этот метод применяли в предыдущих статьях.
Используются статические переменные "hasSpare" и "spare", преобразование Бокса-Мюллера генерирует два независимых случайных числа из нормального распределения за раз, hasSpare — логическая переменная, определяющая, сохранено ли одно из сгенерированных чисел для следующего вызова функции, spare - переменная, которая хранит это "запасное" число.Генерация новых случайных чисел (если необходимо):
Если "запасного" числа нет, то: генерируются две независимые случайные величины "u_val" и "v_val" из равномерного распределения на интервале (0, 1). Функция "u.RNDfromCI" занимается генерацией равномерно распределённых чисел. Применяется преобразование Бокса-Мюллера:
- Вычисляется "mag" (магнитуда) как квадратный корень из -2.0 * Math.log(u_val + 1e-10). Добавление небольшого числа к "u_val" необходимо, чтобы избежать взятия логарифма от нуля, что недопустимо.
- Вычисляется "запасное" число "spare" как mag * Math.cos(2.0 * M_PI * v_val).
- Возвращается значение mag * Math.sin(2.0 * M_PI * v_val).
//———————————————————————————————————————————————————————————————————— // Генерация гауссовского случайного числа с использованием преобразования Бокса-Мюллера double C_AO_ES::GenerateGaussian () { static bool hasSpare = false; static double spare; if (hasSpare) { hasSpare = false; return spare; } hasSpare = true; double u_val = u.RNDfromCI (0.0, 1.0); double v_val = u.RNDfromCI (0.0, 1.0); double mag = MathSqrt (-2.0 * MathLog (u_val + 1e-10)); spare = mag * MathCos (2.0 * M_PI * v_val); return mag * MathSin (2.0 * M_PI * v_val); } //————————————————————————————————————————————————————————————————————
Метод "Gamma" является функцией, аппроксимирующей гамма-функцию для заданного аргумента "z". Поскольку гамма-функция является важной математической функцией, особенно в статистике и оптимизации, но ее точное вычисление может быть трудным и энергоемким, часто используются аппроксимации. Используем аппроксимацию Ланцоша, которая обеспечивает хорошую точность при относительно небольших вычислительных затратах. Обговорим основные моменты.
Если аргумент "z" меньше "0.5", применяется формула отражения Эйлера. Это позволяет вычислять гамма-функцию для аргументов, близких к нулю. Формула отражения связывает гамма-функцию от "z" с гамма-функцией от "1 - z". Воспользуемся фиксированными коэффициентами Ланцоша, они были тщательно подобраны для обеспечения высокой точности аппроксимации, а также коэффициентами и формулой, включающие степенные и экспоненциальные функции. Метод возвращает аппроксимированное значение гамма-функции для заданного аргумента "z".
Аппроксимация Ланцоша предоставляет хорошую точность, достаточную для большинства практических применений. Алгоритм относительно эффективен, поскольку требует только нескольких арифметических операций и табличного поиска коэффициентов. Подходит для широкого диапазона значений аргумента, особенно в сочетании с формулой отражения. В целом, метод "Gamma" представляет собой достаточно точный способ аппроксимации гамма-функции.
//———————————————————————————————————————————————————————————————————— // Аппроксимация гамма-функции с использованием аппроксимации Ланцоша double C_AO_ES::Gamma (double z) { if (z < 0.5) { // Формула отражения для z < 0.5 return M_PI / (MathSin (M_PI * z) * Gamma (1.0 - z)); } // Коэффициенты Ланцоша const double g = 7.0; double coef [] = { 0.99999999999980993, 676.5203681218851, -1259.1392167224028, 771.32342877765313, -176.61502916214059, 12.507343278686905, -0.13857109526572012, 9.9843695780195716e-6, 1.5056327351493116e-7 }; z -= 1.0; double x = coef [0]; for (int i = 1; i < 9; i++) { x += coef [i] / (z + i); } double t = z + g + 0.5; double sqrt2pi = MathSqrt (2.0 * M_PI); return sqrt2pi * MathPow (t, z + 0.5) * MathExp (-t) * x; } //————————————————————————————————————————————————————————————————————
Результаты тестов
Хотя алгоритм и не смог пройти в нашу рейтинговую таблицу, результаты его работы заслуживают внимания.=============================
5 Hilly's; Func runs: 10000; result: 0.7077570016043803
25 Hilly's; Func runs: 10000; result: 0.4307775904381953
500 Hilly's; Func runs: 10000; result: 0.2747545259235643
=============================
5 Forest's; Func runs: 10000; result: 0.7173720280531499
25 Forest's; Func runs: 10000; result: 0.3448423301485268
500 Forest's; Func runs: 10000; result: 0.1597390810339928
=============================
5 Megacity's; Func runs: 10000; result: 0.5184615384615384
25 Megacity's; Func runs: 10000; result: 0.2775384615384615
500 Megacity's; Func runs: 10000; result: 0.11063076923077016
=============================
All score: 3.54187 (39.35%)
На визуализации хорошо заметно как разделяются фазы поиска по стратегиям, когда происходят длинные броски и короткие уточняющие движения.
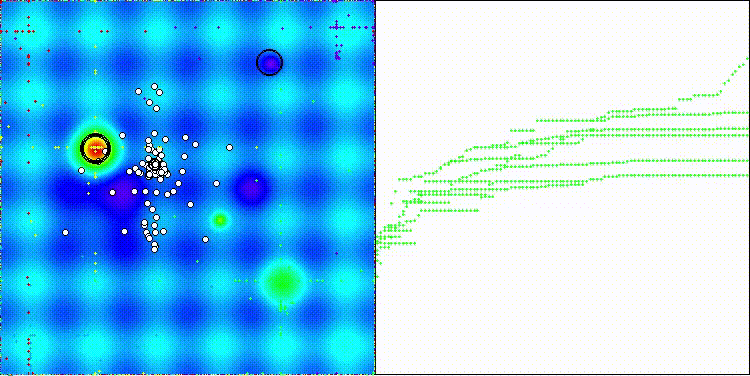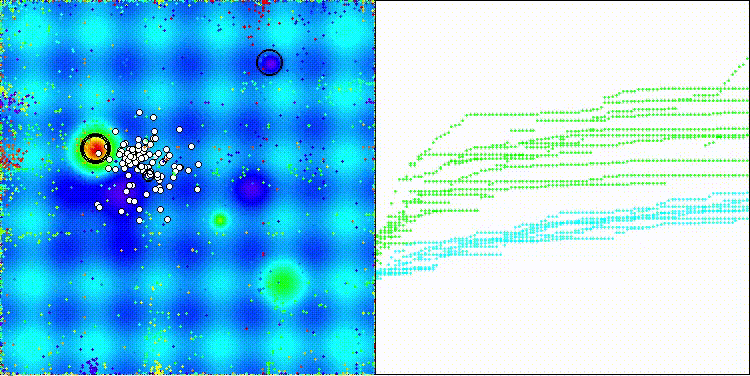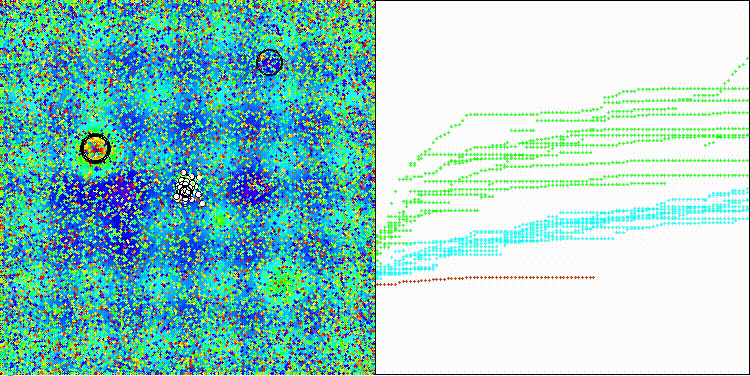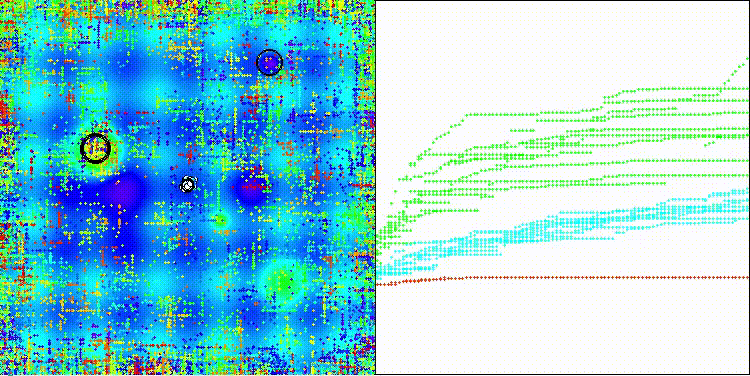
ES на тестовой функции Hilly
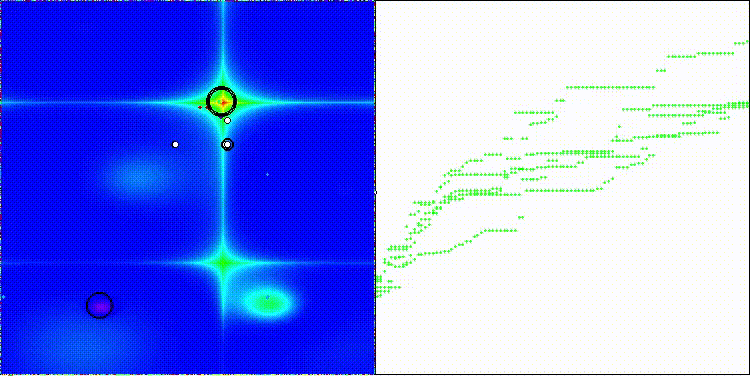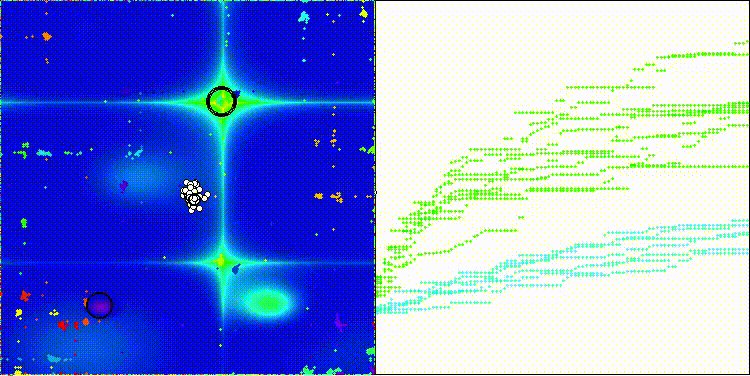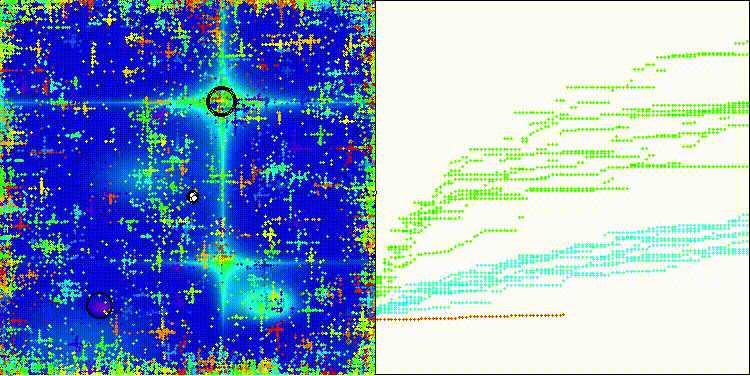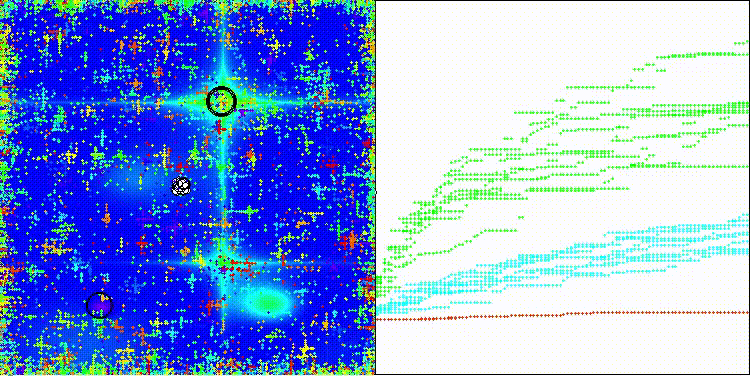
ES на тестовой функции Forest
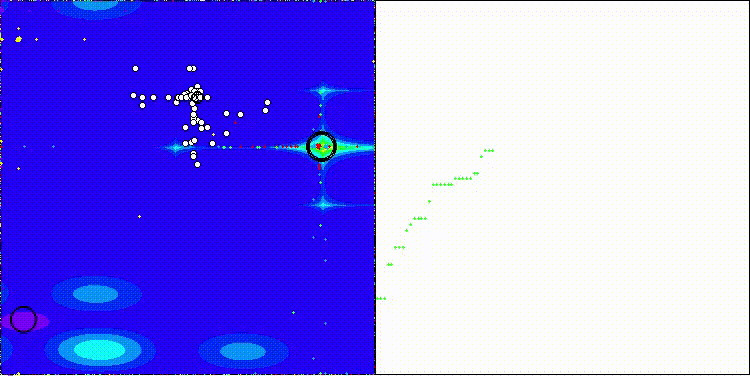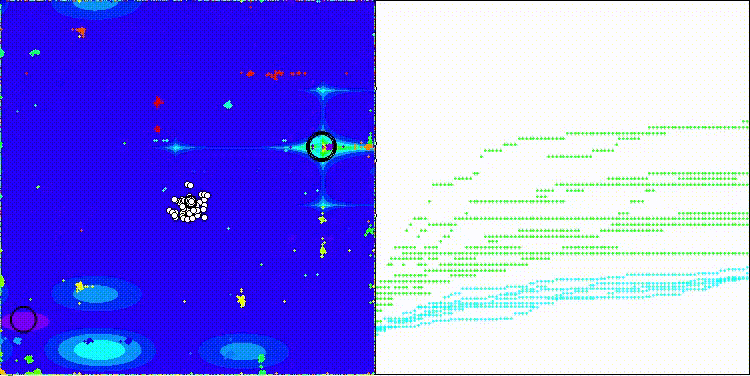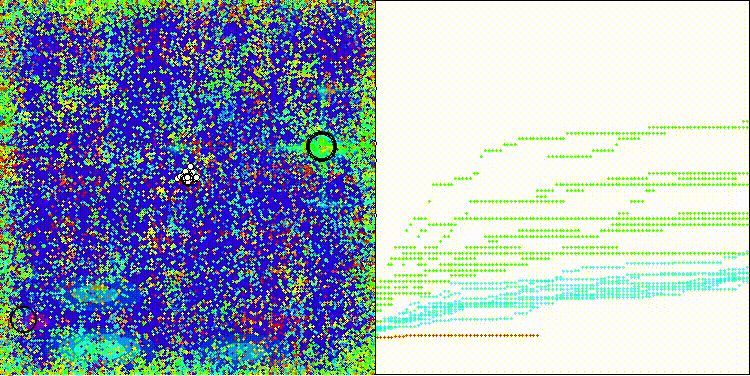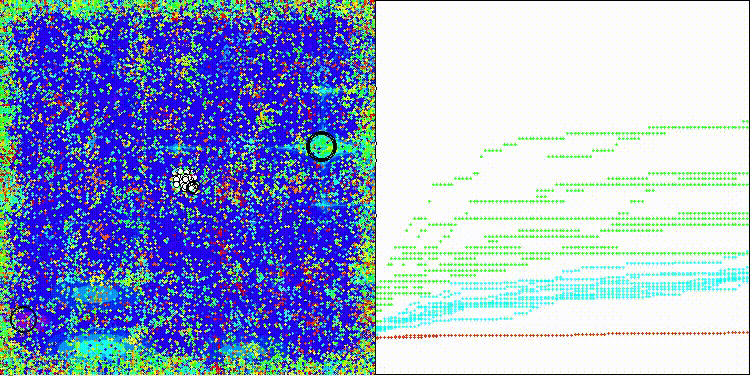
ES на тестовой функции Megacity
Алгоритм ES представлен в рейтинговой таблице ознакомительно.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| 13 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 14 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 15 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 16 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 17 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 18 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 19 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 20 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 21 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 22 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 23 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 24 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 25 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 26 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 27 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 28 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 29 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 30 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 31 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 32 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 33 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 34 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 35 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 36 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 37 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 38 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 39 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 40 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 41 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 42 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 43 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| 44 | CROm | coral reefs optimization M | 0,78512 | 0,46032 | 0,25958 | 1,50502 | 0,86688 | 0,35297 | 0,16267 | 1,38252 | 0,63231 | 0,26738 | 0,10734 | 1,00703 | 3,895 | 43,27 |
| 45 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| ES | eagle_strategy_optimization | 0,70776 | 0,43078 | 0,27475 | 1,41328 | 0,71737 | 0,34484 | 0,15973 | 1,22194 | 0,51846 | 0,27754 | 0,11063 | 0,90663 | 3,542 | 39,35 | |
| RW | neuroboids optimization algorithm 2(joo) | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Алгоритм ES демонстрирует средние результаты в сравнительном тестировании популяционных методов оптимизации, набрав 39% от максимально возможных баллов, что не позволило ему войти в рейтинговую таблицу 45 сильнейших алгоритмов.
Несмотря на это, алгоритм заслуживает внимания, благодаря своей оригинальной концепции двухфазного поиска, основанной на биологически обоснованной модели охотничьего поведения орла. Использование полетов Леви для глобального исследования представляет собой математически красивое решение, теоретически доказавшее свою оптимальность для задач случайного поиска. Адаптивные механизмы реализации, включая динамическое переключение между фазами и автоматическую настройку параметров при стагнации, показывают потенциал для улучшения базовой концепции.
Алгоритм может найти свою нишу в специфических классах задач, где важен баланс между глобальным исследованием и локальной эксплуатацией, особенно при наличии множества локальных оптимумов и зашумленных данных. Интеграция алгоритма светлячков для локального поиска создает интересную синергию двух природно-инспирированных методов, хотя общая производительность указывает на необходимость дальнейшей оптимизации параметров и возможной модификации базовых механизмов.
Алгоритм ES может рассматриваться как учебный пример гибридного подхода к оптимизации и основа для разработки более совершенных методов, комбинирующих различные метаэвристики. Его относительно простая реализация и интуитивно понятная логика делают алгоритм подходящим для исследовательских экспериментов в области эволюционных вычислений.
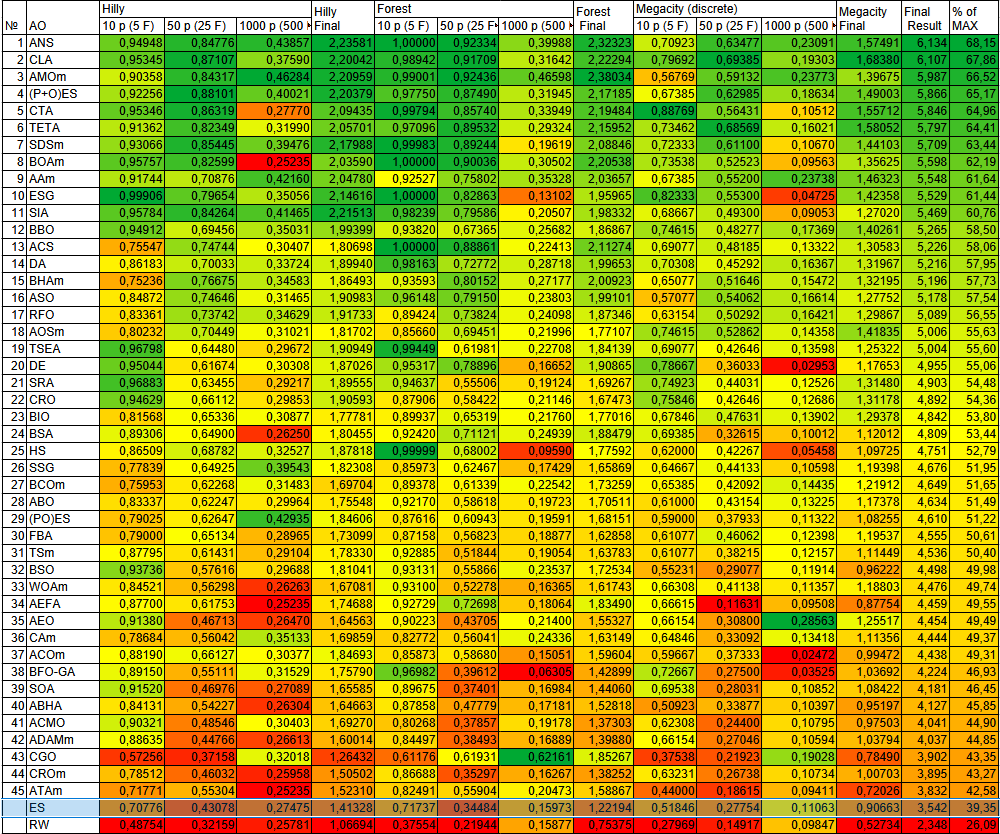
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
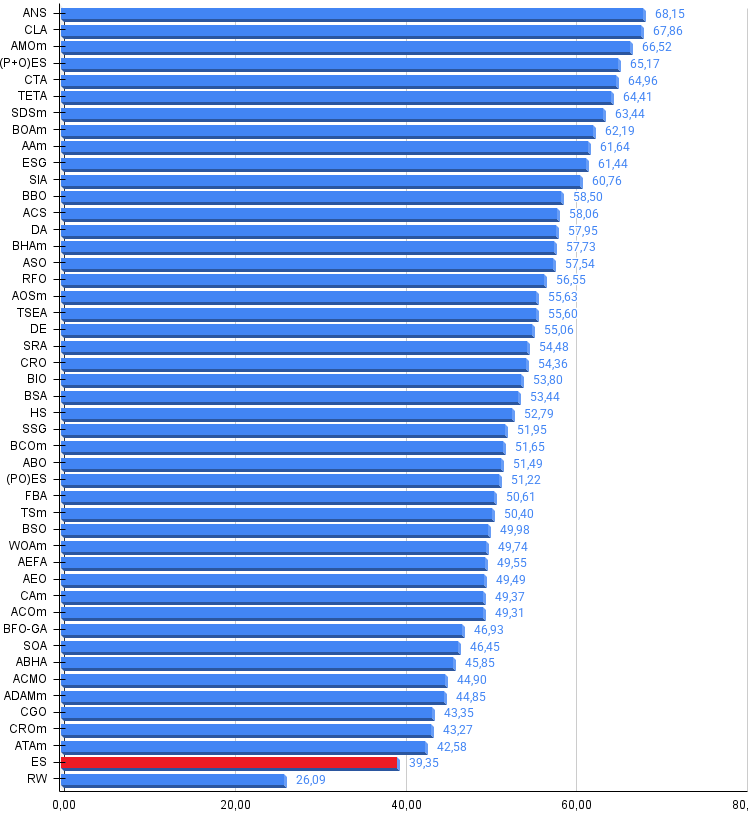
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма ES:
Плюсы:
- Быстрый.
Минусы:
- Большое количество параметров.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_ES.mq5 | Скрипт | Испытательный стенд для ES |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Инженерия признаков с Python и MQL5 (Часть II): Угол наклона цены
Инженерия признаков с Python и MQL5 (Часть II): Угол наклона цены
 Наблюдатель Connexus (Часть 8): Добавление Request Observer (Наблюдатель запросов)
Наблюдатель Connexus (Часть 8): Добавление Request Observer (Наблюдатель запросов)
 Введение в исследование фрактальных рыночных структур с помощью машинного обучения
Введение в исследование фрактальных рыночных структур с помощью машинного обучения
 Нейросети в трейдинге: Интеллектуальный конвейер прогнозов (Окончание)
Нейросети в трейдинге: Интеллектуальный конвейер прогнозов (Окончание)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования