Введение в исследование фрактальных рыночных структур с помощью машинного обучения

Введение: сложность финансовых рынков и нелинейные подходы

Финансовые рынки обладают сложной, нелинейной динамикой, которую традиционные модели часто не отражают. Линейные подходы и классические индикаторы риска, такие как стандартное отклонение и бета, не учитывают особенности, вроде тяжелых хвостов и кластеризации волатильности.

Фрактальная теория, разработанная Мандельбротом, предлагает альтернативу, способную описывать «бурную случайность» и самоподобные структуры в финансовых рядах. Она выявляет скрытые закономерности, ускользающие от традиционного анализа, и способствует более глубокому пониманию рыночного поведения.

Рис 1. Бенуа Мандельброт, создатель фрактальной теории рынков

Фрактальные свойства финансовых временных рядов: самоподобие и масштабная инвариантность

Финансовые данные часто обладают самоподобием — их структура сохраняется при изменении масштаба. Это свойство, характерное для фракталов, проявляется в том, что ценовые графики на разных таймфреймах выглядят схоже, что указывает на масштабную инвариантность.

Наличие самоподобия ставит под сомнение Гипотезу Эффективного Рынка (ГЭР), предполагающую случайные блуждания. Повторяющиеся паттерны в разных масштабах указывают на потенциальную предсказуемость, усиливая интерес к техническому анализу.

Классическим примером является исследование Б. Мандельброта (1963), показавшее распределительное самоподобие в ценах на хлопок и применение устойчивых распределений Леви в моделировании.

Показатель Херста (H) измеряет степень долгосрочной памяти:

• H > 0.5 — трендовая устойчивость;

• H < 0.5 — возврат к среднему;

• H = 0.5 — случайное блуждание.

Он связан с фрактальной размерностью D через D = 2 - H. Эмпирически, H для DAX ≈ 0.54, для сырой нефти — 0.5224, что указывает на отклонение от случайного поведения и наличие устойчивости — важного условия для предсказуемости рынка.

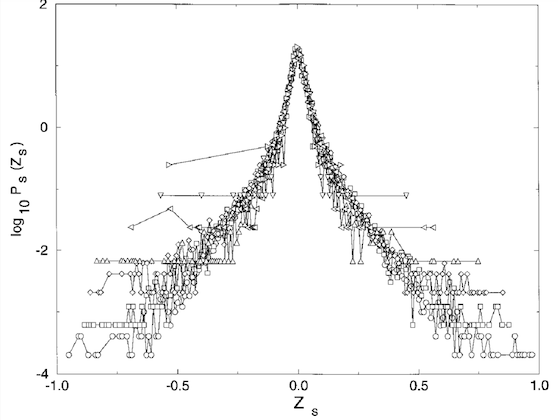
Рис 2. демонстрация масштабной инвариантности в финансовых временных рядах. Источник

Демонстрация масштабной инвариантности в финансовых временных рядах. Мантенья и Стэнли (1995) проанализировали распределение вероятностей P(Z) вариаций индекса S&P Z(t), наблюдаемых на временных интервалах Dt, которые варьируются от 1 до 1000 мин. При увеличении Dt наблюдается разброс распределения вероятностей, характерный для случайного блуждания. Показан масштабированный график распределений вероятностей. Все данные сжимаются до распределения Dt = 1 мин с помощью масштабных преобразований, соответствующих преобразованиям распределения Леви, с a = 1,40. Точки за пределами среднего поведения определяют уровень шума этого конкретного распределения.

Мультифрактальность финансовых временных рядов: многомерность масштабирования

Мультифрактальный анализ отражает сложную природу рыночной динамики. В отличие от монофракталов с единым показателем масштабирования, мультифракталы характеризуются вариациями регулярности сигнала, зависящими от масштаба и порядка статистических моментов. Это означает, что малые и крупные ценовые флуктуации подчиняются разным законам масштабирования.

Мультифрактальный детрендированный флуктуационный анализ (MF-DFA) — один из ключевых методов оценки мультифрактальности, использующий обобщённый показатель Херста H(q). Его нелинейность указывает на наличие мультифрактальной структуры. Метод особенно эффективен для анализа нестационарных рядов с тяжелыми хвостами и долгосрочными корреляциями.

Другие подходы включают мультифрактальную условную диффузионную энтропию (MS-CDE), скользящее среднее (MF-DMA) и кросс-корреляционный анализ (MF-DCCA), позволяя изучать рыночное поведение в разных трендах и масштабах.

Мультифрактальный спектр f(α) описывает распределение сингулярностей и характеризует "шероховатость" рынка. Ширина спектра (Δα) служит количественной мерой сложности и риска, отражая гетерогенность масштабных характеристик и потенциал экстремальных событий.

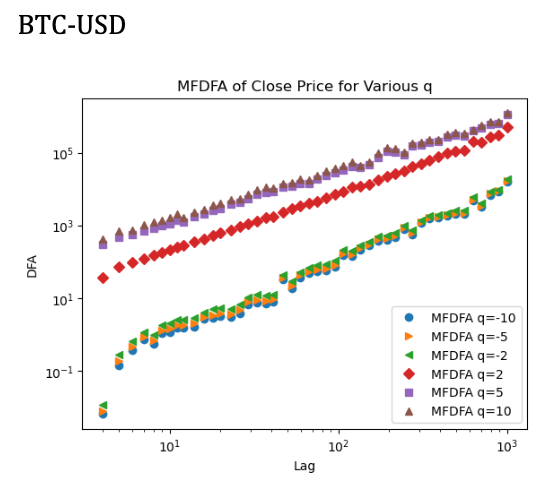
Рис 3. MF-DFA анализ цен BTC/USD. Источник

Симметрия во фрактальных финансовых структурах

Фракталы могут быть "точными" (паттерны повторяются точно) или "статистическими" (повторяются только статистические качества, с введением случайности). Финансовые временные ряды обычно рассматриваются как статистические фракталы, из-за присущего им шума и случайности. В то время как точная симметрия может быть менее заметна в зашумленных финансовых данных, концепция статистической симметрии (или ее отсутствия) имеет решающее значение.

Финансовые временные ряды часто демонстрируют статистические свойства, которые не являются идеально симметричными, такие как тяжелые хвосты и асимметрия, что является отклонением от симметрии нормального распределения. Эта статистическая асимметрия является ключевой фрактальной характеристикой. Это означает, что модели прогнозирования не могут полагаться на идеальное повторение паттернов, но должны использовать статистические закономерности и вероятностное прогнозирование.  

Точные фракталы строятся путем точного повторения паттерна при различных увеличениях, в то время как статистические фракталы вводят случайность, нарушая точное повторение, так что повторяются только статистические качества. Финансовые рынки по своей природе зашумлены и сложны, что делает их более похожими на статистические фракталы, где паттерны не идеально воспроизводятся, но имеют схожие статистические свойства в разных масштабах. Различие между точными и статистическими фракталами имеет решающее значение для реалистичного финансового моделирования. Хотя теоретическая красота точных фракталов обеспечивает концептуальную основу, практическое применение в финансах должно учитывать присущий "шум" и "случайность", которые делают финансовые фракталы статистическими.  

Распределения финансовых доходностей часто демонстрируют асимметрию (скошенность относительно среднего) и эксцесс (тяжелые хвосты), значительно отклоняясь от нормального распределения. Инвесторы обычно предпочитают положительную асимметрию (нечастые большие прибыли) и "тонкие" хвосты (положительный эксцесс, меньше экстремальных убытков).

Мультифрактальный анализ получил широкое распространение благодаря своей способности улавливать асимметричные рыночные риски, выявляя различные реакции на восходящие и нисходящие тренды и идентифицируя различные масштабирующие поведения. Исследования показывают асимметричные мультифрактальные характеристики в фондовых индексах, со значительными различиями в фрактальных спектрах для различных типов активов. Например, мультифрактальность может быть выше в нисходящем тренде для нефти и в восходящем тренде для золота в кризисные периоды.

Наблюдаемая асимметрия в финансовых доходностях, особенно в мультифрактальных свойствах, является прямым вызовом упрощенным рыночным моделям и предлагает сложный путь для управления рисками и прогнозирования. Признание того, что рыночное поведение (и, следовательно, предсказуемость) значительно различается во время восходящих и нисходящих трендов или в периоды кризиса, позволяет разрабатывать более адаптивные и надежные торговые стратегии, учитывающие эти нелинейные, асимметричные реакции.

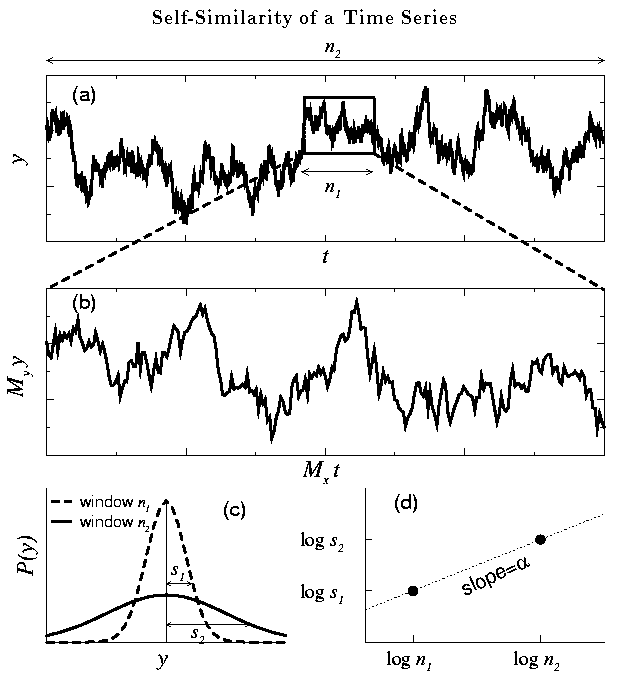
Рис 4. Пример статистической симметрии временного ряда. Источник

Взаимосвязь с теорией хаоса: непредсказуемость и странные аттракторы

Теория хаоса описывает системы с "чувствительной зависимостью от начальных условий", что означает, что крошечная ошибка в начальных условиях может привести к резким долгосрочным изменениям. Это явление часто называют "эффектом бабочки". Хаотические системы непредсказуемы в долгосрочной перспективе из-за этой чувствительности, а также из-за их апериодического поведения, фрактальных размерностей, нелинейности и странных аттракторов.

Финансовые рынки не являются полностью случайными, но функционируют в пределах хаотических, непериодических структур, называемых странными аттракторами, которые ограничивают поведение цен в определённых диапазонах.
Такая ограниченная непредсказуемость позволяет выявлять статистические паттерны и уровни поддержки/сопротивления. Концепция хаотических аттракторов объясняет, почему цены проявляют повторяющиеся, но не идентичные движения.

Гипотеза фрактальных рынков (FMH), предложенная Эдгаром Петерсом, утверждает, что рыночные данные обладают фрактальной структурой, зависящей от инвестиционных горизонтов. При кризисах структура разрушается, что ведёт к росту волатильности и снижению ликвидности. В отличие от ГЭР, FMH допускает периоды рыночной неэффективности и предсказуемости, особенно в стрессовых условиях.

Рис 5. Эффект бабочки на примере аттрактора Лоренца. Источник интерактивный

Синергетика и самоорганизация финансовых рынков

Синергетика изучает самоорганизацию сложных систем, в том числе финансовых рынков, где упорядоченные фрактальные структуры возникают без централизованного управления. Рынки функционируют как открытые нелинейные системы, способные переходить от хаоса к порядку под воздействием внутренних и внешних факторов.

Финансовые рынки обладают способностью самоорганизовываться, формируя фрактальные паттерны через обратные связи, информационные потоки и коллективное поведение участников. Эти паттерны — не внешние эффекты, а эмерджентные свойства системы.

Такая динамика объясняет устойчивость трендов, кластеризацию волатильности и наличие "рыночной памяти", предполагая, что понимание механизмов распространения информации и реакций инвесторов — ключ к анализу и прогнозу фрактального поведения рынков.

Прогностические свойства фрактальных и мультифрактальных характеристик

Фрактальные и мультифрактальные характеристики финансовых рядов дают ценные инструменты для анализа рынка. Показатель Херста (H) оценивает долгосрочную память:

• H > 0.5 — устойчивый тренд,

• H < 0.5 — возврат к среднему,

• H ≈ 0.5 — случайное блуждание.

Высокое значение H помогает точнее прогнозировать поведение рынка и выбирать подходящую стратегию: трендовую или контртрендовую. Также H используется для оценки рыночной турбулентности и обнаружения кризисных фаз.

Мультифрактальный анализ раскрывает степень рыночной «шероховатости» и масштабные закономерности. Ширина спектра (Δα) служит предиктором волатильности, рыночного режима и потенциальной доходности. Например, метод MS-CDE позволяет различать "бычий" и "медвежий" рынки по знаку α.

Фрактальные данные применимы в алгоритмической торговле, улучшая выбор уровней стоп-лосса, размера позиции и структуры портфеля. Анализ самоподобия помогает адаптировать стратегии под меняющиеся рыночные условия. Совмещение фрактальной размерности с машинным обучением повышает точность рыночных прогнозов и эффективность управления рисками.

 

Подход через определение симметричных фрактальных структур

Наш подход будет отличаться от вышеописанных подходов, которые используются, в основном, для оценки риска. Для эффективного краткосрочного предсказания направления рыночных колебаний необходимо определить, на основании чего будут осуществляться предсказания. В теоретической части уже введено понятие странных аттракторов и хаотических паттернов, которые описываются этими аттракторами.

Иными словами, графики котировок способны образовывать некие повторяющиеся структуры, под воздействием внешней организующей их информации. Участники рынка создают сложную динамическую систему, которая имеет элементы памяти, которая принимает вид определенных рыночных симметрий (паттернов). Эти паттерны могут эволюционировать во времени, а могут повторяться. Благодаря самоподобию фрактальных рыночных структур, паттерны могут быть выражены в разных временных масштабах.

В качестве отправной точки рассмотрим всем известное множество Мандельброта, на примере которого можно заметить самоповторение в масштабе.

Рис 6. Изображение множества Мандельброта

Множество Мандельброта можно разделить на отдельные части (крупные и малые), которые подобны друг другу. Возникает прямая аналогия с графиками финансовых котировок, которые формируют похожие структуры вне зависимости от того, какой временной период мы рассматриваем. Если закрыть временную шкалу на часовом и дневном графиках, рядовой трейдер вряд ли сможет отличить, к какому временному масштабу относится каждый из них.

Основные свойства множества Мандельброта:

Множество Мандельброта демонстрирует фрактальную структуру и самоподобие, напоминая графики финансовых котировок: их форма сохраняется на разных временных масштабах. Если скрыть шкалу, сложно отличить часовой график от дневного — как и различные части множества Мандельброта.

Ключевые свойства множества:

• Компактность и ограниченность: все точки лежат в круге радиуса 2; при превышении модуля 2 — точка не принадлежит множеству.

• Связность: множество непрерывно, несмотря на визуальную сложность.

• Приблизительное самоподобие: структура повторяется с вариациями.

• Симметрия по действительной оси.

• Фрактальная граница с бесконечной сложностью.

Дополнительные элементы:

• Кардиоида и луковицы: главная форма и её "спутники", повторяющие структуру множества.

• "Усики" и нити: тонкие соединения, формирующие единую связную структуру.

• Связь с множествами Жюлиа: каждая точка c соответствует множеству Жюлиа, которое может быть связным или нет.

• Периодические области: участки, где последовательность zn = zn² + c сходится к циклу. Это отражает бифуркации удвоения периода, ведущие к хаосу. Такие области визуально организуют сложность множества и указывают на переходы между стабильностью и хаосом.

Множество Мандельброта иллюстрирует, как простые правила порождают сложное поведение, демонстрируя связи с теорией хаоса, бифуркациями и визуализацией динамических систем. Его структура служит моделью для анализа рыночной динамики, сложных циклов и режимов поведения.

Таким образом, каждое конкретное множество Жюлиа, можно определить как отдельный строительный блок множества Мандельброта:

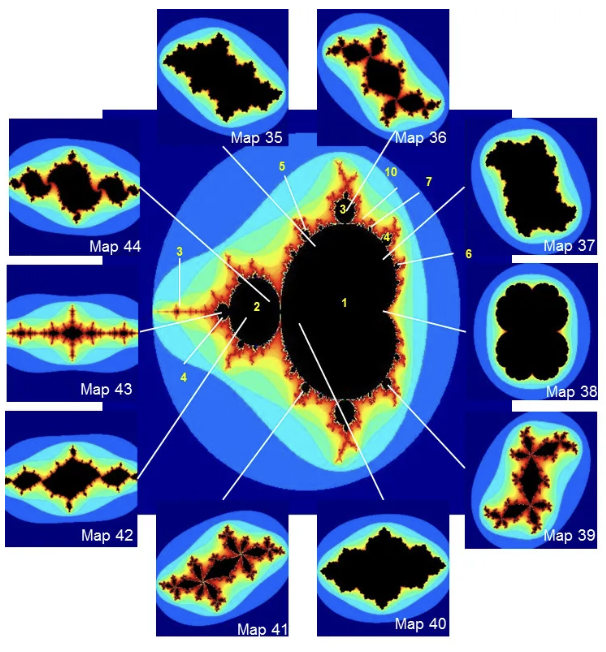
Рис 7. Множества Жюлиа как подмножества множества Мандельброта. Источник

Почему множества Жюлиа имеют притягивающие орбиты? Здесь кроется ключевая связь между множеством Мандельброта и множествами Жюлиа:

1. Связь с множеством Мандельброта:

   • Если параметр c принадлежит множеству Мандельброта (то есть c∈M), то соответствующее множество Жюлиа J(fc​) является связным. В этом случае, заполненное множество Жюлиа содержит притягивающие орбиты. Эти притягивающие орбиты (неподвижные точки или циклы) находятся во внутренней части заполненного множества Жюлиа.
   • Если параметр c не принадлежит множеству Мандельброта (то есть c∈/M), то соответствующее множество Жюлиа J(fc​) является несвязным. В этом случае, заполненное множество Жюлиа не содержит притягивающих орбит (кроме, возможно, бесконечности), и все точки либо уходят на бесконечность, либо являются частью сложной, хаотической динамики на самой границе множества.

2. Роль притягивающих орбит в динамике:

• Притягивающая орбита (аттрактор) — это такая последовательность точек, к которой "притягиваются" другие близлежащие точки. Если вы начнете итерации с точки, которая находится в "бассейне притяжения" (attraction basin) притягивающей орбиты, ваша последовательность zn​ в конечном итоге приблизится к этой орбите и будет оставаться рядом с ней.
• Когда множество Жюлиа связно (т.е. c∈M), это означает, что существует некоторая область точек, которые не "убегают" на бесконечность. Эти точки "застревают" в конечном регионе комплексной плоскости. Они это делают, потому что они притягиваются к притягивающей орбите (или множеству таких орбит), расположенной внутри заполненного множества Жюлиа.

Множества Жюлиа как аналогия "конкретных сценариев развития рынка"

Для каждого конкретного значения c (т.е. для каждой точки на "ландшафте Мандельброта") мы получаем свое уникальное множество Жюлиа. Это множество описывает динамику итераций для данного c: какие начальные точки z0​ останутся ограниченными (принадлежат заполненному множеству Жюлиа) и к каким аттракторам они сойдутся, а какие "убегут" в бесконечность.
Каждое конкретное множество Жюлиа для заданного c (который, в свою очередь, представляет собой "текущее состояние рынка" или "набор преобладающих параметров") может быть аналогией поведения рынка в этот конкретный момент времени или в данном "рыночном режиме".

• Если c находится внутри множества Мандельброта (например, в одной из "луковиц" периода 3), то соответствующее множество Жюлиа будет связным и будет иметь притягивающие орбиты. На рынке это может означать, что, несмотря на кажущуюся сложность, существуют определенные "притягивающие" уровни, цены или циклы, к которым рынок постоянно возвращается или вокруг которых он колеблется. Это могут быть сильные уровни поддержки/сопротивления, средние значения, к которым цена стремится вернуться (т.е. реверсия к среднему).
• Если же c находится вне множества Мандельброта, соответствующее множество Жюлиа является несвязным ("пылью Фату") и не имеет притягивающих орбит (кроме бесконечности). Это может быть аналогией крайне нестабильных или "взрывных" рыночных условий, когда цена не имеет никаких "якорей", стремится в бесконечность (например, гиперболический рост или коллапс), а любые малые возмущения приводят к непредсказуемому и радикально отличающемуся поведению. Любые торговые стратегии, основанные на "возврате к среднему", в таких условиях терпят крах.

Поскольку мы имеем слишком много аналогий, которые подтверждают возможность рассматривать рыночные котировки в качестве самоподобных фракталов, то имеем возможность составить представления о горизонтах прогнозирования таких структур.

• Если мы находимся внутри "тела" заполненного множества Жюлиа (то есть в области Фату), наш "горизонт прогнозирования" достаточно велик. Мы можем быть уверены, что траектория будет стремиться к притягивающей орбите.
• Если мы находимся на границе, которая является самим множеством Жюлиа, то наш "горизонт прогнозирования" стремится к нулю. Любое мельчайшее изменение в нашей начальной точке может отправить нас на совершенно другой путь.

Таким образом, "горизонты прогнозируемости" для множеств Жюлиа не являются фиксированными линиями или числами, а скорее зависят от того, в какой области комплексной плоскости мы находимся по отношению к этим фрактальным структурам. Внутри множества Фату прогнозируемость есть; на множестве Жюлиа её практически нет.

С помощью функции, которая будет предложена в статье, посвященной практическому применению фрактальных рыночных структур, мы сможем найти паттерны, которые удовлетворяют свойствам фракталов Жюлиа. Каждый из них имеет свой центр притяжения (или орбиту), обозначенный вертикальной пунктирной линией, от которой график отображает себя "зеркально" в прошлое и будущее. Это означает, что зеркально перевернутая правая часть графика будет иметь высокую корреляцию с левой частью.

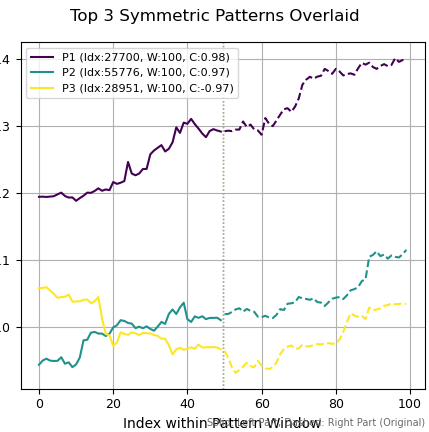
Рис 8. Найденные фракталы на графике EURUSD

На рисунке 8 найдены 3 фрактала, левая и правая части которых сильно коррелируют между собой. То есть, если бы мы знали центр притяжения (аттрактор или орбиту) заранее, а вернее его положение во времени, то могли бы с легкостью предсказать будущую динамику цен. Находясь в этой области фрактала Жюлиа (области Фату), рынки становятся понятными и прогнозируемыми. Мы будем использовать это свойство фракталов для прогнозирования рыночной динамики с помощью машинного обучения.

Изображение ниже было сгенерировано мной при помощи нейросети для того, чтобы визуально подчеркнуть наличие аттрактора и точки притяжения на участке графика. Цены "танцуют" вокруг светящегося центра орбиты, образуя зеркальную симметричную структуру. Это изображение очень точно передает смысл фрактальных симметрий, которые будут исследоваться. Вы можете сравнить Рис 8. и Рис 9. для визуального понимания концепции рыночных фракталов. 

Рис 9. Визуализация аттрактора на финансовом графике

Вызовы и ограничения применения фрактальной теории в финансах

Несмотря на значительный прогностический потенциал фрактальной теории, ее применение в финансах сопряжено с рядом вызовов и ограничений. Финансовые данные известны своей зашумленностью, что усложняет выявление четких самоподобных паттернов. Финансовые временные ряды часто являются нестационарными, то есть их статистические свойства меняются со временем, что создает проблему для традиционных методов анализа. Необходимы надежные методы для улавливания развивающейся рыночной динамики. Оценка точности показателя Херста может быть сложной.

Показатель Херста не является детерминированным, поскольку его можно оценить только на основе наблюдаемых данных. Присущий финансовым данным шум и нестационарность представляют собой значительные методологические препятствия для фрактального анализа. Хотя передовые методы, такие как MF-DFA, разработаны для смягчения этих проблем , они вносят сложности в оценку параметров и проверку моделей. Это означает, что, хотя фрактальные свойства предлагают прогностический потенциал, их извлечение и надежное применение требуют сложной предварительной обработки данных и надежной статистической проверки, признавая динамический характер рыночных параметров.  

Кроме того, сложные модели, основанные на фрактальной теории, часто требуют значительных вычислительных ресурсов и экспертных знаний для правильной реализации. Крайне важно найти баланс между сложностью модели и ее интерпретируемостью. Сложные модели могут улавливать запутанные паттерны в данных, но часто им не хватает прозрачности, что затрудняет их интерпретацию и практическое использование. Анализ больших финансовых наборов данных требует значительных вычислительных ресурсов и масштабируемых алгоритмов.

Вычислительная интенсивность и проблемы интерпретируемости, связанные со сложными фрактальными и мультифрактальными моделями, подчеркивают практический компромисс в финансовых приложениях. Хотя эти модели предлагают более глубокие представления и потенциально лучшую прогностическую силу, их реализация требует значительных технических знаний, что может ограничивать их доступность и применимость в реальном времени для многих пользователей.  

Заключение вводной части и перспективы исследований

Финансовые временные ряды демонстрируют фрактальные и мультифрактальные свойства, включая самоподобие, долгосрочную память (показатель Херста) и масштабную гетерогенность (мультифрактальный спектр). Эти особенности расширяют традиционные подходы, обеспечивая более точное прогнозирование трендов, волатильности и рыночных режимов.

Фрактальный анализ открывает путь к адаптивным алгоритмическим стратегиям и улучшенному управлению рисками, учитывающим нелинейность и асимметрию рынка. Его дальнейшее развитие требует интеграции с машинным обучением, аналитикой больших данных и создания моделей, способных учитывать динамику рыночных режимов и влияние информационных потоков.

Будущие исследования должны сосредоточиться на:

• адаптивных мультифрактальных моделях;
• устойчивости оценки параметров в зашумленных условиях;
• изучении причинно-следственных связей в рыночной самоорганизации;
• поиске "оптимального диапазона сложности" как индикатора рыночной устойчивости.

Будущее фрактального анализа — в его синергии с ИИ, ведущей к "хаотическому обучению": количественным прогнозам на основе кажущейся хаотичности рынка.