
Алгоритм оптимизации динго — Dingo Optimization Algorithm (DOA)
Содержание
Введение
В этой статье мы познакомимся с алгоритмом оптимизации динго (Dingo Optimization Algorithm, DOA), который был разработан в 2021 году международной группой исследователей под руководством Эрнана Пераса-Васкеса (Hernán Peraza-Vázquez). Работа была опубликована в журнале Mathematical Problems in Engineering (DOI: 10.1155/2021/9107547).
Алгоритм вдохновлен охотничьим поведением австралийских динго (Canis lupus dingo) — крупнейших хищных млекопитающих Австралии. Динго демонстрируют сложное социальное поведение и используют различные стратегии охоты в зависимости от размера и типа добычи.
Реализация алгоритма
DOA моделирует три основные охотничьи стратегии динго:
- Групповая атака — динго окружают добычу и атакуют совместно, что особенно эффективно при охоте на крупную дичь, такую как кенгуру;
- Преследование — индивидуальная погоня за мелкой добычей, когда динго преследует жертву до изнеможения;
- Поиск падали — оппортунистическое поведение при исследовании новых территорий и поиске мертвой добычи.
Дополнительно алгоритм включает механизм выживания, который обновляет позиции слабых особей в популяции, имитируя естественный отбор. Алгоритм балансирует между исследованием (exploration) и эксплуатацией (exploitation) пространства поиска через два вероятностных параметра: P — вероятность выбора между охотой и поиском падали и Q — вероятность выбора между групповой атакой и преследованием при охоте.
Представьте, что у вас есть стая из 50 динго, которые ищут оптимальное место для охоты на большой территории. Каждый динго представляет потенциальное решение задачи оптимизации, а территория — это пространство поиска.
1. Групповая атака (вероятность 35%). Танец хищников
В австралийской саванне стая динго окружает стадо кенгуру. Это не хаотичная погоня, а скоординированная операция. Несколько особей — от двух храбрецов до половины стаи — выдвигаются вперед, формируя невидимую сеть позиций.
Каждый атакующий динго делится своим опытом с группой — где он находится, что видит. Их коллективное знание сливается в единую точку понимания, усредненную мудрость стаи. Однако наступает парадокс охоты: новая позиция определяется движением прочь от альфы, от лидера. Почему? Потому что если все будут слепо следовать за вожаком, стая превратится в предсказуемую толпу. Коэффициент β₁ действует как сила ветра — иногда попутного (положительный), иногда встречного (отрицательный), создавая непредсказуемые маневры для стаи. В результате: хаос, управляемый логикой. Динго расходятся веером по территории, исследуя те углы охотничьих угодий, которые лидер мог упустить из виду. Пока это предположения, которые необходимо закрепить практикой.
Когда динго охотятся группой, случайным образом выбирается от 2 до 25 особей для атаки. Новая позиция динго рассчитывается как:
Новая_позиция = β₁ × (Средняя_позиция_атакующих) - Позиция_лидера
Пример: Если 5 динго находятся в точках [10, 20, 30, 40, 50], их средняя позиция = 30. При β₁ = 1.5 и позиции лидера = 45:
Новая позиция = 1.5 × 30 - 45 = 0
Динго движется в сторону от лидера, исследуя новые области.
2. Преследование (вероятность 35%). Одинокий охотник
Молодой динго отделяется от стаи. Перед ним — заяц, быстрый и изворотливый. Это персональная охота, где важна не сила группы, а индивидуальное мастерство. Динго держит в поле зрения две точки: позицию альфы (накопленная мудрость лучшего охотника) и случайного соплеменника поблизости. Расстояние до соседа определяет размах броска — чем дальше сосед, тем смелее прыжок. Экспоненциальная функция e^β₂ работает как адреналин в крови: при положительном β₂ — всплеск энергии, удлинение прыжка; при отрицательном — осторожность, короткие точные движения.
Траектория погони извилиста: динго движется к позиции лидера, но его путь искажается присутствием соседа, создавая спираль преследования, которая постепенно сжимается вокруг цели. Одиночная охота, где динго движется относительно лидера стаи и случайного соседа:
Пример: Лидер в точке 100, текущий динго в точке 60, сосед в точке 80:
При β₁ = 1.5, β₂ = 0.5: Новая позиция = 100 + 1.5 × e^0.5 × |80 - 60| = 100 + 1.5 × 1.65 × 20 ≈ 149.5
Динго движется за лидером, но с учетом расстояния до соседа.
3. Поиск падали (вероятность 30%). Блуждание оппортуниста
Полуденное солнце жжет красную землю. Некоторые динго переключаются в режим падальщика — это не признак слабости, а эволюционная мудрость. Зачем тратить энергию на погоню, если можно найти готовую добычу?
Динго-падальщик выбирает случайного соседа как ориентир, но тут происходит квантовый трюк: с вероятностью 50% его собственная позиция "отражается" через ноль (умножается на -1), словно он видит свое зеркальное отражение в водопое. Это создает огромную дистанцию для расчета — расстояние между реальным соседом и призрачным "анти-собой".
Новая позиция определяется как часть фантомного расстояния, скорректированная с учётом экспоненциального влияния настроения (e^β₂). Результат: непредсказуемые прыжки по территории, исследование самых неожиданных мест. Именно так находятся скрытые оазисы и забытые туши.
Исследовательское поведение для поиска новых областей:
Пример: Текущая позиция = 40, сосед = 70, β₂ = 0.3, знак положительный:
Новая позиция = 0.5 × e^0.3 × |70 - 40| = 0.5 × 1.35 × 30 ≈ 20.25
Это создает более случайное движение для исследования пространства.
4. Механизм выживания. Второй шанс для отстающих
В любой стае есть аутсайдеры. Их показатель выживания падает ниже критической отметки 0.3 — они находятся в невыгодных позициях, их попытки охоты неудачны. Природа дает им шанс на перерождение. Слабый динго получает "генетическую инъекцию" от двух случайных сородичей. Их позиции, возможно с инверсией одной из них (природная мутация), создают вектор изменения. Этот вектор, уменьшенный вдвое для безопасности, добавляется к позиции альфы.
Метафора проста: слабый следует за сильным, но с примесью случайности от генофонда стаи. Это не просто копирование лидера — это управляемая эволюция, где неудачники получают направление, но сохраняют индивидуальность. После каждой итерации рассчитывается "показатель выживания" для каждого динго:
Выживаемость = (Худший_результат - Текущий_результат) / (Худший - Лучший)
Если выживаемость < 0.3 (слабая особь), позиция обновляется:
Пример:
Слабый динго: позиция [5, 5], fitness = 90 (плохой)
Лидер: [45, 50]
Динго r₁: [30, 35]
Динго r₂: [25, 20]
σ = 0 (положительный знак)
Вектор разности = |[30, 35] - [25, 20]| = |[5, 15]| = [5, 15]; Новая позиция = [45, 50] + 0.5 × [5, 15] = [45, 50] + [2.5, 7.5] = [47.5, 57.5]
Перемещаем слабые решения ближе к лидеру с небольшой случайной вариацией. Теперь можем обобщить всю информацию в алгоритм пошагово:
- Инициализация: Размещаем 50 динго случайно в пространстве поиска
- Основной цикл (500 итераций):
- Для каждого динго генерируем β₁ ∈ [-2, 2] и β₂ ∈ [-1, 1]
- Бросаем "монетку" с вероятностью P = 0.5:
- Если выпала охота, бросаем еще раз с Q = 0.7:
- 70% шанс → групповая атака
- 30% шанс → преследование
- Если выпал поиск падали → используем стратегию падали
- Если выпала охота, бросаем еще раз с Q = 0.7:
- Проверяем выживаемость и при необходимости применяем процедуру выживания
- Обновление: Запоминаем лучшее найденное решение
Представленная ниже иллюстрация визуализирует все четыре стратегии алгоритма DOA: групповая атака — показывает, как несколько динго формируют среднюю позицию и движутся от лидера, преследование — демонстрирует движение к лидеру с учетом расстояния до соседа, поиск падали — иллюстрирует случайное исследование с возможной инверсией позиции и выживание — показывает перемещение слабых особей к лидеру с добавлением случайного вектора. Каждая стратегия включает математическую формулу и визуальное представление векторов движения.
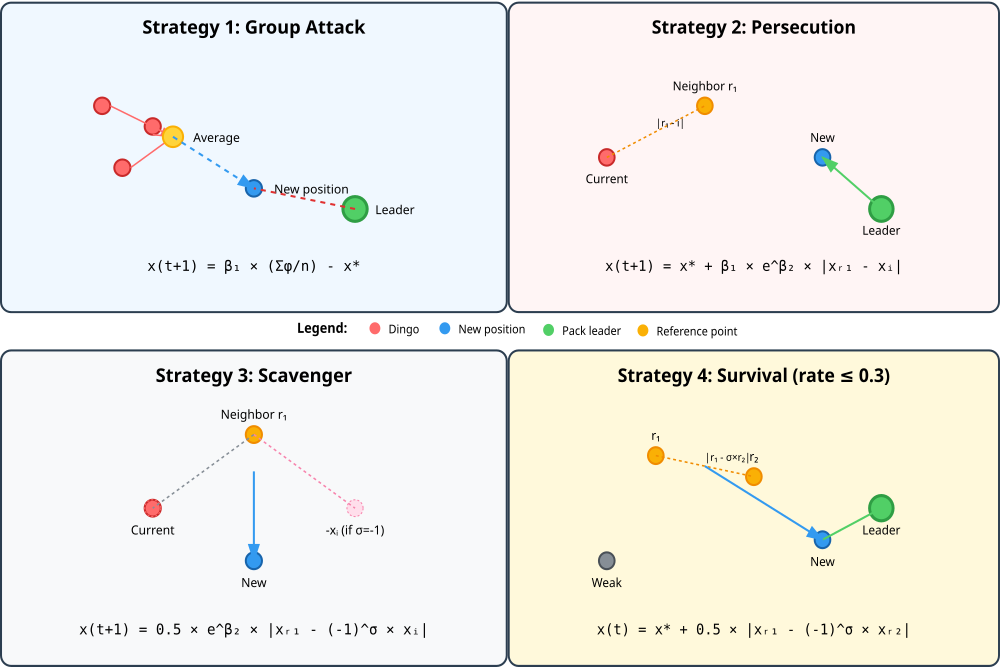
Рисунок 1. Математическое моделирование стратегий охоты динго
После детального разбора, перейдем к написанию кода. Класс "C_AO_DOA_dingo" представляет собой реализацию алгоритма оптимизации DOA и является производным от более общего класса "C_AO", что подразумевает наличие унаследованной функциональности для поддержки алгоритмов оптимизации. Основные характеристики класса.
Параметры алгоритма:- popSize — определяет размер "популяции" (количество "динго").
- P — отвечает за вероятность выбора между двумя стратегиями поведения динго: охотой или поиском падали.
- Q — определяет вероятность групповой атаки или преследования добычи.
Инициализация: метод "Init ()" является точкой входа для инициализации алгоритма, принимая диапазоны допустимых значений параметров, шаги их изменения и количество эпох (циклов работы алгоритма).
Основной цикл:
- Moving () — метод реализует основную фазу "движения" или поиска решения алгоритмом, где агенты (динго) взаимодействуют и перемещаются в пространстве поиска.
- Revision () — метод отвечает за "пересмотр" принятых решений, оценку результатов и корректировку поведения агентов.
- survival — массив, хранящий показатели "выживаемости" каждого агента.
- attackVector — массив, используемый для записи индексов агентов, участвующих в атаке.
- UpdateSurvivalRates () — обновляет показатели выживаемости агентов.
- GroupAttack () — реализует стратегию групповой атаки.
- Persecution () — описывает процесс преследования добычи.
- Scavenger () — реализует поведение поиска падали.
- SurvivalProcedure () — выполняет процедуру, связанную с выживанием агента.
В целом, класс "C_AO_DOA_dingo" моделирует поведение группы динго, используя их природные инстинкты охоты, поиска падали и группового взаимодействия для решения задач оптимизации. Он обладает гибкой системой параметров, позволяющей настраивать его поведение, и использует ряд внутренних методов для симуляции процессов, приводящих к поиску оптимального решения.
//———————————————————————————————————————————————————————————————————— class C_AO_DOA_dingo : public C_AO { public: //---------------------------------------------------------- ~C_AO_DOA_dingo () { } C_AO_DOA_dingo () { ao_name = "DOA"; ao_desc = "Dingo Optimization Algorithm"; ao_link = "https://www.mql5.com/ru/articles/19458"; popSize = 50; // размер популяции (количество динго) P = 0.5; // вероятность охоты или поиска падали Q = 0.7; // вероятность групповой атаки или преследования ArrayResize (params, 3); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "P"; params [1].val = P; params [2].name = "Q"; params [2].val = Q; } void SetParams () { popSize = (int)params [0].val; P = params [1].val; Q = params [2].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); //------------------------------------------------------------------ double P; // вероятность охоты или поиска падали double Q; // вероятность групповой атаки или преследования private: //--------------------------------------------------------- double survival []; // массив показателей выживания int attackVector []; // массив для хранения индексов атакующих // Вспомогательные методы void UpdateSurvivalRates (); void GroupAttack (int agentIdx, int na, double beta1); void Persecution (int agentIdx, double beta1, double beta2); void Scavenger (int agentIdx, double beta2); void SurvivalProcedure (int agentIdx); }; //————————————————————————————————————————————————————————————————————
Метод "Init" является точкой входа для инициализации алгоритма DOA. Он выполняет следующие ключевые задачи:
Стандартная инициализация:
- При первой строке вызывается другой метод "StandardInit", он выполняет общие для всех алгоритмов оптимизации действия по настройке диапазонов поиска параметров (rangeMinP, rangeMaxP) и шагов их изменения (rangeStepP).
- Если стандартная инициализация завершается неудачно (возвращает "false"), то метод также прерывает свою работу.
//———————————————————————————————————————————————————————————————————— //--- Инициализация bool C_AO_DOA_dingo::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; ArrayResize (survival, popSize); ArrayInitialize (survival, 1.0); // Резервируем максимальный размер для вектора атакующих ArrayResize (attackVector, popSize / 2); return true; } //————————————————————————————————————————————————————————————————————
Метод "Moving", является основной функцией, выполняющей один итерационный шаг алгоритма. Он моделирует поведение популяции "динго", направленное на поиск оптимального решения.
Первоначальная инициализация: при первом вызове, когда флаг "revision" установлен в ложное значение, метод случайным образом распределяет значения для всех параметров (координат) каждой особи в популяции. Диапазоны и шаги для этих параметров задаются заранее. После инициализации флаг "revision" устанавливается в истинное значение, и метод завершает работу на этом шаге.
Оценка выживаемости: Если инициализация уже проведена, метод сначала вызывает подпрограмму для обновления показателей "выживаемости" всех особей в популяции. Этот показатель отражает, насколько хорошо текущее решение (позиция особи) соответствует поставленной цели или насколько оно "пригодно". Затем метод проходит по каждой особи в популяции.
Для текущей особи генерируются два случайных параметра. Эти параметры влияют на специфику выбранной стратегии поведения. Основываясь на вероятностных соотношениях, особь выбирает одну из стратегий:- Вероятность P: если случайное число меньше "P", особь переходит к стратегии "охоты".
- Вероятность Q (в рамках охоты): если особь выбрала "охоту", то с вероятностью "Q" она применяет "групповую атаку". При групповой атаке особь перемещается, учитывая позиции нескольких других особей популяции. Количество участвующих других особей определяется случайным образом в определенном диапазоне.
- Преследование (в рамках охоты): если особь выбрала "охоту", но не "групповую атаку" (с вероятностью 1-Q), она применяет стратегию "преследования". При преследовании особь перемещается, ориентируясь на лучшие решения, атакуя "добычу".
- Поиск падали (альтернатива охоте): если случайное число больше или равно "P", особь выбирает стратегию "поиск падали". Эта стратегия, имитирует поиск оставшейся добычи или случайное исследование пространства решений.
- Проверка на выживаемость и корректировка: после применения основной выбранной стратегии (охота/преследование/поиск падали), метод проверяет показатель выживаемости текущей особи. Если выживаемость ниже определенного порога (в данном случае 0.3), применяется специальная "процедура выживания". Эта процедура направлена на то, чтобы помочь слабой особи улучшить свои показатели или выжить, путем изменения позиции.
Таким образом, метод "Moving" управляет эволюцией популяции, позволяя каждой особи принимать решения о своем поведении, взаимодействовать с другими и адаптироваться к условиям, имитируя естественное поведение динго.
//———————————————————————————————————————————————————————————————————— //--- Основной шаг алгоритма void C_AO_DOA_dingo::Moving () { // Начальная инициализация популяции if (!revision) { for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = u.RNDfromCI (rangeMin [j], rangeMax [j]); a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } revision = true; return; } //------------------------------------------------------------------ // Обновляем показатели выживания для всей популяции UpdateSurvivalRates (); // Основной цикл по всем динго for (int i = 0; i < popSize; i++) { // Генерируем beta для каждого агента double beta1 = u.RNDfromCI (-2.0, 2.0); double beta2 = u.RNDfromCI (-1.0, 1.0); // Сначала выбираем стратегию if (u.RNDprobab () < P) // Охота { if (u.RNDprobab () < Q) // Групповая атака { // Стратегия 1: Групповая атака (Eq. 2) int na = 2 + (int)((popSize / 2 - 2) * u.RNDprobab ()); GroupAttack (i, na, beta1); } else // Преследование { // Стратегия 2: Преследование (Eq. 3) Persecution (i, beta1, beta2); } } else // Поиск падали { // Стратегия 3: Поиск падали (Eq. 4) Scavenger (i, beta2); } // После основной стратегии проверяем выживаемость if (survival [i] <= 0.3) { // Стратегия 4: Процедура выживания для слабых особей (Eq. 6) SurvivalProcedure (i); } } } //————————————————————————————————————————————————————————————————————
Следующий метод "GroupAttack" реализует одну из основных стратегий поведения в алгоритме – Стратегия 1: Групповая атака. Он моделирует ситуацию, когда группа динго объединяется для атаки.
Выбор участников атаки. Метод сначала определяет, сколько других особей (динамическое количество "na") будет участвовать в атаке вместе с текущей особью "agentIdx". Затем он случайным образом выбирает "na" уникальных индексов особей из всей популяции. Эти выбранные особи и будут формировать "атакующую группу". Важно, чтобы выбранные особи были разными, чтобы избежать повторного использования одной и той же особи.
Применение формулы атаки. Метод проходит по каждой координате (параметру) решения "c". Для каждой координаты он вычисляет среднее значение этой координаты среди всех особей, входящих в атакующую группу. Затем, используя это среднее значение, параметр "beta1" (который был сгенерирован ранее), и значение "cB [c]" (представляет собой текущее лучшее известное решение), вычисляет новое значение для данной координаты текущей особи "agentIdx". Формула обновления позиции основана на вычитании из лучшего решения произведения "beta1" на среднее значение координаты особей.
После вычисления нового значения для координаты, оно приводится в соответствие с допустимыми границами и шагом дискретизации, аналогично тому, как это делалось при инициализации.
//———————————————————————————————————————————————————————————————————— //--- Стратегия 1: Групповая атака (Equation 2) void C_AO_DOA_dingo::GroupAttack (int agentIdx, int na, double beta1) { // x_i(t+1) = beta1 * [sum(phi_k(t))/na] - x*(t) // Формируем подмножество атакующих динго ArrayResize (attackVector, na); int count = 0; while (count < na) { int idx = u.RNDintInRange (0, popSize - 1); bool unique = true; for (int j = 0; j < count; j++) { if (attackVector [j] == idx) { unique = false; break; } } if (unique) { attackVector [count++] = idx; } } // Применяем формулу for (int c = 0; c < coords; c++) { double sum = 0.0; for (int j = 0; j < na; j++) { sum += a [attackVector [j]].c [c]; } //a [agentIdx].c [c] = beta1 * (sum / na) - cB [c]; a [agentIdx].c [c] = cB [c] - beta1 * (sum / na); a [agentIdx].c [c] = u.SeInDiSp (a [agentIdx].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } //————————————————————————————————————————————————————————————————————
Метод "Persecution" (Преследование), реализует Стратегию 2, основанную на принципе "преследования" некоторого целевого объекта. Данная стратегия предназначена для обновления позиции одной конкретной особи в популяции. Метод сначала выбирает случайную другую особь из популяции. Эта особь будет называться "атакующей" (r1). Важно, чтобы атакующей особью не была сама особь, которую мы обновляем (то есть "agentIdx" не должна совпадать с "r1").
Стратегия "Преследование" пытается переместить целевую особь (agentIdx) в направлении, определяемом комбинацией лучшего найденного решения (cB) и разницы между случайной другой особью и самой целевой особью.
- cB (лучшее решение) обеспечивает, что движение направлено к лучшему известному решению.
- beta1 и exp (beta2), эти параметры контролируют "силу" или "дальность" шага преследования. Большая "beta1" или "beta2" приведет к более значительным смещениям.
- |x_r1 (t) - x_i (t)| (разница)определяет, насколько далеко находится другая особь. Чем больше разница, тем сильнее эффект от преследования.
Таким образом, данная стратегия моделирует поведение, когда одна особь (или, правильнее сказать, ее действия) пытается "догнать" или приблизиться к другой столь же случайной особи, но вся эта динамика смещена в сторону наилучшего найденного в популяции решения.
//———————————————————————————————————————————————————————————————————— //--- Стратегия 2: Преследование (Equation 3) void C_AO_DOA_dingo::Persecution (int agentIdx, double beta1, double beta2) { // x_i(t+1) = x*(t) + beta1 * exp(beta2) * |x_r1(t) - x_i(t)| int r1; do { r1 = u.RNDintInRange (0, popSize - 1); } while (r1 == agentIdx); double expBeta2 = MathExp (beta2); for (int c = 0; c < coords; c++) { double diff = MathAbs (a [r1].c [c] - a [agentIdx].c [c]); a [agentIdx].c [c] = cB [c] + beta1 * expBeta2 * diff; a [agentIdx].c [c] = u.SeInDiSp (a [agentIdx].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } //————————————————————————————————————————————————————————————————————
Метод "Scavenger" описывает Стратегию 3: Поиск падали, имитируя поведение особи (динго), которая ищет останки. В первую очередь, метод выбирает случайным образом другую особь (r1) из всей популяции. Эта особь становится "объектом интереса" для поиска. Выбранная особь не может быть той же самой, что и текущая особь, выполняющая поиск. Для определения направления поиска используется случайный знак "sigma". Этот знак может быть либо +1, либо -1, выбирается случайным образом. Это добавляет элемент непредсказуемости в направление поиска.
Далее, для каждой характеристики (координаты) решения: вычисляется разница между значением данной характеристики у другой особи и у текущей особи, умноженное на случайно выбранный знак "sigma". Это означает, что текущая позиция особи либо добавляется, либо вычитается из позиции другой особи. Из этой разницы берется абсолютное значение (MathAbs), чтобы получить величину расстояния.
Эта абсолютная разница умножается на половину экспоненты от "beta2", этот параметр, возведенный в степень, определяет, насколько сильно будет меняться позиция. Множитель 0.5 масштабирует это влияние. Полученное в результате умножения значение становится новой координатой для текущей особи. Как и в других методах, новое значение координаты затем ограничивается допустимыми пределами, определенными "rangeMin", "rangeMax" и "rangeStep".
Стратегия "Поиск падали" побуждает особь перемещаться на расстояние, зависящее от разницы ее собственного положения с положением другой особи, причем это направление может быть как "впереди", так и "позади" текущей особи, определяемое случайным знаком "sigma". Сила этого перемещения также регулируется через параметр "beta2". Эта стратегия добавляет элемент более случайного и, возможно, менее целенаправленного поиска, моделируя поведение, когда особь может следовать по следу добычи или искать останки.
//———————————————————————————————————————————————————————————————————— //--- Стратегия 3: Поиск падали (Equation 4) void C_AO_DOA_dingo::Scavenger (int agentIdx, double beta2) { // x_i(t+1) = 0.5 * exp(beta2) * |x_r1(t) - (-1)^sigma * x_i(t)| int r1; do { r1 = u.RNDintInRange (0, popSize - 1); } while (r1 == agentIdx); double sigma = u.RNDbool () ? 1.0 : -1.0; double halfExpBeta2 = 0.5 * MathExp (beta2); for (int c = 0; c < coords; c++) { double diff = MathAbs (a [r1].c [c] - sigma * a [agentIdx].c [c]); a [agentIdx].c [c] = halfExpBeta2 * diff; a [agentIdx].c [c] = u.SeInDiSp (a [agentIdx].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } //————————————————————————————————————————————————————————————————————
Метод "SurvivalProcedure" описывает Стратегию 4: Процедура выживания. Он имитирует сценарий, в котором особь (динго) обновляет свое положение, пытаясь выжить или улучшить свои шансы, основываясь на положении других особей.
Метод выбирает двух различных особей (r1 и r2) из популяции, каждая из которых обязательно отличается от текущей особи, выполняющей процедуру выживания (agentIdx). Также, эти две выбранные особи должны быть разными друг от друга.
Для каждой характеристики (координаты) производится случайное изменение знака (sigma). Этот знак может быть либо +1, либо -1, выбирается случайным образом. Это определяет, участвует ли вторая особь (r2) в расчете напрямую или с инвертированным значением. Для каждой координаты:
- вычисляется разница между соответствующими характеристиками выбранной первой особи (a [r1].c [c]) и второй особи (a [r2].c [c]), к которой применяется случайный знак "sigma";
- берется абсолютное значение этой разницы "diff";
- полученная абсолютная разница умножается на 0.5;
- к текущему лучшему известному решению (cB [c]) добавляется половина этой разницы. Это означает, что новая позиция особи сдвигается от лучшего решения в направлении, определяемом разницей между двумя другими особями. Рассчитанное новое значение становится новой координатой для текущей особи;
- как и в предыдущих методах, полученное значение координаты затем корректируется, чтобы остаться в пределах допустимых границ.
Стратегия "Процедура выживания" представляет собой механизм, где индивид обновляет свою позицию, используя информацию от двух других индивидов. Обновление позиции происходит как смещение от текущего лучшего решения (cB), причем величина и направление этого смещения зависят от разницы в положениях двух случайных особей. Это можно интерпретировать как поиск "ниши" или "ресурса", который находится где-то посередине между двумя другими особями, но с некоторой случайностью в определении того, куда именно двигаться.
//———————————————————————————————————————————————————————————————————— //--- Стратегия 4: Процедура выживания (Equation 6) void C_AO_DOA_dingo::SurvivalProcedure (int agentIdx) { // x_i(t) = x*(t) + 0.5 * |x_r1(t) - (-1)^sigma * x_r2(t)| int r1, r2; r1 = u.RNDintInRange (0, popSize - 1); while (r1 == agentIdx) { r1 = u.RNDintInRange (0, popSize - 1); } r2 = u.RNDintInRange (0, popSize - 1); while (r2 == agentIdx || r2 == r1) { r2 = u.RNDintInRange (0, popSize - 1); } double sigma = u.RNDbool () ? 1.0 : -1.0; for (int c = 0; c < coords; c++) { double diff = MathAbs (a [r1].c [c] - sigma * a [r2].c [c]); a [agentIdx].c [c] = cB [c] + 0.5 * diff; a [agentIdx].c [c] = u.SeInDiSp (a [agentIdx].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } //————————————————————————————————————————————————————————————————————
Метод "UpdateSurvivalRates" отвечает за обновление показателей выживания для каждой особи в популяции. Это важный шаг, который помогает определить, насколько вероятно, что каждая особь сможет "выжить" и сохранить свое положение (или, наоборот, быть отброшенной) в процессе эволюции.
Сначала метод проходит по всем особям в популяции, чтобы определить две крайние величины: минимальную пригодность (minFitness) и максимальную пригодность (maxFitness). При этом первая особь берется в качестве начального предположения для этих значений. Затем вычисляется диапазон (range) между максимальной и минимальной пригодностью. Этот диапазон отражает вариативность успешности решений в текущей популяции.
Если диапазон пригодности равен нулю (это означает, что все особи имеют одинаковую пригодность), то показатель выживания для каждой особи устанавливается в значение 0.5. В этом случае делается предположение, что все особи имеют равные шансы на выживание, так как нет явного лидера или аутсайдера.
Если диапазон пригодности не равен нулю, то для каждой особи вычисляется ее показатель выживания (survival [i]), который рассчитывается по формуле: (максимальная пригодность — пригодность текущей особи) / диапазон пригодности.
Метод нормализует пригодность каждой особи к лучшим и худшим в популяции, преобразуя ее в показатель, который затем будет использоваться другими частями алгоритма для принятия решений о том, какие особи должны менять свое положение более активно, а какие — сохранять.
//———————————————————————————————————————————————————————————————————— //--- Обновление показателей выживания (Equation 5) void C_AO_DOA_dingo::UpdateSurvivalRates () { // survival(i) = (fitness_max - fitness(i)) / (fitness_max - fitness_min) double minFitness = a [0].f; double maxFitness = a [0].f; for (int i = 1; i < popSize; i++) { if (a [i].f < minFitness) minFitness = a [i].f; if (a [i].f > maxFitness) maxFitness = a [i].f; } double range = maxFitness - minFitness; if (range < DBL_EPSILON) { ArrayInitialize (survival, 0.5); } else { for (int i = 0; i < popSize; i++) { survival [i] = (maxFitness - a [i].f) / range; } } } //————————————————————————————————————————————————————————————————————
Метод "Revision" является критически важным для большинства эвристических алгоритмов оптимизации. Его задача — сохранить лучшее решение, найденное на данный (или любой предыдущий) момент времени. Это гарантирует, что алгоритм не "забудет" о хорошем решении, даже если другие особи будут развиваться и, возможно, найдут решения, которые временно покажутся менее успешными. Таким образом, "fB" и "cB" всегда хранят наилучшую найденную конфигурацию пригодности и ее соответствующие координаты.
//———————————————————————————————————————————————————————————————————— //--- Обновление лучшего решения void C_AO_DOA_dingo::Revision () { for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //————————————————————————————————————————————————————————————————————
После реализации такого перспективного и многогранного метода оптимизации, наконец, можем приступить к тестированию.
Результаты тестов
По результатам тестов алгоритм набирает 35% от 100% возможных, ожидания, к сожалению, не совсем оправдались.
=============================
5 Hilly's; Func runs: 10000; result: 0.49066480903390775
25 Hilly's; Func runs: 10000; result: 0.399914179876301
500 Hilly's; Func runs: 10000; result: 0.35798310869836164
=============================
5 Forest's; Func runs: 10000; result: 0.29643143556801427
25 Forest's; Func runs: 10000; result: 0.20458050042664944
500 Forest's; Func runs: 10000; result: 0.17091405461356773
=============================
5 Megacity's; Func runs: 10000; result: 0.36615384615384616
25 Megacity's; Func runs: 10000; result: 0.4489230769230771
500 Megacity's; Func runs: 10000; result: 0.45393846153845924
=============================
All score: 3.18950 (35.44%)
На визуализации по сложному рисунку движения агентов можно заметить, как меняются стратегии алгоритма. В целом, странное распределение особей-агентов по "диагонали" пространства поиска указывает на возможную ошибку во внутренней логике алгоритма, допущенную авторами.
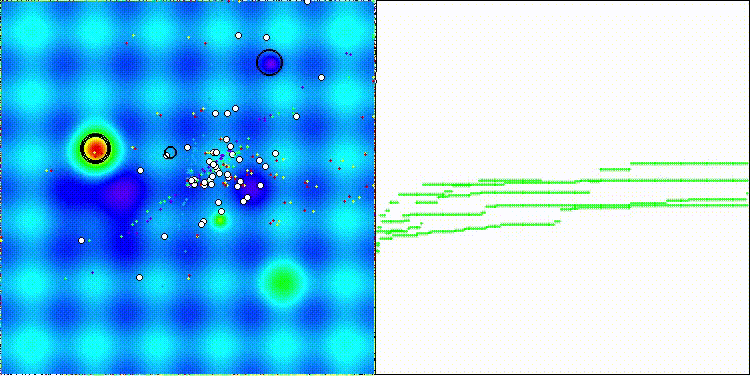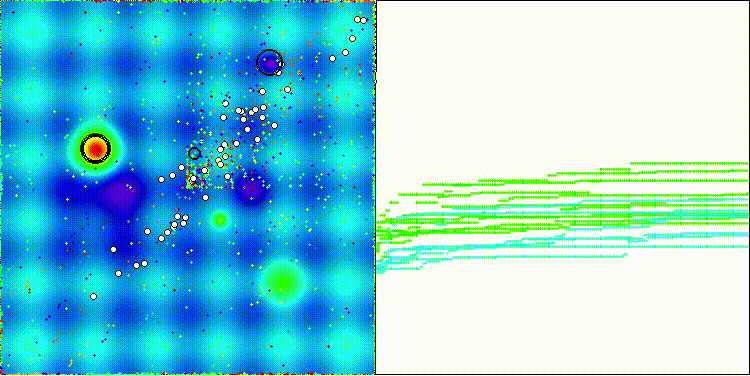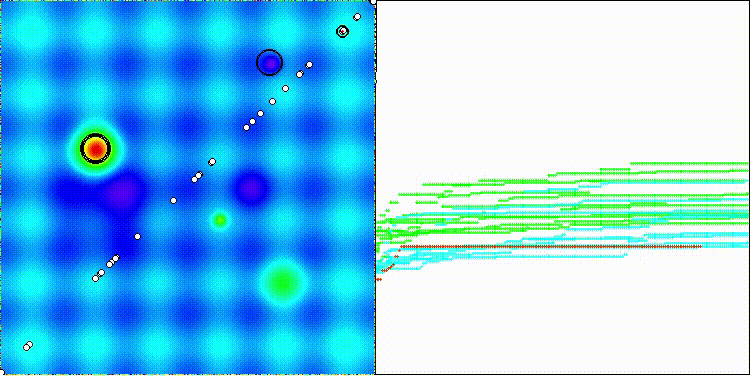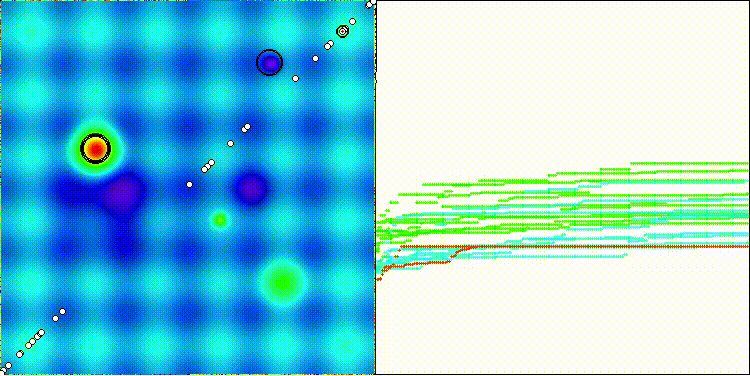
DOA_dingo на тестовой функции Hilly
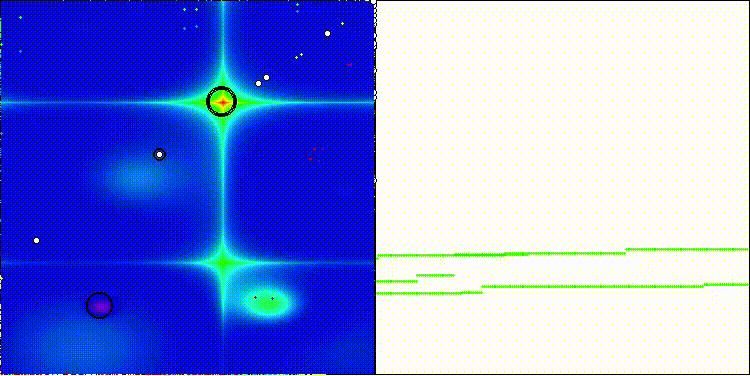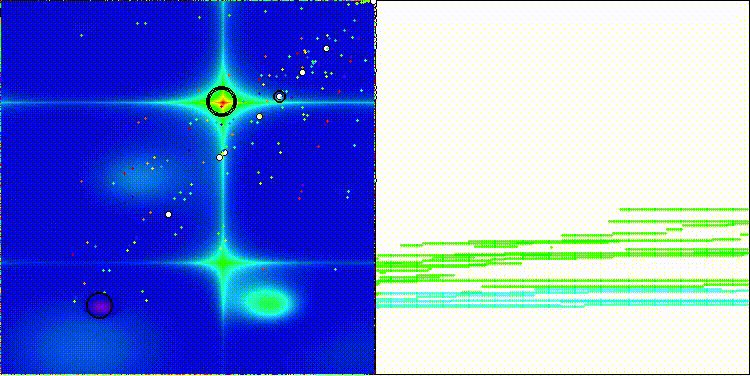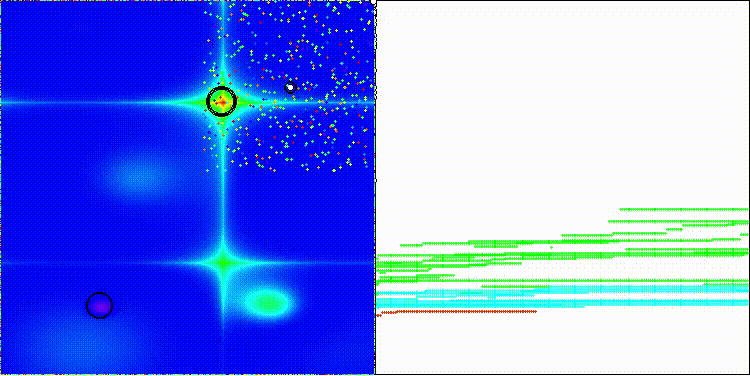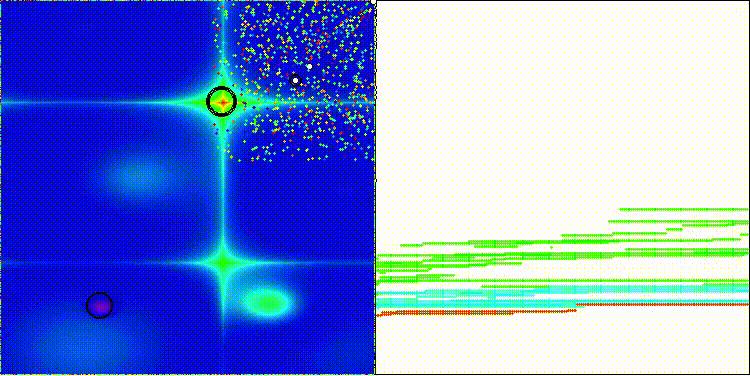
DOA_dingo на тестовой функции Forest
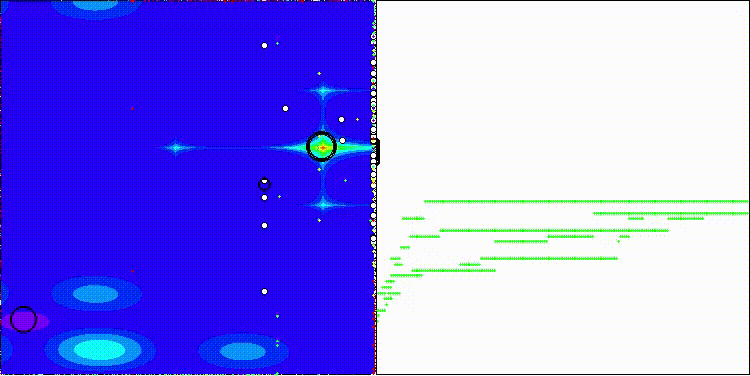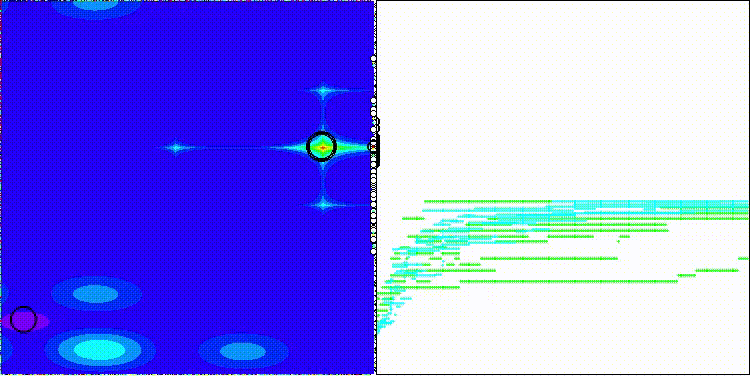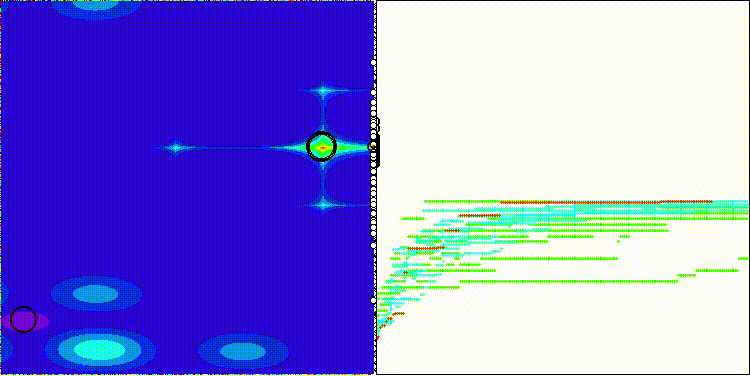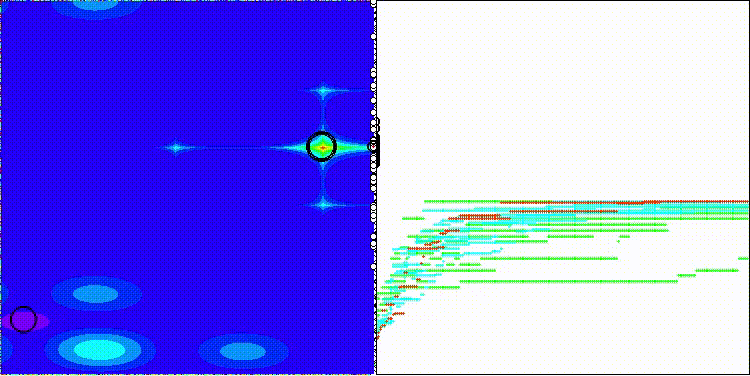
DOA_dingo на тестовой функции Megacity
В рейтинговой таблице алгоритм DOA_dingo после проведенного тестирования представлен ознакомительно.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | EOm | extremal_optimization_M | 0,76166 | 0,77242 | 0,31747 | 1,85155 | 0,99999 | 0,76751 | 0,23527 | 2,00277 | 0,74769 | 0,53969 | 0,14249 | 1,42987 | 5,284 | 58,71 |
| 13 | BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| 14 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 15 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 16 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 17 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 18 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 19 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 20 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 21 | BSA | backtracking_search_algorithm | 0,97309 | 0,54534 | 0,29098 | 1,80941 | 0,99999 | 0,58543 | 0,21747 | 1,80289 | 0,84769 | 0,36953 | 0,12978 | 1,34700 | 4,959 | 55,10 |
| 22 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 23 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 24 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 25 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 26 | DOA | dream_optimization_algorithm | 0,85556 | 0,70085 | 0,37280 | 1,92921 | 0,73421 | 0,48905 | 0,24147 | 1,46473 | 0,77231 | 0,47354 | 0,18561 | 1,43146 | 4,825 | 53,62 |
| 27 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 28 | DEA | dolphin_echolocation_algorithm | 0,75995 | 0,67572 | 0,34171 | 1,77738 | 0,89582 | 0,64223 | 0,23941 | 1,77746 | 0,61538 | 0,44031 | 0,15115 | 1,20684 | 4,762 | 52,91 |
| 29 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 30 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 31 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 32 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 33 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 34 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 35 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 36 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 37 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 38 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 39 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 40 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 41 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 42 | CMAES | covariance_matrix_adaptation_evolution_strategy | 0,76258 | 0,72089 | 0,00000 | 1,48347 | 0,82056 | 0,79616 | 0,00000 | 1,61672 | 0,75846 | 0,49077 | 0,00000 | 1,24923 | 4,349 | 48,33 |
| 43 | DA_duelist | duelist_algorithm | 0,92782 | 0,53778 | 0,27792 | 1,74352 | 0,86957 | 0,47536 | 0,18193 | 1,52686 | 0,62153 | 0,33569 | 0,11715 | 1,07437 | 4,345 | 48,28 |
| 44 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 45 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| DOA_dingo | dingo_optimization_algorithm | 0,49066 | 0,39991 | 0,35798 | 1,24855 | 0,29643 | 0,20458 | 0,17091 | 0,67192 | 0,36615 | 0,44892 | 0,45394 | 1,26901 | 3,189 | 35,44 | |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
В данной статье мы рассмотрели интересный алгоритм оптимизации, примечательный с точки зрения применяемых подходов. На первый взгляд, алгоритм может показаться не самым удачным способом поиска оптимального решения. Однако, в ходе многочисленных экспериментов проявился неожиданный потенциал: при должной доработке заложенных в DOA идей, алгоритм способен продемонстрировать весьма достойные результаты — на уровне лучших популяционных методов.
Что именно было обнаружено — об этом мы расскажем в следующей статье. Кроме того, небольшой подарок ждет очень внимательных любителей оптимизации, в файле можно обнаружить небольшую модификацию в коде алгоритма, которая уже значительно повлияла на результаты работы, можете отписаться в комментариях.
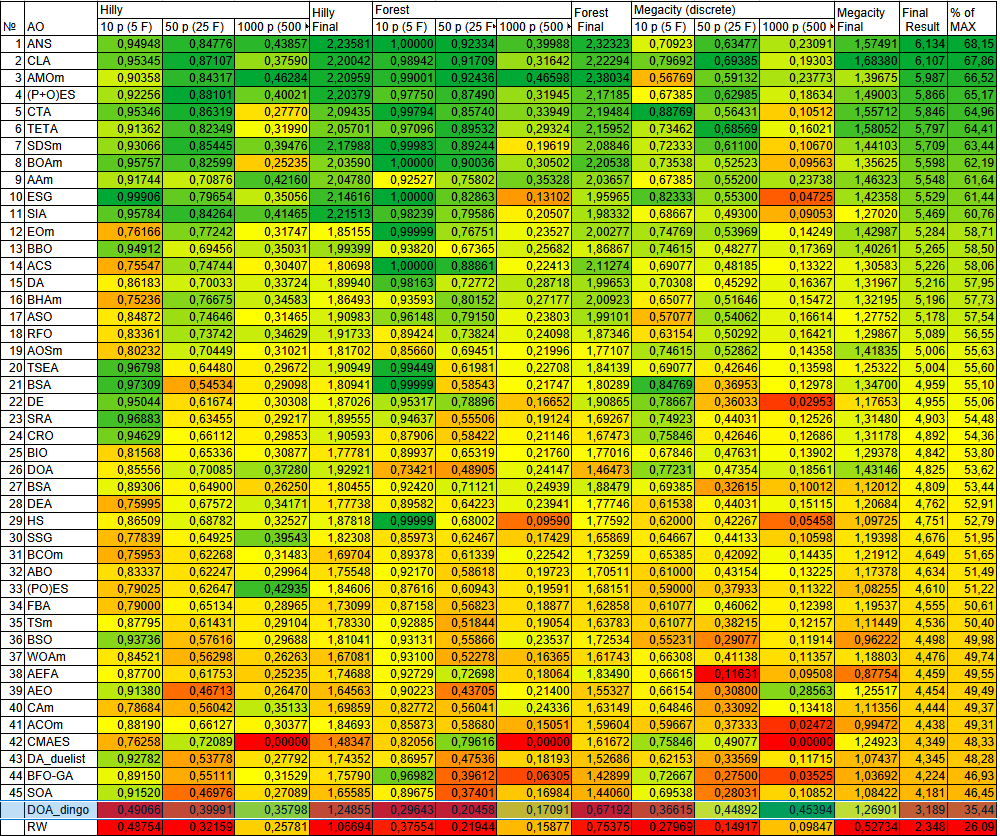
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
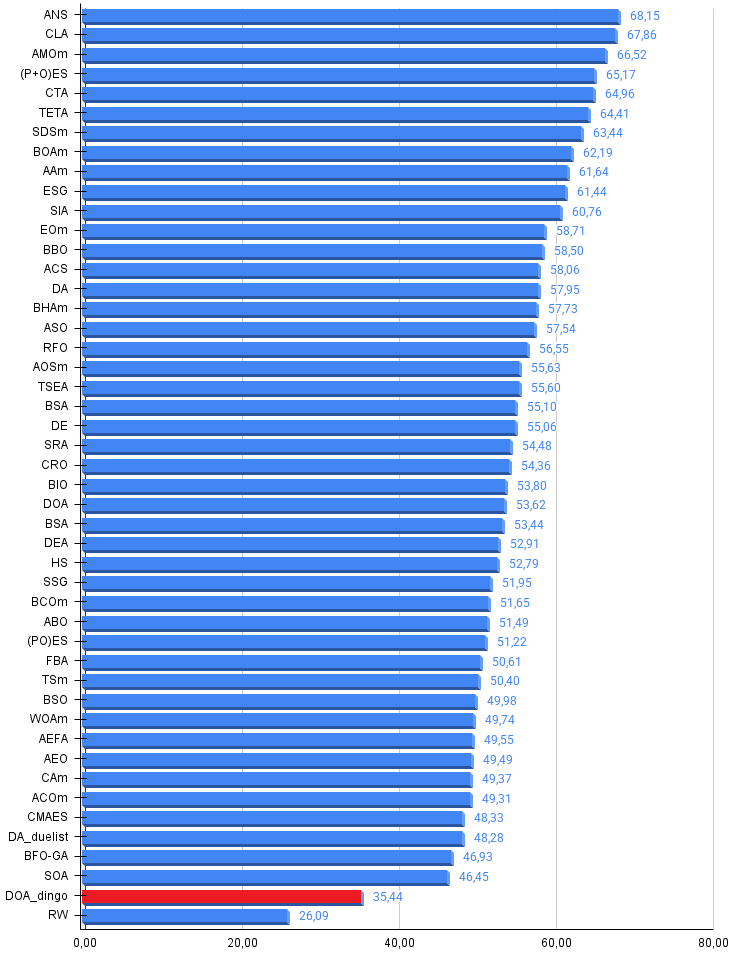
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма DOA_dingo:
Плюсы:
- Быстрый.
Минусы:
- Разброс результатов.
- Слабое исследование пространства поиска.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_DOA_dingo.mq5 | Скрипт | Испытательный стенд для DOA_dingo |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 От новичка до эксперта: Создание анимированного советника для новостей в MQL5 (VIII) — Кнопки быстрой торговли на новостях
От новичка до эксперта: Создание анимированного советника для новостей в MQL5 (VIII) — Кнопки быстрой торговли на новостях
 От новичка до эксперта: Советник Reporting EA - Настройка рабочего процесса
От новичка до эксперта: Советник Reporting EA - Настройка рабочего процесса
 Торговый инструментарий MQL5 (Часть 5): Расширение EX5-библиотеки для управления историей функциями последнего исполненного отложенного ордера
Торговый инструментарий MQL5 (Часть 5): Расширение EX5-библиотеки для управления историей функциями последнего исполненного отложенного ордера
 Нейросети в трейдинге: Единый взгляд на пространство и время (Окончание)
Нейросети в трейдинге: Единый взгляд на пространство и время (Окончание)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования