Скрытые марковские модели для прогнозирования волатильности с учетом тренда

Введение

Скрытые марковские модели(СММ) — это мощный статистический инструмент, позволяющий выявлять скрытые состояния рынка на основе анализа наблюдаемых ценовых движений. В трейдинге СММ позволяют улучшить прогнозирование волатильности и применяются при разработке трендовых стратегий, моделируя изменения рыночных режимов.

В этой статье мы представим пошаговый процесс разработки стратегии следования за трендом, которая использует СММ в качестве фильтра для прогнозирования волатильности. Процесс включает в себя разработку базовой стратегии в MQL5 с использованием MetaTrader 5, получение данных и обучение СММ в Python, а также интеграцию моделей обратно в MetaTrader 5, где мы протестируем стратегию на исторических данных.

Мотивация

В книге "Технический анализ на основе доказательств" Дэйв Аронсон предлагает трейдерам разрабатывать свои стратегии с использованием научных методов. Этот процесс начинается с формирования гипотезы, основанной на интуиции, лежащей в основе идеи, и ее строгом тестировании, чтобы избежать предвзятости от подглядывания в данные. В этой статье мы предпримем аналогичный подход. Сначала разберемся, что такое скрытая марковская модель и почему она может быть полезна для разработки нашей стратегии.

Скрытая модель Маркова (СММ) — это модель машинного обучения без учителя, которая представляет системы, в которых базовое состояние скрыто, но может быть выведено на основе наблюдаемых событий или данных. Она основана на предположении Маркова, согласно которому будущее состояние системы зависит только от ее текущего состояния, а не от прошлых состояний. В СММ система моделируется как набор дискретных состояний, причем каждое состояние имеет определенную вероятность перехода в другое состояние. Эти переходы описываются набором вероятностей, известных как вероятности переходов. Наблюдаемые данные (такие как цены активов или доходность рынка) генерируются системой, но сами состояния не поддаются непосредственному наблюдению, отсюда и термин "скрытая".

Вот ее компоненты:

1. Состояния – это ненаблюдаемые условия или режимы системы. На финансовых рынках эти состояния могут представлять различные рыночные условия, такие как бычий рынок, медвежий рынок или периоды высокой и низкой волатильности. Эти состояния развиваются на основе определенных вероятностных правил.

2. Вероятности перехода – они определяют вероятность перехода из одного состояния в другое. Состояние системы в момент времени t зависит только от состояния в момент времени t-1, что соответствует свойству Маркова. Для количественной оценки этих вероятностей используются матрицы перехода.

3. Вероятности наблюдений – они описывают вероятность наблюдения конкретного фрагмента данных (например, цены акций или доходности) с учетом базового состояния. Каждое состояние имеет вероятностное распределение, которое определяет вероятность наблюдения определенных рыночных условий или движения цен в данном состоянии.

4. Начальные вероятности – они представляют вероятность того, что система начнет работу в определенном состоянии, обеспечивая отправную точку для анализа модели.

Учитывая эти компоненты, модель использует байесовский вывод для определения наиболее вероятной последовательности скрытых состояний во времени на основе наблюдаемых данных. Обычно это делается с помощью алгоритмов, таких как алгоритм Forward-Backward или алгоритм Витерби, которые оценивают вероятность наблюдаемых данных, учитывая последовательность скрытых состояний.

В торговле волатильность является ключевым фактором, влияющим на цены активов и динамику рынка. СММ могут быть особенно эффективны в прогнозировании волатильности, выявляя базовые рыночные режимы, которые не поддаются непосредственному наблюдению, но значительно влияют на поведение рынка.

1. Идентификация рыночных режимов. Путем разделения рыночных условий на отдельные состояния (такие как высокая волатильность или низкая волатильность) СММ могут фиксировать сдвиги в рыночных режимах. Это позволяет трейдерам понять, когда рынок, вероятно, переживет периоды высокой волатильности или стабильных условий, что может напрямую отражаться на ценах активов.

2. Кластеризация волатильности. Финансовые рынки демонстрируют кластеризацию волатильности, когда за периодами высокой волатильности часто следуют периоды высокой волатильности, а за периодами низкой волатильности — периоды низкой волатильности. СММ могут моделировать эту характеристику, присваивая высокие вероятности оставаться в состояниях высокой волатильности или низкой волатильности в течение длительных периодов, тем самым обеспечивая более точные прогнозы будущих движений рынка.

3. Прогнозирование волатильности. Наблюдая за переходами между различными состояниями рынка, СММ могут предоставлять прогнозные данные о будущей волатильности. Например, если модель определяет, что рынок находится в состоянии высокой волатильности, трейдеры могут ожидать более значительных ценовых колебаний и соответствующим образом скорректировать свои стратегии. Кроме того, если рынок переходит в состояние низкой волатильности, модель может помочь трейдерам корректировать уровень риска или адаптировать свои торговые стратегии.

4. Адаптивность. СММ непрерывно обновляют свои вероятностные распределения и переходы между состояниями на основе новых данных, что позволяет им адаптироваться к меняющимся рыночным условиям. Эта способность адаптироваться в режиме реального времени дает трейдерам преимущество в прогнозировании изменений волатильности и динамической корректировке своих стратегий.

В соответствии с исследованиями многих ученых, мы исходим из гипотезы о том, что в условиях высокой волатильности наша стратегия следования за трендом, как правило, работает лучше, поскольку более значительные движения рынка приводят к формированию тренда. Мы планируем использовать скрытые марковские модели (СММ) для кластеризации волатильности и определения состояний высокой и низкой волатильности. Затем мы обучим модель прогнозировать, будет ли следующее состояние волатильности высоким или низким. Если сигнал стратегии появляется в то время, когда модель прогнозирует состояние высокой волатильности, мы входим в сделку; в противном случае мы остаемся вне рынка.

Основная стратегия

Стратегия следования за трендом, которую мы будем использовать, такая же, как и та, которую я реализовал в своей предыдущей статье по машинному обучению. Основная логика включает в себя две скользящие средние: быструю и медленную. Торговый сигнал генерируется, когда две скользящие средние пересекаются, и направление торговли следует за быстрой скользящей средней, отсюда и термин "следование за трендом". Сигнал выхода возникает, когда цена пересекает медленную скользящую среднюю, что дает больше пространства для трейлинг-стопов. Полный код выглядит следующим образом:

#include <Trade/Trade.mqh>
//XAU - 1h.
CTrade trade;

input ENUM_TIMEFRAMES TF = PERIOD_CURRENT;
input ENUM_MA_METHOD MaMethod = MODE_SMA;
input ENUM_APPLIED_PRICE MaAppPrice = PRICE_CLOSE;
input int MaPeriodsFast = 15;
input int MaPeriodsSlow = 25;
input int MaPeriods = 200;
input double lott = 0.01;
ulong buypos = 0, sellpos = 0;
input int Magic = 0;
int barsTotal = 0;
int handleMaFast;
int handleMaSlow;
int handleMa;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   trade.SetExpertMagicNumber(Magic);
   handleMaFast =iMA(_Symbol,TF,MaPeriodsFast,0,MaMethod,MaAppPrice);
   handleMaSlow =iMA(_Symbol,TF,MaPeriodsSlow,0,MaMethod,MaAppPrice);  
   handleMa = iMA(_Symbol,TF,MaPeriods,0,MaMethod,MaAppPrice); 
   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {

  }  

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  //Beware, the last element of the buffer list is the most recent data, not [0]
  if (barsTotal!= bars){
     barsTotal = bars;
     double maFast[];
     double maSlow[];
     double ma[];
     CopyBuffer(handleMaFast,BASE_LINE,1,2,maFast);
     CopyBuffer(handleMaSlow,BASE_LINE,1,2,maSlow);
     CopyBuffer(handleMa,0,1,1,ma);
     double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
     double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
     double lastClose = iClose(_Symbol, PERIOD_CURRENT, 1);
     //The order below matters
     if(buypos>0&& lastClose<maSlow[1]) trade.PositionClose(buypos);
     if(sellpos>0 &&lastClose>maSlow[1])trade.PositionClose(sellpos);   
     if (maFast[1]>maSlow[1]&&maFast[0]<maSlow[0]&&buypos ==sellpos)executeBuy(); 
     if(maFast[1]<maSlow[1]&&maFast[0]>maSlow[0]&&sellpos ==buypos) executeSell();
     if(buypos>0&&(!PositionSelectByTicket(buypos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      buypos = 0;
      }
     if(sellpos>0&&(!PositionSelectByTicket(sellpos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      sellpos = 0;
      }
    }
 }

//+------------------------------------------------------------------+
//| Expert trade transaction handling function                       |
//+------------------------------------------------------------------+
void OnTradeTransaction(const MqlTradeTransaction& trans, const MqlTradeRequest& request, const MqlTradeResult& result) {
    if (trans.type == TRADE_TRANSACTION_ORDER_ADD) {
        COrderInfo order;
        if (order.Select(trans.order)) {
            if (order.Magic() == Magic) {
                if (order.OrderType() == ORDER_TYPE_BUY) {
                    buypos = order.Ticket();
                } else if (order.OrderType() == ORDER_TYPE_SELL) {
                    sellpos = order.Ticket();
                }
            }
        }
    }
}

//+------------------------------------------------------------------+
//| Execute sell trade function                                      |
//+------------------------------------------------------------------+
void executeSell() {      
       double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
       bid = NormalizeDouble(bid,_Digits);
       trade.Sell(lott,_Symbol,bid);  
       sellpos = trade.ResultOrder();  
       }   

//+------------------------------------------------------------------+
//| Execute buy trade function                                       |
//+------------------------------------------------------------------+
void executeBuy() {
       double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
       ask = NormalizeDouble(ask,_Digits);
       trade.Buy(lott,_Symbol,ask);
       buypos = trade.ResultOrder();
}

Я не буду подробно останавливаться на проверке и предложениях по выбору основной стратегии. Более подробную информацию можно найти в моей предыдущей статье по машинному обучению, ссылка на которую приведена здесь.

Получение данных

В этой статье мы определим два состояния: высокая волатильность и низкая волатильность, представленные соответственно цифрами 1 и 0. Волатильность будет определяться как стандартное отклонение доходности за последние 50 свечей следующим образом:

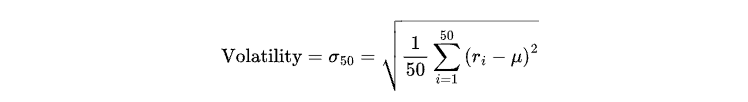
Где:

• ri представляет доходность i-й свечи (рассчитывается как процентное изменение цены между последовательными закрытыми свечами).

• μ — средняя доходность последних 50 закрытых свечей, определяемая следующим образом:

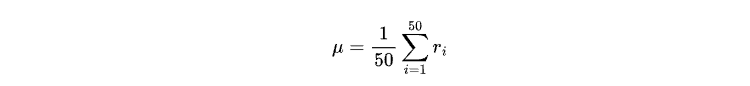
Для обучения модели нам понадобятся только данные о цене закрытия и время. Хотя прямой поиск данных из терминала MetaTrader 5 возможен, большая часть данных, предоставляемых терминалом, ограничена реальными тиковыми данными. Чтобы получить от вашего брокера данные OHLC за более длительный период, мы можем создать советник OHLC getter для решения этой задачи.

#include <FileCSV.mqh>

int barsTotal = 0;
CFileCSV csvFile;

input string fileName = "Name.csv";
string headers[] = {
    "time",
    "close"
};

string data[100000][2];
int indexx = 0;
vector xx;

input bool SaveData = true;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {//Initialize model
   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   if (!SaveData) return;
   if(csvFile.Open(fileName, FILE_WRITE|FILE_ANSI))
     {
      //Write the header
      csvFile.WriteHeader(headers);
      //Write data rows
      csvFile.WriteLine(data);
      //Close the file
      csvFile.Close();
     }
   else
     {
      Print("File opening error!");
     }

  }
  
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  
  if (barsTotal!= bars){
     barsTotal = bars;
   data[indexx][0] =(string)TimeTradeServer() ;
   data[indexx][1] = DoubleToString(iClose(_Symbol,PERIOD_CURRENT,1), 8); 
   indexx++;
   }
 }

Этот код считывает и записывает финансовые данные (время и цену закрытия) в файл CSV. При каждом тике он проверяет, изменилось ли количество баров. Если да, то он обновляет массив данных с текущим временем сервера и ценой закрытия символа. Когда скрипт деинициализируется, он записывает собранные данные в файл CSV, включая заголовки и строки данных. Для обработки файлов он использует классCFileCSV.

Запустите этот советник в тестере стратегий, используя желаемый таймфрейм и период, и CSV-файл будет сохранен в каталоге /Tester/Agent-sth000.

Для обучения мы будем использовать обучающие данные с 1 января 2020 года по 1 января 2024 года. Данные с 1 января 2024 года по 1 января 2025 года будут использоваться для вневыборочного тестирования.

Модели обучения

Теперь откройте любой редактор Python и убедитесь, что вы установили необходимые библиотеки с помощью pip, как требуется в этом разделе.

CSV-файл изначально содержит только один столбец, в котором значения времени и закрытия смешаны и разделены точкой с запятой. Для удобства хранения значения хранятся в виде строк. Чтобы обработать это, мы сначала читаем CSV-файл следующим образом, чтобы разделить два столбца и преобразовать значения из строк в типы datetime и float.

import pandas as pd
data = pd.read_csv("XAU_test.csv",sep=";")
data = data.dropna()
data["close"] = data["close"].astype(float)
data['time'] = pd.to_datetime(data['time'])
data.set_index('time', inplace=True)

Волатильность можно легко рассчитать с помощью этой строки:

data['volatility'] = data['returns'].rolling(window=50).std()

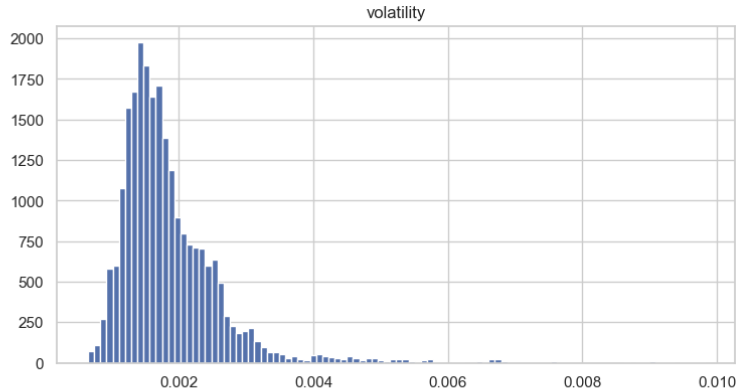
Затем мы визуализируем распределение волатильность, чтобы лучше понимать ее характеристики. В данном случае очевидно, что оно примерно соответствует нормальному распределению.

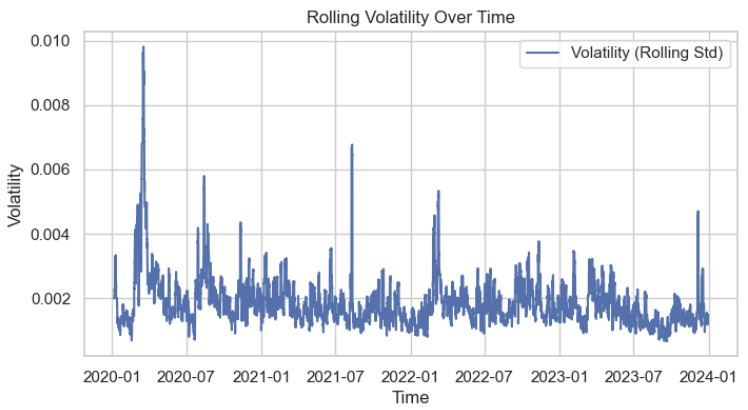
Мы используем расширенный тест Дики-Фуллера для подтверждения того, что данные по волатильности являются стационарными. Вероятнее всего, тест выдаст следующий результат:

Augmented Dickey-Fuller Test: Volatility
ADF Statistic: -13.120552520156329
p-value: 1.5664189630119278e-24
# Lags Used: 46
Number of Observations Used: 23516
=> The series is likely stationary.

Хотя скрытые марковские модели (СММ) не являются строго необходимыми для стационарных данных из-за их поведения с прогрессивным обновлением, наличие стационарных данных значительно облегчает процесс кластеризации и повышает точность модели.

Несмотря на то, что данные о волатильности, скорее всего, стационарны и близки к нормальному распределению, мы все же хотим нормализовать их до стандартного нормального распределения, чтобы диапазон стал более управляемым.

В статистике этот процесс называется "масштабированием", при котором любая нормально распределенная случайная величина x может быть преобразована в стандартное нормальное распределение N(0,1) с помощью следующей операции:

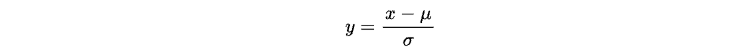
Здесь μ представляет среднее значение, а σ — стандартное отклонение x.

Имейте в виду, что позже, при повторной интеграции в редактор MetaTrader 5, нам нужно будет выполнить те же операции нормализации. Поэтому нам также необходимо сохранить среднее значение и стандартное отклонение.

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaled_volatility = scaler.fit_transform(data[['volatility']])
scaled_volatility = scaled_volatility.reshape(-1, 1)
scaler_mean = scaler.mean_[0]  # Mean of the volatility feature
scaler_std = scaler.scale_[0]  # Standard deviation of the volatility feature

Затем мы обучаем модель на масштабированных данных волатильности следующим образом:

from hmmlearn import hmm
import numpy as np
# Define the number of hidden states
n_states = 2
# Initialize the Gaussian HMM
model = hmm.GaussianHMM(n_components=n_states, covariance_type="full", n_iter=100, random_state=42, verbose = True)
# Fit the model to the scaled volatility data
model.fit(scaled_volatility)

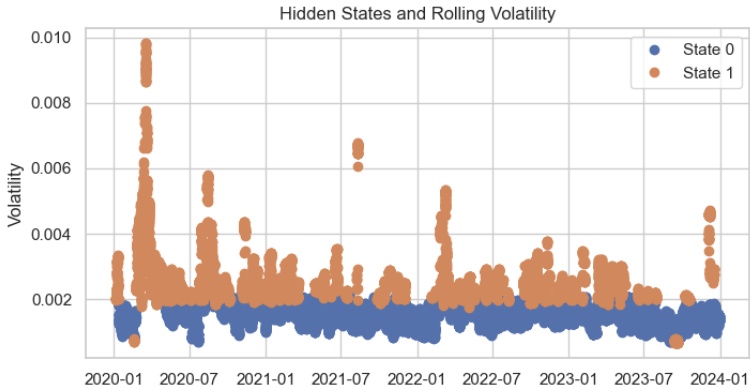
При прогнозировании скрытых состояний для каждой точки обучающих данных распределение кластеров выглядит вполне разумным, с незначительными погрешностями.

# Predict the hidden states
hidden_states = model.predict(scaled_volatility)

# Add the hidden states to your dataframe
data['hidden_state'] = hidden_states
plt.figure(figsize=(14, 6))
for state in range(n_states):
    state_mask = data['hidden_state'] == state
    plt.plot(data.index[state_mask], data['volatility'][state_mask], 'o', label=f'State {state}')
plt.title('Hidden States and Rolling Volatility')
plt.xlabel('Time')
plt.ylabel('Volatility')
plt.legend()
plt.show()

Наконец, мы форматируем желаемый вывод в языке MQL5 и сохраняем его в файле заголовка JSON, что упрощает копирование и вставку соответствующих значений матрицы в редактор MetaTrader 5.

import json

# Your HMM model parameters
transition_matrix = model.transmat_
means = model.means_
covars = model.covars_

# Construct the data in the required format
data = {
    "A": [
        [transition_matrix[0, 0], transition_matrix[0, 1]],
        [transition_matrix[1, 0], transition_matrix[1, 1]]
    ],
    "mu": [means[0, 0], means[1, 0]],
    "sigma_sq": [covars[0, 0], covars[1, 0]],
    "scaler_mean": scaler_mean,
    "scaler_std": scaler_std
}

# Create the output content in the desired format
output_str = """
const double A[2][2] = { 
    {%.16f, %.16f}, 
    {%.16f, %.16f}
};
const double mu[2] = {%.16f, %.16f};
const double sigma_sq[2] = {%.16f, %.16f};
const double scaler_mean = %.16f;
const double scaler_std = %.16f;
""" % (
    data["A"][0][0], data["A"][0][1], data["A"][1][0], data["A"][1][1],
    data["mu"][0], data["mu"][1],
    data["sigma_sq"][0], data["sigma_sq"][1],
    data["scaler_mean"], data["scaler_std"]
)

# Write to a file
with open('model_parameters.h', 'w') as f:
    f.write(output_str)

print("Parameters saved to model_parameters.h")

Полученный в результате файл должен выглядеть примерно так:

const double A[2][2] = { 
    {0.9941485184089348, 0.0058514815910651}, 
    {0.0123877225858242, 0.9876122774141759}
};
const double mu[2] = {-0.4677410059727503, 0.9797900996225393};
const double sigma_sq[2] = {0.1073520489683212, 1.4515804806463273};
const double scaler_mean = 0.0018685496675093;
const double scaler_std = 0.0008350190448735;

Эти значения необходимо вставить в код нашего советника в качестве глобальных переменных.

Интеграция

Теперь вернемся в редактор кода MetaTrader 5 и доработаем наш исходный код стратегии.

Сначала нам нужно создать функции для расчета скользящей волатильности, которая постоянно обновляется.

//+------------------------------------------------------------------+
//| Get volatility Function                                          |
//+------------------------------------------------------------------+
void GetVolatility(){
// Step 1: Get the last two close prices to compute the latest percent change
        double close_prices[2];
        int copied = CopyClose(_Symbol, PERIOD_CURRENT, 1, 2, close_prices);
        if(copied != 2){
            Print("Failed to copy close prices. Copied: ", copied);
            return;
        }
        
        // Step 2: Compute the latest percent change
        double latest_close = close_prices[0];
        double previous_close = close_prices[1];
        double percent_change = 0.0;
        if(previous_close != 0){
            percent_change = (latest_close - previous_close) / previous_close;
        }
        else{
            Print("Previous close price is zero. Percent change set to 0.");
        }
        
        // Step 3: Update the percent_changes buffer
        percent_changes[percent_change_index] = percent_change;
        percent_change_index++;
        if(percent_change_index >= 50){
            percent_change_index = 0;
            percent_change_filled = true;
        }
        
        // Step 4: Once the buffer is filled, compute the rolling std dev
        if(percent_change_filled){
            double current_stddev = ComputeStdDev(percent_changes, 50);
            // Step 5: Scale the std dev
            double scaled_stddev = (current_stddev - scaler_mean) / scaler_std;
            
            // Step 6: Update the volatility array (ring buffer for Viterbi)
            // Shift the volatility array to make room for the new std dev
            for(int i = 0; i < 49; i++){
                volatility[i] = volatility[i+1];
            }
            volatility[49] = scaled_stddev; // Insert the latest std dev
       }
}

//+------------------------------------------------------------------+
//| Compute Standard Deviation Function                              |
//+------------------------------------------------------------------+
double ComputeStdDev(double &data[], int size)
{
    if(size <= 1)
        return 0.0;
    
    double sum = 0.0;
    double sum_sq = 0.0;
    for(int i = 0; i < size; i++)
    {
        sum += data[i];
        sum_sq += data[i] * data[i];
    }
    double mean = sum / size;
    double variance = (sum_sq - (sum * sum) / size) / (size - 1);
    return MathSqrt(variance);
}

• Функция GetVolatility() вычисляет и отслеживает скользящую волатильность во времени, используя масштабированное стандартное отклонение процентных изменений цен.
• Вспомогательная функция ComputeDtsDev() служит для вычисления стандартного отклонения заданного массива данных.

Затем мы пишем две функции, которые вычисляют текущее скрытое состояние на основе наших матриц и текущей скользящей волатильности.

//+------------------------------------------------------------------+
//| Viterbi Algorithm Implementation in MQL5                         |
//+------------------------------------------------------------------+
int Viterbi(double &obs[], int &states[])
{
    // Initialize dynamic programming tables
    double T1[2][50];
    int T2[2][50];

    // Initialize first column
    for(int s = 0; s < 2; s++)
    {
         double emission_prob = (1.0 / MathSqrt(2 * M_PI * sigma_sq[s])) * MathExp(-MathPow(obs[0] - mu[s], 2) / (2 * sigma_sq[s])) + 1e-10;

        T1[s][0] = MathLog(pi[s]) + MathLog(emission_prob);
        T2[s][0] = 0;
    }

    // Fill the tables
    for(int t = 1; t < 50; t++)
    {
        for(int s = 0; s < 2; s++)
        {
            double max_prob = -DBL_MAX; // Initialize to negative infinity
            int max_state = 0;
            for(int s_prev = 0; s_prev < 2; s_prev++)
            {
                double transition_prob = A[s_prev][s];
                if(transition_prob <= 0) transition_prob = 1e-10; // Prevent log(0)
                double prob = T1[s_prev][t-1] + MathLog(transition_prob);
                if(prob > max_prob)
                {
                    max_prob = prob;
                    max_state = s_prev;
                }
            }
            // Calculate emission probability with epsilon
            double emission_prob = (1.0 / MathSqrt(2 * M_PI * sigma_sq[s])) * MathExp(-MathPow(obs[t] - mu[s], 2) / (2 * sigma_sq[s])) + 1e-10;
            T1[s][t] = max_prob + MathLog(emission_prob);
            T2[s][t] = max_state;
        }
    }

    // Backtrack to find the optimal state sequence
    // Find the state with the highest probability in the last column
    double max_final_prob = -DBL_MAX;
    int last_state = 0;
    for(int s = 0; s < 2; s++)
    {
        if(T1[s][49] > max_final_prob)
        {
            max_final_prob = T1[s][49];
            last_state = s;
        }
    }    
    // Initialize the states array
    ArrayResize(states, 50);
    states[49] = last_state;
    // Backtrack
    for(int t = 48; t >= 0; t--)
    {
        states[t] = T2[states[t+1]][t+1];
    }
    return 0; // Success
}

//+------------------------------------------------------------------+
//| Predict Current Hidden State                                     |
//+------------------------------------------------------------------+
int PredictCurrentState(double &obs[])
{   
    // Define states array
    int states[50];
    
    // Apply Viterbi
    int ret = Viterbi(obs, states);
    if(ret != 0)
        return -1; // Error
    
    // Return the most probable current state
    return states[49];
}

Функция Viterbi() реализует алгоритм Витерби, метод динамического программирования для нахождения наиболее вероятной последовательности скрытых состояний в скрытой марковской модели (СММ) на основе наблюдаемых данных (obs[]).

1. Инициализация:

• Таблицы динамического программирования:

  • T1[s][t] – логарифмическая вероятность наиболее вероятной последовательности состояний, которая заканчивается в состоянии s в момент времени t.
  • T2[s][t] – таблица указателей, в которой хранится состояние, которое максимизировало вероятность перехода в состояние s в момент времени t.

• Первый временной шаг (t = 0):

  • Вычислите начальные вероятности, используя априорные вероятности каждого состояния (π[s]) и вероятности появления первого наблюдаемого значения (obs[0]).

2. Рекурсивный расчет:

Для каждого временного шага t от 1 до 49 :

1. Для каждого состояния s:

   Вычислите максимальную вероятность перехода из любого предыдущего состояния s_prev в s с помощью следующего уравнения:

   

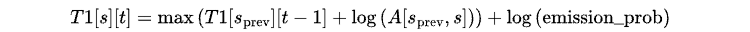
   Здесь вероятность перехода A[s_prev, s] преобразуется в логарифмическое пространство, чтобы избежать числового переполнения.

2. Сохраните состояние s_prev, которое максимизировало вероятность, в T2[s][t].

3. Возвратный проход для извлечения оптимального пути:

1. Начните с состояния с наибольшей вероятностью на последнем временном шаге (t = 49).
2. Проследите T2, чтобы восстановить наиболее вероятную последовательность состояний, сохранив результат в states[].

Конечным результатом является states[], содержащий наиболее вероятную последовательность состояний.

Функция PredictCurrentState() использует функцию Viterbi() для прогнозирования текущего скрытого состояния на основе наблюдений.

1. Для инициализации он определяет массив states[50] для хранения результата, возвращаемого Viterbi().
2. Затем он передает последовательность наблюдений obs[] в функцию Viterbi() для вычисления наиболее вероятной последовательности скрытых состояний.
3. Наконец, он возвращает состояние на последнем временном шаге (states[49]), которое представляет наиболее вероятное текущее скрытое состояние.

Если вас смущает математика, лежащая в основе этого, я настоятельно рекомендую посмотреть более интуитивные иллюстрации в Интернете. Здесь я постараюсь кратко объяснить, что мы делаем.

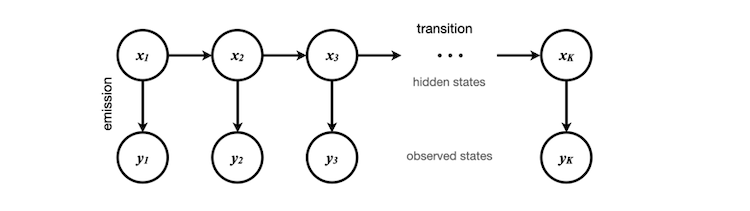
Наблюдаемые состояния — это масштабированные данные о волатильности, которые мы можем получить и сохранить в массиве obs[], содержащем в данном случае 50 элементов. Эти элементы соответствуют y1, y2, ... y50 на диаграмме. Соответствующие скрытые состояния могут быть либо 0, либо 1, что представляет абстрактные условия текущей волатильности (высокая или низкая).

Эти скрытые состояния определяются путем кластеризации в процессе обучения модели, который мы выполнили ранее в Python. Важно отметить, что код Python не знает точно, что представляет каждое число — он только знает, как кластеризовать данные и идентифицировать особенности свойств перехода между состояниями.

Изначально мы случайным образом присваиваем состояние x1, предполагая, что каждое состояние имеет равный вес. Если мы не хотим делать это предположение, мы можем рассчитать стационарное распределение начального состояния, используя наши обучающие данные, которые будут собственным вектором матрицы перехода. Для простоты мы предполагаем, что вектор стационарного распределения равен [0,5, 0,5].

Путем обучения скрытой модели Маркова мы получаем вероятность перехода в другое скрытое состояние и вероятность появления другого наблюдения. Используя теорему Байеса, мы можем рассчитать вероятность всех возможных путей для каждой цепочки Маркова и определить наиболее вероятный путь. Это позволяет нам найти наиболее вероятный результат для x50, конечного скрытого состояния в последовательности.

Наконец, мы корректируем исходную логику функции OnTick(), вычисляя скрытые состояния для каждого закрытия и добавляя критерий входа, согласно которому скрытое состояние должно быть равно 1.

//+------------------------------------------------------------------+
//| Check Volatility is filled Function                              |
//+------------------------------------------------------------------+
bool IsVolatilityFilled(){
     bool volatility_filled = true;
     for(int i = 0; i < 50; i++){
         if(volatility[i] == 0){
             volatility_filled = false;
             break;
         }
     }
     if(!volatility_filled){
         Print("Volatility buffer not yet filled.");
         return false;
     }
     else return true;
}  

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  if (barsTotal!= bars){
     barsTotal = bars;
     double maFast[];
     double maSlow[];
     double ma[];  
     
     GetVolatility();
     if(!IsVolatilityFilled()) return;
     int currentState = PredictCurrentState(volatility);
     
     CopyBuffer(handleMaFast,BASE_LINE,1,2,maFast);
     CopyBuffer(handleMaSlow,BASE_LINE,1,2,maSlow);
     CopyBuffer(handleMa,0,1,1,ma);

     double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
     double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
     double lastClose = iClose(_Symbol, PERIOD_CURRENT, 1);
     //The order below matters
     if(buypos>0&& lastClose<maSlow[1]) trade.PositionClose(buypos);
     if(sellpos>0 &&lastClose>maSlow[1])trade.PositionClose(sellpos);        
     if (maFast[1]>maSlow[1]&&maFast[0]<maSlow[0]&&buypos ==sellpos&&currentState==1)executeBuy(); 
     if(maFast[1]<maSlow[1]&&maFast[0]>maSlow[0]&&sellpos ==buypos&&currentState==1) executeSell();
     
     if(buypos>0&&(!PositionSelectByTicket(buypos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      buypos = 0;
      }
     if(sellpos>0&&(!PositionSelectByTicket(sellpos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      sellpos = 0;
      }
    }
 }

Тестирование на исторических данных

Мы обучили модель, используя обучающие данные с 1 января 2020 года по 1 января 2024 года. Теперь мы хотим протестировать результаты за период с 1 января 2024 года по 1 января 2025 года на XAUUSD в 1-часовом таймфрейме.

Сначала мы сравним производительность с базовым показателем, который представляет собой результат без интеграции СММ.

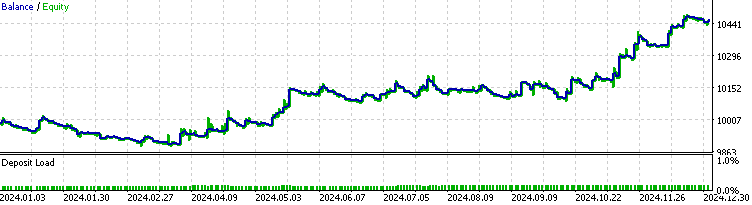
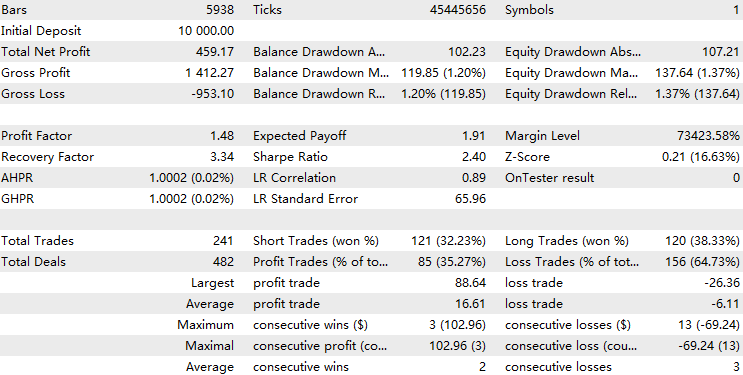
Теперь мы протестируем наш советник с реализованным фильтром модели СММ на исторических данных.

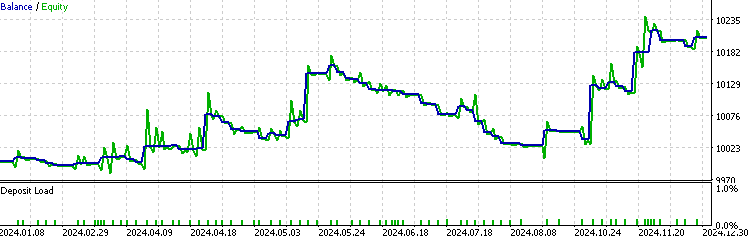
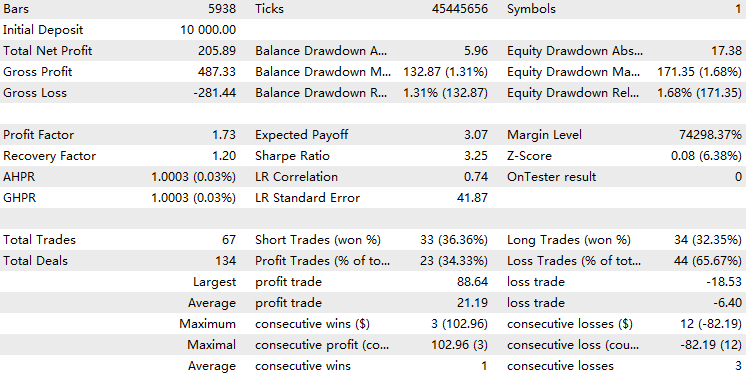
Мы видим, что советник с реализацией СММ отсеял около 70% всех сделок. Он превосходит базовый уровень с коэффициентом прибыли 1,73 (у базового уровня – 1,48), а также с более высоким коэффициентом Шарпа. Это говорит о том, что обученная нами модель СММ демонстрирует определенный уровень предсказуемости.

Если мы проведем скользящее тестирование на исторических данных, в котором повторим эту процедуру 4-летнего обучения и 1-летнего тестирования, начиная с 2004 года, и скомпилируем все результаты в одну кривую капитала, мы получим следующий результат:

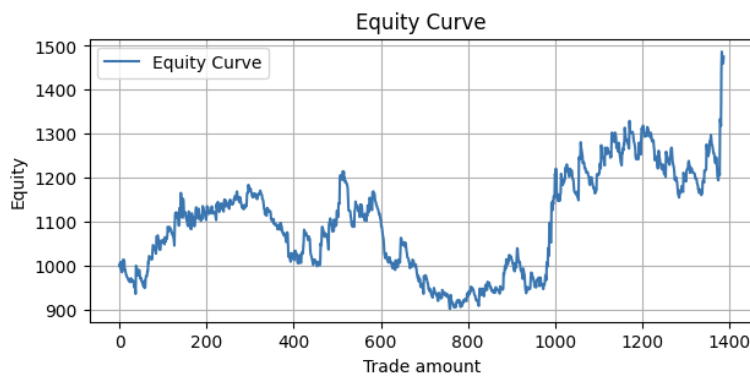
Показатели:

Profit Factor: 1.10
Maximum Drawdown: -313.17
Average Win: 11.41
Average Loss: -5.01
Win Rate: 32.56%

Результаты положительные, хотя остаётся потенциал для дальнейшего улучшения.

Обсуждение результатов

В современном мире трейдинга, где доминируют методы машинного обучения, ведется постоянная дискуссия о том, следует ли использовать более сложные модели, такие как рекуррентные нейронные сети (RNN), или оставаться при более простых моделях, таких как скрытые марковские модели (СММ).

Плюсы:

1. Простота. Проще в реализации и интерпретации по сравнению со сложными моделями, такими как RNN, которые вводят неоднозначность в отношении того, что представляет каждый параметр и операция.
2. Меньшие требования к данным. Требует меньшего количества обучающих выборок для оценки параметров модели и меньшей вычислительной мощности.
3. Меньшее количество параметров. Более устойчива к проблемам переобучения.

Минусы

1. Ограниченная сложность. Может не улавливать сложные закономерности в изменчивых данных, которые могут моделировать RNN.
2. Предположение о процессе Маркова. Предполагает, что переходы волатильности не имеют памяти, что может не соответствовать реальности на рынках.
3. Риск переобучения. Несмотря на свою простоту, если задействовано слишком много состояний, СММ все равно будет подвержен переобучению.

Популярным подходом является прогнозирование волатильности, а не цен с помощью методов машинного обучения, поскольку ученые пришли к выводу, что прогнозы волатильности являются более надежными. Однако ограничением подхода, представленного в этой статье, является то, что наблюдения, которые мы получаем для каждого нового бара (50-периодная скользящая средняя волатильность), и скрытые состояния, которые мы определяем (состояния высокой/низкой волатильности), в некоторой степени коррелируют, что снижает достоверность прогнозов. Это говорит о том, что аналогичные результаты можно было бы получить, просто используя данные наблюдений в качестве фильтров.

Для дальнейшего развития я рекомендую читателям изучить другие определения скрытых состояний, а также поэкспериментировать с более чем двумя состояниями, чтобы улучшить надежность модели и ее прогнозирующую способность.

Заключение

В этой статье мы сначала объяснили мотивацию использования СММ в качестве предиктора состояния волатильности для стратегии следования за трендом, а также представили основные концепции СММ. Затем мы прошли весь процесс разработки стратегии, который включал разработку базовой стратегии в MQL5 с использованием MetaTrader 5, получение данных и обучение СММ в Python, а затем интеграцию моделей обратно в MetaTrader 5. После этого мы провели тестирование на исторических данных и проанализировали его результаты, кратко объяснив математическую логику СММ с помощью диаграммы. В заключение я поделился своими соображениями о стратегии, а также наметил возможные направления для дальнейшего развития данного подхода.

Таблица файлов

Имя файла	Использование
HMM Test.mq5	Реализация торгового советника
Classic Trend Following.mq5	Советник по базовой стратегии
OHLC Getter.mq5	Торговый советник для извлечения данных
FileCSV.mqh	Включаемый файл для хранения данных в CSV
rollingBacktest.ipynb	Для обучения модели и получения матриц