Нейросети в трейдинге: Адаптивная периодическая сегментация (LightGTS)

Введение

Прогнозирование временных рядов давно стало ключевым инструментом во многих сферах — от энергетики и транспорта до здравоохранения и образования. Но именно в финансах, где ценность каждой секунды можно измерить в деньгах, точность прогноза становится критически важной. Здесь не прощают ошибок: малейший промах в модели — и стратегия уходит в минус.

Традиционные подходы, будь то статистика или глубокое обучение, обычно строятся по принципу: одна задача — одна модель. Такие решения хорошо работают в изолированных условиях, но на практике финансовые рынки ведут себя непредсказуемо: смена волатильности, масштабов, циклов и режимов — всё это ставит под сомнение эффективность жёстко привязанных моделей.

На этом фоне появляются так называемые базовые модели временных рядов (Time Series Foundation Models — TSFM). Их обучают на огромных массивах разнородных данных, рассчитывая на универсальность и масштабируемость. Однако, реальность такова, что подобные модели требуют колоссальных вычислительных ресурсов, а прирост точности далеко не всегда оправдывает затраты. Параметров — десятки миллионов, но на практике универсальность нередко теряется в деталях.

Особенность временных рядов — в их ритме. В отличие от текста, где токен — это слово, здесь важны масштаб и периодичность. Одни данные приходят раз в час, другие — каждые 15 минут. Одни содержат дневную или недельную сезонность, другие — квартальную или годовую. Всё это влияет на так называемый внутренний период — повторяющийся паттерн в данных, который критичен для качественного прогноза. Более того, при смене масштаба длина цикла меняется — и если модель не умеет с этим справляться, её обобщающая способность резко падает.

Проблема в том, что большинство существующих моделей используют фиксированную токенизацию. Они просто делят данные на одинаковые по длине куски, не учитывая масштаб и структуру периодов. Это приводит к тому, что одни токены перегружены данными, а другие почти пусты. Информация размывается, повторяющиеся паттерны нарушаются. Особенно это заметно, когда модель, обученная на одном масштабе, применяется к другому — точность прогнозов падает, требуется увеличивать объём параметров, а значит, растёт время и стоимость обучения.

Авторы работы "LightGTS: A Lightweight General Time Series Forecasting Model" решили не использовать в лоб грубую силу, а применить разумный подход — задействовать естественные свойства временных рядов: масштабную инвариантность и периодичность. Результатом их работы стал фреймворк LightGTS — лёгкий, эффективный и точно заточенный под реальные задачи прогнозирования временных рядов. Его ключевая идея — не бороться с масштабами, а подстраиваться под них.

Вместо жёсткой нарезки на одинаковые фрагменты, было предложено использовать периодическую токенизацию. Модель сама адаптивно делит данные на участки, длина которых соответствует одному полному циклу. Это позволяет ей улавливать целостные паттерны независимо от масштаба — будь то дневной график или минутный. Семантика внутри токена остаётся неизменной, а значит, представление признаков становится стабильным и переносимым между задачами.

Для прогнозирования в фреймворке применяется параллельное декодирование: последний токен от энкодера используется как стартовая точка, и на его основе сразу формируются все будущие значения. Это не только сокращает время и снижает накопление ошибок (в отличие от пошаговых авторегрессионных подходов), но и позволяет лучше использовать структуру самого ряда. Последний токен содержит всю суть истории и напрямую связан с будущим, что делает прогнозирование логичным и структурно обоснованными.

Дополнительно авторы фреймворка LightGTS отказались от фиксированной проекции признаков. Вместо этого используется гибкий слой, способный адаптироваться к различной длине циклов и множественным источникам данных. Это особенно актуально в финансовых приложениях, где в одном портфеле могут соседствовать часовые данные по акциям и дневные — по макроэкономике.

Результаты говорят сами за себя. Модель LightGTS показывает точность на уровне лучших решений в индустрии, при этом имеет менее 5 миллионов параметров. Это в 10–100 раз меньше, чем у других TSFM-моделей. А значит — меньше времени на обучение, меньше затрат на инфраструктуру и больше шансов внедрить модель в реальную торговую систему или аналитическую платформу.

Алгоритм LightGTS

Представьте себе типичную задачу прогнозирования на финансовых рынках. У нас есть мультивариантный временной ряд — например, котировки, объёмы, индикаторы и другие рыночные сигналы. Назовём его Xt={xi,t-L:t}i=1,C, где каждая xi — это наблюдения по отдельному каналу за последние L временных шагов. Таких каналов C — сколько угодно: от одного до десятков. Это наше окно в прошлое, скользящий отрезок анализируемой истории.

Наша цель — заглянуть в будущее на F шагов вперёд и спрогнозировать значения Ŷt={ŷi,t:t+F}i=1,C. А для оценки точности в процессе обучения у нас есть и фактические данные — Yt={yi,t:t+F}i=1,C. Всё это укладывается в классическую схему прогнозирования.

Теперь самое интересное. Обучение модели осуществляется в два этапа. Сначала идёт масштабное предварительное обучение на разнородных временных рядах из разных источников. Это могут быть исторические данные по акциям, валютам, экономическим индикаторам, погоде — всё, что проявляет временные зависимости. Затем идёт тонкая настройка (fine-tuning) модели на конкретной задаче.

Интересный момент: модель можно и не дообучать — достаточно просто протестировать её на тестовой выборке, если она изначально была обучена достаточно универсально. Это особенно важно в контексте алгоритмической торговли: не всегда есть возможность дообучать модель под каждый инструмент, особенно в режиме реального времени.

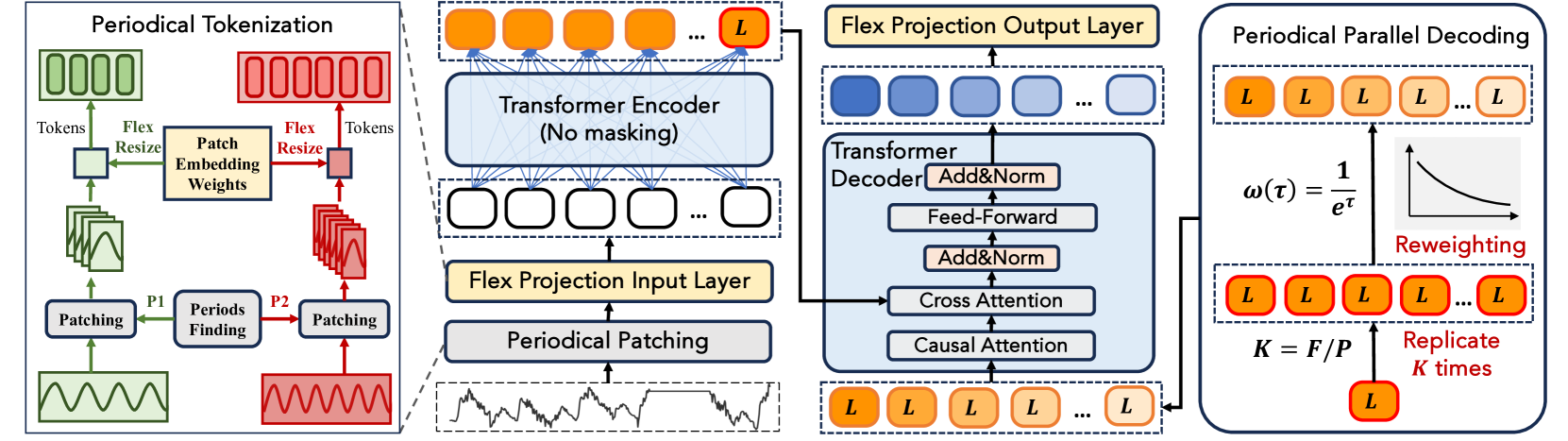
Что делает модель LightGTS уникальной? Всё начинается с периодической токенизации — настоящей волшебной линейки, которая адаптируется к ритму самого ряда. Авторы фреймворка предлагают делить последовательность на периодические патчи — отрезки данных, которые соответствуют одному полному циклу (например, дневному или недельному). Эта операция называется Adaptive Periodical Patching. Она учитывает масштаб и структуру временного ряда и формирует сегменты, идеально вписывающиеся в повторы поведения рынка.

Для описания метода рассмотрим простой случай — одномерный временной ряд. На практике всё легко масштабируется на многомерные данные: каждый канал просто обрабатывается отдельно, без потери структуры.

Представим, что мы работаем с набором временных рядов из разных источников — финансовых активов, рынков, таймфреймов. У каждого ряда есть свой внутренний ритм — так называемый естественный период. Это может быть, например, дневной торговый цикл, недельная волатильность или сезонный тренд. Чтобы эффективно работать с такими рядами, первым делом нужно определить длину этого периода — то есть, сколько временных точек анализируемых данных составляет один полный цикл.

Если есть предварительная информация о частоте данных (например, они поступают раз в час или раз в минуту), то определить длину цикла несложно: скажем, для суточного периода и часовых данных — это 24 точки. Но если данных о частоте нет, на помощь приходит спектральный анализ, в том числе быстрое преобразование Фурье (FFT), которое помогает вынюхать доминирующие частоты в ряду. Именно они и отражают повторяющиеся закономерности — циклы, столь важные в прогнозировании рыночной динамики.

Как только длина цикла, обозначим её P, найдена, весь временной ряд аккуратно нарезается на последовательные, не перекрывающиеся фрагменты ровно по этим периодам. Каждый такой фрагмент или патч содержит P точек и полностью охватывает один цикл. Количество таких патчей — это просто L делённое на P с округлением вниз, где L — длина исходного ряда.

Этот шаг на первый взгляд кажется простым, но на деле он открывает модели доступ к совершенно новому уровню семантической структуры. Разные таймфреймы, частоты и источники теперь интерпретируются в едином, синхронизированном по периоду пространстве. Это исключает шум от разницы масштабов данных и позволяет модели учиться выявлять закономерности, которые действительно повторяются от цикла к циклу — а не просто подстраиваться под локальную волатильность.

Именно такой способ нарезки делает возможным обучение на разнородных источниках. Несмотря на разницу в частотах, все они приводятся к сопоставимому виду, где период — ключевая единица информации. А это значит, что модель может извлекать и обобщать повторяющиеся рыночные сигналы, что критически важно для надёжного прогнозирования в условиях живых торгов.

После того, как временной ряд нарезан на циклические патчи, каждый из которых охватывает полный цикл временного ряда, важно правильно перевести эти патчи в векторное представление. На этом этапе начинается магия проекционного слоя, но, как и в жизни, дьявол кроется в деталях.

Наивное решение — использовать фиксированную проекционную матрицу, которая преобразует каждый патч в токен. Проблема? Разные финансовые данные имеют разные длины циклов: дневной цикл на минутных свечах — это 1440 точек, а недельный на часовых — всего 120. В результате, размер входных патчей варьируется, а фиксированная матрица просто не справляется: она либо урезает данные, либо требует привести всё к общему размеру. Простая интерполяция, конечно, помогает — можно просто растянуть или сжать данные. Но есть подвох: такие операции искажают смысл. Получаем красиво выровненные, но пустые токены, которые мало что значат для модели.

Чтобы избежать таких искажений, вводится гибкий проекционный слой (Flex Projection Layer). Его задача — не просто сжать патч до фиксированной размерности, а сделать это так, чтобы семантика данных осталась прежней. Иными словами, токены, полученные из патча длиной 96, должны быть эквивалентны тем, что пришли бы из патча длиной 144, если оба отражают один и тот же рыночный цикл.

Как это работает технически? Пусть у нас есть проекционные веса θ, обученные для патча длиной P. Мы хотим адаптировать их для нового патча длиной P′, причём так, чтобы произведение данных и весов (а значит и токены) остались максимально близкими. Простая интерполяция тут не подойдёт, слишком уж грубо. Поэтому используется линейное преобразование с адаптацией весов через псевдообратную матрицу — метод, известный в численных методах и регрессионном анализе.

Этот механизм называется flex-resize и он решает оптимизационную задачу: найти такие новые веса θ′, которые при преобразовании новых патчей дадут результат, максимально близкий к старому — по Фробениусовой норме, если уж говорить математически. Тут же вводится коэффициент δ — он учитывает разницу в дисперсиях между оригинальным патчем и интерполированным, что позволяет сохранить статистическую стабильность проекций. Итоговая формула для flex-resize выглядит довольно солидно, но по сути это умный способ сделать весовую матрицу гибкой и адаптивной.

В рамках реализации Flex Projection Layer используются две матрицы параметров — для входа и выхода, каждая рассчитана на эталонный размер патча (например, 96). Во время прямого прохода модели (forward pass), эти матрицы подстраиваются под нужную длину текущего патча с помощью той самой трансформации δ⁻¹(A)+. После этого патчи легко проецируются в скрытое пространство модели — токены готовы и сохраняют всю структуру оригинального рыночного цикла.

Таким образом, независимо от того, анализирует ли модель недельный тренд по дневным свечам, или скальпирует минутные графики, она всегда работает с данными в едином, непротиворечивом представлении. Это устраняет конфликт между разными масштабами и позволяет эффективно использовать предварительно обученные веса без повторного обучения с нуля. А в условиях финансовых рынков, где данные приходят из разных источников и с разной частотой, такая гибкость — не роскошь, а необходимость.

В архитектуре фреймворка LightGTS, аналогично классическому Transformer, используются Энкодер и Декодер, каждый из которых включает модули многоголового внимания и полносвязные слои (Feed-Forward Networks). Однако здесь есть одна ключевая деталь — в модулях внимания применяется вращающее позиционное кодирование (RoPE), которое позволяет учитывать не только абсолютные, но и относительные позиции токенов. Для временных рядов, где важен не просто порядок, а расстояние между точками, это особенно актуально.

После того, как периодические патчи были переведены в токены через Flex Projection, формируется последовательность токенов 𝐗ₑ = {𝐱ₑ₁, 𝐱ₑ₂, …, 𝐱ₑₙ}, где каждый 𝐱ₑᵢ — это векторное представление i-го патча. При обработке этой последовательности Энкодер накладывает позиционную структуру с помощью RoPE: токены не просто запоминают своё положение, они учитывают относительное смещение друг от друга.

Конкретно, для каждого токена вычисляются векторы запроса (Query) и ключа (Key) с помощью обучаемых матриц 𝐖Q и 𝐖K. Далее, на пару векторов (𝐱ₑᵢ, 𝐱ₑⱼ), представляющих позиции i и j, накладывается вращающая матрица 𝐑i−j, которая точно кодирует разницу в их позициях. Полученная мера сходства между токенами i и j вычисляется по формуле:

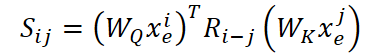
Чем больше эта величина, тем с большим вниманием токен i смотрит на токен j. Все такие значения нормализуются с помощью функции SoftMax и используются для взвешенного суммирования Value-векторов, полученных через ещё одну обучаемую матрицу 𝐖V.

Именно это внимание в прямом смысле определяет для каждого токена, на кого из соседей смотреть и насколько сильно. После внимания каждый токен дополнительно обрабатывается полносвязным блоком — Feed-Forward Network, которая извлекает скрытые признаки и обогащает представление.

В итоге, на выходе Энкодера получается латентное пространство, где каждый вектор 𝐞ⱼ содержит не только локальную информацию патча, но и контекст от всех других токенов с учётом их относительных позиций во временном ряду. Такой механизм позволяет модели понимать структуру, ритм и повторяющиеся паттерны в данных, что критично для финансовых временных рядов, где важна не столько точка, сколько её окружение.

Как уже упоминалось ранее, периодическое разбиение на патчи помогает извлекать повторяющиеся циклы из временных рядов. Но чтобы максимально использовать эту информацию и при генерации прогноза, модель применяет новый подход — периодическое параллельное декодирование. В отличие от классического авторегрессионного подхода, где прогноз строится шаг за шагом, здесь используется неавторегрессионная стратегия, позволяющая сразу обрабатывать весь отрезок будущего.

Ключевая идея проста, но изящна: последний токен 𝐞ₙ из выходного латентного пространства Энкодера содержит сжатую информацию о всей предшествующей последовательности, включая её внутреннюю периодичность. Поэтому мы берём именно его, клонируем K раз (где K = F/P, то есть необходим прогноз на сколько циклов), и получаем матрицу 𝐇, которая и будет входом в декодер.

Однако важно учитывать, что влияние последнего токена на прогнозирование ослабевает по мере продвижения вперёд во времени. Поэтому к каждому клонированному вектору 𝐡ⱼ применяется весовая функция ω(j)=1/eʲ, которая экспоненциально уменьшает вклад по мере удаления от текущего момента. Полученные взвешенные токены ω(j)·𝐡ⱼ подаются в декодер одновременно, что и составляет суть параллельной архитектуры Декодера.

На выходе декодера получается матрица 𝐙 — прогнозные токены, соответствующие будущим циклам. А чтобы эти токены можно было перевести в привычные значения временного ряда, модель использует обратную проекцию с помощью уже знакомого механизма Flex-resize, на этот раз применяя его к параметрам декодера θd.

Так модель генерирует весь прогнозный отрезок 𝐘̂ сразу, без накопления ошибок и задержек, характерных для пошагового предсказания. Это не только ускоряет вычисления, но и лучше сохраняет периодичность, ведь она была заложена ещё на стадии токенизации и теперь проносится сквозь всю архитектуру — от Энкодера до финального выхода.

Под капотом LightGTS работает как часовой механизм: ритмично, точно, без избыточных затрат. Благодаря периодической токенизации и параллельному декодированию, модель обходит стороной классические ловушки громоздкости и плохой переносимости.

В соответствии с устоявшейся практикой в области прогнозирования временных рядов, авторы фреймворка LightGTS в качестве функции потерь используют классическую среднеквадратичную ошибку (Mean Squared Error — MSE). Она измеряет отклонение между прогнозными значениями и реальными наблюдаемыми данными, выступая, как объективный критерий качества прогноза.

Авторская визуализация фреймворка LightGTS представлена ниже.

Реализация средствами MQL5

После подробного рассмотрения теоретических аспектов фреймворка LightGTS, мы переходим к практической части нашей статьи. В этом разделе будет представлено наше собственное видение реализации ключевых компонентов модели средствами MQL5 — с учетом особенностей финансовых временных рядов и ограничений платформы.

Начнем, пожалуй, с одного из базовых и одновременно наиболее интересных элементов — адаптивного периодического патчинга. Именно с этого механизма начинается процесс преобразования временного ряда в структуру, удобную для обработки трансформером. Здесь нас поджидает несколько нетривиальных вызовов.

Один из них — динамическое изменение размера патча — уже упоминается авторами оригинального фреймворка. В статье предлагается элегантный способ решения этой задачи с помощью линейной интерполяции весов. Однако на практике он затрагивает лишь часть проблемы.

Ведь если размер патча меняется, то меняется и их количество — динамически и непредсказуемо. И вот это уже вносит дополнительную сложность в архитектуру модели, особенно при реализации на строго типизированном языке, таком как MQL5. Классические циклы и массивы здесь требуют точного контроля размеров на всех этапах, а значит, необходимо не только адаптировать размерность входных данных, но и разработать механизм адаптивной разбивки временного ряда на переменное количество патчей — при сохранении их периодичности и согласованности с историей наблюдений.

К сожалению, используемые нами архитектурные решения не позволяют использовать динамическую размерность входных или выходных тензоров в процессе выполнения операций. Поэтому нам необходим иной, более прагматичный подход, который обеспечит фиксированные размеры буферов при сохранении возможности работы с переменным числом токенов.

Один из возможных вариантов — создание буфера с заведомо избыточной вместимостью, рассчитанного на максимально возможное количество токенов. В случае, если фактическое число токенов оказывается меньше, лишние ячейки зануляются. Такой подход действительно предоставляет определённую гибкость в работе с разным количеством патчей, однако, эта гибкость достигается ценой неоправданного расхода памяти, значительная часть которой остаётся неиспользованной.

Кроме того, не стоит забывать о ключевой уязвимости архитектуры Transformer — квадратичной сложности внимания по отношению к длине последовательности. Чем больше токенов мы подаём на вход, тем больше времени и ресурсов потребуется для выполнения самих блоков внимания. Иными словами, избыточное количество токенов не только неэффективно с точки зрения памяти, но и прямо вредит вычислительной производительности модели, особенно в условиях реального времени, или при обработке массивов высокочастотных рыночных данных.

Поэтому возникает необходимость в альтернативном, более гибком подходе. В связи с этим, заслуживает внимания предложенная авторами фреймворка LightGTS концепция не перекрывающихся периодических патчей, при которой каждый сегмент временного ряда соответствует одному полному циклу. Это вполне логично: временной ряд часто содержит ярко выраженные периодические компоненты, и обособленное рассмотрение каждого периода позволяет извлечь семантически чистые признаки.

Однако мы предлагаем взглянуть на задачу с иного ракурса. Что если отказаться от жёсткого требования неперекрываемости патчей? Вместо этого можно зафиксировать желаемое количество патчей на выходе и регулировать длину перекрытия между соседними окнами в зависимости от периодичности исходной последовательности.

Такой подход открывает ряд преимуществ. Во-первых, он позволяет гарантировать постоянное количество патчей независимо от исходной цикличности анализируемого временного ряда. А это крайне удобно при проектировании фиксированной архитектуры. Во-вторых, за счёт гибкого перекрытия можно добиться полного покрытия циклической структуры данных, не обрезая её и не теряя информацию между границами окон. И наконец, это даёт возможность более плавно управлять разрешением семантического представления, не нарушая компактности выходного тензора.

Проще говоря, мы предлагаем обменять строгость один патч — один цикл на контролируемую плотность представления, сохраняя при этом общий объём выходной информации и повышая устойчивость модели к изменениям длины входного ряда.

Думаю, концепция понятна. Теперь самое время перейти к практической реализации. Первый шаг — определить периодичность анализируемого временного ряда. Для этого мы воспользуемся классическим и проверенным временем методом, основанным на Быстром преобразовании Фурье (Fast Fourier Transform — FFT).

Суть подхода проста: мы рассматриваем спектр амплитуд частотных компонент временного ряда и находим частоту, обладающую наибольшей энергией. Именно она, как правило, соответствует доминирующему циклу в данных. Период, в свою очередь, вычисляется как обратная величина к обнаруженной частоте.

Почему мы выбираем именно FFT? Во-первых, это быстрый и эффективный алгоритм даже при работе с большими объёмами данных. Во-вторых, он позволяет выявить скрытые периодические зависимости, которые визуально определить бывает невозможно. Ну и наконец, FFT хорош тем, что позволяет работать в условиях отсутствия априорной информации о частотных характеристиках временного ряда — что часто бывает в реальных трейдинговых данных.

И конечно, дополнительным бонусом будет наличие готовой реализации FFT в нашей библиотеке. Напомню, что его мы использовали в рамках работы на фреймворком FITS.

Существующая в нашей библиотеке реализация FFT возвращает действительную и мнимую части спектра, что полностью соответствует классической форме представления результата быстрого преобразования Фурье. Однако сама по себе эта информация ещё не даёт ответа на вопрос, какая частота доминирует в сигнале и определяет структуру колебаний.

Чтобы не перегружать центральный процессор и сохранить параллельную эффективность, мы реализуем кернел, который прямо на стороне OpenCL-контекста определяет доминантную частоту для каждой унитарной последовательности. Каждый поток получает свой спектр, вычисляет энергию всех частотных компонент и выбирает ту, где амплитуда максимальная. Это как слушать сложную мелодию и мгновенно распознать в ней основной ритм, который задаёт структуру. Такой подход особенно важен при работе с мультимодальными временными рядами, когда каждая переменная может иметь собственную характерную частоту.

Алгоритм реализуем в рамках OpenCL-кернела MainFreq, который работает с массивами действительных и мнимых компонент спектра. А на выходе возвращает массив, содержащий индексы наиболее выраженных частот для каждой последовательности.

__kernel void MainFreq(__global const float* freq_r,
                       __global const float* freq_im,
                       __global float *main_freq,
                       int dimension
                      )
  {
   if(dimension <= 0)
      return;
//---
   size_t n = get_global_id(0);
   const int shift = n * dimension;

В теле кернела мы сначала идентифицируем каждый поток операций в одномерном пространстве задач. Полученный индекс указывает на уникальный номер анализируемой унитарной последовательности. И на основании полученного, сразу определяем смещение в массивах спектра так, чтобы обрабатывать только свою последовательность.

Далее инициализируем переменные для хранения максимальной амплитуды (энергии) и соответствующего ей индекса.

float max_f = 0;
float max_id = 0;
float energy;

На этом завершается подготовительная работа, и далее мы организуем цикл по спектру, начиная с первой гармоники.

for(int i = 1; i < dimension; i++)
  {
   float2 freq = (float2)(freq_r[shift + i], freq_im[shift + i]);
   energy = ComplexAbs(freq);
   if(max_f < energy)
     {
      max_f = energy;
      max_id = i + 1;
     }
  }

Нулевую частоту (DC-компоненту) мы намеренно пропускаем — она не несёт информации о периодичности, а отражает постоянную составляющую сигнала.

На каждой итерации формируем комплексное число из реальной и мнимой частей. Модуль этого числа представляет собой силу выраженности соответствующей частоты. Если найденная энергия превышает текущий максимум, то мы обновляем значения.

Наконец, после завершения обхода всего спектра, записываем результат в глобальный буфер данных.

 main_freq[n] = max_id;
}

Алгоритм работает как опытный дирижёр, внимательно следящий за каждым инструментом в оркестре и определяющий, кто играет главную партию. Мы не просто находим частоту — мы вычисляем наиболее выраженный период сигнала, который затем используется для адаптивного построения патчей в модели. А так как каждый ряд (в условиях мультимодальности) обрабатывается независимо, — мы получаем масштабируемую, гибкую и абсолютно автономную систему определения локальной периодичности.

Также стоит особо подчеркнуть, что предложенный алгоритм полностью детерминирован, не содержит обучаемых параметров и не требует затрат на обучение. Он опирается исключительно на физическую природу спектра: оценка амплитуды частотных компонент осуществляется напрямую, без привлечения какой-либо статистики, регрессий или адаптивных весов. Это делает метод прозрачным, надёжным и особенно удобным на этапе предварительной обработки данных — когда критически важно не вносить искажений, связанных с недообучением или переобучением. Иными словами, здесь работает чистая и беспристрастная математика, а не вероятностные допущения, что особенно важно при анализе волатильных рыночных временных рядов.

Следующим этапом нашей работы станет непосредственная реализация алгоритма адаптивного патчинга с динамическим изменением размера сегмента. Однако, как вы понимаете, об этом не расскажешь в двух словах. Реализация требует внимания к множеству технических деталей, а размер текущей статьи и без того уже довольно велик. Поэтому, в лучших традициях сериалов с напряжённым сюжетом, мы предлагаем сделать небольшую паузу и продолжить обсуждение реализации предложенных подходов в следующей статье.

В ней мы шаг за шагом разберём, как реализовать механизм динамического формирования патчей с учётом переменной длины цикла, сохраняя при этом стабильное количество выходных токенов. Рассмотрим возможные компромиссы между гибкостью архитектуры и вычислительной эффективностью.

Заключение

В данной статье мы подробно рассмотрели теоретические основы фреймворка LightGTS, сфокусировавшись на его ключевых компонентах: периодическом патчинге, гибкой проекции токенов и механизме параллельной декодировки. Мы проанализировали, каким образом архитектура справляется с многомодальными временными рядами и адаптируется к различным периодам, без необходимости повторного обучения модели. Особое внимание было уделено техническим аспектам вычисления доминирующей частоты с использованием быстрого преобразования Фурье.

Мы также затронули практические ограничения, связанные с динамической аллокацией памяти и переменным числом токенов, и предложили альтернативные решения на основе перекрывающихся патчей и фиксированной длины выходного вектора. Такой подход не только улучшает совместимость с архитектурой Transformer, но и позволяет более рационально использовать ресурсы, избегая чрезмерного расхода памяти и падения производительности.

Представленный материал служит прочной основой для последующей реализации полной версии адаптивного патчинга и интеграции его в предсказательную архитектуру. В следующей статье мы продолжим этот путь, сфокусировавшись на конкретных реализациях адаптивной сегментации временного ряда и интеграции полученных токенов в обучаемую модель.

Ссылки

• LightGTS: A Lightweight General Time Series Forecasting Model
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Study.mq5	Советник	Советник офлайн обучения моделей
2	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
3	Test.mq5	Советник	Советник для тестирования модели
4	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
5	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
6	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы