
Нейросети в трейдинге: Повышение эффективности Transformer путем снижения резкости (SAMformer)
Введение
Многомерное прогнозирование временных рядов — это классическая задача обучения, которая заключается в анализе временных рядов для прогнозирования будущих тенденций на основе исторической информации. И является сложной задачей из-за корреляции признаков и долгосрочных временных зависимостей во временных рядах. Эта проблема обучения широко распространена в тех реальных приложениях, где наблюдения собираются последовательно (медицинские данные, потребление электроэнергии, цены на акции).
В последнее время архитектуры на основе Transformer достигают прорывной производительности в задачах обработки естественного языка и компьютерного зрения. Transformer особенно эффективен при работе с последовательными данными, что естественно приводит к применению подобных решений на временных рядах. Тем не менее, современное состояние прогнозирования многомерных временных рядов достигается с помощью более простой модели, основанной на MLP.
Недавние работы по применению Transformer к данным временных рядов в основном сосредоточены на эффективных реализациях, снижающих квадратичную стоимость внимания, или декомпозицию временных рядов для лучшего отражения лежащих в их основе закономерностей. Но авторы работы "SAMformer: Unlocking the Potential of Transformers in Time Series Forecasting with Sharpness-Aware Minimization and Channel-Wise Attention" обращают внимание на проблему Transformer, связанную с нестабильностью обучения, проявляющуюся при отсутствии крупномасштабных данных.
В компьютерном зрении и НЛП было обнаружено, что матрицы внимания могут страдать от энтропии или обрушения рангов. Затем было предложено несколько подходов к преодолению этих проблем. Однако, в случае прогнозирования временных рядов, остаются открытыми вопросы о том, как можно эффективно обучать архитектуры трансформаторов без тенденции к переобучению. Авторы упомянутой работы стремятся показать, что устранение неустойчивости обучения позволяет повысить эффективность Transformer в многомерном долгосрочном прогнозировании, вопреки ранее сложившимся представлениям об их ограничениях.
1. Алгоритм SAMformer
Рассматривается многомерная система долгосрочного прогнозирования при заданном D-размерном временном ряде длины L (окно ретроспективного обзора). Исходные данные расположенные в виде матрицы 𝐗 ∈ RD×L. Цель заключается в прогнозировании следующих H значений (горизонт прогнозирования), обозначаемых как 𝐘 ∈ RD×H. Предположим, что у нас есть доступ к обучающему набору, который состоит из N наблюдений. Мы стремимся обучить модель прогнозирования f𝝎: RD×L→RD×L с параметрами 𝝎, которая минимизирует среднеквадратичную ошибку (MSE) на обучающем наборе данных.
Недавно было показано, что трансформаторы работают наравне с простыми линейными нейронными сетями, обученными напрямую проецировать исходные данные на прогнозные значения. С целью поиска причин данного явления, авторы фреймворка SAMformer рассматривают генеративную модель для задачи искусственной регрессии, имитирующей установку прогнозирования временных рядов. Они используют линейную модель для генерации некоего продолжения временного ряда к случайным исходным данным и добавляют небольшой шум к полученным результатам. Таким образом было сгенерировано 15000 наборов исходных данных и результатов, которые разделили на 10000 обучающей выборки и 5000 для валидации модели.
С помощью такой генеративной модели авторы SAMformer разрабатывают архитектуру Transformer, которая могла бы эффективно решить проблему прогнозирования без излишней сложности. Для этого они предлагают упростить обычный энкодер Transformer, оставив блок Self-Attention и остаточного соединения за ним. Вместо блока FeedForward напрямую используется линейный слой для прогнозирования последующих данных.
Здесь стоит обратить внимание, что авторы фреймворка используют внимание по каналам, что упрощает задачу и снижает риск гиперпараметризации, так как матрица внимания становится значительно меньше за счет L>D. Кроме того, внимание по каналам более уместно, поскольку генерация данных следует за процессом идентификации.
Для определения роли внимания в решении задачи, авторы фреймворка рассматривают модель, получившую название Random Transformer. В ней оптимизируется только слой прогнозирования, в то время как все параметры блока Self-Attention фиксируются во время обучения на уровне инициализации случайными значениями. Это фактически заставляет рассматриваемый Transformer действовать как линейная модель. Сравнение локальных минимумов, полученных этими двумя моделями после их оптимизации с помощью метода Adam, с моделью Oracle, которая соответствует решению по методу наименьших квадратов представлено на рисунке ниже (визуализация из авторской статьи).
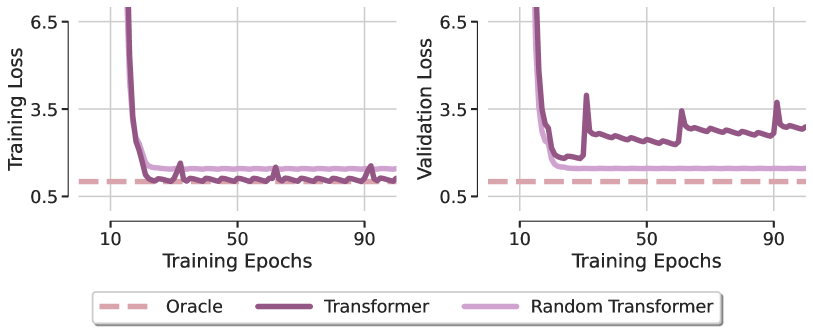
Первый удивительный вывод заключается в том, что оба трансформатора не восстанавливают линейную зависимость искусственной регрессии, подчеркивая, что оптимизация даже такой простой архитектуры с благоприятным дизайном демонстрирует явное отсутствие обобщения. Это наблюдение остается неизменным для различных оптимизаторов и значений скорости обучения. Из этого авторы фреймворка делают вывод, что слабые возможности обобщения Transformer в основном связаны с проблемами обучаемости модуля внимания.
Для лучшего понимания обнаруженного феномена, авторы SAMformer визуализировали матрицы внимания в разные эпохи обучения и обнаружили, что матрица внимания близка к матрице идентичности сразу после самой первой эпохи и почти не меняется впоследствии, особенно когда SoftMax усиливает различия в значениях матрицы. Это показывает возникновение энтропийного коллапса внимания с полноранговой матрицей внимания, которая была идентифицирована, как одна из причин жесткости тренировки трансформеров.
Авторы SAMformer так же обнаруживают связь между коллапсом энтропии и резкостью ландшафта потерь Transformer. Transformer сходится к более резкому минимуму, чем Random Transformer, при этом имея значительно меньшую энтропию (внимание к последнему фиксируется при инициализации, его энтропия остается постоянной на протяжении всего обучения). Эти патологические паттерны позволяют предположить, что Transformer выходит из строя из-за коллапса энтропии и резкости его потери при обучении.
Недавние исследования показали, что ландшафт потерь Transformer более острый по сравнению с другими архитектурами. Это может объяснить нестабильность обучения и низкую производительность Transformer, особенно при обучении на небольших наборах данных.
С целью поиска подходящего решения, позволяющего повысить производительность обобщения и стабильность обучения, авторы фреймворка SAMformer исследуют 2 подхода. Первый предполагает использование системы минимизации с учетом резкости, который заменяет цель обучения:
![]()
где ρ>0 является гиперпараметром, и 𝝎 — параметром модели.
Второй подход включает в себя повторную параметризацию всех весовых матриц с помощью спектральной нормализации и дополнительного обученного скаляра, который называется σReparam.
Результаты подчеркивают успешную сходимость предложенного решения к желаемому результату. Удивительно, но это достигается только с помощью SAM, так как σReparam не удается приблизиться к оптимальной производительности, несмотря на максимизацию энтропии матрицы внимания. Кроме того, резкость при использовании SAM на несколько порядков ниже, чем у Transformer, в то время как энтропия внимания, получаемого с помощью SAM, остается близкой к энтропии базового Transformer с небольшим увеличением на более поздних этапах обучения. Это говорит о том, что коллапс энтропии является доброкачественным в этом сценарии.
Авторы SAMformer дополняют описанное решение реверсивной нормализацией экземпляров (RevIN). Поскольку этот метод показал свою эффективность при обработке сдвига между обучающими и тестовыми данными во временных рядах. Как следует из представленного выше исследования, оптимизация модели осуществляется с помощью SAM, что заставляет ее сходиться к более плоским локальными минимумами. В целом, это дает модель уменьшенного Transformer с одним энкодером, показанную на рисунке ниже (авторская визуализация).
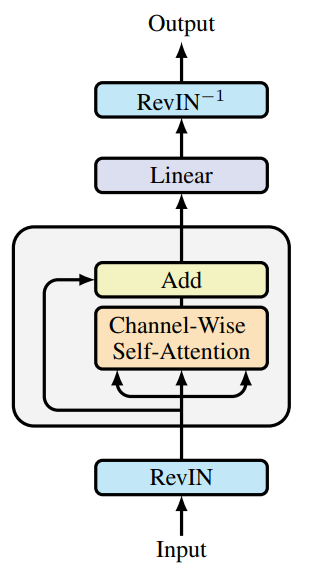
Подчеркнем, что SAMformer сохраняет внимание по каналам, представленное матрицей D×D, в отличие от пространственного (или временного) внимания, задаваемого L×L матрицей, используемой в других моделях. Это дает два важных преимущества:
- обеспечивает инвариантность перестановки признаков, устраняя необходимость позиционного кодирования, обычно предшествующего слою внимания;
- приводит к уменьшению времени и сложности памяти, так как D≤L в большинстве реальных наборов данных.
2. Реализация средствами MQL5
После рассмотрения теоретических аспектов фреймворка SAMformer, мы переходим к реализации предложенных подходов средствами MQL5. И здесь важно сразу определить, что же конкретно мы будем имплементировать в наши модели и каким образом. Давайте детально посмотрим, что же нам предлагают авторы фреймворка SAMformer:
- урезание Энкодера Transformer до уровня блока Self-Attention с остаточной связью;
- внимание по каналам;
- обратимая нормализация;
- SAM оптимизация.
Урезание Энкодера вопрос интересный, но на мой взгляд, основная его практическая ценность в сокращении параметров обучаемой модели. Ведь если откинуть условности, то функционал модели не зависит от нашего отнесения отдельных нейронных слоев к блоку FeedForward Энкодера или блоку прогнозирования, который авторы фреймворка располагают за блоком внимания.
Для организации внимания по каналам нам достаточно транспонировать исходные данные перед их передачей в блок внимания. И для этого нам нет необходимости делать какие-либо доработки.
С обратимой нормализацией RevIN мы уже знакомы. И остается только оптимизация модели методом SAM. SAM функционирует путем поиска параметров, лежащих в окрестностях с равномерно низким значением потерь.
Алгоритм оптимизации SAM работает в несколько этапов. Вначале, по результатам прямого прохода, мы получаем градиент ошибки на уровне параметров модели. Нормируем полученные градиенты ошибки и добавляем к текущим параметрам нормированный градиент ошибки с учетом коэффициента резкости. Повторно осуществляем прямой проход и распределение градиентов ошибки. Возвращаем матрицу весовых коэффициентов в предыдущее состояние, путем вычитания ранее добавленного нормированного градиента. И обновления параметров одним из классических методов SGD или Adam. Авторы фреймворка SAMformer предлагают использовать последний.
И здесь стоит отметить, что авторы метода используют нормализацию градиентов ошибки в рамках всей модели. Это довольно трудоемко. И в этом контексте становится более актуальным вопрос о снижении количества параметров модели. И очевидным решением становится сокращение внутренних слоев и голов внимания. Что и сделали авторы фреймворка SAMformer.
Мы же решили немного отойти от авторской реализации в данном случае, и нормализацию градиентов ошибки будем осуществлять только в рамках одного нейронного слоя. Более того, мы осуществим отдельную нормализацию градиентов для каждой группы параметров, формирующих значение одного нейрона. И начнем мы свою реализацию с построения новых кернелов на стороне OpenCL-программы.
2.1 Дополнение OpenCL-программы
Думаю, вы уже заметили, что в наших работах мы наиболее часто используем 2 типа нейронных слоев: полносвязные и сверточные. Все наши модули внимания, так или иначе построены на использовании сверточных слоев, которые мы используем без перекрытия для анализа и трансформации отдельных элементов анализируемой последовательности. Поэтому функционал именно этих двух нейронных слоев мы решили дополнить SAM оптимизацией. На стороне OpenCL-программы мы создадим кернелы нормирования градиента ошибки и создания весовых коэффициентов ω+ε.
Первым мы создадим кернел для полносвязного слоя CalcEpsilonWeights. В параметрах данного кернела мы получаем указатели на 4 буфера данных и коэффициент рассеивания резкости. Три буфера данных содержат исходную информацию и один для записи результатов.
__kernel void CalcEpsilonWeights(__global const float *matrix_w, __global const float *matrix_g, __global const float *matrix_i, __global float *matrix_epsw, const float rho ) { const size_t inp = get_local_id(0); const size_t inputs = get_local_size(0) - 1; const size_t out = get_global_id(1);
Вызов данного кернела мы планируем в двухмерном пространстве задач с объединением в рабочие группы по первому измерению. В теле кернела мы сразу идентифицируем текущий поток операций во всех измерениях пространства задач.
После чего объявляем массив данных в локальной памяти устройства для организации процесса обмена данных между потоками рабочей группы.
__local float temp[LOCAL_ARRAY_SIZE]; const int ls = min((int)inputs, (int)LOCAL_ARRAY_SIZE);
На следующем шаге мы определим градиент ошибки анализируемого элемента как произведение соответствующих элементов в буферах исходных данных и градиентов на выходе слоя. Полученное значение взвесим по абсолютному значению анализируемого параметра. Это позволит увеличить вес параметров, которые вносят наибольший вклад в результат работы слоя.
const int shift_w = out * (inputs + 1) + inp; const float w =IsNaNOrInf(matrix_w[shift_w],0); float grad = fabs(w) * IsNaNOrInf(matrix_g[out],0) * (inputs == inp ? 1.0f : IsNaNOrInf(matrix_i[inp],0));
И далее нам предстоит найти L2 норму полученных градиентов ошибки. Для этого мы суммируем квадраты полученных значений в рамках рабочей группы с использованием массива в локальной памяти и двух последовательных циклов, как мы это делали в предыдущих работах.
const int local_shift = inp % ls; for(int i = 0; i <= inputs; i += ls) { if(i <= inp && inp < (i + ls)) temp[local_shift] = (i == 0 ? 0 : temp[local_shift]) + IsNaNOrInf(grad * grad,0); barrier(CLK_LOCAL_MEM_FENCE); } //--- int count = ls; do { count = (count + 1) / 2; if(inp < count) temp[inp] += ((inp + count) < inputs ? IsNaNOrInf(temp[inp + count],0) : 0); if(inp + count < inputs) temp[inp + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Квадратный корень из полученной суммы и является искомой нормой градиентов. С её помощью мы найдем скорректированное значение параметра.
float norm = sqrt(IsNaNOrInf(temp[0],0)); float epsw = IsNaNOrInf(w * w * grad * rho / (norm + 1.2e-7), w); //--- matrix_epsw[shift_w] = epsw; }
И сохраним полученное значение в соответствующем элементе глобального буфера результатов.
Аналогичным образом построен кернел CalcEpsilonWeightsConv, который выполняет первичную корректировку параметров сверточного слоя. Однако, как вы знаете, сверточный слой имеет свою специфику. Он обладает меньшим количеством параметров, но каждый параметр взаимодействует с несколькими элементами слоя исходных данных и участвует в формировании значений нескольких элементов в буфере результатов. Соответственно, градиент ошибки параметра формируется путем сбора его доли с нескольких элементов буфера результатов.
Специфика сверточного слоя проявляется и в параметрах кернела. Здесь мы видим появление 2 дополнительных констант, которые определяют размер исходной последовательности и шаг окна исходных данных.
__kernel void CalcEpsilonWeightsConv(__global const float *matrix_w, __global const float *matrix_g, __global const float *matrix_i, __global float *matrix_epsw, const int inputs, const float rho, const int step ) { //--- const size_t inp = get_local_id(0); const size_t window_in = get_local_size(0) - 1; const size_t out = get_global_id(1); const size_t window_out = get_global_size(1); const size_t v = get_global_id(2); const size_t variables = get_global_size(2);
Мы так же увеличивает и размерность пространства задач до 3. Первое измерение соответствует анализируемому окну исходных данных, увеличенному на элемент смещения. Во втором измерении мы укажем количество сверточных фильтров. Третье отвечает за количество независимых последовательностей в исходных данных. Как и ранее, мы объединяем потоки операций в рабочие группы по первому измерению.
В теле кернела мы идентифицируем текущий поток операций по всем измерениям пространства задач. После чего инициализируем массив данных в локальной памяти OpenCL-контекста для обмена информацией в рамках рабочей группы.
__local float temp[LOCAL_ARRAY_SIZE]; const int ls = min((int)(window_in + 1), (int)LOCAL_ARRAY_SIZE);
Затем мы вычислим количество элементов каждого фильтра в буфере результатов и определим смещения в буферах данных.
const int shift_w = (out + v * window_out) * (window_in + 1) + inp; const int total = (inputs - window_in + step - 1) / step; const int shift_out = v * total * window_out + out; const int shift_in = v * inputs + inp; const float w = IsNaNOrInf(matrix_w[shift_w], 0);
Тут же мы сохраним в локальную переменную текущее значение анализируемого параметра, что позволит нам далее сократить количество операций обращения к глобальной памяти.
На следующем этапе мы соберем градиент ошибки со всех элементов буфера результатов, на которые оказывал влияние анализируемый параметр.
float grad = 0; for(int t = 0; t < total; t++) { if(inp != window_in && (inp + t * step) >= inputs) break; float g = IsNaNOrInf(matrix_g[t * window_out + shift_out],0); float i = IsNaNOrInf(inp == window_in ? 1.0f : matrix_i[t * step + shift_in],0); grad += IsNaNOrInf(g * i,0); }
Скорректируем его на абсолютное значение нашего параметра.
grad *= fabs(w);
И воспользуемся выше представленным алгоритмом из двух последовательных циклов для суммирования квадратов полученных значений в рамках рабочей группы.
const int local_shift = inp % ls; for(int i = 0; i <= inputs; i += ls) { if(i <= inp && inp < (i + ls)) temp[local_shift] = (i == 0 ? 0 : temp[local_shift]) + IsNaNOrInf(grad * grad,0); barrier(CLK_LOCAL_MEM_FENCE); } //--- int count = ls; do { count = (count + 1) / 2; if(inp < count) temp[inp] += ((inp + count) < inputs ? IsNaNOrInf(temp[inp + count],0) : 0); if(inp + count < inputs) temp[inp + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Квадратный корень из полученной суммы является искомой нормой градиентов ошибки.
float norm = sqrt(IsNaNOrInf(temp[0],0)); float epsw = IsNaNOrInf(w * w * grad * rho / (norm + 1.2e-7),w); //--- matrix_epsw[shift_w] = epsw; }
Мы вычисляем значение скорректированного параметра и сохраняем его в соответствующем элементе буфера результатов.
На этом мы завершаем работу на стороне OpenCL-программы. А с полным её кодом Вы можете ознакомиться во вложении.
2.2 Полносвязный слой SAM оптимизации
После завершения работы на стороне OpenCL-программы мы переходим к работе с нашей библиотекой, где мы и создадим объект полносвязного слоя с функционалом SAM оптимизации CNeuronBaseSAMOCL. Структура нового класса представлена ниже.
class CNeuronBaseSAMOCL : public CNeuronBaseOCL { protected: float fRho; CBufferFloat cWeightsSAM; //--- virtual bool calcEpsilonWeights(CNeuronBaseSAMOCL *NeuronOCL); virtual bool feedForwardSAM(CNeuronBaseSAMOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronBaseSAMOCL(void) {}; ~CNeuronBaseSAMOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, float rho, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual int Type(void) const { return defNeuronBaseSAMOCL; } virtual int Activation(void) const { return (fRho == 0 ? (int)None : (int)activation); } virtual int getWeightsSAMIndex(void) { return cWeightsSAM.GetIndex(); } //--- virtual CLayerDescription* GetLayerInfo(void); virtual void SetOpenCL(COpenCLMy *obj); };
Как можно заметить в представленной выше структуре нового объекта, основной функционал мы наследуем от базового полносвязного слоя. В принципе перед Вами копия базового полносвязного слоя, в которой мы переопределяем метод обновления параметров с учетом функционала SAM оптимизации.
Тем не менее мы добавили метод-обертку calcEpsilonWeights для одноименного кернела, описанного выше, и сделали копию метода прямого прохода, в котором изменили буфер весовых коэффициентов feedForwardSAM.
Здесь надо сказать, что авторы фреймворка SAMformer сначала добавляли ε к параметрам модели, а затем вычитали, возвращая параметры модели в исходное состояние. Мы поступили немного иначе. И сохранили скорректированные параметры в отдельный буфер. Это позволило нам отказаться от операции вычитания ε и тем самым сократить общее время выполнения операций. Но обо всем по порядку.
Буфер скорректированных параметров модели мы объявили статично, что позволяет нам оставить пустыми конструктор и деструктор класса. Инициализация всех объявленных и унаследованных объектов осуществляется в методе Init.
bool CNeuronBaseSAMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, float rho, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch)) return false;
В параметрах метода мы получаем основные константы, определяющие архитектуру создаваемого объекта. И в теле метода мы сразу вызываем одноименный метод родительского класса, в котором осуществляется контроль полученных параметров и инициализация унаследованных объектов.
После успешного выполнения метода родительского класса мы сохраняем коэффициент области рассеивания во внутренней переменной.
fRho = fabs(rho); if(fRho == 0 || !Weights) return true;
А затем проверяем значение полученного коэффициента рассеивания и наличие матрицы параметров. Если коэффициент рассеивания равен "0" или отсутствует матрица параметров (слой не содержит исходящих связей), то мы завершаем работу метода с положительным результатом. Иначе нам необходимо создать буфер альтернативных параметров. Мы создаем его равным буферу основных параметров, но на данном этапе заполняем нулевыми значениями.
if(!cWeightsSAM.BufferInit(Weights.Total(), 0) || !cWeightsSAM.BufferCreate(OpenCL)) return false; //--- return true; }
И завершаем работу метода.
С методами-обертками постановки кернелов в очередь я предлагаю Вам ознакомиться самостоятельно. Их код представлен во вложении. А мы переходим к рассмотрению метода обновления параметров updateInputWeights.
bool CNeuronBaseSAMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false; if(NeuronOCL.Type() != Type() || fRho == 0) return CNeuronBaseOCL::updateInputWeights(NeuronOCL);
В параметрах метода мы, как всегда, получаем указатель на объект исходных данных. И в теле метода сразу проверяем актуальность полученного указателя. Без наличия актуального указателя на слой исходных данных дальнейшая работа метода не возможна, так как приведет к возникновению критических ошибок.
Мы так же проверяем тип объекта исходных данных, так как в данном случае он имеет значение. Кроме того, коэффициент рассеивания должен быть больше "0". В противном случае SAM вырождается в базовый слой оптимизации. И вызываем соответствующий метод родительского класса.
После успешного прохождения вышеуказанного контрольного блока мы переходим к выполнению операций непосредственно метода SAM. И здесь следует вспомнить, что алгоритм SAM подразумевает полное прохождение прямого и обратного проходов с распределением градиентов ошибки до параметров модели после добавления к ним ε. Однако выше мы определились об организации алгоритма SAM в рамках отдельно взятого слоя. И вполне резонен вопрос, где взять целевые значения для каждого слоя.
На первый взгляд ответ очевиден — достаточно суммировать последний результат прямого прохода и градиент ошибки. Но есть нюанс. При передаче градиента ошибки от последующего слоя, мы корректируем его на производную функции активации. А значит, простое суммирование данных исказит результат. И здесь, казалось бы, необходимо создать механизм отката корректировки градиента ошибки на производную функции активации, но мы нашли более простое решение. Просто переопределили метод возврата функции активации, который при нулевом коэффициенте рассеивания возвращает None. Таким образом, мы получаем от последующего слоя градиент ошибки без корректировки на производную функцию активации. Следовательно, можем сложить результаты прямого прохода и полученный градиент ошибки, что в сумме даст нам цель анализируемого нейронного слоя.
if(!SumAndNormilize(Gradient, Output, Gradient, 1, false, 0, 0, 0, 1)) return false;
Далее мы вызываем метод-обертку для получения скорректированных параметров модели.
if(!calcEpsilonWeights(NeuronOCL)) return false;
И осуществляем прямой проход с измененными параметрами.
if(!feedForwardSAM(NeuronOCL)) return false;
Теперь в буфере градиентов ошибки мы имеем целевые значения, а в буфере результатов вектор, куда нас приведут скорректированные параметры. Для определения отклонения между этими значениями нам достаточно вызвать метод родительского класса определения отклонения от целевых результатов.
float error = 1; if(!calcOutputGradients(Gradient, error)) return false;
И теперь нам остается скорректировать параметры модели с учетом обновленного градиента ошибки. Для этого достаточно вызывать одноименный метод родительского класса.
return CNeuronBaseOCL::updateInputWeights(NeuronOCL);
}
Несколько слов стоит сказать о методах работы с файлами. Для экономии дискового пространства мы не стали сохранять буфер скорректированных параметров cWeightsSAM. Сохранение его данных не несет практической ценности, так как содержимое данного буфера актуально только в рамках работы метода обновления параметров. И при следующем вызове метода будет перезаписано. Таким образом, объем сохраняемых данных увеличился только на один элемент типа float (коэффициент области рассеивания).
bool CNeuronBaseSAMOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false; if(FileWriteFloat(file_handle, fRho) < INT_VALUE) return false; //--- return true; }
С другой стороны, нам необходим буфер cWeightsSAM для выполнения заданного функционала. При этом нам критически важен его размер — он должен быть достаточен для сохранения всех параметров текущего слоя. Поэтому мы должны его восстановить при чтении ранее сохраненной модели. В методе загрузки данных мы сначала выполняем операции одноименного метода родительского класса.
bool CNeuronBaseSAMOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false;
Затем проверяем окончание файла и, при наличии данных, считываем коэффициент области рассеивания.
if(FileIsEnding(file_handle)) return false; fRho = FileReadFloat(file_handle);
И проверяем отличие коэффициента рассеивания от нуля, а так же наличие матрицы параметров (её указатель может быть неактуальны в случае отсутствия исходящих связей нейронного слоя).
if(fRho == 0 || !Weights) return true;
При нахождении хотя бы одного несоответствия, оптимизация параметров вырождается в базовые методы, и нам нет необходимости создавать буфер скорректированных параметров. Поэтому завершаем работу метода с положительным результатом.
Здесь стоит отметить, непрохождение данного блока контролей является критичным для SAM-оптимизации, но не критичным для работы модели. Поэтому мы продолжаем работу с использованием базовых методов оптимизации.
В случае же необходимости создания буфера, мы сначала очищаем имеющийся буфер. При этом мы осознанно не проверяем результат выполнения операций. Ведь возможны ситуации, когда на момент загрузки данных такого буфера еще нет.
cWeightsSAM.BufferFree();
А затем инициализируем буфер достаточного размера нулевыми значениями и создаем его копию в контексте OpenCL.
if(!cWeightsSAM.BufferInit(Weights.Total(), 0) || !cWeightsSAM.BufferCreate(OpenCL)) return false; //--- return true; }
На этот раз мы контролируем процесс выполнения операций, так как их корректное выполнение критично для последующей работы модели. И после выполнения операций мы завершаем работу метода, вернув логический результат выполнения операций вызывающей программе.
На этом мы завершаем рассмотрение алгоритмов построения методов объекта полносвязного слоя с функционалом SAM оптимизации CNeuronBaseSAMOCL. С полным кодом данного класса и всех его методов вы можете ознакомиться самостоятельно во вложении.
К сожалению объем статьи почти исчерпан, а мы еще не завершили всю работу. В следующей статье мы продолжим начатое и посмотрим реализацию сверточного слоя с имплементацией функционала SAM. Посмотрим на внедрение предложенных технологий в архитектуру Transformer и, конечно, проверим эффективность предложенных подходов на реальных исторических данных
Заключение
SAMformer предлагает эффективное решение ключевых проблем Transformer в долгосрочном прогнозировании многомерных временных рядов, таких как сложность обучения и слабая способность к обобщению на малых выборках. Благодаря неглубокой архитектуре и механизму оптимизации с учетом резкости, SAMformer не только избегает плохих локальных минимумов, но и демонстрирует превосходство над современными методами при меньшем количестве параметров. Приведенные в авторской работе результаты подтверждают его потенциал, как универсального инструмента для задач временных рядов.
В практической части нашей статьи мы начали работу по имплементации предложенных подходов средствами MQL5. Но наша работа ещё продолжается. И в следующей статье мы оценим практическую ценность предложенных подходов для решения наших задач.
Ссылки
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | ResearchRealORL.mq5 | Советник | Советник сбора примеров методом Real-ORL |
| 3 | Study.mq5 | Советник | Советник обучения Моделей |
| 4 | StudyEncoder.mq5 | Советник | Советник обучения Энкодера |
| 5 | Test.mq5 | Советник | Советник для тестирования модели |
| 6 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы |
| 7 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 8 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Изучение MQL5 — от новичка до профи (Часть VI): Основы написания советников
Изучение MQL5 — от новичка до профи (Часть VI): Основы написания советников
 Алгоритм атомарного орбитального поиска — Atomic Orbital Search (AOS): Модификация
Алгоритм атомарного орбитального поиска — Atomic Orbital Search (AOS): Модификация
 Скользящая средняя на MQL5 с нуля: Просто и доступно
Скользящая средняя на MQL5 с нуля: Просто и доступно
 Объемный нейросетевой анализ как ключ к будущим трендам
Объемный нейросетевой анализ как ключ к будущим трендам
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования