Нейросети в трейдинге: Оптимизация Transformer для прогнозирования временных рядов (LSEAttention)
571
0
Введение
Многомерное прогнозирование временных рядов критически важно в разнообразных сферах (финансы, здравоохранение и т.д.), где решается задача прогнозирования будущих значений на основе исторических данных. Эта задача становится особенно сложной при долгосрочном прогнозировании, поскольку в таком случае необходимы модели, способные эффективно улавливать корреляции признаков и долгосрочные зависимости в многомерных временных рядах. Последние исследования сосредотачиваются на использовании архитектуры Transformer для прогнозирования временных рядов, благодаря её способности улавливать сложные временные взаимодействия при помощи механизма Self-Attention. Тем не менее, несмотря на существующий потенциал, современные методы многомерного прогнозирования временных рядов в большей степени продолжают полагаться на линейные модели, что поднимает вопросы об эффективности архитектуры Transformer в данном контексте.
Механизм Self-Attention, лежащий в основе этой архитектуры Transformer, сформулирован следующим образом:
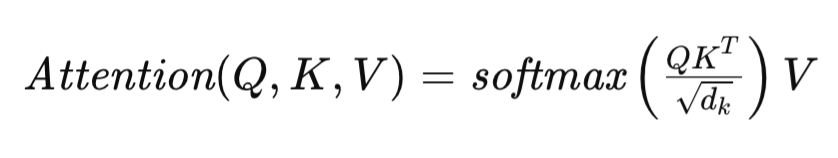
где Q, K и V представляют матрицы Query, Key и Value соответственно, и dk обозначает размерность векторов описания одного элемента последовательности в указанных матрицах. Такая формулировка позволяет Transformer динамически оценивать значимость различных элементов исходной последовательности, облегчая поиск сложных взаимозависимостей в данных.
Различные методы адаптации архитектуры Transformer применяются для долгосрочного прогнозирования временных рядов. К примеру, FEDformer применяет продвинутый модуль Фурье, достигающий линейной сложности по времени и пространству, что существенно повышает масштабируемость и эффективность для обработки длинных последовательностей.
PatchTST отказывается от точечного внимания и сосредотачивается на уровне патчей вместо отдельных временных шагов, позволяя модели улавливать более обширную семантическую информацию многомерных временных рядов, что критически важно для эффективного долгосрочного прогнозирования.
В компьютерном зрении и обработке естественного языка матрицы внимания могут испытывать энтропию или коллапс рангов. Эта проблема усугубляется при прогнозировании временных рядов из-за частых колебаний, присущих временным данным, что приводит к значительному снижению производительности модели. Фундаментальные причины коллапса энтропии остаются недостаточно изученными, что требует дальнейшего изучения его основных механизмов и влияния на производительность модели. Указанные проблемы пытаются решить авторы работы "LSEAttention is All You Need for Time Series Forecasting".
1. Алгоритм LSEAttention
Цель прогнозирования многомерных временных рядов состоит в определении наиболее вероятных будущих P значений для каждого из C каналов, представленных в виде тензора Y ∈ RC×P. Этот прогноз основан на исторических данных временных рядов длины L c C каналами, инкапсулированными в матрицу исходных данных X ∈ RC×L. Для решения поставленной задачи нам необходимо обучить предиктивную модель fωRC×L →RC×P c параметрами ω, чтобы свести к минимуму среднеквадратичную ошибку (MSE) между прогнозируемыми и фактическими значениями.
Transformer в значительной степени зависят от своего механизма точечного Self-Attention для улавливания временных ассоциаций. Однако эта зависимость может привести к явлению, известному как коллапс внимания, когда матрицы внимания сходятся к одинаковым значениям на всех наборах исходных данных и склонны к идентичным матрицам. Это приводит к плохому обобщению данных моделью.
Авторы метода LSEAttention проводят аналогию определения коэффициентов зависимости функцией SoftMax c LSE (Log-Sum-Exp) и предполагают в этом источник проблемы численной нестабильности, которая может быть основной причиной коллапса внимания.
Число обусловленности функции определяет её чувствительность к небольшим изменениям исходных данных. Высокое число обусловленности указывает на то, что незначительные возмущения исходных данных могут привести к значительным изменениям на выходе.
Эта нестабильность может проявляться в виде таких проблем, как чрезмерное внимание или энтропийный коллапс, характеризующихся матрицами внимания с чрезмерно высокими диагональными значениями (указывающими на переполнение) и крайне низкими недиагональными значениями (указывающими на занижение).
Для решения указанных проблем был предложен модуль LSEAttention, который интегрирует трюк Log-Sum-Exp (LSE) вместе с функцией активации линейной единицы гауссовской ошибки (GELU). Трюк LSE смягчает числовую неустойчивость, возникающую из-за переполнения и занижения за счет нормализации. Функция SoftMax может быть переформулирована с помощью LSE следующим образом:
где экспонента от LSE(x) обозначает экспоненциальную величину функции log-sum-exp, повышая числовую стабильность.
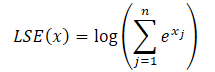
Воспользовавшись свойством степеней мы всегда можем представить значение экспоненты любого числа в виде произведения двух экспоненциальных значений.
где a — константа, используемая для нормализации. На практике в качестве константы обычно используется максимальная величина. Подставим произведение экспонент в формулу LSE и вынесем общее значение за знак суммы:
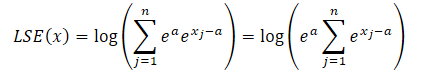
Логарифм произведения равен сумме логарифмов, а натуральный логарифм от экспоненциального значения равен показателю степени. Это позволяет нам упростить представленное выражение:
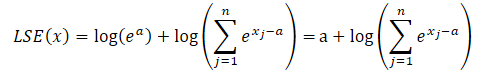
Подставим полученное выражение в функцию SoftMax и воспользуемся свойством степеней:
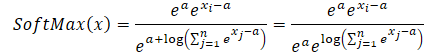
Легко заметить, что общее для числителя и знаменателя экспоненциальное значение константы сокращается. А экспонента от натурального логарифма равна под логарифмическому выражению. Таким образом, мы получаем численно стабильное выражение SoftMax.
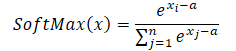
При использовании максимального значения в качестве константы (a = max(x)), мы всегда получаем x-a меньше или равно 0. В таком случае экспоненциальное значение от x-a лежит в диапазоне от 0 до 1, не включая 0. Соответственно, знаменатель функции находится в диапазоне (1, n].
Кроме того, авторы фреймворка LSEAttention предлагают использовать функцию активации GELU, которая обеспечивает более плавную вероятностную активацию. Это помогает стабилизировать экстремальные значения логарифмической вероятности перед применением экспоненциальной функции, тем самым смягчая резкие переходы в оценках внимания. Путем аппроксимации функции ReLU, благодаря плавной кривой, включающей кумулятивную функцию распределения (CDF) стандартного нормального распределения, GELU уменьшает резкие сдвиги в активациях, которые могут произойти при использовании традиционного ReLU. Это свойство особенно выгодно для стабилизации механизмов внимания на основе Transformer, где резкие изменения активации могут привести к численной нестабильности и градиентному взрыву.
Функция GELU формально определяется следующим образом:
где Φ(x) представляет собой CDF стандартного нормального распределения. Эта формулировка гарантирует, что GELU применяет различные уровни масштабирования к входам в зависимости от их величины, уменьшая усиление экстремальных значений. Плавный, вероятностный характер GELU позволяет осуществлять постепенный переход входных значений, что, в свою очередь, смягчает влияние больших колебаний градиента во время обучения.
Это свойство становится важным в сочетании с трюком Log-Sum-Exp (LSE), который нормализует функцию SoftMax в численно стабильной манере. Вместе LSE и GELU предотвращают переполнение и занижение в экспоненциальных операциях в SoftMax, что приводит к стабилизированному диапазону оценок внимания. Эта синергия повышает надежность моделей Transformer, гарантируя хорошее распределение коэффициентов внимания между токенами. В конечном итоге это приводит к более стабильным градиентам и улучшенной сходимости во время обучения.
В традиционных архитектурах Transformer функция активации ReLU (Rectified Linear Unit), используемая в блоке Feed Forward (FFN), подвержена проблеме «умирающего ReLU», когда нейроны могут стать неактивными, выводя ноль для всех отрицательных входных значений. Это приводит к сценарию нулевого градиента для этих нейронов, что эффективно останавливает их процесс обучения и способствует нестабильности во время обучения.
Для решения указанных проблем, в качестве альтернативной функции активации используется параметрический ReLU (PReLU). PReLU вводит обучаемый наклон для отрицательных входных данных, что позволяет получать ненулевой выход даже при отрицательном входе. Эта адаптация не только облегчает проблему умирающего ReLU, но и способствует более плавному переходу между негативными и положительными активациями, тем самым повышая способность модели обучаться на всех областях пространства исходных значений. Наличие ненулевого градиента для отрицательных значений способствует улучшению градиентного потока, что имеет решающее значение для обучения более глубоких архитектур. Следовательно, использование PReLU способствует общей стабильности обучения и помогает поддерживать активные представления, что в конечном итоге приводит к повышению производительности модели.
В Transformer временных рядов LSEAttention (LATST) авторы фреймворка также добавляют обратимую нормализацию данных, что особенно эффективно для устранения расхождений между распределением обучающих и тестовых данных в задачах прогнозирования временных рядов.
Архитектура сохраняет традиционный темпоральный механизм Self-Attention, встроенный в модуль LSEAttention.
В целом, архитектура LATST состоит из одноуровневой структуры Transformer, дополненной модулями замещения, что позволяет проводить адаптивное обучение при сохранении надежности механизмов внимания. Такая конструкция облегчает эффективное моделирование временных зависимостей и повышает производительность в задачах прогнозирования временных рядов. Авторская визуализация фреймворка представлена ниже.
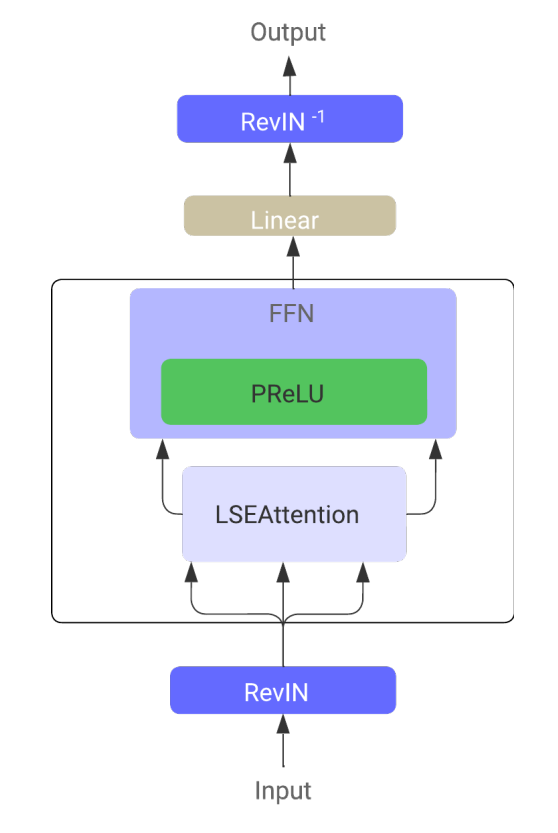
2. Реализация средствами MQL5
После рассмотрения теоретических аспектов фреймворка LSEAttention, мы переходим к практической части нашей работы, в которой рассмотрим один из вариантов реализации предложенных подходов средствами MQL5. И сразу надо сказать, что данная наша работа будет отличаться от всех, проделанных ранее. Дело в том, что в данной реализации мы не будем создавать новый объект для реализации предложенных подходов. Вместо этого мы добавим предложенные подходы в ранее реализованные классы.
2.1 Корректировка слоя SoftMax
Возьмем, к примеру, класс CNeuronSoftMaxOCL, в рамках которого организован слой функции SoftMax. Мы широко используем данный класс как в качестве отдельного слоя нашей модели, так и в составе различных фреймворков. В частности, мы использовали объект CNeuronSoftMaxOCL при построении модуля пулинга на основе зависимостей CNeuronMHAttentionPooling, применяемого нами в нескольких последних работах. И вполне логично добавить в его алгоритм подход численно стабильного вычисления значений функции SoftMax.
С этой целью мы внесем изменения в работу кернела SoftMax_FeedForward. В параметрах кернела мы получаем указатели на 2 буфера данных: исходных значений и результатов.
__kernel void SoftMax_FeedForward(__global float *inputs, __global float *outputs) { const uint total = (uint)get_local_size(0); const uint l = (uint)get_local_id(0); const uint h = (uint)get_global_id(1);
Выполнение кернела мы планируем в двухмерном пространстве задач. Размер первого измерения равен количеству нормализуемых значений в рамках одной унитарной последовательности. По второму измерению мы укажем количество унитарных последовательностей (или голов нормализации). При этом мы объединяем потоки в рабочие группы в рамках отдельных унитарных последовательностей.
В теле кернела мы сразу идентифицируем текущий поток по всем измерениям пространства задач.
Тут же мы объявляем массив данных в локальной памяти, который будет использоваться для обмена данными в рамках рабочих групп.
__local float temp[LOCAL_ARRAY_SIZE];
И определим константы смещения в глобальных буферах данных до соответствующих элементов.
const uint ls = min(total, (uint)LOCAL_ARRAY_SIZE); uint shift_head = h * total;
Для сокращения операций обращений к глобальной памяти, мы скопируем исходные данные в локальные переменные и осуществим контроль полученных значений.
float inp = inputs[shift_head + l]; if(isnan(inp) || isinf(inp) || inp<-120.0f) inp = -120.0f;
Обратите внимание, что мы ограничиваем исходное значение на уровне -120, что практически соответствует минимальному значению степени для вычисления экспоненты типа float и является дополнительным способом предотвращения занижения значений. При этом мы не ограничиваем верхний порог значений, так как с переполнением мы будем бороться путем вычитания максимального значения.
Далее нам предстоит определить максимальное значение анализируемой унитарной последовательности. Для этого мы организуем цикл сбора максимальных значений в отдельных подпоследовательностях рабочей группы с записью их в элементы локального массива.
for(int i = 0; i < total; i += ls) { if(l >= i && l < (i + ls)) temp[l] = (i > 0 ? fmax(inp, temp[l]) : inp); barrier(CLK_LOCAL_MEM_FENCE); }
После чего мы определим максимальное значение в нашем локальном массиве, создав дополнительный цикл перебора значений.
uint count = min(ls, (uint)total); do { count = (count + 1) / 2; if(l < ls) temp[l] = (l < count && (l + count) < total ? fmax(temp[l + count],temp[l]) : temp[l]); barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); float max_value = temp[0]; barrier(CLK_LOCAL_MEM_FENCE);
Полученное максимальное значение элементов текущей рабочей группы мы сохраним в локальную переменную и обязательно синхронизируем потоки на данном этапе. Нам очень важно, чтобы все потоки рабочей группы сохранили корректное максимальное значение до последующего изменения элементов массива локальной памяти.
Теперь мы можем вычесть из исходного значения величину максимального элемента. И здесь мы снова проверяем нижний порог значений. Ведь при вычитании положительного максимального значения мы рискуем выйти из диапазона допустимых значений. После чего вычисляем экспоненту скорректированного значения.
inp = fmax(inp - max_value, -120); float inp_exp = exp(inp); if(isinf(inp_exp) || isnan(inp_exp)) inp_exp = 0;
И с помощью двух последовательных циклов мы осуществим суммирование полученных экспоненциальных значений в рамках рабочей группы. Алгоритм построения циклов аналогичен приведенному выше для нахождения максимального значения. Мы лишь изменяем операцию в теле циклов.
for(int i = 0; i < total; i += ls) { if(l >= i && l < (i + ls)) temp[l] = (i > 0 ? temp[l] : 0) + inp_exp; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)total); do { count = (count + 1) / 2; if(l < ls) temp[l] += (l < count && (l + count) < total ? temp[l + count] : 0); if(l + count < ls) temp[l + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
И теперь, когда мы получили все необходимые значения, мы можем посчитать итоговые значения функции SoftMax, разделим каждое отдельное экспоненциальное значение на их сумму в рамках рабочей группы.
//--- float sum = temp[0]; outputs[shift_head+l] = inp_exp / (sum + 1.2e-7f); }
Результат выполненных операций мы сохраняем в соответствующий элемент глобального буфера результатов.
Здесь стоит обратить внимание, что изменения, внесенные в алгоритм вычисления функции SoftMax при прямом проходе, не требуют пересмотра алгоритмов обратного прохода. Как можно заметить из математических выкладок, представленных в теоретической части данной статьи, использование трюка LSE не изменяет итоговых значений функции. Следовательно, влияние исходных данных на конечный результат остается прежним. И мы вправе использовать уже имеющийся алгоритм распределения градиента ошибки.
2.2 Внесение изменений в модуль относительного внимания
Однако надо заметить, что алгоритм SoftMax мы не всегда используем в качестве отдельного слоя. Практически во всех вариантах нашей реализации различных вариантов использования блоков Self-Attention, мы имплементировали его реализацию в рамках единого кернела построения функционала внимания. Давайте посмотрим на модуль относительного внимания CNeuronRelativeSelfAttention. В нем весь алгоритм модифицированного Self-Attention реализован в рамках кернела MHRelativeAttentionOut. И конечно, нам важно получить стабильный процесс обучения всех наших моделей не зависимо от их архитектуры. Поэтому нам предстоит провести работу по имплементации численно стабильного SoftMax во все аналогичные алгоритмы. При этом параметры кернела и пространства задач мы, по возможности, оставляем без изменений. Именно так мы поступили при модернизации кернела MHRelativeAttentionOut.
Однако стоит обратить внимание, что внесение изменений в параметры кернела и пространства задач постановки его в очередь выполнения, должно сопровождаться соответствующими изменениями во всех методах-обертках такого кернела основной программы. В противном случае, существует риск получения критической ошибки программы при постановке кернела в очередь выполнения. Это относится не только к изменению глобального пространства задач, но и к изменению размера рабочих групп.
__kernel void MHRelativeAttentionOut(__global const float *q, ///<[in] Matrix of Querys __global const float *k, ///<[in] Matrix of Keys __global const float *v, ///<[in] Matrix of Values __global const float *bk, ///<[in] Matrix of Positional Bias Keys __global const float *bv, ///<[in] Matrix of Positional Bias Values __global const float *gc, ///<[in] Global content bias vector __global const float *gp, ///<[in] Global positional bias vector __global float *score, ///<[out] Matrix of Scores __global float *out, ///<[out] Matrix of attention const int dimension ///< Dimension of Key ) { //--- init const int q_id = get_global_id(0); const int k_id = get_local_id(1); const int h = get_global_id(2); const int qunits = get_global_size(0); const int kunits = get_local_size(1); const int heads = get_global_size(2);
В теле кернела мы, как и ранее, идентифицируем текущий поток в пространстве задач. А так же определяем все размерности пространства задач.
Тут же мы определяем целый ряд необходимых констант, среди которых есть как указатели смещения в глобальных буферах данных, так и некоторые вспомогательные величины.
const int shift_q = dimension * (q_id * heads + h); const int shift_kv = dimension * (heads * k_id + h); const int shift_gc = dimension * h; const int shift_s = kunits * (q_id * heads + h) + k_id; const int shift_pb = q_id * kunits + k_id; const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE); float koef = sqrt((float)dimension);
После чего мы объявляем массив в локальной памяти, который мы будем использовать для обмена данными между потоками рабочей группы.
__local float temp[LOCAL_ARRAY_SIZE];
Для определения коэффициента внимания, согласно алгоритму ванильного Self-Attention, вначале нам необходимо выполнить операцию умножения двух соответствующих векторов из тензоров Query и Key. Однако авторы фреймворка R-MAT добавили еще элементы контекстно-зависимого и глобального смещения. Равенство размеров всех используемых векторов позволяет нам выполнить операции в рамках одного цикла с числом итераций, равным размеру векторов. В теле цикла осуществляется поэлементное умножение элементов соответствующих векторов с последующим суммирование полученных значений.
//--- score float sc = 0; for(int d = 0; d < dimension; d++) { float val_q = q[shift_q + d]; float val_k = k[shift_kv + d]; float val_bk = bk[shift_kv + d]; sc += val_q * val_k + val_q * val_bk + val_k * val_bk + gc[shift_q + d] * val_k + gp[shift_q + d] * val_bk; } sc = sc / koef;
Полученный результат мы скорректируем на квадратный корень из размерности векторов. Авторы ванильного Transformer утверждают, что данная операция повышает стабильность работы модели. И мы не будем с этим спорить.
И дальше полученные значения переводятся в область вероятностных величин с помощью функции SoftMax. Здесь мы добавим операции алгоритма повышения численной стабильности. Вначале нам предстоит определить максимальное значение среди полученных коэффициентов в рамках одной рабочей группы. Для этого разделим все потоки рабочей группы на несколько подгрупп, каждая из которых запишет свое максимальное значение в один из элементов нашего массива в локальной памяти.
//--- max value for(int cur_k = 0; cur_k < kunits; cur_k += ls) { if(k_id >= cur_k && k_id < (cur_k + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_k == 0 ? sc : fmax(temp[shift_local], sc)); } barrier(CLK_LOCAL_MEM_FENCE); }
После чего организуем цикл определения максимального значения среди элементов массива.
uint count = min(ls, (uint)kunits); //--- do { count = (count + 1) / 2; if(k_id < ls) temp[k_id] = (k_id < count && (k_id + count) < kunits ? fmax(temp[k_id + count], temp[k_id]) : temp[k_id]); barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
И вычислим экспоненциальное значение из текущего коэффициента внимания за вычетом максимального значения. И не забываем синхронизировать потоки. Так как на следующем этапе мы будем изменять значения элементов локального массива и рискуем перезаписать значение максимального элемента до его использования всеми потоками рабочей группы.
sc = exp(fmax(sc - temp[0], -120)); if(isnan(sc) || isinf(sc)) sc = 0; barrier(CLK_LOCAL_MEM_FENCE);
Следующим шагом нам предстоит вычислить сумму полученных экспоненциальных значений в рамках рабочей группы. Для этого, как и ранее, мы воспользуемся алгоритмом из двух последовательных циклов.
//--- sum of exp for(int cur_k = 0; cur_k < kunits; cur_k += ls) { if(k_id >= cur_k && k_id < (cur_k + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_k == 0 ? 0 : temp[shift_local]) + sc; } barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k_id < ls) temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0); if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
И теперь мы можем привести коэффициенты внимания в область вероятностных значений, разделим текущие величины на общую сумму.
//--- score float sum = temp[0]; if(isnan(sum) || isinf(sum) || sum <= 1.2e-7f) sum = 1; sc /= sum; score[shift_s] = sc; barrier(CLK_LOCAL_MEM_FENCE);
Полученные значения сохраняем в соответствующих элементах глобального буфера данных и синхронизируем потоки операций в рамках рабочей группы.
И в завершении, нам предстоит посчитать взвешенную сумму элементов тензора Value для каждого элемента исходной последовательности. Как вы знаете, взвешивать значения мы будем на основании вышевычисленных коэффициентов внимания. В рамках одного элемента последовательности данная операция представляется умножением вектора коэффициентов внимания на тензор Value, к которому авторы фреймворка R-MAT добавили тензор глобального смещения.
Для выполнения указанных операций мы создаем систему циклов, внешний из которых будет перебирать элементы последнего изменения тензора Value.
//--- out for(int d = 0; d < dimension; d++) { float val_v = v[shift_kv + d]; float val_bv = bv[shift_kv + d]; float val = sc * (val_v + val_bv); if(isnan(val) || isinf(val)) val = 0;
В теле цикла каждый поток вычисляет свое значение для соответствующего элемента, которые затем суммируются в рамках рабочей группы средствами вложенных двух последовательных циклов.
//--- sum of value for(int cur_v = 0; cur_v < kunits; cur_v += ls) { if(k_id >= cur_v && k_id < (cur_v + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_v == 0 ? 0 : temp[shift_local]) + val; } barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k_id < count && (k_id + count) < kunits) temp[k_id] += temp[k_id + count]; if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Сумма полученных значений одним из потоков рабочей группы сохраняется в соответствующем элементе глобального буфера результатов.
//--- if(k_id == 0) out[shift_q + d] = (isnan(temp[0]) || isinf(temp[0]) ? 0 : temp[0]); barrier(CLK_LOCAL_MEM_FENCE); } }
После чего, синхронизируются потоки операций рабочей группы, и мы переходим к следующей итерации цикла.
Как и обсуждалось ранее, внесение изменений в алгоритм функции SoftMax не оказывает влияния на зависимость результатов от исходных данных. Поэтому для функционала обратного прохода мы используем ранее реализованные алгоритмы без изменений.
2.3 Функция активация GELU
Кроме числовой стабилизации функции SofMax, авторы фреймворка LSEAttention предлагают использовать функцию активации GELU. Авторы данной функции активации предложили 2 варианта её реализации. Один из которых представлен ниже.
Реализация подобной функции не вызывает труда. Мы лишь дополним функцию вычисления активаций новым вариантом.
float Activation(const float value, const int function) { if(isnan(value) || isinf(value)) return 0; //--- float result = value; switch(function) { case 0: result = tanh(clamp(value, -20.0f, 20.0f)); break; case 1: //Sigmoid result = 1 / (1 + exp(clamp(-value, -20.0f, 20.0f))); break; case 2: //LReLU if(value < 0) result *= 0.01f; break; case 3: //SoftPlus result = (value >= 20.0f ? 1.0f : (value <= -20.0f ? 0.0f : log(1 + exp(value)))); break; case 4: //GELU result = value / (1 + exp(clamp(-1.702f * value, -20.0f, 20.0f))); break; default: break; } //--- return result; }
Однако, за кроющейся простотой прямого прохода нас ждала довольно сложная задача реализации обратного прохода данной функции. Дело в том, что производная GELU зависит от исходного значения и сигмоиды. А в нашей стандартной реализации нет таких значений.
И нет возможности точно выразить производную функции GELU через имеющийся у нас результат прямого прохода. Поэтому нам пришлось прибегнуть к некоторым эвристикам и приближениям.
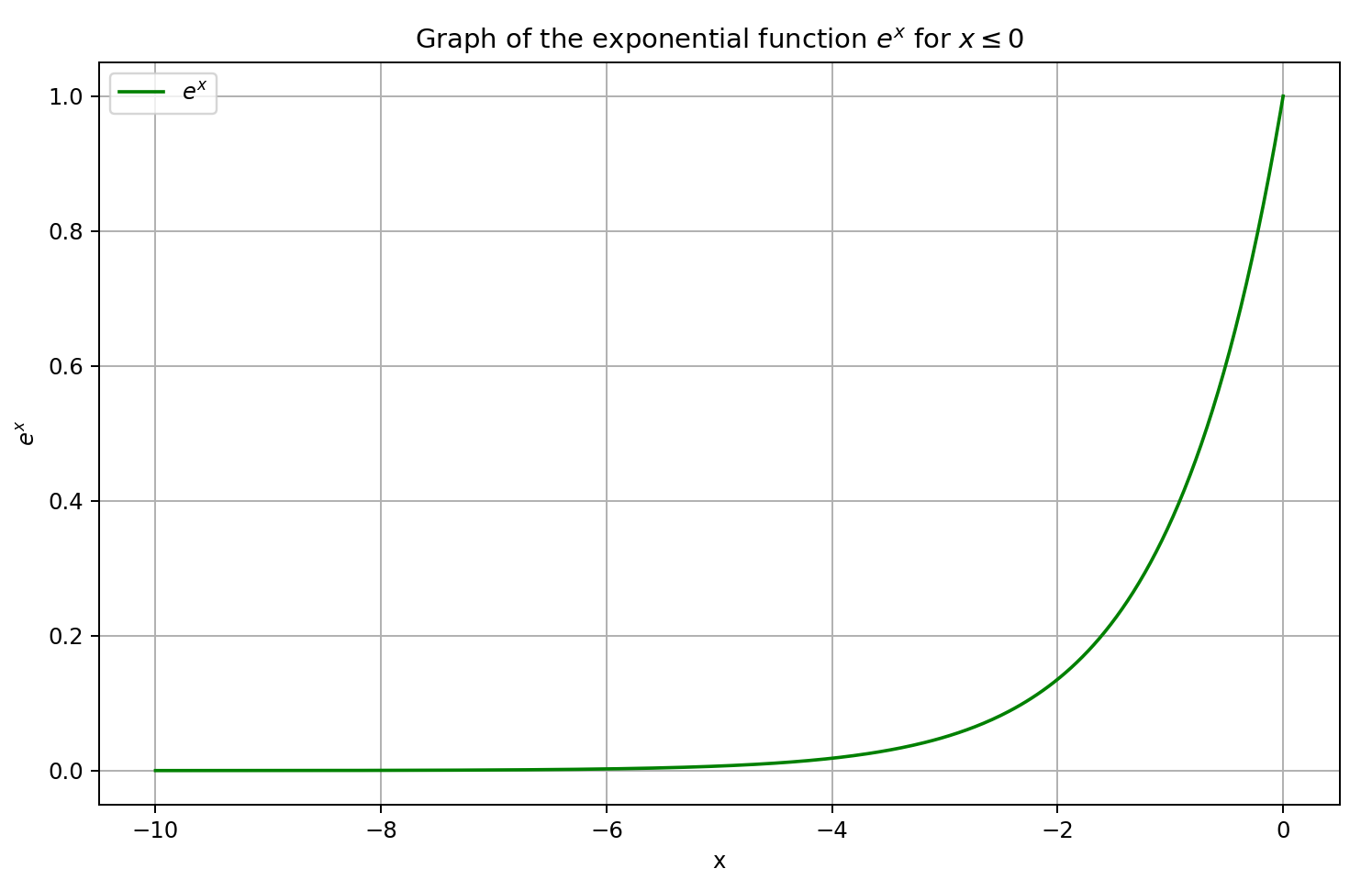
Для начала давайте вспомним график сигмоиды.
При значениях аргумента больше "5" он стремится к "1", а при меньше "-5" — к "0". Следовательно, при достаточно отрицательных значениях X, производная GELU стремится к "0", так как левый множитель уравнения стремится к "0". А при достаточно больших положительных значениях X, производная стремится к "1", так как оба множителя стремятся к "1". Что и подтверждает приведенный ниже график.
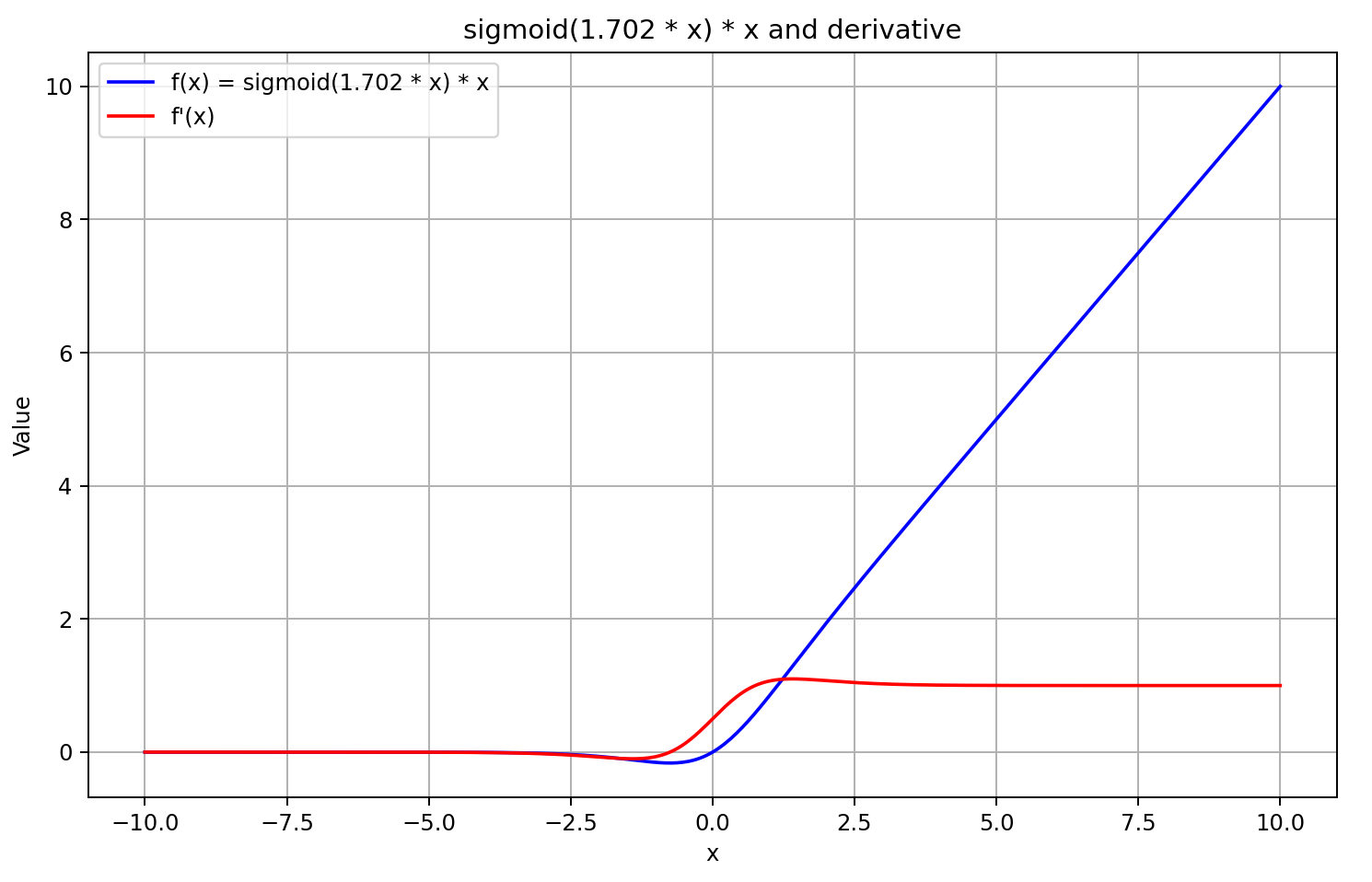
Руководствуясь вышесказанными предположениями, мы аппроксимируем производную как сигмоиду из результата прямого прохода помноженного на 5. Такой подход нам дает относительно быстрое вычисление значения производной с хорошим приближением для результатов GELU больше или равных "0". А при отрицательных значениях функции после прямого прохода, производная фиксируется на уровне 0.5, что не позволяет продолжать обучение модели. В то время как фактическая производная функции стремится к "0" и блокирует передачу градиента ошибки.
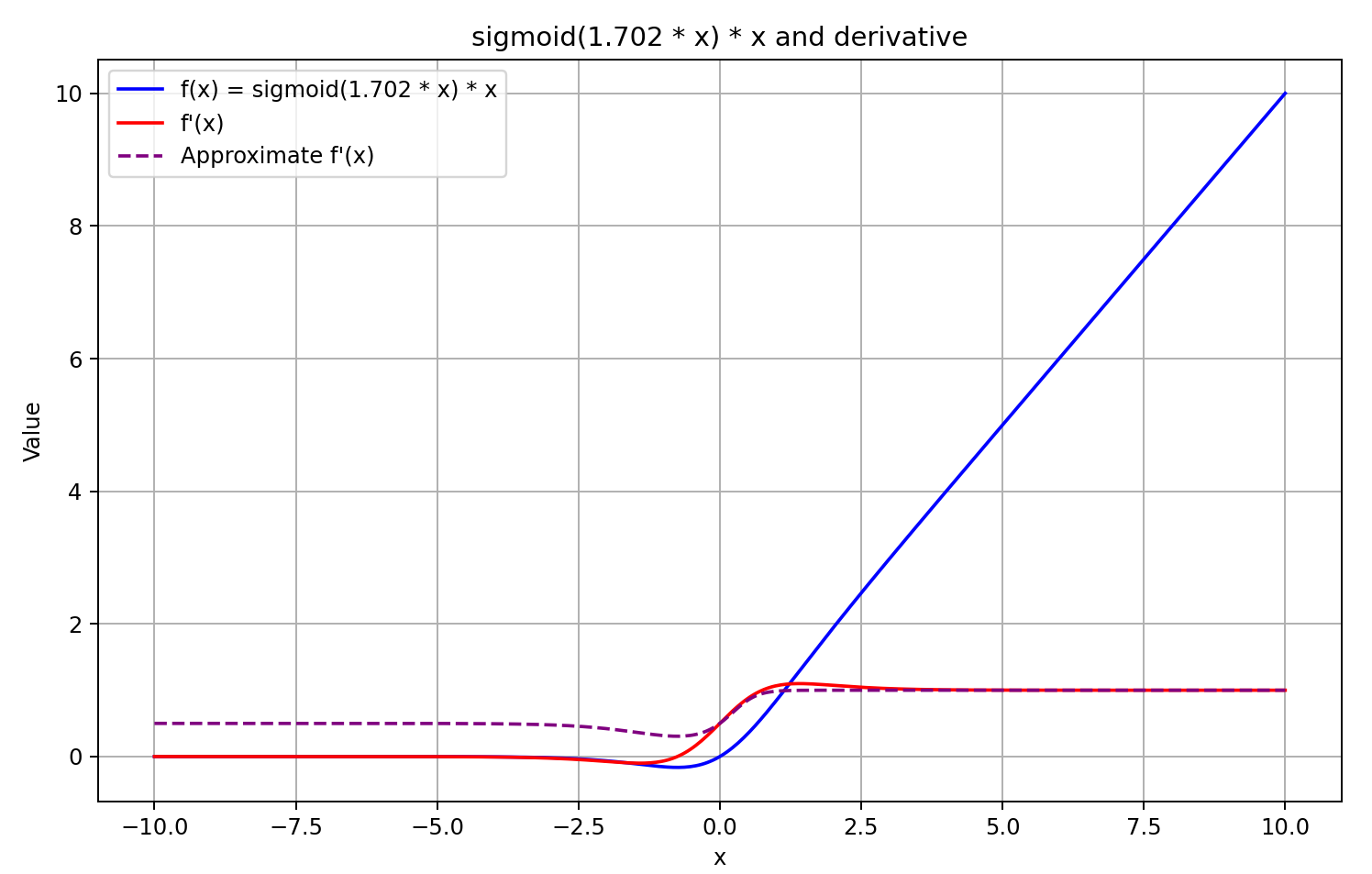
Решение принято. Приступаем к реализации. Для этого мы добавляем ещё один пункт в функции вычисления производной.
float Deactivation(const float grad, const float inp_value, const int function) { float result = grad; //--- if(isnan(inp_value) || isinf(inp_value) || isnan(grad) || isinf(grad)) result = 0; else switch(function) { case 0: //TANH result = clamp(grad + inp_value, -1.0f, 1.0f) - inp_value; result *= 1.0f - pow(inp_value, 2.0f); break; case 1: //Sigmoid result = clamp(grad + inp_value, 0.0f, 1.0f) - inp_value; result *= inp_value * (1.0f - inp_value); break; case 2: //LReLU if(inp_value < 0) result *= 0.01f; break; case 3: //SoftPlus result *= Activation(inp_value, 1); break; case 4: //GELU if(inp_value < 0.9f) result *= Activation(5 * inp_value, 1); break; default: break; } //--- return clamp(result, -MAX_GRAD, MAX_GRAD); }
Обратите внимание, что мы вычисляем функцию активации только при значении результата прямого прохода меньше "0.9". В остальных случаях мы принимаем производную равной "1", что соответствует действительности. Тем самым мы сокращаем количество операций, осуществляемых при распределении градиента ошибки.
Авторы фреймворка предлагают использовать функцию GELU для создания нелинейности между слоями блока FeedForward. В классе CNeuronRMAT в качестве указанного блока мы используем сверточный модуль с обратной связью CResidualConv. Изменим в нем функцию активации между слоями. Данная операция выполняется в методе инициализации класса. Точечная правка выделена в коде подчеркиванием.
bool CResidualConv::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_out, uint count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * count, optimization_type, batch)) return false; //--- if(!cConvs[0].Init(0, 0, OpenCL, window, window, window_out, count, optimization, iBatch)) return false; if(!cNorm[0].Init(0, 1, OpenCL, window_out * count, iBatch, optimization)) return false; cNorm[0].SetActivationFunction(GELU); if(!cConvs[1].Init(0, 2, OpenCL, window_out, window_out, window_out, count, optimization, iBatch)) return false; if(!cNorm[1].Init(0, 3, OpenCL, window_out * count, iBatch, optimization)) return false; cNorm[1].SetActivationFunction(None); //--- ........ ........ ........ //--- return true; }
На этом мы завершаем работу по имплементации подходов, предложенных авторами фреймворка LSEAttention. С полным кодом всех правок вы можете ознакомиться во вложении. Там же вы найдете полный код всех программ, используемых при подготовке данной статьи.
Должен сказать, что все программы взаимодействия с окружающей средой и обучения моделей перенесены полностью из предыдущей статьи. Аналогично и архитектура моделей перенесена без изменений. Тем интереснее будет оценить результат обучения моделей. Ведь на результат обучения могут повлиять только внедренные подходы.
3. Тестирование
В данной статье мы реализовали подходы по оптимизации ванильного алгоритма Transformer, предложенные авторами фреймворка LSEAttention для прогнозирования временных рядов. Как уже было сказано, данная работа отличается от представленных ранее. Мы не создавали новые нейронные слои, как это делалось ранее. Напротив, мы внедрили предложенные подходы в реализованные ранее объекты. Фактически, мы взяли реализованный в предыдущей статье фреймворк HypDiff и добавили в него некоторые оптимизации алгоритма, которые не повлияли на архитектуру модели. Если конечно не считать изменение функции активации в блоке FeedForward. Однако внедренные подходы несколько скорректировали вычислительные операции, добавим им численную стабильность. И, конечно, нам интересно посмотреть, как это повлияет на результаты обучения модели.
Для чистоты эксперимента мы полностью повторяем алгоритм обучения модели HypDiff. Для обучения используем ту же обучающую выборку. Однако на это раз мы не осуществляем итерационного её обновления. Да, это может отрицательно сказаться на результатах обучения, но позволит нам корректно сравнить работу модели до и после оптимизации алгоритма.
Для проверки результатов обучения модели используются реальные исторические данные за первый квартал 2024 года. Результаты тестирования представлены ниже.
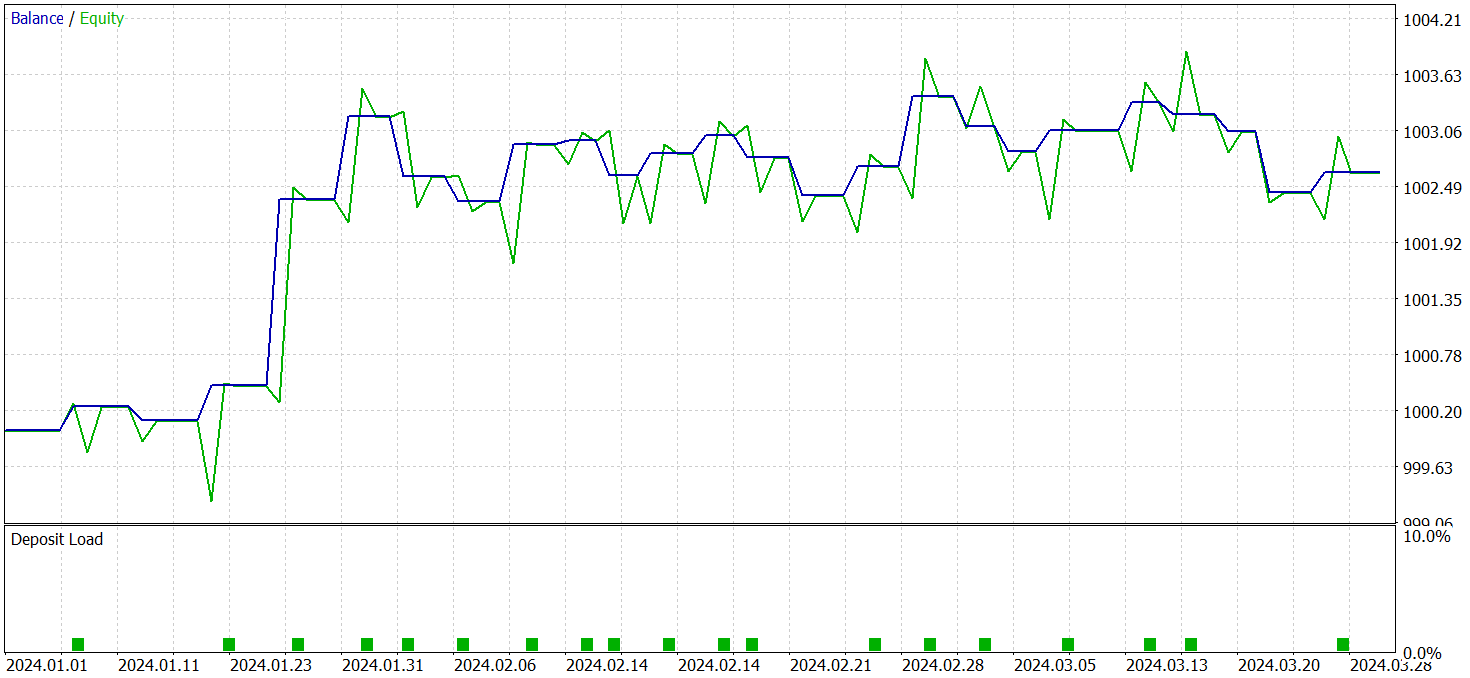
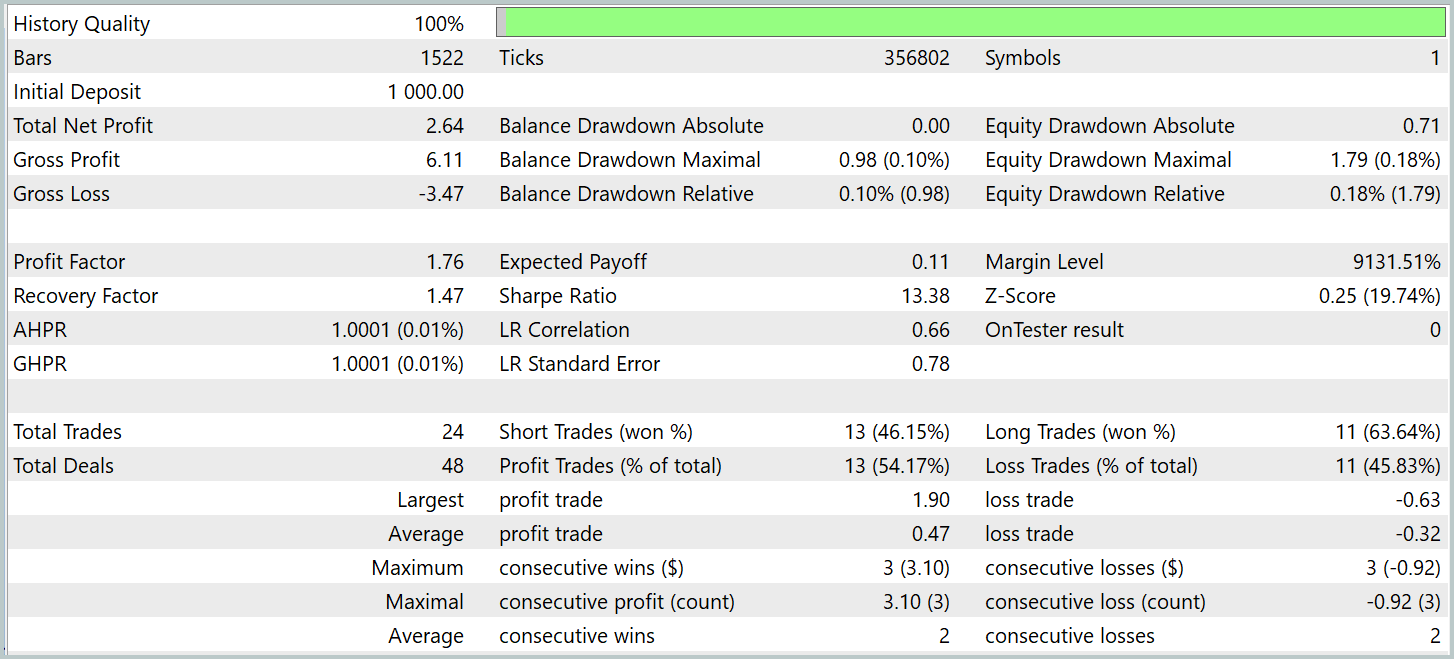
Надо сказать, что результаты работы модели на тестовой выборке до и после модификации довольно близки. За период тестирования обновленная модель совершила 24 сделки. Отклонение об базовой модели в 1 сделку на уровне погрешности. Обе модели сделали 13 прибыльных сделок. Единственное видимое улучшение — отсутствие просадки в феврале месяце.
Заключение
Метод LSEAttention представляет собой развитие механизмов внимания, особенно эффективное в задачах, требующих высокой устойчивости к шуму и вариативности данных. Основное преимущество LSEAttention заключается в использовании логарифмического сглаживания, реализованного с помощью Log-Sum-Exp функции. Что позволяет избежать эффектов численного переполнения и затухания, критичных для глубоких нейронных сетей.
В практической части мы имплементировали предложенные подходы средствами MQL5 в ранее реализованные объекты. Обучили и провели тестирование моделей с использованием предложенных подходов на реальных исторических данных. По результатам тестирования можно сделать вывод, что предложенные подходы повышают стабильность процесса обучения модели.
Ссылки
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | ResearchRealORL.mq5 | Советник | Советник сбора примеров методом Real-ORL |
| 3 | Study.mq5 | Советник | Советник обучения Моделей |
| 4 | Test.mq5 | Советник | Советник для тестирования модели |
| 5 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы |
| 6 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 7 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL |
Объемный нейросетевой анализ как ключ к будущим трендам
Торговый инструментарий MQL5 (Часть 1): Разработка EX5-библиотеки для управления позициями
Алгоритм атомарного орбитального поиска — Atomic Orbital Search (AOS): Модификация
Быстрый тестер торговых стратегий на Python с использованием Numba
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования