
Redes neurais em trading: Modelos bidimensionais do espaço de conexões (Conclusão)
Introdução
No artigo anterior, apresentamos o framework Chimera, um modelo bidimensional do espaço de estados (2D-SSM), baseado em transformações lineares ao longo dos eixos do tempo e das variáveis analisadas. Ele combina modelos de espaço de estados em dois eixos e os mecanismos de sua interação.
Modelos de espaço de estados (SSM) são amplamente aplicados na análise de séries temporais, pois permitem modelar dependências complexas. No entanto, os SSM tradicionais consideram apenas o eixo temporal, o que limita sua aplicação em problemas multidimensionais. Chimera amplia esse conceito ao incluir o eixo de características no processo de modelagem.
O framework trabalha com a forma discretizada do 2D-SSM, introduzindo passos de discretização Δ1 e Δ2. O primeiro parâmetro afeta as dependências temporais, enquanto o segundo regula as conexões entre variáveis. Valores menores de Δ1 ajudam a capturar tendências de longo prazo, enquanto valores maiores destacam mudanças sazonais. Da mesma forma, a discretização em relação às variáveis ajusta o nível de detalhamento da análise.
Para garantir a correta reconstrução dos processos, os autores do framework introduzem restrições estruturais nas matrizes A1, A2 (dependências temporais) e A3, A4 (conexões entre variáveis). A natureza causal do 2D-SSM limita a transmissão de informação ao longo do eixo de características, por isso o Chimera utiliza dois módulos para analisar as interdependências com características anteriores e posteriores do ambiente em estudo.
A flexibilidade do framework Chimera permite o uso de parâmetros Bi, Ci e Δi tanto de forma independente dos dados brutos quanto como funções dos próprios dados brutos. O uso de parâmetros dependentes do contexto torna o modelo mais adaptável às condições de sistemas multidimensionais complexos.
O framework utiliza uma pilha de 2D-SSM com transformações não lineares entre as camadas, aproximando-se da arquitetura de modelos profundos. Ele permite decompor séries temporais em componentes de tendência e sazonais, garantindo uma análise precisa dos padrões.
Abaixo é apresentada a visualização autoral do framework Chimera.
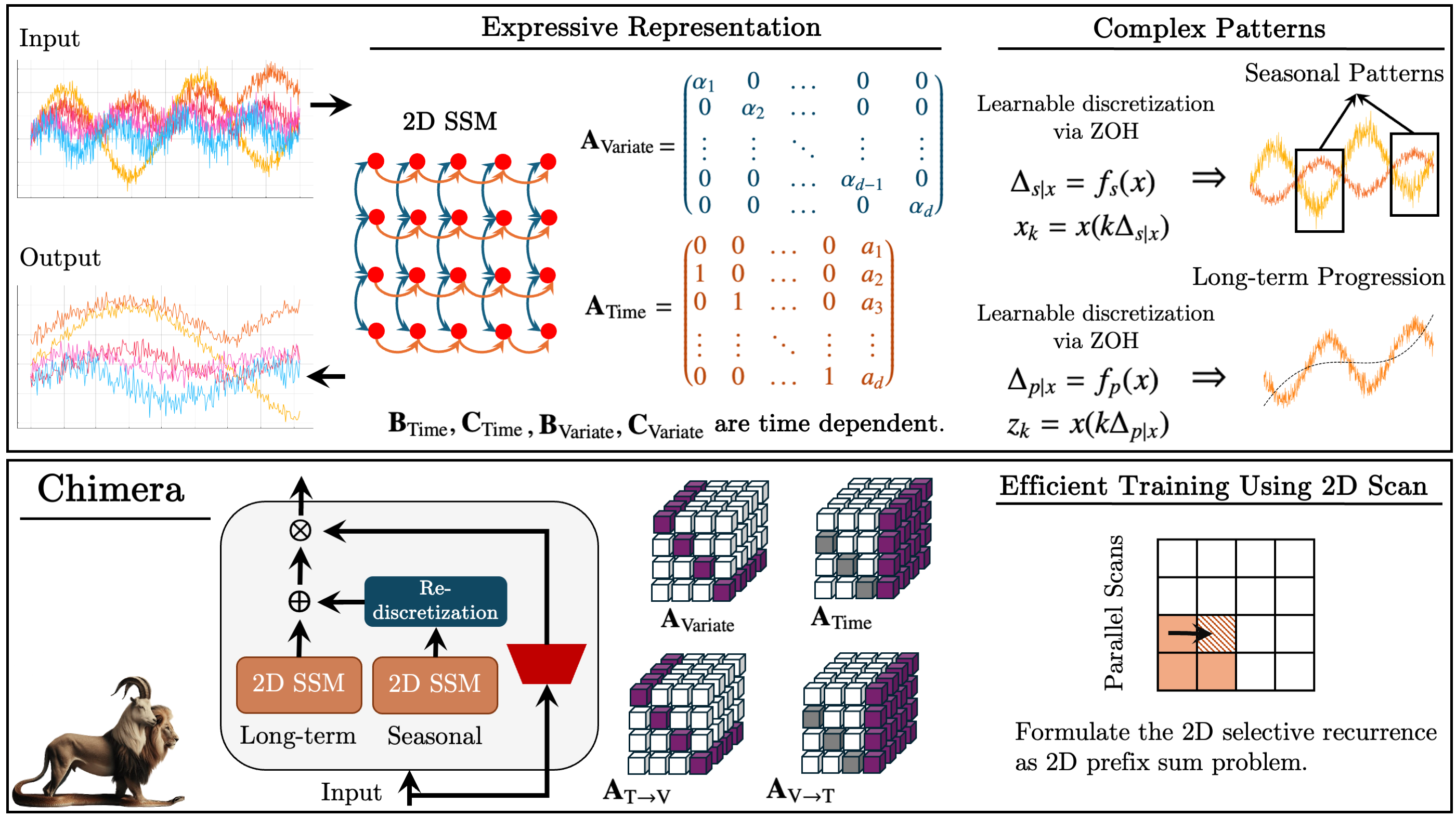
Na parte prática do artigo foi desenvolvida a arquitetura para implementação da visão própria dos métodos propostos utilizando MQL5 e iniciada a etapa de implementação. Foram analisadas as modificações feitas no programa em OpenCL. Foi criada a estrutura do objeto 2D-SSM e apresentado o método de sua inicialização. Hoje damos continuidade à construção dos algoritmos de aplicação dos métodos propostos em nossos próprios modelos.
Objeto 2D-SSM
Encerramos o artigo anterior com a análise do método de inicialização do objeto CNeuron2DSSMOCL, no qual pretendemos implementar o funcional de construção e treinamento do 2D-SSM. A estrutura desse objeto está apresentada abaixo.
class CNeuron2DSSMOCL : public CNeuronBaseOCL { protected: uint iWindowOut; uint iUnitsOut; CNeuronBaseOCL cHiddenStates; CLayer cProjectionX_Time; CLayer cProjectionX_Variable; CNeuronConvOCL cA; CNeuronConvOCL cB_Time; CNeuronConvOCL cB_Variable; CNeuronConvOCL cC_Time; CNeuronConvOCL cC_Variable; CNeuronConvOCL cDelta_Time; CNeuronConvOCL cDelta_Variable; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool feedForwardSSM2D(void); //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradientsSSM2D(void); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuron2DSSMOCL(void) {}; ~CNeuron2DSSMOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_out, uint units_in, uint units_out, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuron2DSSMOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); //--- virtual bool Clear(void) override; };
Damos continuidade ao trabalho iniciado. E hoje, começamos pelo algoritmo de construção do método de propagação para frente deste objeto feedForward.
bool CNeuron2DSSMOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *inp = NeuronOCL; CNeuronBaseOCL *x_time = NULL; CNeuronBaseOCL *x_var = NULL;
Nos parâmetros do método recebemos um ponteiro para o objeto de dados brutos, que imediatamente salvamos em uma variável local. Nesse mesmo ponto, declaramos ainda duas variáveis locais para armazenar ponteiros para os objetos de projeção dos dados brutos no contexto do tempo e no contexto das características. Nesta etapa ainda precisamos formar essas projeções.
Vale lembrar que, para a formação dessas projeções, no método de inicialização foram criadas duas sequências internas, cujos ponteiros para objetos foram armazenados nos arrays dinâmicos cProjectionX_Time e cProjectionX_Variable. Agora podemos utilizá-los para obter as projeções necessárias.
Primeiro, geramos a projeção no contexto do tempo. O ponteiro para o objeto de dados brutos já foi salvo em uma variável local. Em seguida, criamos um laço de iteração sequencial dos objetos do modelo de projeção no contexto do tempo.
//--- Projection Time int total = cProjectionX_Time.Total(); for(int i = 0; i < total; i++) { x_time = cProjectionX_Time.At(i); if(!x_time || !x_time.FeedForward(inp)) return false; inp = x_time; }
No corpo do laço, primeiramente obtemos o ponteiro para o próximo objeto da sequência. Em seguida, verificamos a validade do ponteiro obtido. Após a checagem bem-sucedida do ponto de controle, chamamos o método de propagação para frente do objeto, passando para ele o ponteiro do objeto de dados brutos.
Depois, salvamos o ponteiro para o objeto atual na variável local de dados brutos e passamos para a próxima iteração do laço.
Após a conclusão de todas as iterações do laço, na variável local de projeção dos dados brutos no contexto do tempo estará armazenado o ponteiro para o último objeto da sequência correspondente. No buffer deste objeto estará a projeção que necessitamos.
De forma análoga, obtemos a projeção dos dados brutos no contexto das características.
//--- Projection Variable inp = NeuronOCL; total = cProjectionX_Variable.Total(); for(int i = 0; i < total; i++) { x_var = cProjectionX_Variable.At(i); if(!x_var || !x_var.FeedForward(inp)) return false; inp = x_var; }
Para obter as quatro projeções de dois estados ocultos, basta chamarmos um único método de propagação para frente do objeto das respectivas projeções. Nos seus parâmetros, passamos o ponteiro para o objeto que contém o tensor concatenado dos estados ocultos.
if(!cA.FeedForward(cHiddenStates.AsObject())) return false;
Os demais parâmetros do nosso 2D-SSM são dependentes do contexto. Por isso, em seguida geramos os parâmetros do modelo com base nas respectivas projeções dos dados brutos. Para isso, percorremos sequencialmente os objetos de geração de parâmetros do modelo e chamamos seus métodos de propagação para frente, passando os ponteiros para os objetos das projeções correspondentes dos dados brutos.
if(!cB_Time.FeedForward(x_time) || !cB_Variable.FeedForward(x_var)) return false; if(!cC_Time.FeedForward(x_time) || !cC_Variable.FeedForward(x_var)) return false; if(!cDelta_Time.FeedForward(x_time) || !cDelta_Variable.FeedForward(x_var)) return false;
Neste ponto, finalizamos a preparação dos parâmetros do modelo bidimensional de espaço de estados. Agora, resta gerar os novos valores do estado oculto e os resultados do modelo. Como já vimos no artigo anterior, esses processos foram transferidos para um kernel separado, criado no lado do programa OpenCL. Portanto, basta chamar o método wrapper desse kernel. No entanto, é importante destacar que a geração de um novo estado oculto substitui os valores atuais, que ainda serão necessários para a execução das operações de propagação reversa. Por isso, primeiro realizamos a troca dos ponteiros para os objetos dos buffers de dados e somente depois chamamos o método wrapper feedForwardSSM2D.
if(!cHiddenStates.SwapOutputs()) return false; //--- return feedForwardSSM2D(); }
A próxima etapa do nosso trabalho será a construção dos algoritmos de propagação reversa do nosso objeto. Para isso, proponho observar o método de distribuição do gradiente do erro calcInputGradients. Nos parâmetros deste método, recebemos o ponteiro para o mesmo objeto de dados brutos, mas agora precisamos transmitir a ele o gradiente do erro de acordo com a influência dos dados brutos no resultado geral do modelo.
bool CNeuron2DSSMOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
A transmissão dos dados só é possível quando existe um ponteiro válido para o objeto. Portanto, a primeira etapa do algoritmo é verificar o ponteiro recebido, o que evita o acesso a recursos liberados ou não inicializados. Essa abordagem é fundamental para garantir a estabilidade do processo computacional e prevenir falhas durante o processamento dos dados.
Após a checagem bem-sucedida do bloco de controle, iniciam-se as operações de distribuição do gradiente do erro. Esse processo é realizado a partir do nível dos resultados do objeto em direção aos dados brutos, seguindo o mecanismo de propagação reversa do erro, em conformidade com o fluxo de dados da propagação para frente, mas em ordem inversa.
Encerramos o método de propagação para frente com a chamada do método wrapper do kernel de geração dos estados ocultos e cálculo dos resultados do 2D-SSM. Consequentemente, o processo de propagação do gradiente do erro se inicia com a chamada de um método wrapper semelhante, mas direcionado ao kernel responsável pela distribuição dos erros. Dentro desse kernel, o gradiente é distribuído corretamente entre os elementos do 2D-SSM, de acordo com sua contribuição para a formação dos resultados do modelo.
if(!calcInputGradientsSSM2D()) return false;
É importante destacar que, nesta etapa, está sendo realizada apenas a distribuição dos valores do gradiente entre os componentes estruturais do modelo. Entretanto, a correção direta dos valores em relação às derivadas das funções de ativação dos objetos não é executada dentro deste kernel. Por isso, antes de propagar o gradiente do erro através dos objetos internos do modelo, é necessário verificar a presença de funções de ativação nesses objetos. Caso existam, deve-se aplicar a correção adequada nos valores, levando em conta a influência das transformações não lineares sobre os gradientes transmitidos. Isso garante que cada parâmetro do modelo seja atualizado de acordo com sua real contribuição na formação do sinal de saída.
//--- Deactivation CNeuronBaseOCL *x_time = cProjectionX_Time[-1]; CNeuronBaseOCL *x_var = cProjectionX_Variable[-1]; if(!x_time || !x_var) return false; if(x_time.Activation() != None) if(!DeActivation(x_time.getOutput(), x_time.getGradient(), x_time.getGradient(), x_time.Activation())) return false; if(x_var.Activation() != None) if(!DeActivation(x_var.getOutput(), x_var.getGradient(), x_var.getGradient(), x_var.Activation())) return false; if(cB_Time.Activation() != None) if(!DeActivation(cB_Time.getOutput(), cB_Time.getGradient(), cB_Time.getGradient(), cB_Time.Activation())) return false; if(cB_Variable.Activation() != None) if(!DeActivation(cB_Variable.getOutput(), cB_Variable.getGradient(), cB_Variable.getGradient(), cB_Variable.Activation())) return false; if(cC_Time.Activation() != None) if(!DeActivation(cC_Time.getOutput(), cC_Time.getGradient(), cC_Time.getGradient(), cC_Time.Activation())) return false; if(cC_Variable.Activation() != None) if(!DeActivation(cC_Variable.getOutput(), cC_Variable.getGradient(), cC_Variable.getGradient(), cC_Variable.Activation())) return false; if(cDelta_Time.Activation() != None) if(!DeActivation(cDelta_Time.getOutput(), cDelta_Time.getGradient(), cDelta_Time.getGradient(), cDelta_Time.Activation())) return false; if(cDelta_Variable.Activation() != None) if(!DeActivation(cDelta_Variable.getOutput(), cDelta_Variable.getGradient(), cDelta_Variable.getGradient(), cDelta_Variable.Activation())) return false; if(cA.Activation() != None) if(!DeActivation(cA.getOutput(), cA.getGradient(), cA.getGradient(), cA.Activation())) return false;
Em seguida, passamos ao processo de distribuição dos gradientes do erro através dos objetos internos do nosso 2D-SSM. E, antes de tudo, precisamos distribuir os valores do gradiente pelos objetos de geração dos parâmetros dependentes do contexto do modelo. Vale lembrar que eles são formados com base nas respectivas projeções dos dados brutos.
Aqui é necessário observar que os objetos de projeção dos dados brutos participam do processo principal de formação dos resultados do modelo e já receberam valores de gradiente do erro durante as operações anteriores. Para preservar esses valores previamente obtidos, realizamos a troca dos ponteiros para os respectivos buffers de dados.
//--- Gradient to projections X CBufferFloat *grad_x_time = x_time.getGradient(); CBufferFloat *grad_x_var = x_var.getGradient(); if(!x_time.SetGradient(x_time.getPrevOutput(), false) || !x_var.SetGradient(x_var.getPrevOutput(), false)) return false;
Depois, propagamos o gradiente do erro sequencialmente através dos objetos de formação dos parâmetros dependentes do contexto e, em cada etapa, somamos os valores recebidos com aqueles já acumulados.
//--- B -> X if(!x_time.calcHiddenGradients(cB_Time.AsObject()) || !SumAndNormilize(grad_x_time, x_time.getGradient(), grad_x_time, iWindowOut, false, 0, 0, 0, 1)) return false; if(!x_var.calcHiddenGradients(cB_Variable.AsObject()) || !SumAndNormilize(grad_x_var, x_var.getGradient(), grad_x_var, iWindowOut, false, 0, 0, 0, 1)) return false;
//--- C -> X if(!x_time.calcHiddenGradients(cC_Time.AsObject()) || !SumAndNormilize(grad_x_time, x_time.getGradient(), grad_x_time, iWindowOut, false, 0, 0, 0, 1)) return false; if(!x_var.calcHiddenGradients(cC_Variable.AsObject()) || !SumAndNormilize(grad_x_var, x_var.getGradient(), grad_x_var, iWindowOut, false, 0, 0, 0, 1)) return false;
//--- Delta -> X if(!x_time.calcHiddenGradients(cDelta_Time.AsObject()) || !SumAndNormilize(grad_x_time, x_time.getGradient(), grad_x_time, iWindowOut, false, 0, 0, 0, 1)) return false; if(!x_var.calcHiddenGradients(cDelta_Variable.AsObject()) || !SumAndNormilize(grad_x_var, x_var.getGradient(), grad_x_var, iWindowOut, false, 0, 0, 0, 1)) return false;
Concluída a transmissão dos gradientes do erro de todos os fluxos de informação, restauramos os ponteiros dos objetos para o estado original.
if(!x_time.SetGradient(grad_x_time, false) || !x_var.SetGradient(grad_x_var, false)) return false;
Neste ponto, obtivemos os valores dos gradientes do erro no nível das projeções dos dados brutos em ambos os contextos. Agora precisamos propagar os gradientes através dos modelos internos de projeção correspondentes. Para isso, criamos laços de iteração reversa sobre os objetos das respectivas sequências.
//--- Projection Variable int total = cProjectionX_Variable.Total() - 2; for(int i = total; i >= 0; i--) { x_var = cProjectionX_Variable[i]; if(!x_var || !x_var.calcHiddenGradients(cProjectionX_Variable[i + 1])) return false; }
//--- Projection Time total = cProjectionX_Time.Total() - 2; for(int i = total; i >= 0; i--) { x_time = cProjectionX_Time[i]; if(!x_time || !x_time.calcHiddenGradients(cProjectionX_Time[i + 1])) return false; }
É importante notar que, ao conduzir o gradiente do erro pelos modelos internos das projeções contextuais, interrompemos o processo na primeira camada de cada sequência. Aqui é preciso mencionar que ambas as sequências de projeções geram seus valores com base nos dados brutos, recebidos como parâmetros do método a partir do programa externo. Portanto, agora devemos transmitir o gradiente do erro ao objeto de dados brutos a partir de ambos os modelos internos de projeção.
Como normalmente ocorre em casos desse tipo, primeiro transmitimos o gradiente do erro por um dos fluxos de informação.
//--- Projections -> inputs if(!NeuronOCL.calcHiddenGradients(x_var.AsObject())) return false;
E, em seguida, realizamos a troca dos ponteiros para os objetos dos buffers de gradiente e propagamos os erros através do segundo fluxo de informação.
grad_x_time = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(x_time.getPrevOutput(), false) || !NeuronOCL.calcHiddenGradients(x_time.AsObject()) || !SumAndNormilize(grad_x_time, NeuronOCL.getGradient(), grad_x_time, 1, false, 0, 0, 0, 1) || !NeuronOCL.SetGradient(grad_x_time, false)) return false; //--- return true; }
Por fim, somamos os valores de ambos os fluxos de informação e restauramos os ponteiros dos buffers de dados ao estado original.
É importante observar que não propagamos o gradiente do erro até o nível do objeto de estado oculto, pois esse objeto é utilizado apenas para armazenamento de dados e não contém parâmetros treináveis.
Agora que já distribuímos os valores do gradiente do erro entre todos os objetos internos, resta apenas retornar o resultado lógico da execução das operações para o programa chamador e encerrar o método.
Com isso, concluímos a análise dos algoritmos de construção dos métodos do objeto CNeuron2DSSMOCL. O código completo desse objeto e de todos os seus métodos pode ser consultado em anexo.
Módulo Chimera
A próxima etapa do nosso trabalho é a construção do módulo Chimera. Os autores do framework propõem a utilização de dois 2D-SSM paralelos, com diferentes níveis de discretização e conexões residuais. A combinação de dois modelos independentes de espaço de estados, operando com distintos níveis de discretização, permite uma análise mais profunda das dependências e possibilita a construção de modelos preditivos altamente eficientes, adaptados a dados multiescalares.
O uso de 2D-SSM com diferentes parâmetros de discretização possibilita uma análise diferenciada das séries temporais. O modelo de alta frequência detecta tendências de longo prazo, enquanto o modelo de baixa frequência foca no reconhecimento de ciclos sazonais. Essa divisão melhora a precisão das previsões, já que cada modelo se adapta à sua parte dos dados, minimizando perdas de informação e erros causados pelo excesso de agregação de características temporais. A adição de um módulo de discretização permite alinhar os resultados das duas abordagens em uma forma comparável.
Outro benefício adicional do módulo Chimera é o uso de conexões residuais, que asseguram uma transmissão eficiente da informação entre os níveis do modelo. Elas permitem preservar e transferir o gradiente durante a propagação reversa do erro, evitando o seu enfraquecimento. Isso é especialmente relevante no treinamento de modelos profundos, nos quais o gradiente descendente frequentemente enfrenta problemas de instabilidade numérica. O modelo se mantém mais resistente à perda de informação durante a transmissão de dados entre as camadas, e o processo de treinamento torna-se mais estável, mesmo ao lidar com séries temporais extensas.
O mecanismo proposto é implementado dentro do objeto CNeuronChimera, cuja estrutura está apresentada abaixo.
class CNeuronChimera : public CNeuronBaseOCL { protected: CNeuron2DSSMOCL caSSM[2]; CNeuronConvOCL cDiscretization; CLayer cResidual; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronChimera(void) {}; ~CNeuronChimera(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_out, uint units_in, uint units_out, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronChimera; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); //--- virtual bool Clear(void) override; };
Na estrutura apresentada, vemos um conjunto já familiar de métodos sobrescrevíveis e alguns objetos internos, cujo funcional é fácil de deduzir a partir de seus nomes.
Todos os objetos internos são declarados estaticamente, o que permite deixar o construtor e o destrutor da classe vazios. A inicialização de todos os objetos é realizada no método Init.
bool CNeuronChimera::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_out, uint units_in, uint units_out, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, units_out * window_out, optimization_type, batch)) return false; SetActivationFunction(None);
Nos parâmetros do método, recebemos um conjunto de constantes que permitem interpretar de forma unívoca a arquitetura do objeto em construção. Vale destacar que a lista de parâmetros foi totalmente transferida do método equivalente do objeto CNeuron2DSSMOCL, descrito anteriormente, e aponta para a arquitetura de uma das 2D-SSM internas.
O algoritmo do método de inicialização, como de costume, começa com a chamada do método homônimo da classe pai. Neste caso, trata-se da camada totalmente conectada básica.
Em seguida, passamos à inicialização dos objetos internos. Como já foi mencionado, utilizamos duas modelos bidimensionais de espaço de estados com diferentes níveis de detalhamento. Na estrutura do objeto, os modelos internos são representados pelo array caSSM. Para inicializar os objetos desse array, organizamos um laço.
int index = 0; for(int i = 0; i < 2; i++) { if(!caSSM[i].Init(0, index, OpenCL, window_in, (i + 1)*window_out, units_in, units_out, optimization, iBatch)) return false; index++; }
Para a inicialização da primeira modelo de espaço de estados, utilizam-se os parâmetros recebidos do programa externo. Já a segunda modelo recebe uma dimensionalidade do espaço de características dos resultados duplicada, o que possibilita capturar dependências mais complexas. Como ambas as modelos operam com o mesmo conjunto de dados brutos, os parâmetros principais de sua configuração permanecem inalterados, garantindo a integridade e a consistência da estrutura.
Na sequência, inicializamos a camada de discretização adicional, que cria uma projeção dos resultados da segunda modelo no subespaço da primeira. Trata-se de uma camada convolucional comum, que reduz o espaço de características até o tamanho definido.
if(!cDiscretization.Init(0, index, OpenCL, 2 * window_out, 2 * window_out, window_out, units_out, 1, optimization, iBatch)) return false; cDiscretization.SetActivationFunction(None);
Para evitar perda de dados, desativamos a função de ativação desse objeto.
Após a inicialização dos fluxos de informação das duas modelos de espaço de estados, passamos à organização das conexões residuais. Nesse ponto, surge o problema da soma de tensores, que podem apresentar diferenças de tamanho em um ou mais eixos. Para resolver esse problema, é necessária a projeção prévia dos dados brutos no subespaço definido dos resultados. Para isso, é criada uma modelo interna de projeção de dados, semelhante às modelos de projeções contextuais vistas anteriormente. Esse método permite alinhar corretamente as dimensões dos dados, garantindo a estabilidade da arquitetura e a precisão no processamento das dependências temporais.
Primeiramente, preparamos um array dinâmico para armazenar os ponteiros para os objetos da modelo e declaramos variáveis locais para o armazenamento temporário desses ponteiros.
//--- Residual cResidual.Clear(); cResidual.SetOpenCL(OpenCL); CNeuronConvOCL *conv = NULL; CNeuronTransposeOCL *transp = NULL;
Criamos um objeto de transposição de dados, seguido por uma camada convolucional de projeção das sequências unitárias na dimensionalidade definida da série temporal.
transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, units_in, window_in, optimization, iBatch) || !cResidual.Add(transp)) { delete transp; return false; } index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, units_in, units_in, units_out, window_in, 1, optimization, iBatch) || !cResidual.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None);
Essa abordagem nos permite preservar as dependências estruturais dentro das sequências unitárias individuais da série temporal multidimensional analisada.
Em seguida, adicionamos mais um bloco composto por um objeto de transposição e uma camada convolucional, responsáveis pela projeção dos dados brutos ao longo do eixo das características.
index++; transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, window_in, units_out, optimization, iBatch) || !cResidual.Add(transp)) { delete transp; return false; } index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, window_in, window_in, window_out, units_out, 1, optimization, iBatch) || !cResidual.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None);
Vale destacar que ambas as camadas convolucionais não utilizam funções de ativação, o que possibilita realizar a projeção dos dados brutos com perda mínima de informação.
Na saída do objeto, planejamos somar os três fluxos de informação. E, como costumamos proceder nesses casos, o gradiente do erro será transmitido integralmente por todas as ramificações. Para evitar operações desnecessárias de cópia de dados, sincronizamos os ponteiros para os buffers dos gradientes do erro. Entretanto, é importante notar que as camadas convolucionais usadas para projeção dos dados podem conter funções de ativação. É verdade que, neste caso, não as utilizamos e poderíamos simplesmente ignorar esse detalhe. Mas, com o objetivo de desenvolver uma solução mais universal, não podemos desconsiderá-lo. Assim, transmitiremos o gradiente do erro para as camadas convolucionais somente após a devida correção pela derivada da função de ativação correspondente.
if(!SetGradient(caSSM[0].getGradient(), true)) return false; //--- return true; }
Agora, resta apenas retornar o resultado lógico da execução das operações para o programa chamador e encerrar o método.
Concluída a implementação do método de inicialização, passamos à construção dos algoritmos de propagação para frente dentro do método feedForward.
bool CNeuronChimera::feedForward(CNeuronBaseOCL *NeuronOCL) { for(uint i = 0; i < caSSM.Size(); i++) { if(!caSSM[i].FeedForward(NeuronOCL)) return false; }
O algoritmo de propagação para frente é relativamente simples. Nos parâmetros do método recebemos o ponteiro para o objeto de dados brutos, que será passado para os modelos internos de espaço de estados. Para isso, organizamos um laço de iteração sobre os 2D-SSM internos e chamamos, um a um, seus métodos de propagação para frente.
Após a conclusão de todas as iterações do laço, projetamos os resultados obtidos em uma forma comparável.
if(!cDiscretization.FeedForward(caSSM[1].AsObject())) return false;
Em seguida, precisamos obter a projeção dos dados brutos no subespaço dos resultados. Para isso, organizamos um laço de iteração sequencial sobre os objetos do modelo interno de projeção, chamando os métodos de propagação para frente correspondentes.
CNeuronBaseOCL *inp = NeuronOCL; CNeuronBaseOCL *current = NULL; for(int i = 0; i < cResidual.Total(); i++) { current = cResidual[i]; if(!current || !current.FeedForward(inp)) return false; inp = current; }
E, por fim, somamos os resultados dos três fluxos de informação, aplicando a normalização dos dados em seguida.
if(!SumAndNormilize(caSSM[0].getOutput(), cDiscretization.getOutput(), Output, 1, false, 0, 0, 0, 1) || !SumAndNormilize(Output, current.getOutput(), Output, cDiscretization.GetFilters(), true, 0, 0, 0, 1)) return false; //--- return true; }
Depois disso, retornamos o resultado lógico da execução das operações ao programa chamador e encerramos o método.
No entanto, por trás da aparente simplicidade do algoritmo do método de propagação para frente, está o uso de três fluxos de informação, o que impõe algumas dificuldades na organização do processo de distribuição do gradiente do erro. Esse processo é estruturado dentro do método calcInputGradients.
bool CNeuronChimera::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Nos parâmetros do método, recebemos o ponteiro para o objeto de dados brutos, ao qual, desta vez, devemos transmitir o gradiente do erro, de acordo com sua influência no resultado final do modelo. No corpo do método, verificamos imediatamente a validade do ponteiro recebido. A necessidade desse tipo de controle já foi discutida anteriormente.
Em seguida, corrigimos o gradiente do erro recebido dos objetos subsequentes pela função de ativação da camada de projeção dos resultados da segunda 2D-SSM e o propagamos até o nível desse modelo.
if(!DeActivation(cDiscretization.getOutput(), cDiscretization.getGradient(), Gradient, cDiscretization.Activation())) return false; if(!caSSM[1].calcHiddenGradients(cDiscretization.AsObject())) return false;
De forma semelhante, corrigimos o gradiente do erro pela derivada da função de ativação da última camada do modelo interno de projeção dos dados brutos e o propagamos sequencialmente pelos objetos dessa sequência.
CNeuronBaseOCL *residual = cResidual[-1]; if(!residual) return false; if(!DeActivation(residual.getOutput(), residual.getGradient(), Gradient, residual.Activation())) return false; for(int i = cResidual.Total() - 2; i >= 0; i--) { residual = cResidual[i]; if(!residual || !residual.calcHiddenGradients(cResidual[i + 1])) return false; }
Nesse ponto, chegamos ao passo de transmissão do gradiente do erro até o nível dos dados brutos por meio dos três fluxos de informação. E lembramos que, durante a transmissão do gradiente do erro, os dados previamente armazenados são eliminados. Felizmente, já aprendemos a lidar com esse problema. Primeiro, transmitimos o gradiente do erro de uma das modelos de espaço de estados.
if(!NeuronOCL.calcHiddenGradients(caSSM[0].AsObject())) return false;
Depois, realizamos a troca do ponteiro para o buffer de dados e transmitimos o gradiente do erro pelo segundo fluxo, seguido da soma dos dados provenientes dos dois fluxos de informação.
CBufferFloat *temp = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(residual.getPrevOutput(), false) || !NeuronOCL.calcHiddenGradients(caSSM[1].AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1)) return false;
Da mesma forma, adicionamos os valores do terceiro fluxo de informação.
if(!NeuronOCL.calcHiddenGradients((CObject*)residual) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1) || !NeuronOCL.SetGradient(temp, false) ) return false; //--- return true; }
E somente após a soma dos dados de todos os fluxos, restauramos os ponteiros dos objetos ao estado original.
O resultado lógico da execução das operações é então retornado ao programa chamador, e o método é finalizado.
Com isso, concluímos a análise dos algoritmos de implementação do framework Chimera por meio do MQL5. O código completo dos objetos apresentados e de todos os seus métodos pode ser consultado em anexo.
Arquitetura do modelo
Acima, foi apresentado um detalhamento da implementação dos métodos propostos pelos autores do framework Chimera, em MQL5. No entanto, os autores do framework recomendam o uso de uma arquitetura composta por uma pilha de objetos semelhantes, com a organização de não linearidades entre eles. A utilização dessa arquitetura favorece a criação de um sistema flexível e adaptativo, capaz de reagir dinamicamente às mudanças nas condições de utilização. Por isso, vamos nos deter um pouco na arquitetura dos modelos treináveis.
De início, vale dizer que, no contexto deste experimento, implementamos os métodos do Chimera dentro do framework de aprendizado multitarefa.
A arquitetura dos modelos treináveis está representada no método CreateDescriptions.
bool CreateDescriptions(CArrayObj *&actor, CArrayObj *&probability) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!probability) { probability = new CArrayObj(); if(!probability) return false; }
Nos parâmetros do método, recebemos ponteiros para dois arrays dinâmicos, nos quais devemos armazenar a descrição da arquitetura dos modelos. No corpo do método, verificamos a validade dos ponteiros recebidos e, se necessário, criamos novas instâncias de objetos.
Primeiro, descrevemos a arquitetura do Ator, que inclui também o bloco codificador do estado do ambiente. No input do modelo planejamos alimentar os dados brutos de descrição do estado do ambiente. Estes são enviados para uma camada totalmente conectada de tamanho adequado.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Em seguida, vem a camada de normalização em lote, responsável pelo pré-processamento inicial dos dados brutos e por trazê-los para uma forma comparável.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Os dados processados seguem para o primeiro módulo Chimera, cuja saída esperamos que seja uma sequência temporal multidimensional de 64 elementos, cada um contendo 16 características.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronChimera; //--- Window { int temp[] = {BarDescr, 16}; //In, Out if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } //--- Units { int temp[] = {HistoryBars, 64}; //In, Out if(ArrayCopy(descr.units, temp) < int(temp.Size())) return false; } descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Logo após, adicionamos uma camada convolucional com a função de ativação SoftPlus para introduzir a não linearidade.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = 64; descr.window = 16; descr.step = 16; descr.window_out = 16; descr.activation = SoftPlus; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
De forma semelhante, acrescentamos mais 2 módulos Chimera, incluindo camadas de não linearidade entre eles.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronChimera; //--- Window { int temp[] = {16, 32}; //In, Out if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } //--- Units { int temp[] = {64, 32}; //In, Out if(ArrayCopy(descr.units, temp) < int(temp.Size())) return false; } descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = 32; descr.window = 32; descr.step = 32; descr.window_out = 16; descr.activation = SoftPlus; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronChimera; //--- Window { int temp[] = {16, 32}; //In, Out if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } //--- Units { int temp[] = {32, 16}; //In, Out if(ArrayCopy(descr.units, temp) < int(temp.Size())) return false; } descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Seguindo a mesma lógica do framework ResNeXt, reduzimos o comprimento da sequência e aumentamos proporcionalmente o espaço de características.
Depois disso, estruturamos a cabeça de tomada de decisão, composta por três camadas totalmente conectadas consecutivas.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 512; descr.batch = 1e4; descr.activation = TANH; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 256; descr.activation = TANH; descr.batch = 1e4; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NActions; descr.activation = SoftPlus; descr.batch = 1e4; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Os resultados dessa etapa são normalizados por meio de uma camada de normalização em lote.
//--- layer 10 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Assim como nos modelos analisados anteriormente, ao final da arquitetura do Ator adicionamos o módulo de gerenciamento de risco.
//--- layer 11 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMacroHFTvsRiskManager; //--- Windows { int temp[] = {3, 15, NActions, AccountDescr}; //Window, Stack Size, N Actions, Account Description if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } descr.count = 10; descr.window_out = 16; descr.step = 4; // Heads descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 12 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = NActions / 3; descr.window = 3; descr.step = 3; descr.window_out = 3; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
O modelo de avaliação de probabilidades da direção do próximo movimento de preço foi transferido da parte anterior praticamente sem alterações. Apenas ajustes pontuais foram feitos nas funções de ativação das camadas ocultas. Portanto, não vamos nos aprofundar em sua descrição aqui. O detalhamento completo da arquitetura dos modelos está disponível no anexo, junto com o código integral dos programas de treinamento e teste, que foram reutilizados da implementação anterior sem modificações.
Testes
Após concluir a implementação de nossa própria visão dos métodos propostos pelos autores do framework Chimera, avançamos para a etapa final do trabalho, o treinamento e teste dos modelos com dados históricos reais.
Para o treinamento, utilizamos o mesmo conjunto de dados de aprendizado reunido durante o treinamento dos modelos analisados anteriormente. Vale lembrar que as trajetórias foram coletadas a partir dos dados históricos do par de moedas EURUSD durante todo o ano de 2024, no timeframe M1. Os parâmetros de todos os indicadores analisados foram utilizados em suas configurações padrão. A descrição detalhada do processo de preparação do conjunto de treinamento pode ser consultada no link indicado.
O teste dos modelos treinados foi realizado no testador de estratégias do MetaTrader 5, utilizando dados históricos de janeiro de 2025, mantendo os demais parâmetros de treinamento do modelo. Os resultados do teste estão apresentados abaixo.
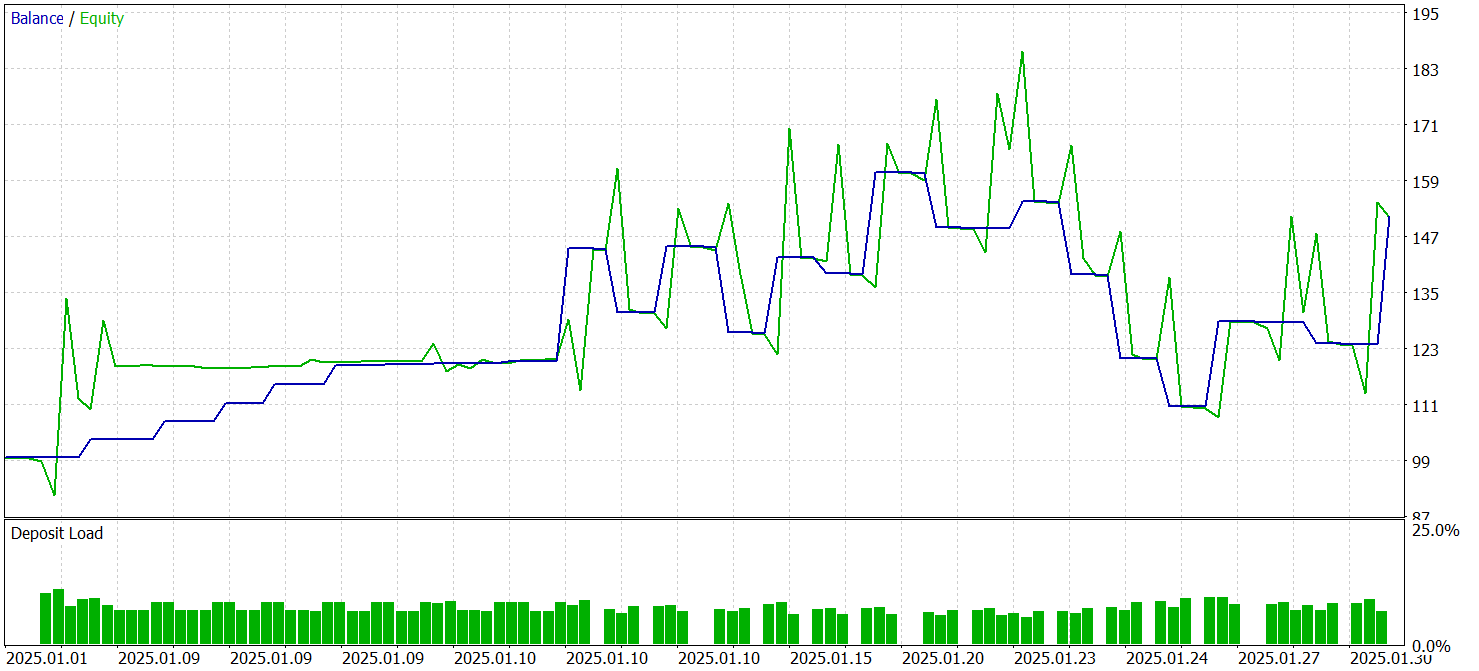
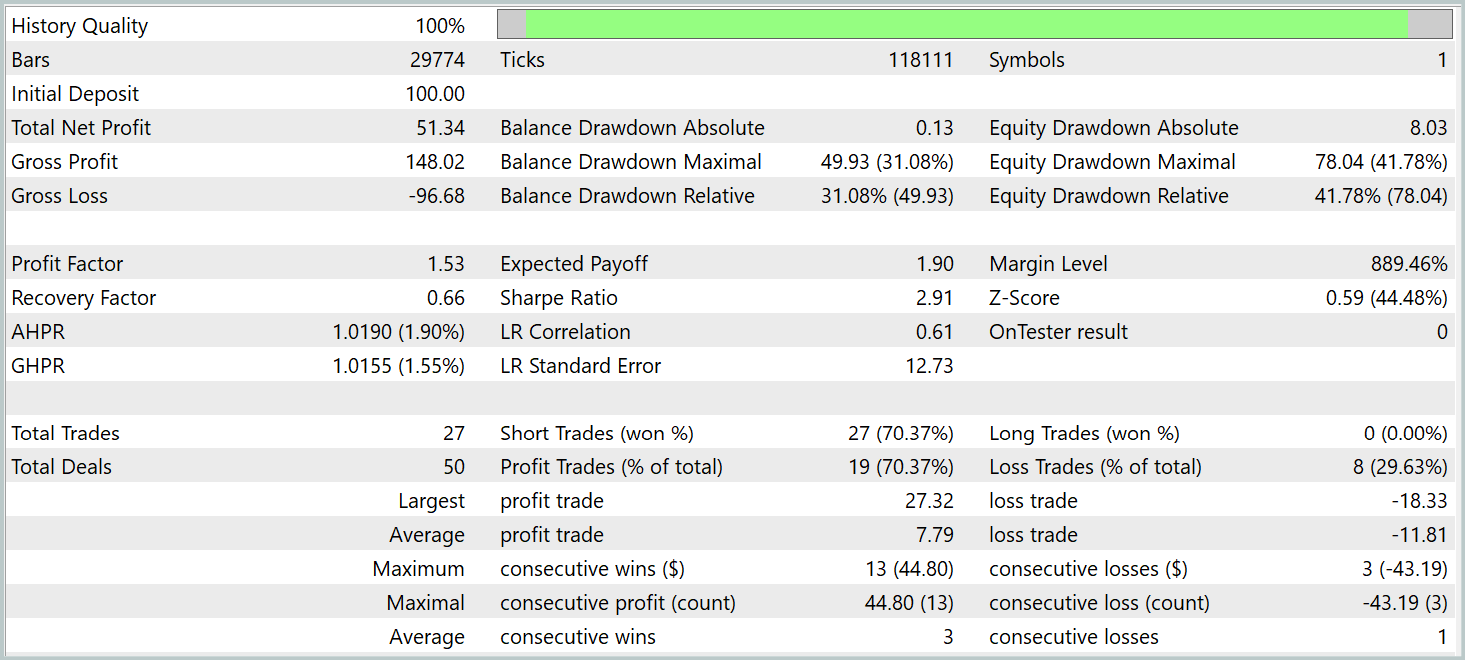
De acordo com os testes, o modelo conseguiu gerar lucro. Mais de 70% das operações foram encerradas com resultado positivo. O profit factor foi registrado no nível de 1.53.
No entanto, alguns pontos merecem atenção. Realizamos o teste dos modelos no timeframe M1. Ainda assim, o modelo executou apenas 27 operações, o que é bastante pouco para uma estratégia de alta frequência em um timeframe mínimo. Além disso, o modelo abriu apenas posições curtas, o que também levanta questionamentos.
O tempo de manutenção das posições também gera dúvidas. A operação mais rápida, por assim dizer, foi encerrada quase uma hora após a abertura. Já o tempo médio de manutenção de uma posição foi superior a 14 horas. E isso durante testes no timeframe M1.
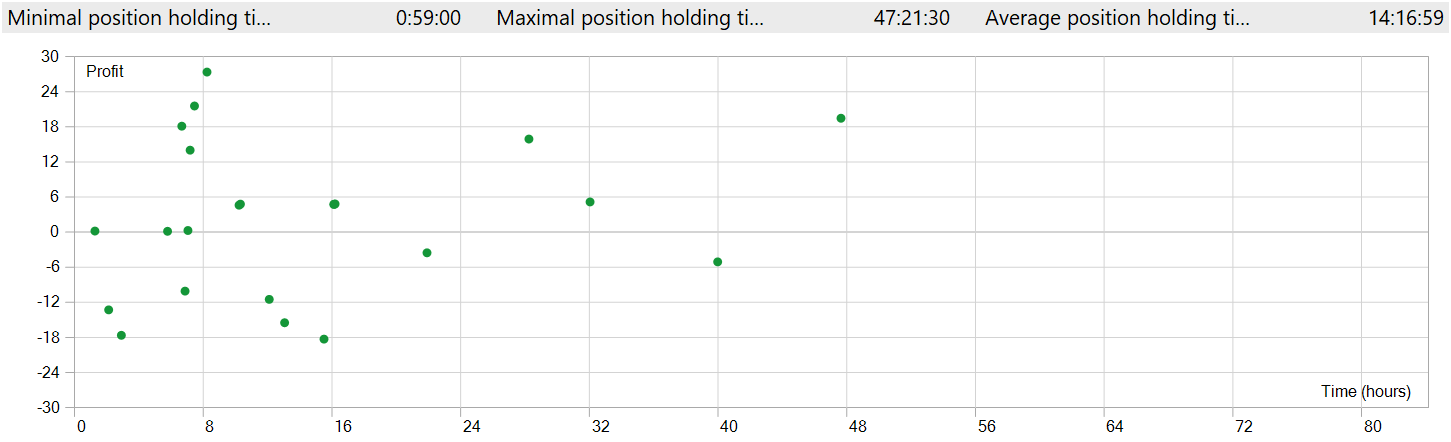
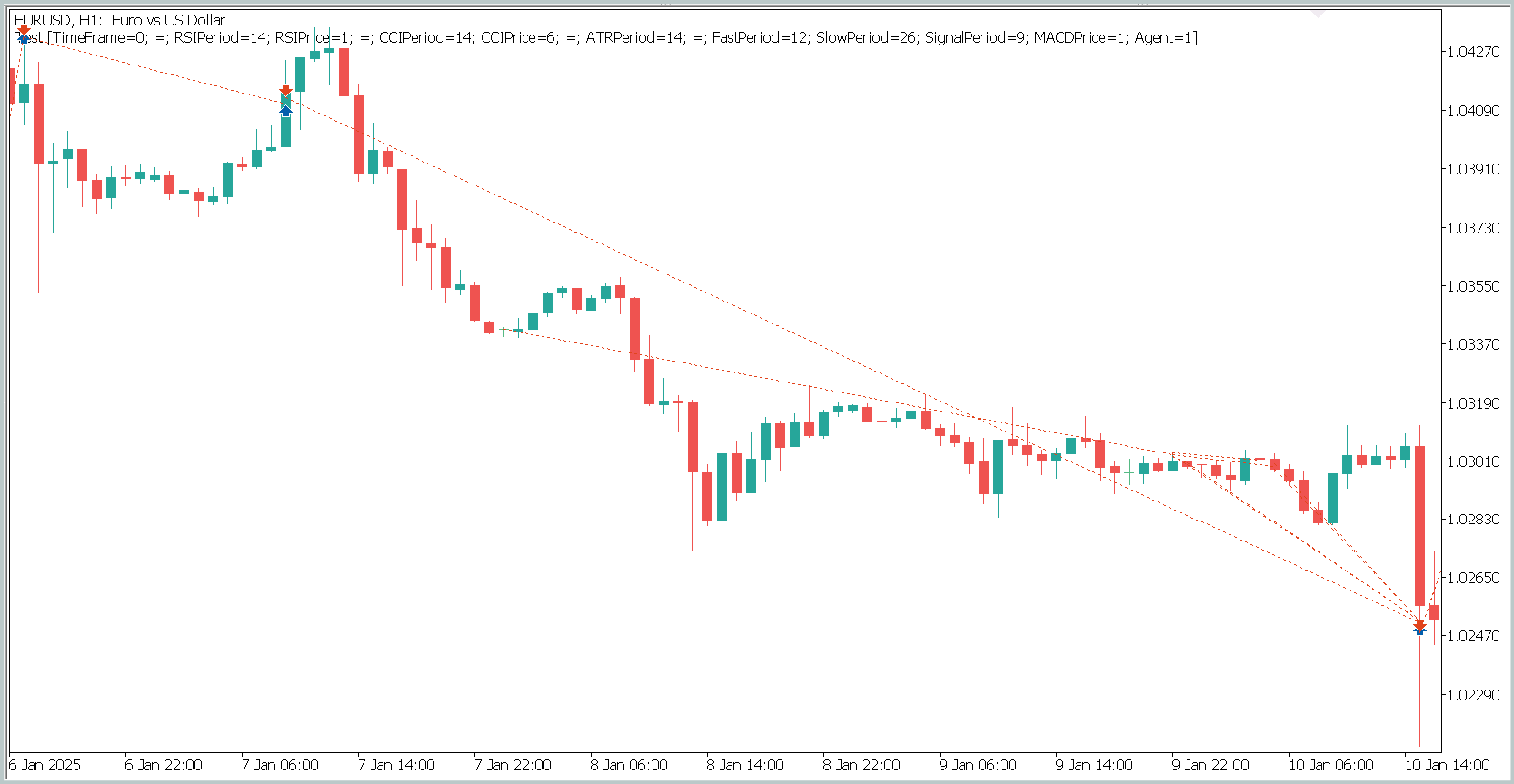
Para exibir em uma única janela de gráfico a abertura e o fechamento das posições, foi necessário aumentar o timeframe. Nessa visualização, vemos claramente operações no sentido da tendência global. Isso, naturalmente, foge da concepção de alta frequência no timeframe M1. Contudo, é evidente que o modelo que implementamos é capaz de capturar tendências de longo prazo, ignorando as flutuações de curto prazo.
Considerações finais
Exploramos o framework Chimera, baseado em um modelo bidimensional de espaço de estados. Essa abordagem introduz metodologias inovadoras para a modelagem de séries temporais multidimensionais, permitindo considerar relações complexas tanto no contexto do tempo quanto no das características.
Na parte prática do nosso trabalho, implementamos nossa própria visão dos métodos propostos por meio do MQL5. O modelo construído foi treinado e testado com dados históricos reais. Os resultados dos testes se mostraram um tanto inesperados. Durante o período de teste, o modelo conseguiu gerar lucro. Mas, ao contrário do esperado, observamos operações alinhadas à tendência global, com longos períodos de manutenção das posições, mesmo que o teste tenha sido realizado no timeframe M1.
#Links
- Chimera: Effectively Modeling Multivariate Time Series with 2-Dimensional State Space Models
- Outros artigos da série
#Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA de coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA de coleta de exemplos pelo método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA de treinamento de modelos |
| 4 | Test.mq5 | Expert Advisor | EA para teste do modelo |
| 5 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema e da arquitetura dos modelos |
| 6 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criação de rede neural |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código do programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/17241
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Análise de todas as variantes do movimento do preço em um computador quântico da IBM
Análise de todas as variantes do movimento do preço em um computador quântico da IBM
 Simulação de mercado: Position View (VII)
Simulação de mercado: Position View (VII)
 Explorando a Criptografia no MQL5: Uma Abordagem Passo a Passo
Explorando a Criptografia no MQL5: Uma Abordagem Passo a Passo
 Do básico ao intermediário: Navegando na SandBox
Do básico ao intermediário: Navegando na SandBox
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso