
Redes neuronales en el trading: Segmentación de datos basada en expresiones de referencia
Introducción
La 3D Referring Expression Segmentation (3D-RES) es una tendencia en franco crecimiento en el campo multimodal que está despertando un gran interés entre los investigadores. Esta tarea tiene como objetivo segmentar las instancias objetivo basándose en las expresiones de lenguaje natural dadas. No obstante, los métodos tradicionales de 3D-RES se limitan a considerar casos con un único objetivo, lo cual restringe considerablemente su aplicación práctica. En el mundo real, las instrucciones conducen con frecuencia a situaciones en las que no se encuentra ningún objetivo o en las que es necesario definir varios objetivos al mismo tiempo. Esta realidad supone un reto al que los modelos 3D-RES existentes no pueden hacer frente. Para colmar esta laguna, los autores del artículo "3D-GRES: Generalized 3D Referring Expression Segmentation" proponen el nuevo método Generalized 3D Referring Expression Segmentation (3D-GRES) para interpretar instrucciones que especifican un número aleatorio de objetivos.
La principal tarea de 3D-GRES consiste en identificar con precisión múltiples objetivos de un grupo de objetos similares. La clave para resolver este problema es la partición de tareas, que permitirá que varias consultas se ocupen simultáneamente de la localización de una instrucción lingüística multiobjeto. En este caso, cada consulta será responsable de una instancia diferente en una escena multiobjeto. Los autores del método 3D-GRES proponen un módulo Multi-Query Decoupled Interaction Network (MDIN), encargado de facilitar la interacción entre las consultas, los superpuntos y el texto. Para gestionar eficazmente un número aleatorio de objetivos, se ha añadido un mecanismo que permite dividir varias consultas y generar de forma conjunta resultados con varios objetivos. En este caso, cada consulta será responsable de un único objetivo en una instancia multiobjeto.
Para abarcar uniformemente los objetivos clave de la nube de puntos con las consultas entrenadas, los autores del método introducen un nuevo módulo de consulta dispersa (TSQ) basado en el texto de las expresiones de referencia. Además, para lograr simultáneamente la distinción entre consultas y mantener la coherencia semántica global, se ha desarrollado una estrategia de optimización de división multiobjeto (MDO) . Esta estrategia divide la máscara multiobjeto en supervisiones separadas de un solo objeto, preservando el carácter distintivo de cada consulta. La vinculación de la característica de consulta y la caracterización de superpuntos en la escena de la nube de puntos con la semántica textual proporciona coherencia semántica para múltiples propósitos.
1. Algoritmo 3D-GRES
La tarea clásica de 3D-RES se centra en la creación de una máscara 3D para un único objeto de destino en una escena de nube de puntos controlado por una expresión de referencia. Esta tarea tradicional posee importantes limitaciones. En primer lugar, no resulta adecuada para escenas en los que ningún objeto de la escena de la nube de puntos coincide con una expresión determinada. En segundo lugar, no considera los casos en que varios objetos cumplen los criterios descritos. Este desfase significativo entre las capacidades del modelo y la aplicabilidad en el mundo real limita la aplicación práctica de las tecnologías 3D-RES.
Para superar las limitaciones existentes, se propone el método de Generalized 3D Referring Expression Segmentation (3D-GRES) para identificar un número aleatorio de objetos a partir de descripciones textuales. 3D-GRES analiza una escena 3D de nube de puntos P y una expresión de texto de referencia E. Como resultado, se generan las correspondientes máscaras M 3D, que pueden estar vacías o contener uno o varios objetos. El método presentado permite encontrar múltiples objetos usando expresiones multiobjetivo y verificar la existencia de objetos específicos en una escena utilizando expresiones «nothing», proporcionando así una mayor flexibilidad y robustez en la recuperación e interacción de objetos.
3D-GRES procesa primero las expresiones de referencia originales codificándolas en tokens de texto 𝒯 usando un modelo RoBERTa preentrenado. Para facilitar la alineación multimodal, los objetos codificados se proyectan en un espacio multimodal de dimensión D. A los tokens resultantes se le añade una codificación posicional.
Para la nube de puntos original con posiciones P y características F, se extraen Superpoints mediante una U-Net 3D dispersa y se proyectan en un espacio multimodal D-dimensional.
Multi-Query Decoupled Interaction Network (MDIN) utiliza múltiples consultas para procesar instancias individuales en escenas con múltiples objetivos, combinándolos en un resultado final. Para las escenas sin objetivos definidos, las predicciones se basan en las puntuaciones de confianza de cada consulta, en este caso, si todas las consultas tienen una puntuación baja, se predicen lecturas objetivo cero.
MDIN consta de varios módulos idénticos, cada uno de ellos compuesto por los módulos Query-Superpoint (QSA) y Query (QLA), que facilitan la interacción entre Query, Superpoint y el texto. A diferencia de los modelos que hemos analizado anteriormente, que usan una inicialización aleatoria de Query, MDIN utiliza un módulo de consultas dispersas basado en texto (TSQ) para generar Query dispersas, lo que proporciona una cobertura eficaz de las escenas. Y para ofrecer soporte a múltiples consultas, se implementa una estrategia de optimización dividida multiobjeto (MDO).
Query puede verse como un ancla en la escena de la nube de puntos. Cuando Query interactúa con Superpoint, captan la información global de la escena de la nube de puntos. En particular, los superpuntos seleccionados por separado sirven como consultas en el proceso de interacción, lo cual posibilita una agregación local más fuerte. Este enfoque local crea un entorno favorable para la separación de consultas.
Inicialmente, se calcula la distribución de similitud entre la característica del superpunto S y la incorporación de consultas Qf. Posteriormente, las consultas añadirán los superpuntos pertinentes relacionados utilizando distribuciones de similitud. A continuación, la escena, considerando la Qs actualizada, se introduce en el módulo QLA para modelar las interacciones Query-Query y Query-Language. QLA consta de un bloque de Self-Attention para las características Qs de la consulta y un bloque de atención cruzada multimodal que modela las dependencias entre cada palabra y cada consulta.
A continuación, la función de consulta considerando las relaciones Qr, las funciones de consulta considerando el lenguaje Ql y las funciones de consulta considerando la escena Qs se juntan y combinan usando MLP.
Para lograr una distribución dispersa de las consultas inicializadas dentro de la escena de la nube de puntos, preservando al mismo tiempo más información geométrica y semántica, los autores de 3D-GRES aplican la técnica de muestreo de los puntos más alejados directamente para Superpoint.
Para mejorar la separación de las consultas y delegarlas en objetos individuales, los autores del método usan los atributos internos de las consultas generadas por TSQ. Cada consulta se origina en un superpunto de la nube de puntos, lo cual la vincula intrínsecamente a un objeto concreto. Las consultas de las instancias objetivo se encargan de segmentar las instancias relacionadas, mientras que las instancias no relacionadas se asignan a la consulta más cercana. Este método usa restricciones visuales previas para desentrañar las consultas y asignarlas a objetos individuales.
A continuación se presenta la visualización de autor del método 3D-GRES.
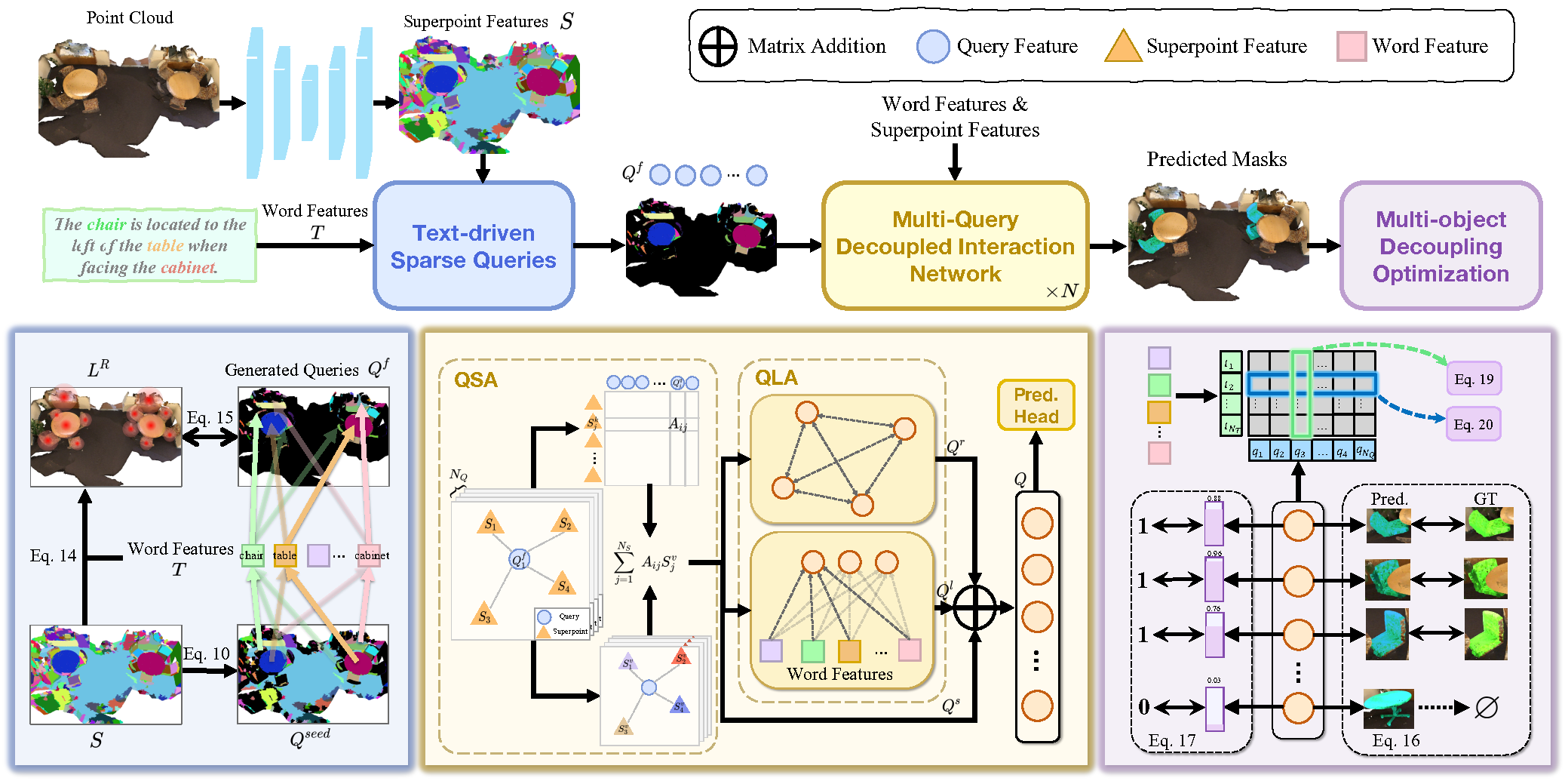
2. Implementación con MQL5
Tras familiarizarnos con los aspectos teóricos del método 3D-GRES, pasaremos a la parte práctica de nuestro artículo, donde implementaremos nuestra visión de los enfoques propuestos utilizando herramientas MQL5. Y en primer lugar, consideraremos qué distingue al algoritmo propuesto de los métodos que hemos analizado anteriormente, así como lo que tienen en común.
Obviamente, lo primero y más importante será la multimodalidad del método 3D-GRES. Primero nos encontraremos con expresiones textuales aclaratorias que deberían orientar mejor nuestros análisis. Y sin duda aprovecharemos esta oportunidad, solo que no utilizaremos el modelo lingüístico. Para el enunciado de la tarea suministraremos al modelo información sobre el estado de la cuenta y las posiciones abiertas. Así, propondremos un modelo que dependa de la incorporación del estado de la cuenta para buscar puntos de entrada o de salida.
Una cosa más a tener en cuenta: 3D-GRES, al igual que los modelos que hemos analizado anteriormente, usa un conjunto de consultas entrenadas. Solo hay una diferencia en su principio de entrenamiento. SPFormer y MAFT usaban consultas estáticas que se optimizaban durante el entrenamiento y permanecían inalteradas cuando el modelo se ejecutaba. Así, el modelo aprendía algunos patrones y luego actuaba según un "esquema preparado de antemano". Los autores de 3D-GRES proponen formar consultas basadas en los datos de origen, haciéndolas más localizadas y dinámicas. Y para maximizar la cobertura del espacio de la escena analizada se aplicarán diversas heurísticas. También tendremos en cuenta esta idea.
Además, el método 3D-GRES usa la codificación posicional de los tokens. Y esto lo combina con el método MAFT, lo cual sirvió como punto de partida para elegir la clase padre en nuestra implementación. Bien, empezaremos nuestro trabajo con la adición de un programa OpenCL.
2.1 Diversificación de las consultas
Para maximizar la cobertura del espacio de la escena por parte de las consultas entrenadas, introduciremos un error de diversificación, diseñado para "alejar" las consultas de sus vecinas:
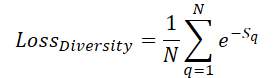
Aquí, Sq indicará la distancia a la consulta q. Obviamente, cuando S=0, el error será igual a 1. Y a medida que aumente la distancia media entre consultas, el error tenderá a "0". De este modo, el modelo se diluirá uniformemente durante el proceso de entrenamiento.
Sin embargo, no nos interesa tanto el valor del error como la dirección de ajuste de los parámetros de consulta para maximizar la distancia respecto a las demás consultas. Por consiguiente, en nuestra aplicación, calcularemos directamente el gradiente de error y lo añadiremos al flujo principal de distribución del error de trabajo con el modelo, seguido de la optimización de los parámetros. Luego implementaremos el algoritmo descrito en el kernel DiversityLoss.
En los parámetros de este kernel transmitiremos los punteros a 2 búferes de datos globales y 2 variables. El primer búfer de datos contendrá las características actuales de las consultas, mientras que en el segundo búfer registraremos el gradiente del error de diversificación.
__kernel void DiversityLoss(__global const float *data, __global float *grad, const int activation, const int add ) { const size_t main = get_global_id(0); const size_t slave = get_local_id(1); const size_t dim = get_local_id(2); const size_t total = get_local_size(1); const size_t dimension = get_local_size(2);
Nuestro kernel trabajará en un espacio tridimensional de tareas. Las dos primeras serán iguales al número de consultas analizadas, y la tercera dimensión definirá la dimensionalidad del vector de características de una sola consulta. Al hacerlo, para minimizar los accesos a la memoria global lenta, agruparemos los flujos en grupos de trabajo a lo largo de las dos últimas dimensiones del espacio de tareas.
En el cuerpo del kernel, como es habitual, primero identificaremos el flujo de trabajo en el espacio de tareas en todas las dimensiones. A continuación, declararemos un array en la memoria local para el intercambio de datos entre flujos separados del grupo de trabajo.
__local float Temp[LOCAL_ARRAY_SIZE];
Y determinaremos el desfase en los búferes de datos globales respecto a los valores analizados.
const int shift_main = main * dimension + dim; const int shift_slave = slave * dimension + dim;
A continuación, cargaremos los valores de los búferes de datos globales y determinaremos la desviación entre ellos.
const int value_main = data[shift_main]; const int value_slave = data[shift_slave]; float delt = value_main - value_slave;
Observe que el espacio de tareas y los grupos de trabajo están organizados de forma que cada subproceso lea solo 2 valores de la memoria global. Y a continuación tendremos que recopilar la suma de las distancias de todos los flujos. Para ello, primero organizaremos un ciclo que recoja la suma de los valores individuales de los elementos del array local.
for(int d = 0; d < dimension; d++) { for(int i = 0; i < total; i += LOCAL_ARRAY_SIZE) { if(d == dim) { if(i <= slave && (i + LOCAL_ARRAY_SIZE) > slave) { int k = i % LOCAL_ARRAY_SIZE; float val = pow(delt, 2.0f) / total; if(isinf(val) || isnan(val)) val = 0; Temp[k] = ((d == 0 && i == 0) ? 0 : Temp[k]) + val; } } barrier(CLK_LOCAL_MEM_FENCE); } }
Y aquí probablemente deberíamos señalar que primero almacenaremos la diferencia simple entre los dos valores en la variable delt. Y solo la elevaremos al cuadrado antes de añadir la distancia al array local. Esto se debe a que es la diferencia la que interviene en la derivada de nuestra función de pérdida. Y la guardaremos para evitar que se recalcule.
En el siguiente paso, recopilaremos la suma de todos los valores de nuestro array local.
const int ls = min((int)total, (int)LOCAL_ARRAY_SIZE); int count = ls; do { count = (count + 1) / 2; if(slave < count) { Temp[slave] += ((slave + count) < ls ? Temp[slave + count] : 0); if(slave + count < ls) Temp[slave + count] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Y solo entonces calcularemos el valor del error de diversificación de la consulta analizada y el gradiente de error del elemento correspondiente.
float loss = exp(-Temp[0]); float gr = 2 * pow(loss, 2.0f) * delt / total; if(isnan(gr) || isinf(gr)) gr = 0;
Después, nos espera un fascinante viaje de recopilación de gradientes de error según las características individuales de la consulta analizada. El algoritmo para recopilar los gradientes de error será similar al descrito anteriormente para sumar las distancias.
for(int d = 0; d < dimension; d++) { for(int i = 0; i < total; i += LOCAL_ARRAY_SIZE) { if(d == dim) { if(i <= slave && (i + LOCAL_ARRAY_SIZE) > slave) { int k = i % LOCAL_ARRAY_SIZE; Temp[k] = ((d == 0 && i == 0) ? 0 : Temp[k]) + gr; } } barrier(CLK_LOCAL_MEM_FENCE); } //--- int count = ls; do { count = (count + 1) / 2; if(slave < count && d == dim) { Temp[slave] += ((slave + count) < ls ? Temp[slave + count] : 0); if(slave + count < ls) Temp[slave + count] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); if(slave == 0 && d == dim) { if(isnan(Temp[0]) || isinf(Temp[0])) Temp[0] = 0; if(add > 0) grad[shift_main] += Deactivation(Temp[0],value_main,activation); else grad[shift_main] = Deactivation(Temp[0],value_main,activation); } barrier(CLK_LOCAL_MEM_FENCE); } }
Obsérvese que el algoritmo descrito combinará iteraciones de pasada directa e inversa. Esto nos permitirá utilizarlo solo cuando se entrene el modelo y eliminar estas operaciones durante el funcionamiento, lo que a su vez influirá en el tiempo toma de decisiones.
Con esto damos por completado nuestro trabajo con el programa OpenCL y podemos pasar a construir nuestra implementación de la clase de los enfoques del método 3D-GRES.
2.2 Clase del método 3D-GRES
Para poner en práctica los planteamientos propuestos por los autores del método 3D-GRES, crearemos un nuevo objeto CNeuronGRES en el lado del programa principal. Como hemos mencionado antes, la funcionalidad básica se heredará de la clase CNeuronMAFT A continuación, le mostraremos la estructura de la nueva clase.
class CNeuronGRES : public CNeuronMAFT { protected: CLayer cReference; CLayer cRefKey; CLayer cRefValue; CLayer cMHRefAttentionOut; CLayer cRefAttentionOut; //--- virtual bool CreateBuffers(void); virtual bool DiversityLoss(CNeuronBaseOCL *neuron, const int units, const int dimension, const bool add = false); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override; public: CNeuronGRES(void) {}; ~CNeuronGRES(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint window_sp, uint units_sp, uint heads_sp, uint ref_size, uint layers, uint layers_to_sp, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronGRES; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Junto con la funcionalidad básica, heredaremos de la clase padre y una amplia gama de objetos internos que abarcarán la mayoría de nuestras necesidades. La mayor parte, pero no todas. Y añadiremos los objetos para trabajar con expresiones de referencia. Luego declararemos todos los objetos como estáticos, lo cual nos permitirá dejar el constructor y el destructor de la clase "vacíos". La inicialización de todos los objetos declarados y heredados se realizará en el método Init, en cuyos parámetros obtendremos las constantes principales que nos permitirán definir inequívocamente la arquitectura del objeto que se va a crear.
bool CNeuronGRES::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint window_sp, uint units_sp, uint heads_sp, uint ref_size, uint layers, uint layers_to_sp, ENUM_OPTIMIZATION optimization_type, uint batch ) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
Desafortunadamente, la estructura de la clase que creamos es muy diferente de la clase padre, lo que no nos permitirá utilizar plenamente todos los métodos de la clase padre. Esto también se reflejará en el algoritmo del método de inicialización. Aquí tendremos que inicializar no solo los objetos añadidos sino también los heredados.
En el cuerpo del método de inicialización, primero llamaremos al método homónimo de la capa básica totalmente conectada, que realizará la validación inicial de los parámetros recibidos y la activación de las interfaces de intercambio de datos entre capas neuronales como parte del funcionamiento del modelo.
Y luego almacenaremos los parámetros obtenidos en las variables internas de nuestra clase.
iWindow = window; iUnits = units_count; iHeads = heads; iSPUnits = units_sp; iSPWindow = window_sp; iSPHeads = heads_sp; iWindowKey = window_key; iLayers = MathMax(layers, 1); iLayersSP = MathMax(layers_to_sp, 1);
Aquí también declararemos algunas variables para almacenar temporalmente los punteros a los objetos de las distintas capas neuronales que inicializaremos como parte de nuestro método.
CNeuronBaseOCL *base = NULL; CNeuronTransposeOCL *transp = NULL; CNeuronConvOCL *conv = NULL; CNeuronLearnabledPE *pe = NULL;
A continuación, crearemos los objetos para generar las consultas entrenadas. Aquí conviene recordar que los autores del método 3D-GRES proponen utilizar consultas dinámicas basadas en la nube de puntos original. No obstante, la nube de puntos analizada puede diferir de las consultas entrenadas tanto en el número de elementos como en el tamaño del vector de características que describe un elemento. Resolveremos este problema en 2 pasos. Primero transpondremos el tensor de los datos de origen y utilizaremos la capa de convolución para cambiar el número de elementos de la secuencia. El uso de la capa de convolución nos permitirá realizar la operación anterior dentro de secuencias unitarias independientes.
//--- Init Querys cQuery.Clear(); transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, 0, OpenCL, iSPUnits, iSPWindow, optimization, iBatch) || !cQuery.Add(transp)) return false; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, 1, OpenCL, iSPUnits, iSPUnits, iUnits, 1, iSPWindow, optimization, iBatch) || !cQuery.Add(conv)) return false; conv.SetActivationFunction(SIGMOID);
En el segundo paso, transpondremos inversamente el tensor y realizaremos su proyección en el espacio multimodal.
transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, 2, OpenCL, iSPWindow, iUnits, optimization, iBatch) || !cQuery.Add(transp)) return false; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, 3, OpenCL, iSPWindow, iSPWindow, iWindow, iUnits, 1, optimization, iBatch) || !cQuery.Add(conv)) return false; conv.SetActivationFunction(SIGMOID);
Ahora todo lo que deberemos hacer es añadir una codificación posicional totalmente entrenable.
pe = new CNeuronLearnabledPE(); if(!pe || !pe.Init(0, 4, OpenCL, iWindow * iUnits, optimization, iBatch) || !cQuery.Add(pe)) return false;
De forma similar al algoritmo de la clase padre, colocaremos los datos de consulta de la codificación posicional en un flujo de información independiente.
base = new CNeuronBaseOCL(); if(!base || !base.Init(0, 5, OpenCL, pe.Neurons(), optimization, iBatch) || !base.SetOutput(pe.GetPE()) || !cQPosition.Add(base)) return false;
Hemos trasladado completamente el algoritmo para generar la arquitectura del modelo Superpoints desde la clase padre sin modificaciones.
//--- Init SuperPoints int layer_id = 6; cSuperPoints.Clear(); for(int r = 0; r < 4; r++) { if(iSPUnits % 2 == 0) { iSPUnits /= 2; CResidualConv *residual = new CResidualConv(); if(!residual || !residual.Init(0, layer_id, OpenCL, 2 * iSPWindow, iSPWindow, iSPUnits, optimization, iBatch) || !cSuperPoints.Add(residual)) return false; } else { iSPUnits--; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, 2 * iSPWindow, iSPWindow, iSPWindow, iSPUnits, 1, optimization, iBatch) || !cSuperPoints.Add(conv)) return false; conv.SetActivationFunction(SIGMOID); } layer_id++; } conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iSPWindow, iSPWindow, iWindow, iSPUnits, 1, optimization, iBatch) || !cSuperPoints.Add(conv)) return false; conv.SetActivationFunction(SIGMOID); layer_id++; pe = new CNeuronLearnabledPE(); if(!pe || !pe.Init(0, layer_id, OpenCL, conv.Neurons(), optimization, iBatch) || !cSuperPoints.Add(pe)) return false; layer_id++;
Y para generar la incorporación de la expresión aclaratoria, utilizaremos un MLP completamente conectado con la adición de una capa de codificación posicional.
//--- Reference cReference.Clear(); base = new CNeuronBaseOCL(); if(!base || !base.Init(iWindow * iUnits, layer_id, OpenCL, ref_size, optimization, iBatch) || !cReference.Add(base)) return false; layer_id++; base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch) || !cReference.Add(base)) return false; base.SetActivationFunction(SIGMOID); layer_id++; pe = new CNeuronLearnabledPE(); if(!pe || !pe.Init(0, layer_id, OpenCL, base.Neurons(), optimization, iBatch) || !cReference.Add(pe)) return false; layer_id++;
Aquí cabe señalar que obtendremos un tensor conmensurado con el tensor de consultas entrenadas en la salida del MLP. Esto se hace para poder descomponer la expresión de referencia en varios componentes semánticos, lo cual permitirá un análisis más completo de la situación actual del mercado.
En esta fase, hemos completado la inicialización de los objetos de procesamiento inicial de los datos de origen. Ahora crearemos el ciclo de inicialización de los objetos de las capas neuronales internas. Pero primero limpiaremos los arrays de colecciones de objetos internos.
//--- Inside layers cQKey.Clear(); cQValue.Clear(); cSPKey.Clear(); cSPValue.Clear(); cSelfAttentionOut.Clear(); cCrossAttentionOut.Clear(); cMHCrossAttentionOut.Clear(); cMHSelfAttentionOut.Clear(); cMHRefAttentionOut.Clear(); cRefAttentionOut.Clear(); cRefKey.Clear(); cRefValue.Clear(); cResidual.Clear(); for(uint l = 0; l < iLayers; l++) { //--- Cross-Attention //--- Query conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1,optimization, iBatch) || !cQuery.Add(conv)) return false; layer_id++;
En el cuerpo del ciclo, primero inicializaremos los objetos de atención cruzada Query-Superpoint. Aquí crearemos un objeto de generación de entidades Query para el bloque de atención. Y, a continuación, añadiremos objetos de generación de entidades Key y Value según sea necesario.
if(l % iLayersSP == 0) { //--- Key conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iSPUnits, 1, optimization, iBatch) || !cSPKey.Add(conv)) return false; layer_id++; //--- Value conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iSPUnits, 1, optimization, iBatch) || !cSPValue.Add(conv)) return false; layer_id++; }
Asimismo, añadiremos una capa de registro de resultados de la atención multicabeza.
//--- Multy-Heads Attention Out base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) || !cMHCrossAttentionOut.Add(base)) return false; layer_id++;
Y una capa de escalado de resultados.
//--- Cross-Attention Out conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 1, optimization, iBatch) || !cCrossAttentionOut.Add(conv)) return false; layer_id++;
El bloque de atención cruzada se completará con una capa de enlaces residuales.
//--- Residual base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch) || !cResidual.Add(base)) return false; layer_id++;
A continuación, inicializaremos el bloque Self-Attention del análisis de dependencias Query-Query. Aquí generaremos todas las entidades basándonos en los resultados del bloque anterior de atención cruzada.
//--- Self-Attention //--- Query conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) || !cQuery.Add(conv)) return false; layer_id++; //--- Key conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) || !cQKey.Add(conv)) return false; layer_id++; //--- Value conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) || !cQValue.Add(conv)) return false; layer_id++;
En este caso, para cada capa interna, generaremos todas las entidades con el mismo número de cabezas de atención.
Añadiremos una capa de registro de resultados de la atención multicabeza.
//--- Multy-Heads Attention Out base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) || !cMHSelfAttentionOut.Add(base)) return false; layer_id++;
Y una capa de escalado de resultados.
//--- Self-Attention Out conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 1, optimization, iBatch) || !cSelfAttentionOut.Add(conv)) return false; layer_id++;
Paralelamente con el bloque Self-Attention funcionará un bloque de atención cruzada Query respecto a las expresiones de referencia semánticas. Aquí, la entidad Query se generará a partir de los resultados del bloque de atención cruzada anterior.
//--- Reference Cross-Attention //--- Query conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) || !cQuery.Add(conv)) return false; layer_id++;
Mientras que el tensor Key-Value se formará a partir de incorporaciones semánticas previamente preparadas.
//--- Key conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) || !cRefKey.Add(conv)) return false; layer_id++; //--- Value conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) || !cRefValue.Add(conv)) return false; layer_id++;
De forma similar al bloque Self-Attention, generaremos todas las entidades en cada nueva capa con un número igual de cabezas de atención.
A continuación, añadiremos las capas de resultados de atención múltiple y de escalado de resultados.
//--- Multy-Heads Attention Out base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) || !cMHRefAttentionOut.Add(base)) return false; layer_id++; //--- Cross-Attention Out conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindowKey*iHeads, iWindowKey*iHeads, iWindow, iUnits, 1, optimization, iBatch) || !cRefAttentionOut.Add(conv)) return false; layer_id++; if(!conv.SetGradient(((CNeuronBaseOCL*)cSelfAttentionOut[cSelfAttentionOut.Total() - 1]).getGradient(), true)) return false;
Y completando este bloque estará la capa de enlaces residuales, que combinará los resultados de los tres bloques de atención.
//--- Residual base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch)) return false; if(!cResidual.Add(base)) return false; layer_id++;
Mientras que el procesamiento final de las consultas enriquecidas se realizará en el bloque FeedForward con enlace residual, cuya estructura será similar a la del Transformer vainilla.
//--- Feed Forward conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, 4*iWindow, iUnits, 1, optimization, iBatch)) return false; conv.SetActivationFunction(LReLU); if(!cFeedForward.Add(conv)) return false; layer_id++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, 1, optimization, iBatch)) return false; if(!cFeedForward.Add(conv)) return false; layer_id++; //--- Residual base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch)) return false; if(!base.SetGradient(conv.getGradient())) return false; if(!cResidual.Add(base)) return false; layer_id++;
Además, incorporaremos de la clase padre un algoritmo para corregir los centros de los objetos, que no fue proporcionado por los autores del método 3D-GRES.
//--- Delta position conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch)) return false; conv.SetActivationFunction(SIGMOID); if(!cQPosition.Add(conv)) return false; layer_id++; base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, conv.Neurons(), optimization, iBatch)) return false; if(!base.SetGradient(conv.getGradient())) return false; if(!cQPosition.Add(base)) return false; layer_id++; }
Y pasaremos a la siguiente iteración del ciclo de creación de objetos de la capa interior. Y una vez ejecutadas con éxito todas las iteraciones del ciclo, intercambiaremos los punteros a los búferes de datos, lo cual nos permitirá reducir el número de operaciones de copiado de datos y acelerar el proceso de entrenamiento.
base = cResidual[iLayers * 3 - 1]; if(!SetGradient(base.getGradient())) return false; //--- SetOpenCL(OpenCL); //--- return true; }
Y al final de las operaciones del método, retornaremos el resultado lógico de las operaciones ejecutadas al programa que realiza la llamada.
Aquí vale la pena señalar que, como en el artículo anterior, hemos trasladado la creación de búferes de datos auxiliares a un método CreateBuffers separado. Le sugiero que se familiarice con este método por sí mismo. Su código completo se encuentra en el archivo adjunto.
Tras inicializar el objeto de nuestra nueva clase, pasaremos a construir el algoritmo de pasada directa, implementado en el método feedForward. Esta vez, obtendremos los dos punteros a los objetos de datos de origen en los parámetros del método. Uno contendrá la nube de puntos analizada, mientras que el segundo presentará la expresión de referencia.
bool CNeuronGRES::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) { //--- Superpoints CNeuronBaseOCL *superpoints = NeuronOCL; int total_sp = cSuperPoints.Total(); for(int i = 0; i < total_sp; i++) { if(!cSuperPoints[i] || !((CNeuronBaseOCL*)cSuperPoints[i]).FeedForward(superpoints)) return false; superpoints = cSuperPoints[i]; }
Y en el cuerpo del método, organizaremos inmediatamente un ciclo de pasada directa de nuestro pequeño modelo de generación Superpoints. A continuación, generaremos las consultas de manera similar.
//--- Query CNeuronBaseOCL *query = NeuronOCL; for(int i = 0; i < 5; i++) { if(!cQuery[i] || !((CNeuronBaseOCL*)cQuery[i]).FeedForward(query)) return false; query = cQuery[i]; }
Pero tendremos que trabajar un poco más con la creación del tensor de incorporaciones semánticas de la expresión de referencia. La cuestión es que obtendremos la expresión de referencia como un búfer de datos. Mientras que el método de pasada directa de los objetos internos requerirá una capa neuronal como entrada. Por consiguiente, utilizaremos la primera capa del modelo interno para generar incorporaciones semánticas de la expresión de referencia para registrar los datos de origen, de forma similar al modelo principal. Solo que en este caso no copiaremos completamente el contenido del búfer, sino que solo sustituiremos los punteros a los objetos.
//--- Reference CNeuronBaseOCL *reference = cReference[0]; if(!SecondInput) return false; if(reference.getOutput() != SecondInput) if(!reference.SetOutput(SecondInput, true)) return false;
Y luego organizaremos el ciclo de pasada directa del modelo interno.
for(int i = 1; i < cReference.Total(); i++) { if(!cReference[i] || !((CNeuronBaseOCL*)cReference[i]).FeedForward(reference)) return false; reference = cReference[i]; }
Aquí finalizaremos el preprocesamiento de los datos de origen y pasaremos al algoritmo principal de descodificación de datos. Para ello, organizaremos un ciclo de iteración de las capas internas de nuestro Decodificador.
CNeuronBaseOCL *inputs = query, *key = NULL, *value = NULL, *base = NULL, *cross = NULL, *self = NULL; //--- Inside layers for(uint l = 0; l < iLayers; l++) { //--- Calc Position bias cross = cQPosition[l * 2]; if(!cross || !CalcPositionBias(cross.getOutput(), ((CNeuronLearnabledPE*)superpoints).GetPE(), cPositionBias[l], iUnits, iSPUnits, iWindow)) return false;
Aquí, primero determinaremos los coeficientes de desplazamiento posicional, de forma similar al método MAFT. Este será nuestro punto de partida con respecto al algoritmo 3D-GRES del autor. En su trabajo, los autores del método utilizaron un MLP para generar una máscara de atención.
A continuación viene el bloque de atención cruzada QSA, donde se realizarán los análisis de dependencia Query-Superpoint. Aquí generaremos primero los tensores de las entidades Query, Key y Value. Los dos últimos solo se generarán cuando sea necesario.
//--- Cross-Attention query = cQuery[l * 3 + 5]; if(!query || !query.FeedForward(inputs)) return false; key = cSPKey[l / iLayersSP]; value = cSPValue[l / iLayersSP]; if(l % iLayersSP == 0) { if(!key || !key.FeedForward(superpoints)) return false; if(!value || !value.FeedForward(cSuperPoints[total_sp - 2])) return false; }
Y analizaremos las dependencias considerando los coeficientes de desplazamiento posicional.
if(!AttentionOut(query, key, value, cScores[l * 3], cMHCrossAttentionOut[l], cPositionBias[l], iUnits, iHeads, iSPUnits, iSPHeads, iWindowKey, true)) return false;
Luego escalaremos los resultados de la atención multicabeza y añadiremos los valores de enlace residuales seguidos de una normalización de datos.
base = cCrossAttentionOut[l]; if(!base || !base.FeedForward(cMHCrossAttentionOut[l])) return false; value = cResidual[l * 3]; if(!value || !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, false, 0, 0, 0, 1)|| !SumAndNormilize(cross.getOutput(), value.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1)) return false; inputs = value;
El siguiente paso consistirá en organizar el funcionamiento del módulo QLA. Aquí tendremos que organizar la pasada directa de dos bloques de atención:
- Self-Attention → Query-Query;
- Cross-Attention → Query-Reference.
Primero organizaremos el bloque Self-Attention. Aquí generaremos al completo los tensores de entidad Query, Key y Value basándonos en los datos obtenidos del bloque anterior del Decodificador.
//--- Self-Atention query = cQuery[l * 3 + 6]; if(!query || !query.FeedForward(inputs)) return false; key = cQKey[l]; if(!key || !key.FeedForward(inputs)) return false; value = cQValue[l]; if(!value || !value.FeedForward(inputs)) return false;
Analizaremos las dependencias en un módulo de atención multicabeza vainilla.
if(!AttentionOut(query, key, value, cScores[l * 3 + 1], cMHSelfAttentionOut[l], -1, iUnits, iHeads, iUnits, iHeads, iWindowKey, false)) return false; self = cSelfAttentionOut[l]; if(!self || !self.FeedForward(cMHSelfAttentionOut[l])) return false;
A continuación, escalaremos los resultados obtenidos.
El bloque de atención cruzada se construirá de forma similar. Solo que las entidades Key y Value se generarán a partir de incorporaciones semánticas de la expresión de referencia.
//--- Reference Cross-Attention query = cQuery[l * 3 + 7]; if(!query || !query.FeedForward(inputs)) return false; key = cRefKey[l]; if(!key || !key.FeedForward(reference)) return false; value = cRefValue[l]; if(!value || !value.FeedForward(reference)) return false; if(!AttentionOut(query, key, value, cScores[l * 3 + 2], cMHRefAttentionOut[l], -1, iUnits, iHeads, iUnits, iHeads, iWindowKey, false)) return false; cross = cRefAttentionOut[l]; if(!cross || !cross.FeedForward(cMHRefAttentionOut[l])) return false;
A continuación, realizaremos la suma de los resultados de los tres bloques de atención y normalizaremos los datos resultantes.
value = cResidual[l * 3 + 1]; if(!value || !SumAndNormilize(cross.getOutput(), self.getOutput(), value.getOutput(), iWindow, false, 0, 0, 0, 1) || !SumAndNormilize(inputs.getOutput(), value.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1)) return false; inputs = value;
A esto le seguirá el bloque FeedForward del Transformer vainilla con enlace residual y normalización de datos.
//--- Feed Forward base = cFeedForward[l * 2]; if(!base || !base.FeedForward(inputs)) return false; base = cFeedForward[l * 2 + 1]; if(!base || !base.FeedForward(cFeedForward[l * 2])) return false; value = cResidual[l * 3 + 2]; if(!value || !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1)) return false; inputs = value;
Ya habrá notado que el algoritmo de pasada directa construido es una especie de simbiosis de los métodos 3D-GRES y MAFT. Solo nos queda añadir el toque final del método MAFT: ajustar las posiciones de las consultas.
//--- Delta Query position base = cQPosition[l * 2 + 1]; if(!base || !base.FeedForward(inputs)) return false; value = cQPosition[(l + 1) * 2]; query = cQPosition[l * 2]; if(!value || !SumAndNormilize(query.getOutput(), base.getOutput(), value.getOutput(), iWindow, false, 0, 0, 0,0.5f)) return false; }
Después pasaremos a la siguiente capa del Decodificador. Y tras finalizar la enumeración de todas las capas internas del Descodificador, resumiremos los valores de consulta enriquecidos con su codificación posicional. Los resultados los transmitiremos a la siguiente capa de nuestro modelo usando interfaces básicas.
value = cQPosition[iLayers * 2]; if(!value || !SumAndNormilize(inputs.getOutput(), value.getOutput(), Output, iWindow, true, 0, 0, 0, 1)) return false; //--- return true; }
Y aquí todo lo que deberemos hacer es retornar el resultado lógico de las operaciones al programa que realiza la llamada.
Aquí concluye nuestro trabajo sobre la construcción de los métodos de pasada directa y procederemos a implementar los algoritmos de pasada inversa. Aquí, como de costumbre, dividiremos el proceso completo en dos pasos:
- La distribución de los gradientes de error (calcInputGradients);
- La optimización de los parámetros del modelo (updateInputWeights).
En el primer caso, nos desplazaremos a través del flujo de operaciones de pasada directa, solo que en orden inverso. En el segundo, nos limitaremos a llamar a los métodos homónimos de las capas internas que contienen los parámetros a entrenar. A primera vista, será lo de siempre, pero hay un matiz en la diversificación de las consultas. Por consiguiente, nos centraremos con más detalle en examinar el algoritmo del método calcInputGradients, que realizará la distribución del gradiente de error.
En los parámetros del método obtendremos los punteros a los tres objetos y la constante de la función de activación utilizada para la segunda fuente de datos.
bool CNeuronGRES::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1) { if(!NeuronOCL || !SecondGradient) return false;
En el cuerpo del método comprobaremos la relevancia de solo dos punteros. Recordemos que en la pasada anterior, hemos guardado el puntero a la segunda fuente de los datos de origen. Por consiguiente, la ausencia de un puntero real en los parámetros no será de importancia crítica para nosotros en esta etapa. Sin embargo, esto no puede decirse del búfer de registro de gradientes de error. Por eso nos aseguraremos de que esté actualizado antes de empezar a trabajar.
Aquí también declararemos una serie de variables para almacenar temporalmente los punteros a los objetos. Y con esto concluirá nuestra etapa de trabajo preparatorio.
CNeuronBaseOCL *residual = GetPointer(this), *query = NULL, *key = NULL, *value = NULL, *key_sp = NULL, *value_sp = NULL, *base = NULL;
A continuación, organizaremos un ciclo para recorrer las capas internas del Decodificador.
//--- Inside layers for(int l = (int)iLayers - 1; l >= 0; l--) { //--- Feed Forward base = cFeedForward[l * 2]; if(!base || !base.calcHiddenGradients(cFeedForward[l * 2 + 1])) return false; base = cResidual[l * 3 + 1]; if(!base || !base.calcHiddenGradients(cFeedForward[l * 2])) return false;
Aquí, gracias a la sustitución correctamente planificada de los punteros por búferes de datos en los objetos internos, nos evitaremos operaciones innecesarias de copiado de datos y empezaremos a trabajar conduciendo el gradiente de error a través del bloque FeedForward.
El gradiente de error obtenido en el nivel de datos de origen del bloque FeedForward lo sumaremos con valores similares en el nivel de resultados de nuestra clase, que se corresponderá con el flujo de datos de enlace residual de este bloque. Pasaremos el resultado de las operaciones al búfer de resultados del bloque de Self-Attention.
//--- Residual value = cSelfAttentionOut[l]; if(!value || !SumAndNormilize(base.getGradient(), residual.getGradient(), value.getGradient(), iWindow, false, 0, 0, 0, 1)) return false; residual = value;
Aquí debemos señalar que suministraremos la suma de los resultados de los tres bloques de atención a la entrada del bloque FeedForward. Y, en consecuencia, tendremos que transferir el gradiente de error resultante de todas las fuentes. Recuerde que al sumar los datos, pasaremos el gradiente de error completo a todos los sumandos. También utilizaremos los resultados del bloque QSA como fuentes para otros módulos de nuestro decodificador. Por consiguiente, recopilaremos su gradiente de error más adelante, de forma similar a los flujos de enlace residuales. Pero para evitar el copiado innecesario de gradientes de error en el bloque de atención cruzada Query-Reference, hemos dispuesto prudentemente el intercambio de punteros durante la inicialización del objeto. Así, cuando transfiramos datos al bloque de Self-Attention, transferiremos simultáneamente los mismos datos al bloque de atención cruzada Query-Reference. Este pequeño truco reducirá el consumo de memoria y el tiempo de entrenamiento del modelo al eliminar operaciones redundantes.
A continuación, pasaremos el gradiente de error por el bloque de atención cruzada Query-Reference.
//--- Reference Cross-Attention base = cMHRefAttentionOut[l]; if(!base || !base.calcHiddenGradients(cRefAttentionOut[l], NULL)) return false; query = cQuery[l * 3 + 7]; key = cRefKey[l]; value = cRefValue[l]; if(!AttentionInsideGradients(query, key, value, cScores[l * 3 + 2], base, iUnits, iHeads, iUnits, iHeads, iWindowKey)) return false;
Y pasaremos el gradiente de error de la entidad Query al módulo QSA, añadiéndole previamente el gradiente de error obtenido del bloque FeedForward (flujo de enlaces residuales).
base = cResidual[l * 3]; if(!base || !base.calcHiddenGradients(query, NULL)) return false; value = cCrossAttentionOut[l]; if(!SumAndNormilize(base.getGradient(), residual.getGradient(),value.getGradient(), iWindow, false, 0, 0, 0, 1)) return false; residual = value;
Del mismo modo, pasaremos el gradiente de error por el bloque de Self-Attention.
//--- Self-Attention base = cMHSelfAttentionOut[l]; if(!base || !base.calcHiddenGradients(cSelfAttentionOut[l], NULL)) return false; query = cQuery[l * 3 + 6]; key = cQKey[l]; value = cQValue[l]; if(!AttentionInsideGradients(query, key, value, cScores[l * 2 + 1], base, iUnits, iHeads, iUnits, iHeads, iWindowKey)) return false;
Solo ahora tendremos que añadir el gradiente de error de las tres entidades al módulo QSA. Para ello, pasaremos sucesivamente el gradiente de error a la capa de enlace residual y añadiremos los valores resultantes a la suma acumulada previamente de los gradientes de los módulos QSA.
base = cResidual[l * 3 + 1]; if(!base.calcHiddenGradients(query, NULL)) return false; if(!SumAndNormilize(base.getGradient(), residual.getGradient(), residual.getGradient(), iWindow, false, 0, 0, 0, 1)) return false; if(!base.calcHiddenGradients(key, NULL)) return false; if(!SumAndNormilize(base.getGradient(), residual.getGradient(), residual.getGradient(), iWindow, false, 0, 0, 0, 1)) return false; if(!base.calcHiddenGradients(value, NULL)) return false; if(!SumAndNormilize(base.getGradient(), residual.getGradient(), residual.getGradient(), iWindow, false, 0, 0, 0, 1)) return false;
La suma de los valores de gradiente acumulados también se transferirá al flujo de información paralelo desde la codificación de posición de las consultas sumándola a los gradientes del otro flujo de información.
//--- Qeury position base = cQPosition[l * 2]; value = cQPosition[(l + 1) * 2]; if(!base || !SumAndNormilize(value.getGradient(), residual.getGradient(), base.getGradient(), iWindow, false, 0, 0, 0, 1)) return false;
Y ahora solo nos quedará pasar el gradiente de error por el módulo QSA. Aquí utilizaremos el mismo algoritmo para propagar el gradiente de error a través del bloque de atención, pero haremos una corrección para recoger los gradientes de error de las entidades Key y Value de múltiples capas del Decodificador. Primero recogeremos los gradientes de error en los búferes de datos temporales y almacenaremos los valores finales en los búferes de objetos correspondientes.
//--- Cross-Attention base = cMHCrossAttentionOut[l]; if(!base || !base.calcHiddenGradients(residual, NULL)) return false; query = cQuery[l * 3 + 5]; if(((l + 1) % iLayersSP) == 0 || (l + 1) == iLayers) { key_sp = cSPKey[l / iLayersSP]; value_sp = cSPValue[l / iLayersSP]; if(!key_sp || !value_sp || !cTempCrossK.Fill(0) || !cTempCrossV.Fill(0)) return false; } if(!AttentionInsideGradients(query, key_sp, value_sp, cScores[l * 2], base, iUnits, iHeads, iSPUnits, iSPHeads, iWindowKey)) return false; if(iLayersSP > 1) { if((l % iLayersSP) == 0) { if(!SumAndNormilize(key_sp.getGradient(), GetPointer(cTempCrossK), key_sp.getGradient(), iWindowKey, false, 0, 0, 0, 1)) return false; if(!SumAndNormilize(value_sp.getGradient(), GetPointer(cTempCrossV), value_sp.getGradient(), iWindowKey, false, 0, 0, 0, 1)) return false; } else { if(!SumAndNormilize(key_sp.getGradient(), GetPointer(cTempCrossK), GetPointer(cTempCrossK), iWindowKey, false, 0, 0, 0, 1)) return false; if(!SumAndNormilize(value_sp.getGradient(), GetPointer(cTempCrossV), GetPointer(cTempCrossV), iWindowKey, false, 0, 0, 0, 1)) return false; } }
Luego pasaremos el gradiente de error de la entidad Query a la capa de datos de origen y añadiremos los datos sobre el flujo de información de los enlaces residuales. Después pasaremos a la siguiente iteración del ciclo de la capa del Decodificador.
if(l == 0) base = cQuery[4]; else base = cResidual[l * 3 - 1]; if(!base || !base.calcHiddenGradients(query, NULL)) return false; //--- Residual if(!SumAndNormilize(base.getGradient(), residual.getGradient(), base.getGradient(), iWindow, false, 0, 0, 0, 1)) return false; residual = base; }
Después de pasar con éxito el gradiente de error por todas las capas del Decodificador, solo tendremos que pasarlo a la capa de datos de origen a través de las operaciones del módulo de preprocesamiento de datos. Primero haremos descender el gradiente de error de nuestras consultas entrenadas. Para ello, pasaremos el gradiente de error por la capa de codificación de posición.
//--- Qeury query = cQuery[3]; if(!query || !query.calcHiddenGradients(cQuery[4])) return false;
Y en este paso, realizaremos la inyección del gradiente de error de codificación de la posición a partir del flujo de información correspondiente.
base = cQPosition[0]; if(!DeActivation(base.getOutput(), base.getGradient(), base.getGradient(), SIGMOID) || !(((CNeuronLearnabledPE*)cQuery[4]).AddPEGradient(base.getGradient()))) return false;
Y luego añadiremos el gradiente de error de diversificación de la consulta, pero aquí ya estaremos trabajando sin información sobre la codificación posicional. Este paso se ha introducido de forma intencional para que el error de diversificación no afecte a la codificación posicional.
if(!DiversityLoss(query, iUnits, iWindow, true)) return false;
Después vendrá un simple ciclo de iteración inversa por las capas de nuestro modelo de generación de consultas pasando el gradiente de error a la capa de datos de origen.
for(int i = 2; i >= 0; i--) { query = cQuery[i]; if(!query || !query.calcHiddenGradients(cQuery[i + 1])) return false; } if(!NeuronOCL.calcHiddenGradients(query, NULL)) return false;
Nótese aquí que tendremos que pasar también el gradiente de error del modelo interno de generación Superpoints a la capa de datos de origen. Para evitar la pérdida de datos, almacenaremos en una variable local el puntero al búfer de gradiente del objeto de datos de origen. Y sustituirlo en el objeto de datos de origen por el correspondiente búfer de capa de transposición del modelo de generación de consultas.
Recordemos que la capa de transposición no contendrá parámetros de entrenamiento, y que la pérdida de gradientes de error no supondrá ningún riesgo para nosotros.
CBufferFloat *inputs_gr = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(query.getGradient(), false)) return false;
En el siguiente paso, distribuiremos el gradiente de error a través del modelo de generación Superpoints. Nótese aquí, sin embargo, que no le transmitiremos el gradiente de error en el proceso de iteración inversa de las capas del Decodificador. Por consiguiente, primero tendremos que recoger el gradiente de error de las entidades Key y Value correspondientes. Al hacerlo, entenderemos que tenemos al menos un tensor de cada entidad. Pero hay un punto más: la entidad Key la hemos generado a partir de los resultados de la última capa del modelo Superpoints (teniendo en cuenta la codificación de posición), mientras que Value se ha generado a partir de la penúltima capa sin tener en cuenta la codificación de posición. Y el gradiente de error que tendremos que distribuir será exactamente ese flujo de datos de información.
Para ello, primero calcularemos el gradiente de error de la primera capa de la entidad Key y lo transmitiremos a la última capa del modelo interno.
//--- Superpoints //--- From Key int total_sp = cSuperPoints.Total(); CNeuronBaseOCL *superpoints = cSuperPoints[total_sp - 1]; if(!superpoints || !superpoints.calcHiddenGradients(cSPKey[0])) return false;
Y, a continuación, comprobaremos el número de capas de la entidad Key y, si es necesario, para evitar la pérdida del gradiente de error obtenido anteriormente, realizaremos la sustitución de los búferes de datos.
if(cSPKey.Total() > 1) { CBufferFloat *grad = superpoints.getGradient(); if(!superpoints.SetGradient(GetPointer(cTempSP), false)) return false;
Y organizaremos un ciclo de iteración de las capas restantes de la entidad dada con cálculo del gradiente de error y la posterior suma con los valores acumulados anteriormente.
for(int i = 1; i < cSPKey.Total(); i++) { if(!superpoints.calcHiddenGradients(cSPKey[i]) || !SumAndNormilize(superpoints.getGradient(), grad, grad, iWindow, false, 0, 0, 0, 1)) return false; }
Una vez ejecutadas con éxito todas las iteraciones del ciclo, retornaremos el puntero al búfer que contiene la suma del gradiente de error acumulado.
if(!superpoints.SetGradient(grad, false)) return false; }
Así, en la última capa del modelo Superpoint, hemos recogido el gradiente de error de todas las capas de la entidad Key y ahora podremos transmitirlo a una capa por debajo del modelo especificado.
superpoints = cSuperPoints[total_sp - 2]; if(!superpoints || !superpoints.calcHiddenGradients(cSuperPoints[total_sp - 1])) return false;
Y ahora al mismo nivel necesitaremos recoger el gradiente de error de la entidad Value. Aquí usaremos el mismo algoritmo. Solo que en este caso, ya tendremos datos de la capa posterior en el búfer de gradiente de error. Por consiguiente, organizaremos directamente el intercambio de búferes de datos y, a continuación, recopilaremos la información con los flujos de datos paralelos en un ciclo.
//--- From Value CBufferFloat *grad = superpoints.getGradient(); if(!superpoints.SetGradient(GetPointer(cTempSP), false)) return false; for(int i = 0; i < cSPValue.Total(); i++) { if(!superpoints.calcHiddenGradients(cSPValue[i]) || !SumAndNormilize(superpoints.getGradient(), grad, grad, iWindow, false, 0, 0, 0, 1)) return false; } if(!superpoints.SetGradient(grad, false)) return false;
Aquí añadiremos también los errores de diversificación, que nos permitirán maximizar la variedad de Superpoints.
if(!DiversityLoss(superpoints, iSPUnits, iSPWindow, true)) return false;
Y además, en un ciclo de iteración inversa de las capas del modelo Superpoints, haremos bajar el gradiente de error hasta el nivel de los datos de origen.
for(int i = total_sp - 3; i >= 0; i--) { superpoints = cSuperPoints[i]; if(!superpoints || !superpoints.calcHiddenGradients(cSuperPoints[i + 1])) return false; } //--- Inputs if(!NeuronOCL.calcHiddenGradients(cSuperPoints[0])) return false;
Aquí conviene recordar que hemos guardado parte del gradiente de error en el nivel de datos de origen después de procesar el flujo de información de la consulta. Fue entonces cuando también sustituimos los búferes de datos. Y ahora sumaremos el gradiente de error de ambos flujos de información. Y luego retornaremos el puntero al búfer de datos.
if(!SumAndNormilize(NeuronOCL.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1)) return false; if(!NeuronOCL.SetGradient(inputs_gr, false)) return false;
De este modo, hemos recogido el gradiente de error de los dos flujos de información para la primera fuente de datos de origen. Pero todavía tendremos que pasar el gradiente de error al segundo objeto de datos de origen. Para ello, primero sincronizaremos los punteros a los búferes de gradiente de error del segundo objeto de datos de origen y de la primera capa del modelo Reference.
base = cReference[0]; if(base.getGradient() != SecondGradient) { if(!base.SetGradient(SecondGradient)) return false; base.SetActivationFunction(SecondActivation); }
A continuación, en la última capa del modelo especificado, recogeremos el gradiente de error de todos los tensores de las entidades Key y Value correspondientes. El algoritmo será similar al descrito anteriormente.
base = cReference[2]; if(!base || !base.calcHiddenGradients(cRefKey[0])) return false; inputs_gr = base.getGradient(); if(!base.SetGradient(GetPointer(cTempQ), false)) return false; if(!base.calcHiddenGradients(cRefValue[0])) return false; if(!SumAndNormilize(base.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1)) return false; for(uint i = 1; i < iLayers; i++) { if(!base.calcHiddenGradients(cRefKey[i])) return false; if(!SumAndNormilize(base.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1)) return false; if(!base.calcHiddenGradients(cRefValue[i])) return false; if(!SumAndNormilize(base.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1)) return false; } if(!base.SetGradient(inputs_gr, false)) return false;
Luego pasaremos el gradiente de error por la capa de codificación de posición.
base = cReference[1]; if(!base.calcHiddenGradients(cReference[2])) return false;
Y añadiremos el error de diversificación vectorial para maximizar la diversidad de componentes semánticos.
if(!DiversityLoss(base, iUnits, iWindow, true)) return false;
A continuación, pasaremos el gradiente de error a la capa de datos de origen.
base = cReference[0]; if(!base.calcHiddenGradients(cReference[1])) return false; //--- return true; }
Cuando el método finalice, todo lo que deberemos hacer es pasar el resultado lógico de las operaciones al programa que realiza la llamada.
Con esto concluirá nuestra revisión de los algoritmos para los métodos de nuestra nueva clase. Podrá ver el código completo de esta clase y todos sus métodos en el archivo adjunto. Allí encontrará también una descripción de la arquitectura de los modelos entrenados y de todos los programas usados en la elaboración de este artículo.
La arquitectura de los modelos entrenados se ha heredado casi por completo de artículos anteriores. Solo hemos cambiado una capa del Codificador de la descripción del estado del entorno.
Además, hemos introducido modificaciones puntuales en los programas de entrenamiento del modelo y de interacción con el entorno, debido a la necesidad de introducir una segunda fuente de datos en el modelo del Codificador del estado del entorno. Pero estas ediciones son momentos puntuales. Como ya hemos mencionado, como expresión de referencia hemos utilizado el vector de descripción del estado de la cuenta. La preparación de este vector se ha realizado antes, ya que ha sido utilizado por nuestro Actor.
3. Simulación
Hemos hecho un buen trabajo: hemos logrado construir con la ayuda de MQL5 una cierta simbiosis de los enfoques propuestos por los autores de los métodos 3D-GRES y MAFT. Ahora es momento de evaluar el trabajo realizado. Tendremos que entrenar el modelo utilizando la técnica propuesta con datos históricos reales y probar la política del Actor entrenada.
Para entrenar el modelo, usaremos los datos históricos reales del instrumento EURUSD para todo el año 2023 en el marco temporal H1. Los parámetros de los indicadores analizados se utilizarán por defecto.
Para entrenar los modelos usaremos un algoritmo comprobado en nuestros artículos anteriores.
La prueba de la política del Actor entrenada se realizará en el Simulador de Estrategias de MetaTrader 5 con los datos históricos de enero de 2024, mientras que los demás parámetros se mantendrán sin cambios. A continuación resumimos los resultados de las pruebas.
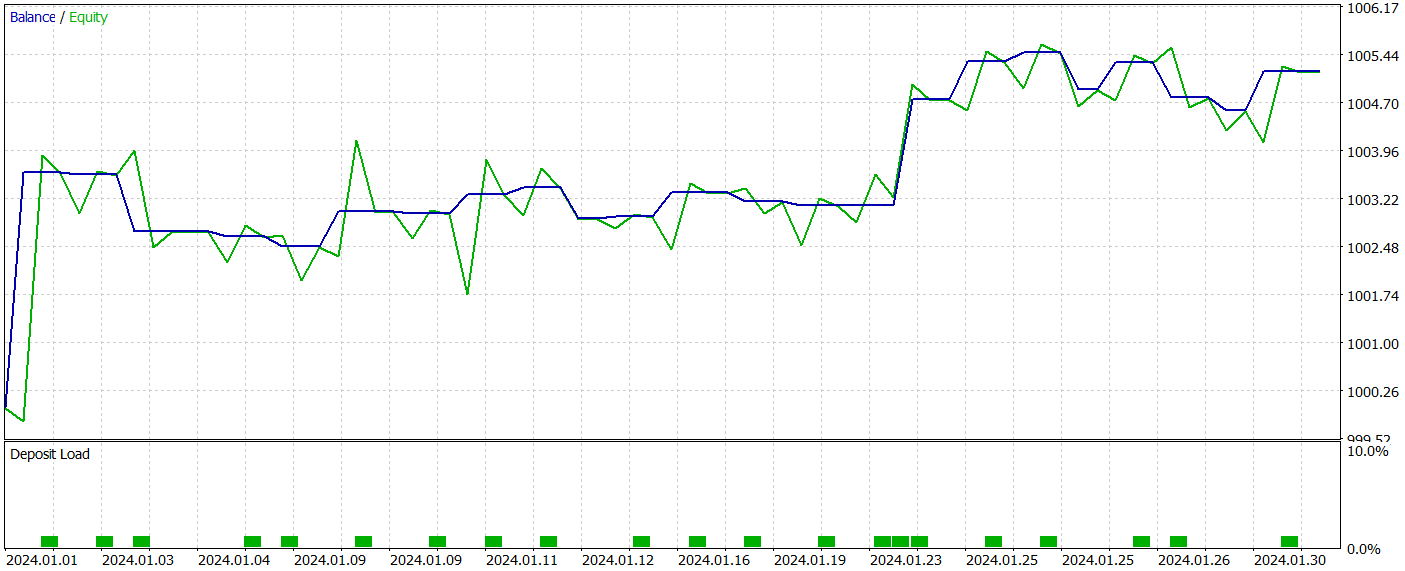
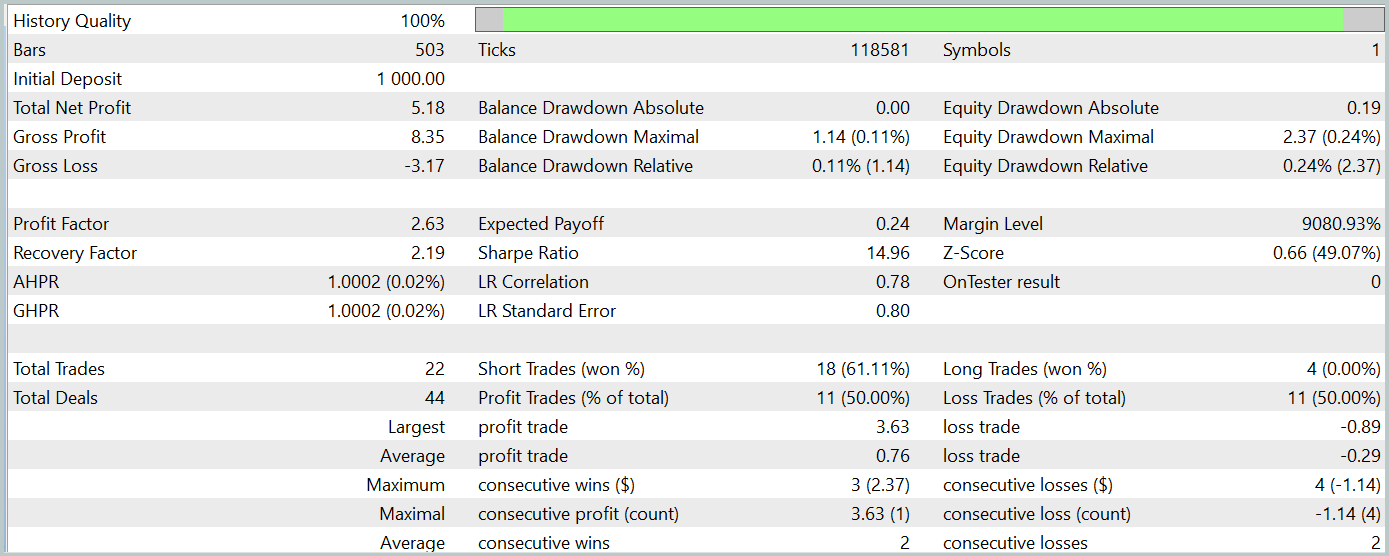
Durante el periodo de prueba, el modelo ha realizado 22 transacciones, y exactamente la mitad de ellas se han cerrado con beneficios. Cabe destacar que la transacción rentable media es más de 2 veces superior a la media de transacciones perdedoras. Y en la transacción de máxima rentabilidad vemos que es cuatro veces superior. Esto ha permitido al modelo registrar una puntuación del factor de beneficio de 2,63. No obstante, el reducido número de transacciones, unido un periodo de prueba tan corto, no nos permiten juzgar la eficacia del modelo a largo plazo. Antes de utilizar el modelo en condiciones reales, deberá entrenarse con un horizonte temporal más largo de datos históricos, seguido de pruebas exhaustivas.
Conclusión
Los enfoques propuestos por los autores del método Generalized 3D Referring Expression Segmentation (3D-GRES) pueden encontrar su aplicación en el comercio, posibilitando un análisis más profundo de los datos del mercado. El método propuesto puede adaptarse para segmentar y analizar múltiples señales de mercado, lo que permitirá una interpretación más precisa de situaciones de mercado complejas, mejorando la calidad de los pronósticos y las decisiones comerciales.
En la parte práctica de este artículo, hemos presentado una de las variantes de implementación de los enfoques propuestos usando los recursos de MQL5. Asimismo, hemos mostrado su uso. Los experimentos realizados demuestran el potencial de las soluciones propuestas para su uso en casos reales.
Enlaces
Programas usados en el artículo| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 5 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 6 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15997
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Métodos de William Gann (Parte III): ¿Funciona la astrología?
Métodos de William Gann (Parte III): ¿Funciona la astrología?
 Ciclos y Forex
Ciclos y Forex
 Algoritmo de Irrigación Artificial — Artificial Showering Algorithm (ASHA)
Algoritmo de Irrigación Artificial — Artificial Showering Algorithm (ASHA)
 El enfoque cuantitativo en la gestión de riesgos: Aplicación de un modelo VaR para la optimización de portafolios multidivisa con Python y MetaTrader 5
El enfoque cuantitativo en la gestión de riesgos: Aplicación de un modelo VaR para la optimización de portafolios multidivisa con Python y MetaTrader 5
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso