Características del Wizard MQL5 que debe conocer (Parte 36): Q-Learning con Cadenas de Markov

Introducción

Las clases de señales personalizadas para los Asesores Expertos ensamblados por el asistente pueden asumir varias funciones, que vale la pena explorar, y continuamos esta búsqueda examinando cómo el algoritmo Q-Learning cuando se empareja con las Cadenas de Markov puede ayudar a refinar el proceso de aprendizaje de una red de perceptrón multicapa. Q-Learning es uno de los varios (aproximadamente 12) algoritmos de aprendizaje de refuerzo, por lo que esencialmente también es una mirada a cómo este tema puede implementarse como una señal personalizada y probarse dentro de un Asesor Experto ensamblado por un asistente.

Entonces, la estructura de este artículo se basará en lo que es el aprendizaje de refuerzo, se centrará en el algoritmo Q-Learning y las etapas de su ciclo, observará cómo se pueden integrar las Cadenas de Markov en Q-Learning y luego concluirá, como siempre, con informes del Probador de estrategias. El aprendizaje por refuerzo puede utilizarse como un generador de señales independiente porque sus ciclos ('episodios') son en esencia una forma de aprendizaje que cuantifica los resultados como 'recompensas' para cada uno de los 'entornos' en los que está involucrado el 'actor'. Estos términos entre comillas se presentan a continuación. Sin embargo, no utilizamos el aprendizaje de refuerzo como una señal bruta, sino que confiamos en sus capacidades para promover el proceso de aprendizaje al complementar un perceptrón multicapa.

Dada la posición del aprendizaje por refuerzo como el tercer estándar en la formación de aprendizaje automático, además del aprendizaje supervisado y el aprendizaje no supervisado, pensé que podríamos involucrarlo más en la función de pérdida de un MLP, ya que en cierto sentido actúa como un punto intermedio entre la supervisión y la no-supervisión mediante el uso de 'CriticRewards' y 'environment-states', respectivamente. Ambos términos citados se presentan en la siguiente sección; sin embargo, esto significa que la mayor parte del pronóstico aún depende del MLP y el aprendizaje de refuerzo juega un papel más subordinado. Además, el uso de cadenas de Markov también es complementario al aprendizaje de refuerzo ya que las selecciones de "actores" del "Q-Map" a menudo son suficientes para implementar el algoritmo Q-Learning; sin embargo, lo incluimos aquí para tener una idea de la diferencia, si la hay, en los resultados de las pruebas que proporciona.

Descripción general del aprendizaje por refuerzo

El aprendizaje de refuerzo, que hemos presentado anteriormente como la tercera pata del entrenamiento del aprendizaje automático, es una forma de equilibrar tanto la exploración como la explotación durante el proceso de entrenamiento. Esto es posible gracias a su enfoque cíclico a la hora de evaluar cada ronda de entrenamiento, donde las rondas de entrenamiento se denominan episodios. Este ciclo se puede representar en el diagrama siguiente:

Fuente

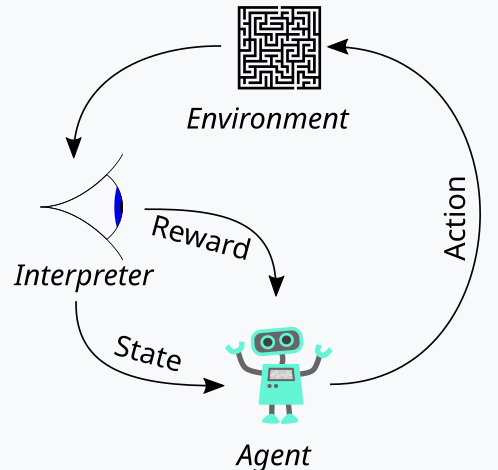
Entonces, con esto, tenemos una secuencia de pasos en el proceso de aprendizaje de refuerzo. Al principio, hay un 'Agente' que actúa en nombre de una parte principal que en nuestro caso es un MLP, para seleccionar el curso de acción ideal cuando se enfrenta a un mapa o núcleo o matriz de Q-Learning actualizado. Este mapa es un registro de todos los posibles estados del entorno más una distribución de probabilidad sobre las posibles acciones a tomar para cada uno de los estados disponibles.

La mejor manera de ilustrar esto podría ser si repasamos la implementación del entorno que hemos elegido para este artículo. Como traders, a menudo buscamos definir los mercados no sólo por su acción a corto plazo, sino también por sus características de moda o de largo plazo. Entonces, si nos centramos en tres métricas básicas, es decir, optimismo, pesimismo y estancamiento, cada una de estas tres puede tener indicadores en un marco temporal más corto y en un marco temporal más largo. Entonces, en esencia, nuestro "entorno" es un espacio de 9 índices (3 x 3 para el corto plazo y el largo plazo) donde un índice como el 0 marca un comportamiento bajista en el corto y largo plazo, el índice 4 marca un mercado lateral tanto en el corto como en el largo plazo, mientras que el índice 8 marca un comportamiento alcista en ambos horizontes temporales, etc.

Los entornos se seleccionan con la ayuda de una función con el mismo nombre, cuya fuente se proporciona a continuación:

//+------------------------------------------------------------------+
// Indexing new Environment data to conform with states
//+------------------------------------------------------------------+
void Cql::Environment(vector &E_Row, vector &E_Col, vector &E)
{  if(E_Row.Size() == E_Col.Size() && E_Col.Size() > 0)
   {  E.Init(E_Row.Size());
      E.Fill(0.0);
      for(int i = 0; i < int(E_Row.Size()); i++)
      {  if(E_Row[i] > 0.0 && E_Col[i] > 0.0)
         {  E[i] = 0.0;
         }
         else if(E_Row[i] > 0.0 && E_Col[i] == 0.0)
         {  E[i] = 1.0;
         }
         else if(E_Row[i] > 0.0 && E_Col[i] < 0.0)
         {  E[i] = 2.0;
         }
         else if(E_Row[i] == 0.0 && E_Col[i] > 0.0)
         {  E[i] = 3.0;
         }
         else if(E_Row[i] == 0.0 && E_Col[i] == 0.0)
         {  E[i] = 4.0;
         }
         else if(E_Row[i] == 0.0 && E_Col[i] < 0.0)
         {  E[i] = 5.0;
         }
         else if(E_Row[i] < 0.0 && E_Col[i] > 0.0)
         {  E[i] = 6.0;
         }
         else if(E_Row[i] < 0.0 && E_Col[i] == 0.0)
         {  E[i] = 7.0;
         }
         else if(E_Row[i] < 0.0 && E_Col[i] < 0.0)
         {  E[i] = 8.0;
         }
      }
   }
}

Este código se aplica estrictamente a nuestro entorno de 9 índices y no se puede utilizar en matrices de entorno de diferentes tamaños. Para definir esta matriz de entorno, utilizamos un parámetro de entrada adicional denominado "escala". Esta escala ayuda a proporcionar o ratioar nuestro horizonte de largo plazo con nuestra ventana de marco de corto plazo. El valor predeterminado para esto es 5, lo que significa que en un eje de la matriz de entorno marcamos el estado como alcista, plano o bajista en función de los cambios en el precio durante un período que es 5 veces más largo que otro período cuyos valores están "graficados" en el otro eje. Digo “graficados” porque estos dos ejes simplemente proporcionan puntos de coordenadas para el estado actual. La indexación de 0 a 8 es simplemente un aplanamiento de esta matriz en una matriz, pero como puede ver en el código fuente adjunto, la referencia continua a 'row' y 'col' simplemente apunta a las posibles lecturas de coordenadas 'x' e 'y' de la matriz de entorno que definen el estado actual.

El mapa Q-Learning reproduce esta serie de estados del entorno añadiendo una ponderación para las posibles acciones a tomar en cualquiera de estos estados del entorno. Como en nuestro caso estamos considerando 3 posibles acciones que se pueden tomar en cada estado, a saber, comprar, vender o no hacer nada, cada estado del mapa de Q-Learning tiene una matriz de 3 tamaños que guarda la puntuación de qué acción es la más adecuada. Cuanto mayor sea el valor de la puntuación, más adecuado será. La otra entidad principal en nuestro diagrama de ciclo anterior es el observador, a quien nos referiremos como el “critic”. Es el crítico el primero en encargarse de determinar las "recompensas" por las acciones del actor. ¿Y qué son las recompensas? Bueno, esto dependerá de para qué se use el aprendizaje de refuerzo, pero para nuestros propósitos, en función de las 3 acciones posibles del actor, utilizamos las ganancias del valor del tick bruto provenientes del cambio de precio como recompensa.

Entonces, si este cambio de precio es negativo y nuestra última acción fue vender, entonces la magnitud de este cambio actúa como una recompensa. Lo mismo se aplicaría si el cambio es positivo después de una acción de compra anterior. Sin embargo, si la última acción fue una compra y tenemos un cambio de precio negativo, entonces el tamaño de este valor negativo actúa como una penalización de la misma manera que los cambios de precio después de una venta siempre se multiplican por menos, lo que significa que cualquier producto negativo resultante actuaría como una penalización para nuestras acciones en ese estado particular (que es nuestro entorno o la indexación de la acción del precio a corto y largo plazo del mercado).  

Sin embargo, este valor de recompensa debe normalizarse y es por eso que utilizamos la función CriticRreward que lo mantiene en el rango de 0,0 a 1,0. Todos los valores negativos están entre 0,0 y 0,5, mientras que los valores positivos están normalizados entre 0,5 y 1,0. El código fuente que hace esto se proporciona a continuación:

//+------------------------------------------------------------------+
// Normalize reward via off-policy
//+------------------------------------------------------------------+
double Cql::CriticReward(double MaxProfit, double MaxLoss, double Float)
{  double _reward = 0.0;
   if(MaxProfit >= Float && Float >= MaxLoss && MaxLoss < MaxProfit)
   {  _reward = (Float - MaxLoss) / (MaxProfit - MaxLoss);
   }
   return(_reward);
}

La actualización del valor de la recompensa siempre ocurrirá a mitad del proceso de entrenamiento y no al principio. Esto implica que debemos pasar constantemente parámetros que actualicen los valores de reward-max, reward-min y reward-float a la función de retropropagación para que puedan incorporarse al proceso. Para lograr esto, comenzamos modificando la estructura de aprendizaje, que se utiliza para almacenar variables de aprendizaje que se pueden llamar en cada ejecución de retropropagación. El uso de una estructura en realidad hace que nuestro código sea fácilmente modificable, ya que solo tenemos que agregar las nuevas variables adicionales que necesitamos a la lista existente de variables dentro de la estructura. Esto es claramente menos propenso a errores y contrasta marcadamente con tener que modificar la lista de parámetros de entrada en una función que requiere las variables en esta estructura. Entonces ciertamente sería difícil de manejar. La estructura de aprendizaje modificada ahora se ve de la siguiente manera:

//+------------------------------------------------------------------+
//| Learning Struct                                                  |
//+------------------------------------------------------------------+
struct Slearning
{  Elearning         type;
   int               epochs;
   double            rate;
   double            initial_rate;
   double            prior_rate;
   double            min_rate;
   double            decay_rate_a;
   double            decay_rate_b;
   int               decay_epoch_steps;
   double            polynomial_power;
   double            ql_reward_max;
   double            ql_reward_min;
   double            ql_reward_float;
   vector            ql_e;

                     Slearning()
   {  type = LEARNING_FIXED;
      rate = 0.005;
      prior_rate = 0.1;
      epochs = 50;
      initial_rate = 0.1;
      min_rate = __EPSILON;
      decay_rate_a = 0.25;
      decay_rate_b = 0.75;
      decay_epoch_steps = 10;
      polynomial_power = 1.0;
      ql_reward_max = 0.0;
      ql_reward_min = 0.0;
      ql_reward_float = 0.0;
      ql_e.Init(1);
      ql_e.Fill(0.0);
   };
                    ~Slearning() {};
};

Además, tenemos que realizar algunos cambios en la función de retropropagación en el momento en que llamamos a la función de pérdida. Esto se debe a que ahora hemos introducido una enumeración nueva o subordinada para las funciones de pérdida, cuyo listado es el siguiente:

//+------------------------------------------------------------------+
//| Custom Loss-Function Enumerator                                  |
//+------------------------------------------------------------------+
enum Eloss
{  LOSS_TYPICAL = -1,
   LOSS_SVR = 1,
   LOSS_QL = 2
};

Una de las enumeraciones es 'LOSS_SVR', que se ocupa de medir la pérdida mediante la regresión de vectores de soporte, un enfoque que abordamos en el último artículo. Los otros dos son 'LOSS_TYPICAL', que cuando se selecciona toma como valor predeterminado la lista de funciones de pérdida integradas en MQL5, y el otro es 'LOSS_QL', donde QL significa Q-Learning y cuando se selecciona esta opción, el aprendizaje de refuerzo con Q-Learning informa el proceso de aprendizaje al proporcionar un vector objetivo (o etiqueta) con el que se pueden comparar los pronósticos de MLP. Las cláusulas 'If' dentro de la función de retropropagación verifican esto de la siguiente manera:

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  

   ...

   if(THIS.loss_custom == LOSS_SVR)
   {  _last_loss = SVR_Loss();
   }
   else if(THIS.loss_custom == LOSS_QL)
   {  double _reward = QL.CriticReward(Learning.ql_reward_max, Learning.ql_reward_min, Learning.ql_reward_float);
      if(QL.act == 0)
      {  _reward *= -1.0;
      }
      else if(QL.act == 1)
      {  _reward = -1.0 * fabs(_reward);
      }
      QL.CriticState(_reward, Learning.ql_e);
      _last_loss = output.LossGradient(QL.Q_Loss(), THIS.loss_typical);
   }
   

...

}

La adición de esta función de pérdida personalizada no necesariamente elimina la necesidad de las antiguas funciones de pérdida que se usaban según las enumeraciones integradas en MQL5. Simplemente hemos cambiado el nombre de pérdida a 'typical_loss' y si la entrada 'custom_loss' es 'LOSS_TYPICAL' entonces se deberá proporcionar este valor.

Una vez normalizado el valor de la recompensa, se utiliza para actualizar el mapa Q-Learning en la función CriticState. La actualización de los valores Q se rige por la siguiente fórmula:

Donde:

• Q(s,a): El valor 'Q' para tomar la acción a en el estado 's'. Esto representa la recompensa futura esperada para ese par estado-acción.
• α: La tasa de aprendizaje, un valor entre 0 y 1, que controla en qué medida la información nueva anula la información anterior. Un 'α' más pequeño significa que el agente aprende más lentamente, mientras que un 'α' más grande lo hace más receptivo a experiencias recientes.
• r: La recompensa más reciente recibida después de realizar la acción a en el estado 's'.
• γ: El factor de descuento, un valor entre 0 y 1, que descuenta las recompensas futuras. Un 'γ' más alto hace que el agente valore más las recompensas a largo plazo, mientras que un 'γ' más bajo hace que se centre más en las recompensas inmediatas.
• max a′ Q(s′,a′): El valor 'Q' máximo para el siguiente estado 's′' sobre todas las posibles acciones 'a′' Representa la estimación del agente de la mejor recompensa futura posible a partir del siguiente estado 's′'.

Y la actualización real del mapa de Q-Learning se puede implementar en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
// Update Q-value using off-policy (Q-learning formula)
//+------------------------------------------------------------------+
void Cql::CriticState(double Reward, vector &E)
{  int _e_row_new = 0, _e_col_new = 0;
   SetMarkov(int(E[E.Size() - 1]), _e_row_new, _e_col_new);
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   e_row[0] = _e_row_new;
   e_col[0] = _e_col_new;
   int _new_best_q = Action();
   double _weighting = Q[e_row[0]][e_col[0]][_new_best_q];
   if(THIS.use_markov)
   {  LetMarkov(e_row[1], e_col[1], E);
      int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _weighting *= markov[_old_index][_new_index];
   }
   Q[e_row[1]][e_col[1]][act] += THIS.alpha * (Reward + (THIS.gamma * _weighting) - Q[e_row[1]][e_col[1]][act]);
}

Al actualizar el mapa, se aplica la regla fuera de política de actualización donde se utiliza la mejor acción del siguiente estado para actualizar la acción anterior. Esto contrasta con la acción según la política, donde la acción actual se utiliza en el siguiente estado para realizar la misma actualización. Esto se debe a que para cualquier estado, que está definido por una coordenada de fila y una coordenada de columna dentro de la matriz de entorno, existe una matriz estándar de posibles acciones que el agente puede realizar. Y con actualizaciones fuera de política, que es lo que utiliza Q-Learning, se elige la acción con mejor ponderación; sin embargo, con algoritmos que utilizan actualizaciones dentro de la política, la acción actual se mantiene al realizar la actualización. La selección de la mejor acción se realiza a través de la función 'Acción', cuyo código se detalla a continuación:

//+------------------------------------------------------------------+
// Choose an action using epsilon-greedy
//+------------------------------------------------------------------+
int Cql::Action()
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q[e_row[0]][e_col[0]][0];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q[e_row[0]][e_col[0]][i] > _best_value)
         {  _best_value = Q[e_row[0]][e_col[0]][i];
            _best_act = i;
         }
      }
   }
   //update last action
   act = _best_act;
   return(_best_act);
}

El aprendizaje de refuerzo es un poco como el aprendizaje supervisado en el sentido de que hay una métrica de recompensa que se utiliza para ajustar y afinar la ponderación de las acciones en cada estado del entorno. Por otra parte, también es como si se tratara de un aprendizaje no supervisado dado el uso de una matriz de entorno cuyos valores de coordenadas (los dos valores para el índice de fila y el índice de columna) sirven como entradas al MLP que la utiliza. Por lo tanto, el MLP sirve como un clasificador que intenta determinar la distribución de probabilidad correcta para las tres acciones aplicables cuando se presentan las coordenadas del estado del entorno como entradas. Luego, el entrenamiento ocurre como en cualquier clasificador MLP, pero esta vez apuntamos a minimizar la diferencia entre la distribución de probabilidad proyectada del MLP y la distribución de probabilidad en el kernel Q-Learning en las coordenadas del mapa Q-Learning proporcionadas como entrada al MLP.

El papel de las transiciones de Markov

Las cadenas de Markov son modelos estocásticos de probabilidad que utilizan matrices de transición para mapear las probabilidades de pasar de un estado a otro cuando se alimentan con una secuencia de series temporales de estos estados. Estos modelos de probabilidad son inherentemente sin memoria, ya que la probabilidad de transición al siguiente estado se basa únicamente en el estado actual y no en la historia de los estados anteriores. Estas transiciones se pueden utilizar para dar importancia a los distintos estados que se definen dentro de la matriz del entorno.

Ahora bien, la matriz de entorno, de nuestro caso de uso en la señal personalizada, solo considera los tres estados del mercado: alcista, bajista y plano en un horizonte corto y un marco temporal largo, lo que la convierte en una matriz de 3 x 3 que implica nueve estados posibles. Debido a que tenemos nueve estados posibles, esto significa que nuestra matriz de transición de Markov será una matriz de 9 x 9 para mapear las transiciones de un estado del entorno a otro. Por lo tanto, es necesario poder convertir el par de índices de la matriz de entorno en un único índice utilizable en la matriz de transición de Markov. En realidad, terminamos necesitando dos funciones: una para convertir el par de índices de fila y columna del entorno en un solo índice para la matriz de Markov y otra para reconstruir los índices de fila y columna de la matriz de entorno cuando se le presenta un índice de matriz de transición de Markov. Estas dos funciones se denominan GetMarkov y SetMarkov respectivamente y su fuente se proporciona a continuación:

//+------------------------------------------------------------------+
// Getting markov index from environment row & col
//+------------------------------------------------------------------+
int Cql::GetMarkov(int Row, int Col)
{  return(Row + (THIS.environments * Col));
}

Y:

//+------------------------------------------------------------------+
// Getting environment row & col from markov index
//+------------------------------------------------------------------+
void Cql::SetMarkov(int Index, int &Row, int &Col)
{  Col = int(floor(Index / THIS.environments));
   Row = int(fmod(Index, THIS.environments));
}

Necesitamos obtener el índice equivalente de Markov de las coordenadas de los dos estados del entorno al comienzo de la realización de los cálculos de Markov, ya que estaríamos haciendo la transición desde este estado. Una vez que obtenemos ese índice, recuperamos las probabilidades de transición a otros estados a lo largo de esta columna en la matriz de transición, ya que cada uno de ellos sirve como un peso. Como era de esperar, todos suman uno y como el actor ya ha seleccionado el siguiente estado del Q-Map, utilizamos su probabilidad como numerador con un denominador de uno, lo que significa que solo su probabilidad se utiliza como peso para incrementar el nuevo valor en el Q-Map durante el proceso de aprendizaje. El código fuente que implementa esto ya se compartió arriba en la función de estado crítico.

Este proceso de aprendizaje esencialmente descuenta el incremento de aprendizaje en proporción a su probabilidad en la matriz de transición de Markov.

Además, realizamos los cálculos de la matriz de transición cada vez que se registra una nueva barra y la serie temporal de precios recibe una actualización. El código para realizar estos cálculos se proporciona a continuación:

//+------------------------------------------------------------------+
// Function to update markov matrix
//+------------------------------------------------------------------+
void Cql::LetMarkov(int OldRow, int OldCol, vector &E)  //
{  matrix _transitions;  // Count the transitions
   _transitions.Init(markov.Rows(), markov.Cols());
   _transitions.Fill(0.0);
   vector _states;  // Count the occurrences of each state
   _states.Init(markov.Rows());
   _states.Fill(0.0);
// Count transitions from state i to state ii
   for (int i = 0; i < int(E.Size()) - 1; i++)
   {  int _old_state = int(E[i]);
      int _new_state = int(E[i + 1]);
      _transitions[_old_state][_new_state]++;
      _states[_old_state]++;
   }
// Reset prior values to zero.
   markov.Fill(0.0);
// Compute probabilities by normalizing transition counts
   for (int i = 0; i < int(markov.Rows()); i++)
   {  for (int ii = 0; ii < int(markov.Cols()); ii++)
      {  if (_states[i] > 0)
         {  markov[i][ii] = double(_transitions[i][ii] / _states[i]);
         }
         else
         {  markov[i][ii] = 0.0;  // No transitions from this state
         }
      }
   }
}

Al ser una matriz de transición sin memoria, nuestro código anterior siempre comienza con una matriz recién declarada y la variable de clase que contiene las probabilidades también se llena con valores cero para cancelar cualquier historial previo. El enfoque para calcular las transiciones es sencillo, ya que obtenemos un recuento de la secuencia de cada estado en el primer bucle for, y seguimos con otro bucle for que divide los recuentos acumulativos que obtuvimos para cada transición por el número total de estados desde los cuales se realizan las transiciones.

Implementación de la clase de señal personalizada

Como ya se mencionó, utilizamos un MLP que es un clasificador para manejar el pronóstico principal, mientras que el aprendizaje de refuerzo solo cumple un papel subordinado como función de pérdida. El aprendizaje de refuerzo también puede optimizarse o entrenarse para generar señales comerciales utilizables al maximizar las recompensas críticas; sin embargo, eso no es lo que estamos haciendo aquí, en cambio, su función es secundaria al perceptrón multicapa, ya que, como en el aprendizaje supervisado y no supervisado, se utiliza para cuantificar la función objetivo.

Como lo hemos hecho en artículos anteriores donde hemos utilizado MLP, utilizamos los cambios de precios como origen para nuestra entrada de datos. Recordemos que la matriz de entorno utilizada para este artículo es una matriz de 3 x 3 que sirve como una cuadrícula de posibles estados del mercado cuando se pondera en el marco temporal corto y en el marco temporal largo. Cada uno de los ejes para el marco temporal corto y el marco temporal largo tiene métricas o lecturas que van desde el optimismo hasta el plano bajista, que constituyen la cuadrícula de 3 x 3. Y similar a esta matriz es la matriz o mapa Q-Learning que también tiene esta cuadrícula de 3 x 3 con el agregado de un array de posibles acciones, abiertas al actor, que llevan la cuenta de la idoneidad de cada acción para cada estado. Es esta matriz de idoneidad la que sirve como etiqueta u objetivo de entrenamiento para nuestro MLP.

Sin embargo, las entradas al MLP no serán cambios de precios brutos como había sido el caso en nuestros artículos recientes con MLP, sino más bien serán las coordenadas del estado del entorno para el cambio de precio más reciente o actual en el marco temporal corto y largo. El uso de un "marco temporal" aquí es puramente para ilustrar las diferentes escalas de tiempo u horizontes en los que se miden los cambios de precios. We do not have two separate timeframes as inputs to the signal class that guide the measuring of these changes, but rather we have a single input integer parameter that is labelled ‘m_scale’ that is a multiple of how much larger the ‘long-timeframe’ is to the short. Dado que el marco temporal corto utiliza cambios en una única barra de precios, el "marco temporal largo" obtiene sus lecturas de cambio durante un período equivalente a este parámetro de entrada de escala. Este procesamiento se realiza en la función de obtención de salida de la siguiente manera:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalQLM::GetOutput(int &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
         if
         (
            _in_row.Init(m_scale) &&
            _in_row.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, m_scale) &&
            _in_row.Size() == m_scale
            &&
            _in_row_old.Init(m_scale) &&
            _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1 + 1, m_scale) &&
            _in_row_old.Size() == m_scale
            &&
            _in_col.Init(m_scale) &&
            _in_col.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, m_scale) &&
            _in_col.Size() == m_scale
            &&
            _in_col_old.Init(m_scale) &&
            _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale + ii + 1, m_scale) &&
            _in_col_old.Size() == m_scale
         )
         {  _in_row -= _in_row_old;
            _in_col -= _in_col_old;
            vector _in_e;
            _in_e.Init(m_scale);
            MLP.QL.Environment(_in_row, _in_col, _in_e);
            int _row = 0, _col = 0;
            MLP.QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
            _in.Init(__MLP_INPUTS);
            _in[0] = _row;
            _in[1] = _col;
            MLP.Set(_in);
            MLP.Forward();
            if(ii > 0)
            {  vector _target, _target_data;
               if
               (
                  _target_data.Init(2) &&
                  _target_data.CopyRates(m_symbol.Name(), m_period, 8, ii, 2) &&
                  _target_data.Size() == 2
               )
               {  _target.Init(__MLP_OUTPUTS);
                  _target.Fill(0.0);
                  double _type = _target_data[0] - _in_row[1];
                  int _index = (_type < 0.0 ? 0 : (_type > 0.0 ? 2 : 1));
                  _target[_index] = 1.0;
                  MLP.Get(_target);
                  m_learning.ql_e = _in_e;
                  m_learning.ql_reward_float = _in_row[m_scale - 1];
                  m_learning.ql_reward_max = _in_row.Max();
                  m_learning.ql_reward_min = _in_row.Min();
                  if(i == m_epochs && ii == m_train_set)
                  {  MLP.QL.Action();
                  }
                  MLP.Backward(m_learning, i);
               }
            }
            Output = (MLP.output.Max()==MLP.output[0]?0:(MLP.output.Max()==MLP.output[1]?1:2));
         }
      }
   }
}

Entonces, como podemos ver en nuestro código fuente anterior, necesitamos 4 vectores para obtener las lecturas de coordenadas para nuestras entradas MLP. Una vez determinados estos, con la ayuda de la función Environment que convierte los dos cambios de precio en un único índice de Markov y la función SetMarkov que proporciona estas dos coordenadas del índice MARKOV, los completamos en el vector 'in' que es nuestra entrada. El clasificador MLP tiene una arquitectura muy básica de 2-8-3 que representa 2 entradas, una capa oculta de tamaño 8 y 3 salidas que corresponden a las tres posibles acciones abiertas al actor. El resultado del MLP es esencialmente un mapa de probabilidad que proporciona valores para tomar posiciones cortas (por debajo del índice 0), no hacer nada (por debajo del índice 1) y tomar posiciones largas (por debajo del índice 2).

El proceso de entrenamiento de aprendizaje de refuerzo mide qué tan lejos están estos resultados de los vectores similares asociados a cada estado del entorno.  

Resultados del Probador de estrategias

Entonces, como siempre, realizamos optimizaciones y ejecuciones de pruebas con datos de ticks reales simplemente con el propósito de demostrar cómo un Asesor Experto ensamblado a través del asistente MQL5 con esta clase de señal podría realizar sus funciones básicas. Puede encontrar guías sobre el uso del código adjunto con el asistente MQL5 aquí y aquí. En estos artículos no se aborda gran parte del trabajo diligente necesario para preparar el Asesor Experto o el sistema comercial ensamblado para una cuenta real, y se deja en manos del lector. Realizamos corridas en el par GBPJPY para el año 2023 en el marco temporal diario. Hemos introducido cadenas de Markov como una alternativa a la ponderación de los valores del mapa Q-Learning y, por lo tanto, ejecutamos dos pruebas, una sin la ponderación de la cadena de Markov y otra con la ponderación. Y aquí están los resultados:

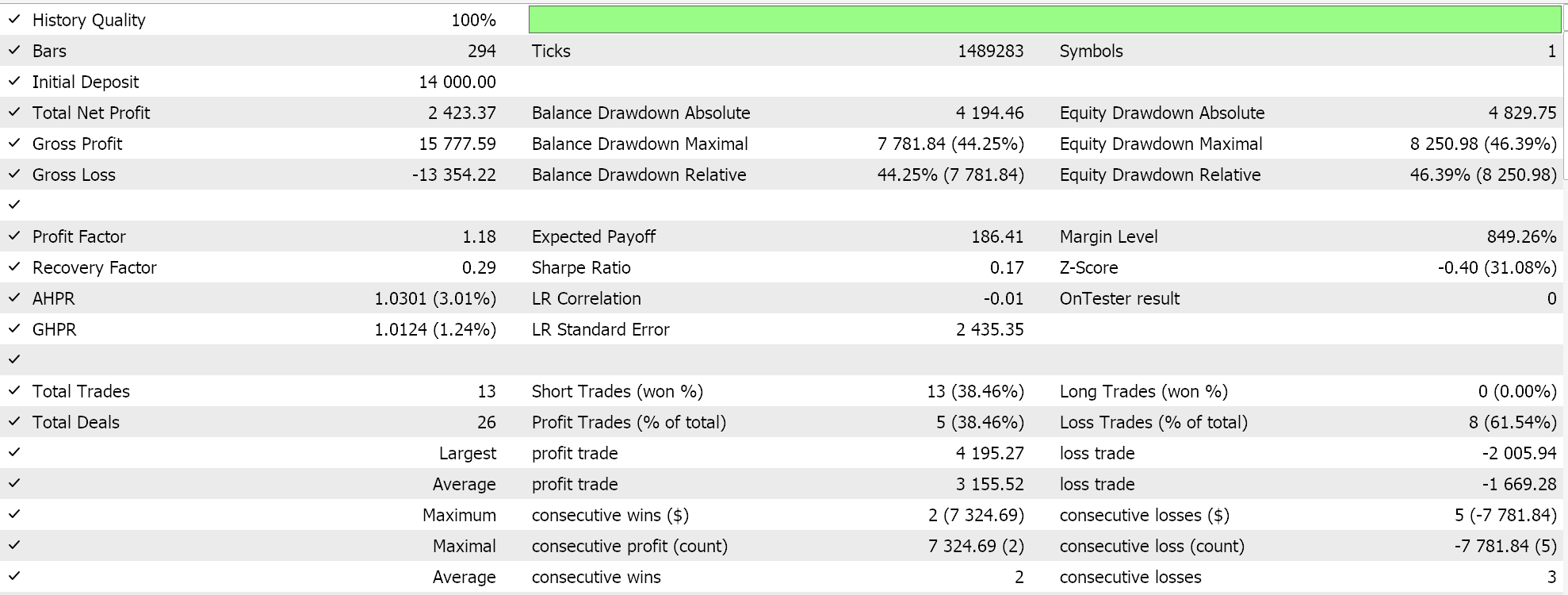
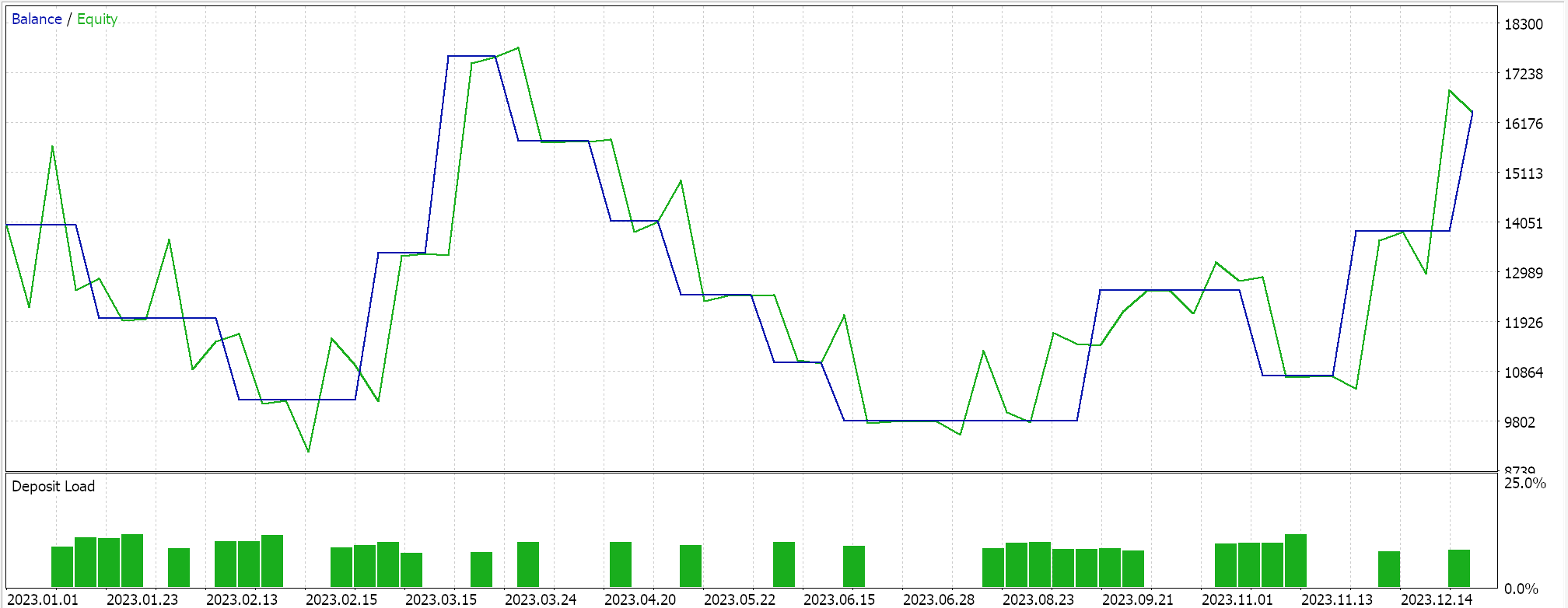
  Y luego los resultados sin ponderación de Markov son:

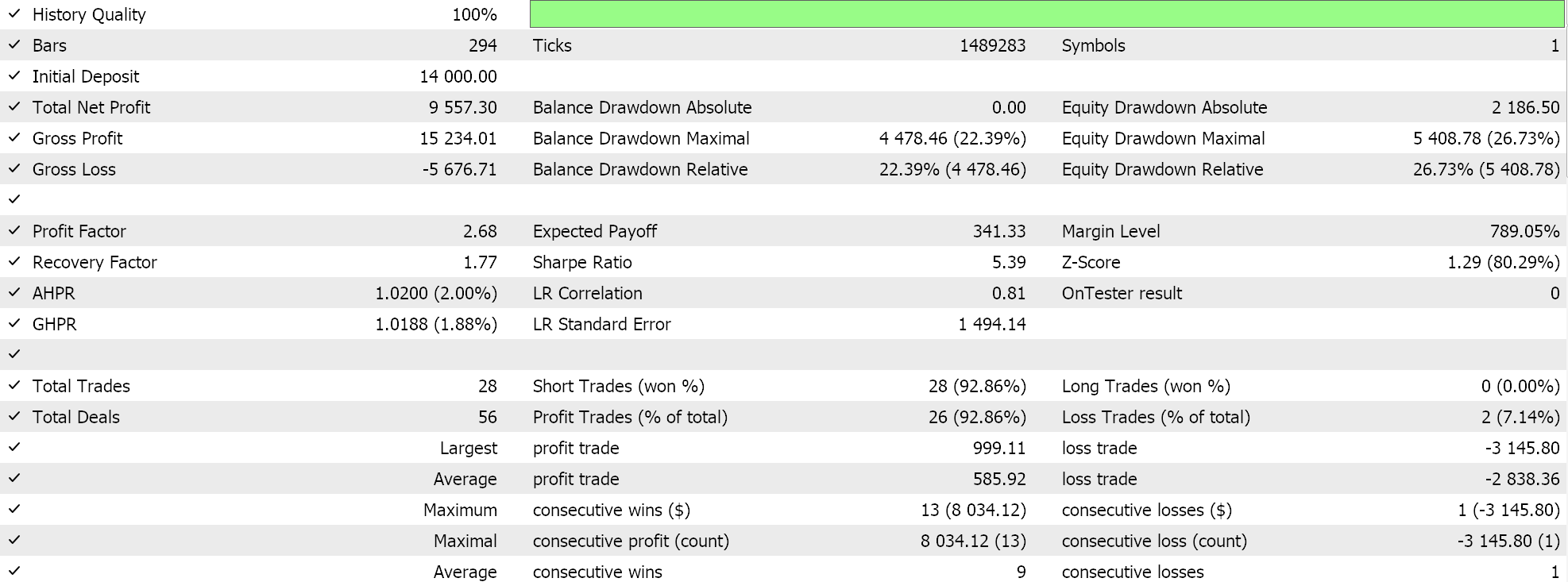
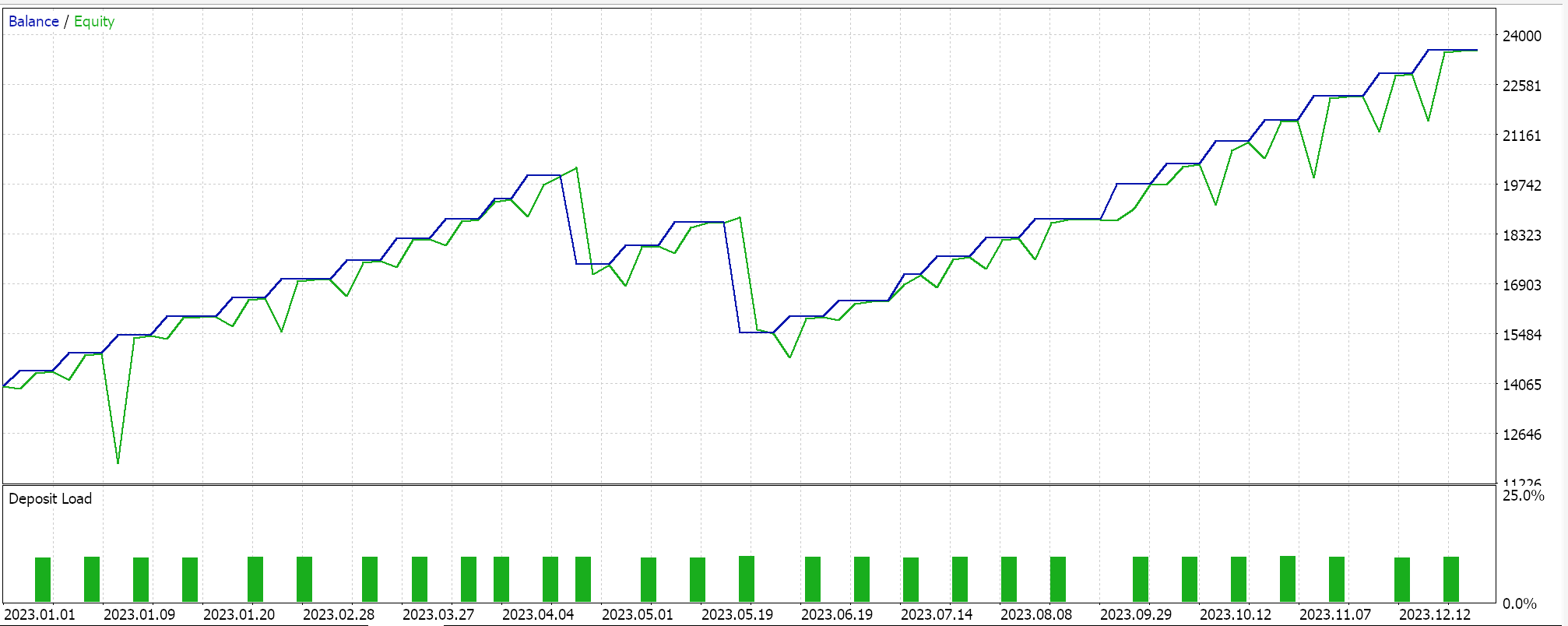
Estos resultados de pruebas no se logran con las mejores configuraciones de optimización ni se realizan pruebas de avance con estas configuraciones; por lo tanto, no son un respaldo para el uso complementario de cadenas de Markov con Q-Learning per se, aunque argumentos sólidos y un régimen de pruebas más completo pueden defender su uso.

Conclusión

En este artículo, destacamos qué más se podría hacer con el asistente MQL5 al introducir el aprendizaje de refuerzo, una alternativa en el entrenamiento de aprendizaje automático además de los métodos establecidos de aprendizaje supervisado y no supervisado. Hemos buscado utilizar esto en el entrenamiento de un clasificador MLP haciendo que informe y guíe el proceso de entrenamiento en lugar de tenerlo como generador de señal bruta, lo que también es posible. Al hacerlo, mientras nos centramos en el algoritmo Q-Learning, explotamos las cadenas de Markov, una matriz de probabilidad de transición que puede actuar como un peso para el proceso de entrenamiento de aprendizaje de refuerzo, y presentamos ejecuciones de prueba de un asesor experto comercial en dos escenarios: cuando se entrena sin las cadenas de Markov y cuando se entrena con ellas.

Creo que esto ha sido un poco más complejo en comparación con mis artículos anteriores, ya que estamos haciendo referencia a 2 clases para nuestra señal personalizada y se han utilizado muchos parámetros de entrada sensibles con sus valores predeterminados sin ningún ajuste importante, es necesario introducir muchos términos nuevos para aquellos que no están familiarizados con el tema. Sin embargo, es el comienzo de nuestro abordaje de este tema amplio y profundo, el aprendizaje por refuerzo, y por eso espero que en futuros artículos, cuando volvamos a tratar este tema, no resulte tan desalentador.