Population optimization algorithms: Fish School Search (FSS)

Contents

1. Introduction
2. Algorithm description
3. Test results

1. Introduction

An aggregation of fish is the general term for any collection of fish that have gathered together in some locality. Fish aggregations can be structured or unstructured. An unstructured aggregation might be a group of mixed species and sizes that have gathered randomly near some local resource, such as food or nesting sites.

If, in addition, the aggregation comes together in an interactive, social way, they may be said to be shoaling. Most of them are in the same phase of their life cycles, are in active contact with each other, and at any moment can exhibit biologically active and organized activities that are useful for members of the group.
In contrast to the individual, the gregarious lifestyle is a compromise between the advantage of living in a group in terms of greater protection from predators and increased competition in obtaining food.

Fish form schools in nature in several ways. As a rule, they prefer larger schools, consisting of individuals only of their own species. Any member of the pack that stands out in its appearance, or has some kind of difference, becomes a prime target for predators. This fact explains why fish prefer schools of identical individuals. This way the homogeneity of the entire school is achieved.

A school is organized quite rigidly when the fish swim synchronously at the same speed and in the same direction. This happens due to the fish being of the same species, age and size moving at a certain distance from each other. Schools of fish are able to perform complex maneuvers, as if they have group intelligence and a common mind.
The subtleties of school formation are far from being fully understood, especially aspects of movement and ways of feeding.

Many hypotheses have been put forward to explain gregarious behavior, including better orientation, hunting synchronization, confusing predators and reduced risk of being caught. Fish in schools seem to share information controlling each other's behavior from a close distance. The feeding behavior of one fish quickly stimulates an active search for food in others. Schooling fish swim in slender phalanxes often making rapid ascents and descents and spinning around their axis, while they change the shape of the school avoiding collisions with each other. Such maneuvers require a very fast response system. A schooling lifestyle implies that fish have sensory systems that can instantly respond to small changes in their position in relation to their neighbor.

To create a more complete picture, mathematical modeling of such behavior is used. The most common mathematical models assume that individual animals in a school follow three basic rules:

1. Move in the same direction as one's neighbor
2. Stay close to neighbors
3. Avoid collisions with neighboring individuals

The question of how schooling fish choose the direction in which to swim remains unresolved. During migrations, it seems that most members of the pack know where to go.If all members of a school are equally aware of the availability of food, there are still certain leaders in the group who are bolder than their other relatives. This schooling behavior prompted many researchers to create not only a mathematical model, but also an algorithmic model for solving various optimization problems.

2. Algorithm description

Fish school search (FSS) is a subfamily of swarm intelligence algorithms belonging to the class of metaheuristic algorithms. It was proposed by Bastos Filho and Lima Neto in 2008 and first published in 2009. In FSS, simple agents are called fish, and each fish has a weight that represents the "success" achieved during the search. The values and variations of the weights affect individual and collective movements. Built-in feeding and coordinated action mechanisms force the school to move in the direction of a positive gradient to gain weight and find the best spots locally and globally. FSS was developed for continuous optimization problems in multimodal search spaces. This also prompted other researchers to propose options for solving other problems, such as optimization in binary problems and multiobjective optimization.

In the FSS algorithm, it can be simplified to imagine that fish swim in a conditional aquarium, the walls of which are the boundaries of the domain of the studied function definition. The fish weight is a measure of success in finding food (solutions). Besides, it plays the role of the fish's memory. The presence of weight is the main idea of the algorithm and the difference from a swarm of particles. This feature of the FSS algorithm eliminates the need to find and fix globally best solutions, as is the case with a swarm of particles.

The FSS algorithm operators are divided into two groups:
- the feeding operator formalizes the success of the area exploration
- swimming operators implement migration algorithms for individual fish and the school as a whole

The feeding operator is a calculation of the weight of the fish. The basic idea is to get the fish to "swim" towards a positive gradient in order to "eat" and "gain weight". Collectively, heavier fish have a greater effect on the overall search process, which causes the center of fish school mass to move towards better locations in the search space over iterations. The weight increment at a given iteration is proportional to the normalized difference in the values of the fitness function:

fishes [f].weight = fishes [f].weight + (fishes [f].delta_fitness / max_delta_fitness);

where:

• weight - fish weight
• delta_fitness - difference between fitness function values
  
• max_delta_fitness - maximum value of the difference in fitness functions among all fish

Floating operators are divided into three types according to the type of movement:

- individual;

- instinctive-collective;

- collective-volitional;

Individual swimming can be interpreted as a local search in the vicinity of the current position of the fish. The motion vector of each individual is directed randomly and has a different value.

fishes [f].new_position [d] = fishes [f].current_position [d] + step_ind [d] * r;

where:

• new_position - new position at the corresponding coordinate
• current_position - current position on the corresponding coordinate
• step_ind - individual move step calculated as

initial_step_ind * (rangeMax [d] - rangeMin [d]);

where:

• initial_step_ind - algorithm parameter for individual movement
• rangeMax and rangeMin - optimized argument value ranges
  
• r - random number [-1.0;1.0]

Schematically, individual swimming is shown in Figure 1.

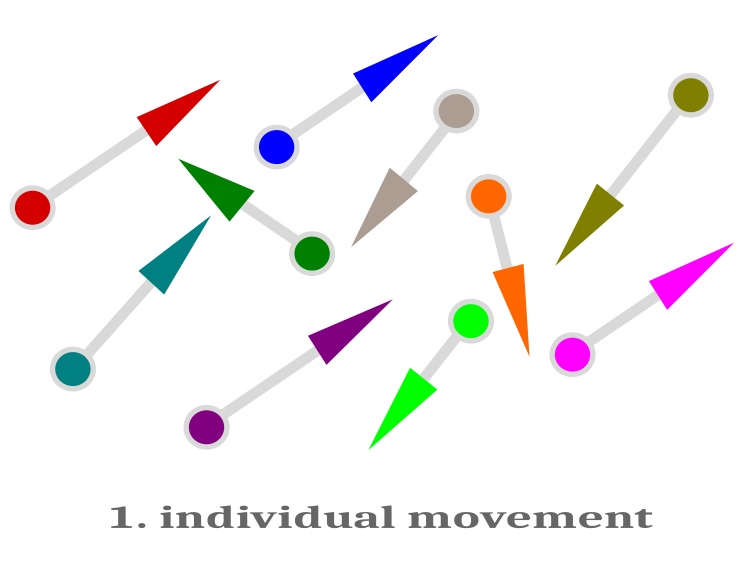
Fig. 1. Individual swimming. The movement vector of each fish is directed in a random direction and has a different scalar value

After individual swimming, the fitness function is measured. If the resulting position of the fish did not improve, then we consider that this particular fish did not have any movement and it remains in place. Only those fish that have improved their fitness functions will move to a new position.

After the completion of the individual swim, the instinctive-collective movement operator is executed. Let's look at Figure 2 first.

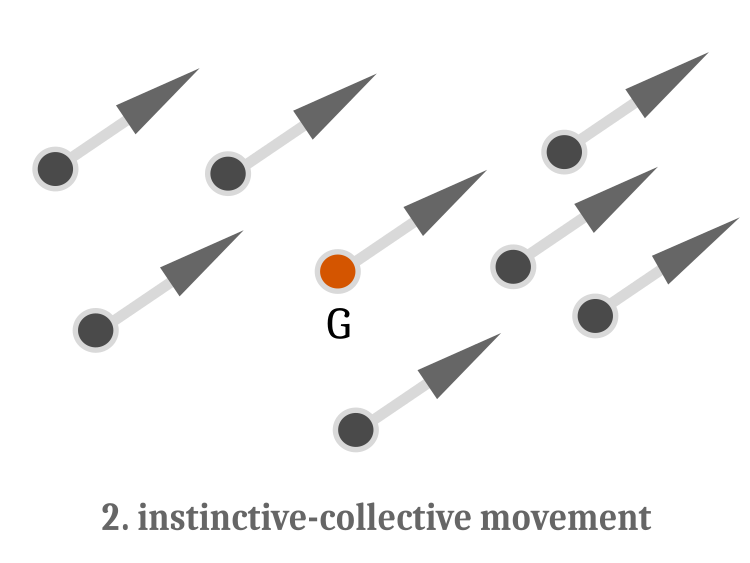
Fig 2. Instinctive-collective swimming The movement is characterized for all fish by the same vector of direction and magnitude relative to the center of mass G.

Instinctive-collective movement serves to correct the general position of the school of fish taking into account the change in the fitness function of each fish at the previous iteration. The new coordinates are calculated as follows:

fishes [f].new_position [d] = fishes [f].current_position [d] + collective_instinct [d];

where:

• new_position - new position of the fish at the corresponding coordinate
• current_position - current position on the corresponding coordinate
• collective_instinct - amount of movement along the corresponding coordinate calculated as:

collective_instinct [d] = fishes [f].delta_position [d] * fishes [f].delta_fitness;

where:

• delta_position - difference between the coordinates of the current and the previous position obtained at the stage of individual swimming
• delta_fitness - change of fitness functions of the current position and the previous one during individual swimming

Instinctive-collective swimming formalizes the group synchronous movement of a school of fish to a new place providing a search for new places of food, while individual movement allows improving the situation locally.

Now let's consider collective-volitional swimming. It is divided into two types:

- from the center of mass - if the improvement in the position of the school as a whole has not occurred compared to the previous position, while the fish spread to the sides symbolizing a further search for food (Figure 3)

- movement to the center of mass if the improvement has occurred. Then the fish move to the center of mass, squeezing the ring and symbolizing the attack on the prey. Algorithmically, this means refining the solution of the optimization problem (Figure 4).

Fig. 3. Collective-volitional swimming. The direction vectors are directed from the center of mass G

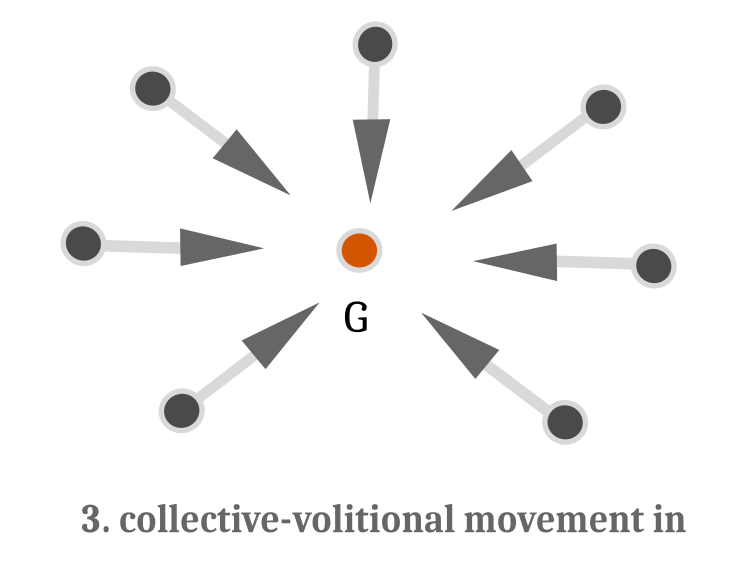
Fig. 4. Collective-volitional swimming. The direction vectors are directed towards the center of mass G

The concept of the center of mass is introduced for the calculation of collective-volitional swimming. From here, the collective-volitional swimming equation will look like this:

fishes [f].new_position [d] = pos + (((pos - barycenter [d]) * step_vol [d] * r) * search_operator);

where:

• pos is the same current_position
• search_operator - 1 if the previous move resulted in a position improvement, and -1 if not
  
• 
  
• step_vol [d] - collective movement step, calculated as:

step_vol [d] = initial_step_vol * (rangeMax [d] - rangeMin [d]);

where:

• initial_step_vol  - algorithm parameter for collective movement
• 
  
• barycenter [d] - center of mass calculated as the sum of fish weights multiplied by the coordinate:

barycenter [d] += fishes [f].weight * fishes [f].current_position [d];

and divided by the total weight of the school of fish:

barycenter [d] /= current_total_weight;

The pseudo code of the algorithm looks like this:

1) initialize fish positions with random numbers

2) individual movements

3) fitness function calculation

4) redefinition of weights for each fish

5) instinctive-collective movement

6) collective-volitional movement

7) recalculate the total weight

8) fitness function calculation

9) repeat from step 2) until the stop criterion is met

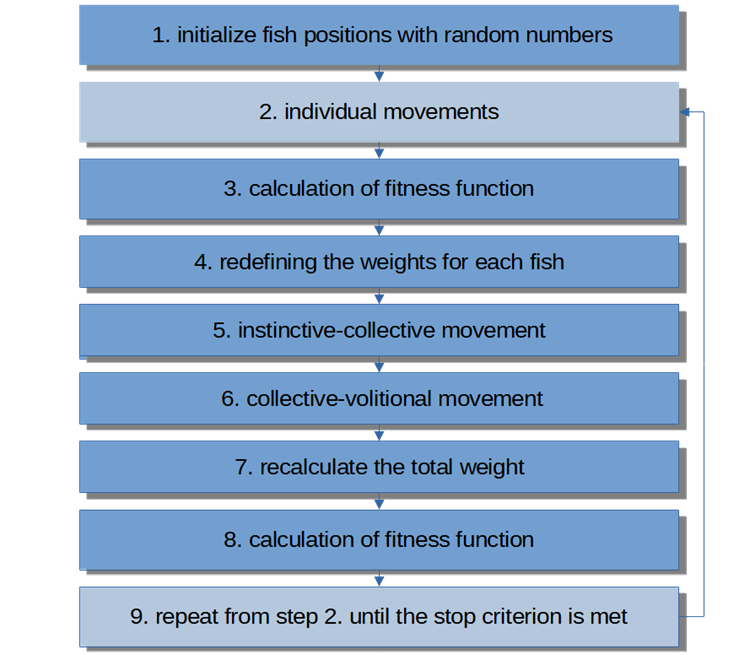
Figure 5. FSS algorithm block diagram

Let's start describing the code.

As you might guess, the simplest logical unit of the algorithm is the structure that describes the fish. Since we will have to initialize the fish several times, it is advisable to “zero out” this structure due to its relatively large size in the special Init () method, which will allow us to slightly optimize the code. The structure includes the arrays of coordinates for the current position, new position, and the difference in coordinates since the last move. The default weight equal to 1000 standard units may have any value. Fish is also characterized by the value of the current fitness function, the previous one and the difference between them. In the Init() method, the fitness function is initialized with the minimum possible 'double' value. So, the fitness difference is zero, since the fish has not yet moved.

//——————————————————————————————————————————————————————————————————————————————
struct S_Fish
{
  void Init (int dimensions)
  {
    ArrayResize (current_position, dimensions);
    ArrayResize (new_position,     dimensions);
    ArrayResize (delta_position,   dimensions);
    weight        = 1000.0;
    fitness       = -DBL_MAX;
    delta_fitness = 0.0;
  }

  double current_position [];
  double new_position     [];
  double delta_position   [];
  double weight;
  double fitness;
  double new_fitness;
  double delta_fitness;
};
//——————————————————————————————————————————————————————————————————————————————

Let's declare the C_AO_FSS class - a school of fish mathematically representing the natural community model. There is nothing unusual here. There are also two public methods required for interaction with the user program - the ranges of values of the optimized function necessary to take into account the coordinates of fish and interaction in a school, as well as the arrays.

In the public method of the Init () initialization class, it is necessary to reset the variables to their original values and allocate memory for arrays. Pay special attention to the init and swimmingRegime variables. According to the pseudo code we saw, the calculation of the fitness function is performed twice: the first time - after an individual movement, the second time - after two types of collective movement. This contradicts the algorithm-application linking scheme adopted by us, which states that each iteration features a sequence: first_method -> calculation_fitness_functions -> second_method. These two variables are applied in order to fix this and change the sequence of actions in the canonical algorithm. The init variable should be 'false' at the beginning of the algorithm. This is a flag that indicates the necessity to initialize the fish, calculate the fitness function and do the movement again, since the entire logic of the algorithm uses the difference between the current and previous value of the coordinates and the fitness function. Without that, we would not have been able to get the value difference. The second important flag is swimmingRegime. It allows us to redefine the order of calling methods that describe the movement of fish so that it matches our structure. The value of 1 corresponds to the call of "individual" swimming, otherwise we use the sequence of group movements we considered above.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::Init (const int    dimensionsP,
                     const int    fishSchSizeP,
                     const double initial_step_indP,
                     const double initial_step_volP)
{
  MathSrand (GetTickCount ());
  init = false;
  swimmingRegime = 1;

  dimensions     = dimensionsP;

  ArrayResize (rangeMax,  dimensions);
  ArrayResize (rangeMin,  dimensions);
  ArrayResize (rangeStep, dimensions);

  num_of_individuos = fishSchSizeP;

  ArrayResize (fishes, num_of_individuos);

  for (int i = 0; i < num_of_individuos; i++)
  {
    fishes [i].Init (dimensions);
  }

  global_best = -DBL_MAX;
  ArrayResize (global_best_position, dimensions);

  total_weight     = num_of_individuos;

  initial_step_ind = initial_step_indP;
  ArrayResize (step_ind, dimensions);

  initial_step_vol = initial_step_volP;
  ArrayResize (step_vol, dimensions);

  ArrayResize (collective_instinct, dimensions);
  ArrayResize (barycenter, dimensions);
}
//——————————————————————————————————————————————————————————————————————————————

The first public method called in each iteration Swimming () determines the sequence of calls to individual and group fish movements. If the method is called for the first time, then the individual and group movement steps are initialized as part of the possible range along the corresponding coordinate by means of the two initial_step_ind and initial_step_vol algorithm parameters. Some authors recommend setting the values to 0.01 and 0.001 respectively. However, I did not get good results with these values. So I use 0.1 and 0.8. Also, at the first run of the algorithm, the current value of the fish position coordinates is initialized with random numbers within the range of optimized parameters. The appropriate movement types will be called during subsequent method calls in accordance with the swimmingRegime flag.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::Swimming (int i)
{
  //----------------------------------------------------------------------------
  if (!init)
  {
    global_best    = -DBL_MAX;
    swimmingRegime = 1;

    for (int d = 0; d < dimensions; d++)
    {
      step_ind [d] = initial_step_ind * (rangeMax [d] - rangeMin [d]);
      step_vol [d] = initial_step_vol * (rangeMax [d] - rangeMin [d]);
    }

    for (int f = 0; f < num_of_individuos; f++)
    {
      fishes [f].Init (dimensions);

      for (int d = 0; d < dimensions; d++)
      {
        fishes [f].new_position [d] = RNDfromCI (rangeMin [d], rangeMax [d]);
        fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
      }
    }
  }
  //----------------------------------------------------------------------------
  else
  {
    switch (swimmingRegime)
    {
    case 1:
      apply_individual_movement ();            //individual movement
      break;
    default:
      apply_instintive_collective_movement (); //instinctively-collective movement
      apply_collective_volitive_movement ();   //collective-volitional movement
      update_total_weight ();                  //recalculate the total weight
      break;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

The second public method called at each iteration Regrouping () is intended primarily to determine the order of calls to the methods of swimming - individual, collective-instinctive, collective-volitional. Additional functionality of the method for ensuring the order of calls is provided by the swimmingRegime flag, which takes the values 1 and 2. This is necessary to redefine the order of calling fish movement methods in the classical version for the structure I have adopted: first_open_method -> _fitness_function_calculation -> second_open_method. Depending on the Init flag, if the algorithm is at the first iteration, we will store the current position of the coordinates and the value of the fitness function for further calculation of their differences, since it is assumed that the method is called after the calculation of the fitness function. If the Init flag indicates that the algorithm is on the second and subsequent iterations, then, after an individual movement, it is necessary to obtain the difference between the current and previous values of the fitness function, as well as the difference between the coordinates of the current and previous positions. The differences are calculated under the condition that the position has improved, otherwise we consider that there was no movement. So, we reset the values of the fish weight to the initial state, and the differences in movements and fitness functions are taken equal to zero. We immediately update the best solution, if it is reached, by calling the updates_optimal_solution() method, as well as apply fish feeding with the apply_feeding() method. If the swimmingRegime flag is not equal to 1, then collective-instinctive and collective-volitional movements were applied. After their execution, set swimmingRegime to 1. An individual movement will be next.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::Regrouping ()
{
  //----------------------------------------------------------------------------
  if (swimmingRegime == 1
  {
    if (!init)
    {
      for (int f = 0; f < num_of_individuos; f++)
      {
        ArrayCopy (fishes [f].current_position, fishes [f].new_position, 0, 0, WHOLE_ARRAY);
        ArrayInitialize (fishes [f].delta_position, 0.0);

        fishes [f].fitness = fishes [f].new_fitness;
        fishes [f].delta_fitness = 0.0;
      }

      init = true;
      return;
    }

    for (int f = 0; f < num_of_individuos; f++)
    {
      //remember the best position for the fish
      if (fishes [f].new_fitness > fishes [f].fitness)
      {
        fishes [f].delta_fitness = fishes [f].new_fitness - fishes [f].fitness; //fabs
        fishes [f].fitness = fishes [f].new_fitness;

        for (int d = 0; d < dimensions; d++)
        {
          fishes [f].delta_position [d] = fishes [f].new_position [d] - fishes [f].current_position [d];
        }

        ArrayCopy (fishes [f].current_position, fishes [f].new_position, 0, 0, WHOLE_ARRAY);
      }
      else
      {
        ArrayInitialize (fishes [f].delta_position, 0.0);
        fishes [f].delta_fitness = 0.0;
      }
    }

    swimmingRegime = 2;
    updates_optimal_solution ();
    apply_feeding ();
    return;
  }

  //----------------------------------------------------------------------------
  swimmingRegime = 1;
  updates_optimal_solution ();
}
//——————————————————————————————————————————————————————————————————————————————

The following simple private method is used to update the best results of the algorithm if they are reached. To do this, we simply compare the fitness values function values of each fish with the global ones. If they are better, then save them.

//——————————————————————————————————————————————————————————————————————————————
// update the best overall solution
void C_AO_FSS::updates_optimal_solution ()
{
  for (int f = 0; f < num_of_individuos; f++)
  {
    if (fishes [f].fitness > global_best)
    {
      global_best = fishes [f].fitness;
      ArrayCopy (global_best_position, fishes [f].current_position, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

We have already considered the equation of the private method that provides individual swimming above. So, everything is simple here: we add an individual step multiplied by a random number in the range from -1.0 to 1.0 to the current coordinates of each fish, which gives an increment both in positive and negative directions. If the optimized parameter values go beyond the range, the border value is set for the coordinate.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_individual_movement ()
{
  // move the fish to new places-----------------------------------------------
  double r = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      r = RNDfromCI (-1.0, 1.0);

      fishes [f].new_position [d] = fishes [f].current_position [d] + step_ind [d] * r;
      fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

The method of feeding should not cause difficulties in understanding. The weight of the fish, in fact, is determined as the quotient of the difference in the fitness-function of the fish itself and the maximum value of the difference among the entire school of fish. However, it may happen that the maximum difference among all fish will be equal to zero. The description of the classical version of the algorithm says that the weight of fish must always be positive. Generally, only cases when the fitness function takes positive values are usually considered, but I did not find practical sense in this requirement. I admit that the weight of fish can take negative values, therefore if the maximum difference of the fitness function (this is the value, to which we must normalize the weight of each fish) is zero among all fish, then the weight of the fish is taken equal to 1.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_feeding ()
{
  double max_delta_fitness = -DBL_MAX;

  //find the maximum weight among fish
  for (int f = 0; f < num_of_individuos; f++)
  {
    if (fishes [f].delta_fitness > max_delta_fitness) max_delta_fitness = fishes [f].delta_fitness;
  }

  //feed the fish
  for (int f = 0; f < num_of_individuos; f++)
  {
    if (max_delta_fitness != 0.0)
    {
      fishes [f].weight = fishes [f].weight + (fishes [f].delta_fitness / max_delta_fitness);
    }
    else fishes [f].weight = 1;
  }
}
//——————————————————————————————————————————————————————————————————————————————

The private method of instinctive-collective movement consists in changing the coordinates of each fish by incrementing by the value of the collective instinct, which in turn is nothing more than the product of the difference in positions on the current and previous iterations by the difference in the fitness function achieved on previous movements. Here, we assign the values of the boundaries when going beyond the boundaries of the optimized parameters.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_instintive_collective_movement ()
{
  double sum_delta_fitness = 0.0;
  for (int f = 0; f < num_of_individuos; f++)
  {
    sum_delta_fitness += fishes [f].delta_fitness;
  }

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      collective_instinct [d] = fishes [f].delta_position [d] * fishes [f].delta_fitness;

      if (sum_delta_fitness != 0.0)
      {
        collective_instinct [d] /= sum_delta_fitness;
      }

      fishes [f].new_position [d] = fishes [f].current_position [d] + collective_instinct [d];
      fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

The private method of collective-volitional swimming, in which the center of mass of a school of fish, as well as the current total weight, are calculated. If the total weight of the school has increased, then the fish begin to move towards the center of mass, otherwise - away from the center. The equation was discussed in detail earlier. The total weight of a school of fish is updated in a special method discussed below.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_collective_volitive_movement ()
{
  //----------------------------------------------------------------------------
  double current_total_weight = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    current_total_weight += fishes [f].weight;
  }

  ArrayInitialize (barycenter, 0.0);

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      barycenter [d] += fishes [f].weight * fishes [f].current_position [d];
    }
  }

  for (int d = 0; d < dimensions; d++)
  {
    barycenter [d] /= current_total_weight;
  }

  //----------------------------------------------------------------------------
  double search_operator = current_total_weight > total_weight ? 1.0 : -1.0;
  double r   = 0.0;
  double pos = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      r = RNDfromCI (0.0, 1.0);
      pos = fishes [f].current_position [d];

      fishes [f].new_position [d] = pos + (((pos - barycenter [d]) * step_vol [d] * r) * search_operator);
      fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Actually, this is the very method of updating the total weight of fish. Everything is simple here. We take the weight of each fish and sum it up.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::update_total_weight ()
{
  total_weight = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    total_weight += fishes [f].weight;
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Test results

Let's move on to the final and most interesting part - the results. The algorithm contains interesting tricks, such as the absence of the need to take into account the global optimum, the introduction of the concepts of the center of mass and instinctive-volitional movement, implying convergence or scatter from the center of the school, depending on whether the position as a whole was improved. All this gave hope for the original behavior of the algorithm on the studied functions.

Generally, there is originality in the behavior in the search area of space, namely there are dispersals of fish into separate parts of space similar to what was observed in the bee algorithm, although a detailed consideration of the equations and the principle of operation of the FSS does not imply the dispersal of the school into separate groups. In general, the algorithm performed poorly, only slightly outperforming the PSO algorithm in terms of the overall result.

If we consider individual tests, FSS still managed to excel in some of them. In particular, on the smooth Skin function, the FSS algorithm turned out to be better than the wolf algorithm, showing good (but not the best) results, which is easy to explain. The algorithm uses the gradient of the surface of the function under study, considered in increments for each of the coordinates, and the change in the fitness function at each iteration. Since the Skin function is smooth, the algorithm "clings" well to surface changes.

As for the Forest function, the algorithm showed results below the average. Smooth changes in the test function to some extent helped the algorithm navigate the space, but it could not find the global maximum. When considering Megacity, then the shortcomings of FSS become even more noticeable. The algorithm really "does not like" it when the function under study does not change in the vicinity of the current position of individual agents, and the algorithm is not able to make long jumps to identify new potentially better places. Therefore, it gets stuck in any local extrema that do not have an increment in the vicinity.

Although the Megacity test is very difficult for any optimization algorithms and the other participants in the comparison table are not much ahead of FSS in general, it is still necessary to recognize the weak abilities of the algorithm on discrete problems. In some tests, the random search showed the best result. As we can see in the animation, no "clustering" can be observed in the algorithm operation. You might remember optimization algorithm "crystallization" described in the previous article.

FSS algorithm results:

2022.12.08 13:14:06.033    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:14:08.388    Test_AO_FSS (EURUSD,M1)    1 Skin's; Func runs 10000 result: 4.892861444841324
2022.12.08 13:14:08.388    Test_AO_FSS (EURUSD,M1)    Score: 0.99391
2022.12.08 13:14:12.557    Test_AO_FSS (EURUSD,M1)    20 Skin's; Func runs 10000 result: 3.11410005347766
2022.12.08 13:14:12.557    Test_AO_FSS (EURUSD,M1)    Score: 0.56920
2022.12.08 13:14:47.176    Test_AO_FSS (EURUSD,M1)    500 Skin's; Func runs 10000 result: 1.20519552002827
2022.12.08 13:14:47.176    Test_AO_FSS (EURUSD,M1)    Score: 0.11341
2022.12.08 13:14:47.176    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:14:49.498    Test_AO_FSS (EURUSD,M1)    1 Forest's; Func runs 10000 result: 1.5057381856551146
2022.12.08 13:14:49.498    Test_AO_FSS (EURUSD,M1)    Score: 0.85172
2022.12.08 13:14:53.825    Test_AO_FSS (EURUSD,M1)    20 Forest's; Func runs 10000 result: 0.21468156279781656
2022.12.08 13:14:53.825    Test_AO_FSS (EURUSD,M1)    Score: 0.12143
2022.12.08 13:15:31.235    Test_AO_FSS (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.056970068652984526
2022.12.08 13:15:31.235    Test_AO_FSS (EURUSD,M1)    Score: 0.03223
2022.12.08 13:15:31.235    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:15:34.066    Test_AO_FSS (EURUSD,M1)    1 Megacity's; Func runs 10000 result: 11.0
2022.12.08 13:15:34.066    Test_AO_FSS (EURUSD,M1)    Score: 0.91667
2022.12.08 13:15:38.467    Test_AO_FSS (EURUSD,M1)    20 Megacity's; Func runs 10000 result: 1.03
2022.12.08 13:15:38.467    Test_AO_FSS (EURUSD,M1)    Score: 0.08583
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.31
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    Score: 0.02583
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    All score for C_AO_FSS: 0.4122477188979048

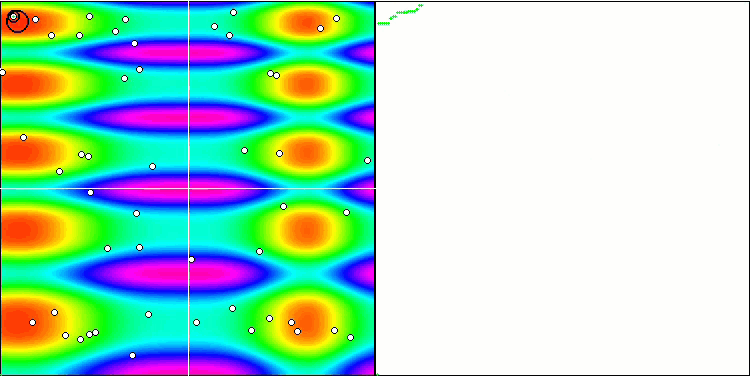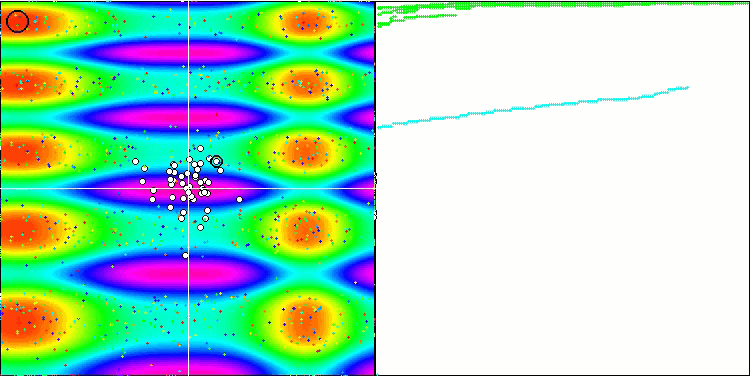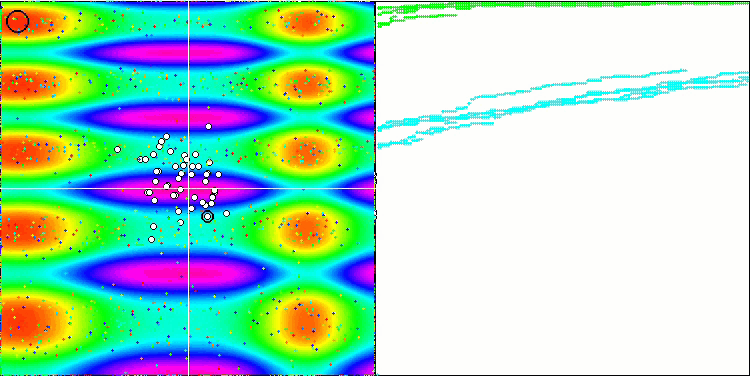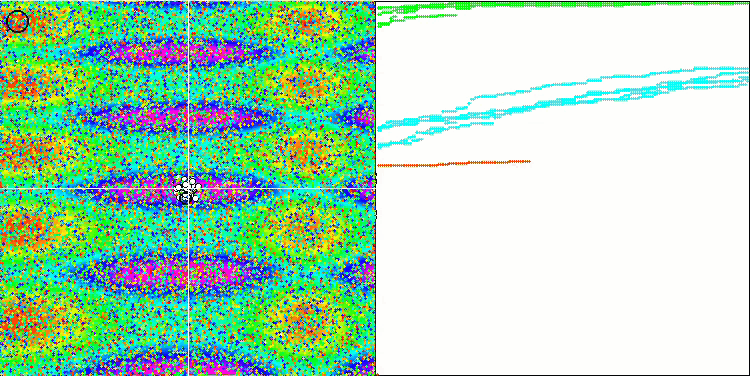
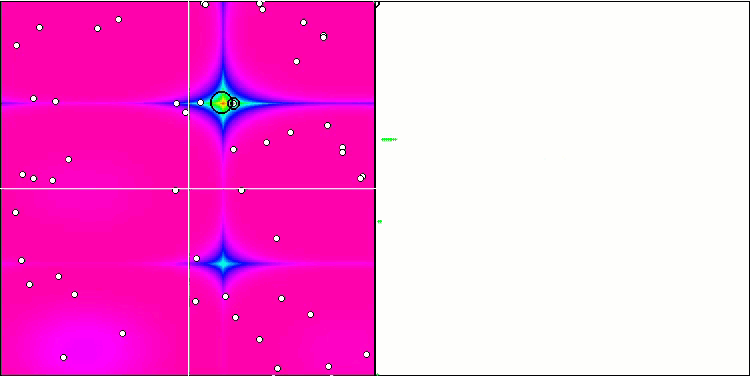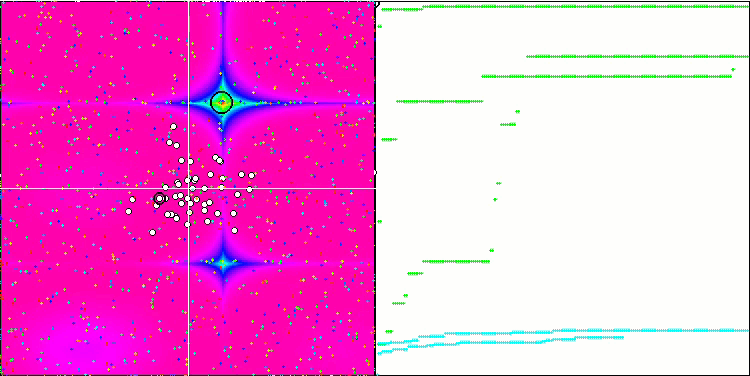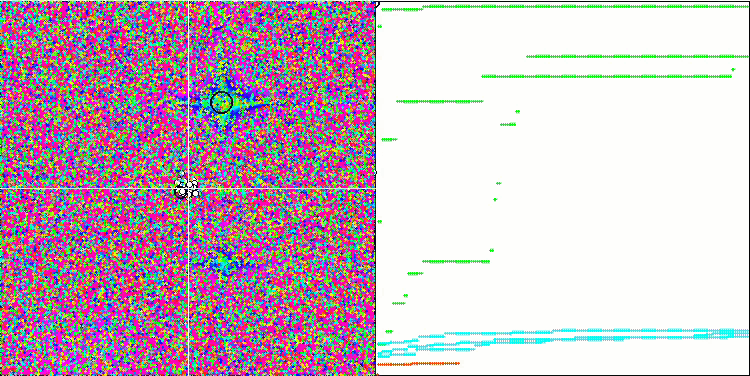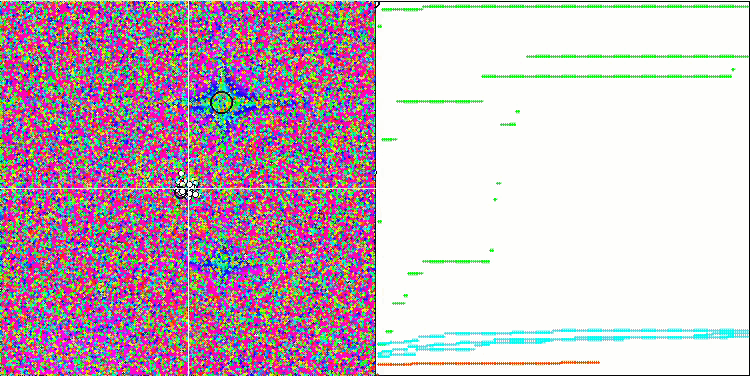
  FSS on the Skin test function.

  FSS on the Forest test function.

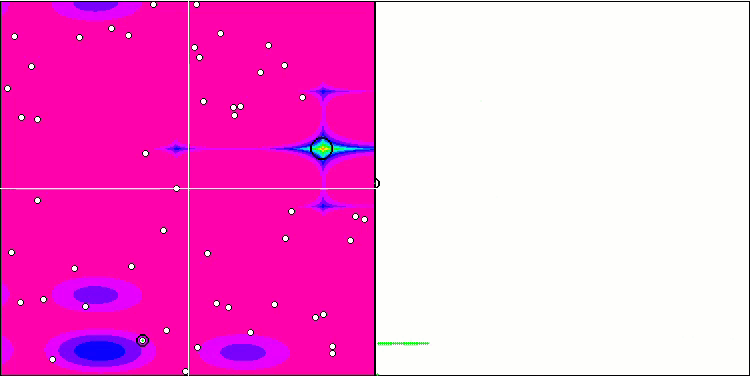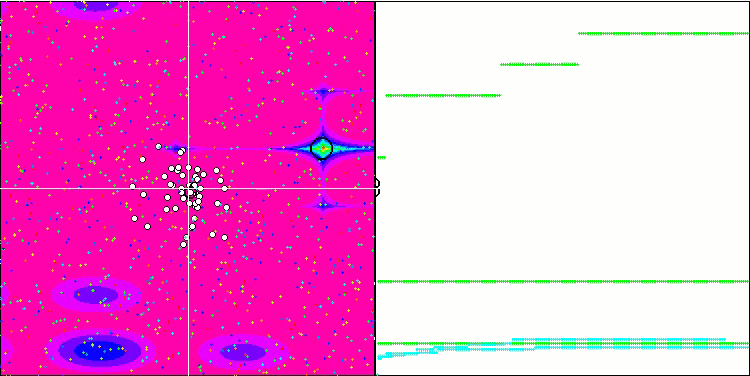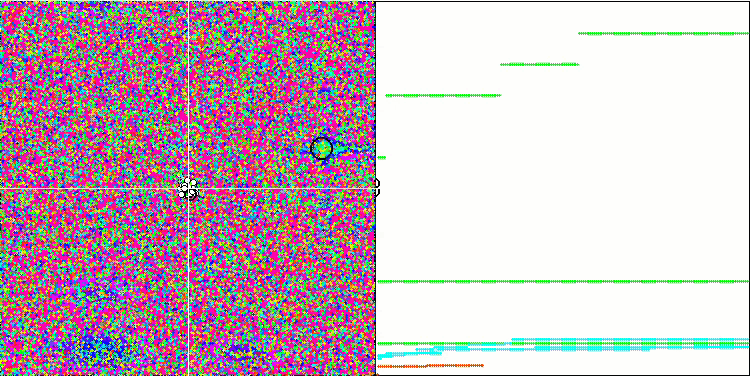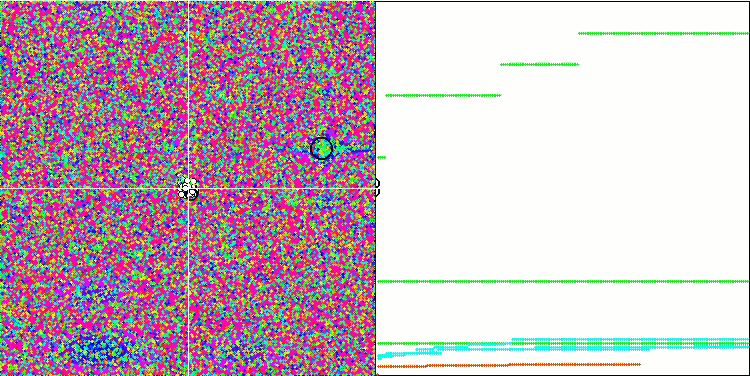
  FSS on the Megacity test function.

Here is the final table. It features additional columns for more convenience in evaluating the algorithms for each test function separately, which allows us to more fairly argue about the applicability of each algorithm for certain tasks.

AO	Description	Skin			Skin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
		2 params (1 F)	40 params (20 F)	1000 params (500 F)		2 params (1 F)	40 params (20 F)	1000 params (500 F)		2 params (1 F)	40 params (20 F)	1000 params (500 F)
COAm	cuckoo optimization algorithm	1.00000	0.85911	0.14316	0.66742	0.99283	0.28787	0.04551	0.44207	1.00000	0.24917	0.03537	0.42818	0.51255778
ACOm	ant colony optimization	0.98229	0.79108	0.12602	0.63313	1.00000	0.62077	0.11521	0.57866	0.38333	0.44000	0.02377	0.28237	0.49805222
ABCm	artificial bee colony M	1.00000	0.63922	0.08076	0.57333	0.99908	0.20112	0.03785	0.41268	1.00000	0.16333	0.02823	0.39719	0.46106556
ABC	artificial bee colony	0.99339	0.73381	0.11118	0.61279	0.99934	0.21437	0.04215	0.41862	0.85000	0.16833	0.03130	0.34988	0.46043000
GWO	grey wolf optimizer	0.99900	0.48033	0.18924	0.55619	0.83844	0.08755	0.02555	0.31718	1.00000	0.10000	0.02187	0.37396	0.41577556
FSS	fish school search	0.99391	0.5692	0.11341	0.55884	0.85172	0.12143	0.03223	0.33513	0.91667	0.08583	0.02583	0.34278	0.41224778
PSO	particle swarm optimisation	0.99627	0.38080	0.05089	0.47599	0.93772	0.14540	0.04856	0.37723	1.00000	0.09333	0.02233	0.37189	0.40836667
RND	random	0.99932	0.44276	0.06827	0.50345	0.83126	0.11524	0.03048	0.32566	0.83333	0.09000	0.02403	0.31579	0.38163222

Stochastic (randomized) heuristic methods do not guarantee a precise solution, but, as a rule, they allow finding solutions close enough for practical use in an acceptable time. However, practice shows that some algorithms are able to demonstrate excellent convergence abilities, although this is not the case with FSS. In general, the search algorithm for a school of fish is a special case of algorithms based on a swarm of particles. Therefore, it inherited both advantages and drawbacks. The unique algorithm features include the division of a school of fish (swarm) into separate groups, which is not observed in the particle swarm. The algorithm copes with smooth functions relatively well, although there is no certainty that FSS will cope well with functions with multiple variables.

Pros:
1. The algorithm handles smooth functions fairly well.
2. The ability of a school of fish to be divided into separate groups, which allows the algorithm to further explore other potentially good local extremes.

Cons:
1. A large scatter of results in individual tests indicates the algorithm instability.
2. Very weak convergence on discrete functions and on functions with breaks. This is almost not applicable for discrete functions.
3. Weak scalability.