Neuronale Netze im Handel: Hierarchische Vektortransformer (HiVT)

Einführung

Die Herausforderungen des autonomen Fahrens überschneiden sich erheblich mit denen der Händler. Die Navigation in dynamischen Umgebungen mit sicheren Manövern ist eine wichtige Aufgabe für autonome Fahrzeuge. Um dies zu erreichen, müssen diese Fahrzeuge ihre Umgebung erfassen und zukünftige Ereignisse auf der Straße vorhersagen. Die genaue Vorhersage der Manöver von Verkehrsteilnehmern in der Nähe, wie z. B. Autos, Fahrrädern und Fußgängern, ist jedoch ein komplexes Problem, vor allem, wenn deren Ziele oder Absichten unbekannt bleiben. In Multi-Agenten-Verkehrsszenarien wird das Verhalten eines Agenten durch komplizierte Interaktionen mit anderen Agenten bestimmt, die durch kartenabhängige Verkehrsregeln noch weiter verkompliziert werden. Es ist daher äußerst schwierig, die verschiedenen Verhaltensweisen mehrerer Akteure in einer Szene zu verstehen.

Neuere Forschungen verwenden einen vektorisierten Ansatz für eine kompaktere Szenendarstellung durch Extraktion von Vektor- oder Punktmengen aus Trajektorien und Kartenelementen. Bestehende vektorisierte Methoden haben jedoch Probleme mit der Bewegungsvorhersage in Echtzeit bei sich schnell ändernden Verkehrsbedingungen. Denn solche Methoden reagieren in der Regel empfindlich auf Verschiebungen des Koordinatensystems. Um dieses Problem zu entschärfen, werden die Szenen so normalisiert, dass sie auf den Zielagenten zentriert sind und mit seiner Bewegungsrichtung übereinstimmen. Dieser Ansatz wird problematisch, wenn die Bewegung einer großen Anzahl von Agenten vorhergesagt werden soll, da die hohen Rechenkosten für die wiederholte Normalisierung der Szene und die Neuberechnung der Merkmale für jeden Zielagenten zu einem Engpass werden. Darüber hinaus modellieren die bestehenden Methoden die Beziehungen zwischen allen Elementen über räumliche und zeitliche Dimensionen hinweg, um detaillierte Interaktionen zwischen vektorisierten Elementen zu erfassen. Dies führt unweigerlich zu einem übermäßigen Rechenaufwand, wenn die Anzahl der Elemente steigt. Da eine genaue Vorhersage in Echtzeit für die Sicherheit des autonomen Fahrens von entscheidender Bedeutung ist, sind viele Forscher bestrebt, diesen Prozess auf die nächste Stufe zu heben, indem sie einen neuen Rahmen entwickeln, der eine schnellere und präzisere Bewegungsvorhersage durch mehrere Agenten ermöglicht.

Ein solcher Ansatz wurde in dem Artikel „HiVT: Hierarchical Vector Transformer for Multi-Agent Motion Prediction“. Diese Methode nutzt Symmetrien und eine hierarchische Struktur für die Vorhersage von Bewegungen mehrerer Agenten. Die Autoren von HiVT zerlegen die Aufgabe der Bewegungsvorhersage in mehrere Stufen und modellieren die Interaktionen zwischen den Elementen hierarchisch mit Hilfe einer auf Transformer basierenden Architektur.

In der ersten Phase vermeidet das Modell die kostspielige Modellierung von Interaktionen zwischen allen Elementen, indem es kontextbezogene Merkmale lokal extrahiert. Die gesamte Szene wird in eine Reihe lokaler Regionen unterteilt, die jeweils auf einen modellierten Agenten zentriert sind. Kontextuelle Merkmale werden aus lokalen vektorisierten Elementen in jeder agenturzentrierten Region extrahiert, die reichhaltige Informationen enthalten, die für den zentralen Agenten relevant sind.

Um die Einschränkungen lokaler Sichtfelder auszugleichen und Abhängigkeiten über große Entfernungen zu erfassen, wird in der zweiten Phase ein globaler Informationsübertragungsmechanismus zwischen agentenzentrierten Regionen eingeführt. Zu diesem Zweck setzen die Autoren einen Transformer ein, der mit geometrischen Verbindungen zwischen lokalen Koordinatensystemen ausgestattet ist.

Die kombinierten lokalen und globalen Darstellungen ermöglichen es dem Decoder, die zukünftigen Trajektorien aller Agenten in einem einzigen Vorwärtsdurchlauf des Modells vorherzusagen. Um die Symmetrie der Aufgabe weiter auszunutzen, führen die Autoren eine Szenendarstellung ein, die gegenüber Verschiebungen des globalen Koordinatensystems invariant ist und relative Positionen zur Beschreibung aller vektorisierten Elemente verwendet. Auf der Grundlage dieser Szenendarstellung implementieren sie rotationsinvariante Kreuzaufmerksamkeitsmodule für räumliches Lernen, die es dem Modell ermöglichen, lokale und globale Darstellungen unabhängig von der Szenenausrichtung zu lernen.

1. HiVT-Algorithmus

Die HiVT-Methode beginnt mit der Darstellung der Straßenszene als eine Sammlung von vektorisierten Elementen. Auf der Grundlage dieser Szenendarstellung aggregiert das Modell hierarchisch raum-zeitliche Informationen. Die Straßenszene besteht aus Agenten und Karteninformationen. Für die strukturierte Darstellung der Szene werden zunächst vektorisierte Elemente extrahiert, darunter Trajektionssegmente von Straßenakteuren und Wegsegmente aus Kartendaten.

Ein vektorisiertes Element ist mit semantischen und geometrischen Attributen verbunden. Im Gegensatz zu früheren vektorisierten Methoden, bei denen die geometrischen Attribute von Agenten oder Wege absolute Punktpositionen enthalten, vermeiden die Autoren absolute Positionen und beschreiben stattdessen geometrische Attribute durch relative Positionen. Dadurch wird die Szene zu einem kompletten Satz von Vektoren. Konkret wird die Flugbahn des Agenten i als „pt,i - pt-1,i“ dargestellt, wobei pt,i der Standort des Agenten i im Zeitschritt t ist.

Für ein Wegsegment xi ist das geometrische Attribut definiert als p1,xi - p0,xi, wobei p0,xi und p1,xi die Anfangs- und Endkoordinaten von xi sind. Die Umwandlung der Punktmenge in eine Menge von Vektoren gewährleistet natürlich Translationsinvarianz. Allerdings gehen die relativen Positionsinformationen zwischen den Elementen verloren. Um räumliche Beziehungen zu erhalten, werden relative Positionsvektoren für Agenten-Agenten- und Agenten-Weg-Paare eingeführt. Zum Beispiel ist der Positionsvektor von Agent j relativ zu Agent i zum Zeitpunkt t ptj - pti, was ihre räumliche Beziehung vollständig beschreibt und gleichzeitig die Translationsinvarianz beibehält. Diese Szenendarstellung stellt sicher, dass alle angewandten Lernfunktionen die Translationsinvarianz einhalten, ohne Informationen zu verlieren.

Um künftige Trajektorien von Agenten in einer hochdynamischen Umgebung genau vorhersagen zu können, muss das Modell räumlich-zeitliche Abhängigkeiten zwischen zahlreichen vektorisierten Elementen effektiv erlernen. Der Transformer hat gezeigt, dass er das Potenzial hat, langfristige Abhängigkeiten zwischen Elementen über verschiedene Aufgaben hinweg zu erfassen. Die direkte Anwendung von Transformers auf raumzeitliche Elemente führt jedoch zu einer Rechenkomplexität von O((NT + L)^2), wobei N, T und L die Anzahl der Agenten, der historischen Zeitschritte bzw. der Wegsegmente sind. Um Informationen aus einer großen Anzahl von Elementen effizient zu extrahieren, faktorisiert HiVT räumliche und zeitliche Dimensionen, indem räumliche Beziehungen in jedem Zeitschritt lokal modelliert werden. Konkret wird der Raum in N lokale Regionen unterteilt, die jeweils auf einen Agenten zentriert sind. Innerhalb jeder lokalen Region wird die lokale Umgebung des zentralen Agenten durch die Trajektorien der benachbarten Agenten und die lokalen Wegsegmente dargestellt. Lokale Informationen werden für jede Region zu einem Merkmalsvektor zusammengefasst, der die Interaktionen zwischen Agenten in jedem Zeitschritt, die zeitlichen Abhängigkeiten zwischen den einzelnen Agenten und die Interaktionen zwischen Agenten und Wege im aktuellen Zeitschritt modelliert. Nach der Aggregation enthält der Merkmalsvektor umfangreiche Informationen über den zentralen Agenten. Dadurch verringert sich die Rechenkomplexität von O((NT + L)^2) auf O(NT^2 + TN^2 + NL) aufgrund der Faktorisierung der räumlichen und zeitlichen Dimensionen und reduziert sich dann weiter auf O(NT^2 + TNk + Nl), indem der Radius der lokalen Regionen begrenzt wird, wenn k < N und l < L.

Während der lokale Kodierer reichhaltige Darstellungen extrahiert, ist sein Informationsvolumen durch lokale Regionen begrenzt. Um eine Verschlechterung der Vorhersagequalität zu verhindern, führen die Autoren ein globales Interaktionsmodul ein, das begrenzte lokale rezeptive Felder kompensiert und die Dynamik auf Szenenebene durch Nachrichtenübermittlung zwischen lokalen Regionen erfasst. Dieses globale Interaktionsmodul erhöht die Ausdruckskraft des Modells mit einem Rechenaufwand von O(N^2) erheblich, was im Vergleich zum lokalen Kodierer relativ leicht ist.

Das Problem der Bewegungsvorhersage durch mehrere Agenten weist Translations- und Rotationssymmetrien auf. Bestehende Methoden renormieren alle vektorisierten Elemente relativ zu jedem Agenten und machen mehrere Vorhersagen pro Agent, um Invarianz zu erreichen. Dieses Paradigma skaliert linear mit der Anzahl der Agenten. Im Gegensatz dazu kann HiVT die Bewegungen aller Agenten in einem einzigen Vorwärtsdurchgang vorhersagen und dabei die Invarianz beibehalten, indem es eine invariante Szenendarstellung und drehungsrobuste räumliche Lernmodule verwendet.

Das Agenten-Agenten-Interaktionsmodul erfasst die Beziehungen zwischen den zentralen und den benachbarten Agenten in jeder lokalen Region in jedem Zeitschritt. Um Problemsymmetrien auszunutzen, schlagen die Autoren einen rotationsinvarianten Block einer Kreuzaufmerksamkeit vor, der räumliche Informationen zusammenfasst. Konkret verwenden sie das letzte Trajektorensegment des zentralen Agenten pT,i — pT-1,i als Referenzvektor für die lokale Region und drehen alle lokalen Vektoren entsprechend der Referenzorientierung ʘi. Die gedrehten Vektoren und ihre zugehörigen semantischen Attribute werden mit einem mehrschichtigen Perzeptron (MLP) verarbeitet, um Einbettungen für den zentralen Agenten zti und jeden benachbarten Agenten ztij zu jedem Zeitschritt t zu erhalten.

Da alle geometrischen Attribute relativ zum zentralen Agenten normalisiert werden, bevor sie in den MLP eingespeist werden, sind diese Einbettungen drehungsinvariant. Zusätzlich zu den Bahnsegmenten enthält die Eingabefunktion фnbr(•) auch die relativen Positionsvektoren der benachbarten Agenten in Bezug auf den zentralen Agenten, wodurch die Einbettung der Nachbarn räumlich bewusst wird. Die Einbettung des zentralen Agenten wird dann in einen Abfragevektor(Query) umgewandelt, während die Einbettungen der Nachbarn zur Berechnung von Schlüssel- (Key) und Wertentitäten (Value) verwendet werden. Die resultierenden Entitäten werden im Aufmerksamkeitsblock verwendet.

Im Gegensatz zum klassischen Transformer schlagen die Autoren von HiVT eine Merkmalsfusionsfunktion vor, die Umweltmerkmale mit den Merkmalen des zentralen Agenten zti. integriert. Dadurch kann der Aufmerksamkeitsblock die Aktualisierung von Merkmalen besser kontrollieren. Ähnlich wie die ursprüngliche Transformer-Architektur kann der vorgeschlagene Aufmerksamkeitsblock auf mehrere Aufmerksamkeitsköpfe erweitert werden. Die Ausgabe des mehrköpfigen Aufmerksamkeitsblocks wird durch einen MLP-Block geleitet, um die räumliche Einbettung sti des Agenten i im Zeitschritt t zu erhalten.

Darüber hinaus verwenden die Autoren der Methode eine Datennormalisierung nach Schichten vor jedem Block und Restverbindungen nach jedem Block. In der Praxis kann dieses Modul durch effiziente parallele Lernoperationen über alle lokalen Regionen und Zeitschritte hinweg implementiert werden.

Die weitere Erfassung der zeitlichen Informationen jeder lokalen Region erfolgt über einen temporalen Transformer-Encoder, der dem Agenten-Agenten-Interaktionsmodul folgt. Für jeden zentralen Agenten i besteht die Anfangssequenz dieses Moduls aus Einbettungen sti, die vom Agenten-Agenten-Interaktionsmodul in verschiedenen Zeitschritten empfangen werden. Die Autoren der Methode fügen ein zusätzliches trainierbares Token sT+1 an das Ende der ursprünglichen Sequenz an. Dann fügen sie die erlernbare Positionskodierung zu allen Token hinzu und platzieren die Token in einer Matrix Si, die in den zeitlichen Aufmerksamkeitsblock eingespeist wird.

Das zeitliche Lernmodul besteht ebenfalls aus abwechselnden Blöcken mit mehrköpfiger Aufmerksamkeit und MLP-Blöcken.

Die lokale Struktur der Karte kann auf die zukünftigen Absichten des zentralen Agenten hinweisen. Daher werden der Einbettung des zentralen Agenten lokale Karteninformationen hinzugefügt. Dazu werden zunächst die lokalen Straßensegmente und die Vektoren der relativen Positionen der Straßenagenten im aktuellen Zeitschritt T gedreht. Die gedrehten Vektoren werden dann mit einem MLP kodiert. Unter Verwendung der raum-zeitlichen Merkmale des zentralen Agenten als Abfrage (Query) und der mit einem MLP kodierten Straßenabschnittsmerkmale als Schlüssel-Wert-Vektoren wird die Kreuzaufmerksamkeit des Agenten-Straße ähnlich wie die oben beschriebenen Ansätze implementiert.

Die Autoren der Methode wenden zusätzlich einen MLP-Block an, um das endgültige lokale Embedding hi des zentralen Agenten i zu erhalten. Nach der sequentiellen Modellierung von Agenten-Agenten-Interaktionen, zeitlichen Abhängigkeiten und Agenten-Straßen-Interaktionen kapseln die Einbettungen angereicherte Informationen in Bezug auf die zentralen Agenten der lokalen Regionen ein.

In der nächsten Stufe des HiVT-Algorithmus werden die lokalen Einbettungen innerhalb des globalen Interaktionsmoduls verarbeitet, um weitreichende Abhängigkeiten in der Szene zu erfassen. Da lokale Merkmale in agenten-zentrierten Koordinatensystemen extrahiert werden, muss das globale Interaktionsmodul die geometrischen Beziehungen zwischen verschiedenen Frames berücksichtigen, wenn Informationen über lokale Regionen hinweg ausgetauscht werden. Um dies zu erreichen, erweitern die Autoren den Transformer-Encoder, um Unterschiede zwischen lokalen Koordinatensystemen einzubeziehen. Bei der Übermittlung von Informationen von Agent j an Agent i verwenden die Autoren ein MLP, um eine paarweise Einbettung zu erhalten, die dann in die Vektortransformation einbezogen wird.

Um paarweise globale Interaktionen zu modellieren, wird derselbe räumliche Aufmerksamkeitsmechanismus wie im lokalen Encoder angewendet, gefolgt von einem MLP-Block, der eine globale Repräsentation für jeden Agenten ausgibt.

Die vorhergesagte Bewegung von Verkehrsteilnehmern ist von Natur aus multimodal. Daher schlagen die Autoren vor, die Verteilung der zukünftigen Trajektorien als Mischmodell zu parametrisieren, bei dem jede Komponente einer Laplace-Verteilung folgt. Die Vorhersagen werden für alle Agenten in einem einzigen Durchgang erstellt. Für jeden Agenten i jeder Komponente f nimmt MLP lokale und globale Repräsentationen als Eingaben. Es gibt dann den Standort des Agenten und die damit verbundene Unsicherheit in jedem zukünftigen Zeitschritt im lokalen Koordinatensystem aus. Der Ausgangstensor des Regressionskopfes hat die Dimensionen [F, N, H, 4], wobei F die Anzahl der Mischungskomponenten, N die Anzahl der Agenten in der Szene und H der Vorhersagehorizont in zukünftigen Zeitschritten ist. Auch hier wird eine MLP verwendet. Es folgt eine SoftMax-Funktion, die die Koeffizienten des Mischmodells für jeden Agenten bestimmt.

Im Folgenden wird die Visualisierung der HiVT-Methode durch die Autoren vorgestellt.

2. Implementation in MQL5

Wir haben den von den HiVT-Autoren vorgeschlagenen umfassenden Algorithmus überprüft. Wir wenden uns nun dem praktischen Aspekt der Umsetzung unserer Interpretation dieser Methoden mit MQL5 zu.

Es ist wichtig, darauf hinzuweisen, dass sich die von den HiVT-Autoren vorgeschlagenen Ansätze erheblich von den Mechanismen unterscheiden, die wir bisher verwendet haben. Infolgedessen steht uns ein erheblicher Arbeitsaufwand bevor.

2.1 Vektorisierung des Ausgangszustands

Wir beginnen damit, den Prozess der Zustandsvektorisierung zu organisieren. Natürlich haben wir zuvor verschiedene Algorithmen zur Zustandsvektorisierung erforscht, darunter die stückweise lineare Darstellung von Zeitreihen, die Datensegmentierung und verschiedene Einbettungstechniken. In diesem Fall schlagen die Autoren jedoch einen radikal anderen Ansatz vor. Wir werden sie auf der OpenCL-Seite im Kernel HiVTPrepare implementieren.

__kernel void HiVTPrepare(__global const float *data,
                          __global float2 *output
                         )
  {
   const size_t t = get_global_id(0);
   const size_t v = get_global_id(1);
   const size_t total_v = get_global_size(1);

In den Kernel-Parametern verwenden wir nur zwei Zeiger auf globale Datenpuffer: einen für die Eingabewerte und einen für die Operationsergebnisse.

Es ist wichtig zu beachten, dass wir im Gegensatz zu den Eingabedaten den Vektortyp float2 für den Ergebnispuffer verwenden. Bisher haben wir diesen Typ für komplexe Werte verwendet. In diesem Fall verwenden wir jedoch nicht die Mathematik der komplexen Zahlen. Die Wahl dieses Datentyps ist vielmehr auf die Notwendigkeit zurückzuführen, die Drehung der Szene in einem zweidimensionalen Raum zu behandeln. Die Verwendung eines Vektors mit zwei Elementen ermöglicht es uns, Koordinaten und Verschiebungen in der Ebene zu speichern.

Wie Sie vielleicht bemerkt haben, enthalten die Kernel-Parameter keine expliziten Konstanten, die die Dimensionen der Eingabe- und Ausgabetensoren definieren. Wir planen, diese Informationen aus dem zweidimensionalen Aufgabenraum abzuleiten. Die erste Dimension gibt die Tiefe des analysierten Verlaufs an, während die zweite Dimension die Anzahl der univariaten Zeitreihen in der zu verarbeitenden multimodalen Sequenz angibt.

Dieser Ansatz basiert auf der Annahme, dass unsere multimodale Sequenz aus einer Sammlung von eindimensionalen univariaten Zeitreihen besteht.

Innerhalb des Kernelkörpers identifizieren wir den aktuellen Thread über alle Dimensionen des Aufgabenraums hinweg. Anschließend werden die Offset-Konstanten in den globalen Datenpuffern entsprechend festgelegt.

   const int shift_data = t * total_v;
   const int shift_out = shift_data * total_v;

Um den Offset im Ergebnispuffer zu verdeutlichen, lohnt es sich, ein wenig über den Algorithmus zu erzählen, den wir in diesem Kernel zu implementieren planen.

Wie bereits im theoretischen Teil erwähnt, schlugen die Autoren der HiVT-Methode vor, die absoluten Werte durch relative Werte zu ersetzen und die Szene um den zentralen Agenten zu drehen.

Dieser Logik folgend, bestimmen wir zunächst den Bias jedes Agenten zu einem bestimmten Zeitpunkt.

   float value = data[shift_data + v + total_v] - data[shift_data + v];

Anschließend berechnen wir den Neigungswinkel der erhaltenen Verschiebung. Für die Bestimmung des Neigungswinkels in einer Ebene sind natürlich zwei Verschiebungskoordinaten erforderlich. Die Eingabedaten enthalten jedoch nur einen einzigen Wert. Da wir mit einer Zeitreihe arbeiten, können wir die zweite Verschiebungskoordinate ableiten, indem wir einen Einheitsschritt entlang der Zeitachse annehmen. Das heißt, wir nehmen „1“ als die Verschiebung entlang der Zeitachse für einen einzelnen Schritt.

   const float theta = atan(value);

Nun können wir den Sinus und den Kosinus des Winkels bestimmen, um die Drehmatrix zu erstellen.

   const float cos_theta = cos(theta);
   const float sin_theta = sin(theta);

Danach können wir den Bewegungsvektor des zentralen Agenten drehen.

   const float2 main = Rotate(value, cos_theta, sin_theta);

Da wir die Rotation für alle Bearbeiter durchführen müssen, habe ich diesen Vorgang in eine separate Funktion ausgelagert.

Bitte beachten Sie, dass durch die Drehung eine Verschiebung entlang von 2 Koordinatenachsen erfolgt. Zum Speichern der Daten verwenden wir eine Vektorvariable float2.

Als Nächstes führen wir eine Schleife über alle Agenten durch, die zu einem bestimmten Zeitschritt anwesend sind.

   for(int a = 0; a < total_v; a++)
     {
      float2 o = main;
      if(a != v)
         o -= Rotate(data[shift_data + a + total_v] - data[shift_data + a], cos_theta, sin_theta);
      output[shift_out + a] = o;
     }
  }

Im Hauptteil der Schleife für den zentralen Agenten speichern wir seine Bewegung, und für die anderen Agenten berechnen wir ihre Bewegung relativ zum zentralen Agenten. Zu diesem Zweck wird zunächst die Schicht jedes Agenten bestimmt. Wir drehen sie entsprechend der Rotationsmatrix des zentralen Agenten. Und wir subtrahieren die resultierende Verschiebung vom Bewegungsvektor des zentralen Agenten.

So erhalten wir für jeden Agenten in jedem Zeitschritt einen Tensor zur Beschreibung der Szene mit 2 Spalten (Koordinaten auf der Ebene), wobei die Anzahl der Zeilen gleich der Anzahl der analysierten univariaten Reihen ist.

Es ist erwähnenswert, dass die Autoren der Methode die Anzahl der Agenten auf den Radius des lokalen Segments begrenzt haben. Wir haben dies nicht getan, da die Divergenz der Indikatorwerte oft recht gute Handelssignale liefert.

2.2 Aufmerksamkeit innerhalb eines einzelnen Zeitschritts

Die nächste Frage, mit der wir uns bei der Umsetzung der vorgeschlagenen Ansätze konfrontiert sahen, war die Organisation von Aufmerksamkeitsmechanismen zwischen Agenten innerhalb eines separaten Zeitschritts.

Wir haben bereits früher Aufmerksamkeitsmechanismen in einzelnen Variablen implementiert. Dies ist jedoch eine „vertikale“ Analyse. Und in diesem Fall brauchen wir eine „horizontale“ Analyse. Wir könnten dieses Problem natürlich lösen, indem wir eine neue Klasse „horizontale Aufmerksamkeit“ schaffen, aber das ist ein ziemlich arbeitsintensiver Ansatz.

Es gibt eine schnellere Lösung. Wir könnten die ursprünglichen Daten übertragen und bestehende Lösungen für „vertikale Aufmerksamkeit“ verwenden. Dennoch gibt es eine Nuance. In diesem Fall ist der bestehende Algorithmus für die Transposition zweidimensionaler Matrizen nicht geeignet. Deshalb werden wir einen Algorithmus für die Transposition eines dreidimensionalen Tensors entwickeln. Bei dieser Transposition werden die 1. und 2. Dimension vertauscht, während die 3. unverändert bleibt.

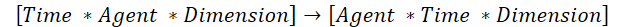
Das ist genau das, was wir brauchen, um die bestehenden Algorithmen der „vertikalen Aufmerksamkeit“ zu nutzen.

Um diesen Prozess zu organisieren, werden wir einen TransposeRCD-Kernel erstellen.

__kernel void TransposeRCD(__global const float *matrix_in, ///<[in] Input matrix
                           __global float *matrix_out ///<[out] Output matrix
                          )
  {
   const int r = get_global_id(0);
   const int c = get_global_id(1);
   const int d = get_global_id(2);
   const int rows = get_global_size(0);
   const int cols = get_global_size(1);
   const int dimension = get_global_size(2);
//---
   matrix_out[(c * rows + r)*dimension + d] = matrix_in[(r * cols + c) * dimension + d];
  }

Ich muss sagen, dass der Kernel-Algorithmus den ähnlichen Kernel für die Transposition einer zweidimensionalen Matrix fast vollständig kopiert. Es wird nur eine weitere Dimension des Aufgabenraums hinzugefügt. Dementsprechend wird der Offset in den Datenpuffern unter Berücksichtigung der zusätzlichen Dimension angepasst.

Dasselbe gilt für die Klassenstruktur CNeuronTransposeRCDOCL. Hier verwenden wir die 2D-Matrix-Transportklasse CNeuronTransposeOCL als Elternteil. 

class CNeuronTransposeRCDOCL  :  public CNeuronTransposeOCL
  {
protected:
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronTransposeRCDOCL(void){};
                    ~CNeuronTransposeRCDOCL(void){};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint count, uint window, uint dimension, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) const { return defNeuronTransposeRCDOCL; }
  };

Beachten Sie, dass wir keine zusätzlichen Variablen oder Objekte im Klassenkörper deklarieren. Zur Umsetzung des Prozesses reichen uns die ererbten völlig aus. Auf diese Weise können wir nur die Methoden zum Aufruf des Kernels außer Kraft setzen, während alle anderen Funktionen von den Methoden der übergeordneten Klasse abgedeckt werden. Daher werden wir die Algorithmen der Klassenmethoden nicht im Detail besprechen. Ich schlage vor, dass Sie sie selbst prüfen. Der vollständige Code dieser Klasse und alle ihre Methoden sind in den beigefügten Dateien enthalten.

2.3 Agent-Agent-Aufmerksamkeitsblock

Als Nächstes gehen wir zur Implementierung des Agent-Agent-Aufmerksamkeitsblocks über. Im Rahmen dieses Blocks wird davon ausgegangen, dass die Aufmerksamkeit zwischen lokalen Einbettungen von Agenten innerhalb eines Zeitschritts aufgebaut wird. Die oben geschaffene dreidimensionale Tensortranspositionsklasse hat unsere Arbeit stark vereinfacht. Die Verwendung des von den Autoren vorgeschlagenen Kontrollmechanismus für die Merkmalsvereinheitlichung erfordert jedoch eine Anpassung des Algorithmus.

Um die Prozesse des spezifizierten Aufmerksamkeitsblocks zu organisieren, werden wir eine neue Klasse CNeuronHiVTAAEncoder erstellen. In diesem Fall wird die unabhängige Variable Aufmerksamkeitsschicht verwendet CNeuronMVMHAufmerksamkeitMLKV als die übergeordnete Klasse.

class CNeuronHiVTAAEncoder : public CNeuronMVMHAttentionMLKV
  {
protected:
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronHiVTAAEncoder(void){};
                    ~CNeuronHiVTAAEncoder(void){};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint heads, uint heads_kv, 
                          uint units_count, uint layers, uint layers_to_one_kv, uint variables, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronMVMHAttentionMLKV;   }
  };

Wie Sie sehen können, deklarieren wir keine zusätzlichen Variablen oder Objekte in der Struktur dieser Klasse. Die Struktur der übergeordneten Klasse ist mehr als ausreichend. Die Klasse CNeuronMVMHAttentionMLKV verwendet dynamische Sammlungen von Datenpuffern, die ihrerseits von den Methoden der Klasse bearbeitet werden. Und wir können den bestehenden Sammlungen so viele Datenpuffer hinzufügen, wie wir brauchen.

Die Initialisierung einer neuen Instanz unseres Klassenobjekts ist in der Methode Init implementiert.

bool CNeuronHiVTAAEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                uint window, uint window_key, uint heads, uint heads_kv, 
                                uint units_count, uint layers, uint layers_to_one_kv, uint variables, 
                                ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables, 
                                                                   optimization_type, batch))
      return false;

In den Methodenparametern erhalten wir die wichtigsten Konstanten, mit denen wir die Architektur des vom Nutzer angegebenen Objekts genau bestimmen können. Im Hauptteil der Methode rufen wir dieselbe Methode der Basisklasse der neuronalen Schicht auf.

Beachten Sie, dass wir eine Methode der Basisklasse und nicht der direkten Elternklasse aufrufen, weil wir später noch einige Datenpuffer neu definieren müssen.

Nach erfolgreicher Ausführung der Methode der Elternklasse speichern wir die vom externen Programm erhaltenen Konstanten der Objektarchitekturdefinition in internen Variablen.

   iWindow = fmax(window, 1);
   iWindowKey = fmax(window_key, 1);
   iUnits = fmax(units_count, 1);
   iHeads = fmax(heads, 1);
   iLayers = fmax(layers, 1);
   iHeadsKV = fmax(heads_kv, 1);
   iLayersToOneKV = fmax(layers_to_one_kv, 1);
   iVariables = variables;

Als Nächstes berechnen wir die Konstanten, die die Größe der internen Objekte bestimmen.

   uint num_q = iWindowKey * iHeads * iUnits * iVariables;      //Size of Q tensor
   uint num_kv = iWindowKey * iHeadsKV * iUnits * iVariables;   //Size of KV tensor
   uint q_weights = (iWindow * iHeads + 1) * iWindowKey;        //Size of weights' matrix of Q tenzor
   uint kv_weights = (iWindow * iHeadsKV + 1) * iWindowKey;     //Size of weights' matrix of KV tenzor
   uint scores = iUnits * iUnits * iHeads * iVariables;         //Size of Score tensor
   uint mh_out = iWindowKey * iHeads * iUnits * iVariables;     //Size of multi-heads self-attention
   uint out = iWindow * iUnits * iVariables;                    //Size of attention out tensore
   uint w0 = (iWindowKey * iHeads + 1) * iWindow;               //Size W0 weights matrix
   uint gate = (2 * iWindow + 1) * iWindow;                     //Size of weights' matrix gate layer
   uint self = (iWindow + 1) * iWindow;                         //Size of weights' matrix self layer

Der Algorithmus wird im Wesentlichen von der übergeordneten Klasse geerbt, es wurden nur einige kleinere Änderungen vorgenommen.

Nach Abschluss der vorbereitenden Arbeiten erstellen wir eine Schleife mit einer Anzahl von Iterationen, die der angegebenen Anzahl von verschachtelten Ebenen entspricht. Im Hauptteil dieser Schleife werden bei jeder Iteration Objekte erstellt, die für die Ausführung der Funktionen der einzelnen verschachtelten Ebenen erforderlich sind.

   for(uint i = 0; i < iLayers; i++)
     {
      CBufferFloat *temp = NULL;
      for(int d = 0; d < 2; d++)
        {
         //--- Initilize Q tensor
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(num_q, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!QKV_Tensors.Add(temp))
            return false;

Hier legen wir zunächst Puffer für Zwischendaten und Ergebnisse einzelner Blöcke sowie für die Aufnahme der entsprechenden Fehlergradienten an.

Beachten Sie, dass der Datenpuffer und die entsprechenden Fehlergradienten die gleiche Größe haben. Um die manuelle Arbeit zu reduzieren, werden wir daher eine verschachtelte Schleife mit 2 Iterationen erstellen. Während der ersten Iteration der Schleife werden Datenpuffer angelegt, während der zweiten Iteration werden Puffer für die entsprechenden Fehlergradienten angelegt.

Zunächst wird ein Puffer erstellt, in den die Abfrageobjekte geschrieben werden. Es folgen die Puffer für Schlüssel und Werte (key und value).

         //--- Initilize KV tensor
         if(i % iLayersToOneKV == 0)
           {
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit(num_kv, 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!K_Tensors.Add(temp))
               return false;
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit(num_kv, 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!V_Tensors.Add(temp))
               return false;
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit(2 * num_kv, 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!KV_Tensors.Add(temp))
               return false;
           }

Die Algorithmen zur Erstellung und Initialisierung von Datenpuffern sind völlig identisch. Der einzige Unterschied ist, dass unser Algorithmus die Möglichkeit bietet, einen Schlüssel-Wert-Tensor für mehrere verschachtelte Ebenen zu verwenden. Daher prüfen wir vor der Erstellung von Puffern, ob diese Aktion auf der aktuellen Ebene notwendig ist.

Als Nächstes initialisieren wir einen Puffer mit Abhängigkeitskoeffizienten zwischen Objekten.

         //--- Initialize scores
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(scores, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!S_Tensors.Add(temp))
            return false;

Und der mehrköpfige Aufmerksamkeits-Ausgangspuffer.

         //--- Initialize multi-heads attention out
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(mh_out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!AO_Tensors.Add(temp))
            return false;

In Übereinstimmung mit dem Algorithmus der mehrköpfigen Selbstaufmerksamkeit werden die Ergebnisse der mehrköpfigen Aufmerksamkeit mithilfe einer Projektionsschicht auf die ursprüngliche Datenebene komprimiert. Wir erstellen einen Puffer, um die resultierende Projektion zu speichern.

         //--- Initialize attention out
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

Der bis hierher beschriebene Algorithmus wiederholt fast vollständig die Methode der übergeordneten Klasse. Im weiteren Verlauf werden jedoch Änderungen vorgenommen, um den Mechanismus zur Verwaltung der Vereinheitlichung von Merkmalen zu implementieren. Hier müssen wir nach dem vorgeschlagenen Algorithmus zunächst die Quelldaten mit den Ergebnissen des Aufmerksamkeitsblocks verketten.

         //--- Initialize Concatenate
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(2 * out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

Die Ergebnisse werden dann zur Berechnung der Kontrollkoeffizienten verwendet.

         //--- Initialize Gate
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

Danach führen wir eine Projektion der ursprünglichen Daten durch.

         //--- Initialize Self
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

Am Ende der verschachtelten Schleife erstellen wir einen Ausgabepuffer der aktuellen verschachtelten Schicht.

         //--- Initialize Out
         if(i == iLayers - 1)
           {
            if(!FF_Tensors.Add(d == 0 ? Output : Gradient))
               return false;
            continue;
           }
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;
        }

Dabei ist zu beachten, dass wir Output- und Gradientenpuffer nur für interne Zwischenschichten erstellen. Für die letzte verschachtelte Ebene kopieren wir einfach die Zeiger auf die entsprechenden Puffer unserer Klasse.

Nach der Erstellung der Zwischenergebnispuffer und der entsprechenden Fehlergradienten werden die Trainingsparametermatrizen initialisiert. Wir werden mehrere davon haben. Zuerst haben wir die Abfrageentität der Generierungsmatrix.

      //--- Initilize Q weights
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(q_weights))
         return false;
      float k = (float)(1 / sqrt(iWindow + 1));
      for(uint w = 0; w < q_weights; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!QKV_Weights.Add(temp))
         return false;

Hier erstellen wir zunächst einen Puffer und füllen ihn dann mit zufälligen Parametern. Diese Parameter werden während des Modelltrainings optimiert.

In ähnlicher Weise erstellen wir Parameter für die Erzeugung von Schlüssel- und Wertentitäten. Wir erstellen jedoch nicht für jede verschachtelte Ebene eine Matrize.

      //--- Initialize K weights
      if(i % iLayersToOneKV == 0)
        {
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.Reserve(kv_weights))
            return false;
         for(uint w = 0; w < kv_weights; w++)
           {
            if(!temp.Add(GenerateWeight() * 2 * k - k))
               return false;
           }
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!K_Weights.Add(temp))
            return false;
         //---
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.Reserve(kv_weights))
            return false;
         for(uint w = 0; w < kv_weights; w++)
           {
            if(!temp.Add(GenerateWeight() * 2 * k - k))
               return false;
           }
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!V_Weights.Add(temp))
            return false;
        }

Darüber hinaus benötigen wir eine Projektionsmatrix der Ergebnisse der mehrköpfigen Aufmerksamkeit.

      //--- Initialize Weights0
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(w0))
         return false;
      for(uint w = 0; w < w0; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!FF_Weights.Add(temp))
         return false;

Hier fügen wir auch Parameter für den Kontrollblock der Merkmalskombination hinzu.

      //--- Initialize Gate Weights
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(gate))
         return false;
      k = (float)(1 / sqrt(2 * iWindow + 1));
      for(uint w = 0; w < gate; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!FF_Weights.Add(temp))
         return false;

Und Projektionen der Quelldaten.

      //--- Self
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(self))
         return false;
      k = (float)(1 / sqrt(iWindow + 1));
      for(uint w = 0; w < self; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!FF_Weights.Add(temp))
         return false;

Als Nächstes müssen wir Datenpuffer hinzufügen, um Momente auf der Ebene der Gewichtsmatrix zu schreiben, die bei der Parameteroptimierung verwendet werden.

      //---
      for(int d = 0; d < (optimization == SGD ? 1 : 2); d++)
        {
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? q_weights : iWindowKey * iHeads), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!QKV_Weights.Add(temp))
            return false;
         if(i % iLayersToOneKV == 0)
           {
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit((d == 0 || optimization == ADAM ? kv_weights : iWindowKey * iHeadsKV), 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!K_Weights.Add(temp))
               return false;
            //---
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit((d == 0 || optimization == ADAM ? kv_weights : iWindowKey * iHeadsKV), 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!V_Weights.Add(temp))
               return false;
           }
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? w0 : iWindow), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Weights.Add(temp))
            return false;
         //--- Initilize Gate Momentum
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? gate : 2 * iWindow), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Weights.Add(temp))
            return false;
         //--- Initilize Self Momentum
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? self : iWindow), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Weights.Add(temp))
            return false;
        }
     }

Nach erfolgreicher Initialisierung von verschachtelten Ebenenobjekten wird ein zusätzlicher Puffer angelegt, der zur vorübergehenden Speicherung von Zwischenergebnissen verwendet wird.

   if(!Temp.BufferInit(MathMax(2 * num_kv, out), 0))
      return false;
   if(!Temp.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Ende der Methode. Danach geben wir das boolesche Ergebnis der Methodenoperationen an das aufrufende Programm zurück.

Der nächste Schritt nach der Initialisierung des Objekts besteht darin, einen Algorithmus für die Vorwärtsdurchgänge zu konstruieren, der in der Methode feedForward implementiert wird.

bool CNeuronHiVTAAEncoder::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(NeuronOCL) == POINTER_INVALID)
      return false;

In den Parametern dieser Methode erhalten wir einen Zeiger auf das Objekt mit den Ausgangsdaten und prüfen sofort die Relevanz des erhaltenen Zeigers. Nach erfolgreichem Abschluss dieser Kontrolle führen wir eine Schleife aus, in der wir die sequentielle Ausführung der Operationen jeder verschachtelten Schicht implementieren.

   CBufferFloat *kv = NULL;
   for(uint i = 0; (i < iLayers && !IsStopped()); i++)
     {
      //--- Calculate Queries, Keys, Values
      CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(10 * i - 6));
      CBufferFloat *q = QKV_Tensors.At(i * 2);
      if(IsStopped() || 
         !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), inputs, q, 
                                                       iWindow, iWindowKey * iHeads, None))
         return false;

Zunächst erzeugen wir Abfrageentitäten. Dann bilden wir, falls erforderlich, einen Schlüssel-Wert-Tensor.

      if((i % iLayersToOneKV) == 0)
        {
         uint i_kv = i / iLayersToOneKV;
         kv = KV_Tensors.At(i_kv * 2);
         CBufferFloat *k = K_Tensors.At(i_kv * 2);
         CBufferFloat *v = V_Tensors.At(i_kv * 2);
         if(IsStopped() || 
           !ConvolutionForward(K_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, k, 
                                                        iWindow, iWindowKey * iHeadsKV, None))
            return false;
         if(IsStopped() || 
            !ConvolutionForward(V_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, v, 
                                                         iWindow, iWindowKey * iHeadsKV, None))
            return false;
         if(IsStopped() || 
            !Concat(k, v, kv, iWindowKey * iHeadsKV * iVariables, iWindowKey * iHeadsKV * iVariables, iUnits))
            return false;
        }

Nach der Bildung der Tensoren der erforderlichen Entitäten können wir die Ergebnisse der mehrköpfigen Aufmerksamkeit berechnen.

      //--- Score calculation and Multi-heads attention calculation
      CBufferFloat *temp = S_Tensors.At(i * 2);
      CBufferFloat *out = AO_Tensors.At(i * 2);
      if(IsStopped() || !AttentionOut(q, kv, temp, out))
         return false;

Dann komprimieren wir sie auf die Dimension der Ausgangsdaten.

      //--- Attention out calculation
      temp = FF_Tensors.At(i * 10);
      if(IsStopped() || 
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out, temp, 
                                                       iWindowKey * iHeads, iWindow, None))
         return false;

Um die Kontrollkoeffizienten zu berechnen, werden zunächst die Ergebnisse des Aufmerksamkeitsblocks und die Ausgangsdaten miteinander verknüpft.

      //--- Concat
      out = FF_Tensors.At(i * 10 + 1);
      if(IsStopped() || !Concat(temp, inputs, out, iWindow, iWindow, iUnits))
         return false;

Dann berechnen wir die Kontrollkoeffizienten.

      //--- Gate
      if(IsStopped() || 
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), out, 
                                 FF_Tensors.At(i * 10 + 2), 2 * iWindow, iWindow, SIGMOID))
         return false;

Dann müssen wir nur noch eine Projektion der ursprünglichen Eingaben vornehmen.

      //--- Self
      if(IsStopped() || 
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), inputs, 
                                         FF_Tensors.At(i * 10 + 3), iWindow, iWindow, None))
         return false;

Danach kombinieren wir die erhaltene Projektion mit den Ergebnissen des Aufmerksamkeitsblocks, wobei wir die Kontrollkoeffizienten berücksichtigen.

      //--- Out
      if(IsStopped() || 
        !GateElementMult(FF_Tensors.At(i * 10 + 3), temp, FF_Tensors.At(i * 10 + 2), 
                                                          FF_Tensors.At(i * 10 + 4)))
         return false; 
     }
//---
   return true;
  }

Danach geht es weiter mit der nächsten verschachtelten Ebene in einer neuen Iteration des Zyklus.

Nach erfolgreichem Abschluss der Operationen aller verschachtelten Ebenen innerhalb des Blocks schließen wir die Ausführung der Methode ab und geben ein logisches Ergebnis an den Aufrufer zurück, das den Abschlussstatus der Operationen angibt.

Damit ist unsere Arbeit an der Implementierung des Feed-Forward-Algorithmus abgeschlossen. Ich schlage vor, dass Sie sich selbständig mit den Algorithmen der Methoden für Backpropagation vertraut machen. Den vollständigen Code aller Klassen und ihrer Methoden sowie alle Programme, die bei der Erstellung des Artikels verwendet wurden, finden Sie im Anhang.

Schlussfolgerung

In diesem Artikel haben wir eine recht interessante und vielversprechende Methode des Hierarchical Vector Transformer (HiVT) untersucht, die vorgeschlagen wurde, um die Bewegung mehrerer Agenten vorherzusagen. Diese Methode bietet einen effektiven Ansatz zur Lösung des Vorhersageproblems, indem das Problem in Phasen lokaler Kontextextextraktion und globaler Interaktionsmodellierung zerlegt wird.

Die Autoren der Methode verfolgten einen umfassenden Ansatz zur Lösung des Problems und schlugen eine Reihe von Ansätzen zur Verbesserung der Wirksamkeit des vorgeschlagenen Modells vor. Leider übersteigt der Arbeitsaufwand für die Umsetzung der vorgeschlagenen Ansätze den Rahmen dieses Artikels. Dieser Teil bezog sich also nur auf die vorbereitenden Arbeiten. Die begonnenen Arbeiten werden im nächsten Artikel abgeschlossen. Die Ergebnisse der Prüfung der vorgeschlagenen Ansätze anhand realer historischer Daten werden ebenfalls im zweiten Teil vorgestellt.

Referenzen

HiVT: Hierarchical Vector Transformer for Multi-Agent Motion Prediction

Weitere Artikel aus dieser Serie

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	EA	EA-Beispielsammlung
2	ResearchRealORL.mq5	EA	EA zum Sammeln von Beispielen mit der Real-ORL-Methode
3	Study.mq5	EA	Trainings-EA des Modells
4	StudyEncoder.mq5	EA	Trainings-EA des Encoders
5	Test.mq5	EA	Modeltest-EA
6	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
7	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
8	NeuroNet.cl	Code Base	OpenCL-Programmcode-Bibliothek