Neuronales Netz in der Praxis: Das erste Neuron

Einführung

Hallo und herzlich willkommen zu einem neuen Artikel über neuronale Netze. Im vorherigen Artikel Neuronales Netzwerk in der Praxis: Skizze eines Neurons, haben wir eine erste grundlegende Skizze für die Konstruktion eines einfachen Neurons erstellt. Doch trotz unserer Bemühungen ist das von uns gebaute Neuron nicht genau das, was wir brauchen. Das liegt daran, dass es sozusagen einen kleinen Makel enthält. Dennoch, mein lieber und geschätzter Leser, ist es mein Ziel, dass Sie den schrittweisen Aufbau eines neuronalen Netzes vollständig nachvollziehen können. Dieser kleine Fehler wirkt sich nicht wesentlich auf die Funktionalität unseres einfachen Neurons aus.

Das werden Sie sich vielleicht fragen: Auf welchen Fehler beziehen Sie sich? Ich habe nichts bemerkt. Das Neuron hat in meinen Tests perfekt funktioniert. Gehen wir in dieser Artikelserie über neuronale Netze ein wenig zurück, um zu verstehen, wovon ich spreche.

In den ersten Artikeln über neuronale Netze habe ich gezeigt, wie wir die Maschine zwingen können, eine lineare Gleichung zu formulieren. Ursprünglich musste diese Gleichung durch den Ursprung der kartesischen Ebene gehen, d. h. die Linie musste sich im Punkt (0, 0) schneiden. Dies lag daran, dass die Konstante < b > in der nachstehenden Gleichung auf Null gesetzt wurde.

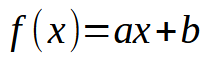
Obwohl wir die Methode der kleinsten Quadrate angewandt haben, um eine geeignete Gleichung zu finden, die sicherstellt, dass der Datensatz oder das in der Datenbank gespeicherte Vorwissen angemessen in mathematischer Form dargestellt werden kann, hat uns dieser Modellierungsansatz nicht geholfen, die am besten geeignete Gleichung zu finden. Diese Einschränkung ergab sich, weil die Konstante < b > je nach Datensatz in der Wissensbasis einen von Null verschiedenen Wert haben muss.

Wenn Sie die vorangegangenen Artikel aufmerksam lesen, werden Sie feststellen, dass wir bestimmte mathematische Manöver anwenden mussten, um die bestmöglichen Werte sowohl für die Konstante < a >, die die Steigung darstellt, als auch für die Konstante < b >, die den Achsenabschnitt bezeichnet, zu bestimmen. Diese Anpassungen ermöglichten es uns, die am besten geeignete lineare Gleichung zu finden. Wir haben zwei Methoden untersucht, um dies zu erreichen: eine durch Ableitungsberechnungen und die andere durch Matrixberechnungen.

Von diesem Zeitpunkt an sind solche Berechnungen jedoch nicht mehr sinnvoll. Das liegt daran, dass wir eine alternative Methode zur Bestimmung der Konstanten in unserer linearen Gleichung entwickeln müssen. Im vorherigen Artikel habe ich gezeigt, wie man die Konstante der Steigung findet. Ich hoffe, es hat Ihnen Spaß gemacht, mit diesem Code zu experimentieren, denn jetzt werden wir uns an eine etwas komplexere Aufgabe machen. Dieser nächste Schritt ist zwar nur eine kleine Herausforderung, eröffnet aber zahlreiche Möglichkeiten. In der Tat könnte dies der interessanteste Artikel in unserer Serie über neuronale Netze sein, da alles, was folgt, wesentlich einfacher und praktischer wird.

Warum verkomplizieren die Menschen die Dinge so sehr?

Bevor wir uns mit dem Code befassen, möchte ich Ihnen, liebe Leser, einige wichtige Begriffe näher bringen. Wenn Sie anfangen, sich mit neuronalen Netzen zu beschäftigen, werden Sie wahrscheinlich auf eine Flut von Fachbegriffen stoßen - eine Lawine, wirklich. Ich bin mir nicht sicher, warum diejenigen, die neuronale Netze erklären, dazu neigen, etwas grundsätzlich Einfaches zu kompliziert zu machen. Meiner Meinung nach gibt es keinen Grund für eine solche Komplexität. Es geht mir hier jedoch nicht darum, andere zu kritisieren oder herabzusetzen, sondern zu klären, wie die Dinge hinter den Kulissen ablaufen.

Um die Dinge so einfach wie möglich zu machen, wollen wir uns auf einige wiederkehrende Begriffe im Zusammenhang mit neuronalen Netzen konzentrieren. Die erste ist die Gewichte. Dieser Begriff bezieht sich einfach auf den Steigungskoeffizienten in einer linearen Gleichung. Unabhängig davon, wie andere es beschreiben, entspricht der Begriff „Gewicht“ im Wesentlichen der Steigung. Ein weiterer häufig verwendeter Begriff ist „Bias“. Dies ist weder ein esoterisches Konzept noch ist es ausschließlich auf neuronale Netze oder künstliche Intelligenz beschränkt. Im Gegensatz dazu stellt das „Bias“ einfach den Achsenabschnitt einer linearen Gleichung dar. Da wir es mit einer Sekantenlinie zu tun haben, sollten Sie diese Begriffe nicht verwechseln.

Ausgehend von diesen scheinbar komplexen Begriffen ergeben sich zahlreiche weitere Fachausdrücke. In Wirklichkeit sind dies nur verschiedene Namen für dieselben Dinge. Ich werde nicht darauf eingehen, warum vertraute Begriffe unterschiedlich benannt werden. Wenn Sie beim Studium neuronaler Netze oder anderer damit zusammenhängender Themen auf unbekannte Begriffe stoßen, sollten Sie sich die Zeit nehmen, die mathematische Formel dahinter zu verstehen. Sie werden bald feststellen, dass sie im Grunde viel einfacher sind, als sie erscheinen.

Ich sage das, weil viele Menschen dazu neigen, die Dinge zu sehr zu verkomplizieren.

Sie nehmen etwas Einfaches und fügen Schichten von Komplexität, Ausschmückungen und unnötigen Elementen hinzu, sodass etwas, das jeder verstehen könnte, letztendlich kompliziert erscheint. Beim Programmieren und in den exakten Wissenschaften ist Einfachheit der Schlüssel. Wenn die Dinge anfangen, mit unnötigen Zusätzen, Ablenkungen und übermäßigen Details überladen zu werden, ist es am besten, innezuhalten, alle unnötige Komplexität zu entfernen und die zugrunde liegende Wahrheit aufzudecken. Viele werden darauf bestehen, dass das Thema kompliziert ist, dass man ein Experte auf dem Gebiet sein muss, um ein neuronales Netz zu verstehen oder zu implementieren, und dass es nur mit einer bestimmten Sprache oder einem bestimmten Tool möglich ist. Inzwischen sollten Sie, liebe Leserin, lieber Leser, jedoch erkannt haben, dass ein neuronales Netz nicht kompliziert ist. Es ist eigentlich ganz einfach.

Kommen wir nun zu einem neuen Thema. Wir werden verstehen, wie man die Konstante < b > einbezieht, die den Schnittpunkt darstellt, oder wie manche es lieber nennen: das „Bias“. Dies ist notwendig, um die Gleichung der Linie so anzupassen, dass sie den Datensatz, den wir zum Trainieren unseres Neurons verwenden, genauer darstellt.

Die Geburt des ersten Neurons

Damit unser erstes Neuron Gestalt annimmt - und wenn es einmal Gestalt angenommen hat, brauchen wir es nicht mehr zu verändern, wie Sie gleich sehen werden - müssen wir zunächst verstehen, womit wir arbeiten. Unser aktuelles Neuron verhält sich wie in der folgenden Animation dargestellt.

Dies ist dieselbe Animation, die im Artikel Neuronales Netz in der Praxis: Die Sekante vorgestellt wird. Mit anderen Worten: Wir haben soeben den ersten Schritt zum Aufbau eines Neurons getan, das in der Lage ist, eine Aufgabe auszuführen, die zuvor manuell mit Richtungstasten erledigt wurde. Vielleicht haben Sie jedoch festgestellt, dass dies allein nicht ausreicht. Um die Gleichung weiter zu verfeinern, müssen wir die Schnittmengenkonstante einbeziehen. Man könnte annehmen, dass dies extrem kompliziert ist, aber das ist es nicht. Es ist sogar so einfach, dass es fast trivial wirkt. Unten sehen Sie, wie wir die Schnittmengenkonstante zum Neuron hinzufügen. Dies lässt sich am besten verstehen, wenn man das folgende Fragment betrachtet.

01. //+------------------------------------------------------------------+
02. double Cost(const double w, const double b)
03. {
04.     double err, fx, x;
05. 
06.     err = 0;
07.     for (uint c = 0; c < nTrain; c++)
08.     {
09.         x = Train[c][0];
10.         fx =  a * w + b;
11.         err += MathPow(fx - Train[c][1], 2);
12.     }
13. 
14.     return err / nTrain;
15. }
16. //+------------------------------------------------------------------+

Ich versuche, den Code in kleinere Fragmente zu zerlegen, damit Sie, liebe Leserin und lieber Leser, im Detail verstehen können, was getan wird. Und dann können Sie es mir sagen: Ist es wirklich kompliziert? Oder erfordert es all die unnötige Komplexität, die viele gerne hinzufügen, wenn sie über neuronale Netze diskutieren?

Passen Sie gut auf, denn der Grad der Komplexität ist fast absurd. (Lacht.) In Zeile neun nehmen wir unseren Trainingswert und weisen ihn der Variablen X zu. In Zeile zehn führen wir dann eine Faktorisierung durch. Wow! Was für eine unglaublich komplexe Berechnung! Aber Moment mal - ist das nicht dieselbe Gleichung, die wir am Anfang gesehen haben? Die Gleichung einer geraden Linie? Sie machen wohl Witze! Dieses Ding kann unmöglich wie ein Neuron funktionieren, das in Programmen für künstliche Intelligenz verwendet wird.

Entspannen Sie sich, lieber Leser. Sie werden sehen, dass dies genauso funktioniert wie jedes andere Programm für künstliche Intelligenz oder neuronale Netze. Ganz gleich, wie kompliziert die Leute versuchen, es klingen zu lassen, Sie werden feststellen, dass es sich im Grunde um dasselbe Konzept handelt, das in jedem neuronalen Netz umgesetzt wird. Der Unterschied liegt im nächsten Schritt, auf den wir gleich eingehen werden. Die Veränderung ist jedoch nicht so drastisch, wie Sie vielleicht denken. Lassen Sie uns einen Schritt nach dem anderen tun.

Nach der Aktualisierung der Fehlerberechnung kann das für die Anpassung dieser beiden Parameter zuständige Fragment der Kostenfunktion geändert werden. Dies wird schrittweise geschehen, damit Sie einige wichtige Details erfassen können. Der erste Schritt besteht darin, den ursprünglichen Code aus dem vorangegangenen Artikel zu ändern und durch die unten gezeigte neue Version zu ersetzen.

01. //+------------------------------------------------------------------+
02. void OnStart()
03. {
04.     double weight, ew, eb, e1, bias;
05.     int f = FileOpen("Cost.csv", FILE_COMMON | FILE_WRITE | FILE_CSV);
06. 
07.     Print("The first neuron...");
08.     MathSrand(512);
09.     weight = (double)macroRandom;
10.     bias = (double)macroRandom;
11. 
12.     for(ulong c = 0; (c < ULONG_MAX) && ((e1 = Cost(weight, bias)) > eps); c++)
13.     {
14.         ew = (Cost(weight + eps, bias) - e1) / eps;
15.         eb = (Cost(weight, bias + eps) - e1) / eps;
16.         weight -= (ew * eps);
17.         bias -= (eb * eps);
18.         if (f != INVALID_HANDLE)
19.             FileWriteString(f, StringFormat("%I64u;%f;%f;%f;%f;%f\n", c, weight, ew, bias, eb, e1));
20.     }
21.     if (f != INVALID_HANDLE)
22.         FileClose(f);
23.     Print("Weight: ", weight, "  Bias: ", bias);
24.     Print("Error Weight: ", ew);
25.     Print("Error Bias: ", eb);
26.     Print("Error: ", e1);
27. }
28. //+------------------------------------------------------------------+

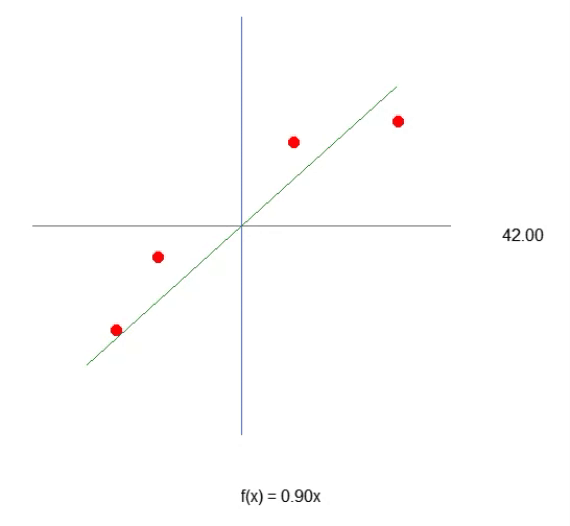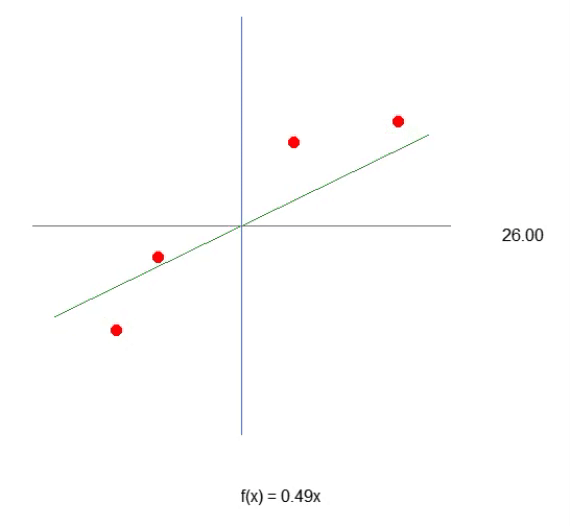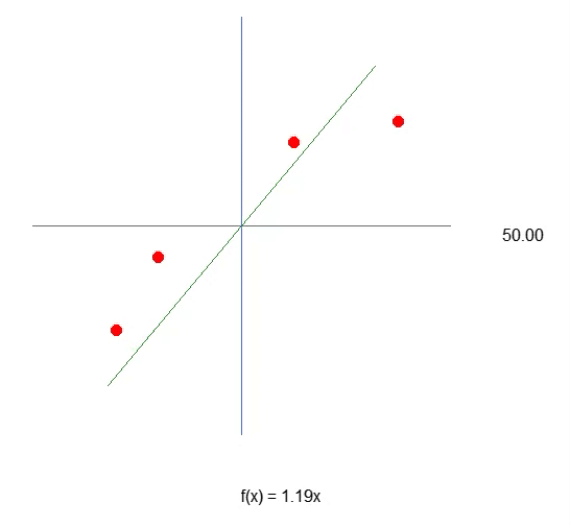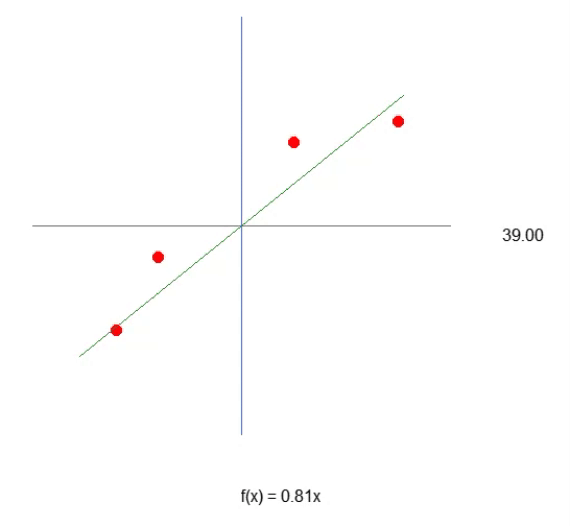
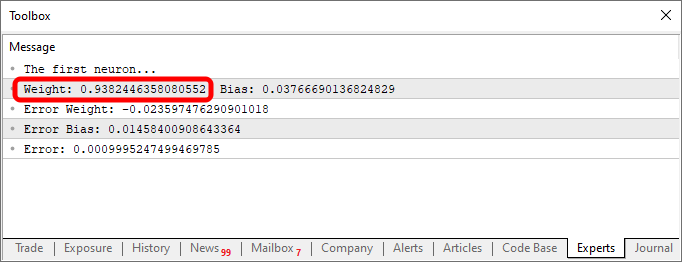
Nachdem Sie das Skript mit diesen Änderungen ausgeführt haben, sehen Sie etwas Ähnliches wie das folgende Bild.

Konzentrieren wir uns nun ausschließlich auf dieses zweite Codefragment. In Zeile vier fügen wir einige Variablen hinzu und ändern sie - nichts Komplexes. In Zeile 10 weisen wir dann die Anwendung an, dem „Bias“ oder unserer Schnittpunktkonstante einen Zufallswert zuzuweisen. Beachten Sie, dass wir diesen Wert auch an die Funktion Kosten weitergeben müssen. Dies geschieht in den Zeilen 12, 14 und 15. Interessant ist jedoch, dass wir zwei Arten von aggregierten Fehlern erzeugen: einen Wert für das Gewicht und einen für das „Bias“. Es ist wichtig zu verstehen, dass beide zwar Teil derselben Gleichung sind, aber unterschiedlich angepasst werden müssen. Daher müssen wir den spezifischen Fehler bestimmen, den jeder einzelne innerhalb des Gesamtsystems darstellt.

In diesem Sinne passen wir in den Zeilen 16 und 17 die Werte für die nächste Iteration der for-Schleife richtig an. Außerdem speichern wir diese Werte, wie im vorherigen Artikel, in einer CSV-Datei. So können wir ein Diagramm erstellen und analysieren, wie sich die Werte im Laufe der Zeit verändern.

In diesem Stadium ist unser erstes Neuron nun vollständig aufgebaut. Es gibt jedoch noch einige Details, die Sie verstehen können, wenn Sie sich den vollständigen Code für dieses Neuron ansehen, den Sie unten finden. Hier ist der vollständige Code, den ich entwickelt habe.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define macroRandom (rand() / (double)SHORT_MAX)
05. //+------------------------------------------------------------------+
06. double Train[][2] {
07.                     {0, 0},
08.                     {1, 2},
09.                     {2, 4},
10.                     {3, 6},
11.                     {4, 8},
12.                   };
13. //+------------------------------------------------------------------+
14. const uint nTrain = Train.Size() / 2;
15. const double eps = 1e-3;
16. //+------------------------------------------------------------------+
17. double Cost(const double w, const double b)
18. {
19.     double err, fx, a;
20. 
21.     err = 0;
22.     for (uint c = 0; c < nTrain; c++)
23.     {
24.         a = Train[c][0];
25.         fx =  a * w + b;
26.         err += MathPow(fx - Train[c][1], 2);
27.     }
28. 
29.     return err / nTrain;
30. }
31. //+------------------------------------------------------------------+
32. void OnStart()
33. {
34.     double weight, ew, eb, e1, bias;
35.     int f = FileOpen("Cost.csv", FILE_COMMON | FILE_WRITE | FILE_CSV);
36. 
37.     Print("The first neuron...");
38.     MathSrand(512);
39.     weight = (double)macroRandom;
40.     bias = (double)macroRandom;
41. 
42.     for(ulong c = 0; (c < ULONG_MAX) && ((e1 = Cost(weight, bias)) > eps); c++)
43.     {
44.         ew = (Cost(weight + eps, bias) - e1) / eps;
45.         eb = (Cost(weight, bias + eps) - e1) / eps;
46.         weight -= (ew * eps);
47.         bias -= (eb * eps);
48.         if (f != INVALID_HANDLE)
49.             FileWriteString(f, StringFormat("%I64u;%f;%f;%f;%f;%f\n", c, weight, ew, bias, eb, e1));
50.     }
51.     if (f != INVALID_HANDLE)
52.         FileClose(f);
53.     Print("Weight: ", weight, "  Bias: ", bias);
54.     Print("Error Weight: ", ew);
55.     Print("Error Bias: ", eb);
56.     Print("Error: ", e1);
57. }
58. //+------------------------------------------------------------------+

Interessant sind sowohl der Code als auch die Ergebnisse in der obigen Abbildung. In Zeile sechs sehen Sie die Werte, die zum Training des Neurons verwendet wurden. Es ist deutlich zu erkennen, dass der Multiplikationsfaktor zwei ist. Das Neuron meldet ihn jedoch als 1.9804357049081742. In ähnlicher Weise können wir sehen, dass der Schnittpunkt Null sein sollte, aber das Neuron gibt ihn als 0.054422740828113325 an. Wenn man bedenkt, dass wir in Zeile 15 eine Fehlermarge von 0,001 akzeptieren, ist dieses Ergebnis gar nicht so schlecht. Immerhin lag der vom Neuron gemeldete endgültige Fehler bei 0,0009994343288155726 und damit unter der von uns als akzeptabel festgelegten Schwelle.

Diese kleinen Unterschiede, die Sie deutlich erkennen können, stellen den Wahrscheinlichkeitsindex dar, der angibt, wie nahe die Information an der Richtigkeit ist. Dieser wird in der Regel als Prozentsatz ausgedrückt. Sie werden jedoch nie 100 % erreichen. Die Zahl kann sich sehr stark annähern, wird aber aufgrund dieses unvermeidlichen Näherungsfehlers nie genau 100 % betragen.

Allerdings ist dieser Wahrscheinlichkeitsindex nicht dasselbe wie ein Gewissheitsindex in Bezug auf die Information. In diesem Stadium arbeiten wir noch nicht an der Erstellung eines solchen Indexes. Wir trainieren lediglich das Neuron und überprüfen, ob es eine Korrelation zwischen den Trainingsdaten herstellen kann. Aber an dieser Stelle werden Sie vielleicht denken: Diese ganze Neuronensache ist nutzlos. So wie es gebaut ist, dient es keinem wirklichen Zweck. Es findet einfach eine Zahl, die wir bereits kennen. Was ich wirklich möchte, ist ein System, das mir Dinge sagen kann, das Text erzeugt oder sogar Code schreibt. Vielleicht sogar ein Programm, das auf den Finanzmärkten agieren kann und für mich Geld verdient, wann immer ich es brauche.

Na gut. Sie haben sicherlich große Ambitionen. Aber wenn Sie, liebe Leserin, lieber Leser, neuronale Netze oder künstliche Intelligenz nur als Mittel zum Zweck des Geldverdienens betrachten, habe ich eine schlechte Nachricht für Sie: Sie werden auf diese Weise keinen Erfolg haben. Die einzigen, die wirklich von diesem Bereich profitieren, sind diejenigen, die KI- und neuronale Netzwerksysteme verkaufen. Sie versuchen, alle anderen davon zu überzeugen, dass KI qualifizierte Fachkräfte übertreffen kann. Abgesehen von diesen Personen, die aus dem Verkauf dieser Lösungen Kapital schlagen, wird niemand sonst damit Geld verdienen. Wenn es so einfach wäre, warum würde ich dann diese Artikel schreiben und erklären, wie alles funktioniert? Oder warum sollten andere Experten offen darüber sprechen, wie diese Mechanismen funktionieren? Das würde keinen Sinn machen. Sie könnten einfach schweigen und von einem gut trainierten neuronalen Netz profitieren. Aber in der Realität sieht die Sache anders aus. Vergessen Sie also die Vorstellung, dass Sie ein neuronales Netzwerk zusammenstellen, hier und da ein paar Codeschnipsel einfügen und sofort damit beginnen können, ohne wirkliche Kenntnisse Geld zu verdienen.

Nichtsdestotrotz, geschätzter Leser, nichts hindert Sie daran, ein kleines neuronales Netz zu entwickeln, das Ihnen bei der Entscheidungsfindung hilft, sei es beim Kauf, beim Verkauf oder einfach nur, um bestimmte Trends auf den Finanzmärkten besser zu erkennen. Ist es möglich, dies zu erreichen? Ja: Wenn man alles Notwendige studiert, auch wenn es langsam und mit viel Mühe und Hingabe geschieht, kann man ein neuronales Netz für diesen Zweck trainieren. Aber wie ich bereits erwähnt habe, müssen Sie sich die Mühe machen. Das ist durchaus machbar, aber nicht ohne Arbeit.

Jetzt haben wir erfolgreich unser erstes Neuron gebaut. Doch bevor Sie sich zu sehr aufregen und sich überlegen, wie Sie das Programm nutzen können, sollten Sie sich den Aufbau des Programms genauer ansehen. Zur Verdeutlichung sehen Sie sich das folgende Bild an.

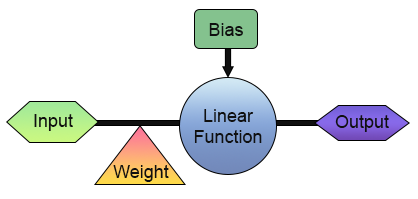
In der Abbildung oben sehen wir, wie unser Neuron implementiert ist. Beachten Sie, dass es aus einem Eingang und einem Ausgang besteht. Diese einzelne Eingabe erhält ein Gewicht. Auf den ersten Blick mag dies nicht sehr nützlich erscheinen. Was nützt es, nur einen Eingang und einen Ausgang zu haben? Ich verstehe Ihre Skepsis gegenüber dem, was wir gerade aufgebaut haben. Je nach Ihrem Hintergrund und Ihren Kenntnissen in verschiedenen Bereichen ist Ihnen jedoch vielleicht nicht bewusst, dass es in der digitalen Elektronik Schaltungen gibt, die genau so funktionieren: mit einem einzigen Eingang und einem einzigen Ausgang. In der Tat gibt es zwei solcher Schaltungen: den Inverter und den Puffer. Beide sind integrale Bestandteile noch komplexerer Systeme, und unsere Neuronen können tatsächlich darauf trainiert werden, ihr Verhalten nachzuahmen. Um dies zu erreichen, müssen Sie lediglich die Trainingsmatrix ändern, wie unten dargestellt.

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
double Train[][2] {
                    {0, 1},
                    {1, 0},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 2;
const double eps = 1e-3;
//+------------------------------------------------------------------+

Wenn Sie diesen Code verwenden, erhalten Sie ein ähnliches Ergebnis wie in der folgenden Abbildung:

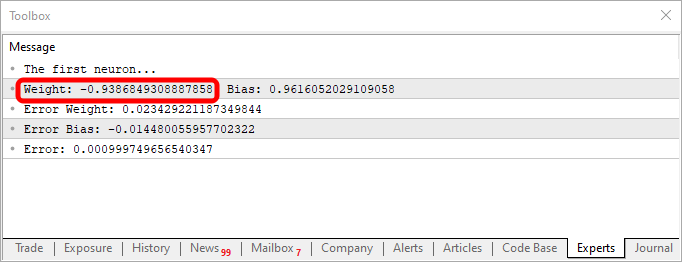
Beachten Sie, dass der Wert des Gewichts negativ ist, was bedeutet, dass wir in den Eingabewert investieren werden. Mit anderen Worten: Wir haben einen Inverter. Mit dem folgenden Code können wir eine andere Ausgabe erhalten.

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
double Train[][2] {
                    {0, 0},
                    {1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 2;
const double eps = 1e-3;
//+------------------------------------------------------------------+

Die Ausgabe ist in diesem Fall in der nachstehenden Abbildung dargestellt.

Beachten Sie, dass der Gewichtswert jetzt positiv ist. Dies bedeutet, dass wir den Eingang direkt zum Ausgang puffern. Mit anderen Worten: Wir haben einen Puffer. Sehen Sie, wie viel Spaß es macht, damit zu experimentieren?

Durch einfaches Ändern der Daten in der Wissensbasis, die in unserem Fall ein zweidimensionales Array ist, kann derselbe Code eine Gleichung erzeugen, die verschiedene Verhaltensweisen darstellt. Genau aus diesem Grund arbeiten alle, die sich für das Programmieren interessieren, gerne mit neuronalen Netzen. Es macht unglaublich viel Spaß, mit ihnen zu experimentieren.

Allerdings ist dieses erste Neuron recht begrenzt. Nicht wegen seiner Struktur, sondern weil er nur eine einzige Eingabe zulässt. In der Praxis können Neuronen in neuronalen Netzen so viele Eingänge haben, wie benötigt werden. Ebenso können sie so viele Ausgänge haben, wie zur Erfüllung ihrer Aufgaben erforderlich sind. Ich führe diese Konzepte schrittweise ein, damit Sie sich nicht überfordert fühlen. Mein Ziel ist es, Ihnen dabei zu helfen, zu verstehen, wie und warum dieser Mechanismus funktioniert. Natürlich wird es nie möglich sein, alles zu zeigen, was mit dieser Technologie möglich ist, egal wie sehr ich oder andere versuchen, es zu erklären. Denn die Möglichkeiten sind nur durch Ihre Kreativität begrenzt. Aber jetzt wollen wir die Dinge ein wenig interessanter machen und noch mehr Spaß.

Die Sigmoidfunktion

Von nun an wird alles, was ich vorstelle, nur die Spitze des Eisbergs sein. Ganz gleich, wie aufregend, komplex oder unterhaltsam das Programmieren zu sein scheint, alles, was von nun an geschieht, wird nur ein kleiner Ausschnitt dessen sein, was möglich ist. Deshalb, liebe Leserin, lieber Leser, sollten Sie jetzt damit beginnen, dieses Thema etwas selbständiger zu studieren. Mein Ziel ist es einfach, Sie auf einen Weg zu führen, der Ihnen als Inspiration für weitere Entdeckungen dient. Fühlen Sie sich frei zu erkunden, zu experimentieren und Spaß zu haben mit dem, was ich als Nächstes zeigen werde. Wie ich bereits erwähnt habe, ist die einzige wirkliche Grenze die eigene Vorstellungskraft.

Damit unser einzelnes Neuron mit mehreren Eingaben lernen kann, müssen Sie nur ein einfaches, aber entscheidendes Detail verstehen. Dies ist in der nachstehenden Abbildung dargestellt.

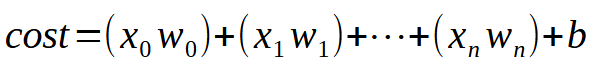
Kurz gesagt, die gleiche Gleichung ist unten angegeben.

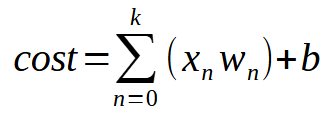
Der Wert < k > steht für die Anzahl der Eingänge, die unser Neuron haben kann. Das bedeutet, dass wir unabhängig von der Anzahl der benötigten Eingänge nur die erforderliche Anzahl von Eingängen hinzufügen müssen, damit das Neuron lernen kann, mit jeder neuen Situation umzugehen. Sobald wir jedoch eine zweite Eingabe einführen, ist die Funktion keine lineare Gleichung mehr (eine gerade Linie). Stattdessen wird sie zu einer Gleichung, die jede mögliche Form darstellen kann. Diese Änderung ist notwendig, damit sich das Neuron an eine Vielzahl von Trainingsszenarien anpassen kann.

Jetzt wird es ernst. Mit dieser Anpassung kann ein einziges Neuron nun mehrere verschiedene Muster lernen. Es gibt jedoch eine kleine Herausforderung, wenn man über einfache lineare Gleichungen hinausgeht. Um dies zu verstehen, ändern wir unser Programm wie unten gezeigt:

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
double Train[][3] {
                    {0, 0, 0},
                    {0, 1, 1},
                    {1, 0, 1},
                    {1, 1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 3;
const double eps = 1e-3;
//+------------------------------------------------------------------+
double Cost(const double w0, const double w1, const double b)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow(((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2], 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
void OnStart()
{
    double  w0, w1, err, ew0, ew1, eb, bias;

    Print("The Mini Neuron...");
    MathSrand(512);
    w0 = (double)macroRandom;
    w1 = (double)macroRandom;
    bias = (double)macroRandom;

    for (ulong c = 0; (c < 3000) && ((err = Cost(w0, w1, bias)) > eps); c++)
    {
        ew0 = (Cost(w0 + eps, w1, bias) - err) / eps;
        ew1 = (Cost(w0, w1 + eps, bias) - err) / eps;
        eb  = (Cost(w0, w1, bias + eps) - err) / eps;
        w0 -= (ew0 * eps);
        w1 -= (ew1 * eps);
        bias -= (eb * eps);
        PrintFormat("%I64u > w0: %.4f %.4f || w1: %.4f %.4f || b: %.4f %.4f || %.4f", c, w0, ew0, w1, ew1, bias, eb, err);
    }
    Print("w0 = ", w0, " || w1 = ", w1, " || Bias = ", bias);
    Print("Error Weight 0: ", ew0);
    Print("Error Weight 1: ", ew1);
    Print("Error Bias: ", eb);
    Print("Error: ", err);
}
//+------------------------------------------------------------------+

Wenn Sie diesen Code ausführen, erhalten Sie ein ähnliches Ergebnis wie in der folgenden Abbildung:

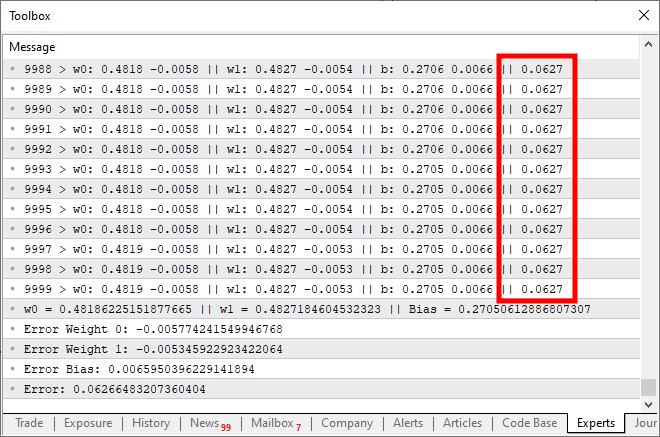
Was ist hier schief gelaufen? Wenn Sie sich den Code ansehen, sehen Sie, dass wir nur die Möglichkeit von Mehrfacheingaben hinzugefügt haben, was auch richtig gemacht wurde. Es ist jedoch interessant zu beobachten, dass die Kostenfunktion bei etwa zehntausend Iterationen nicht mehr abnimmt. Oder wenn sie immer noch abnimmt, dann extrem langsam. Warum? Der Grund dafür ist, dass unserem Neuron etwas fehlt. Etwas, das nicht notwendig war, als wir nur einen einzigen Eingang hatten, aber wesentlich wird, wenn wir mehrere Eingänge einführen. Dieses fehlende Element wird auch bei der Arbeit mit Schichten von Neuronen verwendet, einer Technik, die beim Deep Learning eingesetzt wird. Aber darauf gehen wir später noch ein. Konzentrieren wir uns erst einmal auf das Hauptthema. Unser Neuron erreicht einen Punkt der Stagnation, an dem es die Kosten einfach nicht mehr weiter senken kann. Dieses Problem lässt sich durch das Hinzufügen einer Aktivierungsfunktion am Ausgang lösen. Die spezifische Aktivierungsfunktion und ihr Verhalten hängen von der Art des Problems ab, das wir lösen wollen. Es gibt keine allgemeingültige Lösung, und es gibt viele verschiedene Aktivierungsfunktionen, die wir verwenden können. Die Sigmoidfunktion ist jedoch eine der am häufigsten verwendeten. Und der Grund dafür ist einfach. Die Sigmoidfunktion wandelt Werte, die von negativ unendlich bis positiv unendlich reichen, in einen begrenzten Bereich zwischen 0 und 1 um. In einigen Fällen werden wir sie ändern, um Werte zwischen -1 und 1 abzubilden, aber für den Moment werden wir die Basisversion verwenden. Die Sigmoidfunktion wird durch die folgende Formel definiert:

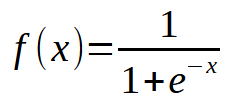
Wie können wir dies nun auf unseren Code anwenden? Auf den ersten Blick mag das kompliziert erscheinen. Aber, liebe Leserin, lieber Leser, es ist viel einfacher, als es aussieht. Tatsächlich müssen wir nur einige geringfügige Änderungen am bestehenden Code vornehmen, wie unten dargestellt:

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
#define macroSigmoid(a) (1.0 / (1 + MathExp(-a)))
//+------------------------------------------------------------------+
double Train[][3] {
                    {0, 0, 0},
                    {0, 1, 1},
                    {1, 0, 1},
                    {1, 1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 3;
const double eps = 1e-3;
//+------------------------------------------------------------------+
double Cost(const double w0, const double w1, const double b)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2]), 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
void OnStart()
{
    double  w0, w1, err, ew0, ew1, eb, bias;

    Print("The Mini Neuron...");
    MathSrand(512);
    w0 = (double)macroRandom;
    w1 = (double)macroRandom;
    bias = (double)macroRandom;

    for (ulong c = 0; (c < ULONG_MAX) && ((err = Cost(w0, w1, bias)) > eps); c++)
    {
        ew0 = (Cost(w0 + eps, w1, bias) - err) / eps;
        ew1 = (Cost(w0, w1 + eps, bias) - err) / eps;
        eb  = (Cost(w0, w1, bias + eps) - err) / eps;
        w0 -= (ew0 * eps);
        w1 -= (ew1 * eps);
        bias -= (eb * eps);
        PrintFormat("%I64u > w0: %.4f %.4f || w1: %.4f %.4f || b: %.4f %.4f || %.4f", c, w0, ew0, w1, ew1, bias, eb, err);
    }
    Print("w0 = ", w0, " || w1 = ", w1, " || Bias = ", bias);
    Print("Error Weight 0: ", ew0);
    Print("Error Weight 1: ", ew1);
    Print("Error Bias: ", eb);
    Print("Error: ", err);
}
//+------------------------------------------------------------------+

Wenn der obige Code ausgeführt wird, sieht die Ausgabe wie im folgenden Bild aus:

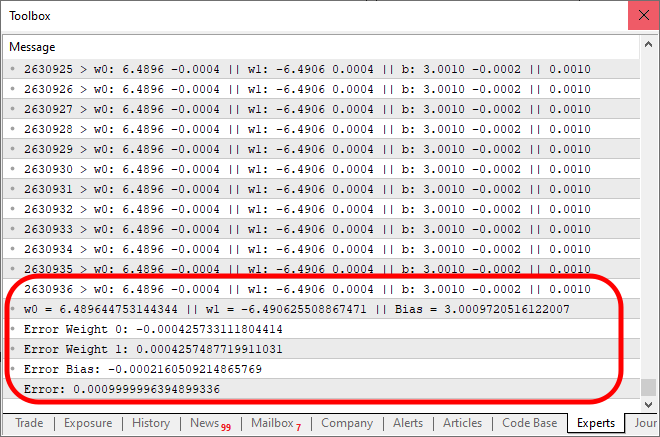
Beachten Sie: Es dauerte 2.630.936 Iterationen, bis das Ergebnis innerhalb der erwarteten Fehlerspanne konvergierte. Das ist gar nicht so schlecht. An diesem Punkt haben Sie vielleicht das Gefühl, dass das Programm etwas langsam wird, besonders wenn es auf einer CPU läuft. Diese Verlangsamung ist jedoch in erster Linie auf die Tatsache zurückzuführen, dass wir bei jeder Iteration eine Nachricht drucken. Eine einfache Möglichkeit, die Dinge zu beschleunigen, besteht darin, die Art und Weise, wie wir die Ausgabe präsentieren, zu ändern. Gleichzeitig fügen wir einen kleinen Test hinzu, um die Fähigkeiten unserer Neuronen zu bewerten. Die endgültige Version des Codes ist unten abgebildet:

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
#define macroSigmoid(a) (1.0 / (1 + MathExp(-a)))
//+------------------------------------------------------------------+
double Train[][3] {
                    {0, 0, 0},
                    {0, 1, 1},
                    {1, 0, 1},
                    {1, 1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 3;
const double eps = 1e-3;
//+------------------------------------------------------------------+
double Cost(const double w0, const double w1, const double b)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2]), 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
void OnStart()
{
    double  w0, w1, err, ew0, ew1, eb, bias;
    ulong count;

    Print("The Mini Neuron...");
    MathSrand(512);
    w0 = (double)macroRandom;
    w1 = (double)macroRandom;
    bias = (double)macroRandom;

    for (count = 0; (count < ULONG_MAX) && ((err = Cost(w0, w1, bias)) > eps); count++)
    {
        ew0 = (Cost(w0 + eps, w1, bias) - err) / eps;
        ew1 = (Cost(w0, w1 + eps, bias) - err) / eps;
        eb  = (Cost(w0, w1, bias + eps) - err) / eps;
        w0 -= (ew0 * eps);
        w1 -= (ew1 * eps);
        bias -= (eb * eps);
    }
    PrintFormat("%I64u > w0: %.4f %.4f || w1: %.4f %.4f || b: %.4f %.4f || %.4f", count, w0, ew0, w1, ew1, bias, eb, err);
    Print("w0 = ", w0, " || w1 = ", w1, " || Bias = ", bias);
    Print("Error Weight 0: ", ew0);
    Print("Error Weight 1: ", ew1);
    Print("Error Bias: ", eb);
    Print("Error: ", err);

    Print("Testing the neuron...");
    for (uchar p0 = 0; p0 < 2; p0++)
        for (uchar p1 = 0; p1 < 2; p1++)
            PrintFormat("%d OR %d IS %f", p0, p1, macroSigmoid((p0 * w0) + (p1 * w1) + bias));
}
//+------------------------------------------------------------------+

Wenn Sie diesen aktualisierten Code ausführen, wird in Ihrem Terminal eine Meldung ähnlich der in der folgenden Abbildung angezeigt:

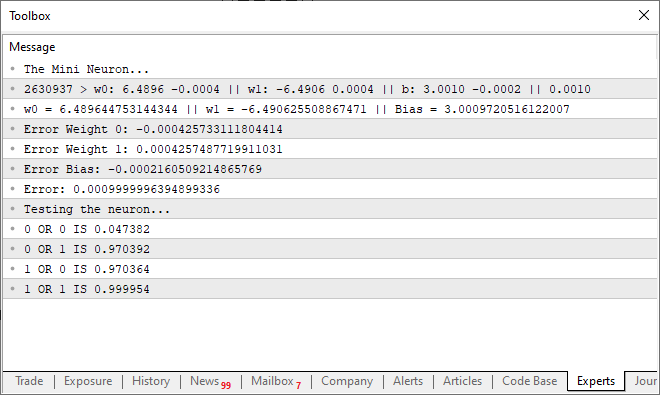
Mit anderen Worten: Wir haben unserem einfachen Neuron erfolgreich beigebracht zu verstehen, wie ein ODER-Gatter funktioniert. An diesem Punkt haben wir einen Weg eingeschlagen, der nicht mehr zurückführt. Unser einzelnes Neuron ist nun in der Lage, komplexere Beziehungen zu lernen und nicht nur festzustellen, ob zwei Werte miteinander korrelieren.

Abschließende Überlegungen

In diesem Artikel haben wir etwas gebaut, das die Leute oft verblüfft, wenn sie es in Aktion sehen. Mit nur wenigen Zeilen Code in MQL5 haben wir ein voll funktionsfähiges künstliches Neuron geschaffen. Viele glauben, dass man dafür unzählige Mittel braucht, aber ich hoffe, dass Sie, liebe Leserin, lieber Leser, jetzt sehen, wie sich die Dinge Schritt für Schritt entwickeln. In nur wenigen Artikeln habe ich Forschungsergebnisse zusammengefasst, für deren Entwicklung viele Wissenschaftler Jahre gebraucht haben. Dieses Neuron ist zwar einfach, aber es hat lange gedauert, die Logik dahinter zu entwerfen, wie es funktioniert. Auch heute noch arbeitet die Forschung daran, diese Berechnungen noch effizienter und schneller zu machen. Hier haben wir nur ein einziges Neuron mit zwei Eingängen, fünf Parametern und einem Ausgang verwendet. Sie sehen aber auch, dass es immer noch einige Zeit dauert, die richtige Gleichung zu finden.

Natürlich könnten wir OpenCL verwenden, um die Berechnungen über die GPU zu beschleunigen. Meiner Meinung nach ist es jedoch noch zu früh, eine solche Optimierung einzuführen. Wir können noch weiter fortschreiten, bevor wir wirklich eine GPU-Beschleunigung für die Berechnungen benötigen. Wenn Sie sich jedoch ernsthaft mit neuronalen Netzen befassen wollen, empfehle ich Ihnen dringend die Investition in einen Grafikprozessor. Sie wird bestimmte Prozesse beim Training neuronaler Netze erheblich beschleunigen.

Im Anhang finden Sie den endgültigen Code aus diesem Artikel. Sie können es gerne verwenden, damit experimentieren und Spaß haben. Beobachten Sie, wie dieses Neuron mit verschiedenen Situationen umgeht, und versuchen Sie, seine Grenzen zu erkennen, denn es gibt sie. Deshalb gibt es noch viel mehr zu erforschen.