Новый подход к пользовательским критериям при оптимизациях (Часть 1): Примеры функций активации

Введение

Поиск идеальной оптимизации для получения правильного сочетания параметров продолжается. Форум переполнен предложениями методов, чтобы убедить оптимизатор MetaTrader возвращать и ранжировать разные проходы для обеспечения разработчику возможности выбора комбинации (или комбинаций) параметров, которые будут сохранять стабильность. Появление на рынке частных компаний с их четкими границами, которые, по понятным причинам, намного строже тех, что могут потребоваться индивидуальному трейдеру, усложнило ситуацию.

Возможность определить пользовательский критерий и даже использовать такой критерий с его непрозрачной методологией повлекла за собой возможность сократить парсинг или, как минимум, анализ результатов в Excel, Python, R или собственном программном обеспечении для получения наилучшего сочетания параметров.

Проблема в том, что в опубликованных пользовательских критериях до сих пор нередко можно встретить использование return(0). Это чревато реальными или потенциальными рисками, включая возможность сброса (вряд ли) нежелательных результатов, или еще хуже — отклонить процесс генетической оптимизации от потенциально продуктивных путей.

В попытке вернуться к некоторым первоосновам и проведя несколько очень эмпирических экспериментов, я попытался найти некоторые уравнения кривых. Для этого я просмотрел статью «Activation Functions in Neural Networks» и кое-что из нее использовал здесь с некоторыми изменениями. Кроме того, разобравшись с этим, я предложил некоторые методы для практической реализации.

Вот план этой серии статей:

1. Введение и стандартные функции активации при помощи MQL5-кода
2. Модификации, масштабирование и взвешивание, а также примеры из реальной практики
3. Инструмент для использования различных кривых, масштабирования и взвешивания
4. и иные возникающие вопросы...

Текущее состояние применения пользовательских критериев

Два участника, к которым я испытываю огромное уважение, сделали несколько отличных замечаний, чтобы проиллюстрировать проблему, выразив обеспокоенность по поводу использования return(0) и результатов, которые возвращает Complex Criterion (сложный критерий). Модератор форума Ален Верлейен сообщает о проходе, вернувшем убыток в размере 6000, то есть более высокий результат, чем у прохода, вернувшего прибыль 1736, с более высоким количеством сделок (и показавшего существенно более хорошие данные по профит-фактору, фактору риска, коэффициенту Шарпа И просадке). Как говорит Ален, «таинственный «комплексный критерий» выдает какие-то странные результаты». Я бы даже сказал, что это без сомнения ставит под сомнение методологию, лежащую в основе комплексного критерия. Если действительно, как комментирует Мухаммад Фахад позднее в той же ветке, - и я уверен, что он прав, - «отрицательные результаты по балансу не так уж плохи для оптимизации, ведь они играют решающую роль в суждении будущего поколения о плохом из худшего при скрещивании генов», возвращение такой положительной оценки, вероятно, может сбить с толку генетический оптимизатор.

Прошло очень много времени с тех пор, как я пользовался MT4, но смутно припоминаю возможность вводить ограничения на определенные статистические данные о результатах. На первый взгляд кажется, что в MQL5 невозможно сделать это, если только не использовать в пользовательском критерии очень простой инструмент return(0), потенциальные недостатки которого уже упоминались. Мне представляется, что если мы сможем получить возвращаемое значение, очень близкое к 1, когда соотношение или показатель равны или выше нашего желаемого минимума, равны или ниже нашего желаемого максимума или даже равны или близки к конкретному целевому значению, а затем перемножить значения каждого показателя или соотношения, а затем умножить результат на 100, то, возможно, мы в чем-то разберемся...

Зачем искать вдохновение в нейронных сетях?

i) Генетическая оптимизация как нейросеть... 

Независимо от того, основан генетический алгоритм на нейросети или нет, логический процесс представляется одинаковым: попробовать параметрическую комбинацию, оценить ее (в соответствии с выбранным критерием оптимизации), сохранить потенциально прибыльные варианты для последующего улучшения и отбросить остальные. Это повторяется до тех пор, пока не будет достигнуто максимальное улучшение выбранного показателя.

ii) Впадины, взрывные градиенты, взвешивание, нормализация и ручной отбор 

Проблема невыпуклой поверхности ошибок хорошо известна в области машинного обучения. Аналогичным образом, представляется, что при генетической оптимизации мы могли бы прийти к локальным минимумам или седловым точкам, неверно направленным операторами return(0), из-за чего генетический алгоритм отбрасывал бы «знания».

Кроме того, обработка различных показателей для создания пользовательского критерия требует серьёзных размышлений... мои ранние попытки были очень грубыми, с использованием различных коэффициентов для деления и умножения, не говоря уже об экспоненциальных множителях, что приводило к результатам, близким к невероятно высоким (взрывной градиент)... Алгоритм оценки комплексного критерия явно использует функцию для ограничения оценки в диапазоне от 0 до 100, что указывает на использование в нем функции сигмоидного или логистического типа.

Необходимость применения весовых коэффициентов к отдельным компонентам пользовательского критерия понятна: нужно использовать весовые коэффициенты для определения приоритетности разных компонентов и нормализации как входных данных для настройки чувствительности нашей модели, так и выходных — для обеспечения возможности сравнения моделей. Взвешивание и нормализацию рассмотрим в следующей статье.

Просматривая прогон оптимизации вручную или с помощью электронной таблицы, мы можем сортировать их по различным выходным показателям, отфильтровывать результаты и быстро, практически на подсознательном уровне, выделять наборы параметров по цвету ключевых показателей. Здесь мы просто повторно применяем описанные процессы, которые сами являются попыткой имитировать нашу собственную интеллектуальную обработку полного результата.

Функции активации в нейросетях

Мне приходит в голову, что функции, которые я искал, были похожи на те, которые мне встретились год или два назад, когда я просматривал статью Activation Functions in Neural Networks.

Функции активации в нейросетях можно условно разделить на три типа: бинарные, линейные и нелинейные.

• Бинарные функции относят значения к 1 из 2 классов, возвращая 1 или 0. В нашем случае они не особенно полезны.
• Линейные функции возвращают преобразования путем простого сложения, умножения, вычитания или деления либо их сочетания. В нашем случае они тоже малополезны.
• Нелинейные функции возвращают кривые результатов, ограниченные крайними значениями x, но позволяют различать значения x в пределах диапазона с центром в 0. Этот диапазон и центр можно изменять с помощью смещений.

Следует отметить, что использование

return(0);

а также неограниченное возвращение многочисленных показателей результатов (причем я был повинен в обоих и продолжаю наблюдать их на форумах), являются методами, которые воспроизводят проблемы, связанные с этими первыми двумя классами; с другой стороны, нелинейные функции, как правило, ограничиваются предотвращением взрывных градиентов, сохраняя при этом градиент от -∞ до ∞.

В качестве пояснения приведу несколько стандартных примеров. Рассмотрим ReLU, Softplus, Sigmoid и Tanh, а также (в следующей статье) мои собственные модификации: Flipped ReLU, Point ReLU, Flipped Sigmoid, Point Sigmoid, Flipped Tanh и Point Tanh.

a) Функция активации ReLU

Задача этой функции — возвращать ноль, когда x <= 0, или x, если x > 0 или, в математической записи, f(x) = max(0,x). Полученная линия показана ниже, а функцию MQL5 можно определить следующим образом:

double ReLU(double x) {
   return(MathMax(0, x));
}

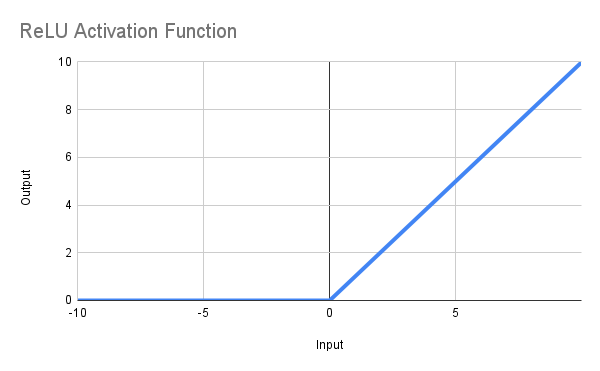
Пока все хорошо, можете сказать вы, но я хочу установить минимальное значение Recovery Factor на 5 или выше... ну, просто изменим код на *:

input double MinRF = 5.0;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double DeviationRF = RF - MinRF;

double ReLU(double x) {
   return(MathMax(0, x));
}

double ScoreRF = ReLU(DeviationRF);

смещая таким образом линию вправо, начиная с 0 при RF = 5.0, как показано на рисунке:

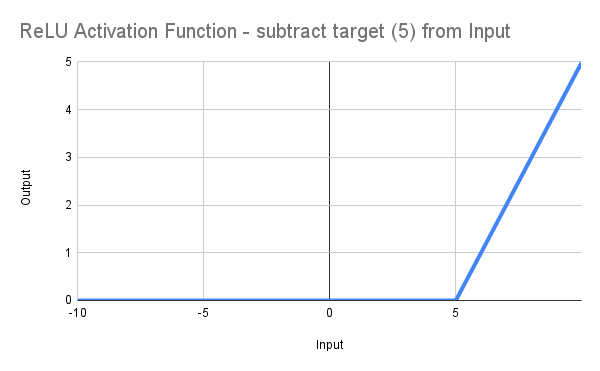
Это, конечно, едва ли такой высокий уровень, как написать*

input double MinRF = 5.0;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double ScoreRF = (RF - MinRF);

но позволяет нам начать...

*еще одна проблема состоит в том, что целевое значение 5 фактически вернет 0 и только значения >5 вернут ненулевое значение. Я не намерен тратить время на этот вопрос, поскольку разнообразные другие проблемы с этой функцией исключают возможность ее дальнейшего использования в нашем случае.

Проблемы

Вскоре становится понятно, что у нас по-прежнему 2 проблемы, и обе они представляют собой функцию от простоты, присущей нашему коду... Выше я сказал:

«Это, конечно, едва ли такой высокий уровень, как написать

input double MinRF = 5.0;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double ScoreRF = (RF - MinRF);

но позволяет нам начать...»

В нейросетях хорошо распознаются следующие проблемы:

• Умирающий ReLU: главной слабостью ReLU является тот факт, что нейроны могут постоянно «умирать», если на выходе будут только нули. Это происходит, когда сильные отрицательные входные сигналы создают нулевые градиенты, делая эти нейроны неактивными и неспособными продолжать обучение. Это также называется проблемой исчезающего градиента.

• Неограниченный выход: выходные данные ReLU могут становиться бесконечно большими для положительных входных данных, в отличие от функций Sigmoid и Tanh, у которых имеются встроенные верхние пределы. Такое отсутствие ограничения сверху иногда может стать причиной проблем взрывного градиента во время обучения глубоких нейросетей. Это также называется проблемой взрывного градиента.

В статистике вторую из проблем решают при помощи нормализации значений в пределах окна наблюдения, но в пределах возможностей оптимизатора этот метод нам недоступен.

Поэтому нам нужно решение, которое будет

1. математически генерировать ограничение, обеспечивая автоматическую нормализацию; а также
2. обеспечивать некоторую степень линейности, а не возвращать 0, на значительной части выборки...

b) Функция активации Softplus

В рамках данной статьи я не собираюсь вдаваться в подробности, но вскользь упомяну об этой функции как об этапе между ReLU и функциями более высокого порядка. Она хорошо описана на сайте Geeksforgeeks, так что я просто опубликую следующее изображение, формулу и код. Должно быть очевидно, что при решении задачи умирающего ReLU сохраняется проблема неограниченного выхода. Кроме того, существует плавный переход между очень пологим «хвостом» и уклоном справа. Это приводит к необходимости учитывать смещение коррекции - концепция, к которой мы вернемся позднее:

Формула: Softplus(x) = ln(1 + e^x), а MQL5-код:

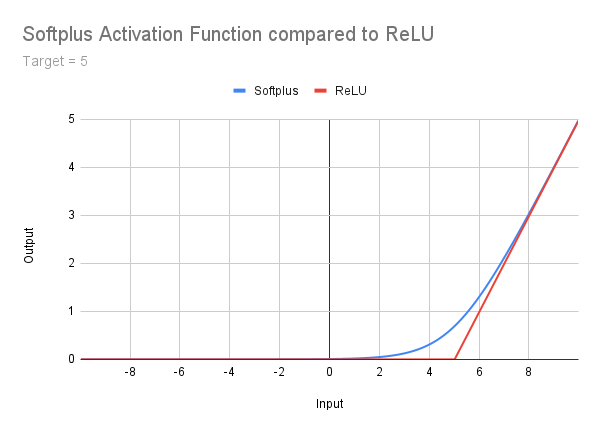
double Softplus(double x) {
   return(MathLog(1 + MathExp(x)));
}

Наслаждайтесь чтением, если желаете, но мы сейчас переходим к функциям, которые дают нам ограниченные результаты в диапазоне от 0 до 1...

c) Функция активации Sigmoid

Сигмоидная функция математически выражается как f(x) = 𝛔(x) = 1 / (1 + e^(-x)). Она идентична производной от функции Softplus, и в MQL5 ее можно запрограммировать следующим образом:

double Sigmoid(double x) {
   return(1 / (1 + MathExp(-x)));
}

Глядя на кривую (ниже), сразу бросается в глаза, что

1. она ограничивается диапазоном от 0 до 1, решая таким образом нашу проблему неограниченного выхода;

2. хотя ее трудно оценить в таком масштабе, переменный градиент, который никогда не становится равным нулю, поддерживается в диапазоне от -∞ до ∞; 

3. при значении 0 несмещенная кривая оценивается как 0.5.

Чтобы разобраться с 3), то есть приблизиться к 1, когда x == наше пороговое (целевое) значение, необходимо сместить кривую влево не только на наше пороговое значение, но и на поправку, что практически достигается с помощью применения значения поправки >= 5. 

Поэтому реализация на языке MQL5 выглядит так:

input double MinRF = 5.0;
sinput double SigCorrection = 5;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double DeviationRF = RF - MinRF;

double CorrectedSigmoid(double x) {
   return(1 / (1 + MathExp(-(x - SigCorrection))));
}

double ScoreRF = CorrectedSigmoid(DeviationRF);

Ниже представлена кривая нескорректированной сигмоидной функции для целевого значения 5 вместе с производной (умноженной на 4), которая будет обсуждаться далее.

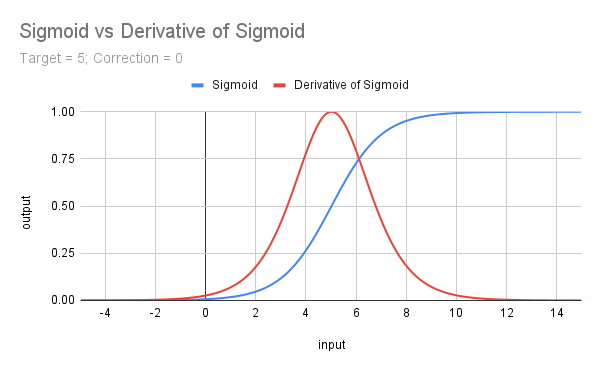
d) Производная сигмоиды (𝛔')

Она дает нам прекрасную фигуру, расположенную в центре и увеличенную до максимума при x = 0... Она представляет собой наклон сигмоидной функции, а формула имеет вид f(x) = 𝛔(x) - 𝛔^2(x) или 𝛔(x) * (1 - 𝛔(x)). 

Потенциально функция (как и все нефункции, которые мы будем рассматривать) от проблемы исчезающего градиента, риск которой можно уменьшить простым приемом умножения ее на 4 (поскольку 𝛔’(x) = 0.25), что тоже полезно, так как еще раз ограничивает результат в пределах от 0 до 1. Центрирование на значении x позволяет нам нацелиться на точку или, точнее, на диапазон с центром в точке.

В MQL5 мы можем сделать так:

input double TargetTrades = 100;

double Trades = TesterStatistics(STAT_TRADES);
double DeviationTrades = Trades - TargetTrades;

double Sigmoid(double x) {
   return(1 / (1 + MathExp(-x)));
}

double Deriv4Sigmoid(double x) {
   return(4 * (Sigmoid(x) * (1 - Sigmoid(x))));
}

double ScoreTrades = Deriv4Sigmoid(DeviationTrades);

Примечание: поскольку наши результаты для сигмоиды, ее производной (умноженной на 4) и рассмотренных ниже Tanh и ее производной, масштабированных до диапазона от 0 до 1, ограничены диапазоном от 0 до 1, нам нет необходимости добавлять в произведение какую-либо дополнительную скалярную величину. Конечно, мы можем умножить их на любой коэффициент, чтобы нормализовать их или отдать им приоритет по сравнению с любыми другими коэффициентами оптимизации, которые мы можем включить в наш окончательный пользовательский критерий. Рассмотрим этот вопрос в следующей статье.

Нам осталось рассмотреть еще одну последнюю стандартную функцию, и это — Tanh...

e) Гиперболический тангенс, или Tanh

Tanh — последняя из наших функций активации, которую мы собираемся изучить в своих поисках полезного зерна в пользовательских критериях. Буду следовать аналогичной схеме, но с меньшим количеством объяснений, чем в предыдущих описаниях, но с применением тех же принципов.

На следующем изображении показан график функции Tanh и ее производной.

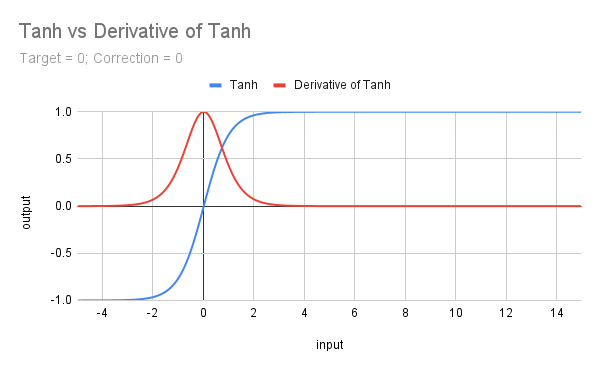
Формула для Tanh: f(x) = (e^x - e^(-x))/(e^x + e^(-x)), и в MQL5 у нее есть собственная функция, так что код написать не составит труда. Конечно, придется иметь дело с целевыми значениями и поправочными коэффициентами, но это все равно упрощает жизнь:

input double MinRF = 5.0;
sinput double TanhCorrection = 2.5; // Anything between 2 and 3 would be reasonable (see last figure)

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double DeviationRF = RF - MinRF;

double CorrectedRSTanh(double x) {
   return((MathTanh(x  + TanhCorrection) + 1) / 2);  // rescaled and corrected
}

double ScoreRF = CorrectedRSTanh(DeviationRF);

Приведенный выше код изменяет масштаб базовой функции, ограничивая ее в диапазоне от 0 до 1 (путем прибавления 1 и деления на 2). Кроме того, он вводит поправочный коэффициент и целевой показатель, а результирующая кривая показана на следующем графике, иллюстрирующем производную Tanh. Ни для кого не должно остаться незамеченным, что Tanh имеет схожую форму с сигмоидой, а производные — друг с другом; мы рассмотрим эти признаки сходства в следующей статье.

f) Производная от Tanh

Математическая формула для производной от Tanh: f(x) = 1 - Tanh^2(x).

В MQL5 мы можем сделать так:

input double TargetTrades = 100;

double Trades = TesterStatistics(STAT_TRADES);
double DeviationTrades = Trades - TargetTrades;

double DerivTanh(double x) {
   return(1 - MathPow(x, 2));

}double ScoreTrades = DerivTanh(DeviationTrades);

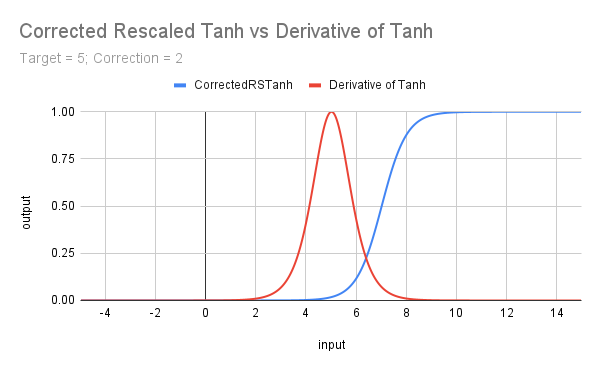
На этом следующем графике показан эффект изменения масштаба Tanh, корректируя его для приближения начала от 0 с целевым (пороговым) значением x и вводя целевое значение как для Tanh, так и для производной от Tanh.

Обобщение и следующие шаги

В этой статье мы кратко рассмотрели взаимосвязь между машинным обучением, с одной стороны, и процессом оптимизации с «постобработкой» (генетической или полной), а также постобработкой в Excel или вручную. Мы начали изучать способы, которыми различные типы функций активации могут уточнять пользовательские критерии, а также способы их кодирования.

Проблемы исчезающих и взрывных градиентов в функциях ReLU и Softplus заставили нас обратить внимание на функции с кривыми, подобными кривым сигмоидной функции, а также кривым ее производной. Мы увидели, как они позволяют нам отдавать в своих оценках предпочтение диапазонам с одной границей (т. е. x > t) или диапазонам, ограниченным с обеих сторон (t1 < x < t2), устраняя при этом проблему взрывных градиентов и уменьшая воздействие проблемы исчезающих градиентов.

Мы рассмотрели использование корректировочных смещений и целевых смещений, чтобы обеспечить концентрацию на желаемых диапазонах значений атрибутов.

В следующей статье рассмотрим некоторые модификации этого списка стандартных функций со сходными, но не идентичными атрибутами. Кроме того, изучим идею масштабирования и взвешивания, прежде чем рассматривать примеры использования различных функций в пользовательских критериях.