
Возможности Мастера MQL5, которые вам нужно знать (Часть 23): CNN
Введение
Мы продолжаем рассматривать идеи машинного обучения и статистики, которые могут быть полезны трейдерам, в контексте быстрого тестирования и прототипирования в Мастере MQL5. Цель по-прежнему заключается в рассмотрении одной идеи в рамках одной статьи. Изначально я думал, что для этой части потребуется как минимум две статьи, но всё же рискнул втиснуть информацию в одну. Как следует из названия, сверточные нейронные сети (Convolutional Neural Networks, CNNs) обрабатывают многомерные данные в свертках с помощью ядер.
Эти ядра несут на себе сетевые веса и, как и многомерные входные данные, обычно имеют матричную форму. Они имеют меньшие общие размеры по сравнению с входными данными. Выполняя итерацию по матрице входных данных при прямом распространении (feed forward), каждая итерация по сути циклически проходит по входным данным. Именно из-за этого "цикла" сети и называют "сверточными".
Итак, в этой статье мы познакомимся с ключевыми этапами работы CNN, создадим простой класс MQL5, реализующий эти этапы, интегрируем этот класс в пользовательский класс сигналов Мастера MQL5 и, наконец, выполним тестовые запуски с помощью советника, собранного из этого класса сигналов.
CNN, как правило, представляют собой сложные нейронные сети, основные области применения которых — обработка видео и изображений, как мы видели в случае с генеративно-состязательными сетями (GAN) в предыдущей статье. Однако в отличие от сетей GAN, которые обучены отличать реальные изображения и/или объекты на изображениях от подделок, сети CNN, как правило, работают скорее как классификаторы, поскольку они разделяют входные данные (которые часто представляют собой пиксели изображения) на различные подгруппы данных, причем каждая подгруппа призвана фиксировать ключевое или очень важное свойство входных данных. Эти созданные подгруппы часто называют картами признаков (feature maps).
Для получения этих карт признаков необходимы следующие шаги: заполнение (padding), прямое распространение (feeding fotwards), активация (activation), субдискретизация (pooling) и, наконец, если сеть обучена, обратное распространение (back propagation). Ниже мы рассмотрим каждый из этих шагов на примере очень простой однослойной сверточной нейронной сети. Говоря об одном слое, мы подразумеваем, что входные данные обрабатываются проходя один слой ядер. В случае со сверточными нейронными сетям такое происходит не всегда, поскольку они могут охватывать много слоев, так что каждый из четырех упомянутых выше шагов (заполнение, прямое распространение, активация и субдискретизация) повторяется для каждого слоя. В многослойных конфигурациях подразумевается, что для каждой карты признаков, созданной на более высоком уровне, существуют другие ключевые свойства компонентов, которые в дальнейшем разделяются на новые карты признаков.
Заполнение (padding)
Этот необязательный этап знаменует начало CNN. Что такое заполнение? Это просто добавление границы данных по краям входных данных. По сути, входные данные получают отступы. Напомним, что входные данные обычно имеют более одного измерения, фактически они часто двумерны, поэтому матричное представление часто оказывается целесообразным. Изображения состоят из пикселей в плоскости XY, поэтому их классификация с помощью сверточной нейронной сети проста.
Для чего нужно заполнение? Необходимость в нем возникает из-за характера свертки с ядрами на этапе прямого распространения. Ядра, как и входные данные, также имеют матричную форму. Они содержат веса сети. Обычно слой имеет более одного ядра, поскольку каждое ядро отвечает за вывод определенной карты признаков.
Процесс умножения весов в ядре на входные данные происходит в течение итерации или цикла, или, что является синонимом, свертки. Конечным результатом умножения является матрица карты признаков, размеры которой всегда меньше входных данных. Таким образом, смысл заполнения заключается в том, что в случае, если пользователь захочет, чтобы карта признаков имела те же размеры, что и необработанные входные данные, к входным данным необходимо будет добавить дополнительные границы данных.
Если мы рассмотрим матрицу входных данных размером 6 x 6 и ядро весов размером 3 x 3, то прямое умножение весов даст нам матрицу размером 4 x 4, как указано выше. Формула для размера выходной матрицы с учетом размера входных данных и размера матрицы ядра имеет вид:
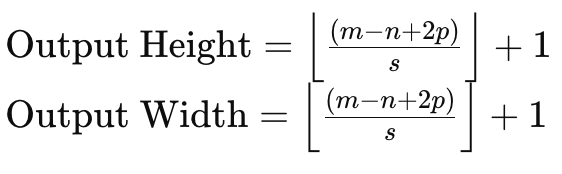
где:
- m — размерность матрицы входных данных,
- n — размерность ядра весов,
- p — размер заполнения,
- s — размер шага.
Таким образом, если нам необходимо сохранить размер матрицы входных данных в картах признаков, нам необходимо будет дополнить матрицу входных данных на величину, которая учитывает не только размер матрицы входных данных и матриц ядра, но и величину используемого шага.
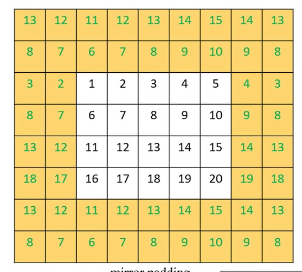
В основном существует 3 метода заполнения. Первый — это заполнение нулями, при котором вдоль границы входной матрицы добавляются нули для соответствия требуемой ширине. Вторая форма отступа — это отступ по краю, при котором числа на краю матрицы повторяются вдоль новой границы также для соответствия новому целевому размеру. И, наконец, есть отраженное заполнение, при котором числа на новой увеличенной границе берутся из матрицы входных данных, а числа вдоль ее края действуют как зеркальная линия.
< 
После завершения заполнения можно приступать к этапу прямого заполнения. Как уже упоминалось, заполнение является необязательным. Если пользователю не требуются карты объектов соответствующего размера, его можно пропустить. Например, рассмотрим ситуацию, когда CNN должна просматривать множество изображений и извлекать из них фотографии человеческих лиц.
Карта признаков или выходные изображения из каждой итерации неизбежно будут иметь меньше пикселей и, следовательно, размеров, чем входное изображение, поэтому в этом случае делать начальную загрузку или увеличивать входное изображение может оказаться бессмысленным занятием. Заполнение реализуется в следующем листинге:
//+------------------------------------------------------------------+ //| Pad | //+------------------------------------------------------------------+ void Ccnn::Pad() { if(!validated) { printf(__FUNCSIG__ + " network invalid! "); return; } if(padding != PADDING_NONE) { matrix _padded; _padded.Init(inputs.Rows() + 2, inputs.Cols() + 2); _padded.Fill(0.0); for(int i = 0; i < int(_padded.Cols()); i++) { for(int j = 0; j < int(_padded.Rows()); j++) { if(i == 0 || i == int(_padded.Cols()) - 1 || j == 0 || j == int(_padded.Rows()) - 1) { if(padding == PADDING_ZERO) { _padded[j][i] = 0.0; } else if(padding == PADDING_EDGE) { if(i == 0 && j == 0) { _padded[j][i] = inputs[0][0]; } else if(i == 0 && j == int(_padded.Rows()) - 1) { _padded[j][i] = inputs[inputs.Rows() - 1][0]; } else if(i == int(_padded.Cols()) - 1 && j == 0) { _padded[j][i] = inputs[0][inputs.Cols() - 1]; } else if(i == int(_padded.Cols()) - 1 && j == int(_padded.Rows()) - 1) { _padded[j][i] = inputs[inputs.Rows() - 1][inputs.Cols() - 1]; } else if(i == 0) { _padded[j][i] = inputs[j - 1][i]; } else if(j == 0) { _padded[j][i] = inputs[j][i - 1]; } else if(i == int(_padded.Cols()) - 1) { _padded[j][i] = inputs[j - 1][inputs.Cols() - 1]; } else if(j == int(_padded.Rows()) - 1) { _padded[j][i] = inputs[inputs.Rows() - 1][i - 1]; } } else if(padding == PADDING_REFLECT) { if(i == 0 && j == 0) { _padded[j][i] = inputs[1][1]; } else if(i == 0 && j == int(_padded.Rows()) - 1) { _padded[j][i] = inputs[inputs.Rows() - 2][1]; } else if(i == int(_padded.Cols()) - 1 && j == 0) { _padded[j][i] = inputs[1][inputs.Cols() - 2]; } else if(i == int(_padded.Cols()) - 1 && j == int(_padded.Rows()) - 1) { _padded[j][i] = inputs[inputs.Rows() - 2][inputs.Cols() - 2]; } else if(i == 0) { _padded[j][i] = inputs[j - 1][1]; } else if(j == 0) { _padded[j][i] = inputs[1][i - 1]; } else if(i == int(_padded.Cols()) - 1) { _padded[j][i] = inputs[j - 1][inputs.Cols() - 2]; } else if(j == int(_padded.Rows()) - 1) { _padded[j][i] = inputs[inputs.Rows() - 2][i - 1]; } } } else { _padded[j][i] = inputs[j - 1][i - 1]; } } } // Set(_padded, false); } }
Так как мы трейдеры, а не специалисты по визуализации, нам понадобится матрица входных данных значений индикаторов. Значения этих индикаторов можно настраивать в соответствии с широким спектром параметров, однако мы выбрали близкие ценовые разрывы из различных индикаторов скользящих средних.
Прямое распространение (свертка, Convolve)
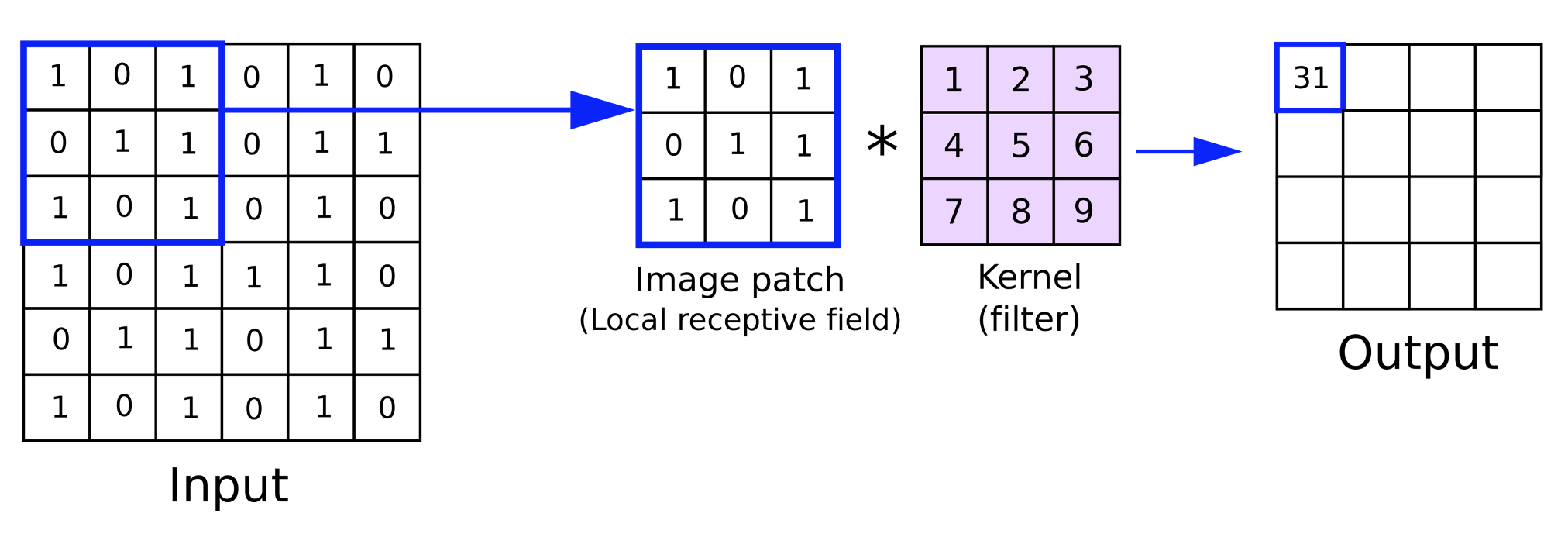
После подготовки входных данных выполняется умножение весов для входных данных для каждого ядра в слое для создания карты признаков. Помимо умножения весов, которое дает матрицу меньшего размера, к каждому значению матрицы добавляется смещение, и это смещение, как и соответствующие веса, является уникальным для каждого ядра.
Каждое ядро имеет веса и смещение, которые специализируются на извлечении ключевого признака или свойства входных данных. Таким образом, чем больше функций кто-то хочет собрать, тем больше ядер он будет использовать в сети. Прямое распространение выполняется функцией Convolve:
//+------------------------------------------------------------------+ //| Convolve through all kernels | //+------------------------------------------------------------------+ void Ccnn::Convolve() { if(!validated) { printf(__FUNCSIG__ + " network invalid! "); return; } // Loop through kernel at set padding_stride for (int f = 0; f < kernels; f++) { bool _stop = false; int _stride_row = 0, _stride_col = 0; output[f].Fill(0.0); for (int g = 0; g < int(output[f].Cols()); g++) { for (int h = 0; h < int(output[f].Rows()); h++) { for (int i = 0; i < int(kernel[f].weights.Cols()); i++) { for (int j = 0; j < int(kernel[f].weights.Rows()); j++) { output[f][h][g] += (kernel[f].weights[j][i] * inputs[_stride_row + j][_stride_col + i]); } } output[f][h][g] += kernel[f].bias; _stride_col += padding_stride; if(_stride_col + int(kernel[f].weights.Cols()) > int(inputs.Cols())) { _stride_col = 0; _stride_row += padding_stride; if(_stride_row + int(kernel[f].weights.Rows()) > int(inputs.Rows())) { _stride_col = 0; _stride_row = 0; } } } } } }
Активация (activation)
После свертки полученные матрицы будут активированы так же, как и при нескольких слоях. Однако при обработке изображений наиболее распространенной целью активации является внедрение в модель возможности отображать нелинейные данные таким образом, чтобы можно было фиксировать и более сложные соотношения (например, квадратные уравнения). Распространенными алгоритмами активации являются ReLU, "дырявый" (leaky) ReLU, Sigmoid и Tanh.
ReLU, пожалуй, является наиболее популярным алгоритмом активации, поскольку он гораздо лучше справляется с проблемами исчезающего градиента, однако он сталкивается с проблемой мертвых нейронов, которая устраняется с помощью "дырявого" ReLU. Проблема мертвых нейронов относится к ситуациям, когда выходные данные сети обновляются до постоянных значений независимо от изменений входных данных. Это может иметь большое значение в сетях, которые инициализируются с весами и предоставляют отрицательные входные данные. В таком случае статические выходные данные будут получены независимо от изменчивости отрицательных входных данных. Это может произойти даже в ходе обучения, что неизбежно приведет к деформации весов. Это привело бы к потере репрезентативной способности, что сделало бы модель неспособной представлять более сложные закономерности. При обратном распространении поток градиентов через сеть будет происходить с более медленной сходимостью или даже с полной стагнацией.
Таким образом, "дырявый" ReLU частично смягчает проблему, позволяя назначать небольшое оптимизируемое положительное значение alpha в качестве небольшого наклона для отрицательных входных данных, так что нейроны с отрицательными входными данными не погибают, а по-прежнему вносят вклад в процесс обучения. Более плавный градиентный поток при обратном распространении также приводит к более стабильному и эффективному обучению, чем в обычном ReLU.
Субдискретизация (pooling)
После активации характерных изображений, которые являются результатами свертки, они проверяются на наличие шума в ходе субдискретизации. Это процесс уменьшения размеров карт признаков по высоте и ширине. Целью субдискретизации является снижение вычислительной нагрузки и уменьшение количества параметров, с которыми приходится иметь дело сети. Объединение также способствует инвариантности трансляции, позволяя определять ключевые свойства каждой карты признаков с минимальными данными.
В основном существует 3 типа субдискретизации, а именно: максимальная, средняя и глобальная. Максимальная выбирает максимальное значение в каждом фрагменте матрицы признаков в точке свертки. И каждая из выбранных точек объединяется в новую матрицу Сторонники подхода утверждают, что он сохраняет большинство критических свойств объединенной карты признаков, одновременно снижая вероятность переобучения.
Средняя субдискретизация вычисляет среднее значение каждого участка во время свертки и, как и в предыдущем случае, возвращает его в объединенную матрицу. На размер объединенной матрицы влияет не только размер окна субдискретизации и его отличие от карты признаков, но и шаг. Часто используются шаги со значением больше 1, что неизбежно делает объединенную матрицу значительно меньше карты признаков. В этой статье мы используем шаг, равный единице, поскольку хотим упростить задачу, учитывая вводный характер статьи. Сторонники средней субдискретизации утверждают, что этот подход более тонкий и менее агрессивный, и поэтому при нем меньше вероятность упустить из виду критически важные особенности.
В случае глобальной субдискретизации свертки не выполняются, вместо этого вся карта признаков сводится к одному значению путем взятия среднего значения карты признаков или выбора ее максимального значения. Такой подход можно применять на последнем уровне многослойных сверточных нейронных сетей, где для каждого ядра назначается одно значение.
Размеры окна и шага субдискретизации являются основными факторами, определяющими размер объединенных данных. Более крупные шаги, как правило, приводят к меньшим объемам объединенных данных, в то время как, с другой стороны, размер карты признаков и размер окна находятся в обратной зависимости. Меньшие размеры объединенных данных значительно сокращают количество сетевых активаций и требования к памяти. Листинг субдискретизации в MQL5:
//+------------------------------------------------------------------+ //| Pool | //+------------------------------------------------------------------+ void Ccnn::Pool() { if(!validated) { printf(__FUNCSIG__ + " network invalid! "); return; } if(pooling != POOLING_NONE) { for(int f = 0; f < int(output.Size()); f++) { matrix _pooled; if(output[f].Cols() > 2 && output[f].Rows() > 2) { _pooled.Init(output[f].Rows() - 2, output[f].Cols() - 2); _pooled.Fill(0.0); for (int g = 0; g < int(_pooled.Cols()); g++) { for (int h = 0; h < int(_pooled.Rows()); h++) { if(pooling == POOLING_MAX) { _pooled[h][g] = DBL_MIN; } for (int i = 0; i < int(output[f].Cols()); i++) { for (int j = 0; j < int(output[f].Rows()); j++) { if(pooling == POOLING_MAX) { _pooled[h][g] = fmax(output[f][j][i], _pooled[h][g]); } else if(pooling == POOLING_AVERAGE) { _pooled[h][g] += output[f][j][i]; } } } if(pooling == POOLING_AVERAGE) { _pooled[h][g] /= double(output[f].Cols()) * double(output[f].Rows()); } } } output[f].Copy(_pooled); } } } }
Обратное распространение (Evolve)
Как и в любой нейронной сети, это этап, на котором веса и смещения сети "обучаются" посредством корректировки. Корректировка выполняется в процессе обучения, и частота этого обучения определяется используемой моделью. Что касается финансовых моделей, используемых трейдерами, некоторые модели можно запрограммировать на обучение своих сетей раз в квартал, например, для корректировки последних новостей о доходах компаний, в то время как другие могут проводить обучение раз в месяц в даты после выхода ключевых новостей экономического календаря. Суть в том, что наличие правильных весов и смещений сети, безусловно, важно, но, возможно, еще важнее наличие четкого предустановленного режима обучения и обновления этих весов и смещений.
Существуют ли сети, которые можно было бы обучить один раз и использовать после этого, не беспокоясь об обучении? Возможно, хотя во многих случаях маловероятно. Поэтому разумно всегда иметь под рукой календарь обучения сети, если вы собираетесь торговать с использованием нейронной сети.
Таким образом, три типичных шага при любом обратном распространении включают в себя: вычисление ошибки и использование дельты ошибки для расчета градиентов, а затем применение этих градиентов для обновления весов и смещений. Мы выполняем все три этих шага в функции Evolve, код которой представлен ниже:
//+------------------------------------------------------------------+ //| Evolve pass through the neural network to update kernel | //| and biases using gradient descent | //+------------------------------------------------------------------+ void Ccnn::Evolve(double LearningRate = 0.05) { if(!validated) { printf(__FUNCSIG__ + " network invalid! "); return; } for(int f = 0; f < kernels; f++) { matrix _output_error = target[f] - output[f]; // Calculate output layer gradients matrix _output_gradients; _output_gradients.Init(output[f].Rows(),output[f].Cols()); for (int g = 0; g < int(output[f].Rows()); g++) { for (int h = 0; h < int(output[f].Cols()); h++) { _output_gradients[g][h] = LeakyReLUDerivative(output[f][g][h]) * _output_error[g][h]; } } // Update output layer kernel weights and biases int _stride_row = 0, _stride_col = 0; for (int g = 0; g < int(output[f].Cols()); g++) { for (int h = 0; h < int(output[f].Rows()); h++) { double _bias_sum = 0.0; for (int i = 0; i < int(kernel[f].weights.Cols()); i++) { for (int j = 0; j < int(kernel[f].weights.Rows()); j++) { kernel[f].weights[j][i] += (LearningRate * _output_gradients[_stride_row + j][_stride_col + i]); // output[f][_stride_row + j][_stride_col + i]); _bias_sum += _output_gradients[_stride_row + j][_stride_col + i]; } } kernel[f].bias += LearningRate * _bias_sum; _stride_col += padding_stride; if(_stride_col + int(kernel[f].weights.Cols()) > int(_output_gradients.Cols())) { _stride_col = 0; _stride_row += padding_stride; if(_stride_row + int(kernel[f].weights.Rows()) > int(_output_gradients.Rows())) { _stride_col = 0; _stride_row = 0; } } } } } }
Наши выходные данные в конечном итоге представляют собой матрицы, поэтому дельты ошибок также должны быть зафиксированы в матричном формате. После того, как мы получим эти дельты ошибок, нам нужно будет скорректировать их с учетом произведения активации, поскольку до перехода на этот последний уровень они были активированы. И эта корректировка активации выполняется путем умножения дельты ошибки на производную функции активации.
Также имейте в виду, что даже если выходные ошибки и выходные градиенты представлены в матричной форме, этот процесс необходимо повторить для каждого ядра. Вот почему мы заключили каждую из этих операций в еще один общий цикл for, индексатором которого является целое число f, а максимальный размер никогда не превышает количества ядер. Число наших выходных матриц для тестового класса CNN, который мы демонстрируем в этой статье, равно трем. Они предоставляют карты бычьего, медвежьего тренда и быстрых разворотов для ценных бумаг, ценовые разрывы которых с различными скользящими средними были предоставлены в качестве входных данных в CNN. Эти ценовые разрывы также представлены в матричной форме.
Поскольку значения выходной ошибки и выходного градиента представлены в матричной форме и были объединены на предыдущем этапе, уже отмеченном выше, их размеры не соответствуют размерам весов матрицы ядра. Это изначально создает проблему при определении того, как использовать градиенты для корректировки весов ядра. Однако решение довольно простое, поскольку оно следует сверточному подходу, который мы применили в прямом распространении, где матрицы весов ядра, размеры которых отличаются от матрицы входных данных (и ее заполнения), циклически умножаются таким образом, что в каждой точке из всех произведений ядра в активном окне суммируется одно значение, и они помещаются в выходную матрицу.
Процесс выполняется пошагово. В нашем тестировании шаг только один, поскольку он должен соответствовать шагу, используемому при прямом распространении. Однако обновление - немного более сложная задача, поскольку они представляют собой всего лишь одно значение. Тем не менее, решение всегда состоит в том, чтобы суммировать градиенты в матрице и умножать эту сумму на старое смещение (после корректировки с помощью скорости обучения).
Интеграция в класс сигналов
Чтобы использовать наш класс CNN в пользовательском сигнале, нам надо определиться с двумя вещами. Во-первых, какую форму входных данных мы собираемся использовать, а во-вторых, какой целевой тип данных мы ожидаем в выходных матрицах. Ответы на оба эти вопроса, по сути, уже были даны выше, поскольку входными данными являются ценовые разрывы между текущей ценой закрытия и многими (по умолчанию 25) значениями скользящей средней цены. Множество скользящих средних отличаются своим уникальным периодом, и мы заполняем ими входную матрицу с помощью функции GetOutput, как показано ниже:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSignalCNN::GetOutput() { int _index = 5; matrix _inputs; vector _ma, _h, _l, _c; _inputs.Init(m_input_size, m_input_size); for(int g = 0; g < m_epochs; g++) { for(int h = m_train_set - 1; h >= 0; h--) { _inputs.Fill(0.0); _index = 0; for(int i = 0; i < m_input_size; i++) { for(int j = 0; j < m_input_size; j++) { if(_ma.CopyIndicatorBuffer(m_ma[_index].Handle(), 0, h, __KERNEL + 1)) { _inputs[i][j] = _c[0] - _ma[0]; _index++; } } } // ... } } ... ... }
С целевыми данными в наших выходных матрицах не всё так просто. Как упоминалось выше, мы хотим получить карты бычьего или медвежьего тренда. Для простоты они должны отображать только эти показатели (без меры флэтовости), но читатель может при необходимости изменить исходный код. Мы проводим измерения, рассматривая последующее ценовое действие для каждой точки входных данных. Опять же, наша точка данных отправляет показания индикатора, для которых мы решили закрыть ценовые разрывы, в массив скользящих средних цен, но это поведение можно легко настроить по вашему усмотрению.
Теперь выбранной нами мерой бычьего настроя, которую мы хотим отразить в матрице, а не в едином значении, будут изменения максимальной цены за различные периоды. Аналогичным образом, чтобы зафиксировать возможный медвежий тренд после регистрации точки данных, мы записываем изменения низких цен за различные периоды в матрицу. Необходимый код представлен ниже:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSignalCNN::GetOutput() { ... for(int g = 0; g < m_epochs; g++) { for(int h = m_train_set - 1; h >= 0; h--) { _inputs.Fill(0.0); _index = 0; ... // _h.CopyRates(m_symbol.Name(), m_period, 2, h, __KERNEL + 1); _l.CopyRates(m_symbol.Name(), m_period, 4, h, __KERNEL + 1); _c.CopyRates(m_symbol.Name(), m_period, 8, h, __KERNEL + 1); //Print(" inputs are: \n", _inputs); CNN.Set(_inputs); CNN.Pad(); //Print(" padded inputs are: \n", CNN.inputs); CNN.Convolve(); CNN.Activate(); CNN.Pool(); // targets as eventual price changes with each matrix a proxy for bullishness, bearishness, or whipsaw action // implying matrices for eventual: // high price changes // low price changes // close price changes, // respectively // // price changes in each column are over 1 bar, 2 bar and 3 bars respectively // & price changes in each row are over different weightings of the applied price with other applied prices // so high is: highs only(H); (Highs + Highs + Close)/3 (HHC); and (Highs + Close)/3 (HC) // while low is: lows only(L); (Lows + Lows + Close)/3 (LLC); and (Lows + Close)/3 (LC) // and close is: closes only(C); (Highs + Lows + Close + Close)/3 (HLCC); and (Highs + Lows + Close)/3 (HLC) // // assumptions here are: // large values in highs mean bullishness // large values in lows mean bearishness // and small magnitude in close imply a whipsaw market matrix _targets[]; ArrayResize(_targets, __KERNEL_SIZES.Size()); for(int i = 0; i < int(__KERNEL_SIZES.Size()); i++) { _targets[i].Init(__KERNEL_SIZES[i], __KERNEL_SIZES[i]); // for(int j = 0; j < __KERNEL_SIZES[i]; j++) { if(i == 0)// highs for 'bullishness' { _targets[i][j][0] = _h[j] - _h[j + 1]; _targets[i][j][1] = ((_h[j] + _h[j] + _c[j]) / 3.0) - ((_h[j + 1] + _h[j + 1] + _c[j + 1]) / 3.0); _targets[i][j][2] = ((_h[j] + _c[j]) / 2.0) - ((_h[j + 1] + _c[j + 1]) / 2.0); } else if(i == 1)// lows for 'bearishness' { _targets[i][j][0] = _l[j] - _l[j + 1]; _targets[i][j][1] = ((_l[j] + _l[j] + _c[j]) / 3.0) - ((_l[j + 1] + _l[j + 1] + _c[j + 1]) / 3.0); _targets[i][j][2] = ((_l[j] + _c[j]) / 2.0) - ((_l[j + 1] + _c[j + 1]) / 2.0); } else if(i == 2)// close for 'whipsaw' { _targets[i][j][0] = _c[j] - _c[j + 1]; _targets[i][j][1] = ((_h[j] + _l[j] + _c[j] + _c[j]) / 3.0) - ((_h[j + 1] + _l[j + 1] + _c[j + 1] + _c[j + 1]) / 3.0); _targets[i][j][2] = ((_h[j] + _l[j] + _c[j]) / 2.0) - ((_h[j + 1] + _l[j + 1] + _c[j + 1]) / 2.0); } } // //Print(" targets for: "+IntegerToString(i)+" are: \n", _targets[i]); } CNN.Get(_targets); CNN.Evolve(m_learning_rate); } } ... }
Наша третья выходная матрица, которая также регистрирует, насколько флэтовыми становятся рынки после каждой точки данных, представлена путем сосредоточения внимания на величине изменений цен закрытия снова в различных диапазонах, а различные длины этих диапазонов соответствуют размерам, используемым для измерения как бычьего, так и медвежьего настроя, упомянутых выше. Сбор этих целевых данных для каждого нового бара означает, что наша модель обучается для каждого нового бара, и это, опять же, всего лишь один из подходов, поскольку, как упоминалось выше, можно выбрать, чтобы обучение проводилось реже, например ежемесячно или ежеквартально.
Однако после каждого сеанса обучения нам необходимо делать прогноз относительно того, какими будут бычьи и медвежьи перспективы с учетом текущих данных. Часть нашего кода, которая занимается обработкой этой информации, представлена ниже:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSignalCNN::GetOutput() { ... ... _index = 0; _h.CopyRates(m_symbol.Name(), m_period, 2, 0, __KERNEL + 1); _l.CopyRates(m_symbol.Name(), m_period, 4, 0, __KERNEL + 1); _c.CopyRates(m_symbol.Name(), m_period, 8, 0, __KERNEL + 1); for(int i = 0; i < m_input_size; i++) { for(int j = 0; j < m_input_size; j++) { if(_ma.CopyIndicatorBuffer(m_ma[_index].Handle(), 0, 0, __KERNEL + 1)) { _inputs[i][j] = _c[__KERNEL] - _ma[__KERNEL]; _index++; } } } CNN.Set(_inputs); CNN.Pad(); CNN.Convolve(); CNN.Activate(); CNN.Pool(); double _long = 0.0, _short = 0.0; if(CNN.output[0].Median() > 0.0) { _long = fabs(CNN.output[0].Median()); } if(CNN.output[1].Median() < 0.0) { _short = fabs(CNN.output[1].Median()); } double _neutral = fabs(CNN.output[2].Median()); if(_long+_short+_neutral == 0.0) { return(0.0); } return((_long-_short)/(_long+_short+_neutral)); }
Матрица содержит множество точек данных, поэтому наилучшим подходом для оценки медвежьего или бычьего тренда на основе выходных матриц является считывание соответствующих медианных значений каждой матрицы. Таким образом, для бычьей матрицы мы хотели бы получить большое положительное значение, а для медвежьей матрицы — очень большое отрицательное значение. Для нашей плоской рыночной матрицы нам нужна величина этой медианы, и чем она меньше, тем более флэтовыми, по прогнозам, будут рынки.
Таким образом, результатом функции GetOutput будет значение с плавающей точкой. Если оно ниже 0,5, это указывает на дальнейшее усиление медвежьего тренда, а если выше 0,5, - бычьего. В результате тестовых запусков, выполненных с использованием однослойной сверточной нейронной сети с матрицей входных данных 5 x 5 и ядрами 3 x 3, которая также использует заполнение для получения выходных матриц размером 3 x 3 для EURJPY на дневном таймфрейме, мы получили выходные данные, которые были очень близки к значению 0,5. Это означает, что в данной реализации всему, что выше 0,5, присваивалось значение 100 в функции условий на покупку, а всему, что ниже 0,5, присваивалось значение 100 в функции условий на продажу.
Отчеты тестера стратегий
Собранный класс сигнала собирается в советник с помощью Мастера MQL5. Инструкцию можно найти здесь и здесь. При тестировании на EURJPY за 2023 год на дневном таймфрейме получаем следующие результаты:
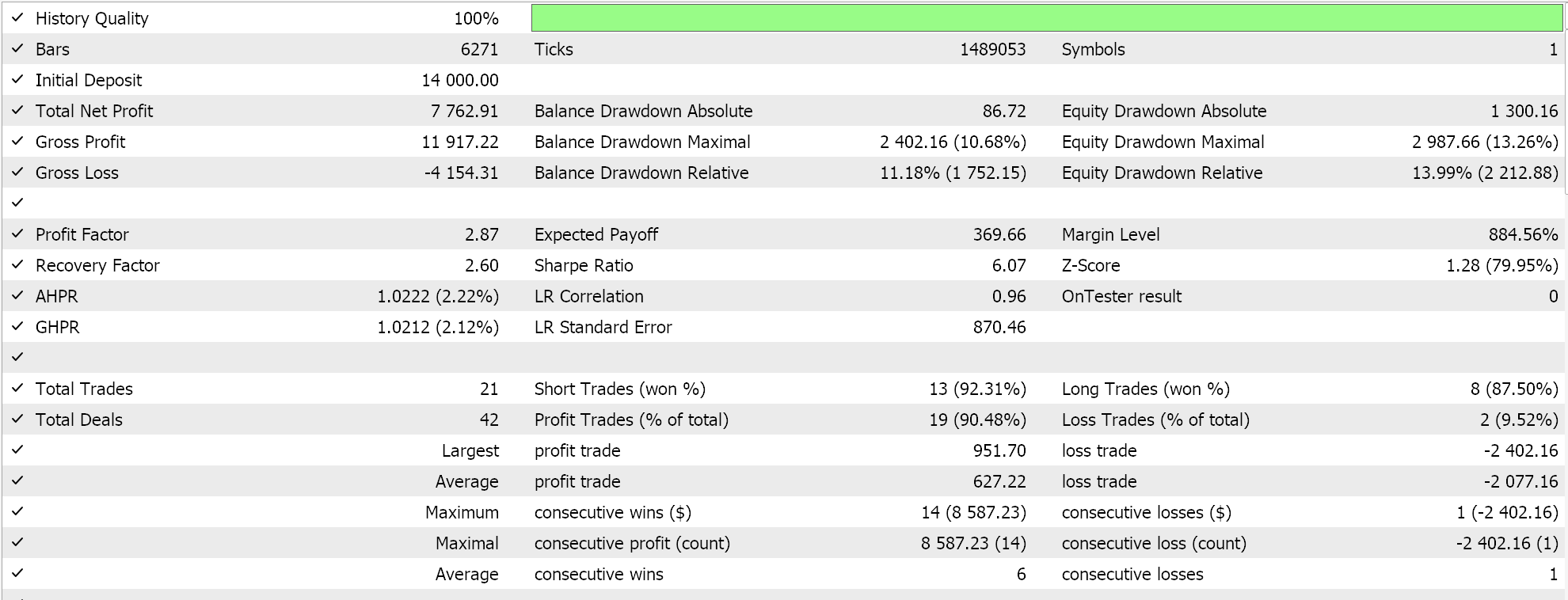
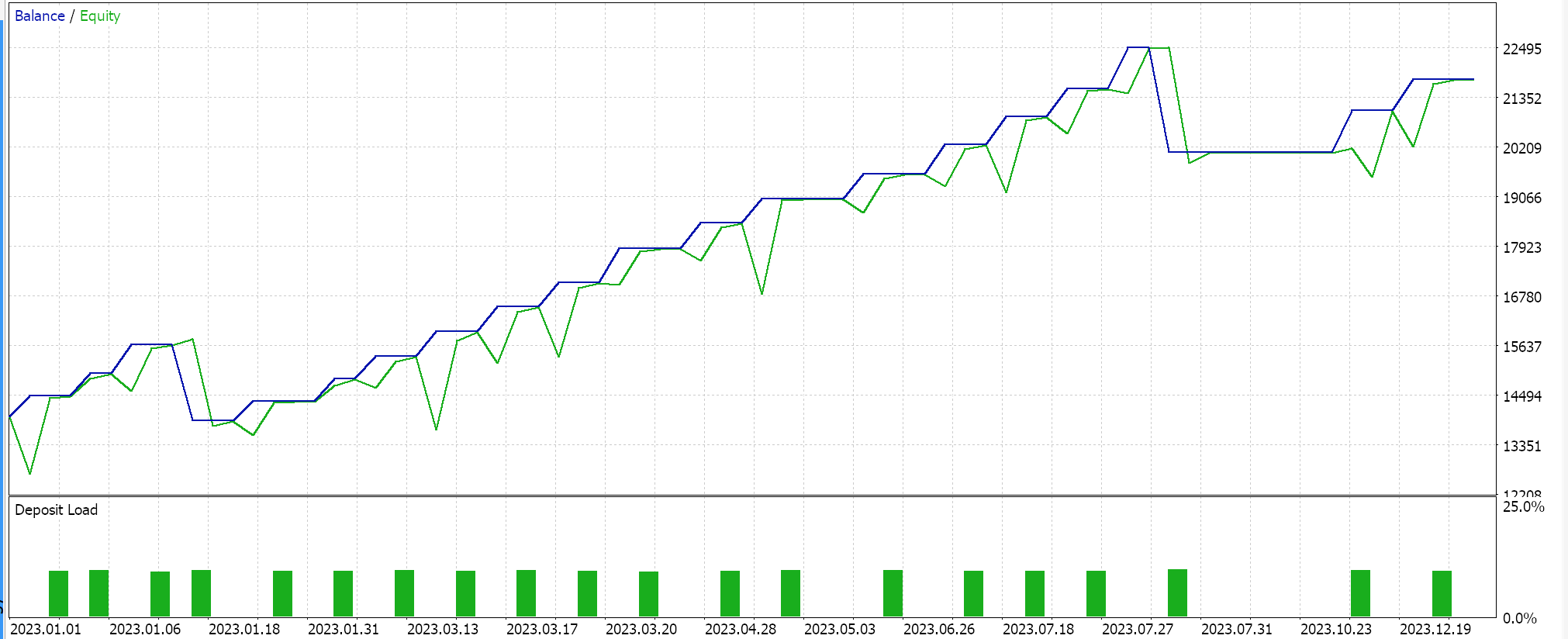
Эти результаты получены из результатов условий на покупку и продажу, которые равны либо 0, либо 100, поскольку выходное значение сети не нормализовано. Попытка нормализовать результаты работы сети должна обеспечить более "чувствительный" результат, поскольку пороговые значения открытия и закрытия можно будет тонко настраивать.
Заключение
Мы рассмотрели сверточные нейронные сети (CNN) — алгоритм машинного обучения, часто используемый при обработке изображений, — с точки зрения трейдера. Мы изучили и рассмотрели в коде ключевые этапы заполнения, прямого распространения, активации и субдискретизации в файле независимого класса MQL5. Мы также рассмотрели процесс обучения, углубившись в обратное распространение CNN и подчеркнув роль сверток в сопряжении матриц неравного размера. В статье была продемонстрирована однослойная сверточная нейронная сеть, поэтому здесь открывается широкое поле для исследований. Читатели могут не только объединить этот однослойный класс в трансформере(ах), но и рассмотреть различных типов входных данных и целевых наборов выходных данных.
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/15101
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Популяционный ADAM (Adaptive Moment Estimation)
Популяционный ADAM (Adaptive Moment Estimation)
 Создаем 3D-бары на основе времени, цены и объема
Создаем 3D-бары на основе времени, цены и объема
 Нейросети в трейдинге: Мультиагентная адаптивная модель (Окончание)
Нейросети в трейдинге: Мультиагентная адаптивная модель (Окончание)
 Нейросети в трейдинге: Мультиагентная адаптивная модель (MASA)
Нейросети в трейдинге: Мультиагентная адаптивная модель (MASA)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Невозможно скомпилировать , потому что многие файлы потеряны. например
//--- доступный трейлинг
Здравствуйте
Файлы, на которые вы ссылаетесь, поставляются с MQL5 IDE. Здесь и здесь есть руководства по использованию мастера.
Спасибо, что прочитали.