Selección de características paso a paso en MQL5
Introducción
La selección tradicional de características por pasos es una técnica que se utiliza para identificar un subconjunto óptimo de variables de un grupo más amplio de características candidatas para una tarea de aprendizaje automático. Este proceso comienza evaluando cada característica candidata individualmente para seleccionar la variable más prometedora para su inclusión en el modelo final. Posteriormente, se evalúan otros candidatos para comprobar su contribución en combinación con los ya elegidos, y así sucesivamente hasta alcanzar un nivel objetivo de rendimiento predictivo o de clasificación.
En este artículo, examinamos las limitaciones de la selección de características paso a paso convencional, como su potencial de sobreajuste y sus desafíos para capturar interacciones entre características. Luego presentamos un algoritmo mejorado diseñado para abordar estos problemas, implementado en MQL5, que proporciona una integración flexible con varios métodos de aprendizaje supervisado.
Este enfoque mejorado fue desarrollado por Timothy Masters y descrito en su libro 'Modern Data Mining Algorithms in C++ and CUDA C'. Finalmente, mostramos la aplicación práctica del algoritmo al usarlo para seleccionar variables óptimas para una tarea de regresión de muestra, ilustrando su efectividad.
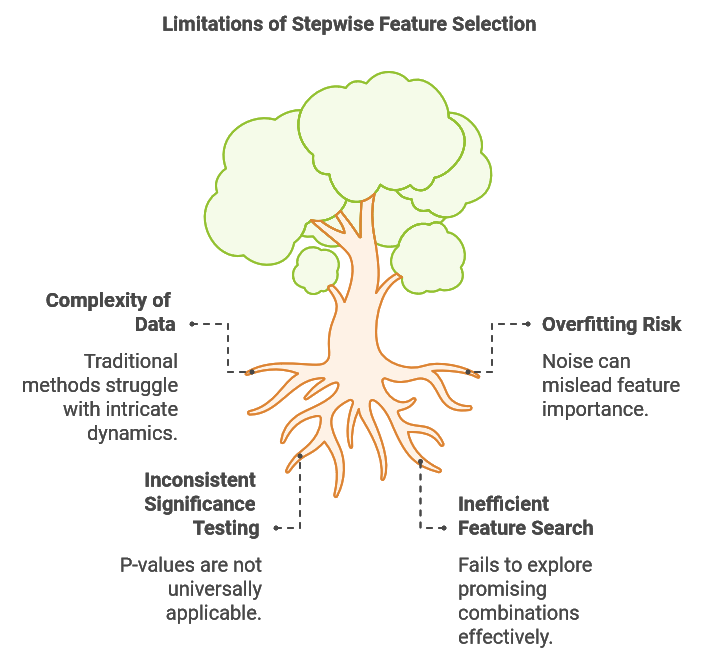
Limitaciones de la selección de características por pasos
Los conjuntos de datos utilizados en tareas de aprendizaje automático suelen ser inherentemente complejos y, a veces, presentan relaciones no lineales, patrones que varían en el tiempo y numerosos factores interconectados. Esta complejidad plantea desafíos importantes para la selección de características, ya que los métodos tradicionales, como la selección por pasos, pueden tener dificultades para capturar estas dinámicas intrincadas. Una limitación clave de la selección por pasos es su incapacidad para evaluar el impacto de diversas combinaciones de características. Con frecuencia, una característica que parece poco informativa por sí sola o cuando se combina con ciertas otras variables puede volverse altamente predictiva cuando se combina con características complementarias específicas.
Consideremos la tarea de construir un modelo predictivo para los tipos de cambio. En este escenario, podríamos recopilar varios indicadores técnicos y fundamentales. Algunos indicadores fundamentales pueden parecer ofrecer poco valor predictivo individualmente o cuando se combinan con datos técnicos no complementarios. Sin embargo, la combinación de indicadores como los próximos resultados electorales con la tendencia actual del mercado podría producir una predicción más sólida que confiar únicamente en las tendencias del mercado. Además, comprender el clima económico general y anticipar cómo el liderazgo entrante podría responder a las condiciones macroeconómicas podría mejorar significativamente la precisión predictiva del modelo. Estos desafíos resaltan la necesidad de un método mejorado de selección paso a paso que pueda probar combinaciones de características prometedoras sin recurrir a una búsqueda exhaustiva que resulte computacionalmente prohibitiva.
Un segundo desafío con la selección escalonada es su susceptibilidad al sobreajuste debido al ruido. Cada vez que se agrega una nueva variable, el algoritmo corre el riesgo de confundir fluctuaciones aleatorias con información valiosa, lo que puede llevarlo a aprender patrones que no se pueden generalizar. Por ejemplo, agregar múltiples indicadores técnicos puede aumentar el rendimiento dentro de la muestra si el modelo comienza a ajustarse al ruido del mercado en lugar de a las tendencias significativas, comprometiendo así su robustez en datos fuera de la muestra. Este problema surge a menudo cuando el rendimiento del modelo se juzga únicamente por el ajuste dentro de la muestra, lo que da como resultado la inclusión de más variables de las necesarias y, en última instancia, degrada el rendimiento fuera de la muestra.
La significancia estadística de la selección de características a menudo se evalúa utilizando valores 'p'. En la selección por pasos basada en regresión tradicional, los valores 'p' evalúan la probabilidad de que el coeficiente de una característica sea cero, lo que refleja su poder predictivo. Los intervalos de confianza proporcionan además un rango para el coeficiente de población real, teniendo en cuenta la incertidumbre del muestreo. Un valor 'p' bajo indica evidencia sólida contra la hipótesis nula (que el coeficiente es cero), lo que respalda la importancia de la característica. Estos valores 'p' se derivan de pruebas de hipótesis, donde la hipótesis nula supone un coeficiente cero y la hipótesis alternativa supone un coeficiente distinto de cero. Para obtener el valor 'p', calculamos una puntuación t basada en la estimación del coeficiente y su error estándar.
Sin embargo, este enfoque es específico de los modelos de regresión. Para otras técnicas de aprendizaje automático, obtener valores 'p' comparables requeriría una prueba de hipótesis personalizada, lo que agregaría complejidad a la aplicación práctica del algoritmo. Lo ideal sería que una técnica con una aplicación más universal proporcionara una medida relevante de significancia y produjera un valor 'p' o una métrica equivalente que se mantuviera consistente en los distintos tipos de métodos de aprendizaje automático.
Teniendo en cuenta las limitaciones de la selección de características paso a paso convencional, el algoritmo modificado presentado aquí ofrece tres mejoras clave respecto del método tradicional. La primera mejora aborda el desafío de buscar eficientemente subconjuntos de características prometedores. Al mantener múltiples subconjuntos de alto potencial y evaluar nuevos candidatos en combinación con estos subconjuntos, el algoritmo modificado logra un equilibrio entre la exploración integral y la eficiencia computacional. Este enfoque permite descubrir relaciones sinérgicas entre características que la selección tradicional por pasos puede pasar por alto.
Para reducir el riesgo de sobreajuste, el algoritmo utiliza el rendimiento de la validación cruzada como base para evaluar conjuntos de características. Este riguroso método de evaluación minimiza las posibilidades de confundir ruido aleatorio con información predictiva significativa y proporciona un mecanismo sencillo para detener automáticamente la inclusión de características adicionales cuando se detectan rendimientos decrecientes.
Además, para cada nueva característica añadida, el algoritmo calcula dos probabilidades:
- Probabilidad de ocurrencia casual: esta probabilidad mide la probabilidad de que el rendimiento observado del conjunto de características actual pueda atribuirse al azar, asumiendo que todas las características seleccionadas son irrelevantes.
- Probabilidad de mejora espuria: esta probabilidad evalúa la posibilidad de que la mejora en el rendimiento derivada de la última incorporación de una función se deba al azar y no a un valor predictivo genuino.
Estas probabilidades ofrecen información sobre la importancia estadística del proceso de selección de características y ayudan a distinguir el poder predictivo genuino del ruido estadístico. En particular, estas probabilidades calculadas son independientes del modelo, lo que permite que el algoritmo se integre perfectamente con una amplia gama de modelos de aprendizaje automático. En las siguientes secciones, examinaremos partes clave del código que implementan este algoritmo. Los fragmentos de código proporcionados se extraen de la clase CStepwisebase, definida en stepwise.mqh. Esta clase es abstracta y requiere que los usuarios creen una clase derivada que implemente ciertos miembros virtuales, lo que permite la integración de cualquier tipo de modelo.
El procedimiento paso a paso
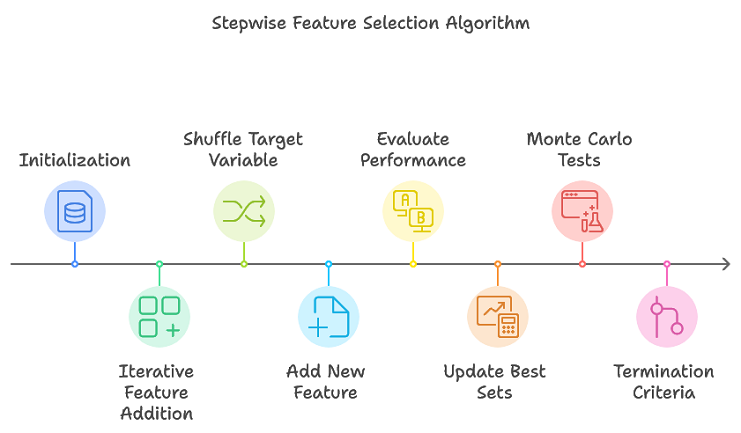
El algoritmo propuesto mejora la selección tradicional por pasos mediante el seguimiento de múltiples subconjuntos de características prometedoras, evitando la necesidad de una búsqueda exhaustiva. Este enfoque limita de manera eficiente los subconjuntos de características que probablemente formarán el conjunto óptimo final. A continuación se ofrece una descripción general del procedimiento:
- Inicialización: Se inicializan las estructuras de datos utilizadas durante todo el proceso para almacenar información acerca de las pruebas de conjuntos de características.
- Adición de características iterativas: para cada iteración, realice múltiples réplicas de permutación. Baraja la variable de destino para crear una nueva permutación. Añade una nueva característica al conjunto de características actual. Evalúe el rendimiento del conjunto de características actualizado mediante la validación cruzada. Actualice los conjuntos de características de mejor rendimiento y sus métricas de rendimiento correspondientes.
- Criterios de terminación: el algoritmo finaliza cuando se alcanza el número máximo de características (según lo definido por max_num_predictors) o cuando la mejora del rendimiento cae por debajo de un umbral predefinido.
Los pasos principales se implementan en stepwiseSearch(), y el proceso está gobernado por varios hiperparámetros que controlan diferentes aspectos de la búsqueda. Estos hiperparámetros son:
- num_kept: La cantidad de subconjuntos de características candidatas con el mejor rendimiento, según el criterio, para conservar en cada iteración. Se considera que es probable que estos candidatos formen el conjunto de características óptimo.
- num_folds: El número de pliegues utilizados en la validación cruzada. Si bien los valores más grandes mejoran la precisión de las estimaciones de rendimiento, también aumentan el costo computacional.
- min_num_predictors: El número mínimo de predictores que puede contener el conjunto de características final, lo que permite a los usuarios definir un límite inferior para la complejidad del modelo.
- max_num_predictors: el número máximo de predictores permitidos en el conjunto de características final, que proporciona un límite superior para la complejidad del modelo.
- num_replications: El número de iteraciones para la prueba de permutación de Monte Carlo, que ayuda a evaluar la importancia estadística del rendimiento de las características.
- verbose_output: Determina si los resultados de cada paso en el proceso de selección de características se muestran en la pestaña Expertos de MetaTrader 5.
Estos parámetros proporcionan flexibilidad y permiten a los usuarios ajustar el proceso de selección de funciones para adaptarlo a sus necesidades. Se pueden especificar invocando setParams().
//+------------------------------------------------------------------+ //| set the stepwise selection parameters | //+------------------------------------------------------------------+ void setParams(ulong num_kept, ulong num_folds, ulong min_num_predictors, ulong max_num_predictors,long num_replications,bool verbose_output) { m_keptvars = num_kept>0?num_kept:1; m_folds = num_folds>0?num_folds:ULONG_MAX; m_min_num_preds = min_num_predictors; m_max_num_preds = max_num_predictors; m_reps = num_replications>0?num_replications:1; m_verbose = verbose_output; return; }
El método stepwiseSearch() comienza inicializando estructuras de datos internas para realizar un seguimiento de las distintas pruebas de conjuntos de características. Luego ingresa a un bucle principal que continúa hasta que se alcanza el número máximo de predictores. Durante cada iteración del bucle, la variable de destino se mezcla aleatoriamente para múltiples repeticiones y se agrega una nueva variable al modelo llamando a addFeature(). El algoritmo almacena las características del modelo con mejor rendimiento y, si agregar una nueva variable genera una degradación del rendimiento, puede finalizar antes de tiempo. Si el rendimiento continúa mejorando, el proceso persiste hasta alcanzar el número máximo de predictores. Finalmente, los índices de las variables seleccionadas se guardan en la matriz m_var_indices.
//+------------------------------------------------------------------+ //| coordinates main stepwise search operation | //+------------------------------------------------------------------+ int stepwiseSearch(void) { int done = 1; int btrials; m_trial_length = m_max_num_preds*m_vars*m_keptvars; reset(); if(!m_prior_best_crits.Resize(m_keptvars) || !m_all_best_crits.Resize(m_reps,m_keptvars)) { Print(__FUNCTION__," data structure resizing error ", GetLastError()); return done; } if(ArrayResize(m_all_best_trials,int(m_reps*m_max_num_preds*m_keptvars))<0 || ArrayResize(m_already_tried,int(m_trial_length))<0 || ArrayResize(m_trial_vars,int(m_max_num_preds))<0 || ArrayResize(m_prior_best_trials,int(m_max_num_preds*m_keptvars))<0) { Print(__FUNCTION__," error resizing array ", GetLastError()); return done; } ArrayInitialize(m_all_best_trials,-1); ArrayInitialize(m_already_tried,-1); ArrayInitialize(m_trial_vars,-1); ArrayInitialize(m_prior_best_trials,-1); vector target; int n_so_far =0; int rval, rem, j,n_this_rep = 0; int mcpt_mod_count, mcpt_change_count; mcpt_mod_count = mcpt_mod_count = mcpt_change_count = -1; double temp,prior_crit; double original_crit, original_change, new_crit; original_crit = original_change = new_crit = -DBL_MIN; if(m_verbose) { if(m_reps>1) Print("Criterion || New pval || Diff pval || Column Indices"); else Print("Criterion || Column Indices"); } while(true) { target = m_target; for(ulong rep=0; rep<m_reps; rep++) { if(rep) { rval = 17*int(rep) + 11; unif(rval); unif(rval); rem = int(m_samples); while(rem>1) { j = (int)(unif(rval))*rem; if(j>=rem) j = rem-1; temp = target[--rem]; target[rem] = target[j]; target[j] = temp; } } btrials = int(rep*m_max_num_preds*m_keptvars); if(n_so_far == 0) prior_crit = -1.e60; else prior_crit = m_all_best_crits[rep][0]; n_this_rep = n_so_far; done = addFeature(target,n_this_rep,btrials,rep); if(done || n_this_rep!=(n_so_far+1)) { Print(__FUNCTION__, " internal error "); return 1; } if(m_all_best_crits[rep][0]<=prior_crit && n_so_far>=int(m_min_num_preds) && !rep) { for(ulong i = 0 ; i<m_keptvars; i++) { m_all_best_crits[rep][i] = m_prior_best_crits[i]; if(ArrayCopy(m_all_best_trials,m_prior_best_trials,btrials+int(i*n_so_far),int(i*n_so_far),n_so_far)<0) { Print(__FUNCTION__, " ArrayCopy error ", GetLastError()); return 1; } } if(m_verbose) Print(__FUNCTION__, " procedure terminated early because adding a new variable caused performance degradation"); return 0; } if(prior_crit < 0.0) prior_crit = 0.0; new_crit = m_all_best_crits[rep][0]; if(new_crit<0.0) new_crit = 0.0; if(rep == 0) { original_crit = new_crit; original_change = new_crit - prior_crit; mcpt_mod_count = mcpt_change_count = 1; } else { if(new_crit >= original_crit) ++mcpt_mod_count; if(new_crit - prior_crit >= original_change) ++mcpt_change_count; } } if(n_so_far == 0) mcpt_change_count = mcpt_mod_count; if(!m_decision_matrix.Resize(n_so_far+1,m_reps>1?3:1,100) || ArrayResize(m_var_indices,int(m_var_indices.Size())+n_this_rep,100)<0) { Print(__FUNCTION__, " container resize error ", GetLastError()); return 1; } string msg; if(m_reps>1) { double mod_pval = (double) mcpt_mod_count / (double) m_reps; double change_pval = (double) mcpt_change_count / (double) m_reps; if(m_verbose) msg = StringFormat("%10.8lf %10.8lf %10.8lf ", original_crit,mod_pval,change_pval); m_decision_matrix[n_so_far][0] = original_crit; m_decision_matrix[n_so_far][1] = mod_pval; m_decision_matrix[n_so_far][2] = change_pval; } else { msg = m_verbose?StringFormat("%10.8lf", original_crit):NULL; m_decision_matrix[n_so_far][0] = original_crit; } if(m_verbose) { for(int i = 0; i<n_this_rep; i++) { msg += StringFormat(" %s",IntegerToString(m_all_best_trials[i])); } } if(ArrayCopy(m_var_indices,m_all_best_trials,(n_so_far*(n_so_far+1))/2,0,n_this_rep)<0) { Print(__FUNCTION__, " array copy error ", GetLastError()); return 1; } if(m_verbose) Print(msg); ++n_so_far; if(n_so_far == int(m_max_num_preds)) { if(m_verbose) Print(" Stepwise selection successfully completed "); break; } } return 0; }
Cálculo del criterio de validación cruzada
Confiar en un único conjunto de datos de entrenamiento para la selección de características a menudo produce resultados subóptimos debido al riesgo de sobreajuste. Para mitigar este riesgo, se utiliza la validación cruzada. La validación cruzada implica dividir el conjunto de datos en múltiples conjuntos de entrenamiento y validación, lo que permite una evaluación más completa del rendimiento del modelo y la importancia de las características. Al entrenar y probar iterativamente en diferentes subconjuntos de datos, la validación cruzada reduce el sobreajuste y mejora la generalización.
Si bien la validación cruzada es muy eficaz, presenta un equilibrio entre la eficiencia computacional y la confiabilidad estadística. Un mayor número de pliegues generalmente proporciona una estimación más precisa del rendimiento del modelo, pero aumenta las demandas computacionales. El número ideal de pliegues depende tanto de las características del conjunto de datos como de los recursos computacionales disponibles. En la práctica, determinar el número apropiado de pliegues requiere una consideración cuidadosa del tamaño del conjunto de datos y el nivel deseado de confianza estadística. Al comprender los principios y las limitaciones de la validación cruzada, los profesionales pueden aplicar esta técnica para mejorar la confiabilidad y la solidez de sus procesos de selección de características y construcción de modelos.
El procedimiento de validación cruzada se implementa mediante el método crossEval().
//+------------------------------------------------------------------+ //| evaluates a predictor set using cross validation | //+------------------------------------------------------------------+ int crossEval(ulong num_vars,vector &target,double &criterion) { ulong ifold, n_remaining, test_start, test_stop ; double error, evalresult ; n_remaining = m_samples; test_start = 0; error = 0.0; for(ifold = 0; ifold<m_folds; ifold++) { test_stop = test_start + (n_remaining/(m_folds-ifold)); if(!fitModel(num_vars,test_start,test_stop,target)) { criterion = -DBL_MIN; Print(__FUNCTION__, " fit() failed "); return 1; } evalresult = evalModel(num_vars,test_start,test_stop,target); if(evalresult==EMPTY_VALUE) { criterion = -DBL_MIN; Print(__FUNCTION__, " evalModel() failed "); return 1; } error+=evalresult; n_remaining -= test_stop - test_start; test_start = test_stop; } criterion = 1.0 - error/double(m_samples); return 0; }
Esta función toma como entrada el número de predictores a evaluar, un vector de valores objetivo mezclados y una referencia a una variable que devolverá el valor de un criterio, utilizado como una de las variables de decisión para identificar el subconjunto de características más adecuado. La función devuelve 0 si se ejecuta correctamente. Funciona primero ajustando un modelo y luego evaluando su desempeño en todos los aspectos de los datos de muestra.
El método fitModel() es responsable de entrenar un modelo en un subconjunto de características candidatas. Toma las siguientes entradas:
- num_preds: El número de predictores,
- row_start: El índice de la primera muestra,
- row_stop: El índice uno después de la última muestra que se excluirá del conjunto de entrenamiento, y
- targets: El vector de valores objetivo mezclados.
Esta función devuelve un valor booleano que indica si el modelo se entrenó correctamente.
La función evalModel() tiene las mismas entradas que fitModel(), pero esta vez, la partición especificada de filas representa las muestras utilizadas para evaluar el modelo entrenado. Esta función devuelve un valor que proporciona una indicación del rendimiento del modelo. Tanto fitModel() como evalModel() son miembros virtuales, que requieren implementación en una clase derivada para integrar el tipo de modelo específico que se utiliza.
//+------------------------------------------------------------------+ //| fit a model | //+------------------------------------------------------------------+ virtual bool fitModel(ulong num_preds,ulong row_start,ulong row_stop, vector& targets) { return false;} //+------------------------------------------------------------------+ //| evaluate a model | //+------------------------------------------------------------------+ virtual double evalModel(ulong num_preds,ulong row_start,ulong row_stop, vector& targets) { return EMPTY_VALUE;}
Encontrar la primera característica
El método addFirstFeature() es invocado por addFeature() para identificar el primer predictor en un conjunto dado.
//+------------------------------------------------------------------+ //| finds the first predictor in the set | //+------------------------------------------------------------------+ int addFirstFeature(vector &targ, int bindex,ulong rep_index) { double crit; for(ulong i = 0; i<m_keptvars; i++) { m_all_best_crits[rep_index][i] = -1.e60; m_all_best_trials[bindex+i] = -1; } for(int i = 0; i<int(m_vars); i++) { m_trial_vars[0] = i; if(crossEval(1,targ,crit)) { Print(__FUNCTION__, " xval error "); return 1; } ulong j; for(j = 0; j<m_keptvars; j++) { if(crit > m_all_best_crits[rep_index][j]) break; } if(j<m_keptvars) { for(long k = long(m_keptvars-2); k>=long(j); k--) { m_all_best_trials[bindex+k+1] = m_all_best_trials[bindex+k]; m_all_best_crits[rep_index][k+1] = m_all_best_crits[rep_index][k]; } m_all_best_trials[bindex+j] = i; m_all_best_crits[rep_index][j] = crit; } } return 0; }
Itera sobre cada variable, evaluando su desempeño mediante validación cruzada. El rendimiento se evalúa en función de un criterio definido en una clase derivada, que, a su vez, informa la técnica de aprendizaje que determina el modelo.
Durante esta evaluación, el método mantiene una lista de las variables con mejor rendimiento junto con sus valores de criterio correspondientes. A medida que se evalúa cada variable, se compara su rendimiento con el de las mejores variables actuales. Si una nueva variable supera a una de las variables de mejor rendimiento existentes, se inserta en la lista, lo que hace que las variables de menor rendimiento se desplacen hacia abajo.
Este proceso continúa hasta que se hayan evaluado todas las variables, culminando con la identificación del primer predictor. Para las llamadas posteriores a addFeature(), se introduce una nueva variable invocando addNewFeature(), lo que garantiza un enfoque sistemático para la adición de características.
Añadiendo al conjunto de funciones
El método addNewFeature() identifica el próximo predictor a incluir en el conjunto de características del modelo.
//+------------------------------------------------------------------+ //| looks for next predictor to include | //+------------------------------------------------------------------+ int addNewFeature(vector& target,int &ind, int bindex,ulong rep_index) { int i, j, k, ivar, ir ; int npred, n_already_tried,nbest, rootvars; nbest = -1; double crit; ind = npred = ind+1; for(i = 0; i<int(m_keptvars); i++) { m_prior_best_crits[i] = m_all_best_crits[rep_index][i]; if(ArrayCopy(m_prior_best_trials,m_all_best_trials,int(i*(npred-1)),bindex+int(i*(npred-1)),npred-1)<0) { Print(__FUNCTION__, " ArrayCopy error ", GetLastError()); return 1; } m_all_best_crits[rep_index][i] = -1.e60; } n_already_tried = 0; for(ir = 0; ir<int(m_keptvars); ir++) { if(m_prior_best_crits[ir] < -1.e59) break; } nbest = ir; for(ir = 0; ir<nbest; ir++) { rootvars = ir*(npred-1); for(ivar=0; ivar<int(m_vars); ivar++) { for(i = 0; i<npred-1; i++) { if(m_prior_best_trials[rootvars+i] == ivar) break; } if(i < npred-1) continue; k = 0; for(i = 0; i<int(m_vars); i++) { for(j=0; j<npred-1; j++) { if(m_prior_best_trials[rootvars+j] == i) { m_trial_vars[k++] = i; break; } } if(ivar == i) m_trial_vars[k++] = i; } for(i = 0; i<n_already_tried; i++) { for(j = 0; j<npred; j++) { if(m_trial_vars[j] != m_already_tried[i*npred+j]) break; } if(j == npred) break; } if(i < n_already_tried) continue; for(i =0; i<npred; i++) m_already_tried[n_already_tried*npred+i]=m_trial_vars[i]; ++n_already_tried; if(crossEval(ulong(npred),target,crit)) { Print(__FUNCTION__, " xval error "); return 1; } for(i = 0; i< int(m_keptvars); i++) { if(crit > m_all_best_crits[rep_index][i]) break; } if(i<int(m_keptvars)) { for(j = int(m_keptvars-2); j>=i; j--) { m_all_best_crits[rep_index][j+1] = m_all_best_crits[rep_index][j]; if(ArrayCopy(m_all_best_trials,m_all_best_trials,bindex+int((j+1)*npred),bindex+int(j*npred),npred)<0) { Print(__FUNCTION__, " array copy error ", GetLastError()); return 1; } } m_all_best_crits[rep_index][i] = crit; if(ArrayCopy(m_all_best_trials,m_trial_vars,bindex+int(i*npred),0,npred)<0) { Print(__FUNCTION__, " array copy error ", GetLastError()); return 1; } } } } return 0; }
Se basa en el conjunto existente de predictores examinando todas las combinaciones posibles de los mejores predictores actuales con variables adicionales. Para cada combinación, el método realiza una validación cruzada para evaluar su desempeño, que se mide utilizando un criterio específico. Después de examinar los elementos centrales del código de selección de características paso a paso, ahora exploraremos cómo estos fragmentos se integran para formar la implementación completa.
La clase CStepwisebase
La clase CStepwisebase sirve como una implementación fundamental para la selección de características paso a paso, diseñada para seleccionar características predictivas de forma iterativa a partir de un conjunto de candidatos. Este proceso de selección agrega sistemáticamente variables en función de sus contribuciones al rendimiento de un modelo predictivo. Como clase abstracta, permite la integración de cualquier tipo de técnica de aprendizaje y su criterio correspondiente dentro de una clase derivada implementando los métodos fitModel() y evalModel(). En la siguiente sección se proporcionará un ejemplo de esta implementación.
El método stepwiseSelection() actúa como el principal punto de entrada de acceso público, iniciando el proceso preparando los datos y ejecutando stepwiseSearch().
//+------------------------------------------------------------------+ //| main method to execute stepwise feature selection | //+------------------------------------------------------------------+ bool stepwiseSelection(matrix& predictors, vector& targets) { if(targets.Size()!=predictors.Rows() || !targets.Size()) { Print(__FUNCTION__, " invalid inputs "); return false; } m_data = stdmat(predictors); m_target = (targets-targets.Mean())/(targets.Std()+1e-10); m_vars = predictors.Cols(); m_samples = predictors.Rows(); if(m_keptvars>m_vars || m_keptvars<1) m_keptvars = m_vars; if(m_folds<1) m_folds = 1; if(m_folds>m_samples) m_folds = m_samples; if(m_min_num_preds==0 || m_min_num_preds>m_vars || m_min_num_preds>m_max_num_preds) m_min_num_preds = m_vars; if(m_max_num_preds==0 || m_max_num_preds>m_vars || m_max_num_preds<m_min_num_preds) m_max_num_preds = m_vars; if(m_reps<1) m_reps = 1; if(m_verbose) { Print(" STEPWISE SELECTION PARAMETERS "); Print(" Number of retained candidate variables for each iteration ", m_keptvars); Print(" Number of folds in cross validation procedure ", m_folds); Print(" Final minimum number of selected predictors ", m_min_num_preds); Print(" Final maximum number of selected predictors ", m_max_num_preds); Print(" Number of replications for MCP test ", m_reps); } return (stepwiseSearch()==0); }
Para configurar los parámetros para el proceso de selección de características de antemano, está disponible el método setParams(). El resultado del proceso de selección de características se puede mostrar en la pestaña Expertos de MetaTrader 5 configurando el último parámetro de setParams() en verdadero. Además, los resultados del procedimiento de selección se pueden recuperar utilizando los siguientes métodos:
- Al llamar a getCriticalVals() se devuelve una matriz con una cantidad variable de columnas dependiendo de si se especifica una prueba de permutación de Monte Carlo (MCP) como parte de la búsqueda paso a paso. Esto se logra configurando num_replications en setParams() en cualquier valor mayor que 1. En este caso, getCriticalVals() devuelve una matriz con tres columnas, donde cada fila contiene valores que cuantifican la adición de una característica adicional. El número de filas en esta matriz corresponde al número de iteraciones a través del bucle más externo del algoritmo paso a paso. Los tres valores en cada fila constan del criterio, un valor 'p' que indica la probabilidad de que el rendimiento observado sea atribuible al azar (asumiendo que las características seleccionadas son irrelevantes) y otro valor 'p' que refleja la probabilidad de que la mejora del rendimiento resultante de la adición de características a la iteración se deba al azar.
//+------------------------------------------------------------------+ //| get all crit values and corresponding p-values | //+------------------------------------------------------------------+ matrix getCriticalVals(void) { return m_decision_matrix; }
- Cuando no se especifica ninguna prueba MCP, la función devuelve una sola columna que contiene los valores de criterio respectivos para cada iteración de la ejecución del algoritmo. La cantidad de mejores subconjuntos de características encontrados se puede consultar utilizando getNumFeatureSets(), mientras que los conjuntos de características en sí se pueden recuperar llamando getFeatureSetAt(), que acepta un índice correspondiente a la iteración deseada y una referencia a una matriz donde se copiarán los índices de las columnas que representan el subconjunto de características.
//+------------------------------------------------------------------+ //| get the selected features at a specific iteration of the process| //| iterations denoted as zero based indices | //| eg, first selected feature located at iteration index 0 | //+------------------------------------------------------------------+ bool getFeatureSetAt(ulong iteration_index,ulong &selectedvars[]) { if(ArrayCopy(selectedvars,m_var_indices,0,int((iteration_index*(iteration_index+1))/2),int(iteration_index+1))>0) return true; else { Print(__FUNCTION__, " ArrayCopy error ", GetLastError()); return false; } } //+---------------------------------------------------------------------+ //| get maximum number of iterations cycled through in selection process| //+---------------------------------------------------------------------+ ulong getNumFeatureSets(void) { return m_decision_matrix.Rows(); }
Con esto concluye nuestra discusión de la clase base. En la siguiente sección, exploraremos cómo aplicar este código integrando un modelo y ejecutando pruebas.
Un ejemplo que utiliza un modelo de regresión lineal-cuadrática
Para ilustrar el algoritmo de selección por pasos mejorado, demostraremos su aplicación en la evaluación de un conjunto de datos de predictores candidatos para ajustar un modelo de regresión lineal-cuadrática. Esta implementación se proporciona en el script de MetaTrader 5, StepWiseFeatureSelection_Demo.mq5. En este script, describiremos el proceso de selección de las características más predictivas a través del método de selección paso a paso mejorado, mostrando cómo el algoritmo identifica predictores óptimos para el modelo de regresión lineal-cuadrática. La demostración práctica incluirá la configuración del conjunto de datos, la configuración de los parámetros del modelo y la ejecución del proceso de selección de características dentro del entorno MetaTrader 5.
La regresión lineal-cuadrática es una extensión de la regresión lineal que incorpora términos lineales y cuadráticos (al cuadrado) de las variables predictoras. Este enfoque permite que el modelo capture relaciones no lineales ajustando una curva a los datos en lugar de una línea recta. La forma general de una ecuación de regresión lineal-cuadrática para una única variable predictora X se da mediante la fórmula general a continuación.
Donde:
- 'y' es la variable dependiente,
- 'x' es la variable independiente,
- β0, β1, y β2 son coeficientes a estimar,
- 'x-cuadrado' es el término cuadrático, que permite que el modelo tenga en cuenta la curvatura,
- 'ϵ' es el término de error.
En esta ecuación, el término βx modela la relación lineal, mientras que β(x-cuadrado) captura la curvatura, lo que hace que el modelo sea útil para datos que muestran una tendencia parabólica o curva. El coeficiente β0 representa la intersección, β1 controla la pendiente de la porción lineal y β2 afecta la curvatura, determinando si la parábola se abre hacia arriba (β2>0) o hacia abajo (β2<0).
En la práctica, la regresión lineal-cuadrática se aplica en situaciones donde la relación entre las variables dependientes e independientes no es estrictamente lineal. La implementación de la regresión lineal-cuadrática en nuestro script se habilita aprovechando la clase de Mínimos Cuadrados Ordinarios (Ordinary Least Squares, OLS) definida en OLS.mqh.
A continuación, analizaremos cómo se integra este modelo de regresión en el proceso de selección paso a paso, lo que permite la identificación de predictores óptimos de nuestro conjunto de datos.
El script StepWiseFeatureSelection_Demo.mq5 implementa de manera efectiva el algoritmo de selección de características por pasos mejorado, diseñado para modelos de regresión lineal-cuadrática. Lo que sigue es un desglose de los componentes y funcionalidades del script. La clase CStepwise hereda de CStepwisebase y proporciona una implementación concreta de los métodos abstractos definidos en la clase base. Este diseño permite la integración de lógica de modelo específica para la regresión lineal-cuadrática. La lógica central para ajustar y evaluar el modelo lineal-cuadrático está encapsulada dentro de la clase CStepwise. Esto incluye los ajustes necesarios para acomodar los términos lineales y cuadráticos de las variables predictoras.
El método fitModel() es responsable de construir la matriz de diseño basada en las muestras de entrenamiento. Excluye el rango especificado de datos destinados a la validación durante la validación cruzada. Se crea una instancia de la clase OLS (denotada como m_ols), que administra las operaciones de regresión de mínimos cuadrados ordinarios.
//+------------------------------------------------------------------+ //| fit the OLS model | //+------------------------------------------------------------------+ virtual bool fitModel(ulong num_preds,ulong row_start,ulong row_stop,vector& targets) { int k1,k2; ulong nvars = num_preds + num_preds * (num_preds+1)/2; ulong ntrain = m_samples - (row_stop - row_start); vector dependent(ntrain); matrix independent(ntrain,nvars+1); ntrain = 0; for(ulong sample=0; sample<m_samples; sample++) { if(sample>=row_start && sample<row_stop) continue; k1=0; k2=1; for(ulong var=0; var<nvars; var++) { if(var<num_preds) independent[ntrain][var]=m_data[sample][m_trial_vars[var]]; else { if(var<(num_preds*2)) { independent[ntrain][var]=pow(m_data[sample][m_trial_vars[var-num_preds]],2.0); } else { independent[ntrain][var]=m_data[sample][m_trial_vars[k1]]*m_data[sample][m_trial_vars[k2]]; ++k2; if(ulong(k2)==num_preds) { ++k1; k2 = k1 + 1; } } } } independent[ntrain][nvars] = 1.0; dependent[ntrain++] = targets[sample]; } return m_ols.Fit(dependent,independent); }
En evalModel(), el método evalúa el rendimiento del modelo lineal-cuadrático entrenado utilizando los datos que se omitieron durante la fase de entrenamiento. Aquí se especifica el criterio para evaluar el rendimiento del modelo, que en este caso es la suma de errores al cuadrado (SSE). Este criterio mide qué tan bien se alinean las predicciones del modelo con los resultados reales.
//+------------------------------------------------------------------+ //| evaluate the model | //+------------------------------------------------------------------+ virtual double evalModel(ulong num_preds,ulong row_start,ulong row_stop,vector& targets) { if(m_ols.Loglikelihood()==EMPTY_VALUE) { Print(__FUNCTION__, " OLS error "); return EMPTY_VALUE; } int k1,k2; ulong nvars = num_preds + num_preds * (num_preds+1)/2; double prediction; vector row(nvars); double error = 0.0; for(ulong sample=row_start; sample<row_stop; sample++) { k1=0; k2=1; for(ulong var=0; var<nvars; var++) { if(var<num_preds) row[var]=m_data[sample][m_trial_vars[var]]; else { if(var<(num_preds*2)) { row[var]=pow(m_data[sample][m_trial_vars[var-num_preds]],2.0); } else { row[var]=m_data[sample][m_trial_vars[k1]]*m_data[sample][m_trial_vars[k2]]; ++k2; if(ulong(k2)==num_preds) { ++k1; k2 = k1 + 1; } } } } prediction = m_ols.Predict(row); if(prediction == EMPTY_VALUE) { Print(__FUNCTION__, " OLS predict() error "); return EMPTY_VALUE; } error+=pow(prediction-targets[sample],2.0); } return error; }
Siguiendo la definición de la clase derivada CStepwise, el script genera una matriz aleatoria de 100 por 10, denotada como mat, que se genera con valores que oscilan entre 0 y 1. Esta matriz sirve como conjunto de datos que contiene las variables predictoras.
//--- MathSrand(120); //--- matrix mat(100,10); //--- mat.Random(0.0,1.0); //---
Un vector de destino se crea sumando columnas específicas. La variable objetivo se define como la suma de los valores de las columnas 0, 5, 4 y 6 de la matriz. Esto define la variable dependiente (o salida) que el modelo pretende predecir basándose en las variables independientes (las columnas restantes).
//--- vector target = mat.Col(0) + mat.Col(5) + mat.Col(4) + mat.Col(6); //---
Se crea una instancia de la clase CStepwise, denominada stepwise. Esta instancia gestionará el proceso de selección de características paso a paso adaptado al modelo de regresión lineal-cuadrática. El método setParams() se invoca en la instancia paso a paso para configurar los parámetros para el proceso de selección paso a paso.
//--- CStepwise stepwise; stepwise.setParams(NumKeptVars,NumFolds,MinNumVars,MaxNumVars,NumReplications,true); if(!stepwise.stepwiseSelection(mat,target)) return;
Los parámetros, que pueden ser ajustados por el usuario, incluyen:
input ulong NumKeptVars = 1; input ulong NumFolds = 10; input ulong MinNumVars = 3; input ulong MaxNumVars = 5; input long NumReplications = 1;
- NumKeptVars: especifica la cantidad deseada de características a conservar en cada iteración del proceso de selección.
- NumFolds: determina la cantidad de pliegues que se utilizarán para la validación cruzada, lo que facilita una evaluación sólida del rendimiento del modelo.
- MinNumVars: establece la cantidad mínima de características que puede contener el conjunto de características final seleccionado, lo que garantiza que el modelo permanezca adecuadamente equipado para la predicción.
- MaxNumVars: establece la cantidad máxima de características permitidas en el conjunto de características final, lo que evita el sobreajuste al controlar la complejidad del modelo.
- NumReplications: Indica el número de iteraciones para la prueba de permutación de Monte Carlo, lo que mejora la confiabilidad de las pruebas de significancia realizadas durante la selección de características.
Una vez que se invoca el método stepwiseSelection(), comienza el proceso de selección de características paso a paso. Este método orquesta todo el algoritmo de selección, implementando las estrategias discutidas anteriormente para identificar los predictores más relevantes para el modelo de regresión lineal-cuadrática. La salida generada por el script StepWiseFeatureSelection_Demo.mq5 puede proporcionar información valiosa sobre cómo los diferentes hiperparámetros influyen en el proceso de selección de características. Profundicemos en los distintos aspectos de la salida y cómo se relacionan con los parámetros de entrada especificados.
Los componentes clave de salida del algoritmo son:
- Conjuntos de características seleccionadas: el resultado principal es el conjunto de características seleccionadas por el algoritmo después de ejecutar la selección paso a paso. Cada conjunto de características representa una combinación de predictores considerados más relevantes en función de su contribución al rendimiento del modelo.
- Métricas de rendimiento: para cada iteración del proceso de selección, el script normalmente generará métricas de rendimiento como:
- Valor del criterio: la suma de los errores cuadrados u otro criterio elegido, que proporciona una medida cuantificable del ajuste del modelo.
- Valores 'p': si se emplean pruebas de permutación de Monte Carlo, el resultado incluirá valores 'p' que indican la probabilidad de que las mejoras de rendimiento observadas se deban al azar.
En la ejecución inicial del script StepWiseFeatureSelection_Demo.mq5 con parámetros predeterminados, preparamos el escenario para observar cómo funciona el proceso de selección por pasos en una configuración restringida. A continuación se presenta un desglose de lo que se puede esperar del resultado, la lógica detrás de estas expectativas y cómo los resultados se alinean con nuestras observaciones.
Dado que no se especifica ninguna prueba MCP, la salida será solo una única columna con los valores de criterio correspondientes a cada iteración. Esto reflejará el rendimiento del modelo a medida que se agreguen predictores. Se espera que los valores del criterio aumenten en cada iteración. Esto indica que el rendimiento del modelo está mejorando a medida que se agregan predictores relevantes. El algoritmo selecciona estratégicamente características que mejoran la precisión predictiva, elevando así el criterio. Finalmente, a medida que se identifiquen los predictores relevantes, el criterio alcanzará un valor óptimo (en este caso, 1). Esto sugiere que el modelo ha incorporado con éxito los predictores más informativos y está funcionando lo mejor que puede, dadas las limitaciones del modelo.
MM 0 20:20:28.754 StepWiseFeatureSelection_Demo (BTCUSD,D1) Stepwise selection successfully completed QM 0 21:05:21.050 StepWiseFeatureSelection_Demo (BTCUSD,D1) STEPWISE SELECTION PARAMETERS KG 0 21:05:21.050 StepWiseFeatureSelection_Demo (BTCUSD,D1) Number of retained candidate variables for each iteration 1 QH 0 21:05:21.050 StepWiseFeatureSelection_Demo (BTCUSD,D1) Number of folds in cross validation procedure 10 FI 0 21:05:21.050 StepWiseFeatureSelection_Demo (BTCUSD,D1) Final minimum number of selected predictors 3 FM 0 21:05:21.050 StepWiseFeatureSelection_Demo (BTCUSD,D1) Final maximum number of selected predictors 5 PM 0 21:05:21.050 StepWiseFeatureSelection_Demo (BTCUSD,D1) Number of replications for MCP test 1 KR 0 21:05:21.050 StepWiseFeatureSelection_Demo (BTCUSD,D1) Criterion || Column Indices ED 0 21:05:21.067 StepWiseFeatureSelection_Demo (BTCUSD,D1) 0.26300861 6 NO 0 21:05:21.089 StepWiseFeatureSelection_Demo (BTCUSD,D1) 0.57220902 4 6 RG 0 21:05:21.122 StepWiseFeatureSelection_Demo (BTCUSD,D1) 0.75419718 4 5 6 HH 0 21:05:21.170 StepWiseFeatureSelection_Demo (BTCUSD,D1) 1.00000000 0 4 5 6 GL 0 21:05:21.240 StepWiseFeatureSelection_Demo (BTCUSD,D1) CStepwisebase::stepwise_search procedure terminated early because adding a new variable caused performance degradation
En el registro de salida, cada iteración mostrará el valor del criterio actual después de evaluar los predictores seleccionados. La tendencia creciente proporcionará una imagen clara de cómo cada adición de características contribuye al rendimiento del modelo. La salida también debe indicar el motivo de la finalización, que probablemente mencionará que las características adicionales no llevaron a un mejor rendimiento, lo que confirma el proceso de toma de decisiones del algoritmo en tiempo real. Esto se habilita mediante el parámetro que especifica el número mínimo de predictores permitidos en un conjunto de características.
En una ejecución posterior del script StepWiseFeatureSelection_Demo.mq5, introducimos una prueba de permutación de Monte Carlo (MCP) con 100 permutaciones mientras mantenemos los valores predeterminados para los demás parámetros. Este ajuste enriquece significativamente el resultado y proporciona información más profunda sobre el proceso de selección de características.
Con la prueba MCP habilitada, la salida ahora constará de múltiples columnas. Cada fila corresponderá a una iteración, mostrando el valor del criterio y la probabilidad de ocurrencia aleatoria y la probabilidad de mejora espuria. Un valor 'p' bajo (normalmente ≤ 0,05) indica que es probable que el rendimiento observado no se deba al azar, lo que respalda la inclusión de la característica correspondiente.
Los dos valores 'p' presentados guiarán a los usuarios en la evaluación de la confiabilidad de los predictores seleccionados.
RI 0 21:10:57.100 StepWiseFeatureSelection_Demo (BTCUSD,D1) STEPWISE SELECTION PARAMETERS LK 0 21:10:57.100 StepWiseFeatureSelection_Demo (BTCUSD,D1) Number of retained candidate variables for each iteration 1 RD 0 21:10:57.100 StepWiseFeatureSelection_Demo (BTCUSD,D1) Number of folds in cross validation procedure 10 EM 0 21:10:57.100 StepWiseFeatureSelection_Demo (BTCUSD,D1) Final minimum number of selected predictors 3 EQ 0 21:10:57.100 StepWiseFeatureSelection_Demo (BTCUSD,D1) Final maximum number of selected predictors 5 OQ 0 21:10:57.100 StepWiseFeatureSelection_Demo (BTCUSD,D1) Number of replications for MCP test 100 PI 0 21:10:57.101 StepWiseFeatureSelection_Demo (BTCUSD,D1) Criterion || New pval || Diff pval || Column Indices RD 0 21:10:58.851 StepWiseFeatureSelection_Demo (BTCUSD,D1) 0.26300861 0.01000000 0.01000000 6 EI 0 21:11:01.243 StepWiseFeatureSelection_Demo (BTCUSD,D1) 0.57220902 0.01000000 0.01000000 4 6 KM 0 21:11:04.482 StepWiseFeatureSelection_Demo (BTCUSD,D1) 0.75419718 0.01000000 0.01000000 4 5 6 FP 0 21:11:09.151 StepWiseFeatureSelection_Demo (BTCUSD,D1) 1.00000000 0.01000000 0.01000000 0 4 5 6 CI 0 21:11:09.214 StepWiseFeatureSelection_Demo (BTCUSD,D1) CStepwisebase::stepwise_search procedure terminated early because adding a new variable caused performance degradation
Esta ejecución, mejorada con la inclusión de una prueba de permutación de Monte Carlo, proporciona un resultado más rico e informativo. Las columnas múltiples permiten a los usuarios tomar decisiones más informadas sobre el conjunto de características óptimo en función de los criterios de rendimiento y la significancia estadística. Como resultado, los usuarios pueden identificar con confianza qué predictores deben conservarse en el modelo final, guiados por valores de criterio altos y valores 'p' bajos.
LL 0 07:22:46.657 StepWiseFeatureSelection_Demo (BTCUSD,D1) STEPWISE SELECTION PARAMETERS GH 0 07:22:46.658 StepWiseFeatureSelection_Demo (BTCUSD,D1) Number of retained candidate variables for each iteration 1 ID 0 07:22:46.658 StepWiseFeatureSelection_Demo (BTCUSD,D1) Number of folds in cross validation procedure 5 FH 0 07:22:46.658 StepWiseFeatureSelection_Demo (BTCUSD,D1) Final minimum number of selected predictors 10 JO 0 07:22:46.658 StepWiseFeatureSelection_Demo (BTCUSD,D1) Final maximum number of selected predictors 10 FL 0 07:22:46.658 StepWiseFeatureSelection_Demo (BTCUSD,D1) Number of replications for MCP test 100 FL 0 07:22:46.658 StepWiseFeatureSelection_Demo (BTCUSD,D1) Criterion || New pval || Diff pval || Column Indices LG 0 07:22:47.303 StepWiseFeatureSelection_Demo (BTCUSD,D1) 0.26726680 0.01000000 0.01000000 6 LJ 0 07:22:48.153 StepWiseFeatureSelection_Demo (BTCUSD,D1) 0.56836766 0.01000000 0.01000000 4 6 FH 0 07:22:49.518 StepWiseFeatureSelection_Demo (BTCUSD,D1) 0.74542884 0.01000000 0.01000000 4 5 6 NM 0 07:22:51.488 StepWiseFeatureSelection_Demo (BTCUSD,D1) 1.00000000 0.01000000 0.01000000 0 4 5 6 KQ 0 07:22:54.163 StepWiseFeatureSelection_Demo (BTCUSD,D1) 1.00000000 0.01000000 0.71000000 0 1 4 5 6 JF 0 07:22:57.793 StepWiseFeatureSelection_Demo (BTCUSD,D1) 1.00000000 0.01000000 0.85000000 0 1 2 4 5 6 DD 0 07:23:02.436 StepWiseFeatureSelection_Demo (BTCUSD,D1) 1.00000000 0.01000000 0.94000000 0 1 2 3 4 5 6 MK 0 07:23:08.007 StepWiseFeatureSelection_Demo (BTCUSD,D1) 1.00000000 0.01000000 1.00000000 0 1 2 3 4 5 6 7 DH 0 07:23:13.842 StepWiseFeatureSelection_Demo (BTCUSD,D1) 1.00000000 0.01000000 1.00000000 0 1 2 3 4 5 6 7 8 HO 0 07:23:18.949 StepWiseFeatureSelection_Demo (BTCUSD,D1) 1.00000000 0.01000000 1.00000000 0 1 2 3 4 5 6 7 8 9 PL 0 07:23:18.949 StepWiseFeatureSelection_Demo (BTCUSD,D1) Stepwise selection successfully completed
En la ejecución final del script StepWiseFeatureSelection_Demo.mq5, el foco está en ampliar el alcance del proceso de selección de características aumentando el parámetro MinNumVars para permitir un mínimo de 10 predictores. Al permitir más predictores en el subconjunto final, el algoritmo podrá evaluar combinaciones más grandes de características y potencialmente descubrir interacciones o relaciones no lineales que un subconjunto más pequeño podría pasar por alto. Si bien aumentar el número mínimo de predictores permite una búsqueda más amplia, es esencial tener en cuenta que esto también conducirá a un mayor tiempo de ejecución del algoritmo. La complejidad adicional que supone evaluar conjuntos de características más grandes requiere más recursos computacionales y tiempo.
Las comprobaciones integradas del algoritmo garantizan que si MinNumVars o MaxNumVars se establecen en valores que exceden el número total de predictores candidatos (en este caso, 10), se ajustarán automáticamente para que coincidan con la cantidad disponible de predictores en el conjunto de datos. Esta protección evita errores de configuración que podrían provocar problemas de tiempo de ejecución o un comportamiento incorrecto en la selección de funciones. Al modificar el parámetro MinNumVars, los usuarios pueden adaptar el proceso de selección de características paso a paso para explorar una gama más amplia de características, lo que potencialmente conduce al descubrimiento de conjuntos de predictores más informativos. Esta flexibilidad mejora la usabilidad del algoritmo, permitiendo a los profesionales adaptar el proceso de selección a las características específicas de sus conjuntos de datos y objetivos de análisis.
El tiempo de ejecución del algoritmo depende de los hiperparámetros seleccionados. La prueba de permutación de Monte Carlo puede ralentizar significativamente el proceso, especialmente a medida que aumenta el número de permutaciones. Cada permutación requiere una evaluación completa del modelo, lo que se suma al número total de cálculos realizados. Por lo tanto, si bien más permutaciones pueden mejorar la robustez de los resultados de significancia estadística, también exigen más tiempo de procesamiento.
Fuera de la prueba MCP, el siguiente parámetro que puede afectar el tiempo de ejecución del algoritmo es la cantidad de pliegues especificados para la validación cruzada. La validación cruzada implica dividir el conjunto de datos en varios subconjuntos y entrenar y probar repetidamente el modelo en estos diferentes subconjuntos. A medida que aumenta el número de pliegues, el algoritmo debe realizar más iteraciones de entrenamiento y evaluación. Esto requiere mucho tiempo, sobre todo con conjuntos de datos grandes, ya que cada pliegue requiere un ajuste y una evaluación completos del modelo.
Por último, se debe prestar especial atención al seleccionar el número mínimo y máximo apropiado de predictores permitidos en el modelo final. Al considerar más predictores para su inclusión, el algoritmo debe evaluar más combinaciones durante el proceso de selección de características, lo que genera un aumento en la cantidad de ciclos de búsqueda necesarios para descubrir los subconjuntos de características óptimos. Considerando las compensaciones involucradas en estos parámetros, es importante que los profesionales seleccionen cuidadosamente los hiperparámetros en función de su caso de uso específico.
Conclusión
En este artículo, exploramos un algoritmo mejorado de selección de características paso a paso, diseñado para optimizar la identificación de características predictivas a partir de un conjunto más amplio de variables. Complementado con validación cruzada y pruebas de permutación de Monte Carlo opcionales, el algoritmo proporciona un marco que aborda las limitaciones de los métodos tradicionales por pasos, lo que permite la selección de subconjuntos de características que maximizan el rendimiento predictivo y minimizan el riesgo de sobreajuste.
Examinamos la importancia del ajuste de hiperparámetros para equilibrar la eficiencia computacional y la confiabilidad estadística, destacando cómo parámetros como el número de pliegues para la validación cruzada, el número de permutaciones para las pruebas de significancia y las restricciones en el número mínimo y máximo de predictores pueden afectar significativamente el tiempo de ejecución del algoritmo.
La demostración práctica con el script StepWiseFeatureSelection_Demo.mq5 ilustró cómo el algoritmo se puede aplicar de manera efectiva a conjuntos de datos reales, generando información sobre la importancia de subconjuntos de características seleccionados. En conclusión, el método propuesto no solo mejora el proceso de selección de características, sino que también podría permitir a los profesionales tomar decisiones informadas sobre la construcción de modelos. Todo el código referenciado en el texto se adjunta en los archivos a continuación.
| Archivo | Descripción |
|---|---|
| MQL5/include/np.mqh | Contiene la definición de funciones de utilidad para manipular matrices y vectores. |
| MQL5/include/OLS.mqh | Archivo de encabezado para la clase OLS que implementa la regresión de mínimos cuadrados ordinarios. |
| MQL5/include/stepwise.mqh | Archivo de encabezado para la clase CStepwisebase que implementa un método de selección de características paso a paso mejorado. |
| MQL5/scripts/StepWiseFeatureSelection_Demo.mq5 | Una secuencia de comandos que aplica la clase CStepwisebase para realizar una selección de características paso a paso en un conjunto de datos arbitrario. |
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/16285
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Algoritmo de Big Bang y Big Crunch
Algoritmo de Big Bang y Big Crunch
 Del básico al intermedio: Plantilla y Typename (IV)
Del básico al intermedio: Plantilla y Typename (IV)
 Del básico al intermedio: Struct (II)
Del básico al intermedio: Struct (II)
 Indicador de fuerza y dirección de la tendencia en barras 3D
Indicador de fuerza y dirección de la tendencia en barras 3D
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso