
Métodos de optimización de la biblioteca ALGLIB (Parte II)
Contenido
- Introducción
- Métodos de optimización de la biblioteca ALGLIB:
- BC (Box Constrained Optimization)
- NLC (Nonlinearly Constrained Optimization with Lagrangian Algorithm)
- LM (Levenberg-Marquardt Method)
- Tabla de funciones utilizadas en los métodos ALGLIB
- Probamos los métodos
Introducción
En la primera parte de nuestra investigación dedicada a los algoritmos de optimización de la biblioteca ALGLIB en el paquete estándar del terminal MetaTrader 5, nos familiarizamos en detalle con los algoritmos: BLEIC (Boundary, Linear Equality-Inequality Constraints), L-BFGS (Limited-memory Broyden–Fletcher–Goldfarb–Shanno) и NS (Nonsmooth Nonconvex Optimization Subject to box/linear/nonlinear - Nonsmooth Constraints). No solo analizamos sus fundamentos teóricos, sino que también deconstruimos una forma sencilla de aplicarlos a problemas de optimización.
En este artículo seguiremos investigando los métodos restantes del arsenal ALGLIB. Prestaremos especial atención a su prueba con funciones multivariantes complejas, lo cual nos permitirá hacernos una visión holística de la eficacia de cada método. Concluiremos con un análisis exhaustivo de los resultados obtenidos y presentaremos recomendaciones prácticas para seleccionar el algoritmo óptimo para determinados tipos de problemas.
BC (Box Constrained Optimization)
La Optimización con restricciones de caja es una rutina que minimiza una función F(x) con N argumentos en presencia de restricciones de caja (siendo algunas de las restricciones de caja en realidad igualdades). Este optimizador utiliza un algoritmo similar al algoritmo BLEIC (optimizador de restricciones lineales), pero al tener solo restricciones de caja permite estrategias de activación de restricciones más rápidas. En problemas a gran escala, con múltiples restricciones activas en la solución, este optimizador puede resultar más rápido que el BLEIC.
Permítame explicar de forma más sencilla en qué consiste la optimización de las restricciones de caja. Se trata de un algoritmo de optimización que busca la mejor solución, trabaja con restricciones de caja (donde cada variable debe encontrarse dentro de ciertos límites) y esencialmente busca el mínimo de una función donde todas las variables deben estar dentro de rangos dados. La principal característica del algoritmo es que resulta similar al BLEIC, pero más rápido, optimizado específicamente para el funcionamiento con restricciones de rango.
Requisitos: el punto de partida debe ser una región admisible o cercana a una región admisible, y la función deberá estar definida en toda la región admisible.
Para utilizar el método BC y otros de la biblioteca ALGLIB, necesitaremos conectar el archivo (la biblioteca se suministra con el terminal MetaTrader 5, el usuario no necesitará instalar nada adicional).
#include <Math\Alglib\alglib.mqh> Luego escribiremos un script, un ejemplo para trabajar eficientemente con métodos ALGLIB. También debemos destacar los principales pasos característicos para trabajar con los métodos ALGLIB, que resaltaremos bloques de código idénticos en el color correspondiente.
1. Definiremos las condiciones límite del problema, como el número de ejecuciones de la función de aptitud (función objetivo), los rangos de los parámetros a optimizar y su paso. Para los métodos ALGLIB será necesario asignar los valores iniciales de los parámetros optimizados "x" (los métodos son deterministas y los resultados dependen totalmente de los valores iniciales, por lo que aplicaremos la generación de números aleatorios en el rango de parámetros de la tarea), así como la escala "s" (los métodos son sensibles a la escala de los parámetros entre sí, en este caso fijaremos la escala "1").
2. Declararemos los objetos necesarios para que el algoritmo funcione.
3. Estableceremos los parámetros externos del algoritmo (ajustes).
4. Inicializaremos el algoritmo pasando al método los rangos y pasos de los parámetros a optimizar, así como los parámetros externos del algoritmo.
5. Efectuaremos la optimización.
6. Obtendremos los resultados de la optimización para su uso posterior.
Hay un aspecto importante a considerar: el usuario no tiene forma de influir o detener el proceso de optimización en ningún momento. El método realizará todas las operaciones de forma independiente llamando a una función de aptitud dentro de su proceso. El algoritmo podrá acceder a la función de aptitud un número arbitrario de veces (aunque se guie por un parámetro especificado por el usuario). El propio usuario podrá controlar el número máximo permitido de llamadas transmitiendo una orden de parada al método.
//—————————————————————————————————————————————————————————————————————————————— void OnStart () { // Initialization of optimization parameters--------------------------------------- int numbTestFuncRuns = 10000; int params = 1000; // Create and initialize arrays for range bounds--------------------- CRowDouble rangeMin, rangeMax; rangeMin.Resize (params); rangeMax.Resize (params); double rangeStep; for (int i = 0; i < params; i++) { rangeMin.Set (i, -10); rangeMax.Set (i, 10); } rangeStep = DBL_EPSILON; CRowDouble x; x.Resize (params); CRowDouble s; s.Resize (params); s.Fill (1); // Generate random initial parameter values in given ranges---- for (int i = 0; i < params; i++) { x.Set (i, rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0)); } // Create objects for optimization------------------------------------------ C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns); CObject obj; CNDimensional_Rep frep; CMinBCReport rep; // Set the parameters of the BC optimization algorithm------------------------------ double diffStep = 0.00001; double epsg = 1e-16; double epsf = 1e-16; CAlglib::MinBCCreateF (x, diffStep, fFunc.state); CAlglib::MinBCSetBC (fFunc.state, rangeMin, rangeMax); CAlglib::MinBCSetScale (fFunc.state, s); CAlglib::MinBCSetCond (fFunc.state, epsg, epsf, rangeStep, numbTestFuncRuns); CAlglib::MinBCOptimize (fFunc.state, fFunc, frep, obj); CAlglib::MinBCResults (fFunc.state, x, rep); // Output of optimization results----------------------------------------------- Print ("BC, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches); } //——————————————————————————————————————————————————————————————————————————————
Como el método accede a la función de aptitud por sí mismo (y no desde el programa del usuario), tendremos que envolver la llamada a la función de aptitud en una clase que herede de una clase padre en ALGLIB (estas clases padre son diferentes para los distintos métodos). Declararemos la clase de envoltorio como "C_OptimisedFunction" y escribiremos los siguientes métodos en la clase:
1. Func () — método virtual que se sobrescribe en las clases derivadas.2. Init () — inicializa los parámetros de la clase. Dentro del método:
- Se inicializarán las variables asociadas al número de ejecuciones y al mejor valor de función encontrado.
- Los arrays "c" y "cB" estarán reservados para almacenar coordenadas.
Variables:
- state — objeto de tipo CMinBCState específico para el método BC; se utilizará al llamar a métodos estáticos del algoritmo y al llamar al método break.
- numberLaunches — número actual de inicios (necesario para evitar una ejecución incontrolada o demasiado larga de la función de aptitud).
- maxNumbLaunchesAllowed — número máximo de inicios permitidos.
- fB — mejor valor encontrado de la función de aptitud.
- c [] — array de coordenadas actuales.
- cB [] — array para almacenar las mejores coordenadas de búsqueda.
//—————————————————————————————————————————————————————————————————————————————— // Class for function optimization, inherits from CNDimensional_Func class C_OptimizedFunction : public CNDimensional_Func { public: //-------------------------------------------------------------------- C_OptimizedFunction (void) { } ~C_OptimizedFunction (void) { } // A virtual function to contain the function being optimized-------- virtual void Func (CRowDouble &x, double &func, CObject &obj); // Initialization of optimization parameters--------------------------------------- void Init (int coords, int maxNumberLaunchesAllowed) { numberLaunches = 0; maxNumbLaunchesAllowed = maxNumberLaunchesAllowed; fB = -DBL_MAX; ArrayResize (c, coords); ArrayResize (cB, coords); } //---------------------------------------------------------------------------- CMinBCState state; // State int numberLaunches; // Launch counter double fB; // Best found value of the objective function (maximum) double cB []; // Coordinates of the point with the best function value private: //------------------------------------------------------------------- double c []; // Array for storing current coordinates int maxNumbLaunchesAllowed; // Maximum number of function calls allowed }; //——————————————————————————————————————————————————————————————————————————————
El método "Func" de la clase "C_OptimisedFunction" está diseñado para abordar la función de aptitud del usuario. Tomaremos como argumentos el vector "x" (una de las variantes de los parámetros del problema optimizado que ofrece el método de optimización), el argumento "func" al que deberá devolverse el valor calculado de la función de aptitud, y el objeto "obj" (cuya finalidad no tengo clara, quizá reservada a la posibilidad de pasar información adicional al/del método). Las principales etapas de la ejecución del método serán las siguientes:
- Incrementaremos el contador "numberLaunches", que lleva la cuenta del número de llamadas al método "Func".
- Si el número de ejecuciones supera el valor permitido "maxNumbLaunchesAllowed", la función establecerá el valor "func" en "DBL_MAX" (valor máximo de tipo "double", los métodos ALGLIB están diseñados para minimizar funciones, este valor significa la peor solución posible). A continuación, se llamará a la función "MinBCRequestTermination", diseñada para indicar al método BC que detenga el proceso de optimización.
- Luego el ciclo copiará los valores del vector "x" en el array "c". Esto será necesario para usar estos valores para la transmisión a la función de aptitud del usuario.
- Después llamaremos a la función "ObjectiveFunction", que calculará el valor de la función objetivo para los valores actuales en el array "c". El resultado se almacenará en "ffVal", y el valor "func" se establecerá en el valor negativo de "ffVal" (estamos optimizando un paraboloide invertido que necesita ser maximizado, y BC minimiza la función, por lo que invertiremos el valor).
- Si el valor actual "ffVal" es superior al mejor valor anterior "fB", "fB" se actualizará y el array "cB" copiará el estado "c" actual. De este modo, se mantendrá un registro del mejor valor encontrado de la función objetivo con los parámetros correspondientes y se podrá consultar posteriormente si es necesario.
La función "Func" implementará una llamada a una función de aptitud personalizada y realizará un seguimiento del número de veces que se ejecuta, actualizando los mejores resultados. También gestionará las condiciones de parada si el número de inicios supera un límite establecido.
//—————————————————————————————————————————————————————————————————————————————— // Implementation of the function to be optimized void C_OptimizedFunction::Func (CRowDouble &x, double &func, CObject &obj) { // Increase the function launch counter and limitation control---------------- numberLaunches++; if (numberLaunches >= maxNumbLaunchesAllowed) { func = DBL_MAX; CAlglib::MinBCRequestTermination (state); return; } // Copy input coordinates to internal array------------------------- for (int i = 0; i < x.Size (); i++) c [i] = x [i]; // Calculate objective function value---------------------------------------- double ffVal = ObjectiveFunction (c); func = -ffVal; // Update the best solution found-------------------------------------- if (ffVal > fB) { fB = ffVal; ArrayCopy (cB, c); } } //——————————————————————————————————————————————————————————————————————————————
Después de ejecutar el script de prueba con el algoritmo BC para optimizar la función paraboloide, obtendremos el siguiente resultado en la impresión:
Desafortunadamente, a pesar de las peticiones para detener la optimización mediante el método "MinBCRequestTermination", el algoritmo ha continuado el proceso y ha intentando acceder a la función de aptitud más allá del límite de 10.000 ejecuciones.
Ahora intentaremos no coartar a BC y dejaremos que actúe como crea conveniente. El resultado ha sido el siguiente:
Como podemos ver, el BC es capaz de converger completamente a una función paraboloide, pero en este caso no es posible estimar de antemano el número necesario de ejecuciones de la función objetivo.
En el algoritmo, el paso de diferenciación resulta importante. Por consiguiente, si utilizamos un paso muy pequeño, como 1e-16 en lugar de 0,00001, el algoritmo se detendrá prematuramente, en esencia, se quedará atascado, con este resultado:
NLC (Nonlinearly Constrained Optimization with Preconditioned Augmented Lagrangian Algorithm)
Este algoritmo de optimización no lineal con restricciones permite minimizar una función objetivo compleja F(x) con N variables teniendo en cuenta diversas restricciones: restricciones en los límites de las variables (min <= x <= max), desigualdades e igualdades lineales, igualdades no lineales G(x) = 0, desigualdades no lineales H(x) <= 0.
Imagine que tenemos un objetivo ambicioso que queremos alcanzar, pero también unas limitaciones que no podemos superar. Por ejemplo, queremos maximizar nuestros beneficios sobre las ventas, pero no podemos superar determinados gastos generales. El algoritmo de ALGLIB ayuda a resolver este tipo de problemas de optimización con restricciones. Así funciona:
1. Ofrecemos al algoritmo un punto de partida, una suposición inicial sobre cómo lograr el objetivo. Este punto debe ser factible, es decir, debe cumplir todas las restricciones.
2. A continuación, el algoritmo comienza a moverse lentamente desde este punto de partida, acercándose paso a paso a la solución óptima. En cada paso, resuelve algún problema auxiliar para entender qué dirección tomar a continuación.
3. Para acelerar este proceso, el algoritmo usa una técnica especial: el "pre-acondicionamiento". Esto significa que el algoritmo ajusta sus "pasos" a la estructura de la tarea para avanzar más rápido.
4. Al final, tras varias iteraciones, el algoritmo encuentra una solución que minimiza su función objetivo (por ejemplo, minimiza la sobrecarga) y sigue cumpliendo todas las restricciones.
El usuario puede elegir entre tres solucionadores diferentes que resultan adecuados para problemas de diferente escala y complejidad implementados en ALGLIB:
La SQP (programación cuadrática secuencial) se recomienda para problemas de tamaño medio con funciones objetivo difíciles.
El método AUL (método lagrangiano aumentado pre-acondicionado) se recomienda para problemas a gran escala o con funciones objetivo baratas (rápidas).
La SLP (programación lineal secuencial) resulta más lenta pero más robusta en casos complejos.
Los experimentos con funciones de prueba han demostrado la eficacia del solucionador AUL; los demás solucionadores se comentan en el código.
//—————————————————————————————————————————————————————————————————————————————— void OnStart () { // Initialization of optimization parameters--------------------------------------- int numbTestFuncRuns = 10000; int params = 1000; // Create and initialize arrays for range bounds--------------------- CRowDouble rangeMin, rangeMax; rangeMin.Resize (params); rangeMax.Resize (params); double rangeStep; for (int i = 0; i < params; i++) { rangeMin.Set (i, -10); rangeMax.Set (i, 10); } rangeStep = DBL_EPSILON; CRowDouble x; x.Resize (params); CRowDouble s; s.Resize (params); s.Fill (1); // Generate random initial parameter values in given ranges---- for (int i = 0; i < params; i++) { x.Set (i, rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0)); } // Create objects for optimization------------------------------------------ C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns); CObject obj; CNDimensional_Rep frep; CMinNLCReport rep; // Setting parameters of the NLC optimization algorithm----------------------------- double diffStep = 0.00001; double rho = 1000.0; int outerits = 5; CAlglib::MinNLCCreateF (x, diffStep, fFunc.state); CAlglib::MinNLCSetBC (fFunc.state, rangeMin, rangeMax); CAlglib::MinNLCSetScale (fFunc.state, s); CAlglib::MinNLCSetCond (fFunc.state, rangeStep, numbTestFuncRuns); //CAlglib::MinNLCSetAlgoSQP (fFunc.state); CAlglib::MinNLCSetAlgoAUL (fFunc.state, rho, outerits); //CAlglib::MinNLCSetAlgoSLP (fFunc.state); CAlglib::MinNLCOptimize (fFunc.state, fFunc, frep, obj); CAlglib::MinNLCResults (fFunc.state, x, rep); // Output of optimization results----------------------------------------------- Print ("NLC, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches); } //——————————————————————————————————————————————————————————————————————————————
En NLC, el tipo de variable "state" lo estableceremos en "CMinNLCState".
//—————————————————————————————————————————————————————————————————————————————— // Class for function optimization, inherits from CNDimensional_FVec class C_OptimizedFunction : public CNDimensional_FVec { public: //-------------------------------------------------------------------- C_OptimizedFunction (void) { } ~C_OptimizedFunction (void) { } // A virtual function to contain the function being optimized-------- virtual void FVec (CRowDouble &x, CRowDouble &fi, CObject &obj); // Initialization of optimization parameters--------------------------------------- void Init (int coords, int maxNumberLaunchesAllowed) { numberLaunches = 0; maxNumbLaunchesAllowed = maxNumberLaunchesAllowed; fB = -DBL_MAX; ArrayResize (c, coords); ArrayResize (cB, coords); } //---------------------------------------------------------------------------- CMinNLCState state; // State int numberLaunches; // Launch counter double fB; // Best found value of the objective function (maximum) double cB []; // Coordinates of the point with the best function value private: //------------------------------------------------------------------- double c []; // Array for storing current coordinates int maxNumbLaunchesAllowed; // Maximum number of function calls allowed }; //——————————————————————————————————————————————————————————————————————————————
Luego detendremos el proceso de optimización con el comando "MinNLCRequestTermination".
//—————————————————————————————————————————————————————————————————————————————— // Implementation of the function to be optimized void C_OptimizedFunction::FVec (CRowDouble &x, CRowDouble &fi, CObject &obj) { // Increase the function launch counter and limitation control---------------- numberLaunches++; if (numberLaunches >= maxNumbLaunchesAllowed) { fi.Set (0, DBL_MAX); CAlglib::MinNLCRequestTermination (state); return; } // Copy input coordinates to internal array------------------------- for (int i = 0; i < x.Size (); i++) c [i] = x [i]; // Calculate objective function value---------------------------------------- double ffVal = ObjectiveFunction (c); fi.Set (0, -ffVal); // Update the best solution found-------------------------------------- if (ffVal > fB) { fB = ffVal; ArrayCopy (cB, c); } } //——————————————————————————————————————————————————————————————————————————————
Tras ejecutar el script de prueba con el algoritmo NLC para optimizar la función paraboloide, obtendremos el siguiente resultado en la impresión:
NLC, best result: 0.8858935739350294, number of function launches: 28007
Sin límite en el número de ejecuciones de la función objetivo, el NLC converge completamente, pero sigue realizando más de un millón de iteraciones:
NLC, best result: 1.0, number of function launches: 1092273
Utilizando un paso muy pequeño de 1e-16, el algoritmo no se detendrá prematuramente como, por ejemplo, el método BC, pero mostrará un resultado ligeramente peor que con un paso de 0,00001.
NLC, best result: 0.8543715192632731, number of function launches: 20005
LM (Levenberg-Marquardt Method)
El método de Levenberg-Marquardt (LM) es un algoritmo de optimización ampliamente usado para resolver problemas de mínimos cuadrados no lineales. Este método resulta eficaz en problemas de ajuste de curvas y superficies.
La idea básica de LM combina dos técnicas de optimización: el método de descenso del gradiente y el método de Gauss-Newton. Esto permite al algoritmo adaptarse a la forma de la función objetivo. Cómo funciona:
- En cada iteración, el algoritmo calcula la dirección del paso usando una combinación de descenso de gradiente y aproximación de segundo orden.
- El coeficiente de atenuación (λ) se ajusta automáticamente para controlar el tamaño del paso y el equilibrio entre los dos métodos.
Imagine que intentamos encontrar el punto más bajo de una zona montañosa, pero todo lo que tenemos es un mapa con contornos borrosos. El método Levenberg-Marquardt sería como un navegador inteligente que combina dos formas de encontrar un camino:
1. El primer método (método de Gauss-Newton) es rápido pero arriesgado. Sería como si estuviéramos corriendo cuesta abajo. Funciona muy bien cuando estamos cerca de nuestro objetivo, pero podemos "tropezar" si el terreno es difícil.
2. El segundo método (descenso por gradiente) es lento pero fiable. Sería como si descendiéramos cuidadosamente en pequeños pasos, más lentos pero más seguros. Funciona bien incluso en terrenos difíciles.
El algoritmo alterna de manera inteligente entre estas dos formas. Cuando el camino está despejado, usa el modo rápido, pero cuando la situación es difícil, cambia al modo cauteloso, ajustando automáticamente el tamaño del paso.
Podría quedar atascado en un mínimo localizado. Requiere una buena aproximación inicial (hay que saber aproximadamente dónde buscar) y no resulta muy eficiente para problemas con un gran número de parámetros (más de 100).
//—————————————————————————————————————————————————————————————————————————————— void OnStart () { // Initialization of optimization parameters--------------------------------------- int numbTestFuncRuns = 10000; int params = 1000; double rangeMin [], rangeMax [], rangeStep; ArrayResize (rangeMin, params); ArrayResize (rangeMax, params); for (int i = 0; i < params; i++) { rangeMin [i] = -10; rangeMax [i] = 10; } rangeStep = DBL_EPSILON; double x []; double s []; ArrayResize (x, params); ArrayResize (s, params); ArrayInitialize (s, 1); // Generate random initial parameter values in given ranges---- for (int i = 0; i < params; i++) { x [i] = rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0); } // Create objects for optimization------------------------------------------ C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns); CObject obj; CNDimensional_Rep frep; CMinLMReportShell rep; // Set the parameters of the LM optimization algorithm------------------------------ double diffStep = 1e-16;//0.00001; CAlglib::MinLMCreateV (1, x, diffStep, fFunc.state); CAlglib::MinLMSetBC (fFunc.state, rangeMin, rangeMax); CAlglib::MinLMSetScale (fFunc.state, s); CAlglib::MinLMSetCond (fFunc.state, rangeStep, numbTestFuncRuns); CAlglib::MinLMOptimize (fFunc.state, fFunc, frep, 0, obj); CAlglib::MinLMResults (fFunc.state, x, rep); // Output of optimization results----------------------------------------------- Print ("LM, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches); } //——————————————————————————————————————————————————————————————————————————————
Para el LM, estableceremos el tipo de variable "state" en "CMinLMStateShell".
//—————————————————————————————————————————————————————————————————————————————— // Class for function optimization, inherits from CNDimensional_FVec class C_OptimizedFunction : public CNDimensional_FVec { public: //-------------------------------------------------------------------- C_OptimizedFunction (void) { } ~C_OptimizedFunction (void) { } // A virtual function to contain the function being optimized-------- virtual void FVec (CRowDouble &x, CRowDouble &fi, CObject &obj); // Initialization of optimization parameters--------------------------------------- void Init (int coords, int maxNumberLaunchesAllowed) { numberLaunches = 0; maxNumbLaunchesAllowed = maxNumberLaunchesAllowed; fB = -DBL_MAX; ArrayResize (c, coords); ArrayResize (cB, coords); } //---------------------------------------------------------------------------- CMinLMStateShell state; // State int numberLaunches; // Launch counter double fB; // Best found value of the objective function (maximum) double cB []; // Coordinates of the point with the best function value private: //------------------------------------------------------------------- double c []; // Array for storing current coordinates int maxNumbLaunchesAllowed; // Maximum number of function calls allowed }; //——————————————————————————————————————————————————————————————————————————————
Al igual que en los métodos de optimización anteriores, limitaremos el número de veces que se accede a la función objetivo, pero el método LM es el único para el que no existe un comando break, así que sería lógico esperar una función "MinLMRequestTermination".
//—————————————————————————————————————————————————————————————————————————————— // Implementation of the function to be optimized void C_OptimizedFunction::FVec (CRowDouble &x, CRowDouble &fi, CObject &obj) { // Increase the function launch counter and limitation control---------------- numberLaunches++; if (numberLaunches >= maxNumbLaunchesAllowed) { fi.Set (0, DBL_MAX); //CAlglib::MinLMRequestTermination (state); // such method does not exist return; } // Copy input coordinates to internal array------------------------- for (int i = 0; i < x.Size (); i++) c [i] = x [i]; // Calculate objective function value---------------------------------------- double ffVal = ObjectiveFunction (c); fi.Set (0, -ffVal); // Update the best solution found-------------------------------------- if (ffVal > fB) { fB = ffVal; ArrayCopy (cB, c); } } //——————————————————————————————————————————————————————————————————————————————
Después de ejecutar el script de prueba con el algoritmo LM para optimizar la función paraboloide, obtendremos el siguiente resultado en la impresión:
LM, best result: 0.6776047308612422, number of function launches: 4003
El método LM se ha detenido en la 4003ª ejecución de la función objetivo, en consecuencia, la eliminación de las restricciones en el número de iteraciones dará el mismo resultado porque el algoritmo se ha atascado antes de alcanzar el "techo" de 10.000 iteraciones:
Utilizando un paso muy pequeño de 1e-16, el algoritmo se detendrá prematuramente incluso antes, en la ejecución 2001ª de la función objetivo:
LM, best result: 0.6670839162547625, number of function launches: 2001
Tabla de funciones usadas en los métodos ALGLIB
Los métodos de optimización ALGLIB usan diferentes tipos de variables como valores iniciales y restricciones de caja, así como diferentes tipos de clases padre de la función objetivo y conjuntos de objetos necesarios para la optimización, y una lista diferente de funciones llamadas. Esto puede dificultar la escritura intuitiva de programas que usen estos métodos.
Para simplificar la comprensión y estructurar el conocimiento sobre los métodos de optimización de ALGLIB, hemos preparado una tabla resumen. Esta ayudará a los programadores a navegar rápidamente e iniciar correctamente la optimización en sus proyectos.
| Optimization algorithm | Type FF function | Type of variable | List of objects | List of called methods |
| BLEIC | Func | double | 1) Cobject 2) CNDimensional_Rep 3) CMinBLEICReportShell 4) CminBLEICStateShell | 1) Calglib::MinBLEICCreateF 2) Calglib::MinBLEICSetBC 3) Calglib::MinBLEICSetInnerCond 4) Calglib::MinBLEICSetOuterCond 5) Calglib::MinBLEICOptimize 6) Calglib::MinBLEICResults 7) Calglib::MinBLEICRequestTermination |
| LBFGS | Func | double | 1) Cobject 2) CNDimensional_Rep 3) CminLBFGSReportShell 4) CminLBFGSStateShell | 1) Calglib::MinLBFGSCreateF 2) Calglib::MinLBFGSSetCond 3) Calglib::MinLBFGSSetScale 4) Calglib::MinLBFGSOptimize 5) Calglib::MinLBFGSResults 6) Calglib::MinLBFGSRequestTermination |
| NS | FVec | CRowDouble | 1) CObject 2) CNDimensional_Rep 3) CminNSReport 4) CminNSState | 1) Calglib::MinNSCreateF 2) CAlglib::MinNSSetBC 3) CAlglib::MinNSSetScale 4) CAlglib::MinNSSetCond 5) CAlglib::MinNSSetAlgoAGS 6) CAlglib::MinNSOptimize 7) Calglib::MinNSResults 8) Calglib::MinNSRequestTermination |
| BC | Func | CRowDouble | 1) CObject 2) CNDimensional_Rep 3) CminBCReport 4) CminBCState | 1) CAlglib::MinBCCreateF 2) CAlglib::MinBCSetBC 3) CAlglib::MinBCSetScale 4) CAlglib::MinBCSetCond 5) CAlglib::MinBCOptimize 6) Calglib::MinBCResults 7) Calglib::MinBCRequestTermination |
| NLC | Fvec | CRowDouble | 1) Cobject 2) CNDimensional_Rep 3) CminNLCReport 4) CminNLCState | 1) CAlglib::MinNLCCreateF 2) CAlglib::MinNLCSetBC 3) CAlglib::MinNLCSetScale 4) CAlglib::MinNLCSetCond 5) Calglib::MinNLCSetAlgoAUL 6) Calglib::MinNLCOptimize 7) Calglib::MinNLCResults 8) Calglib::MinNLCRequestTermination |
| LM | FVec | double | 1) Cobject 2) CNDimensional_Rep 3) CminLMReportShell 4) CminLMStateShell | 1) Calglib::MinLMCreateV 2) Calglib::MinLMSetBC. 3) Calglib::MinLMSetScale 4) Calglib::MinLMSetCond 5) Calglib::MinLMOptimize 6) Calglib::MinLMResults 7) Calglib::MinLMRequestTermination (does not exist) |
Probamos los métodos
Tras estudiar los métodos de optimización de la biblioteca ALGLIB, nos surge una pregunta natural: ¿cuál de ellos elegir para tareas específicas? Los diferentes tipos de problemas de optimización pueden resolverse con distinta eficacia en función del método elegido. Para responder a esta importante pregunta, usaremos sofisticadas funciones de prueba que han demostrado ser las más parecidas a los problemas del mundo real. Estas funciones reflejan casos típicos: las funciones suaves están representadas por la función de prueba Hilly, las funciones suaves con vértices agudos (diferenciables no sobre toda su definición) por Forest, y una función puramente discreta por Megacity.
Las pruebas se realizarán con 50 reinicios de cada prueba y un límite de 10.000 llamadas a las funciones objetivo. Prepararemos un script de banco de pruebas usando el método BC como ejemplo. Este enfoque nos permitirá obtener resultados más precisos y representativos que nos ayudarán a elegir el método de optimización más adecuado para cada problema específico.
Luego escribiremos la función "FuncTests" que realizará ejecuciones de prueba de la optimización utilizando el método ALGLIB correspondiente. La función recopilará datos sobre el rendimiento de los métodos y visualizará su rendimiento, además de trazar gráficos de convergencia.
Vamos a enumerar brevemente lo que hace la función "FuncTests":
- Acepta la función objetivo de la prueba, el número de pruebas, el color para la visualización y las variables para el resultado global.
- Si el vídeo está activado, construirá el gráfico de la función.
- Establece los límites de la prueba e inicializa las variables para los resultados.
- Genera datos de entrada aleatorios y realiza la optimización usando la biblioteca "CAlglib".
- Guarda el número de llamadas a la función de destino y los mejores resultados.
- Calcula y muestra los resultados medios.
- Actualiza la puntuación total basándose en las pruebas actuales.
//—————————————————————————————————————————————————————————————————————————————— void FuncTests (C_Function &f, // Reference to the target function object const int funcCount, // Number of functions to test const color clrConv, // Visualization color double &allScore, // Total score of all tests double &allTests) // Total number of tests { if (funcCount <= 0) return; // If the number of functions = 0, exit the function allTests++; // Increase the total number of tests if (Video_P) // If visualization is enabled { ST.DrawFunctionGraph (f); // Draw the function graph ST.SendGraphToCanvas (); // Send the graph to the canvas ST.MaxMinDr (f); // Determine the maximum and minimum of the function ST.Update (); // Update the visualization } //---------------------------------------------------------------------------- C_AO_Utilities Ut; // Utilities for handling numbers int xConv = 0.0; // Variable for converting along the X axis int yConv = 0.0; // Variable for converting along the Y axis double aveResult = 0.0; // Average test result int aveRunsFF = 0; // Average number of function runs int params = funcCount * 2; // Number of parameters (2 for each function) int epochCount = NumbTestFuncRuns_P / PopSize_P; // Number of epochs //---------------------------------------------------------------------------- CRowDouble bndl; bndl.Resize (params); // Array for lower bounds CRowDouble bndu; bndu.Resize (params); // Array for upper bounds for (int i = 0; i < funcCount; i++) // Fill the boundaries for each function { bndu.Set (i * 2, f.GetMaxRangeX ()); // Set the upper boundary by X bndl.Set (i * 2, f.GetMinRangeX ()); // Set the lower boundary by X bndu.Set (i * 2 + 1, f.GetMaxRangeY ()); // Set the upper bound by Y bndl.Set (i * 2 + 1, f.GetMinRangeY ()); // Set the lower boundary by Y } CRowDouble x; x.Resize (params); // Array for parameter values CRowDouble s; s.Resize (params); // Array for scaling s.Fill (1); // Fill the array with ones for (int test = 0; test < NumberRepetTest_P; test++) // Run the tests { for (int i = 0; i < funcCount; i++) // For each function { x.Set (i * 2, Ut.RNDfromCI (bndl [i * 2], bndu [i * 2])); // Generate random values by X x.Set (i * 2 + 1, Ut.RNDfromCI (bndl [i * 2 + 1], bndu [i * 2 + 1])); // Generate random values by Y } //-------------------------------------------------------------------------- CObject obj; // Object for storing results C_OptimizedFunction fFunc; fFunc.Init (params, NumbTestFuncRuns_P, PopSize_P, clrConv); // Initialize the optimization function CNDimensional_Rep frep; // Representation of multidimensional space CMinBCState state; // State of the minimization method CMinBCReport rep; // Minimization report double epsg = 1e-16; // Parameter for gradient stop condition double epsf = 1e-16; // Parameter for the stop condition by function value CAlglib::MinBCCreateF (x, DiffStep_P, state); // Create minimization state CAlglib::MinBCSetBC (state, bndl, bndu); // Set the boundaries CAlglib::MinBCSetScale (state, s); // Set scaling CAlglib::MinBCSetCond (state, epsg, epsf, ArgumentStep_P, NumbTestFuncRuns_P); // Set conditions CAlglib::MinBCOptimize (state, fFunc, frep, obj); // Optimization CAlglib::MinBCResults (state, x, rep); // Get results //-------------------------------------------------------------------------- aveRunsFF += fFunc.numberLaunches; // Sum up the number of function runs aveResult += -fFunc.bestMIN; // Sum up the best minimum found } aveRunsFF /= NumberRepetTest_P; // Calculate the average number of runs aveResult /= NumberRepetTest_P; // Calculate the average result double score = aveResult; // Estimate based on average result Print (funcCount, " ", f.GetFuncName (), "'s; Func runs: ", aveRunsFF, "(", NumbTestFuncRuns_P, "); result: ", aveResult); // Output test results allScore += score; // Update the overall score } //——————————————————————————————————————————————————————————————————————————————
Ahora iniciaremos el banco de pruebas secuencialmente para todos los métodos considerados de optimización de la biblioteca ALGLIB. Más abajo mostramos los resultados de las pruebas de los métodos correspondientes, que deben leerse como sigue:
BLEIC|bound-constrained limited-memory optimizer with equality and inequality constraints|0.8|: Abreviatura del método, nombre completo, paso de diferenciación (opcional, parámetros adicionales del método).
5 Hilly's: Número de funciones objetivo de prueba relevantes dentro del problema multivariante.
Func runs: 2178(10000): Número de ejecuciones de la función objetivo: número de intentos de los métodos para abordar la función objetivo y "techo" determinado deseado en el número de ejecuciones.
result: 0.38483704535107116: Resultado medio de 50 inicios de pruebas.
Impresión del funcionamiento del método BLEIC en las funciones objetivo de la prueba:
BLEIC|bound-constrained limited-memory optimizer with equality and inequality constraints|0.8|
=============================
5 Hilly's; Func runs: 2178(10000); result: 0.38483704535107116
25 Hilly's; Func runs: 10130(10000); result: 0.3572376879336238
500 Hilly's; Func runs: 11989(10000); result: 0.2676346390264618
=============================
5 Forest's; Func runs: 1757(10000); result: 0.28835869530001046
25 Forest's; Func runs: 9383(10000); result: 0.22629722977214342
500 Forest's; Func runs: 14978(10000); result: 0.16606494305819486
=============================
5 Megacity's; Func runs: 1211(10000); result: 0.13815384615384615
25 Megacity's; Func runs: 9363(10000); result: 0.12640000000000004
500 Megacity's; Func runs: 15147(10000); result: 0.09791692307692391
=============================
All score: 2.05290 (22.81%)
Impresión del rendimiento del método L-BFGS en funciones objetivo de prueba:
L-BFGS|limited memory BFGS method for large scale optimization|0.9|
=============================
5 Hilly's; Func runs: 5625(10000); result: 0.38480050402327626
25 Hilly's; Func runs: 10391(10000); result: 0.2944296786579764
500 Hilly's; Func runs: 41530(10000); result: 0.25091140645623417
=============================
5 Forest's; Func runs: 3514(10000); result: 0.2508946897150378
25 Forest's; Func runs: 9105(10000); result: 0.19753907736098766
500 Forest's; Func runs: 40010(10000); result: 0.1483916309143011
=============================
5 Megacity's; Func runs: 916(10000); result: 0.12430769230769222
25 Megacity's; Func runs: 4639(10000); result: 0.10633846153846153
500 Megacity's; Func runs: 39369(10000); result: 0.09022461538461606
=============================
All score: 1.84784 (20.53%)
Impresión del rendimiento del método NS en las funciones objetivo de prueba:
NS|nonsmooth nonconvex optimization|0.5|0.8|50.0|
=============================
5 Hilly's; Func runs: 10171(10000); result: 0.3716823351189392
25 Hilly's; Func runs: 11152(10000); result: 0.30271115043870767
500 Hilly's; Func runs: 1006503(10000); result: 0.2481831526729561
=============================
5 Forest's; Func runs: 10167(10000); result: 0.4432983184931045
25 Forest's; Func runs: 11221(10000); result: 0.20891527876847327
500 Forest's; Func runs: 1006503(10000); result: 0.15071828612481414
=============================
5 Megacity's; Func runs: 7530(10000); result: 0.15076923076923068
25 Megacity's; Func runs: 11069(10000); result: 0.12480000000000002
500 Megacity's; Func runs: 1006503(10000); result: 0.09143076923076995
=============================
All score: 2.09251 (23.25%)
Impresión del rendimiento del método BC en las funciones objetivo de prueba:
BC|box constrained optimization with fast activation of multiple box constraints|0.9|
=============================
5 Hilly's; Func runs: 1732(10000); result: 0.37512809463286956
25 Hilly's; Func runs: 9763(10000); result: 0.3542591015005374
500 Hilly's; Func runs: 22312(10000); result: 0.26434986025328294
=============================
5 Forest's; Func runs: 1564(10000); result: 0.28431712294752914
25 Forest's; Func runs: 8844(10000); result: 0.23891148588644037
500 Forest's; Func runs: 15202(10000); result: 0.16925473100070892
=============================
5 Megacity's; Func runs: 1052(10000); result: 0.12307692307692313
25 Megacity's; Func runs: 9095(10000); result: 0.12787692307692308
500 Megacity's; Func runs: 20002(10000); result: 0.09740000000000082
=============================
All score: 2.03457 (22.61%)
Impresión del funcionamiento del método NLC en las funciones del objetivo de prueba:
NLC|nonlinearly constrained optimization with preconditioned augmented lagrangian algorithm|0.8|1000.0|5|
=============================
5 Hilly's; Func runs: 8956(10000); result: 0.4270442612182801
25 Hilly's; Func runs: 10628(10000); result: 0.3222093696838907
500 Hilly's; Func runs: 48172(10000); result: 0.24687323917487405
=============================
5 Forest's; Func runs: 8357(10000); result: 0.3230697968403923
25 Forest's; Func runs: 10584(10000); result: 0.2340843463074393
500 Forest's; Func runs: 48572(10000); result: 0.14792910131023018
=============================
5 Megacity's; Func runs: 5673(10000); result: 0.13599999999999995
25 Megacity's; Func runs: 10560(10000); result: 0.1168615384615385
500 Megacity's; Func runs: 47611(10000); result: 0.09196923076923148
=============================
All score: 2.04604 (22.73%)
Impresión del funcionamiento del método LM en las funciones objetivo de prueba:
LM|improved levenberg-marquardt algorithm|0.0001|
=============================
5 Hilly's; Func runs: 496(10000); result: 0.2779179366819541
25 Hilly's; Func runs: 4383(10000); result: 0.26680986645907423
500 Hilly's; Func runs: 10045(10000); result: 0.27253276065962373
=============================
5 Forest's; Func runs: 516(10000); result: 0.1549127879839302
25 Forest's; Func runs: 3727(10000); result: 0.14964009375922901
500 Forest's; Func runs: 10051(10000); result: 0.1481206726095718
=============================
5 Megacity's; Func runs: 21(10000); result: 0.0926153846153846
25 Megacity's; Func runs: 101(10000); result: 0.09040000000000001
500 Megacity's; Func runs: 2081(10000); result: 0.08909230769230835
=============================
All score: 1.54204 (17.13%)
Ahora podemos analizar de forma visual el comportamiento de los algoritmos en las funciones de prueba. La mayoría de los métodos se caracterizan por detenerse prematuramente antes de agotar el límite del número de ejecuciones de la función objetivo (hemos indicado un límite de 10.000 iteraciones en los parámetros). Por ejemplo, el método de Levenberg-Marquardt (LM) en el problema discreto "Megacity" con una dimensionalidad de 1.000 parámetros se ha detenido en una media de 2.081 iteraciones, pero con una dimensionalidad de 10 solo se ha detenido en 21 iteraciones. Al mismo tiempo, en las funciones Hilly suaves, este método ha intentado encontrar el mínimo en un número mucho mayor de iteraciones. En cambio, otros métodos han realizado más de un millón de llamadas a la función objetivo.
A continuación mostramos los resultados del método NS (que ha obtenido la puntuación más alta) y del método LM (que ha obtenido la puntuación más baja).
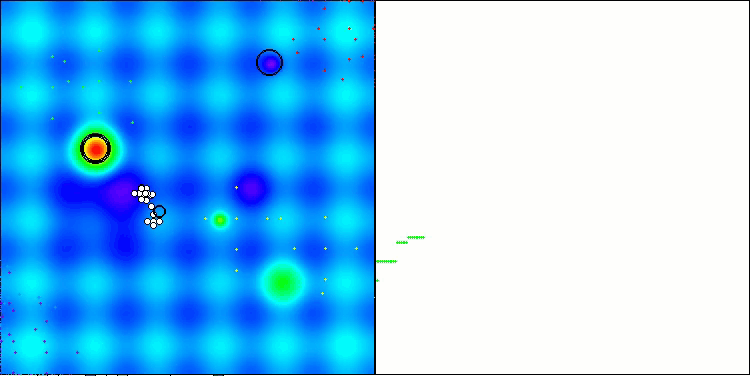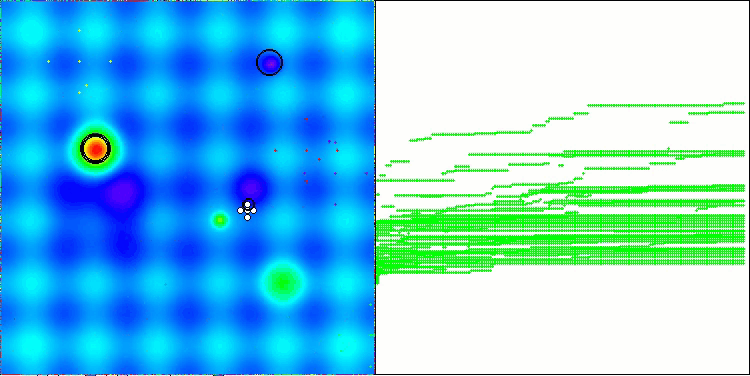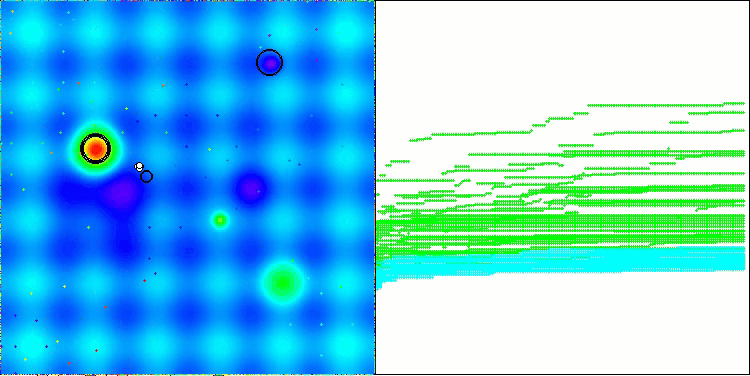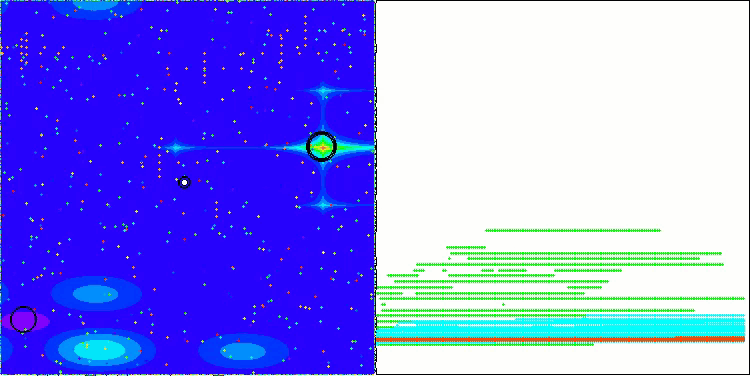
NS en la función de prueba Hilly
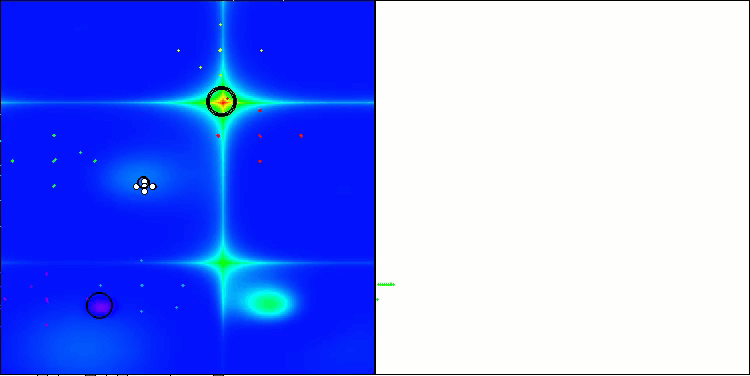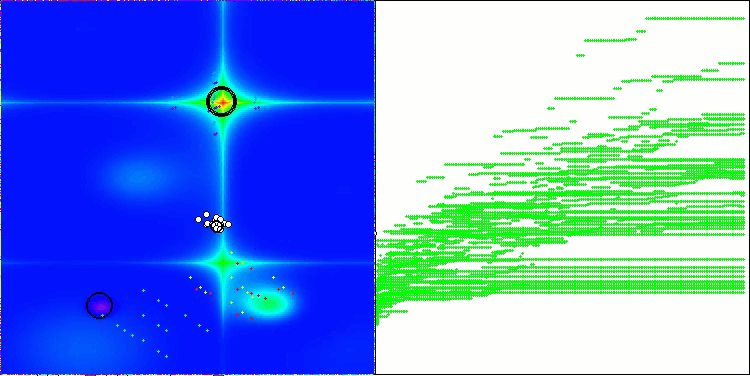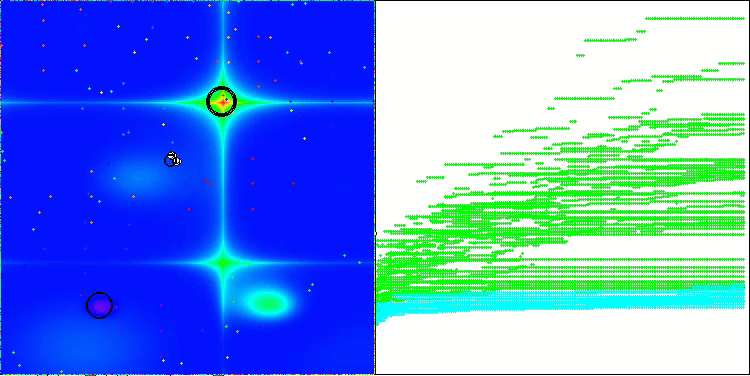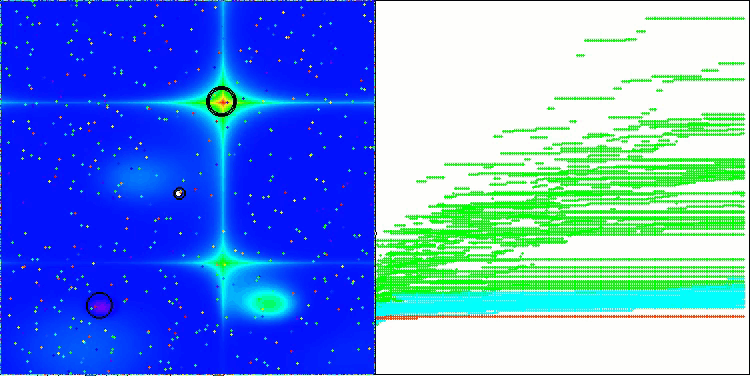
NS en la función de prueba Forest
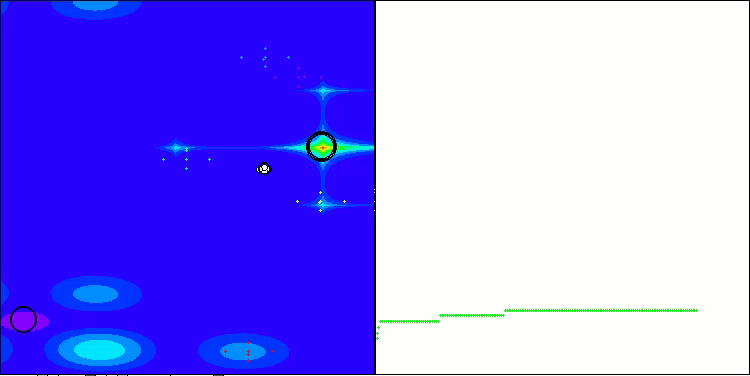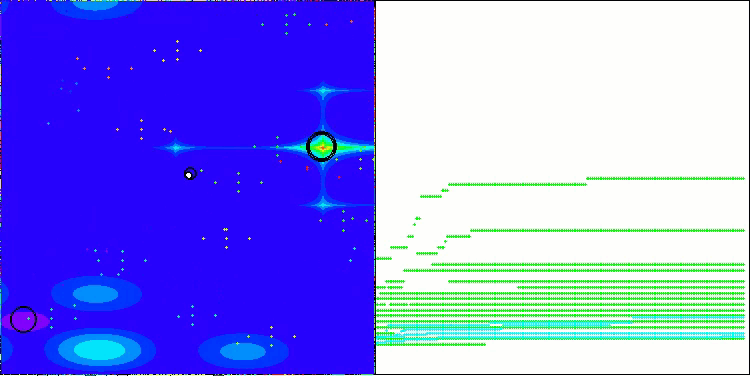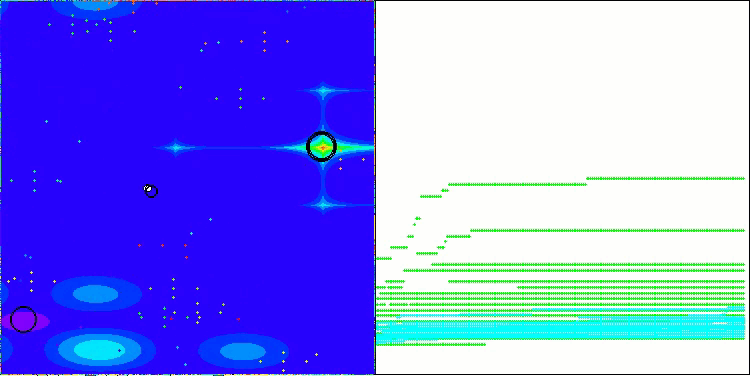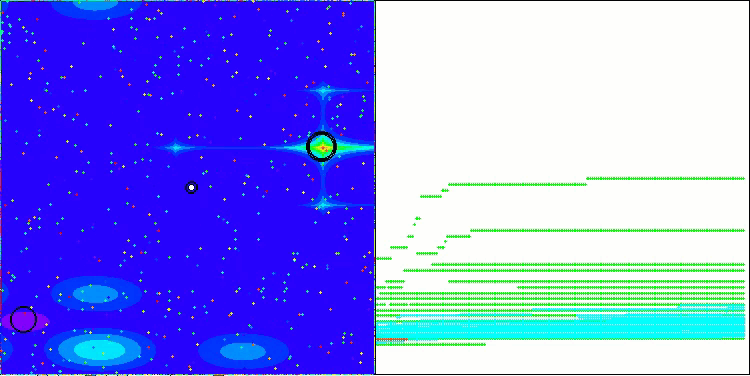
NS en la función de prueba Megacity
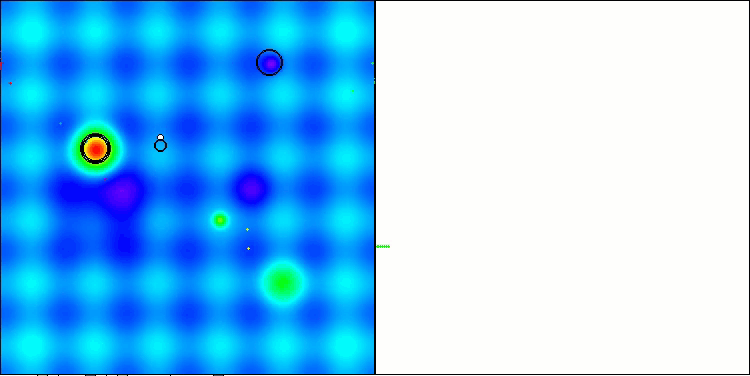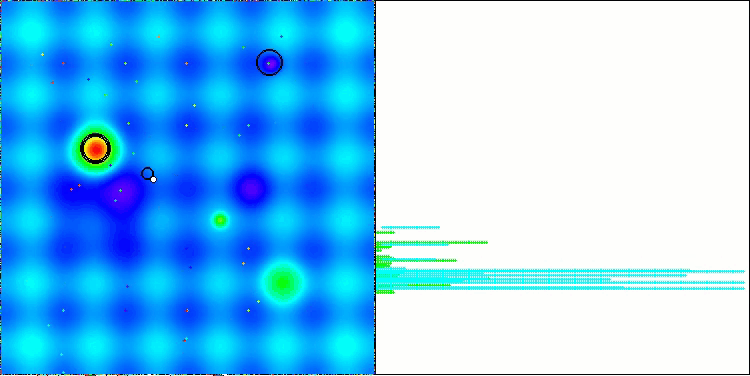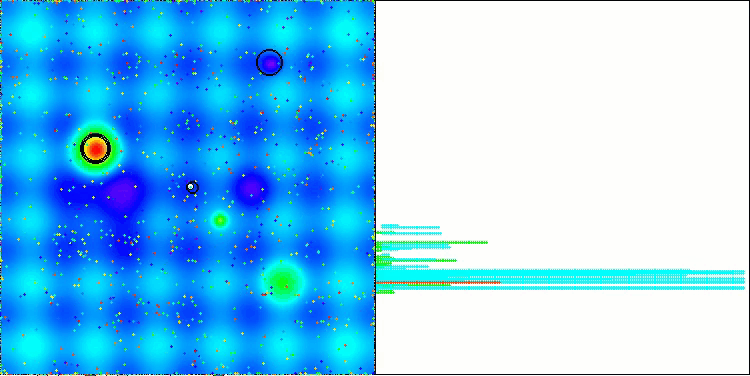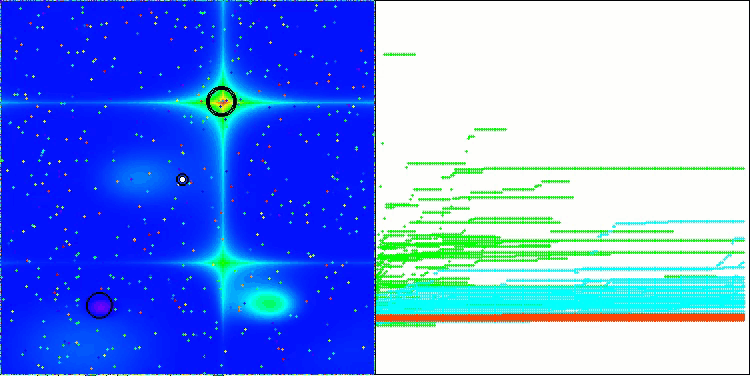
LM en la función de prueba Hilly
LM en la función de prueba Forest
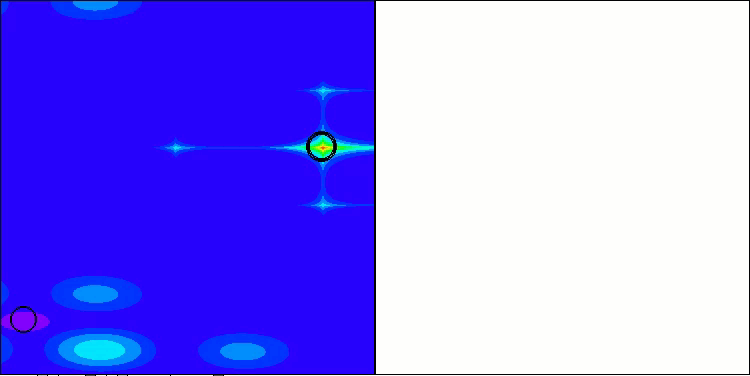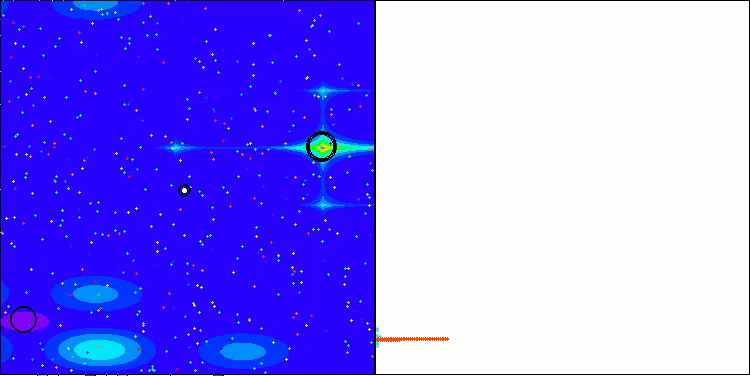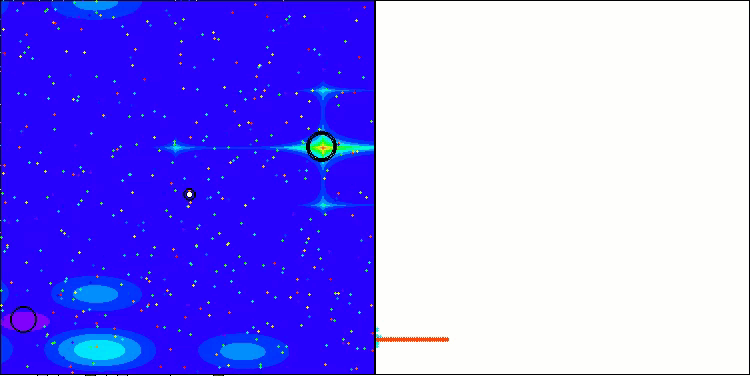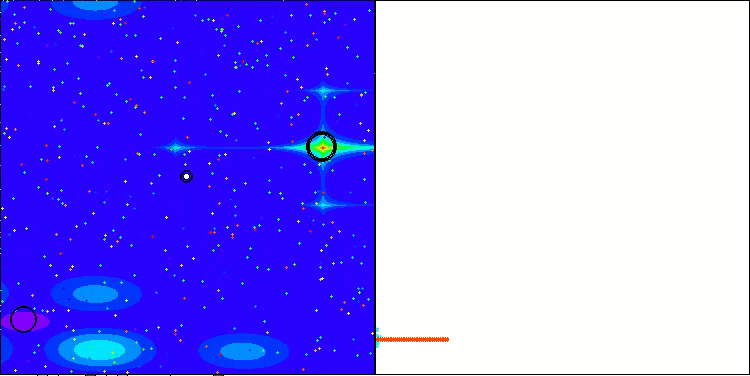
LM en la función de prueba Megacity
Vamos a recopilar los resultados obtenidos en una tabla.

Clasificación por colores de los algoritmos según las pruebas correspondientes
Conclusiones
En los dos últimos artículos hemos analizado los métodos de optimización de la biblioteca ALGLIB y estudiado sus formas de integración en los programas personalizados, así como las peculiaridades de interacción con las funciones de estos métodos. Además, hemos realizado pruebas para identificar los puntos fuertes y débiles de los algoritmos. Resumamos brevemente los resultados:
- En las funciones suaves (Hilly) de baja dimensionalidad, el método NLC ha obtenido los mejores resultados, mientras que en las de alta dimensionalidad el método LM se sitúa en cabeza.
- En funciones suaves con extremos agudos (Forest), el método NS ha obtenido mejores resultados en baja dimensionalidad y el método BC ha obtenido mejores resultados en alta dimensionalidad.
- En el problema discreto "Megacity" en baja dimensionalidad, el método NS ha sido el mejor, mientras que en alta dimensionalidad, el método BLEIC se ha situado en cabeza.
Las diferencias en los resultados de los métodos no son significativas; las desviaciones están dentro de la dispersión de sus propios resultados, pero el método NS puede calificarse de más universal, y no es posible detenerlo por la fuerza.
Los códigos adjuntos a este artículo incluyen todo lo necesario para empezar a usar las técnicas de optimización en nuestros proyectos, y para ver y evaluar visualmente sus posibilidades.
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Simple test ALGLIB BLEIC.mq5 | Script | Script de prueba para trabajar con BLEIC |
| 2 | Simple test ALGLIB LBFGS.mq5 | Script | Script de prueba para trabajar con L-BFGS |
| 3 | Simple test ALGLIB NS.mq5 | Script | Script de prueba para trabajar con NS |
| 4 | Simple test ALGLIB BC.mq5 | Script | Script de prueba para trabajar con BC |
| 5 | Simple test ALGLIB NLC.mq5 | Script | Script de prueba para trabajar con NLC |
| 6 | Simple test ALGLIB LM.mq5 | Script | Script de prueba para trabajar con LM |
| 7 | Test_minBLEIC.mq5 | Script | Banco de pruebas para BLEIC |
| 8 | Test_minLBFGS.mq5 | Script | Banco de pruebas para L-BFGS |
| 9 | Test_minNS.mq5 | Script | Banco de pruebas para NS |
| 10 | Test_minBC.mq5 | Script | Banco de pruebas para BC |
| 11 | Test_minNLC.mq5 | Script | Banco de pruebas para NLC |
| 12 | Test_minLM.mq5 | Script | Banco de pruebas para LM |
| 13 | CalculationTestResults.mq5 | Script | Script para calcular los resultados en una tabla comparativa |
| 14 | TestFunctions.mqh | Archivo de inclusión | Biblioteca de funciones de prueba |
| 15 | TestStandFunctions.mqh | Archivo de inclusión | Biblioteca de funciones del banco de pruebas |
| 16 | Utilities.mqh | Archivo de inclusión | Biblioteca de funciones auxiliares |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16164
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Aprendizaje automático y Data Science (Parte 30): La pareja ideal para predecir el mercado bursátil: redes neuronales convolucionales (CNN) y recurrentes (RNN)
Aprendizaje automático y Data Science (Parte 30): La pareja ideal para predecir el mercado bursátil: redes neuronales convolucionales (CNN) y recurrentes (RNN)
 Creación de un asesor experto integrado de MQL5 y Telegram (Parte 7): Análisis de comandos para la automatización de indicadores en los gráficos
Creación de un asesor experto integrado de MQL5 y Telegram (Parte 7): Análisis de comandos para la automatización de indicadores en los gráficos
 Capacidades de SQLite en MQL5: Ejemplo de panel interactivo con estadísticas comerciales por símbolos y números mágicos
Capacidades de SQLite en MQL5: Ejemplo de panel interactivo con estadísticas comerciales por símbolos y números mágicos
 Redes neuronales en el trading: Representación adaptativa de grafos (NAFS)
Redes neuronales en el trading: Representación adaptativa de grafos (NAFS)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
1. Todavía no es un hecho que los optimizadores de alglib se utilicen correctamente.
1. Puedes cuestionar cualquier cosa, pero siempre es mucho más constructivo hablar desde la posición de códigos fuente completos y pruebas correctas reproducibles.
2. Se puede obtener un resultado óptimo en una Megaciudad bidimensional si se pide a 9.000 millones de personas que introduzcan sus dedos al azar en una hoja de papel en blanco, tras la cual se oculta la superficie de la función (una de ellas acabará sin duda muy cerca de la global y dirá que es la que ha resuelto con éxito el problema). Pero tenemos que encontrar la solución óptima no en 9.000 millones de intentos pinchando al azar, sino en 10.000 utilizando una estrategia.
Cuanto más alto sea el resultado medio de una serie de pruebas independientes (estabilidad, repetibilidad de los resultados), más alto será el método probado en comparación con el aporreo aleatorio para un tipo concreto de problema (para algunos problemas algunos métodos no difieren mucho del aporreo aleatorio, y para otros son muy eficaces).
Este es el sentido de probar y comparar diferentes algoritmos, para lo cual no se toma como referencia una sola función de prueba, sino tres diferentes con diferentes propiedades, de forma que se pueda ver claramente la aplicabilidad de diferentes algoritmos en diferentes tareas, sus limitaciones y capacidades en diferentes tareas. Esto permite abordar la solución de problemas de optimización de una manera significativa.
En el futuro, prefiero responder a preguntas concretas sobre el contenido del artículo y sobre los códigos.
Tomamos los métodos de optimización local, los aplicamos al problema global y los comparamos con los métodos de optimización global. A eso me refiero.
Estoy hablando de cómo podemos adaptar estos métodos para la optimización global. La opción más sencilla es aumentar el número de inicializaciones.
Si no he entendido mal, Adam, etc. se perfeccionan en función de la velocidad, no de la calidad.
Sería interesante ver la puntuación cuando se limita por el tiempo en lugar de por el número de iteraciones.
Si no he entendido mal, Adam y otros se centran en la velocidad, no en la calidad.
Sería interesante ver la clasificación cuando se limita por el tiempo en lugar de por el número de iteraciones.
La familia de algoritmos ADAM (AdamW, RAdam, AdaBelief y otros) así como SGD, SGRAD y otros (hay muchos de ellos) se desarrollan como un reemplazo moderno de los métodos de gradiente clásicos y están diseñados para resolver problemas de grandes dimensiones sin conocimiento de la fórmula analítica, a menudo para el entrenamiento de redes neuronales (todos ellos tienen sus ventajas y desventajas). También son interesantes los métodos de León de Google (2023) y algunos otros muy recientes. Este tema es muy interesante para estudiar, especialmente en el contexto de la formación de redes neuronales, donde será útil e informativo para construir una superficie de destino en algún ejemplo simple (o tal vez complejo) y llevar a cabo experimentos (con el análisis de sus entrañas, con un estudio profundo de las propiedades de los métodos, la evaluación cuidadosa de sus capacidades - todo lo que nos gusta).
Con las limitaciones de tiempo, no hay nada a lo que estar atado. Un usuario hará 1 millón de accesos al objetivo en 1 minuto, y otro hará 1.000 millones. ¿Cómo podemos comparar algos en tales condiciones? Por eso utilizamos un límite en el número de accesos y comparamos la eficacia dentro de este límite.
Con limitaciones de tiempo, no hay nada a lo que vincularse. Un usuario hará 1 millón de accesos al objetivo en 1 minuto, mientras que otro hará 1.000 millones. ¿Cómo podemos comparar algos entre ellos en esas condiciones? Por eso utilizamos un límite en el número de accesos y comparamos la eficacia dentro de ese límite.
Vinculación al PC del autor. Tome el tiempo de 10000 iteraciones de ANS como base.
Mis resultados en el código de fxsaber:
Tamaño del código PS como métrica adicional (grado de complejidad de la implementación del algoritmo)