Data Science and ML (Part 44): Forex OHLC Time series Forecasting using Vector Autoregression (VAR)
1 379
0
Contents
- What is vector autoregression (VAR)
- Mathematics behind Vector Autoregression (VAR) model
- Assumptions underlying the VAR model
- Implementing the VAR model on OHLC values in Python
- Out-of-sample forecasting using VAR
- Making the VAR-Based Trading robot
- Final Thoughts
What is Vector Autoregression (VAR)?
This is a traditional and statistical time series forecasting tool used to investigate the dynamic relationships between multiple time series variables. Unlike univariate autoregressive models such as ARIMA (discussed in the previous article) which only forecast a single variable based on its previous values, VAR models investigate the interconnectivity of many variables.
They accomplish this by modeling each variable as a function of not only its previous values but also of the past values of other variables in the system. In this article, we will explore the fundamentals of Vectorautoregression and its application to trading.
Their origin
Vector Autoregression was first presented in the 1960s by economist Clive Granger. Granger's significant discoveries laid the framework for understanding and modeling the dynamic interactions that exist among economic factors. VAR models acquired significant momentum in econometrics and macroeconomics during the 1970s and 1980s.
This technique is a multivariate extension of auto-regression (AR) models. While traditional AR models such as ARIMA, analyze the relationship between a single variable and its lagged values, VAR models consider multiple variables simultaneously. In a VAR model, each variable is regressed on its own lagged values as well as the lagged values of other variables in the system.
In the previous article of this series, we discussed ARIMA and found out that it cannot incorporate multiple variables into its training and forecasting process, In this article we will discuss VAR which most people might consider to be ARIMA's predecessor as it aims to fix univariate time series forecasting issue.
To understand this simple technique (model) let us look at its mathematics.
Mathematics Behind the Vector Autoregression (VAR) model
The main difference between other autoregressive models (AR, ARMA, and ARIMA) and the VAR model is that former models are unidirectional (the predictors variable influences the target variable not vice versa) but VAR is bidirectional.
Mathematically, a VAR(p) model with 'p' lags can be represented as.
Where:
- c = The constant term (intercept) of the model
-
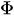= Coefficient of lags Y till order p. -
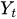= The value of the timeseries at time t -
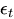= The error term at time t.
A K-dimensional VAR model of order P, denoted as VAR(p), considering k=2, the equation will be as follows.
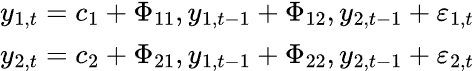
For the VAR model, we have multiple time series variables that influence each other; It is modeled as a system of equations with one equation per time series variable. Below is the formula in matrix form.
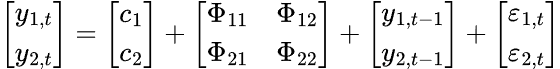
The final VAR equation becomes.
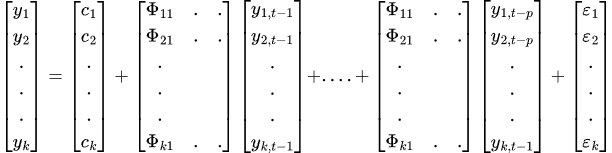
To ensure the validity and trustworthiness of the results obtained from the VAR model, various assumptions and requirements must be met.
Assumptions Underlying the VAR Model
- Linearity
As we have seen from its formula, VAR is a linear model at its core, so all the variables deployed in this model must be linear (i.e., expressed as weighted sums of lagged values). - Stationarity
All variables deployed in this model must be stationary, i.e., the mean, variance, and covariance of each feature of the time series must be constant over time. We have to convert all non-stationary features to stationary if we have any in the dataset. - No perfect multicollinearity between features
For VAR to work effectively, no explanatory variable can be an exact linear combination of others. This matters because it helps in preventing singular matrices in OLS estimation (i.e.,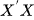
must be invertible). We have to drop redundant features or use a regularization technique to tackle this issue. - No autocorrelation in residuals
It assumes the residuals are not serially correlated, they should be white noise. Autocorrelation biases standard errors and invalidates statistical tests. - Sufficient observations
VAR assumes that it has received sufficient data for parameter estimation. So, we need to feed this model with as much information as possible for maximum efficiency.
Now let's see how you can implement this model in the Python programming language.
Implementing the VAR Model on OHLC values in Python
Start by installing all Python dependencies, requirements.txt file can be found in the attachments section.
pip install -r requirements.txt
Imports.
import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt import warnings # Suppress all warnings warnings.filterwarnings("ignore") sns.set_style("darkgrid")
We start by importing Open, High, Low, and Close OHLC values from MetaTrader 5.
symbol = "EURUSD" timeframe = mt5.TIMEFRAME_D1 if not mt5.symbol_select(symbol, True): print("Failed to select and add a symbol to the MarketWatch, Error = ",mt5.last_error) quit() rates = mt5.copy_rates_from_pos(symbol, timeframe, 1, 10000) df = pd.DataFrame(rates) # convert rates into a pandas dataframe df
Outputs.
| time | open | high | low | close | tick_volume | spread | real_volume | |
|---|---|---|---|---|---|---|---|---|
| 0 | 611280000 | 1.00780 | 1.01050 | 1.00630 | 1.00760 | 821 | 50 | 0 |
| 1 | 611366400 | 0.99620 | 1.00580 | 0.99100 | 0.99600 | 2941 | 50 | 0 |
| 2 | 611452800 | 0.99180 | 0.99440 | 0.98760 | 0.99190 | 1351 | 50 | 0 |
| 3 | 611539200 | 0.99330 | 0.99370 | 0.99310 | 0.99310 | 101 | 50 | 0 |
| 4 | 611798400 | 0.97360 | 0.97360 | 0.97320 | 0.97360 | 81 | 50 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 9995 | 1748390400 | 1.13239 | 1.13453 | 1.12838 | 1.12910 | 153191 | 0 | 0 |
| 9996 | 1748476800 | 1.12918 | 1.13849 | 1.12105 | 1.13659 | 191948 | 0 | 0 |
| 9997 | 1748563200 | 1.13630 | 1.13901 | 1.13127 | 1.13470 | 186924 | 0 | 0 |
| 9998 | 1748822400 | 1.13435 | 1.14500 | 1.13412 | 1.14436 | 168697 | 0 | 0 |
| 9999 | 1748908800 | 1.14385 | 1.14549 | 1.13642 | 1.13708 | 147424 | 0 | 0 |
We obtained 10000 bars from the daily timeframe, which we can consider a lot because, according to the models' assumption, data must be sufficient.
Since we want to use this model on OHLC values, let's drop other columns.
ohlc_df = df.drop(columns=[ "time", "tick_volume", "spread", "real_volume" ]) ohlc_df
I chose to use OHLC values only because I believe there is a strong relationship between these values that the model could help us spot, not to mention these four variables are the fundamental features we can extract from financial instruments.
Since this model assumes stationarity in its features, we can tell that OHLC values aren't stationary so, let us make them stationary by differentiating each value with from its previous value(s) once.
stationary_df = pd.DataFrame() for col in df.columns: stationary_df["Diff_"+col] = df[col].diff() stationary_df.dropna(inplace=True) stationary_df
Outputs.
| Diff_Open | Diff_High | Diff_Low | Diff_Close | |
|---|---|---|---|---|
| 1 | 0.00080 | 0.00180 | -0.01670 | -0.00950 |
| 2 | -0.00960 | -0.00840 | -0.01370 | -0.01880 |
| 3 | -0.01870 | -0.01930 | -0.00350 | -0.00190 |
| 4 | -0.00180 | -0.00210 | -0.00590 | -0.00870 |
| 5 | -0.00890 | -0.00310 | -0.01300 | -0.01200 |
| ... | ... | ... | ... | ... |
Optionally, we can check for stationarity if unsure of the newly obtained variables.
from statsmodels.tsa.stattools import adfuller for col in stationary_df.columns: result = adfuller(stationary_df[col]) print(f'{col} p-value: {result[1]}')
Outputs.
Diff_Open p-value: 0.0 Diff_High p-value: 1.0471939301334604e-28 Diff_Low p-value: 1.1015540451195308e-23 Diff_Close p-value: 0.0
The P-value must be less than 0.05 (<0.05) for the data to be considered stationary. As we can see the p-value is smaller than 0.05 so, our data is good for now.
Again, according to VAR assumptions, perfect multicollinearity must not exist between the features so, let's ensure that.
stationary_df.corr()
Outputs.
| Diff_Open | Diff_High | Diff_Low | Diff_Close | |
|---|---|---|---|---|
| Diff_Open | 1.000000 | 0.565829 | 0.563516 | 0.036347 |
| Diff_High | 0.565829 | 1.000000 | 0.452775 | 0.564026 |
| Diff_Low | 0.563516 | 0.452775 | 1.000000 | 0.557139 |
| Diff_Close | 0.036347 | 0.564026 | 0.557139 | 1.000000 |
The correlation matrix among the features seems fine, we can even check for the mean absolute correlation coefficient of the whole matrix, ensuring |p| < 0.8.
print("Mean absolute |p|:", np.abs(np.corrcoef(stationary_df, rowvar=False).mean()))
Outputs.
Mean absolute |p|: 0.5924538886295351 Selecting the best number of lags
We've seen in the formula that the VAR model uses the past information (lags) to forecast the future, we have to know which number of lags to use yields the best outcome. Luckily, VAR offered by stats models offers the function to help us determine this value according to a couple of criteria:
- AIC (Akaike Information Criterion)
- BIC (Bayesian/Schwarz Information Criterion)
- FPE (Final prediction Error)
- HQIC (Hannan-Quin Information Criterion)
# Select optimal lag using AIC lag_order = model.select_order(maxlags=30) print(lag_order.summary())
Outputs.
VAR Order Selection (* highlights the minimums) ================================================== AIC BIC FPE HQIC -------------------------------------------------- 0 -41.87 -41.87 6.537e-19 -41.87 1 -45.15 -45.14 2.457e-20 -45.15 2 -45.63 -45.60 1.530e-20 -45.62 3 -45.85 -45.81 1.225e-20 -45.84 4 -45.99 -45.94 1.065e-20 -45.97 5 -46.18 -46.12 8.805e-21 -46.16 6 -46.24 -46.17 8.256e-21 -46.22 7 -46.28 -46.20 7.951e-21 -46.25 8 -46.31 -46.22 7.708e-21 -46.28 9 -46.34 -46.24 7.471e-21 -46.31 10 -46.36 -46.24 7.368e-21 -46.32 11 -46.41 -46.28 6.979e-21 -46.37 12 -46.42 -46.28 6.890e-21 -46.38 13 -46.44 -46.28 6.806e-21 -46.38 14 -46.45 -46.28 6.730e-21 -46.39 15 -46.45 -46.28 6.697e-21 -46.39 16 -46.46 -46.28 6.628e-21 -46.40 17 -46.49 -46.29* 6.460e-21 -46.42 18 -46.50 -46.28 6.419e-21 -46.42 19 -46.50 -46.28 6.383e-21 -46.43 20 -46.50 -46.27 6.358e-21 -46.43 21 -46.51 -46.27 6.306e-21 -46.43 22 -46.52 -46.26 6.292e-21 -46.43 23 -46.53 -46.26 6.216e-21 -46.44 24 -46.53 -46.25 6.185e-21 -46.44 25 -46.54 -46.24 6.162e-21 -46.44 26 -46.54 -46.24 6.113e-21 -46.44 27 -46.55 -46.23 6.092e-21 -46.44 28 -46.55 -46.22 6.086e-21 -46.44 29 -46.56* -46.22 6.031e-21* -46.44* 30 -46.56 -46.21 6.033e-21 -46.44 --------------------------------------------------
Each row shows values for different lag orders, a value marked with an asterisk is the minimum value for that criterion, indicating the "best" lag order according to that criterion.
So, according to this lag order summary.
- For AIC, the best model is at lag 29 (value -46.56)
- For BIC, the best model is at lag 17 (value -46.29)
- For FPE, the best model is at lag 29 (value -6.031e-21)
- For HQIC, the best model is at lag 29 (value -46.44)
Most people use AIC and BIC information to select a model. Simply put, AIC tends to select more complex models (higher lags) while BIC penalizes complexity more strongly, often selecting simpler models.
HQIC is the middle ground between AIC and BIC while FPE focuses on prediction error.
For now, let us fit the model with the lag value according to the AIC criteria.
# Fit the model with selected lag results = model.fit(lag_order.aic) print(results.summary())
Outputs.
Summary of Regression Results ================================== Model: VAR Method: OLS Date: Wed, 04, Jun, 2025 Time: 10:40:37 -------------------------------------------------------------------- No. of Equations: 4.00000 BIC: -46.2188 Nobs: 9970.00 HQIC: -46.4425 Log likelihood: 175968. FPE: 6.03280e-21 AIC: -46.5571 Det(Omega_mle): 5.75774e-21 -------------------------------------------------------------------- Results for equation diff_open ================================================================================= coefficient std. error t-stat prob --------------------------------------------------------------------------------- const -0.000002 0.000013 -0.115 0.908 L1.diff_open -0.959329 0.010918 -87.867 0.000 L1.diff_high 0.009878 0.004957 1.993 0.046 L1.diff_low 0.006869 0.005010 1.371 0.170 L1.diff_close 0.995718 0.004583 217.244 0.000 L2.diff_open -0.935345 0.015071 -62.062 0.000 L2.diff_high 0.007118 0.006749 1.055 0.292 L2.diff_low 0.022288 0.006819 3.268 0.001 L2.diff_close 0.939861 0.011863 79.226 0.000 L3.diff_open -0.906595 0.018115 -50.045 0.000 L3.diff_high 0.003072 0.007954 0.386 0.699 L3.diff_low 0.018535 0.008097 2.289 0.022 L3.diff_close 0.910898 0.015703 58.006 0.000 L4.diff_open -0.898803 0.020501 -43.841 0.000 L4.diff_high 0.003670 0.008912 0.412 0.681 L4.diff_low 0.015668 0.009103 1.721 0.085 L4.diff_close 0.886824 0.018628 47.606 0.000 L5.diff_open -0.867308 0.022560 -38.445 0.000 L5.diff_high 0.001318 0.009676 0.136 0.892 L5.diff_low -0.000027 0.009942 -0.003 0.998 L5.diff_close 0.884632 0.020996 42.133 0.000 ... ... ... L29.diff_open -0.005922 0.004617 -1.283 0.200 L29.diff_high 0.007026 0.004956 1.418 0.156 L29.diff_low 0.004387 0.005005 0.876 0.381 L29.diff_close 0.035169 0.010568 3.328 0.001 ================================================================================= Results for equation diff_high ================================================================================= coefficient std. error t-stat prob --------------------------------------------------------------------------------- const 0.000008 0.000048 0.165 0.869 L1.diff_open -0.010294 0.038697 -0.266 0.790 L1.diff_high -0.887555 0.017570 -50.515 0.000 L1.diff_low -0.020634 0.017757 -1.162 0.245 L1.diff_close 0.969305 0.016245 59.667 0.000 L2.diff_open 0.006028 0.053418 0.113 0.910 L2.diff_high -0.838250 0.023920 -35.043 0.000 L2.diff_low -0.057396 0.024169 -2.375 0.018 L2.diff_close 0.914246 0.042047 21.744 0.000 L3.diff_open -0.160354 0.064208 -2.497 0.013 L3.diff_high -0.807663 0.028191 -28.650 0.000 L3.diff_low -0.042960 0.028698 -1.497 0.134 L3.diff_close 0.869460 0.055659 15.621 0.000 L4.diff_open -0.168775 0.072664 -2.323 0.020 L4.diff_high -0.785399 0.031589 -24.863 0.000 L4.diff_low -0.054113 0.032265 -1.677 0.094 L4.diff_close 1.013851 0.066026 15.355 0.000 L5.diff_open -0.146275 0.079959 -1.829 0.067 L5.diff_high -0.746785 0.034295 -21.775 0.000 L5.diff_low -0.098885 0.035238 -2.806 0.005 L5.diff_close 1.012989 0.074419 13.612 0.000 ... ... ... L27.diff_open 0.020345 0.053645 0.379 0.705 L27.diff_high -0.153391 0.028136 -5.452 0.000 L27.diff_low -0.065690 0.028874 -2.275 0.023 L27.diff_close 0.251005 0.062004 4.048 0.000 L28.diff_open -0.005863 0.040235 -0.146 0.884 L28.diff_high -0.087603 0.023901 -3.665 0.000 L28.diff_low 0.008246 0.024229 0.340 0.734 L28.diff_close 0.134924 0.051754 2.607 0.009 L29.diff_open -0.000480 0.016364 -0.029 0.977 L29.diff_high -0.051136 0.017564 -2.911 0.004 L29.diff_low 0.035083 0.017741 1.977 0.048 L29.diff_close 0.054123 0.037457 1.445 0.148 ================================================================================= Results for equation diff_low ================================================================================= coefficient std. error t-stat prob --------------------------------------------------------------------------------- const 0.000005 0.000047 0.101 0.920 L1.diff_open 0.024212 0.038141 0.635 0.526 L1.diff_high -0.058570 0.017317 -3.382 0.001 L1.diff_low -0.904567 0.017501 -51.686 0.000 L1.diff_close 0.976598 0.016012 60.993 0.000 L2.diff_open 0.067049 0.052650 1.274 0.203 L2.diff_high -0.084679 0.023576 -3.592 0.000 L2.diff_low -0.866233 0.023822 -36.363 0.000 L2.diff_close 0.937652 0.041442 22.626 0.000 L3.diff_open 0.065284 0.063284 1.032 0.302 L3.diff_high -0.108128 0.027785 -3.892 0.000 L3.diff_low -0.791679 0.028285 -27.989 0.000 L3.diff_close 0.844047 0.054858 15.386 0.000 L4.diff_open 0.018366 0.071619 0.256 0.798 L4.diff_high -0.116216 0.031134 -3.733 0.000 L4.diff_low -0.747223 0.031801 -23.497 0.000 L4.diff_close 0.816060 0.065076 12.540 0.000 L5.diff_open -0.040872 0.078809 -0.519 0.604 L5.diff_high -0.110998 0.033802 -3.284 0.001 L5.diff_low -0.731241 0.034731 -21.054 0.000 L5.diff_close 0.832344 0.073348 11.348 0.000 ... ... ... L29.diff_open 0.024357 0.016128 1.510 0.131 L29.diff_high 0.026179 0.017312 1.512 0.130 L29.diff_low -0.072592 0.017486 -4.151 0.000 L29.diff_close 0.051738 0.036919 1.401 0.161 ================================================================================= Results for equation diff_close ================================================================================= coefficient std. error t-stat prob --------------------------------------------------------------------------------- const 0.000013 0.000071 0.185 0.853 L1.diff_open 0.037592 0.057827 0.650 0.516 L1.diff_high 0.007085 0.026256 0.270 0.787 L1.diff_low 0.011658 0.026535 0.439 0.660 L1.diff_close -0.020373 0.024276 -0.839 0.401 L2.diff_open 0.150341 0.079825 1.883 0.060 L2.diff_high -0.035345 0.035745 -0.989 0.323 L2.diff_low -0.041114 0.036117 -1.138 0.255 L2.diff_close -0.012920 0.062832 -0.206 0.837 L3.diff_open -0.000054 0.095949 -0.001 1.000 L3.diff_high -0.047439 0.042126 -1.126 0.260 L3.diff_low 0.028500 0.042884 0.665 0.506 L3.diff_close -0.113979 0.083173 -1.370 0.171 L4.diff_open -0.083562 0.108585 -0.770 0.442 L4.diff_high -0.083193 0.047204 -1.762 0.078 L4.diff_low 0.055907 0.048215 1.160 0.246 L4.diff_close 0.026375 0.098665 0.267 0.789 L5.diff_open -0.148622 0.119487 -1.244 0.214 L5.diff_high -0.065192 0.051248 -1.272 0.203 L5.diff_low 0.011819 0.052658 0.224 0.822 L5.diff_close 0.125327 0.111207 1.127 0.260 ... ... ... L29.diff_open 0.002852 0.024453 0.117 0.907 L29.diff_high -0.011652 0.026247 -0.444 0.657 L29.diff_low -0.004191 0.026511 -0.158 0.874 L29.diff_close 0.070689 0.055974 1.263 0.207 ================================================================================= Correlation matrix of residuals diff_open diff_high diff_low diff_close diff_open 1.000000 0.223818 0.241416 0.126479 diff_high 0.223818 1.000000 0.452061 0.770309 diff_low 0.241416 0.452061 1.000000 0.765777 diff_close 0.126479 0.770309 0.765777 1.000000
The VAR model, similarly to other statistical/traditional time series models, they provide a detailed summary of the model performance and its features. This summary helps us understand the model in detail, let us briefly analyze the above model's summary.
-------------------------------------------------------------------- No. of Equations: 4.00000 BIC: -46.2188 Nobs: 9970.00 HQIC: -46.4425 Log likelihood: 175968. FPE: 6.03280e-21 AIC: -46.5571 Det(Omega_mle): 5.75774e-21
- No. of Equations: 4, means the system (model) contains 4 endogenous variables; diff_open, diff_high, diff_low, diff_close.
- Nobs (Number of observations used): Since we chose the AIC criteria, which uses 29 lags, 29+1 features weren't included in the training (estimation) process, as those values before were used as initial lags.
- AIC, BIC, HQIC, and FPE: All these values are negative (normal,) which is a good indication of a better fit.
- Log Likelihood: A high positive value indicates a good model fit.
Each equation results
For each variable (diff_open, diff_high, diff_low, and diff_close), you see.
- Coefficients
These represent the impact of each lagged variable (L1, L2, etc.) on the current value. The closer to 1 this value is the more positive impact a variable has on the current equation variable and vice versa.
For example.
Results for equation diff_open ================================================================================= coefficient std. error t-stat prob --------------------------------------------------------------------------------- const -0.000002 0.000013 -0.115 0.908 L1.diff_open -0.959329 0.010918 -87.867 0.000
The coefficient of -0.959329 here means that A 1-unit increase in yesterday's (lag-1) diff_open value is associated with a decrease of 0.959329 units in today's diff_open value, holding all other variables constant. -
Std. Error
These represent the precision of coefficient estimates. -
t-stat
This stands for statistical significance. The greater the absolute value |t-stat| of this metric is, the more significant the variable is. A large absolute value (e.g., |t|>2) indicates statistical significance.
The value of |(-87.867)| = +87.876 is large indicating that the effect of the variable diff_open at lag-1 is highly significant (not due to random chance). -
prob
This represents the p-value associated with each coefficient's t-statistic. It tells you whether a specific lagged variable has a significant effect on the current value of the dependent variable.
When the prob value is less than or equal to 0.05, a variable is statistically significant.
Residual correlation matrix
Correlation matrix of residuals diff_open diff_high diff_low diff_close diff_open 1.000000 0.223818 0.241416 0.126479 diff_high 0.223818 1.000000 0.452061 0.770309 diff_low 0.241416 0.452061 1.000000 0.765777 diff_close 0.126479 0.770309 0.765777 1.000000
This shows correlations between prediction errors across equations.
A high correlation between diff_high/diff_close (0.77) and diff_low/diff_close (approximately: 0.766) suggests common unexplained factors affect these pairs.
Out-of-Sample Forecasting using VAR
Similarly to the ARIMA model discussed in the previous article, forecasting out-of-sample data using VAR is quite tricky. Unlike machine learning models, these traditional models have to be updated regularly with new information.
Let's make a function for the task.
def forecast_next(model_res, symbol, timeframe): forecast = None # Get required lags for prediction rates = mt5.copy_rates_from_pos(symbol, timeframe, 0, model_res.k_ar+1) # Get rates starting at the current bar to bars=lags used during training if rates is None or len(rates) < model_res.k_ar+1: print("Failed to get copy rates Error =", mt5.last_error()) return forecast, None # Prepare input data and make forecast input_data = pd.DataFrame(rates)[["open", "high", "low", "close"]].values stationary_input = np.diff(input_data, axis=0)[-model_res.k_ar:] # get the recent values equal to the number of lags used by the model try: forecast = model_res.forecast(stationary_input, steps=1) # predict the next price except Exception as e: print("Failed to forecast: ", str(e)) return forecast, None try: updated_data = np.vstack([model_res.endog, stationary_input[-1]]) # concatenate new/last datapoint to the data used during previous training updated_model = VAR(updated_data).fit(maxlags=model_res.k_ar) # Retrain the model with new data except Exception as e: print("Failed to update the model: ", str(e)) return forecast, None return forecast, updated_model
To get a prediction we have to equip the model with the initial trained model and re-update the new model after each prediction by reassigning a model variable to itself.
res_model = results # Initial model forecast, res_model = forecast_next(model_res=res_model, symbol=symbol, timeframe=timeframe) forecast_df = pd.DataFrame(forecast, columns=stationary_df.columns) print("next forecasted:\n", forecast_df)
Outputs.
next forecasted: diff_open diff_high diff_low diff_close 0 0.00435 0.003135 0.001032 -0.000655
We can simplify the training and prediction process by wrapping all these into a class.
File VAR.py
import pandas as pd import numpy as np import MetaTrader5 as mt5 from statsmodels.tsa.api import VAR class VARForecaster: def __init__(self, symbol: str, timeframe: int): self.symbol = symbol self.timeframe = timeframe self.model = None def train(self, start_bar: int=1, total_bars: int=10000, max_lags: int=30): """Trains the VAR model using the collected OHLC from given bars from MetaTrader5 start_bar: int: The recent bar according to copyrates_from_pos total_bars: int: Total number of bars to use for training max_lags: int: The maximum number of lags to use """ self.max_lags = max_lags if not mt5.symbol_select(self.symbol, True): print("Failed to select and add a symbol to the MarketWatch, Error = ",mt5.last_error()) quit() rates = mt5.copy_rates_from_pos(self.symbol, self.timeframe, start_bar, total_bars) if rates is None: print("Failed to get copy rates Error =", mt5.last_error()) return if total_bars < max_lags: print(f"Failed to train, max_lags: {max_lags} must be > total_bars: {total_bars}") return train_df = pd.DataFrame(rates) # convert rates into a pandas dataframe train_df = train_df[["open", "high", "low", "close"]] stationary_df = np.diff(train_df, axis=0) # Convert OHLC values into stationary ones by differenciating them self.model = VAR(stationary_df) # Select optimal lag using AIC lag_order = self.model.select_order(maxlags=self.max_lags) print(lag_order.summary()) # Fit the model with selected lag self.model_results = self.model.fit(lag_order.aic) print(self.model_results.summary()) def forecast_next(self): """Gets recent OHLC from MetaTrader5 and predicts the next differentiated prices Returns: np.array: predicted values """ forecast = None # Get required lags for prediction rates = mt5.copy_rates_from_pos(self.symbol, self.timeframe, 0, self.model_results.k_ar+1) # Get rates starting at the current bar to bars=lags used during training if rates is None or len(rates) < self.model_results.k_ar+1: print("Failed to get copy rates Error =", mt5.last_error()) return forecast # Prepare input data and make forecast input_data = pd.DataFrame(rates)[["open", "high", "low", "close"]] stationary_input = np.diff(input_data, axis=0)[-self.model_results.k_ar:] # get the recent values equal to the number of lags used by the model try: forecast = self.model_results.forecast(stationary_input, steps=1) # predict the next price except Exception as e: print("Failed to forecast: ", str(e)) return forecast try: updated_data = np.vstack([self.model_results.endog, stationary_input[-1]]) # concatenate new/last datapoint to the data used during previous training updated_model = VAR(updated_data).fit(maxlags=self.model_results.k_ar) # Retrain the model with new data except Exception as e: print("Failed to update the model: ", str(e)) return forecast self.model = updated_model return forecast
Let's wrap this up in a Python-based trading robot.
Making the VAR-Based Trading Robot
Given the above class, which can aid us in training and making forecasts on the next value, let us incorporate the predicted outcomes into a trading strategy.
Firstly, in the previous example, we used stationary values produced by differencing the current values from the previous one to get stationary values. At the same time, the approach works, it is not very practical when it comes to building a trading strategy.
Instead, let's find the difference between open and high value, to get how much the price moves upward from the opening price and the difference between open and low value, to get how much the price moves downward from the opening price.
By getting these two values, one for tracking the upward movement of the candle and the other for tracking the downward movement of the candle we can use the predicted outcomes for setting stop loss and take profit values.
Let us change the features used in our model.
# Prepare input data and make forecast input_data = pd.DataFrame(rates)[["open", "high", "low", "close"]] stationary_input = pd.DataFrame({ "high_open": input_data["high"] - input_data["open"], "open_low": input_data["open"] - input_data["low"] })
The resulting features obtained by differentiating are most likely a stationary variable (no need to check for now).
Inside the main robot file, let's schedule the training process and print the forecasted values.
Filename: VAR-TradingRobot.py
import MetaTrader5 as mt5 import schedule import time from VAR import VARForecaster symbol = "EURUSD" timeframe = mt5.TIMEFRAME_D1 mt5_path = r"c:\Users\Omega Joctan\AppData\Roaming\Pepperstone MetaTrader 5\terminal64.exe" # replace this with a desired MT5 path if not mt5.initialize(mt5_path): # initialize MetaTrader5 print("Failed to initialize MetaTrader5, error =", mt5.last_error()) quit() var_model = VARForecaster(symbol=symbol, timeframe=timeframe) var_model.train(start_bar=1, total_bars=10000, max_lags=30) # Train the VAR Model def get_next_forecast(): print(var_model.forecast_next()) schedule.every(1).minutes.do(get_next_forecast) while True: schedule.run_pending() time.sleep(60) else: mt5.shutdown()
Outputs.
[[0.00464001 0.00439884]]
Now that we have these two separate forecasted outcomes for high_open and open_low, let us create a simple trading strategy based on a simple moving average.
Filename: VAR-TradingRobot.py
import MetaTrader5 as mt5 import schedule import time import ta from VAR import VARForecaster from Trade.Trade import CTrade from Trade.SymbolInfo import CSymbolInfo from Trade.PositionInfo import CPositionInfo import numpy as np import pandas as pd symbol = "EURUSD" timeframe = mt5.TIMEFRAME_D1 mt5_path = r"c:\Users\Omega Joctan\AppData\Roaming\Pepperstone MetaTrader 5\terminal64.exe" # replace this with a desired MT5 path if not mt5.initialize(mt5_path): # initialize MetaTrader5 print("Failed to initialize MetaTrader5, error =", mt5.last_error()) quit() var_model = VARForecaster(symbol=symbol, timeframe=timeframe) var_model.train(start_bar=1, total_bars=10000, max_lags=30) # Train the VAR Model # Initlalize the trade classes MAGICNUMBER = 5062025 SLIPPAGE = 100 m_trade = CTrade(magic_number=MAGICNUMBER, filling_type_symbol=symbol, deviation_points=SLIPPAGE) m_symbol = CSymbolInfo(symbol=symbol) m_position = CPositionInfo() ##################################################### def pos_exists(pos_type: int, magic: int, symbol: str) -> bool: """Checks whether a position exists given a magic number, symbol, and the position type Returns: bool: True if a position is found otherwise False """ if mt5.positions_total() < 1: # no positions whatsoever return False positions = mt5.positions_get() for position in positions: if m_position.select_position(position): if m_position.magic() == magic and m_position.symbol() == symbol and m_position.position_type()==pos_type: return True return False def trading_strategy(): forecasts_arr = var_model.forecast_next().flatten() high_open = forecasts_arr[0] open_low = forecasts_arr[1] print(f"high_open: ",high_open, " open_low: ",open_low) # Get the information about the market rates = mt5.copy_rates_from_pos(symbol, timeframe, 0, 50) # Get the last 50 bars information rates_df = pd.DataFrame(rates) if rates is None: print("Failed to get copy rates Error =", mt5.last_error()) return sma_buffer = ta.trend.sma_indicator(close=rates_df["close"], window=20) m_symbol.refresh_rates() if rates_df["close"].iloc[-1] > sma_buffer.iloc[-1]: # current closing price is above sma20 if pos_exists(pos_type=mt5.POSITION_TYPE_BUY, symbol=symbol, magic=MAGICNUMBER) is False: # If a buy position doesn't exist m_trade.buy(volume=m_symbol.lots_min(), symbol=symbol, price=m_symbol.ask(), sl=m_symbol.ask()-open_low, tp=m_symbol.ask()+high_open) else: # if the closing price is below the moving average if pos_exists(pos_type=mt5.POSITION_TYPE_SELL, symbol=symbol, magic=MAGICNUMBER) is False: # If a buy position doesn't exist m_trade.sell(volume=m_symbol.lots_min(), symbol=symbol, price=m_symbol.bid(), sl=m_symbol.bid()+high_open, tp=m_symbol.bid()-open_low) schedule.every(1).minutes.do(trading_strategy) while True: schedule.run_pending() time.sleep(60) else: mt5.shutdown()
Using the trade classes discussed in this article, we check if a position of the same kind exists; if it doesn't, we open a position of the same type. The predicted values high_open and open_low are used for setting the take profit and stop loss of a trade respectively for a buy trade and vice versa for a sell trade.
A simple moving average indicator of the period (window) = 20 is used as a confirmation signal. If the current close price is above the moving average indicator, we open a buy trade; otherwise, we do the opposite for a sell trade.
Outputs.
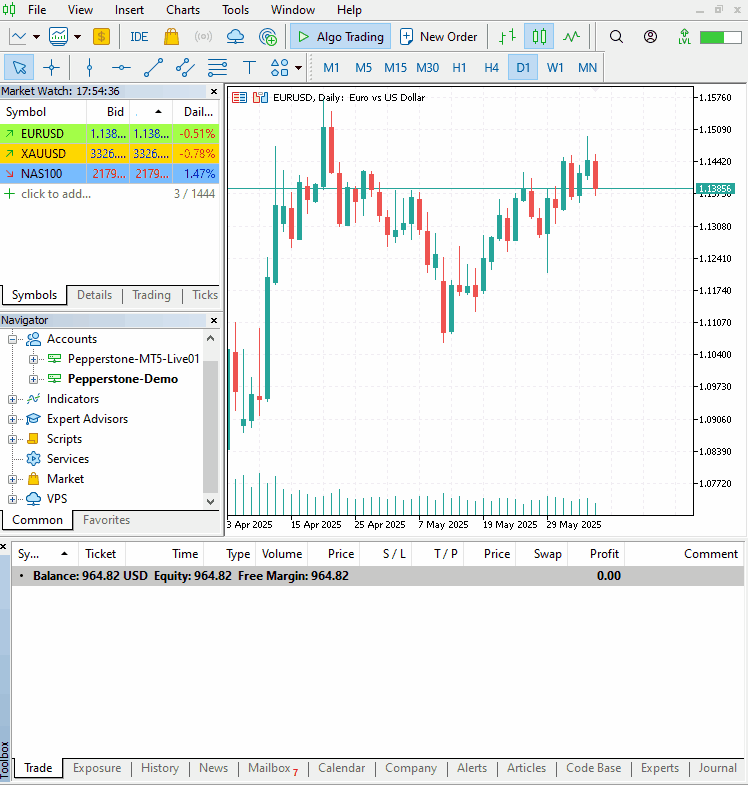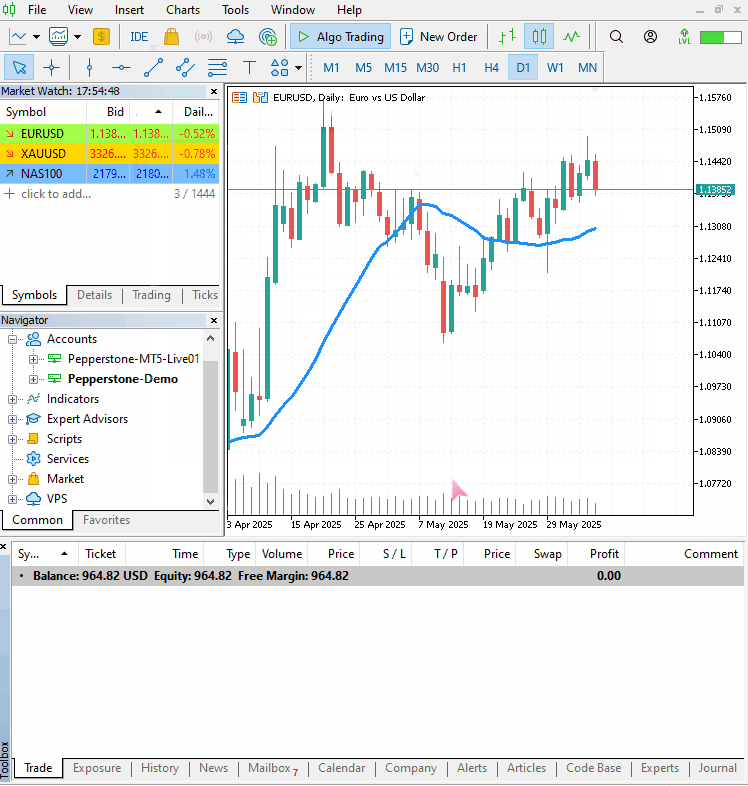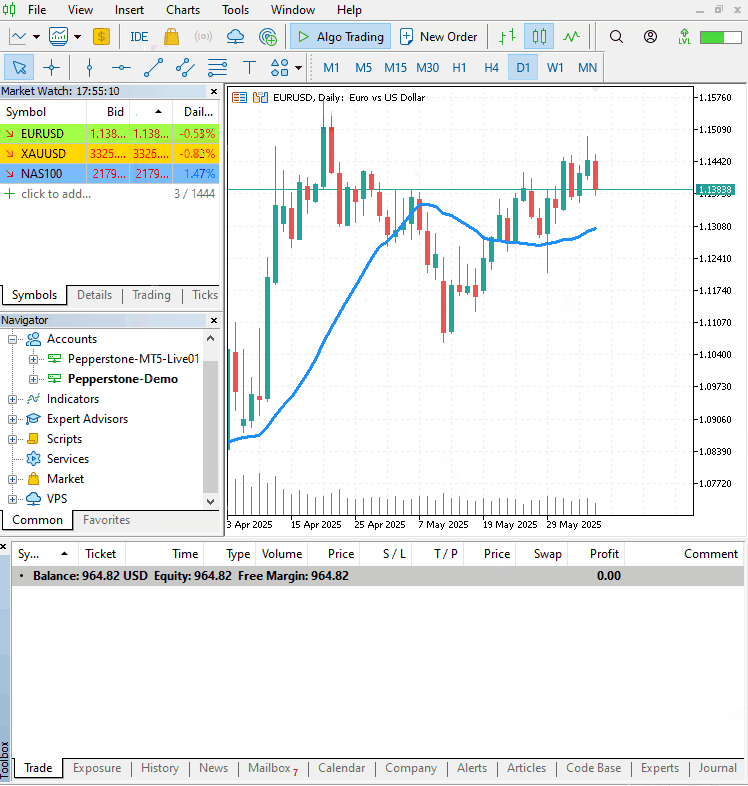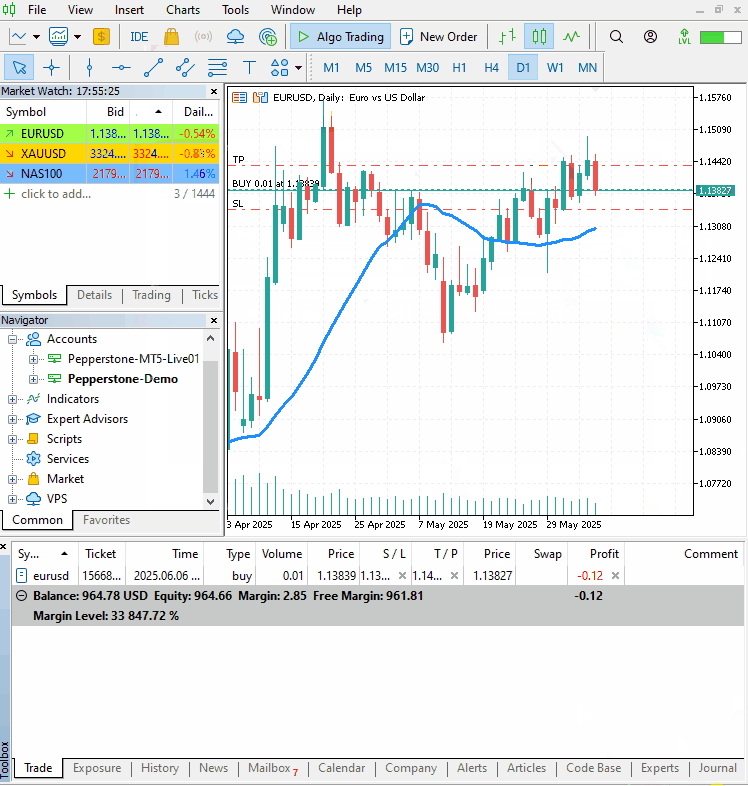
Final Thoughts
Vector Auto-Regression is a decent classical time series model with the ability to forecast multiple regression features, an ability that most machine learning models don't have.
These models offer a couple of advantages such as:
- A flexible lag structure which allows different lag lengths for different variables,
- They capture interdependencies (dynamic relationships between variables),
- They have no strict exogeneity assumption, often present in traditional regression models.
Some of their drawbacks include:
- Their sensitivity to stationary variables, as they only work best in stationary data.
- They assume a linear relationship between a variable and its lags, something not always feasible in the financial markets.
- They can also suffer from overfitting when given many variables and lags.
This article was aimed at raising awareness about this model, its composition, and how it can be applied to trading data, as I found it less documented online on this particular subject. Please don't hesitate to improve the idea to suit your needs.
Best regards.
Attachments Table
| Filename | Descrition & Usage |
|---|---|
| Trade/* | MQL5-like trade classes in Python language. |
| error_description.py | Contains MetaTrader 5 error codes descriptions. |
| forex-ts-forecasting-using-var.ipynb | A Jupyter notebook containing examples for learning purposes. |
| VAR.py | Contains the class that utilizes the VAR model for training and making forecasts. |
| VAR-TradingRobot.py | A trading robot that opens buy and sell trades based on predictions made by the VAR model. |
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
Atomic Orbital Search (AOS) algorithm
Price Action Analysis Toolkit Development (Part 28): Opening Range Breakout Tool
Installing MetaTrader 5 and Other MetaQuotes Apps on HarmonyOS NEXT
From Novice to Expert: Animated News Headline Using MQL5 (II)
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use