MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português
preview
最负盛名的人工协作搜索算法的改进版本（AXSm）

最负盛名的人工协作搜索算法的改进版本（AXSm）

MetaTrader 5 — 示例 |
519 0
Andrey Dik
Andrey Dik

内容

  1. 引言
  2. 算法的实现
  3. 测试结果


1. 引言

在上一篇文章中，我们了解了一种有趣且很有前途的优化算法，即人工协作搜索(ACS)。该算法的灵感来自于对自然界中生物体相互作用和协作的观察，它们团结起来实现共同目标并获得互利。ACS 的基本思想是模拟“捕食者”和“猎物”之间的这种互利关系，以优化复杂的多维问题。

现在我们已经熟悉了 ACS 的基本版本，我们将尝试使用该算法的改进版本来扩展其功能。这些增强版 ACS 将使用受自然生态系统观察启发的附加机制来提高寻找最优解决方案的效率。

研究已知的ACS改进版本将使我们更深入地了解如何成功地运用生物体的合作与互利共存原则来解决复杂的优化问题，并有助于揭示人工智能领域的新视角并激发这一激动人心的领域的进一步发展。


2. 算法实现

ACS（改进型人工协作搜索算法）的第一次小修改包括两个主要变化：

1. 使用 A 和 B 矩阵（种群）的增强形式：
- 在此修改中，A 和 B 矩阵具有附加列。矩阵的每一行包含 N 个变量和一个附加列，用于存储根据前 N 个变量计算出的函数值。这使得跟踪函数值变得更容易，并提高了解决方案的准确性。

2. 改变 M 二进制矩阵的创建方式：
- 在原始算法中，M 矩阵用“0”值填充，然后选择一些元素并将其设置为“1”。这一变化至少对于进行实验的测试函数而言，解决方案的准确性略有提高。

因此，ACS 算法的第一次和微小修改中的这些变化旨在提高解决方案的准确性和算法解决优化问题的效率。我们不会像作者建议的那样添加额外的列来存储个体的拟合度值，而是在智能体结构中使用已经熟悉的“f”字段来描述种群中的个体。

ACS 算法的第二次显著修改包括以下与原始版本不同的变化点：

1. 改变填充捕食者和猎物矩阵的方法：
- 在此修改中，增强的 A 和 B 矩阵中的每一行都按拟合函数值排序。然后比较排序后的 A 和 B 矩阵中的行，并根据此比较确定哪些行将进入捕食者和猎物矩阵。此方法允许根据其优点（特征值）而不是随机选择来选择要更新的候选者。

2. 随机比较以更新 A 和 B 矩阵：
- 在本修改中，在主循环的每次迭代结束时，通过随机比较来更新 A 和 B 矩阵。这意味着两个矩阵具有相同的更新概率。这种方法允许两个种群均匀更新，并提高寻找最优解的多样性。

因此，ACS 算法的第二个修改版本改进了候选者的选择，并更新了 A 和 B 种群，使其在寻找最优解时更加高效和多样化。它与算法的原始版本不同之处在于捕食者和猎物种群的形成方式以及使用随机比较来更新矩阵。

ACS 算法的第三次主要修改代表了捕食者和猎物矩阵形成的完全不同的方法。第三次修改的详细描述如下：

1.Pop 种群：
- 此修改创建了一个新的矩阵 Pop，该矩阵结合了增强的 A 和 B 矩阵。Pop 包含来自 A 和 B 矩阵的所有行。然后按拟合函数值对其进行排序。Pop 中的前 popSize 行成为捕食者种群，而最后 popSize 行成为猎物种群。

2.更新捕食者和猎物：
- 在形成捕食者和猎物种群后，算法根据个体的拟合度不断更新。优先选择最优解作为捕食者，这有助于提高算法的准确性和收敛速度。

3. 使用随机比较：
- 与第二次修改类似，在主循环的每次迭代结束时，通过随机比较更新 A 和 B 矩阵。这种方法确保两个种群的更新机会均等，并促进了寻找最佳解决方案的多样性。

因此，ACS 算法的第三个修改版本专注于利用拟合度来形成捕食者和猎物种群。它代表了一种更先进、更有效的方法来选择候选者和更新种群，同时寻找最优解决方案。

在回顾了算法基本版本（ACS）的可能修改后，我们现在准备着手实现这一有前途的优化方法的第一个改进版本。我们的目标是提高寻找最优解的效率。我们将逐步将新元素引入 ACS 的基本结构，仔细分析它们对算法性能和收敛性的影响。

让我们开始实现该算法的第一个修改版本并探索其潜力。在该算法的每个后续版本中，与前一个版本不同的代码部分都以绿色表示。

C_AO_ACSm1类的代码说明：

1. C_AO_ACSm1是从C_AO基类派生的类。
2. 该类具有公共的构造函数和析构函数。
3. 在构造函数中初始化以下数据成员：

  • ao_name，ao_desc，ao_link - 有关算法的描述行。
  • popSize - 种群大小
  • bioProbab - 生物相互作用的概率
  • params - 算法参数数组，在本例中我们有两个参数：popSize 和 bioProbab

4. SetParams() - 方法根据params 数组中的参数，设置popSize 和 bioProbab 的值。
5. Init() - 方法将范围和搜索步骤以及周期数作为输入，并返回表示初始化成功的逻辑值。
6. Moving() 和 Revision() - 方法包含用于移动和修改智能体的算法的基本逻辑。
7. 私有数据成员包括结构数组 S_AO_Agent 和 S_C ，以及算法中使用的Key和phase变量。
8. ArrayShuffle() - 私有方法，用于对数组元素进行乱序。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACSm1 : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ACSm1 () { }
  C_AO_ACSm1 ()
  {
    ao_name = "ACS";
    ao_desc = "Artificial Cooperative Search m1";
    ao_link = "https://www.mql5.com/ru/articles/15014";

    popSize   = 1;   //population size
    bioProbab = 0.9; //biological interaction probability

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "bioProbab"; params [1].val = bioProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    bioProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double bioProbab; //biological interaction probability

  private: //-------------------------------------------------------------------
  S_AO_Agent A        [];
  S_AO_Agent B        [];
  S_AO_Agent Predator [];
  S_AO_Agent Prey     [];

  S_C M               [];

  int Key;
  int phase;

  void ArrayShuffle (double &arr []);
};
//——————————————————————————————————————————————————————————————————————————————

Init 方法是 C_AO_ACSm1 类中用于对象初始化的方法：

1. Init() - 方法声明。它接受四个参数：最小搜索范围 rangeMinP，最大搜索范围 rangeMaxP，搜索步长 rangeStepP 和迭代次数 epochsP，后者默认为0。
2. if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false - 调用 StandardInit 函数，该函数执行基类的标准初始化。如果 StandardInit 返回 false，则 Init 方法立即终止并返回 false。
3. 在循环 for (int i = 0; i < popSize; i++) 中，使用 Init 方法初始化 A、B、Predator、Prey 和 M 数组的每个元素。
4. ArrayResize (A, popSize) 和类似的行将 A、B、Predator、Prey 和 M 数组的大小更改为 popSize。
5. 在嵌套循环 for (int j = 0; j < coords; j++) 中，使用给定范围内的随机值初始化 A 和 B 数组中每个对象的每个 c 元素（个体坐标）。
6. phase = 0 将 phase 设置为0。
7. 如果初始化成功，该方法返回 true。

该代码负责初始设置和准备进一步算法操作所需的数据。它创建对象数组、初始化它们的值并设置算法的初始状态。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ACSm1::Init (const double &rangeMinP [], //minimum search range
                       const double &rangeMaxP  [], //maximum search range
                       const double &rangeStepP [], //step search
                       const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (A,        popSize);
  ArrayResize (B,        popSize);
  ArrayResize (Predator, popSize);
  ArrayResize (Prey,     popSize);

  ArrayResize (M,         popSize);

  for (int i = 0; i < popSize; i++)
  {
    A        [i].Init (coords);
    B        [i].Init (coords);
    Predator [i].Init (coords);
    Prey     [i].Init (coords);

    M        [i].Init (coords);
  }

  // Initialization
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
    }
  }

  phase = 0;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ACSm1 类的 Moving 方法实现了算法中个体移动的基本逻辑：

1. 当 phase == 0 时，将 A 种群中的个体复制到 a 数组（a 数组用于传递个体以计算拟合度函数）。

  • 在循环 for (int i = 0; i < popSize; i++) 中，将 A 中的个体坐标复制到 a 数组。
  • phase 变量的值增加1，然后方法返回。

2. 当 phase == 1 时，为 A 种群中的个体分配拟合度，并将 B 种群中的个体复制过来。

  • 在循环 for (int i = 0; i < popSize; i++) 中，将 a[i].f 的拟合度值复制到 A[i].f。
  • 接下来，在循环 for (int i = 0; i < popSize; i++) 中，将 B 中的个体坐标复制到 a 数组，以便进一步计算个体的拟合度。
  • phase 的值增加1，然后方法返回。

3. 当 phase == 2 时，将拟合度返回给 B 种群的个体。

  • 在循环 for (int i = 0; i < popSize; i++) 中，将 a[i].f 的拟合度值复制到 B[i].f。
  • phase 的值增加1，然后执行算法的后续逻辑。

4. Selection - 在此处进行选择操作。

  • 如果 u.RNDprobab() 的随机值小于0.5，则在循环 for (int i = 0; i < popSize; i++) 中，将 A[i] 个体复制到 Predator[i]，并将 Key 设置为1。
  • 否则，在循环 for (int i = 0; i < popSize; i++) 中，将 B[i] 个体复制到 Predator[i]，并将 Key 设置为2。
  • Prey 数组的选择操作以类似方式执行。

5. Permutation of Prey - 在此处随机置换 Prey 种群中每个个体的坐标。

  • 在循环 for (int i = 0; i < popSize; i++) 中，对每个个体执行 ArrayShuffle(Prey[i].c)，以混合个体坐标（每个个体的坐标分别混合，而个体之间的坐标不混合）。

6. Mutation 和 Crossover - 在此处执行变异和交叉操作。

  • 根据随机数计算 R 值。
  • 将 M 二进制矩阵填充为1。
  • 根据生物相互作用概率 bioProbab，将 M 矩阵中的某些元素更改为0或1，以执行额外的操作。
  • 在循环 for (int i = 0; i < popSize; i++) 中，对每个个体执行变异和交叉操作，更新 a 种群数组中的值。

7. Boundary control - 此代码块执行边界控制，将 a 种群中位于优化参数指定范围之外的个体坐标替换为范围内的随机值。

此方法实现了算法的基本操作，如选择、变异、交叉和边界控制，这些操作应用于个体种群以找到最优解。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm1::Moving ()
{
  //----------------------------------------------------------------------------
  if (phase == 0)
  {
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 1)
  {
    for (int i = 0; i < popSize; i++) A [i].f = a [i].f;
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 2)
  {
    for (int i = 0; i < popSize; i++) B [i].f = a [i].f;

    phase++;
  }

  //----------------------------------------------------------------------------
  // Selection
  if (u.RNDprobab () < 0.5)
  {
    for (int i = 0; i < popSize; i++)
    {
      Predator [i] = A [i];                                                       
    }

    Key = 1;
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      Predator [i] = B [i];                             
    }

    Key = 2;
  }

  if (u.RNDprobab () < 0.5)
  {
    for (int i = 0; i < popSize; i++)
    {
      Prey [i] = A [i];                                 
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      Prey [i] = B [i];                                 
    }
  }

  // Permutation of Prey
  for (int i = 0; i < popSize; i++)
  {
    ArrayShuffle (Prey [i].c);
  }

  double R;

  if (u.RNDprobab () < 0.5)
  {
    R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0);
  }
  else R = 1 / MathExp (4 * MathRand () / 32767.0);

  // Fill binary matrix M with 0s
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      M [i].c [j] = 0;
    }
  }

  // Additional operations with matrix M
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    int sum = 0;

    for (int c = 0; c < coords; c++) sum += M [i].c [c];

    if (sum == coords)
    {
      int j = MathRand () % coords;
      M [i].c [j] = 0;
    }
  }

  // Mutation
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]);

      // Crossover
      if (M [i].c [j] > 0)
      {
        a [i].c [j] = Predator [i].c [j];
      }

      // Boundary control
      if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j])
      {
        a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      }
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

接下来，让我们考虑C_AO_ACSm1类的 Revision方法代码。它执行以下操作：

1. 检查phase是否已完成种群准备阶段，即phase >= 3。如果此条件不满足，该方法将不执行任何进一步的操作并返回。

2. 更新Selection update个体的选择：

  • 对于a种群中的每个个体，检查其f拟合度值是否超过Predator数组中对应位置的值。如果是，则更新Predator中的值。
  • 根据Key变量的值，将Predator种群中的个体复制到A或B种群中。

3. 确定Predator数组中Ybest（最佳拟合度值）及其Ibest（最佳索引）：

  • 遍历Predator数组，找到最大拟合度值及其索引。

4. 更新fB（最佳全局解）：

  • 如果Ybest超过当前最佳fB值，则更新fB，同时从Predator数组中复制相应的a和cB数组元素。

该方法更新个体选择，确定最佳解并更新优化算法中的全局最佳解。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm1::Revision ()
{
  if (phase < 3) return;

  // Selection update
  for (int i = 0; i < popSize; i++)
  {
    double d = a [i].f;

    if (d > Predator [i].f)
    {                      
      Predator [i] = a [i];
    }                                    
  }

  if (Key == 1)
  {
    for (int i = 0; i < popSize; i++)
    {
      A [i] = Predator [i];
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      B [i] = Predator [i];
    }
  }

  double Ybest = -DBL_MAX;
  int Ibest = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (Predator [i].f > Ybest)
    {
      Ybest = Predator [i].f;
      Ibest = i;
    }
  }

  if (Ybest > fB)
  {
    fB = Ybest;
    ArrayCopy (a [Ibest].c, Predator [Ibest].c);
    ArrayCopy (cB, Predator [Ibest].c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ACS类的ArrayShuffle方法在所有三个修改版中都得到了应用，并且该方法用于对数组中的元素进行随机乱序：

1. 使用ArraySize函数定义“arr”数组的大小。
2. 从最后一个元素开始，以逆序遍历arr数组。
3. 对于每个i元素，生成一个从0到i的随机索引j。
4. 使用临时变量tmp交换arr[i]和arr[j]元素。

因此，arr数组的元素被随机打乱顺序。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm1::ArrayShuffle (double &arr [])
{
  int n = ArraySize (arr);
  for (int i = n - 1; i > 0; i--)
  {
    int j = MathRand () % (i + 1);
    double tmp = arr [i];
    arr [i] = arr [j];
    arr [j] = tmp;
  }
}
//——————————————————————————————————————————————————————————————————————————————

现在是时候分析ACS算法的第二次修改的代码了。C_AO_ACSm2类的Moving方法代码，所做的更改如下：
1. Phase 0：

  • 如果phase等于0，则a种群中的每个个体将从A种群中获取值。
  • phase值递增，然后方法返回。

2. Phase 1：

  • 如果phase是1，则a种群中的每个个体将获得A种群中的f拟合度值。
  • 此外，a种群中的每个个体还将从B种群中获取值。
  • phase值递增，然后方法返回。

3. Phase 2：

  • 如果phase是2，则B种群中的每个个体将从a种群中获取“f”拟合度值。
  • phase值递增，算法继续执行后续逻辑。

4. 选择：

  • 比较A和B种群中每个个体的f拟合度值。
  • 如果A中的f值超过B中的值，则将A中的一个个体复制到Predator，同时将B中的一个个体复制到Prey。否则，情况相反（拟合度最高的个体被指定为“捕食者”，而最低的个体成为“猎物”）。

5. 猎物互换：

  • 使用ArrayShuffle函数对Prey种群中每个个体的坐标进行置换。

6. 变异和交叉：

  • 根据随机数定义R值。
  • 将M二进制矩阵填充为零。
  • 根据bioProbab概率，对M矩阵执行额外操作，将其中一些元素设置为1。

   对于a种群中的每个个体：

  • 执行变异操作：a[i].c[j]元素计算为Predator[i].c[j]与R乘以Prey[i].c[j]和Predator[i].c[j]之间差值的乘积之和。
  • 执行交叉操作：如果M[i].c[j]等于1，则a[i].c[j]被替换为Predator[i].c[j]。
  • 边界检查：如果a[i].c[j]超出rangeMin[j]和rangeMax[j]的范围，则将其替换为该范围内的随机值。

7. 检查坐标：

  • 对于a种群中的每个个体，使用SeInDiSp函数检查坐标。
//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm2::Moving ()
{
  //----------------------------------------------------------------------------
  if (phase == 0)
  {
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 1)
  {
    for (int i = 0; i < popSize; i++) A [i].f = a [i].f;
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 2)
  {
    for (int i = 0; i < popSize; i++) B [i].f = a [i].f;

    phase++;
  }

  //----------------------------------------------------------------------------
  // Selection                     
  for (int i = 0; i < popSize; i++)
  {                                
    if (A [i].f > B [i].f)         
    {                              
      Predator [i] = A [i];        
      Prey     [i] = B [i];        
    }                              
    else                           
    {                              
      Predator [i] = B [i];        
      Prey     [i] = A [i];        
    }                              
  }                                

  // Permutation of Prey
  for (int i = 0; i < popSize; i++)
  {
    ArrayShuffle (Prey [i].c);
  }

  double R;

  if (u.RNDprobab () < 0.5)
  {
    R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0);
  }
  else R = 1 / MathExp (4 * MathRand () / 32767.0);

  // Fill binary matrix M with 0s
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      M [i].c [j] = 0;
    }
  }

  // Additional operations with matrix M
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    int sum = 0;

    for (int c = 0; c < coords; c++) sum += M [i].c [c];

    if (sum == coords)
    {
      int j = MathRand () % coords;
      M [i].c [j] = 0;
    }
  }

  // Mutation
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]);

      // Crossover
      if (M [i].c [j] > 0)
      {
        a [i].c [j] = Predator [i].c [j];
      }

      // Boundary control
      if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j])
      {
        a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      }
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

我不会在这里考虑第二次算法修改的修订方法，因为它保持不变。

我们继续讨论第三种修改从C_AO基类派生的C_AO_ACSm3第三种修改类的定义中已进行以下更改：

数据成员列表已更改：

  • bioProbab - 生物间相互作用的概率。
  • A[]，B[]，Predator[]，Prey[]，Pop[]，pTemp[] - 存储不同个体种群的数组。
  • M[] - 存储与个体相关的附加数据的数组。
  • phase - 算法的当前阶段。
//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACSm3 : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ACSm3 () { }
  C_AO_ACSm3 ()
  {
    ao_name = "ACS";
    ao_desc = "Artificial Cooperative Search m3";
    ao_link = "https://www.mql5.com/ru/articles/15014";

    popSize   = 10;   //population size
    bioProbab = 0.9; //biological interaction probability

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "bioProbab"; params [1].val = bioProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    bioProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double bioProbab; //biological interaction probability

  private: //-------------------------------------------------------------------
  S_AO_Agent A        [];
  S_AO_Agent B        [];
  S_AO_Agent Predator [];
  S_AO_Agent Prey     [];
  S_AO_Agent Pop      [];
  S_AO_Agent pTemp    [];

  S_C M               [];

  int phase;

  void ArrayShuffle (double &arr []);
};
//——————————————————————————————————————————————————————————————————————————————

对C_AO_ACSm3类的Init初始化方法进行以下更改：

1. 为A、B、Predator、Prey、Pop、pTemp和M数组分配了popSize或popSize * 2的内存空间。

2. 使用Init方法初始化了A、B、Predator、Prey、Pop和M数组的每个元素。

算法原始版本的作者没有将代码进行逻辑分段。为了将所有种群算法的实现保持一致的风格，我添加了阶段的划分。这是必要的，因为ACS需要使用预先计算的拟合度来评估А和B种群中的个体。这些操作应该按顺序在方法中执行。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ACSm3::Init (const double &rangeMinP [], //minimum search range
                       const double &rangeMaxP  [], //maximum search range
                       const double &rangeStepP [], //step search
                       const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (A,        popSize);
  ArrayResize (B,        popSize);
  ArrayResize (Predator, popSize);
  ArrayResize (Prey,     popSize);
  ArrayResize (Pop,      popSize * 2);
  ArrayResize (pTemp,    popSize * 2);

  ArrayResize (M,        popSize);

  for (int i = 0; i < popSize; i++)
  {
    A        [i].Init (coords);
    B        [i].Init (coords);
    Predator [i].Init (coords);
    Prey     [i].Init (coords);

    M        [i].Init (coords);
  }

  for (int i = 0; i < popSize * 2; i++) Pop [i].Init (coords);

  // Initialization
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
    }
  }

  phase = 0;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

现在，让我们来看一下第三次修改中C_AO_ACSm3类的Moving方法的代码。以下代码段做了修改：

  • 将A和B种群合并为一个单一的Pop种群。
  • 根据个体的拟合度值对Pop种群进行排序。
  • 从排序后的Pop数组中填充Predator和Prey种群，其中种群中最好的一半成为“捕食者”，另一半成为“猎物”。
  • 用1填充M二进制矩阵。
  • 对M矩阵进行额外的操作，其中一些元素会根据随机数以及bioProbab（生物交互的概率）变为0或1。
//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm3::Moving ()
{
  //----------------------------------------------------------------------------
  if (phase == 0)
  {
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 1)
  {
    for (int i = 0; i < popSize; i++) A [i].f = a [i].f;
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 2)
  {
    for (int i = 0; i < popSize; i++) B [i].f = a [i].f;

    phase++;
  }

  //----------------------------------------------------------------------------
  // Merge matrices A and B to create matrix Pop      
  for (int i = 0; i < popSize; i++)                   
  {                                                   
    Pop [i]           = A [i];                        
    Pop [i + popSize] = B [i];                        
  }                                                   
                                                      
  // Sort matrix Pop using column N as sort key values
  u.Sorting (Pop, pTemp, popSize * 2);                
                                                      
  // Populate Predator and Prey matrices              
  for (int i = 0; i < popSize; i++)                   
  {                                                   
    Predator [i] = Pop [i];                           
    Prey     [i] = Pop [i + popSize];                 
  }                                                   

  // Permutation of Prey
  for (int i = 0; i < popSize; i++)
  {
    ArrayShuffle (Prey [i].c);
  }

  double R;

  if (u.RNDprobab () < 0.5)
  {
    R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0);
  }
  else R = 1 / MathExp (4 * MathRand () / 32767.0);

  // Fill binary matrix M with 1s
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      M [i].c [j] = 1;                
    }
  }

  // Additional operations with matrix M
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 0;              
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        if (u.RNDprobab() < bioProbab)
        {                             
          M[i].c[j] = 1;              
        }                             
        else                          
        {                             
          M[i].c[j] = 0;              
        }                             
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    int sum = 0;

    for (int c = 0; c < coords; c++) sum += M [i].c [c];

    if (sum == coords)
    {
      int j = MathRand () % coords;
      M [i].c [j] = 0;
    }
  }

  // Mutation
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]);

      // Crossover
      if (M [i].c [j] > 0)
      {
        a [i].c [j] = Predator [i].c [j];
      }

      // Boundary control
      if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j])
      {
        a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      }
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————


3. 测试结果

我们已经仔细审阅并分析了该算法的所有已知版本。现在是时候关注它们的实际结果以及我们可以得出的结论了。我提议详细探讨每一项修改如何影响产出率、准确性和效率。这将有助于我们更好地了解哪些更改最为成功，以及我们接下来应该朝哪个方向努力。

修改的第一版本在总体得分上显示出大致相当的结果，但在具有1000个变量的Hilly函数以及具有50个和1000个变量的Forest函数上，结果有了显著改善。

ACS|人工协作搜索 m1|1.0|0.7|
=============================
5 Hilly's；函数运行次数：10000；结果：0.7130880902279995
25 Hilly's；函数运行次数：10000；结果：0.7565145335137569
500 Hilly's；函数运行次数：10000；结果：0.31899537529427235
=============================
5 Forest's；函数运行次数：10000；结果：0.9999999999866176
25 Forest's；函数运行次数：10000；结果：0.9555551824899264
500 Forest's；函数运行次数：10000；结果：0.24186829565864398
=============================
5 Megacity's；函数运行次数：10000；结果：0.6607692307692307
25 Megacity's；函数运行次数：10000；结果：0.5038461538461539
500 Megacity's；函数运行次数：10000；结果：0.13922307692307825
=============================
全部得分：5.28986 (58.78%)

算法的第二版本在所有具有50个和1000个变量的测试函数上的结果都有了明显的改善，但在与基本版本相比时，具有10个变量的Megacity函数上的结果却显著变差（结果分散性极大）。这表明朝这个方向发展是有前景的（尽管存在一些有争议的地方），并且值得继续对进一步的修改进行研究。

ACS|人工协作搜索 m2|2.0|0.7|
=============================
5 Hilly's；函数运行次数：10000；结果：0.7682797921658492
25 Hilly's；函数运行次数：10000；结果：0.7664893907210706
500 Hilly's；函数运行次数：10000；结果：0.31831672493319296
=============================
5 Forest's；函数运行次数：10000；结果：0.9999997349437437
25 Forest's；函数运行次数：10000；结果：0.9534110489423269
500 Forest's；函数运行次数：10000；结果：0.24425762117784502
=============================
5 Megacity's；函数运行次数：10000；结果：0.6176923076923077
25 Megacity's；函数运行次数：10000；结果：0.5384615384615385
500 Megacity's；函数运行次数：10000；结果：0.14057692307692446
=============================
全部得分：5.34749 (59.42%)

遗憾的是，看似最有前景的第三项修改并未达到预期效果，其总体结果甚至略逊于算法的基本版本。尽管值得注意的是，在具有10个变量的平滑Hilly函数上，结果有了显著改善。该算法在具有少量变量的平滑函数上表现出了更高的收敛准确性。

ACS|人工协作搜索 m3|10.0|0.9|
=============================
5 Hilly's；函数运行次数：10000；结果：0.8836798635515516
25 Hilly's；函数运行次数：10000；结果：0.715438105666966
500 Hilly's；函数运行次数：10000；结果：0.3011611038405591
=============================
5 Forest's；函数运行次数：10000；结果：0.9893902762645717
25 Forest's；函数运行次数：10000；结果：0.7954795408759185
500 Forest's；函数运行次数：10000；结果：0.21910399769909533
=============================
5 Megacity's；函数运行次数：10000；结果：0.6315384615384615
25 Megacity's；函数运行次数：10000；结果：0.49876923076923074
500 Megacity's；函数运行次数：10000；结果：0.12683076923077044
=============================
全部得分：5.16139 (57.35%)

算法第二次修改版本的可视化。在变量数量较少的情况下，Hilly和Megacity函数的结果存在相当大的离散度，而算法在尖峰平滑的Forest函数上表现极佳。

Hilly Mod

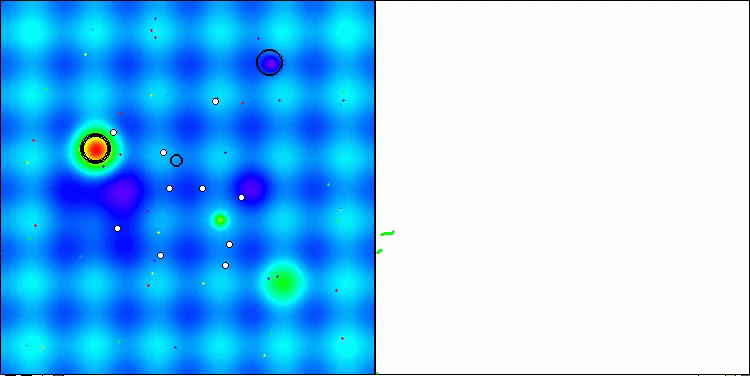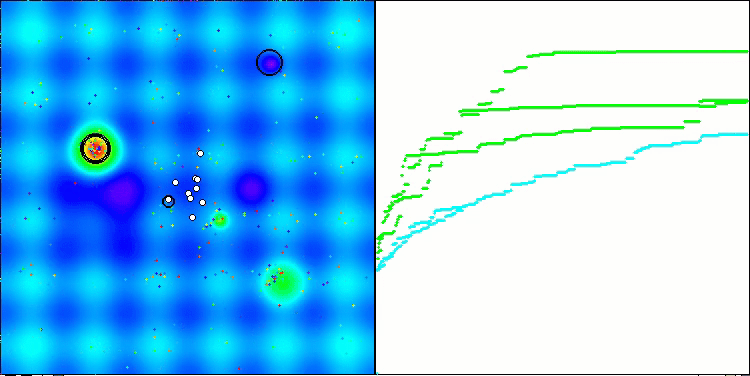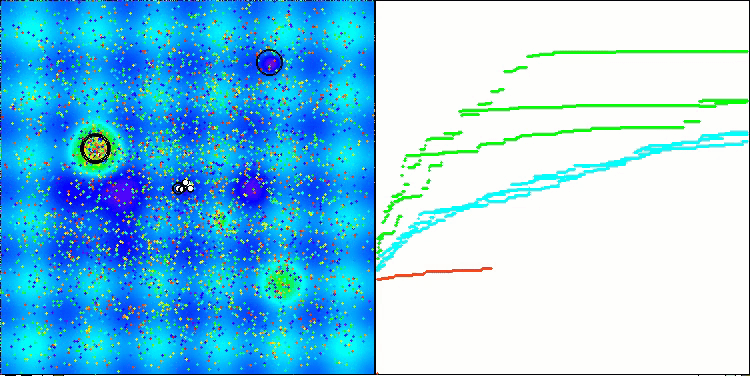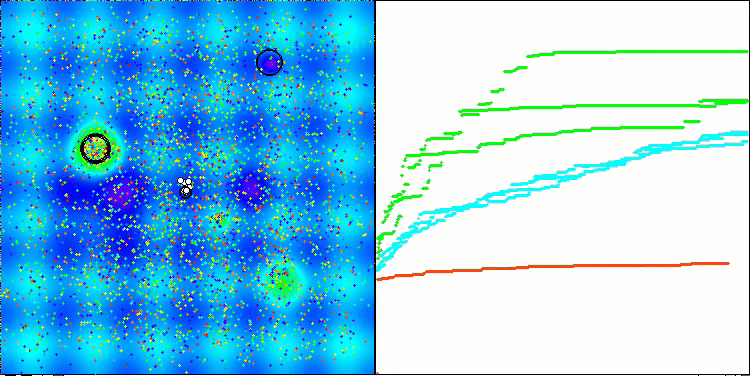
  ACSm2在Hilly测试函数上的表现

Forest Mod

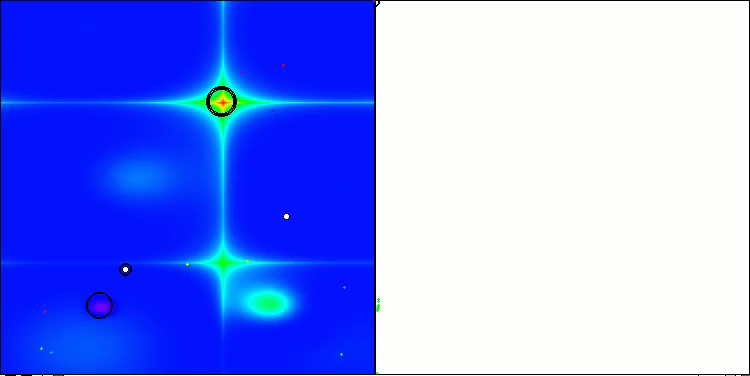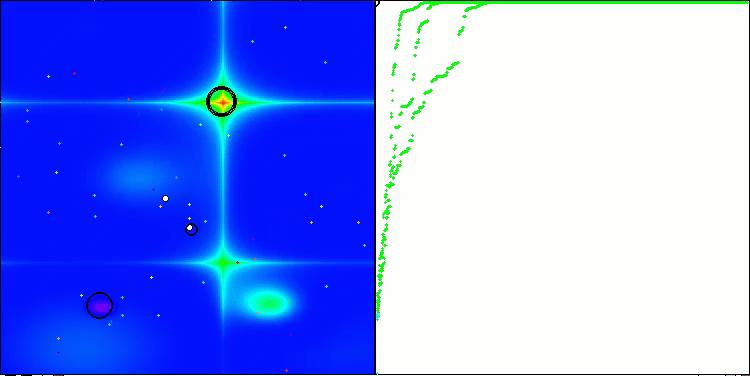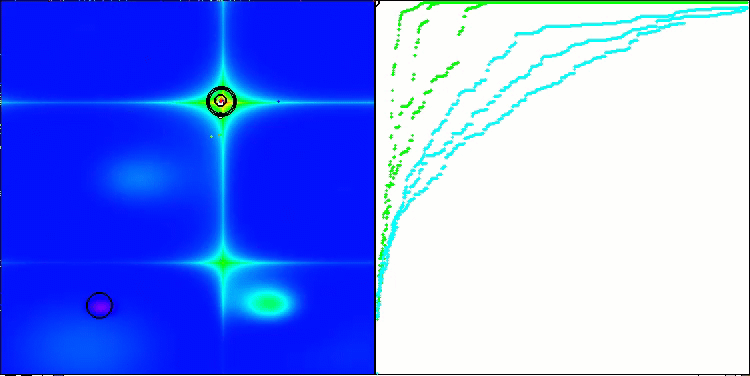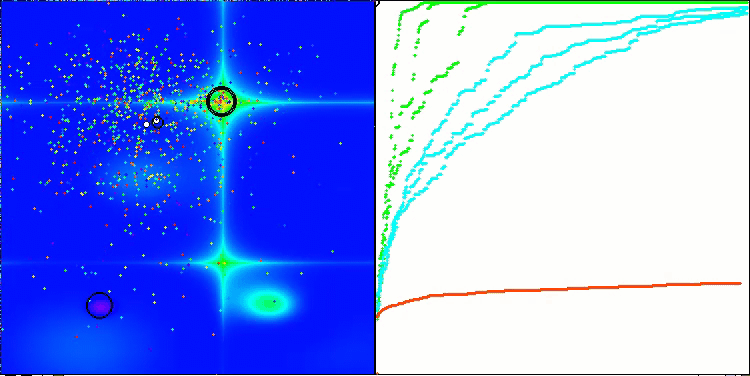
ACSm2在Forest测试函数上的表现

Hilly Mod

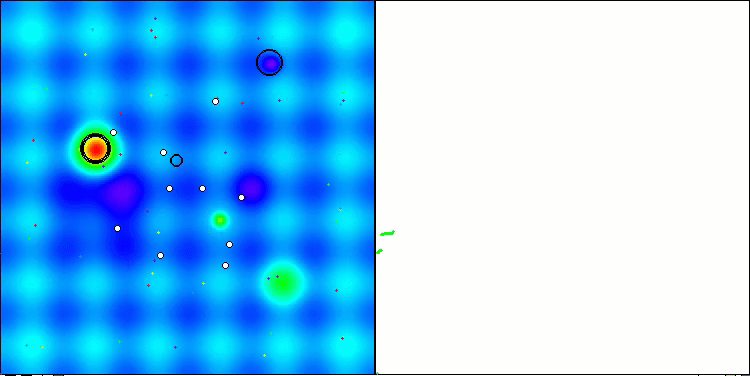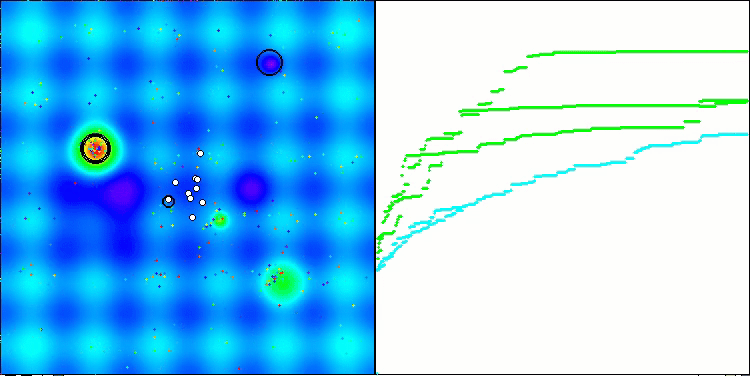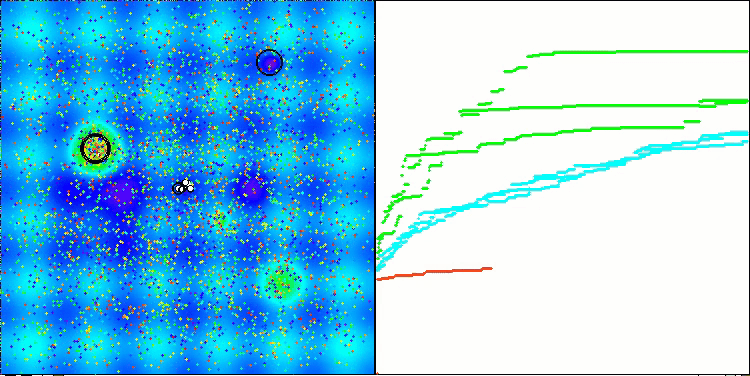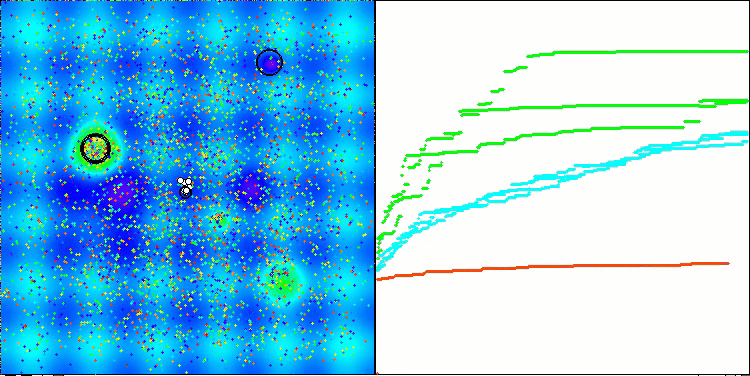
  ACSm2在Megacity测试函数上的表现


总结

总结如下：

1. 对ACS算法进行了第一次修改，增加了A和B矩阵的扩展形式，提高了解的准确性，尤其是对于具有1000个变量的Hilly函数和具有50和1000个变量的Forest函数。

2. 第二次修改改变了填充捕食者和猎物矩阵的方法，并使用随机比较来更新矩阵，结果显示所有具有 50 和 1000 个变量的测试函数的结果都有明显改善，但导致具有 10 个变量的 Megacity 函数的结果分布更加分散。

3. 第三项修改侧重于使用拟合度来形成Predator和Prey种群，但并未达到预期，其总体结果甚至略逊于算法的基本版本，尽管它在具有少量变量的平滑函数上提高了收敛的准确性。

因此，每个修改都有自己的优点和缺点，为了进一步开发算法，必须考虑到这些特点，以便创建更高效​​、更通用的 ACS 算法版本。

可能需进一步改进的地方：

1. 修改搜索机制

  • 分析算法中当前使用的搜索机制，并考虑进一步优化的可能性。
  • 探索是否可以引入自适应搜索步长等附加机制来提高搜索效率。

2.探索混合方法：

  • 考虑将当前算法与其他优化方法相结合，以利用不同方法的优势。例如，我们可以尝试整合进化算法或群体智能方法的元素，以增加多样性和收敛速度。

3. 分析和改进种群间相互作用机制：

  • 研究如何改进A和B种群相互作用的方式，以便在搜索过程中更有效地相互补充。在种群之间引入更复杂的信息共享或合作学习结构可能值得一试。

tab模式

图例 1. 根据相关测试对算法修改进行颜色分级，以便与基本版本进行比较。大于或等0.99 的结果以白色突出显示

图表模式

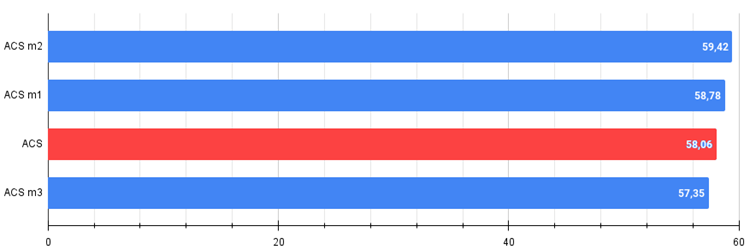
图例 2. 算法修改结果的直方图（范围从0到100，越多越好，

其中100是理论上的最大可能结果，附件提供了一个计算评级表格的脚本）


修改后的 ACS 算法版本的一般优缺点：

优势：

  1. 外部参数少（仅有一个）。
  2. 在各种类型的函数上都能表现出良好的收敛性。

缺点：

  1. 在低维函数上，算法的结果呈现出较大的离散性或分散性。

本文附带了一个文档，其中包含了算法代码的当前版本。文章作者不对典型算法描述的绝对准确性负责。对其中进行了多处修改，从而提升搜索能力。文章中表述的结论和论断是基于实验的结果。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/15014

附加的文件 |
下载ZIP
ACS_mods.zip (36.55 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.

该作者的其他文章

前往讨论
在MQL5中相关性分析的要素：皮尔逊卡方独立性检验和相关比率 在MQL5中相关性分析的要素：皮尔逊卡方独立性检验和相关比率
该文章探讨了相关性分析中的经典工具。文章重点介绍了皮尔逊卡方独立性检验和相关比率的理论背景概述，以及它们的实际应用。
开发多币种 EA 交易（第 8 部分）：负载测试和处理新柱 开发多币种 EA 交易（第 8 部分）：负载测试和处理新柱
随着我们的进步，我们在一个 EA 中使用了越来越多的同时运行的交易策略实例。让我们试着弄清楚在遇到资源限制之前，我们可以得到多少实例。
开发回放系统（第 47 部分）：Chart Trade 项目（六） 开发回放系统（第 47 部分）：Chart Trade 项目（六）
最后，我们的 Chart Trade 指标开始与 EA 互动，以交互方式传输信息。因此，在本文中，我们将对该指标进行改进，使其功能足以与任何 EA 配合使用。这样，我们就可以访问 Chart Trade 指标，并像实际连接 EA 一样使用它。不过，我们将以比以前更有趣的方式来实现这一目标。
人工协作搜索算法 (ACS) 人工协作搜索算法 (ACS)
人工协作搜索算法ACS (Artificial Cooperative Search) 是一种创新方法，它利用二进制矩阵和基于互利共生与合作的多个动态种群来快速准确地找到最优解。ACS在捕食者与猎物问题上的独特处理方法使其能够在数值优化问题中取得卓越成果。