MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português
preview
在训练中激活神经元的函数：快速收敛的关键？

在训练中激活神经元的函数：快速收敛的关键？

MetaTrader 5 — 示例 |
167 9
Andrey Dik
Andrey Dik

引言

在之前的文章中，我们研究了一个简单的 MLP 神经网络作为逼近器（强化学习）在交易中的特性。当时，我们没有特别关注激活函数的特性，而是使用了流行的双曲正切 Sigmoid 函数。此外，在其中一篇文章中，我们讨论了广为人知且广泛使用的 ADAM 算法的能力。我将其修改为一种独立的ADAMm全局优化种群方法。

在本文中，我们将深入探讨神经网络作为数据插值器（监督学习）的能力，重点关注神经元激活函数的特性。我们将使用神经网络内置的 ADAM 优化算法（这是神经网络应用中的常规做法），并研究激活函数及其导数对优化算法收敛速度的影响。

想象一条有许多支流的河流。在正常状态下，水自由流动，形成复杂的洋流和漩涡模式。但如果我们开始建造一套船闸和水坝系统会怎么样呢？我们将能够控制水流，将其引向正确的方向，并调节水流的力量。神经网络中的激活函数扮演着类似的角色：它决定哪些信号可以通过，哪些信号需要延迟或衰减。没有它，神经网络将只是一组线性变换。

激活函数为神经网络的操作增加了动态性，使其能够捕捉数据中的细微差别。例如，在人脸识别任务中，激活函数帮助网络注意到微小的细节，如眉毛的弧度或下巴的形状。正确选择激活函数会影响神经网络在各种任务上的表现。一些函数更适合训练的早期阶段，提供清晰且易于理解的信号。其他函数则允许网络在高级阶段捕捉更微妙的模式，而还有一些函数则负责筛选掉不必要的部分，只留下最重要的部分。

如果我们不了解激活函数的特性，就可能会遇到问题。神经网络可能会在简单任务上“磕磕绊绊”，或者“忽略”重要的细节。激活函数的主要目的是为神经网络引入非线性，并归一化输出值。

本文旨在识别当使用不同的激活函数，及其在最小化误差时，对神经网络精确遍历样本点（插值）影响的相关问题。我们还将弄清楚激活函数是否真的影响收敛速度，或者这仅仅是所用优化算法的特性。作为参考算法，我们将使用改进的种群 ADAMm，它利用了随机性元素，并与 MLP 内置的 ADAM（经典用法）进行测试比较。后者凭直觉应该具有优势，因为它通过激活函数的导数，可以直接访问适应度函数表面的梯度。与此同时，种群随机 ADAMm 无法访问导数，并且对优化问题的表象一无所知。让我们看看结果如何，并得出一些结论。

本文具有探索性质，叙述按照实验的顺序展开。


内置 ADAM 的 MLP 神经网络实现

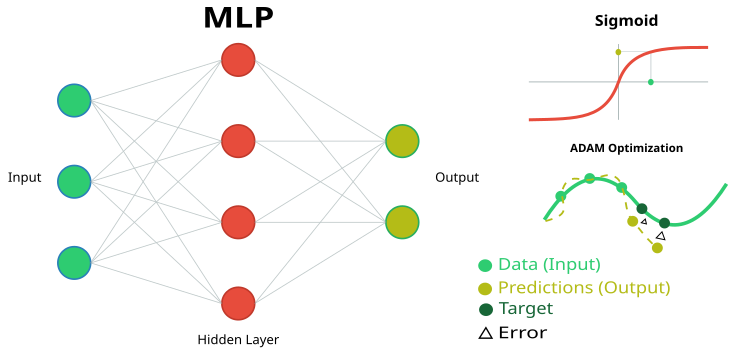
图例 1. MLP 神经网络及其训练的示意图

为了进行当前的研究，我们需要一个简单且透明的 MLP 神经网络代码，不使用 MQL5 语言内置的专用矩阵计算。这将使我们能够清晰地理解神经网络逻辑中究竟发生了什么，以及弄清楚某些结果依赖于什么。

我们将实现一个内置 ADAM（自适应矩估计）优化算法的多层感知机（MLP）。一个类和结构体代表了神经网络实现的一部分，其中定义了主要组件：神经元、神经元层和权重。

1. C_Neuro 类代表一个神经元，它是神经网络中的基本单元。

  • C_Neuron() 是一个构造函数，用于将 “m” 和 “v” 属性的值初始化为零。这些值用于优化算法。
  • out — 神经元在应用激活函数后的输出值。
  • delta — 用于在训练期间计算梯度的误差增量。
  • bias — 添加到神经元输入的偏置值。
  • m 和 v 用于存储偏置的一阶矩和二阶矩，供 ADAM 优化方法使用。

2. S_NeuronLayer 结构体代表一个神经元层。C_Neuron n[] 是神经网络层中神经元的数组。

为了存储神经元之间的权重，我们采用了一种面向对象的方法，而不是简单的二维数组。该方法基于 C_Weight 类，该类不仅存储连接权重本身，还存储优化参数——ADAM 算法中使用的一阶矩和二阶矩。数据结构是分层排列的：S_WeightsLayer 包含一个 S_WeightsLayerR 结构体数组，后者又包含 C_Weight 对象数组。这使得通过清晰的索引链可以轻松访问网络中的任何权重。

例如，要引用第 0 层的第一个神经元与下一层第二个神经元之间的连接权重，我们使用以下表示法：wL [0].nOnL [1].nOnR [2].w。这里，第一个索引表示一对相邻层，第二个索引表示左侧层中的一个神经元，第三个索引表示右侧层中的一个神经元。

//——————————————————————————————————————————————————————————————————————————————
// Neuron class
class C_Neuron
{
  public:
  C_Neuron ()
  {
    m = 0.0;
    v = 0.0;
  }
  double out;   // Neuron output after the activation function
  double delta; // Error delta
  double bias;  // Bias
  double m;     // First moment of displacement
  double v;     // Second moment of displacement
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Structure of the neuron layer
struct S_NeuronLayer
{
    C_Neuron n []; // neurons in the layer
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Weight class
class C_Weight
{
  public:
  C_Weight ()
  {
    w = 0.0;
    m = 0.0;
    v = 0.0;
  }

  double w; // Weight
  double m; // First moment
  double v; // Second moment
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Weight structure for neurons on the right
struct S_WeightsLayerR
{
    C_Weight nOnR [];
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Weight structure for neurons on the left
struct S_WeightsLayer
{
    S_WeightsLayerR nOnL [];
};
//——————————————————————————————————————————————————————————————————————————————

C_MLPa 多层感知机（MLP）类实现了一个神经网络的基本功能，包括使用 ADAM 优化算法进行前向传播和反向传播学习。让我们来看看它能做什么：

网络结构：
    • 网络由连续的层组成：输入层 -> 隐藏层 -> 输出层。
    • 每一层中的每个神经元都与下一层的所有神经元相连接（全连接网络）。
    主要功能：
      • Init — 用于根据给定配置创建网络的方法。
      • ImportWeights 和 ExportWeights — 加载和保存网络权重。
      • ForwProp — 前向传播：获取网络对输入数据的响应。
      • BackProp — 基于误差反向传播的网络训练方法。
      训练参数（ADAM 算法）：
        • alpha (0.001) — 网络的学习速度。
        • beta1 (0.9) 和 beta2 (0.999) — 帮助网络稳定学习的参数。
        • epsilon (1e-8) — 一个用于防止除零错误的小数。
        内部组件：
          • BackProp 存储有关每一层大小（layersSize）的信息。
          • 它包含所有神经元（nL）以及它们之间的权重（wL），
          • 并跟踪权重（wC）和层（nLC）的数量。
          • actFunc 使用选定的激活函数。

          本质上，这个类是神经网络的“大脑”，它可以接收输入数据，通过神经元和权重系统进行处理，产生结果，并从错误中学习，逐步提高其预测的准确性。

          //+-----------------------------------------------------------------------------------------+
//| Multilayer Perceptron (MLP) class                                                       |
//| Implements forward pass through a fully connected neural network and training using the |
//| backpropagation of error by ADAM optimization algorithm                                 |
//| Architecture: Lin -> L1 -> L2 -> ... Ln -> Lout                                         |
//+-----------------------------------------------------------------------------------------+
class C_MLPa
{
  public: //--------------------------------------------------------------------
  ~C_MLPa ()
  {
    delete actFunc;
  }
  C_MLPa ()
  {
    alpha   = 0.001;   // Training speed
    beta1   = 0.9;     // Decay ratio for the first moment
    beta2   = 0.999;   // Decay ratio for the second moment
    epsilon = 1e-8;    // Small constant for numerical stability
  }

  // Network initialization with the given configuration, Returns the total number of weights in the network, or 0 in case of an error
  int    Init          (int &layerConfig [], int actFuncType, int seed);
  bool   ImportWeights (double &weights []);  // Import weights
  bool   ExportWeights (double &weights []);  // Export weights

  // Forward pass through the network
  void   ForwProp (double &inLayer  [],  // input values
                   double &outLayer []); // output layer values

  // Error backpropagation with ADAM optimization algorithm
  void   BackProp (double &errors []);

  // Get the total number of weights in the network
  int    GetWcount () { return wC; }

  // ADAM optimization parameters 
  double alpha;          // Training speed
  double beta1;          // Decay ratio for the first moment
  double beta2;          // Decay ratio for the second moment
  double epsilon;        // Small constant for numerical stability

  int layersSize    [];  // Size of each layer (number of neurons)
  S_NeuronLayer  nL [];  // Layers of neurons, example of access: nLayers [].n [].a
  S_WeightsLayer wL [];  // Layers of weights between layers of neurons, example of access: wLayers [].nOnLeft [].nOnRight [].w

  private: //-------------------------------------------------------------------
  int            wC;       // Total number of weights in the network (including biases)
  int            nLC;      // Total number of neuron layers (including input and output ones)
  int            wLC;      // Total number of weight layers (between neuron layers)
  int            t;        // Iteration counter
  C_Base_ActFunc *actFunc; // Activation functions and their derivatives
};
//——————————————————————————————————————————————————————————————————————————————

          Init 方法通过设置每层的神经元数量、选择激活函数以及为神经元生成初始权重，来初始化多层感知机的结构。它会检查网络配置的有效性，并返回所需权重的总数，如果出错则返回 0。

          参数：

          • layerConfig [] — 包含每一网络层中神经元数量的数组。
          • actFuncType — 神经网络中要使用的激活函数类型（例如，sigmoid 等）。
          • seed — 一个用于初始化随机数生成器的种子，这使得在初始化权重时可以获得可复现的结果。

          操作逻辑：

          1. 该方法根据传入的 layerConfig 数组确定层数。
          2. 它确保层数至少为 2，并且每一层都包含正数个神经元。如果发生错误，它会显示一条消息并终止执行。
          3. 该方法将层的大小复制到 layersSize 数组，并初始化用于存储神经元和权重的数组。
          4. 它计算连接各层神经元所需的总权重数。
          5. 此外，它使用 Xavier 方法初始化权重，该方法理论上有助于避免梯度消失或梯度爆炸问题。
          6. 根据传入的激活函数类型，该方法创建一个相应的激活函数对象。
          7. 它将迭代计数器初始化为零，该计数器用于 ADAM 算法中。
          //+----------------------------------------------------------------------------+
//| Initialize the network                                                     |
//| layerConfig - array with the number of neurons in each layer               |
//| Returns the total number of weights needed, or 0 in case of an error       |
//+----------------------------------------------------------------------------+
int C_MLPa::Init (int &layerConfig [], int actFuncType, int seed)
{
  nLC = ArraySize (layerConfig);

  if (nLC < 2)
  {
    Print ("Network configuration error! Less than 2 layers!");
    return 0;
  }

  // Check configuration
  for (int i = 0; i < nLC; i++)
  {
    if (layerConfig [i] <= 0)
    {
      Print ("Network configuration error! Layer #" + string (i + 1) + " contains 0 neurons!");
      return 0;
    }
  }

  wLC = nLC - 1;
  ArrayCopy (layersSize, layerConfig, 0, 0, WHOLE_ARRAY);

  // Initialize neuron layers
  ArrayResize (nL, nLC);
  for (int i = 0; i < nLC; i++)
  {
    ArrayResize (nL [i].n, layersSize [i]);
  }

  // Initialize weight layers
  ArrayResize (wL, wLC);
  for (int w = 0; w < wLC; w++)
  {
    ArrayResize (wL [w].nOnL, layersSize [w]);
    for (int n = 0; n < layersSize [w]; n++)
    {
      ArrayResize (wL [w].nOnL [n].nOnR, layersSize [w + 1]);
    }
  }

  // Calculate the total number of weights
  wC = 0;
  for (int i = 0; i < nLC - 1; i++) wC += layersSize [i] * layersSize [i + 1] + layersSize [i + 1];

  // Initialize weights
  double weights [];  ArrayResize (weights, wC);

  srand (seed);
  
  //Xavier: U(-√(6/(n₁+n₂)), √(6/(n₁+n₂)))
  double n = sqrt (6.0 / (layersSize [0] + layersSize [nLC - 1]));
  for (int i = 0; i < wC; i++)
  {
    weights [i] = (2.0 * n) * (rand () / 32767.0) - n;
  }

  ImportWeights (weights);

  switch (actFuncType)
  {
    case eActACON:      actFunc = new C_ActACON      (); break;
    case eActAlgSigm:   actFunc = new C_ActAlgSigm   (); break;
    case eActBentIdent: actFunc = new C_ActBentIdent (); break;
    case eActRatSigm:   actFunc = new C_ActRatSigm   (); break;
    case eActSiLU:      actFunc = new C_ActSiLU      (); break;
    case eActSoftPlus:  actFunc = new C_ActSoftPlus  (); break;
    default:            actFunc = new C_ActTanh      (); break;
  }

  t = 0;
  return wC;
}
//——————————————————————————————————————————————————————————————————————————————

          让我们进一步来看两个方法——ImportWeights 和 ExportWeights。这些方法用于导入和导出多层感知机的权重和偏置。ImportWeights 负责将权重和偏置从“weights”数组导入到神经网络结构中。

          首先，该方法会检查传入的“weights”数组的大小是否与存储在 wC 变量中的权重数量相匹配。如果大小不匹配，该方法将返回 ‘false’ 以表示出错。

          wCNT 变量用于跟踪“weights”数组中的当前索引。
          遍历层和神经元：

          • 外层循环遍历每一层，从第二层（索引 1）开始，因为第一层是输入层，没有权重或偏置。
          • 内层循环遍历当前层中的每个神经元。
          • 对于每个神经元，其“bias”（偏置）值从“weights”数组中设置，并且 wCNT 计数器会递增。
          • 一个嵌套循环会遍历前一层中的所有神经元，用于设置连接当前层神经元和前层神经元的权重。

          ExportWeights — 该方法负责将权重和偏置从神经网络结构导出到“weights”数组。该方法的逻辑与 ImportWeights 方法类似。这两个方法都允许将权重和偏置相对于网络类保存在外部程序中，以便将来使用训练好的网络，同时也允许使用外部优化算法，例如种群算法。

          //+----------------------------------------------------------------------------+
//| Import network weights and biases                                          |
//+----------------------------------------------------------------------------+
bool C_MLPa::ImportWeights (double &weights [])
{
  if (ArraySize (weights) != wC) return false;

  int wCNT = 0;

  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      nL [ln].n [n].bias = weights [wCNT++];

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        wL [ln - 1].nOnL [w].nOnR [n].w = weights [wCNT++];
      }
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

//+----------------------------------------------------------------------------+
//| Export network weights and biases                                          |
//+----------------------------------------------------------------------------+
bool C_MLPa::ExportWeights (double &weights [])
{
  ArrayResize (weights, wC);

  int wCNT = 0;

  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      weights [wCNT++] = nL [ln].n [n].bias;

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        weights [wCNT++] = wL [ln - 1].nOnL [w].nOnR [n].w;
      }
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

          ForwProp 方法（前向传播）按顺序计算多层感知机从输入层到输出层的所有层的值。它接收输入值，通过隐藏层处理它们，并生成输出值。参数：

          • inLayer [] - 神经网络的输入值数组（在图 1 中以绿色显示）。
          • outLayer [] - 处理后输出层值将被设置到的数组（在图 1 中以黄色显示）。

          该方法通过将输入值从 inLayer 数组复制到相应的神经元，来初始化输入层神经元的激活值。

          处理隐藏层和输出层：

          • 外层循环遍历所有层，从第二层（索引 1）开始，因为第一层是输入层。
          • 内层循环遍历当前层的每个神经元。
          • 对于每个神经元，计算其加权输入的总和：
            • 首先，向该神经元添加一个偏置。
            • 嵌套循环遍历前一层的所有神经元，将前一神经元的输出值与相应权重的乘积加到 “val” 上。
          • 计算完总和后，对 “val” 应用激活函数，并将结果存储在当前层神经元的输出值中。
          处理完所有层后，该方法将最后一层（即输出层）的输出值复制到 outLayer 数组中。 
            //+----------------------------------------------------------------------------+
//| Direct network pass                                                        |
//| Calculate the values of all layers sequentially from input to output       |
//+----------------------------------------------------------------------------+
void C_MLPa::ForwProp (double &inLayer  [],  // input values
                       double &outLayer [])  // output layer values
{
  double val;

  // Set the input layer activation values
  for (int n = 0; n < layersSize [0]; n++)
  {
    nL [0].n [n].out = inLayer [n];
  }

  // Handle hidden and output layers
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      val = nL [ln].n [n].bias;

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        val += nL [ln - 1].n [w].out * wL [ln - 1].nOnL [w].nOnR [n].w;
      }

      nL [ln].n [n].out = actFunc.Activ (val); // Apply activation function
    }
  }

  // Set the output layer values
  for (int n = 0; n < layersSize [nLC - 1]; n++) outLayer [n] = nL [nLC - 1].n [n].out;
}
//——————————————————————————————————————————————————————————————————————————————

            BackProp 方法实现了多层感知机中的误差反向传播。它使用 ADAM 优化算法，从输出层到输入层更新所有层的权重和偏置。操作逻辑：

            “t” 变量递增，用于跟踪迭代次数，并在 ADAM 逻辑方程中使用。

            为所有层计算 delta（误差项）：

            • 外层循环以反向顺序遍历各层，从输出层开始，到输入层结束。
            • 内层循环遍历当前层的神经元。
            • 如果当前层是输出层，则 delta 的计算方式为误差（errors[nCurr]）与输出神经元激活函数导数的乘积。
            • 对于隐藏层，delta 的计算方式为下一层的 delta 与相应权重的乘积之和。
            • 然后，delta 会通过激活函数的导数进行调整，结果存储在 nL [ln].n [nCurr].delta 中。
            使用 ADAM 更新偏置：
            • 外层循环遍历所有层，从第二层开始。
            • 对于当前层的每个神经元，使用 beta1 和 beta2 参数更新偏置的动量 “m” 和 “v”。
            • 然后，调整 m_hat 和 v_hat 偏置矩。
            • 最后，使用调整后的矩来更新偏置。
            使用 ADAM 更新权重：
            • 外层循环遍历所有权重层。
            • 内层循环遍历当前层和下一层的神经元。
            • 对于每个权重，计算其梯度，然后用该梯度来更新 “m” 和 “v” 矩。
            • 在调整了 m_hat 和 v_hat 权重矩之后，使用调整后的矩来更新权重。
            //+----------------------------------------------------------------------------+
//| Backward network pass                                                      |
//| Update the weights and biases of all layers from output to input           |
//+----------------------------------------------------------------------------+
void C_MLPa::BackProp (double &errors [])
{
  t++;  // Increase the iteration counter

  double delta;     // current neuron delta
  double deltaNext; // delta of the neuron in the next layer connected to the current neuron
  double out;       // neuron value after applying the activation function
  double deriv;     // derivative
  double w;         // weight for connecting the current neuron to the neuron of the next layer

  // 1. Calculating deltas for all layers ----------------------------------------
  for (int ln = nLC - 1; ln > 0; ln--)                  // walk through layers in reverse order from output to input
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)        // iterate through the neurons of the current layer
    {
      if (ln == nLC - 1)
      {
        delta = errors [nCurr] * actFunc.Deriv (nL [ln].n [nCurr].out);
      }
      else
      {
        delta = 0.0;

        // Sum the products of the deltas of the next layer by the corresponding weights
        for (int nNext = 0; nNext < layersSize [ln + 1]; nNext++) // pass the neurons of the next layer in the usual order
        {
          deltaNext = nL [ln + 1].n [nNext].delta;
          w         = wL [ln].nOnL [nCurr].nOnR [nNext].w;
          delta    += deltaNext * w;
        }
      }

      // Delta considering the derivative of the sigmoid
      out   = nL [ln].n [nCurr].out;
      deriv = actFunc.Deriv (out);
      nL [ln].n [nCurr].delta = delta * deriv;
    }
  }

  // 2. Update biases using ADAM ------------------------------
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)
    {
      delta = nL [ln].n [nCurr].delta;

      // Update displacement moments
      nL [ln].n [nCurr].m = beta1 * nL [ln].n [nCurr].m + (1.0 - beta1) * delta;
      nL [ln].n [nCurr].v = beta2 * nL [ln].n [nCurr].v + (1.0 - beta2) * delta * delta;

      // Adjust displacement moments
      double m_hat = nL [ln].n [nCurr].m / (1.0 - pow (beta1, t));
      double v_hat = nL [ln].n [nCurr].v / (1.0 - pow (beta2, t));

      // Update bias
      nL [ln].n [nCurr].bias += alpha * m_hat / (sqrt (v_hat) + epsilon);
    }
  }

  // 3. Update weights using ADAM ---------------------------------
  for (int lw = 0; lw < wLC; lw++)
  {
    for (int nCurr = 0; nCurr < layersSize [lw]; nCurr++)
    {
      for (int nNext = 0; nNext < layersSize [lw + 1]; nNext++)
      {
        deltaNext = nL [lw + 1].n [nNext].delta;
        out       = nL [lw].n [nCurr].out;
        double gradient = deltaNext * out;

        // Update moments for weights
        wL [lw].nOnL [nCurr].nOnR [nNext].m = beta1 * wL [lw].nOnL [nCurr].nOnR [nNext].m + (1.0 - beta1) * gradient;
        wL [lw].nOnL [nCurr].nOnR [nNext].v = beta2 * wL [lw].nOnL [nCurr].nOnR [nNext].v + (1.0 - beta2) * gradient * gradient;

        // Adjust weight moments
        double m_hat = wL [lw].nOnL [nCurr].nOnR [nNext].m / (1.0 - pow (beta1, t));
        double v_hat = wL [lw].nOnL [nCurr].nOnR [nNext].v / (1.0 - pow (beta2, t));

        // Update weight
        wL [lw].nOnL [nCurr].nOnR [nNext].w += alpha * m_hat / (sqrt (v_hat) + epsilon);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————


            用于渲染激活函数的测试台代码

            该测试台旨在测试神经网络中使用的各种激活函数是否正确运行，并将其以图形形式显示。生成的图像稍后将在文章中用于直观地评估它们的外观。代码相当简单，无需过多描述。

            #include <Graphics\Graphic.mqh>
#include <Math\AOs\NeuroNets\MLPa.mqh>

#define SIZE_X 750
#define SIZE_Y 200

//--- input parameters
input E_Act ACT = eActTanh;
input int   CNT = 10000;

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  ObjectDelete (ChartID (), "Test");
  double activ [];
  double deriv [];

  //----------------------------------------------------------------------------
  C_Base_ActFunc *act;
  switch (ACT)
  {
    default:            act = new C_ActTanh      (); break;
    case eActAlgSigm:   act = new C_ActAlgSigm   (); break;
    case eActRatSigm:   act = new C_ActRatSigm   (); break;
    
    case eActSoftPlus:  act = new C_ActSoftPlus  (); break;
    case eActBentIdent: act = new C_ActBentIdent (); break;
    case eActSiLU:      act = new C_ActSiLU      (); break;
    
    case eActACON:      act = new C_ActACON      (); break;
    case eActSnake:     act = new C_ActSnake     (); break;
    case eActSERF:      act = new C_ActSERF      (); break;
  }
  
  //----------------------------------------------------------------------------
  ActFuncTest (act, activ, deriv, CNT, -10, 10);
  
  //----------------------------------------------------------------------------
  CGraphic gr_test;
  gr_test.Create (0, "Test", 0, 0, 20, SIZE_X, SIZE_Y + 20);
  gr_test.YAxis ().Name (act.GetFuncName () + ": Value");
  gr_test.YAxis ().NameSize (13);
  gr_test.HistorySymbolSize (10);
  gr_test.CurveAdd (activ, ColorToARGB (clrRed,  255), CURVE_LINES, "activ");
  gr_test.CurveAdd (deriv, ColorToARGB (clrBlue, 255), CURVE_LINES, "deriv");
  gr_test.CurvePlotAll ();
  gr_test.Redraw (true);
  gr_test.Update ();
  
  //----------------------------------------------------------------------------
  delete act;
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void ActFuncTest (C_Base_ActFunc &act, double &arrayAct [], double &arrayDer [], int testCount, double min, double max)
{
  Print (act.GetFuncName (), " [", min, "; ", max, "]");
  Print (act.Activ (min), " ", act.Activ (0), " ", act.Activ (max));
  Print (act.Deriv (min), " ", act.Deriv (0), " ", act.Deriv (max));

  ArrayResize (arrayAct, testCount);
  ArrayResize (arrayDer, testCount);
  double x    = 0.0;
  double step = (max - min) / testCount;
  
  for (int i = 0; i < testCount; i++)
  {
    x = min + step * i;

    arrayAct [i] = act.Activ (x);
    arrayDer [i] = act.Deriv (x);
  }
}
//——————————————————————————————————————————————————————————————————————————————


            激活函数类的代码

            在解决各种神经网络问题时，会使用许多不同的神经元激活函数。我尝试选择的函数既包括众所周知的双曲正切函数，也包括像 Snake 激活函数这样不太为人所知的函数，同时排除了在外观和特性上非常相似的函数。它们可以大致分为三组：

            1. Sigmoid 函数，
            2. 非线性开关，
            3. 周期性函数。

            为神经元激活函数实现 C_Base_ActFunc 基类。它包含两个虚函数：用于计算激活值的 Activ 和用于计算导数的 Deriv。GetFuncName() 方法返回存储在受保护成员 funcName 中的激活函数名称。该类旨在被继承，以创建激活函数的具体实现。通过创建激活函数对象，我们可以通过避免多次使用 “if” 和 “switch” 来加速计算。

            //——————————————————————————————————————————————————————————————————————————————
// Base class of the neuron activation function
class C_Base_ActFunc
{
  public:
  virtual double Activ (double inp) = 0; // Virtual activation function
  virtual double Deriv (double inp) = 0; // Virtual derivative function
  string         GetFuncName () {return funcName;}
  protected:
  string funcName;
};
//——————————————————————————————————————————————————————————————————————————————

            C_ActTanh 类实现了双曲正切激活函数及其导数，并继承自 C_Base_ActFunc 基类。在类的构造函数中，激活函数的名称在 funcName 变量中被设置为 ActTanh。激活方法：

            • Activ (double x) 使用公式 f(x) = 2 / (1 + exp ( − 2 ⋅ (x)) − 1 计算双曲正切激活函数的值。该公式将输入 “x” 转换到 -1 到 1 的范围内。
            导数方法：
            • Deriv(double x) 计算激活函数的导数。双曲正切的导数表示为：f′(x) = 1 − (f (x)) ^ 2，其中 f(x) 是为当前 “x” 计算出的激活函数值。导数显示了函数相对于输入值的变化速度。

            //——————————————————————————————————————————————————————————————————————————————
// Hyperbolic tangent
class C_ActTanh : public C_Base_ActFunc
{
  public:
  C_ActTanh () {funcName = "ActTanh";}

  double Activ (double x)
  {
    return 2.0 / (1.0 + exp (-2 * (x))) - 1.0;
  }

  double Deriv (double x)
  {
    //1 - (f(x))^2
    double fx = Activ (x);
    return 1.0 - fx * fx;
  }
};
//——————————————————————————————————————————————————————————————————————————————

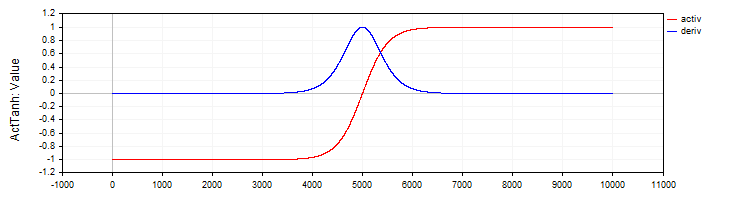
            图例 2. 双曲正切及其导数

            C_ActAlgSigm 类与 C_ActTanh 类类似，它将代数 Sigmoid 实现为一种激活函数，并提供了计算其激活值和导数的方法。

            //——————————————————————————————————————————————————————————————————————————————
// Algebraic sigmoid
class C_ActAlgSigm : public C_Base_ActFunc
{
  public:
  C_ActAlgSigm () {funcName = "ActAlgSigm";}

  double Activ (double x)
  {
    return x / sqrt (1.0 + x * x);
  }

  double Deriv (double x)
  {
    // (1 / sqrt (1 + x * x))^3
    double d = 1.0 / sqrt (1.0 + x * x);
    return d * d * d;
  }
};
//——————————————————————————————————————————————————————————————————————————————

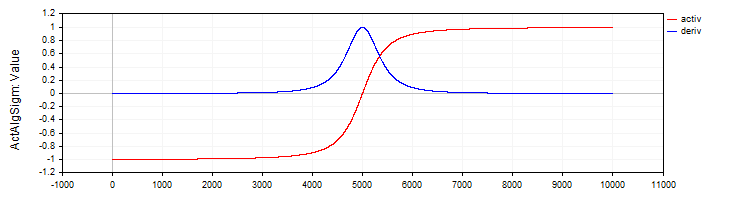
            图例 3. 代数 Sigmoid 及其导数

            C_ActRatSigm 类实现了一个有理 Sigmoid，其中包含激活函数和导数计算方法。

            //——————————————————————————————————————————————————————————————————————————————
// Rational sigmoid
class C_ActRatSigm : public C_Base_ActFunc
{
  public:
  C_ActRatSigm () {funcName = "ActRatSigm";}

  double Activ (double x)
  {
    return x / (1.0 + fabs (x));
  }

  double Deriv (double x)
  {
    //1 / (1 + abs (x))^2
    double d = 1.0 + fabs (x);
    return 1.0 / (d * d);
  }
};
//——————————————————————————————————————————————————————————————————————————————

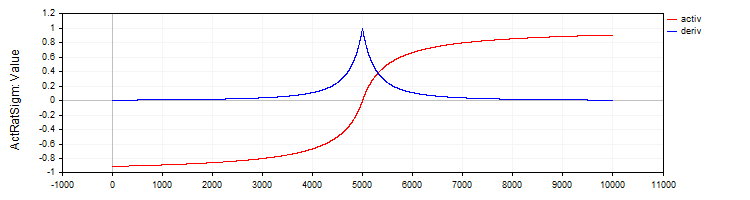
            图例 4. 有理 Sigmoid 及其导数

            C_ActSoftPlus 类实现了 Softplus 激活函数及其导数。

            //——————————————————————————————————————————————————————————————————————————————
// Softplus
class C_ActSoftPlus : public C_Base_ActFunc
{
  public:
  C_ActSoftPlus () {funcName = "ActSoftPlus";}

  double Activ (double x)
  {
    return log (1.0 + exp (x));
  }

  double Deriv (double x)
  {
    return 1.0 / (1.0 + exp (-x));
  }
};
//——————————————————————————————————————————————————————————————————————————————

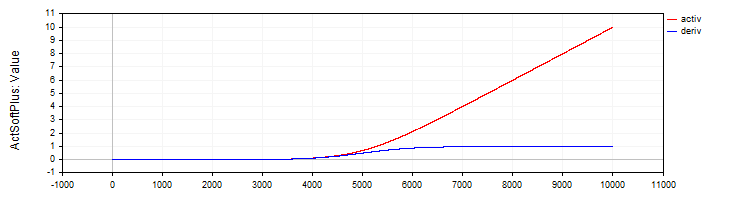
            图例 5. SoftPlus 函数及其导数

            C_ActBentIdent 类实现了 Bent Identity 激活函数及其导数。

            //——————————————————————————————————————————————————————————————————————————————
// Bent Identity
class C_ActBentIdent : public C_Base_ActFunc
{
  public:
  C_ActBentIdent () {funcName = "ActBentIdent";}

  double Activ (double x)
  {
    return (sqrt (x * x + 1.0) - 1.0) / 2.0 + x;
  }

  double Deriv (double x)
  {
    return x / (2.0 * sqrt (x * x + 1.0)) + 1.0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

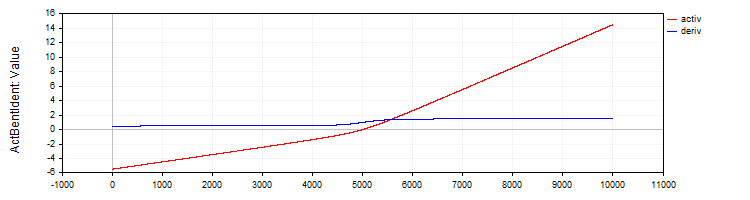
            图例 6. Bent Identity 函数及其导数

            C_ActSiLU 类提供了 SiLU 激活函数及其导数的实现。

            //——————————————————————————————————————————————————————————————————————————————
// SiLU (Swish)
class C_ActSiLU : public C_Base_ActFunc
{
  public:
  C_ActSiLU () {funcName = "ActSiLU";}

  double Activ (double x)
  {
    return x / (1.0 + exp (-x));
  }

  double Deriv (double x)
  {
    if (x == 0.0) return 0.5;

    // f(x) + (f(x)*(1 - f(x)))/ x
    double fx = Activ (x);
    return fx + (fx * (1.0 - fx)) / x;
  }
};
//——————————————————————————————————————————————————————————————————————————————

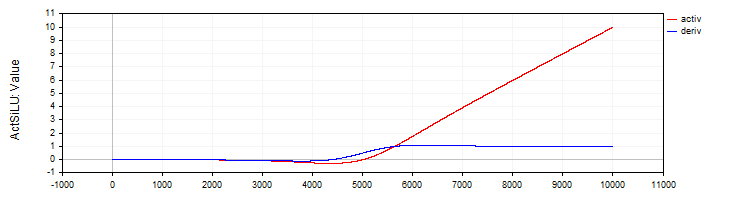
            图例 7. SiLU 函数及其导数

            C_ActACON 类实现了 ACON 激活函数及其导数。 

            //——————————————————————————————————————————————————————————————————————————————
// ACON
class C_ActACON : public C_Base_ActFunc
{
  public:
  C_ActACON () {funcName = "ActACON";}

  double Activ (double x)
  {
    return (x * cos (x) + sin (x)) / (1.0 + fabs (x));
  }

  double Deriv (double x)
  {
    if (x == 0.0) return 2.0;

    //[2 * cos(x) - x * sin(x)] / [|x| + 1] - x * (sin(x) + x * cos(x)) / [|x| * ((|x| + 1)²)]
    double sinX   = sin  (x);
    double cosX   = cos  (x);
    double fabsX  = fabs (x);
    double fabsXp = fabsX + 1.0;

    // Divide the equation into two parts
    double part1 = (2.0 * cosX - x * sinX) / fabsXp;
    double part2 = -x * (sinX + x * cosX) / (fabsX * fabsXp * fabsXp);
    return part1 + part2;
  }
};
//——————————————————————————————————————————————————————————————————————————————

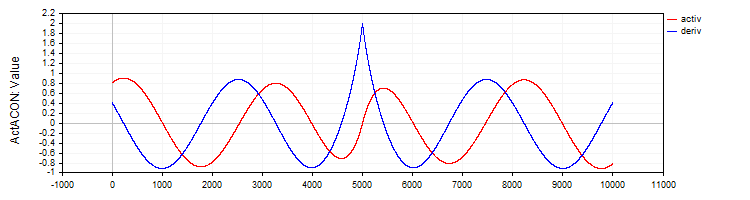
            图例 8. ACON 函数及其导数

            C_ActSERF 类实现了 SERF 激活函数及其导数。 

            //——————————————————————————————————————————————————————————————————————————————
// SERF (sigmoid-weighted exponential straightening function)
class C_ActSERF : public C_Base_ActFunc
{
  public:
  C_ActSERF ()
  {
    alpha    = 0.5;
    funcName = "ActSERF";
  }

  double Activ (double x)
  {
    double sigmoid = 1.0 / (1.0 + exp (-alpha * x));

    if (x >= 0) return sigmoid * x;
    else return sigmoid * (exp (x) - 1.0);
  }

  double Deriv (double x)
  {
    double sigmoid = 1.0 / (1.0 + exp (-alpha * x));
    double sigmoidDeriv = alpha * sigmoid * (1.0 - sigmoid);
    double e = exp (x);
    if (x >= 0) return sigmoid + x * sigmoidDeriv;
    else return sigmoid * e + (e - 1.0) * sigmoidDeriv;
  }

  private:
  double alpha;
};
//——————————————————————————————————————————————————————————————————————————————

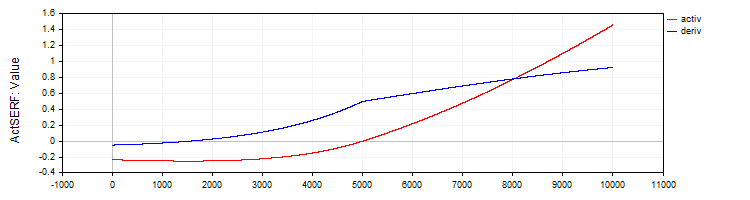
            图例 9. SERF 函数及其导数

            C_ActSNAKE 类实现了 SNAKE 激活函数及其导数。 

            //——————————————————————————————————————————————————————————————————————————————
// Snake (periodic activation function)
class C_ActSnake : public C_Base_ActFunc
{
  public:
  C_ActSnake ()
  {
    frequency = 1;
    funcName  = "ActSnake";
  }

  double Activ (double x)
  {
    double sinx = sin (frequency * x);
    return x + sinx * sinx;
  }

  double Deriv (double x)
  {
    double fx = frequency * x;
    return 1.0 + 2.0 * sin (fx) * cos (fx) * frequency;
  }

  private:
  double frequency;
};
//——————————————————————————————————————————————————————————————————————————————

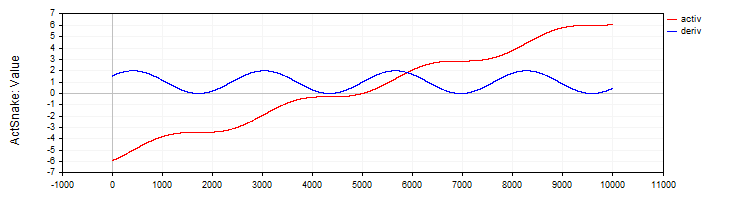
            图例 10. SNAKE 函数及其导数


            测试激活函数

            现在，是时候来看看 MLP 网络如何使用不同的激活函数进行训练了。对于优化算法而言，激活函数的复杂性可以在 1-1-1 的 MLP 配置上，通过仅使用一个训练样本（一个输入值和一个目标值）得到清晰的展示。

            乍一看，这可能并不明显。为什么这样一个简单的任务会引人关注？这里有一个重要的方法论要点：使用单个数据点可以让我们分离并检验激活函数本身的复杂性及其对优化的影响。当我们处理大型数据集时，许多因素会影响训练：数据的分布、样本之间的相互依赖关系，以及它们的影响在通过激活函数时如何体现。通过只使用一个点，我们消除了所有这些外部因素，可以专注于优化算法在处理特定激活函数时的难度。

            关键在于，一个只通过插值函数单个点的神经网络，可以有无穷多种权重选项。这可能看起来不可思议，但它源于方程 in * w + b = out，其中 in 是网络输入，w 是权重，b 是偏置，而 out 是 1-1 配置的网络输出。

            对于 1-1 配置，这没有问题，但当增加另一层——即 1-1-1 配置时，问题就出现了。在这种情况下，即使是最简单的问题对优化算法来说也变得非同小可，因为解的搜索空间变得显著复杂：现在必须通过带有其激活函数的中间层来找到正确的权重组合。正是这种复杂性，使我们能够评估不同的优化算法在使用不同激活函数时，能够多有效地进行权重调整。

            以下是经典实现的 ADAM 算法和种群 ADAMm 算法的结果表。两种算法都执行了 10,000 次迭代。对于基于种群的算法，考虑了种群的存在，但神经网络计算的总次数保持不变。打印输出显示了伪随机数生成器的种子（用于复现有问题的训练过程）、产生最佳结果的迭代次数，以及当前 epoch（以 1000 为倍数）的结果。

            权重使用 Xavier 方法为 ADAM 进行初始化，并为 ADAMm 使用 [-10; 10] 范围内的随机数。使用不同的种子进行了多次测试，并选择了最差的结果。权重选择过程在达到最大迭代次数或误差降至 0.000001 以下时结束。

            Sigmoid 激活函数的结果表：

            Tanh     AlgSigm   RatSigm
            MLP 配置：1|1|1，权重：4，激活函数：eActTanh，种子：4
            -----集成 ADAM-----
            0: 0.2415125490594974, 0: 0.24151254905949734
            0: 0.2415125490594974, 1000: 0.24987227299268625
            0: 0.2415125490594974, 2000: 0.24999778562849811
            0: 0.2415125490594974, 3000: 0.24999995996010888
            0: 0.2415125490594974, 4000: 0.2499999992693791
            0: 0.2415125490594974, 5000: 0.24999999998663514
            0: 0.2415125490594974, 6000: 0.2499999999997553
            0: 0.2415125490594974, 7000: 0.24999999999999556
            0: 0.2415125490594974, 8000: 0.25
            0: 0.2415125490594974, 9000: 0.25
            最佳结果迭代：0，误差：0.241513
            -----基于种群的 ADAMm-----
            0: 0.2499999999999871
            最佳结果迭代：883，误差：0.000001
            		 MLP 配置：1|1|1，权重：4，激活函数：eActAlgSigm，种子：4
            -----集成 ADAM-----
            0: 0.1878131682539310, 0: 0.18781316825393096
            0: 0.1878131682539310, 1000: 0.22880505258129305
            0: 0.1878131682539310, 2000: 0.2395439537933131
            0: 0.1878131682539310, 3000: 0.24376284285887292
            0: 0.1878131682539310, 4000: 0.24584964230029535
            0: 0.1878131682539310, 5000: 0.2470364071634453
            0: 0.1878131682539310, 6000: 0.24777681648987268
            0: 0.1878131682539310, 7000: 0.2482702131676117
            0: 0.1878131682539310, 8000: 0.24861563983949608
            0: 0.1878131682539310, 9000: 0.2488669473265396
            最佳结果迭代：0，误差：0.187813
            -----基于种群的 ADAMm-----
            0: 0.2481251241755712
            1000: 0.0000009070157679
            最佳结果迭代：1000，误差：0.000001
            		 MLP 配置：1|1|1，权重：4，激活函数：eActRatSigm，种子：4
            -----集成 ADAM-----
            0: 0.0354471509280691, 0: 0.03544715092806905
            0: 0.0354471509280691, 1000: 0.10064226929576263
            0: 0.0354471509280691, 2000: 0.13866170841306655
            0: 0.0354471509280691, 3000: 0.16067944018111643
            0: 0.0354471509280691, 4000: 0.17502946224977484
            0: 0.0354471509280691, 5000: 0.18520767592761297
            0: 0.0354471509280691, 6000: 0.19285431843628092
            0: 0.0354471509280691, 7000: 0.1988366186290051
            0: 0.0354471509280691, 8000: 0.20365853142896836
            0: 0.0354471509280691, 9000: 0.20763502064394074
            最佳结果迭代：0，误差：0.035447
            -----基于种群的 ADAMm-----
            0: 0.1928944265733889
            最佳结果迭代：688，误差：0.000000

            SiLU 类型激活函数的结果表：

              SoftPlus   BentIdent   SiLU
            MLP 配置：1|1|1，权重：4，激活函数：eActSoftPlus，种子：2
            -----集成 ADAM-----
            0: 0.5380138004155748, 0: 0.5380138004155747
            0: 0.5380138004155748, 1000: 131.77685264891647
            0: 0.5380138004155748, 2000: 1996.1250363225556
            0: 0.5380138004155748, 3000: 8050.259717531171
            0: 0.5380138004155748, 4000: 20321.169969814575
            0: 0.5380138004155748, 5000: 40601.21872791767
            0: 0.5380138004155748, 6000: 70655.44591598355
            0: 0.5380138004155748, 7000: 112311.81150857621
            0: 0.5380138004155748, 8000: 167489.98562842538
            0: 0.5380138004155748, 9000: 238207.27978678182
            最佳结果迭代：0，误差：0.538014
            -----基于种群的 ADAMm-----
            0: 18.4801637203493884
            778: 0.0000022070092175
            最佳结果迭代：1176，误差：0.000001
            		 MLP 配置：1|1|1，权重：4，激活函数：eActBentIdent，种子：4
            -----集成 ADAM-----
            0: 15.1221330593320857, 0: 15.122133059332086
            0: 15.1221330593320857, 1000: 185.646717568436
            0: 15.1221330593320857, 2000: 1003.1026112225994
            0: 15.1221330593320857, 3000: 2955.8393027057205
            0: 15.1221330593320857, 4000: 6429.902382962495
            0: 15.1221330593320857, 5000: 11774.781156010686
            0: 15.1221330593320857, 6000: 19342.379583340015
            0: 15.1221330593320857, 7000: 29501.355075464813
            0: 15.1221330593320857, 8000: 42640.534930000824
            0: 15.1221330593320857, 9000: 59168.850722337185
            最佳结果迭代：0，误差：15.122133
            -----基于种群的 ADAMm-----
            0: 7818.0964949082390376
            最佳结果迭代：15：0.000001
            		 MLP 配置：1|1|1，权重：4，激活函数：eActSiLU，种子：2
            -----集成 ADAM-----
            0: 0.0021199944516222, 0: 0.0021199944516222444
            0: 0.0021199944516222, 1000: 4.924850697388685
            0: 0.0021199944516222, 2000: 14.827133542234415
            0: 0.0021199944516222, 3000: 28.814259008218087
            0: 0.0021199944516222, 4000: 45.93517121925276
            0: 0.0021199944516222, 5000: 65.82077308420028
            0: 0.0021199944516222, 6000: 88.26782602934948
            0: 0.0021199944516222, 7000: 113.15535264604428
            0: 0.0021199944516222, 8000: 140.41067538093935
            0: 0.0021199944516222, 9000: 169.9878269747845
            最佳结果迭代：0，误差：0.002120
            -----基于种群的 ADAMm-----
            0: 17.2288020548757288
            1000: 0.0000030959186317
            最佳结果迭代：1150，误差：0.000001

            周期性激活函数的结果表：

            ACON     SERF   Snake
            MLP 配置：1|1|1，权重：4，激活函数：eActACON，种子：3
            -----集成 ADAM-----
            0: 0.8183728267492676, 0: 0.8183728267492675
            160: 0.5853150801288914, 1000: 1.2003151947973498
            2000: 0.0177702331540612, 2000: 0.017770233154061187
            3000: 0.0055801976952827, 3000: 0.005580197695282676
            4000: 0.0023096724537356, 4000: 0.002309672453735598
            5000: 0.0010238849157595, 5000: 0.0010238849157594616
            6000: 0.0004581612824611, 6000: 0.0004581612824611273
            7000: 0.0002019092359805, 7000: 0.00020190923598049711
            8000: 0.0000867118074097, 8000: 0.00008671180740972474
            9000: 0.0000361764073840, 9000: 0.00003617640738397845
            最佳结果迭代：9999，误差：0.000015
            -----基于种群的 ADAMm-----
            0: 1.3784017183806672
            最佳结果迭代：481，误差：0.000000
            		 MLP 配置：1|1|1，权重：4，激活函数：eActSERF，种子：4
            -----集成 ADAM-----
            0: 0.2415125490594974, 0: 0.24151254905949734
            0: 0.2415125490594974, 1000: 0.24987227299268625
            0: 0.2415125490594974, 2000: 0.24999778562849811
            0: 0.2415125490594974, 3000: 0.24999995996010888
            0: 0.2415125490594974, 4000: 0.2499999992693791
            0: 0.2415125490594974, 5000: 0.24999999998663514
            0: 0.2415125490594974, 6000: 0.2499999999997553
            0: 0.2415125490594974, 7000: 0.24999999999999556
            0: 0.2415125490594974, 8000: 0.25
            0: 0.2415125490594974, 9000: 0.25
            最佳结果迭代：0，误差：0.241513
            -----基于种群的 ADAMm-----
            0: 0.2499999999999871
            最佳结果迭代：883，误差：0.000001
            		 MLP 配置：1|1|1，权重：4，激活函数：eActSnake，种子：4
            -----集成 ADAM-----
            0: 0.2415125490594974, 0: 0.24151254905949734
            0: 0.2415125490594974, 1000: 0.24987227299268625
            0: 0.2415125490594974, 2000: 0.24999778562849811
            0: 0.2415125490594974, 3000: 0.24999995996010888
            0: 0.2415125490594974, 4000: 0.2499999992693791
            0: 0.2415125490594974, 5000: 0.24999999998663514
            0: 0.2415125490594974, 6000: 0.2499999999997553
            0: 0.2415125490594974, 7000: 0.24999999999999556
            0: 0.2415125490594974, 8000: 0.25
            0: 0.2415125490594974, 9000: 0.25
            最佳结果迭代：0，误差：0.241513
            -----基于种群的 ADAMm-----
            0: 0.2499999999999871
            最佳结果迭代：883，误差：0.000001

            我们现在可以就经典梯度 ADAM 和种群 ADAMm 所用激活函数的复杂性，得出一些初步结论。尽管常规 ADAM 拥有关于激活函数梯度的直接信息，也就是说，它明确知道最陡下降的方向，但它却未能处理好这样一个看似简单的任务。ACON 被证明是 ADAM 最简单的函数。正是在这种类型的函数上，它才能够稳定地将误差最小化。但像 SiLU 这样的函数对它来说却是个问题：误差不仅没有下降，反而迅速增长。很明显，由于 ADAM 没有权重和偏置的边界条件，它选择了错误的方向并增大了权重值。权重自由地向两边发散，不受约束，简直被激活函数导数这股“定向风”给吹跑了。

            如果在层中使用更多的神经元，问题只会变得更糟，因为每个神经元的输入是前一层神经元的输出与相应权重乘积的总和。因此，这个总和可能会变得非常大，以至于无法正确计算指数函数。

            正如我们所见，没有任何一种激活函数对种群 ADAMm 构成问题。它在所有这些函数上都能稳定收敛，并且只在少数几种函数上，迭代次数略微超过了 1000。


            优化激活函数类、MLP 和 ADAM

            为了纠正神经网络中权重发散的问题，我们将对激活函数类进行修改。这将使我们能够追踪相应函数的边界，防止在输入神经元时累积过大的总和，同时也会限制权重和偏置本身的值。

            我将在基类中添加 GetBoundUp 和 GetBoundLo 方法，它们提供对相应激活函数边界的访问，允许其他类或函数获取关于允许值范围的信息。

            以下是基类和双曲正切类的代码，其中进行了一些修改（其余代码保持不变）。其他激活函数的其余类也以类似方式实现，并带有它们自己相应的边界。

            //——————————————————————————————————————————————————————————————————————————————
// Base class of the neuron activation function
class C_Base_ActFunc
{
  public:
  double         GetBoundUp  () { return boundUp;}
  double         GetBoundLo  () { return boundLo;}
  protected:
  double boundUp;  // upper bound of the input range
  double boundLo;  // lower bound of the input range
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Hyperbolic tangent
class C_ActTanh : public C_Base_ActFunc
{
  public:
  C_ActTanh ()
  {
    boundUp  =  6.0;
    boundLo  = -6.0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

            现在，在将总和值输入神经元激活函数之前，将对其添加验证到 MLP 前向传播方法的代码中，以确保它们不会超出指定的边界。将总和增加到超出指定限制是没有意义的。此外，当为具有大量神经元的网络配置计算总和时，这将允许提前停止，从而可以显著加快计算速度。

            上限检查：此代码片段检查总和的当前值是否大于设定的上限。如果该值大于此边界，则将其设置为等于此边界，并终止循环执行。下限的检查方式类似。

            //+----------------------------------------------------------------------------+
//| Direct network pass                                                        |
//| Calculate the values of all layers sequentially from input to output       |
//+----------------------------------------------------------------------------+
void C_MLPa::ForwProp (double &inLayer  [],  // input values
                       double &outLayer [])  // output layer values
{
  double val;

  // Set the input layer activation values
  for (int n = 0; n < layersSize [0]; n++)
  {
    nL [0].n [n].out = inLayer [n];
  }

  // Handle hidden and output layers
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      val = nL [ln].n [n].bias;

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        val += nL [ln - 1].n [w].out * wL [ln - 1].nOnL [w].nOnR [n].w;

        if (val >  actFunc.GetBoundUp ())
        {
          val =  actFunc.GetBoundUp ();
          break;
        }
        if (val < actFunc.GetBoundLo ())
        {
          val = actFunc.GetBoundLo ();
          break;
        }
      }

      nL [ln].n [n].out = actFunc.Activ (val); // Apply activation function
    }
  }

  // Set the output layer values
  for (int n = 0; n < layersSize [nLC - 1]; n++) outLayer [n] = nL [nLC - 1].n [n].out;
}
//——————————————————————————————————————————————————————————————————————————————

            现在，让我们将边界验证的代码添加到反向传播方法中。这些附加项实现了将偏置和权重值从给定边界反射到反向边界的逻辑。这对于确保值不会超出可接受范围是必要的，从而防止权重和偏置不受控制地增加或减少。

            简单地在边界处截断值将导致训练停滞，因为权重会直接撞到边界，从而无法再改变权重。正是为了防止这种情况，才实现了反射，而不是值截断。这在调整权重和偏置时提供了一种“重振”或某种“抖动”效果。 

            //+----------------------------------------------------------------------------+
//| Backward network pass                                                      |
//| Update the weights and biases of all layers from output to input           |
//+----------------------------------------------------------------------------+
void C_MLPa::BackProp (double &errors [])
{
  t++;  // Increase the iteration counter

  double delta;     // current neuron delta
  double deltaNext; // delta of the neuron in the next layer connected to the current neuron
  double out;       // neuron value after applying the activation function
  double deriv;     // derivative
  double w;         // weight for connecting the current neuron to the neuron of the next layer
  double bias;      // bias

  // 1. Calculating deltas for all layers ----------------------------------------
  for (int ln = nLC - 1; ln > 0; ln--)                  // walk through layers in reverse order from output to input
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)        // iterate through the neurons of the current layer
    {
      if (ln == nLC - 1)
      {
        delta = errors [nCurr] * actFunc.Deriv (nL [ln].n [nCurr].out);
      }
      else
      {
        delta = 0.0;

        // Sum the products of the deltas of the next layer by the corresponding weights
        for (int nNext = 0; nNext < layersSize [ln + 1]; nNext++) // pass the neurons of the next layer in the usual order
        {
          deltaNext = nL [ln + 1].n [nNext].delta;
          w         = wL [ln].nOnL [nCurr].nOnR [nNext].w;
          delta    += deltaNext * w;
        }
      }

      // Delta considering the derivative of the sigmoid
      out   = nL [ln].n [nCurr].out;
      deriv = actFunc.Deriv (out);
      nL [ln].n [nCurr].delta = delta * deriv;
    }
  }

  // 2. Update biases using ADAM ------------------------------
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)
    {
      delta = nL [ln].n [nCurr].delta;

      // Update displacement moments
      nL [ln].n [nCurr].m = beta1 * nL [ln].n [nCurr].m + (1.0 - beta1) * delta;
      nL [ln].n [nCurr].v = beta2 * nL [ln].n [nCurr].v + (1.0 - beta2) * delta * delta;

      // Adjust displacement moments
      double m_hat = nL [ln].n [nCurr].m / (1.0 - pow (beta1, t));
      double v_hat = nL [ln].n [nCurr].v / (1.0 - pow (beta2, t));

      // Update bias
      nL [ln].n [nCurr].bias += alpha * m_hat / (sqrt (v_hat) + epsilon);
      bias = nL [ln].n [nCurr].bias;

      if (bias < actFunc.GetBoundLo ())
      {
        nL [ln].n [nCurr].bias = actFunc.GetBoundUp () - (actFunc.GetBoundLo () - bias);  // reflect from the bottom border 
      }
      else
        if (bias > actFunc.GetBoundUp ())
        {
          nL [ln].n [nCurr].bias = actFunc.GetBoundLo () + (bias - actFunc.GetBoundUp ());  // reflect from the upper border
        }
    }
  }

  // 3. Update weights using ADAM ---------------------------------
  for (int lw = 0; lw < wLC; lw++)
  {
    for (int nCurr = 0; nCurr < layersSize [lw]; nCurr++)
    {
      for (int nNext = 0; nNext < layersSize [lw + 1]; nNext++)
      {
        deltaNext = nL [lw + 1].n [nNext].delta;
        out       = nL [lw].n [nCurr].out;
        double gradient = deltaNext * out;

        // Update moments for weights
        wL [lw].nOnL [nCurr].nOnR [nNext].m = beta1 * wL [lw].nOnL [nCurr].nOnR [nNext].m + (1.0 - beta1) * gradient;
        wL [lw].nOnL [nCurr].nOnR [nNext].v = beta2 * wL [lw].nOnL [nCurr].nOnR [nNext].v + (1.0 - beta2) * gradient * gradient;

        // Adjust weight moments
        double m_hat = wL [lw].nOnL [nCurr].nOnR [nNext].m / (1.0 - pow (beta1, t));
        double v_hat = wL [lw].nOnL [nCurr].nOnR [nNext].v / (1.0 - pow (beta2, t));

        // Update weight
        wL [lw].nOnL [nCurr].nOnR [nNext].w += alpha * m_hat / (sqrt (v_hat) + epsilon);
        w = wL [lw].nOnL [nCurr].nOnR [nNext].w;

        if (w < actFunc.GetBoundLo ())
        {
          wL [lw].nOnL [nCurr].nOnR [nNext].w = actFunc.GetBoundUp () - (actFunc.GetBoundLo () - w);  // reflect from the lower border
        }
        else
          if (w > actFunc.GetBoundUp ())
          {
            wL [lw].nOnL [nCurr].nOnR [nNext].w = actFunc.GetBoundLo () + (w - actFunc.GetBoundUp ());  // reflect from the upper border
          }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

            现在让我们重复上述相同的测试，并查看所获得的结果。现在不再有权重爆炸，训练过程中也不会出现雪崩式的误差增长。

            Sigmoid 激活函数的结果表：

            Tanh     AlgSigm   RatSigm
            MLP 配置：1|1|1，权重：4，激活函数：eActTanh，种子：2
            -----集成 ADAM-----
            0: 0.0169277701441132, 0: 0.016927770144113192
            0: 0.0169277701441132, 1000: 0.24726166610109795
            0: 0.0169277701441132, 2000: 0.24996248252671016
            0: 0.0169277701441132, 3000: 0.2499877118017991
            0: 0.0169277701441132, 4000: 0.2260068617570163
            0: 0.0169277701441132, 5000: 2.2499589217599363
            0: 0.0169277701441132, 6000: 2.2499631351033904
            0: 0.0169277701441132, 7000: 2.248459789732414
            0: 0.0169277701441132, 8000: 2.146138260175548
            0: 0.0169277701441132, 9000: 0.15279792149898394
            最佳结果迭代：0，误差：0.016928
            -----基于种群的 ADAMm-----
            0: 0.2491964938729135
            1000: 0.0000010386817829
            最佳结果迭代：1050，误差：0.000001
            		 MLP 配置：1|1|1，权重：4，激活函数：eActAlgSigm，种子：2
            -----集成 ADAM-----
            0: 0.0095411465043040, 0: 0.009541146504303972
            0: 0.0095411465043040, 1000: 0.20977102640908893
            0: 0.0095411465043040, 2000: 0.23464558094398064
            0: 0.0095411465043040, 3000: 0.23657904914082925
            0: 0.0095411465043040, 4000: 0.17812555648593617
            0: 0.0095411465043040, 5000: 2.1749975763135927
            0: 0.0095411465043040, 6000: 2.2093668968051166
            0: 0.0095411465043040, 7000: 2.1657244506071813
            0: 0.0095411465043040, 8000: 1.9330415523200173
            0: 0.0095411465043040, 9000: 0.10441382194622865
            最佳结果迭代：0，误差：0.009541
            -----基于种群的 ADAMm-----
            0: 0.2201830630768654
            最佳结果迭代：750，误差：0.000001
            		 MLP 配置：1|1|1，权重：4，激活函数：eActRatSigm，种子：1
            -----集成 ADAM-----
            0: 1.2866075458561122, 0: 1.2866075458561121
            1000: 0.2796061866784148, 1000: 0.2796061866784148
            2000: 0.0450819127087337, 2000: 0.04508191270873367
            3000: 0.0200306843648248, 3000: 0.020030684364824806
            4000: 0.0098744349153286, 4000: 0.009874434915328582
            5000: 0.0049448920462547, 5000: 0.00494489204625467
            6000: 0.0024344513388710, 6000: 0.00243445133887102
            7000: 0.0011602603038120, 7000: 0.0011602603038120354
            8000: 0.0005316894732581, 8000: 0.0005316894732581081
            9000: 0.0002339388712666, 9000: 0.00023393887126662818
            最佳结果迭代：9999，误差：0.000099
            -----基于种群的 ADAMm-----
            0: 1.8418367346938778
            最佳结果迭代：645，误差：0.000000

            SiLU 类型激活函数的结果表：

              SoftPlus   BentIdent   SiLU
            MLP 配置：1|1|1，权重：4，激活函数：eActSoftPlus，种子：2
            -----集成 ADAM-----
            0: 0.5380138004155748, 0: 0.5380138004155747
            0: 0.5380138004155748, 1000: 12.377378915308087
            0: 0.5380138004155748, 2000: 12.377378915308087
            3000: 0.1996421769021168, 3000: 0.19964217690211675
            4000: 0.1985425345613517, 4000: 0.19854253456135168
            5000: 0.1966512639256550, 5000: 0.19665126392565502
            6000: 0.1933509943676914, 6000: 0.1933509943676914
            7000: 0.1874142582090466, 7000: 0.18741425820904659
            8000: 0.1762132792048514, 8000: 0.17621327920485136
            9000: 0.1538331138702293, 9000: 0.15383311387022927
            最佳结果迭代：9999，误差：0.109364
            -----基于种群的 ADAMm-----
            0: 12.3773789153080873
            最佳结果迭代：677，误差：0.000001
            		 MLP 配置：1|1|1，权重：4，激活函数：eActBentIdent，种子：4
            -----集成 ADAM-----
            0: 15.1221330593320857, 0: 15.122133059332086
            0: 15.1221330593320857, 1000: 25.619316876852988
            1922: 8.6344718719116980, 2000: 8.634471871911698
            1922: 8.6344718719116980, 3000: 8.634471871911698
            1922: 8.6344718719116980, 4000: 8.634471871911698
            1922: 8.6344718719116980, 5000: 8.634471871911698
            1922: 8.6344718719116980, 6000: 8.634471871911698
            6652: 4.3033564303197833, 7000: 8.634471871911698
            6652: 4.3033564303197833, 8000: 8.634471871911698
            6652: 4.3033564303197833, 9000: 7.11489380279475
            最佳结果迭代：9999，误差：3.589207
            -----基于种群的 ADAMm-----
            0: 25.6193168768529880
            最佳结果迭代：15：0.000001
            		 MLP 配置：1|1|1，权重：4，激活函数：eActSiLU，种子：4
            -----集成 ADAM-----
            0: 0.6585816582701970, 0: 0.658581658270197
            0: 0.6585816582701970, 1000: 5.142928362480306
            1393: 0.3271208998291733, 2000: 0.32712089982917325
            1393: 0.3271208998291733, 3000: 0.32712089982917325
            1393: 0.3271208998291733, 4000: 0.4029355474095988
            5000: 0.0114993205601383, 5000: 0.011499320560138332
            6000: 0.0003946998191595, 6000: 0.00039469981915948605
            7000: 0.0000686308316624, 7000: 0.00006863083166239227
            8000: 0.0000176901182322, 8000: 0.000017690118232197302
            9000: 0.0000053723044223, 9000: 0.000005372304422295116
            最佳结果迭代：9999，误差：0.000002
            -----基于种群的 ADAMm-----
            0: 19.9499415647445524
            1000: 0.0000057228950379
            最佳结果迭代：1051，误差：0.000000

            周期性激活函数的结果表：

            ACON     SERF   Snake
            MLP 配置：1|1|1，权重：4，激活函数：eActACON，种子：3
            -----集成 ADAM-----
            0: 0.8183728267492676, 0: 0.8183728267492675
            160: 0.5853150801288914, 1000: 1.2003151947973498
            2000: 0.0177702331540612, 2000: 0.017770233154061187
            3000: 0.0055801976952827, 3000: 0.005580197695282676
            4000: 0.0023096724537356, 4000: 0.002309672453735598
            5000: 0.0010238849157595, 5000: 0.0010238849157594616
            6000: 0.0004581612824611, 6000: 0.0004581612824611273
            7000: 0.0002019092359805, 7000: 0.00020190923598049711
            8000: 0.0000867118074097, 8000: 0.00008671180740972474
            9000: 0.0000361764073840, 9000: 0.00003617640738397845
            最佳结果迭代：9999，误差：0.000015
            -----基于种群的 ADAMm-----
            0: 1.3784017183806672
            最佳结果迭代：300，误差：0.000000
            		 MLP 配置：1|1|1，权重：4，激活函数：eActSERF，种子：2
            -----集成 ADAM-----
            0: 0.0169277701441132, 0: 0.016927770144113192
            0: 0.0169277701441132, 1000: 0.24726166610109795
            0: 0.0169277701441132, 2000: 0.24996248252671016
            0: 0.0169277701441132, 3000: 0.2499877118017991
            0: 0.0169277701441132, 4000: 0.2260068617570163
            0: 0.0169277701441132, 5000: 2.2499589217599363
            0: 0.0169277701441132, 6000: 2.2499631351033904
            0: 0.0169277701441132, 7000: 2.248459789732414
            0: 0.0169277701441132, 8000: 2.146138260175548
            0: 0.0169277701441132, 9000: 0.15279792149898394
            最佳结果迭代：0，误差：0.016928
            -----基于种群的 ADAMm-----
            0: 0.2491964938729135
            1000: 0.0000010386817829
            最佳结果迭代：1050，误差：0.000001
            		 MLP 配置：1|1|1，权重：4，激活函数：eActSnake，种子：2
            -----集成 ADAM-----
            0: 0.0169277701441132, 0: 0.016927770144113192
            0: 0.0169277701441132, 1000: 0.24726166610109795
            0: 0.0169277701441132, 2000: 0.24996248252671016
            0: 0.0169277701441132, 3000: 0.2499877118017991
            0: 0.0169277701441132, 4000: 0.2260068617570163
            0: 0.0169277701441132, 5000: 2.2499589217599363
            0: 0.0169277701441132, 6000: 2.2499631351033904
            0: 0.0169277701441132, 7000: 2.248459789732414
            0: 0.0169277701441132, 8000: 2.146138260175548
            0: 0.0169277701441132, 9000: 0.15279792149898394
            最佳结果迭代：0，误差：0.016928
            -----基于种群的 ADAMm-----
            0: 0.2491964938729135
            1000: 0.0000010386817829
            最佳结果迭代：1050，误差：0.000001


            总结

            那么，让我们来总结一下我们的研究。我先重申一下实验的实质：我们采用了两种基于相同逻辑构建、但工作方式根本不同的优化算法。第一种（经典 ADAM）是一个内置优化器，它在神经网络内部运行，可以直接访问激活函数和整个内部结构——就像一个拥有该区域详细地图的导航员。第二种（种群 ADAMm）是一个外部优化器，它将神经网络视为一个“黑箱”来处理，对其内部结构或任务的具体细节一无所知——就像一个依靠星辰和总体方向来寻找道路的旅行者。

            我们使用同一个神经网络作为两种算法的研究对象。这一点至关重要，因为它使我们能够定位潜在问题的根源：如果我们在使用某些激活函数时遇到困难，我们就可以确信这不是神经网络本身的问题，而是优化算法与这些函数交互方式的问题。

            这种实验设置让我们可以清晰地看到，在不同的优化方法背景下，不同的激活函数表现如何。需要注意的是，我们有意识地不考虑网络的泛化能力或其在新数据上的性能。我们的目标是研究激活函数与优化算法之间的相互影响、它们的兼容性以及交互的效率。

            这种方法让我们能够清晰地看到不同优化策略在不同激活函数上的表现，而不受外部因素的影响。实验结果清楚地表明，有时一个“盲目”的外部优化器可能比一个拥有网络结构全部信息的算法更高效。

            对于所有激活函数，外部的 ADAMm 都表现出快速且稳定的收敛，这表明激活函数的属性对它来说并不起决定性作用。另一方面，传统的内置 ADAM 则遇到了严重的问题。

            现在，让我们来看看内置 ADAM 在每个激活函数上的行为，并将其总结为以下结论：

            1. 有问题的函数（陷入停滞或收敛缓慢）：

            • TanH（双曲正切）
            • AlgSigm（代数 Sigmoid）
            • SERF（Sigmoid 加权指数线性单元）
            • Snake（周期性函数）

            2. 成功的案例（能够收敛）：

            • RatSigm（有理 Sigmoid），Sigmoid 函数中表现最好的
            • SoftPlus
            • BentIdent
            • SiLU (Swish)，第二组中表现最好的
            • ACON（自适应函数），周期性函数中表现最好的

            3. 规律：

            经典的 Sigmoid 函数（TanH, AlgSigm）表现出陷入停滞的问题。更现代的自适应函数（ACON, SiLU）展现出更好的收敛性。在周期性函数中，ACON 表现出收敛性，而 Snake 则会陷入停滞。

            因此，本研究提出了一种综合性的神经网络优化方法，该方法将权重控制、激活函数边界和学习过程整合到一个相互关联的系统中。关键的创新在于引入了 GetBoundUp 和 GetBoundLo 方法，这些方法允许每个激活函数定义自己的边界，然后这些边界被用来管理网络的权重。该机制辅以一个在达到边界时提前终止求和的系统，这不仅防止了冗余计算（尤其是在大型网络中），而且还确保了在应用激活函数之前对值的控制。

            一个特别重要的元素是权重反射机制。与传统的剪裁或归一化不同，它通过在权重达到极限时“抖动”权重来防止学习停滞。这种解决方案即使在临界情况下也能保持改变权重的能力，确保了训练过程的连续性。所有这些组件的系统化集成，创造了一个有效的防止权重发散的机制，同时又不会损失训练的灵活性，这在处理不同激活函数时尤为重要。这种集成方法不仅解决了权重控制问题，还为理解训练过程中各种神经网络组件的相互作用开辟了新的视角。

            本研究并非表明 ADAM 在训练神经网络中毫无用处，而是将注意力集中在它对某些激活函数的响应上。或许对于大型神经网络来说，根本没有替代方案（除了它的现代梯度下降方法同类算法）。这可以作为下一个研究主题，即在大规模神经网络的背景下，探讨 ADAM（作为使用反向传播方法的现代优化算法的代表）的效率，以及研究激活函数的选择对网络泛化能力及其在新数据上运行稳定性的影响。

            文中所用程序

            # 名称 类型 说明
            1 #C_AO.mqh
            		 包含
            		 种群优化算法的父类
            2 #C_AO_enum.mqh
            		 包含
            		 群体优化算法枚举
            3
            		 MLPa.mqh
            		 脚本
            		带有 ADAM 的 MLP 神经网络
            4
            		 Tests and Drawing act func.mq5 脚本 用于可视化构建激活函数的脚本
            5
            		Test act func in training.mq5
            		 脚本
            		使用 ADAM 和 ADAMm 的 MLP 训练脚本


            本文由MetaQuotes Ltd译自俄文
            原文地址： https://www.mql5.com/ru/articles/16845

            附加的文件 |
            下载ZIP
            MLP_ADAM.zip (141.41 KB)

            注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

            本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

            该作者的其他文章

            最近评论 | 前往讨论 (9)
            CODE X
            CODE X | 28 6月 2025 在 23:41

            我想，我想说的话和我实际用文字表述的内容之间存在误解。

            这次我会尽量说得清楚一些。 明确 当我们要对事物进行分类时，比如图像、物体、数字、声音，简而言之，就是对概率进行分类。我们需要限制神经网络中的数值，使其在给定的范围内。这个范围通常在-1 和 1 之间，但也可以在 0 和 1 之间，这取决于我们希望神经网络接触到的输入信息的速度、命中率和处理方式，以及它如何更好地指导自己的学习，以创建对事物的分类。 在这种情况下，我们确实需要 激活函数。正是为了将值保持在这个范围内。最终，我们将有办法根据输入为某一事物的概率生成数值。这是事实，我不否认。因此，我们经常需要对输入数据进行规范化或标准化处理。

            然而，神经网络不仅用于对事物进行分类，还可以而且也在用于保留知识。在这种情况下，激活函数在很多情况下都应被摒弃。细节：在某些情况下，我们需要限制一些东西。但这些都是非常特殊的情况。这是因为这些函数会妨碍网络实现其目的。这正是为了保留知识。事实上，我部分同意斯坦尼斯拉夫-科罗特基 的观点，即在这些情况下，如果我们不使用激活函数，网络就可以被折叠成相当于单层的东西。但是，当这种情况发生时，这只是几种情况中的一种，因为在有些情况下，一个包含多个变量的多项式不足以表示或保留知识。在这种情况下，我们需要使用额外的层，这样才能真正复制结果。或者可以生成新的多项式。在没有适当演示的情况下，这样解释有点令人困惑。但这是可行的。

            最大的问题是，由于现在什么都流行，在过去的十多年里，如果没记错的话，它一直与人工智能和神经网络联系在一起。尽管这项业务在最近五年才真正兴起。很多人完全不知道它们到底是什么。也不知道它们究竟是如何工作的。这是因为我看到的每个人都在使用现成的框架。这根本无助于理解神经网络的工作原理。它们只是一个多变量方程。它们在学术界已经被研究了几十年。即使它们走出学术界，也从未大张旗鼓地宣布过。在初始阶段和很长一段时间内 没有使用激活函数.但这些网络（当时甚至还不叫神经网络）的目的是不同的。然而，因为有三个人想从中获利，所以在我看来，他们的宣传方式有些错误。至少在我看来，正确的做法应该是对它们进行适当的解释。恰恰是这样，才不会给这么多人的思想造成混乱。不过这样也好，他们三个人赚了大钱，而人们却比从搬运车上掉下来的狗还迷茫。无论如何，我不想打击你写新文章的积极性，安德烈-迪克，但我确实希望你能继续学习，努力深入研究这个问题。我看到您尝试使用纯 MQL5 来创建系统。顺便说一句，这非常好。这引起了我的注意，让我意识到你的文章写得很好，也很有计划性。我只是想提请您注意这一点，并让您多思考一下。事实上，这个话题非常有趣，有很多东西很少有人知道。但你还是去研究了。

            Debates em alto nível, são sempre interessantes, pois nos faz crescer e pensar fora da caixa. Brigas não nos leva a nada, e só nos faz perder tempo. 👍

            Andrey Dik
            Andrey Dik | 29 6月 2025 在 07:42
            CODE X #:
            ...

            你的帖子就像是在说："涡轮喷气发动机实际上是蒸汽发动机，因为它最初的设计就是这样的"。

            Rorschach
            Rorschach | 29 6月 2025 在 17:05

            任何激活函数都可以使用，甚至余弦函数也可以，其结果与常用激活函数相同。 建议使用 relu（偏置为 0.1（不建议与 随机行走初始化一起使用 ）），因为它简单（计数速度快），学习效果更好：这些区块很容易优化，因为它们与线性区块非常相似。唯一 不同的是，线性整流区块在 其定义域 的一半范围内 输出 0。 因此，线性整流 区块 的导数 在该区块处于活动状态的任何地方都很大。不仅梯度大，而且 一致。整流运算的二阶导数在任何地方都为 0，而 一阶导数在任何地方都为 1。这意味着梯度的方向 比 激活函数受 二阶效应影响时 更有助于学习 ...在初始化仿射变换参数时，建议给b的所有元素赋一个 小的正值，例如 0.1.这样， 对于大多数训练示例， 线性修正块 很可能 在 初始时刻 处于激活状态， 导数也将不同于零。

            与分线性方程块 不同的是，正余弦方程块 在 其定义域的大部分范围 内 都接近于 渐近线 -- 当 z 趋于 无穷大 时 接近于 高值 ，而 当 z趋于负无穷大时 接近 于 低值。它们仅在 零点附近 具有较高的灵敏度。由于西格码块的饱和度，梯度 学习会受到严重影响。因此， 现在不建议在前向传播网络 中 使用它们 作为隐藏块 ...如果必须使用西格玛激活函数，最好使用 双曲正切 而不是对数西格玛 。 从 tanh(0) = 0 而 σ(0) = 1/2 的意义上讲， 它更接近于 同一函数。由于 tanh 类似于 零邻域的同一函数 ，因此训练深度神经网络 类似于训练线性模型， 前提是网络激活信号可以保持在较低水平。在这种情况下，使用激活函数 tanh 的网络训练 就得到了简化。

            对于 lstm，我们需要使用 sigmoid 或 arctangent（建议将遗忘风口的偏移量设为 1）：西格玛激活函数仍在使用，但不适用于前馈 网络 。 递归网络、许多概率模型和 一些自动编码器都有一些额外的要求，这些要求排除了 使用片断线性激活函数的 可能性 ，因此 尽管存在饱和问题，西格码块还是更适合使用。

            线性激活和参数缩减：如果网络的每一层都只包含 线性变换，那么 整个 网络 将是线性的。不过，某些层 也可能是 纯线性的 ，这也没有问题。假设一个 神经网络 的某一层 有 n 个 输入和 p 个 输出。可以用两层来代替，一层是权重矩阵 U， 另一层 是权重矩阵 V。 如果 U 产生 q个 输出，那么 U 和 V 加起来只包含 (n + p)q 个 参数， 而 W 则 包含 np 个 参数。对于较小的 q ， 节省的参数可能非常可观。代价是一个限制 --线性变换必须 具有较低的秩，但这种低秩链接通常就足够了。因此， 线性隐藏块是减少网络参数数量的有效方法。

            Relu更适合深度网络：尽管整流 在 早期模型 中 很受欢迎 ，但 在二十世纪八十年代，它几乎被sigmoid普遍取代，因为它 更适合 非常小的神经网络。

            但它在一般情况下效果更好：对于小型数据集 ，使用整流非线性比学习 隐层权重更为重要 。随机权重足以通过网络 传播有用的线性整流信息 ，从而训练分类输出层将不同的特征向量映射到类别标识符上。 如果有更多的数据，学习过程就会开始提取大量 有用的知识，从而超越随机选择的参数... 与 激活函数具有曲率或双向饱和特征的深度网络相比，整流线性 网络的学习要容易得多 ...

            [删除] | 31 7月 2025 在 16:48
            CODE X #:

            我想，我想说的话和我实际用文字表述的内容之间存在误解。

            这次我会尽量说得清楚一点。 进行分类时 当我们要对图像、物体、形状、声音等事物进行分类时，简而言之，就是对概率进行分类。我们需要对神经网络中的值进行限制，使其在给定的范围内。通常这个范围在-1 和 1 之间，但也可以在 0 和 1 之间，这取决于我们希望神经网络学习的输入信息的处理速度、速率和方式，以及神经网络如何以最佳方式引导其学习，以创建事物分类。 在这种情况下，我们需要 激活函数。它的作用是将数值保持在该范围内。最终，我们将根据输入为二者之一的概率来生成数值。这是事实，我并不否认。因此，我们经常需要对输入数据进行归一化或标准化处理。

            然而，神经网络不仅可用于分类，也可用于知识保留。在这种情况下，激活函数在很多情况下都应被摒弃。细节：在某些情况下，我们需要限制一些东西。但这些都是非常特殊的情况。问题的关键在于，这些功能会妨碍网络实现其目的。And that is to preserve knowledge.事实上，我部分同意斯坦尼斯拉夫-科罗茨基（Stanislav Korotsky ）的观点，即在这种情况下，如果不使用激活函数，网络可以简化为单层。但是，当这种情况发生时，它只是几种情况中的一种，因为在有些情况下，一个包含多个变量的多项式不足以表示或存储知识。在这种情况下，我们必须使用额外的层，以便能够实际复制结果。或者，也可以生成新的层。在没有适当演示的情况下，这样解释有点令人困惑。但这是可行的。

            最大的问题是，由于现在什么都流行，在过去 10 年左右的时间里，如果我没记错的话，人们一直在谈论人工智能和神经网络。尽管这项业务在过去五年中才真正蓬勃发展起来。很多人完全不知道这些东西到底是什么。以及它们究竟是如何工作的。这是因为我看到的每个人都在使用现成的框架。这根本无助于理解神经网络的工作原理。它只是一个有几个变量的等式。几十年来，学术界一直在研究神经网络。即使它们走出了学术界，也从未如此隆重地宣布过。最初，在很长一段时间里 激活函数并没有.但这些网络（当时甚至还不叫神经网络）的目的是不同的。然而，因为有三个人想利用它们，所以它们被炒得沸沸扬扬，我认为这有些不妥。至少在我看来，正确的做法应该是正确解释其本质。这样才不会让很多人产生混淆。不过没关系，他们三人赚了不少钱，人们比从垃圾车上掉下来的狗还迷茫。总之，我不想打击你写更多文章的积极性，安德鲁-迪克，但我希望你能继续学习，努力钻研这个课题。我看到你尝试使用纯 MQL5 创建一个系统。顺便说一句，这非常好。这引起了我的注意，我意识到你的文章写得很好，也很有计划性。我只是想提请您注意这一点，并让您多思考一下。这个话题其实非常有趣，知道的人并不多。但你却把它拿出来研究了一番。

            是的，非线性是激活 phs 的一种间接影响。它们的初衷是将目标定义从一个领域转换到另一个领域，例如，用于分类任务。"非线性 "可以通过不同的方式实现，例如通过增加特征数量或转换特征，或者通过转换特征的核来实现。

            最简单的例子就是逻辑回归，尽管最后的激活函数仍是线性的。

            但在多层网络中，非线性是由于具有激活函数的层数而产生的，这仅仅是核类型转换的结果。
            [删除] | 31 7月 2025 在 17:05

            历史背景：

            你说得对， 逻辑 回归和早期神经网络的基本概念要早于 现代深度神经网络。

            让我们看看时间顺序：

            1. 逻辑函数 是在 19 世纪开发的。将其用作分类统计模型（逻辑回归）在 20 世纪中期（大约20 世纪 40-50 年代）开始流行。

            2. 第一个带有激活函数的神经元数学模型（McCulloch 和 Pitts 模型）出现于1943 年。它使用了一个简单的阈值函数。

            3. 感知器是一种单层神经网络，由弗兰克-罗森布拉特（Frank Rosenblatt）于1958 年 开发。它使用阈值激活函数，只能解决线性可分离问题。

            4. 1986年，Rumelhart、Hinton和Williams推广了反向传播 算法，深度学习 和多层网络才有了突破性进展。

            正是该算法使多层神经网络的训练变得切实可行，并表明它不仅需要阈值，还需要可微分的非线性激活函数（如 sigmoid 和后来的 ReLU）。

            结论

            历史证明

            • 首先，有一些模型（逻辑回归、感知器）本质上是单层模型。

            • 在这些模型中，激活函数实际上是对所需领域的转换（从线性和到二元类或概率），因为整个模型仍然是线性的。

            • 后来，随着多层网络的出现，激活函数出现了一个新的、从根本上说更为重要的作用--将非线性引入隐层，从而使网络能够学习。

            构建MQL5自优化智能交易系统（EA）（第四部分）：动态头寸规模调整 构建MQL5自优化智能交易系统（EA）（第四部分）：动态头寸规模调整
            成功运用算法交易需要持续的跨学科学习。然而，无限的可能性可能会耗费数年努力，却无法取得切实成果。为解决这一问题，我们提出一个循序渐进增加复杂性的框架，让交易者能够迭代优化策略，而非将无限时间投入不确定的结果中。
            开发多币种 EA 交易（第 20 部分）：整理自动项目优化阶段的输送机（一） 开发多币种 EA 交易（第 20 部分）：整理自动项目优化阶段的输送机（一）
            我们已经创建了不少有助于安排自动优化的组件。在创建过程中，我们遵循了传统的循环结构：从创建最小的工作代码到重构和获得改进的代码。是时候开始清理我们的数据库了，这也是我们正在创建的系统中的一个关键组件。
            开发回放系统（第 76 部分）：新 Chart Trade（三） 开发回放系统（第 76 部分）：新 Chart Trade（三）
            在本文中，我们将看看上一篇文章中缺少的 DispatchMessage 代码是如何工作的。我们还会介绍下一篇文章的主题。因此，在继续下一个主题之前，了解这段代码的工作原理非常重要。此处提供的内容仅用于教育目的。在任何情况下，除了学习和掌握所提出的概念外，都不应出于任何目的使用此应用程序。
            您应当知道的 MQL5 向导技术（第 51 部分）：配以 SAC 的强化学习 您应当知道的 MQL5 向导技术（第 51 部分）：配以 SAC 的强化学习
            柔性参与者评论者是一种利用 3 个神经网络的强化学习算法。一名参与者网络和 2 个评论者网络。这些机器学习模型按主从伙伴关系配对，其中所建模评论者能提升参与者网络的预测准确性。在这些序列中引入 ONNX 的同时，我们探讨了如何将这些思路作为由向导汇编的智能系统的自定义信号，推进测试。