数据分组处理方法：在MQL5中实现多层迭代算法。

简介

数据分组处理方法（GMDH）是一系列用于计算机数据建模的归纳算法。这些算法自动从数据中构建和优化多项式神经网络模型，为揭示输入变量和输出变量之间的关系提供了一种独特的方法。通常，GMDH框架包含四个主要算法：组合算法（COMBI）、组合选择算法（MULTI）、多层迭代算法（MIA）和松弛迭代算法（RIA）。在本文中，我们将探讨如何在MQL5中实现多层迭代算法。我们将讨论其内部工作原理，并展示如何将其应用于从数据集中构建预测模型。

理解GMDH

数据处理的分组方法 是一种用于数据分析和预测的算法类型。它是一种机器学习技术，旨在找到描述给定数据集的最佳数学模型。GMDH由苏联数学家阿列克谢·伊瓦赫宁科（Alexey Ivakhnenko）于20世纪60年代开发。旨在解决基于经验数据对复杂系统进行建模所面临的挑战。GMDH算法采用数据驱动的建模方法，根据观察到的数据生成和完善模型，而不是依赖于先入为主的概念或理论假设。

GMDH的主要优势之一是通过迭代生成和评估潜在模型，能够将模型的构建过程自动化。它根据系统数据反馈，选择最佳的模型并持续优化它。这种自动化的建模能力，使得在模型构建过程中无需人工干预和专业知识。

GMDH背后的核心理念是通过迭代选择和组合变量来构建一系列复杂度和精确性逐步提升的模型。算法从一组简单模型（通常是线性模型）开始，通过添加额外的变量和项目来逐步提高其复杂性。在每个阶段，算法都会评估模型的表现，并选择表现最好的模型作为下一轮迭代的基础。这个过程一直持续到获得令人满意的模型或达到停止标准为止。

GMDH特别适合于对有大量输入变量和复杂关系的数据集进行建模。GMDH算法产生的模型将输入与输出相关联，这可以通过无限 Volterra–Kolmogorov–Gabor （VKG）多项式来表示。VKG多项式是一种在建模非线性系统和近似复杂数据时使用的特殊类型的多项式。VKG多项式具有如下形式：

其中：

• Yn是系统的输出。
• Xi，Xj，和 Xk分别是i，j，k时刻的输入变量。
• ai，aj， ak等是多项式的系数。

这样的多项式可以视为多项式神经网络（PNN）。多项式神经网络（PNN）是一种人工神经网络（ANN）架构，其神经元使用多项式激活函数。多项式神经网络的结构与其他神经网络类似，包含输入节点、隐藏层和输出节点。然而，在多项式神经网络中，应用于神经元的激活函数是多项式函数。参数化GMDH算法是专门为处理连续变量而开发的。当被建模的对象具有在表示或定义上有明确的属性时，就可以使用这些算法。多层迭代算法是参数化GMDH算法的一个例子。

多层迭代算法

MIA是构建多项式神经网络模型时GMDH框架 的一种变体。其结构与多层前馈神经网络几乎一致。信息从输入层经过中间层流向最终输出层. 每一层都对数据进行特定的变换。与GMDH的一般方法相比，MIA的关键区别在于它选择最能描述数据的最终多项式的最优子函数。这意味着根据预定标准，在训练过程中获得的一些信息会被舍弃。

要使用MIA构建模型，我们首先需要将要研究的数据集划分为训练集和测试集。我们希望训练集尽可能多样化，以便充分捕捉潜在过程的特征。完成数据集划分后，我们就开始进行层的构建。 

构建网络层级

类似于多层前馈神经网络，我们从输入层开始，该层是预测变量或自变量的集合。这些输入每次取两个，并发送到网络的第一层。因此，第一层将由“M个2的组合”节点组成，其中M是预测变量的数量。

上面的图示展示了当处理4个输入（表示为x1至x4）时，输入层和第一层可能呈现的样子。在第一层中，将基于节点的输入（使用训练数据集）构建局部模型，并使用测试数据集对所得的部分模型进行评估。然后，比较该层中所有局部模型的预测误差。记录下表现最好的N个模型，并用于生成下一层的输入。以某种方式结合第一层中前N个模型的预测误差，得出一个单一指标，该指标能够反映模型生成的总体进度。将这个指标与上一层的指标进行比较。如果它更小，则创建一个新层，并重复该过程。否则，如果没有改进。则停止模型生成，并丢弃当前层的数据，这表明模型训练已完成。

节点和局部模型

在每一层的每个节点上，都会将前一层的输出作为成对输入，计算出一个多项式来估计训练数据集中的观测值。这就是所谓的局部模型。一个用于根据节点的输入来建模训练集输出的函数示例如下所示。

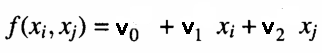
其中“v”是拟合线性模型的系数。模型的好坏是通过计算测试数据集中预测值与实际值之间的均方误差来测试的。这些测试误差然后以某种方式组合。要么通过计算它们的平均值，要么简单地选择均方误差最小的节点。最终指标值指表明了当前层的近似值（预测误差）是否相对于其他层有所改善或和其他层无关。同时，会记录下预测误差最小的前N个节点。并使用它们对应的系数来生成下一层的一组新输入值。如果当前层的近似值（此处指误差更小）优于前一层，则会构建一个新层。

一旦网络构建完成，就只会保留每层中预测误差最小的节点的系数，并使用这些系数来定义最能描述数据的最终模型。在下一节中，我们将深入介绍实现上述过程的代码。该代码是从GitHub上可用的C++版本的GMDH（Group Method of Data Handling，数据处理的分组方法）改编而来的。

MQL5实现

C++ 实现模型的训练，并将它们以 JSON 格式保存到文本文件中以供后续使用。它利用多线程来加速训练过程，并使用 Boost 和 Eigen 库构建模型。对于我们的 MQL5 实现，大部分功能都将保留，但多线程训练和用于求解线性方程的QR分解的可选方案将不可用。

我们的程序将包含三个头文件。第一个是gmdh_internal.mqh。此文件包含各种自定义数据类型的定义。它首先定义了三个枚举类型：

• PolynomialType - 定义在进行下一轮训练之前，用于转换现有变量的多项式类型。
  

  //+---------------------------------------------------------------------------------------------------------+
  //|  Enumeration for specifying the polynomial type to be used to construct new variables from existing ones|
  //+---------------------------------------------------------------------------------------------------------+
  enum PolynomialType
    {
     linear,
     linear_cov,
     quadratic
    };

  "PolynomialType"提供三种选项，它们代表了以下多项式函数。在这里，x1和x2是函数 f(x1, x2) 的输入，而v0...vN是需要确定的系数。这个枚举值代表了生成解集的方程类型：

选项	Function f(x1,x2)
linear	线性方程：v0 + v1*x1 + v2*x2
linear_cov	含系数的线性方程：v0 + v1*x1 + v2*x2 + v3*x1*x2
quadratic	二次方程：v0 + v1*x1 + v2*x2 + v3*x1*x2 + v4*x1^2 + v5*x2^2

• Solver - 定义用于求解线性方程的QR分解方法。我们的程序将仅提供一个可选项。C++版本使用Eigen库，通过Householder方法的变形来进行QR分解。
  

  //+-----------------------------------------------------------------------------------------------+
  //|  Enum  for specifying the QR decomposition method for linear equations solving in models.     |
  //+-----------------------------------------------------------------------------------------------+
  enum Solver
    {
     fast,
     accurate,
     balanced
    };

• CriterionType - 允许用户选择一个特定的外部标准，该规则将作为评估候选模型的基础。此枚举列出了在训练模型时可以用作停止准则的选项。
  

  //+------------------------------------------------------------------+
  //|Enum for specifying the external criterion                        |
  //+------------------------------------------------------------------+
  enum CriterionType
    {
     reg,
     symReg,
     stab,
     symStab,
     unbiasedOut,
     symUnbiasedOut,
     unbiasedCoef,
     absoluteNoiseImmun,
     symAbsoluteNoiseImmun
    };

  枚举值选项的意义将在下面的表格中一一解释：

CriterionType	说明
reg	常规准则：基于测试数据集的目标值与使用训练数据集计算得出的系数所做出的预测值之间的差异，使用常规平方误差总和（SSE）。
symReg	对称准则：是指基于以下两部分平方误差（SSE）的总和：一是基于测试数据集的目标值与使用训练数据集计算得出的系数所做出的预测值之间的差异；二是基于训练数据集的目标值与使用测试数据集计算得出的系数所做出的预测值之间的差异。
stab	稳定性：使用基于所有目标值与使用训练数据集计算得出的系数（结合所有预测变量）所做出的预测值之间差异的平方误差总和（SSE）来衡量。
symStab	对称稳定性（Symetric Stability）：这一标准结合了两种平方和误差（SSE）的计算方法。一种是类似于“稳定性”标准中的SSE计算方式；另一种是基于所有目标值，与使用测试数据集结合数据集中所有预测变量计算得到的系数所做出的预测值之间差异的SSE计算方式。
unbiasedOut	无偏输出（Unbiased Outputs）：这一标准是基于使用训练数据集计算的系数所做出的预测值与使用测试数据集计算的系数（两者都使用测试数据集中的预测变量）所做出的预测值之间差异的平方和误差（SSE）来衡量的。
symUnbiasedOut	对称无偏输出（Symmetric Unbiased Outputs）：这一标准以与“无偏输出”（Unbiased Outputs）标准相同的方式计算平方和误差（SSE），但不同的是，这次我们使用了所有的预测变量。
unbiasedCoef	无偏系数（Unbiased Coefficients）：这是指使用训练数据计算得到的系数与使用测试数据计算得到的系数之间平方差的总和。
absoluteNoiseImmun	绝对噪声免疫（Absolute Noise Immunity）：该标准计算整个数据集训练模型与训练数据集训练模型对测试数据集预测值的平方差的点积，以及测试数据集训练模型与训练数据集训练模型对测试数据集预测值的平方差点积之和。
symAbsoluteNoiseImmun	对称绝对噪声免疫（Symmetric Absolute Noise Immunity）：该标准通过计算两个模型预测值的点积来评估模型的噪声免疫能力。一个值是训练整个数据集所得的模型与仅训练训练数据集所得模型在训练数据集上预测值的差异。另一个值是训练整个数据集所得的模型与训练测试数据集所得模型在所有观察值上的预测值的差异。

枚举值后面是四个自定义结构体：

• BufferValues - 是一个向量结构，用于存储通过测试集和训练集以多种方式计算得到的系数和预测值。
  

  //+-------------------------------------------------------------------------------------+
  //| Structure for storing coefficients and predicted values calculated in different ways|
  //+--------------------------------------------------------------------------------------+
  struct BufferValues
    {
     vector            coeffsTrain; // Coefficients vector calculated using training data
     vector            coeffsTest; // Coefficients vector calculated using testing data
     vector            coeffsAll; // Coefficients vector calculated using learning data
     vector            yPredTrainByTrain; // Predicted values for *training* data calculated using coefficients vector calculated on *training* data
     vector            yPredTrainByTest; // Predicted values for *training* data calculated using coefficients vector calculated on *testing* data
     vector            yPredTestByTrain; // Predicted values for *testing* data calculated using coefficients vector calculated on *training* data
     vector            yPredTestByTest; //Predicted values for *testing* data calculated using coefficients vector calculated on *testing* data
  
                       BufferValues(void)
       {
  
       }
  
                       BufferValues(BufferValues &other)
       {
        coeffsTrain = other.coeffsTrain;
        coeffsTest =  other.coeffsTest;
        coeffsAll = other.coeffsAll;
        yPredTrainByTrain = other.yPredTrainByTrain;
        yPredTrainByTest = other.yPredTrainByTest;
        yPredTestByTrain = other.yPredTestByTrain;
        yPredTestByTest = other.yPredTestByTest;
       }
  
     BufferValues      operator=(BufferValues &other)
       {
        coeffsTrain = other.coeffsTrain;
        coeffsTest =  other.coeffsTest;
        coeffsAll = other.coeffsAll;
        yPredTrainByTrain = other.yPredTrainByTrain;
        yPredTrainByTest = other.yPredTrainByTest;
        yPredTestByTrain = other.yPredTestByTrain;
        yPredTestByTest = other.yPredTestByTest;
  
        return this;
       }
  
    };

  
  
• PairDVXd - 封装了一个数据结构，该结构将一个标量（scalar）和与之对应的向量（vector）组合在一起。
  

  //+------------------------------------------------------------------+
  //|  struct PairDV                                                   |
  //+------------------------------------------------------------------+
  struct PairDVXd
    {
     double            first;
     vector            second;
  
                       PairDVXd(void)
       {
        first = 0.0;
        second = vector::Zeros(10);
       }
  
                       PairDVXd(double &_f, vector &_s)
       {
        first = _f;
        second.Copy(_s);
       }
  
                       PairDVXd(PairDVXd &other)
       {
        first = other.first;
        second = other.second;
       }
  
     PairDVXd          operator=(PairDVXd& other)
       {
        first = other.first;
        second = other.second;
  
        return this;
       }
    };

  
  
• PairMVXd - 是一个组合了矩阵和向量的结构体。它们共同存储了输入及其对应的输出或目标值。输入被保存在矩阵中，而向量则是输出的集合。矩阵中的每一行都与向量中的一个值相对应。
  

  //+------------------------------------------------------------------+
  //| structure PairMVXd                                               |
  //+------------------------------------------------------------------+
  struct PairMVXd
    {
     matrix            first;
     vector            second;
  
                       PairMVXd(void)
       {
        first = matrix::Zeros(10,10);
        second = vector::Zeros(10);
       }
  
                       PairMVXd(matrix &_f,  vector& _s)
       {
        first = _f;
        second = _s;
       }
  
                       PairMVXd(PairMVXd &other)
       {
        first = other.first;
        second = other.second;
       }
  
     PairMVXd          operator=(PairMVXd &other)
       {
        first = other.first;
        second = other.second;
  
        return this;
       }
    };

• SplittedData - 这一数据结构用于存储被分割成训练集和测试集的数据。
  

  //+------------------------------------------------------------------+
  //|  Structure for storing parts of a split dataset                  |
  //+------------------------------------------------------------------+
  struct SplittedData
    {
     matrix            xTrain;
     matrix            xTest;
     vector            yTrain;
     vector            yTest;
  
                       SplittedData(void)
       {
        xTrain = matrix::Zeros(10,10);
        xTest = matrix::Zeros(10,10);
        yTrain = vector::Zeros(10);
        yTest = vector::Zeros(10);
       }
  
                       SplittedData(SplittedData &other)
       {
        xTrain = other.xTrain;
        xTest =  other.xTest;
        yTrain = other.yTrain;
        yTest =  other.yTest;
       }
  
     SplittedData      operator=(SplittedData &other)
       {
        xTrain = other.xTrain;
        xTest =  other.xTest;
        yTrain = other.yTrain;
        yTest =  other.yTest;
  
        return this;
       }
    };

  
  

结构体之后，我们来定义类：

• Combination类表示一个候选模型。它存储评估标准、输入的组合以及用于构建模型的系数。
  

  //+------------------------------------------------------------------+
  //| Сlass representing the candidate model of the GMDH algorithm     |
  //+------------------------------------------------------------------+
  class Combination
    {
     vector            _combination,_bestCoeffs;
     double            _evaluation;
  public:
                       Combination(void) { _combination = vector::Zeros(10); _bestCoeffs.Copy(_combination); _evaluation = DBL_MAX; }
                       Combination(vector &comb) : _combination(comb) { _bestCoeffs=vector::Zeros(_combination.Size()); _evaluation = DBL_MAX;}
                       Combination(vector &comb, vector &coeffs) : _combination(comb),_bestCoeffs(coeffs) { _evaluation = DBL_MAX; }
                       Combination(Combination &other) { _combination = other.combination(); _bestCoeffs=other.bestCoeffs(); _evaluation = other.evaluation();}
     vector            combination(void) { return _combination;}
     vector            bestCoeffs(void)  { return _bestCoeffs; }
     double            evaluation(void)  { return _evaluation; }
  
     void              setCombination(vector &combination) { _combination = combination; }
     void              setBestCoeffs(vector &bestcoeffs) { _bestCoeffs = bestcoeffs; }
     void              setEvaluation(double evaluation)  { _evaluation = evaluation; }
  
     bool              operator<(Combination &combi) { return _evaluation<combi.evaluation();}
     Combination       operator=(Combination &combi)
       {
        _combination = combi.combination();
        _bestCoeffs = combi.bestCoeffs();
        _evaluation = combi.evaluation();
  
        return this;
       }
    };

• CVector - 定义了一个自定义的类似向量的容器，用于存储Combination类的实例。为候选模型做一个容器。

  //+------------------------------------------------------------------+
  //| collection of Combination instances                              |
  //+------------------------------------------------------------------+
  class CVector
    {
  protected:
     Combination       m_array[];
     int               m_size;
     int               m_reserve;
  public:
     //+------------------------------------------------------------------+
     //| default constructor                                              |
     //+------------------------------------------------------------------+
                       CVector(void) :m_size(0),m_reserve(1000) { }
     //+------------------------------------------------------------------+
     //| parametric constructor specifying initial size                   |
     //+------------------------------------------------------------------+
                       CVector(int size, int mem_reserve = 1000) :m_size(size),m_reserve(mem_reserve)
       {
        ArrayResize(m_array,m_size,m_reserve);
       }
     //+------------------------------------------------------------------+
     //| Copy constructor                                                 |
     //+------------------------------------------------------------------+
                       CVector(CVector &other)
       {
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]=other[i];
       }
  
  
     //+------------------------------------------------------------------+
     //| destructor                                                       |
     //+------------------------------------------------------------------+
                      ~CVector(void)
       {
  
       }
     //+------------------------------------------------------------------+
     //| Add element to end of array                                      |
     //+------------------------------------------------------------------+
     bool              push_back(Combination &value)
       {
        ResetLastError();
  
        if(ArrayResize(m_array,int(m_array.Size()+1),m_reserve)<m_size+1)
          {
           Print(__FUNCTION__," Critical error: failed to resize underlying array ", GetLastError());
           return false;
          }
  
        m_array[m_size++]=value;
  
        return true;
       }
     //+------------------------------------------------------------------+
     //| set value at specified index                                     |
     //+------------------------------------------------------------------+
     bool              setAt(int index, Combination &value)
       {
        ResetLastError();
  
        if(index < 0 || index >= m_size)
          {
           Print(__FUNCTION__," index out of bounds ");
           return false;
          }
  
        m_array[index]=value;
  
        return true;
  
       }
     //+------------------------------------------------------------------+
     //|access by index                                                   |
     //+------------------------------------------------------------------+
  
     Combination*      operator[](int index)
       {
        return GetPointer(m_array[uint(index)]);
       }
  
     //+------------------------------------------------------------------+
     //|overload assignment operator                                      |
     //+------------------------------------------------------------------+
  
     CVector           operator=(CVector &other)
       {
        clear();
  
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]= other[i];
  
  
        return this;
       }
     //+------------------------------------------------------------------+
     //|access last element                                               |
     //+------------------------------------------------------------------+
  
     Combination*      back(void)
       {
        return GetPointer(m_array[m_size-1]);
       }
     //+-------------------------------------------------------------------+
     //|access by first index                                             |
     //+------------------------------------------------------------------+
  
     Combination*      front(void)
       {
        return GetPointer(m_array[0]);
       }
     //+------------------------------------------------------------------+
     //| Get current size of collection ,the number of elements           |
     //+------------------------------------------------------------------+
  
     int               size(void)
       {
        return ArraySize(m_array);
       }
     //+------------------------------------------------------------------+
     //|Get the reserved memory size                                      |
     //+------------------------------------------------------------------+
     int               reserve(void)
       {
        return m_reserve;
       }
     //+------------------------------------------------------------------+
     //|set the reserved memory size                                      |
     //+------------------------------------------------------------------+
     void              reserve(int new_reserve)
       {
        if(new_reserve > 0)
           m_reserve = new_reserve;
       }
     //+------------------------------------------------------------------+
     //| clear                                                            |
     //+------------------------------------------------------------------+
     void              clear(void)
       {
        ArrayFree(m_array);
  
        m_size = 0;
       }
  
    };

• CVector2d - 是另一个自定义的类似向量的容器，用于存储一组CVector实例。
  

  //+------------------------------------------------------------------+
  //| Collection of CVector instances                                  |
  //+------------------------------------------------------------------+
  class CVector2d
    {
  protected:
     CVector           m_array[];
     int               m_size;
     int               m_reserve;
  public:
     //+------------------------------------------------------------------+
     //| default constructor                                              |
     //+------------------------------------------------------------------+
                       CVector2d(void) :m_size(0),m_reserve(1000) { }
     //+------------------------------------------------------------------+
     //| parametric constructor specifying initial size                   |
     //+------------------------------------------------------------------+
                       CVector2d(int size, int mem_reserve = 1000) :m_size(size),m_reserve(mem_reserve)
       {
        ArrayResize(m_array,m_size,m_reserve);
       }
     //+------------------------------------------------------------------+
     //| Copy constructor                                                 |
     //+------------------------------------------------------------------+
                       CVector2d(CVector2d &other)
       {
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]= other[i];
       }
  
  
     //+------------------------------------------------------------------+
     //| destructor                                                       |
     //+------------------------------------------------------------------+
                      ~CVector2d(void)
       {
  
       }
     //+------------------------------------------------------------------+
     //| Add element to end of array                                      |
     //+------------------------------------------------------------------+
     bool              push_back(CVector &value)
       {
        ResetLastError();
  
        if(ArrayResize(m_array,int(m_array.Size()+1),m_reserve)<m_size+1)
          {
           Print(__FUNCTION__," Critical error: failed to resize underlying array ", GetLastError());
           return false;
          }
  
        m_array[m_size++]=value;
  
        return true;
       }
     //+------------------------------------------------------------------+
     //| set value at specified index                                     |
     //+------------------------------------------------------------------+
     bool              setAt(int index, CVector &value)
       {
        ResetLastError();
  
        if(index < 0 || index >= m_size)
          {
           Print(__FUNCTION__," index out of bounds ");
           return false;
          }
  
        m_array[index]=value;
  
        return true;
  
       }
     //+------------------------------------------------------------------+
     //|access by index                                                   |
     //+------------------------------------------------------------------+
  
     CVector*          operator[](int index)
       {
        return GetPointer(m_array[uint(index)]);
       }
  
     //+------------------------------------------------------------------+
     //|overload assignment operator                                      |
     //+------------------------------------------------------------------+
  
     CVector2d         operator=(CVector2d &other)
       {
        clear();
  
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]= other[i];
  
        return this;
       }
     //+------------------------------------------------------------------+
     //|access last element                                               |
     //+------------------------------------------------------------------+
  
     CVector*          back(void)
       {
        return GetPointer(m_array[m_size-1]);
       }
     //+-------------------------------------------------------------------+
     //|access by first index                                             |
     //+------------------------------------------------------------------+
  
     CVector*          front(void)
       {
        return GetPointer(m_array[0]);
       }
     //+------------------------------------------------------------------+
     //| Get current size of collection ,the number of elements           |
     //+------------------------------------------------------------------+
  
     int               size(void)
       {
        return ArraySize(m_array);
       }
     //+------------------------------------------------------------------+
     //|Get the reserved memory size                                      |
     //+------------------------------------------------------------------+
     int               reserve(void)
       {
        return m_reserve;
       }
     //+------------------------------------------------------------------+
     //|set the reserved memory size                                      |
     //+------------------------------------------------------------------+
     void              reserve(int new_reserve)
       {
        if(new_reserve > 0)
           m_reserve = new_reserve;
       }
     //+------------------------------------------------------------------+
     //| clear                                                            |
     //+------------------------------------------------------------------+
     void              clear(void)
       {
  
        for(uint i = 0; i<m_array.Size(); i++)
           m_array[i].clear();
  
        ArrayFree(m_array);
  
        m_size = 0;
       }
  
    };

• Criterion - 这个类实现了基于所选规则类型下，各种外部规则的计算方法。
  

  //+---------------------------------------------------------------------------------+
  //|Class that implements calculations of internal and individual external criterions|
  //+---------------------------------------------------------------------------------+
  class Criterion
    {
  protected:
     CriterionType     criterionType; // Selected CriterionType object
     Solver            solver; // Selected Solver object
  
  public:
     /**
     Implements the internal criterion calculation
     param xTrain Matrix of input variables that should be used to calculate the model coefficients
     param yTrain Target values vector for the corresponding xTrain parameter
     return Coefficients vector representing a solution of the linear equations system constructed from the parameters data
     */
     vector            findBestCoeffs(matrix& xTrain,  vector& yTrain)
       {
        vector solution;
  
        matrix q,r;
  
        xTrain.QR(q,r);
  
        matrix qT = q.Transpose();
  
        vector y = qT.MatMul(yTrain);
  
        solution = r.LstSq(y);
  
  
        return solution;
       }
  
     /**
      Calculate the value of the selected external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param _criterionType Selected external criterion type
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of external criterion and calculated model coefficients
      */
     PairDVXd          getResult(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                 CriterionType _criterionType, BufferValues& bufferValues)
       {
        switch(_criterionType)
          {
           case reg:
              return regularity(xTrain, xTest, yTrain, yTest, bufferValues);
           case symReg:
              return symRegularity(xTrain, xTest, yTrain, yTest, bufferValues);
           case stab:
              return stability(xTrain, xTest, yTrain, yTest, bufferValues);
           case symStab:
              return symStability(xTrain, xTest, yTrain, yTest, bufferValues);
           case unbiasedOut:
              return unbiasedOutputs(xTrain, xTest, yTrain, yTest, bufferValues);
           case symUnbiasedOut:
              return symUnbiasedOutputs(xTrain, xTest, yTrain, yTest, bufferValues);
           case unbiasedCoef:
              return unbiasedCoeffs(xTrain, xTest, yTrain, yTest, bufferValues);
           case absoluteNoiseImmun:
              return absoluteNoiseImmunity(xTrain, xTest, yTrain, yTest, bufferValues);
           case symAbsoluteNoiseImmun:
              return symAbsoluteNoiseImmunity(xTrain, xTest, yTrain, yTest, bufferValues);
          }
  
        PairDVXd pd;
        return pd;
       }
     /**
      Calculate the regularity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     param inverseSplit True, if it is necessary to swap the roles of training and testing data, otherwise false
     return The value of the regularity external criterion and calculated model coefficients
      */
     PairDVXd          regularity(matrix& xTrain, matrix& xTest, vector &yTrain, vector& yTest,
                                  BufferValues& bufferValues, bool inverseSplit = false)
       {
        PairDVXd pdv;
        vector f;
        if(!inverseSplit)
          {
           if(bufferValues.coeffsTrain.Size() == 0)
              bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
           if(bufferValues.yPredTestByTrain.Size() == 0)
              bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
           f = MathPow((yTest - bufferValues.yPredTestByTrain),2.0);
           pdv.first = f.Sum();
           pdv.second = bufferValues.coeffsTrain;
          }
        else
          {
           if(bufferValues.coeffsTest.Size() == 0)
              bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
           if(bufferValues.yPredTrainByTest.Size() == 0)
              bufferValues.yPredTrainByTest = xTrain.MatMul(bufferValues.coeffsTest);
  
           f = MathPow((yTrain - bufferValues.yPredTrainByTest),2.0);
           pdv.first = f.Sum();
           pdv.second = bufferValues.coeffsTest;
          }
  
        return pdv;
       }
     /**
      Calculate the symmetric regularity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmertic regularity external criterion and calculated model coefficients
      */
     PairDVXd          symRegularity(matrix& xTrain, matrix& xTest, vector& yTrain, vector& yTest,
                                     BufferValues& bufferValues)
       {
        PairDVXd pdv1,pdv2,pdsum;
  
        pdv1 = regularity(xTrain,xTest,yTrain,yTest,bufferValues);
        pdv2 = regularity(xTrain,xTest,yTrain,yTest,bufferValues,true);
  
        pdsum.first = pdv1.first+pdv2.first;
        pdsum.second = pdv1.second;
  
        return pdsum;
       }
  
     /**
      Calculate the stability external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     param inverseSplit True, if it is necessary to swap the roles of training and testing data, otherwise false
     return The value of the stability external criterion and calculated model coefficients
      */
     PairDVXd          stability(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                 BufferValues& bufferValues, bool inverseSplit = false)
       {
        PairDVXd pdv;
        vector f1,f2;
        if(!inverseSplit)
          {
           if(bufferValues.coeffsTrain.Size() == 0)
              bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
           if(bufferValues.yPredTrainByTrain.Size() == 0)
              bufferValues.yPredTrainByTrain = xTrain.MatMul(bufferValues.coeffsTrain);
  
           if(bufferValues.yPredTestByTrain.Size() == 0)
              bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
           f1 = MathPow((yTrain - bufferValues.yPredTrainByTrain),2.0);
           f2 = MathPow((yTest - bufferValues.yPredTestByTrain),2.0);
  
           pdv.first = f1.Sum()+f2.Sum();
           pdv.second = bufferValues.coeffsTrain;
          }
        else
          {
           if(bufferValues.coeffsTest.Size() == 0)
              bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
           if(bufferValues.yPredTrainByTest.Size() == 0)
              bufferValues.yPredTrainByTest = xTrain.MatMul(bufferValues.coeffsTest);
  
           if(bufferValues.yPredTestByTest.Size() == 0)
              bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
           f1 = MathPow((yTrain - bufferValues.yPredTrainByTest),2.0);
           f2 = MathPow((yTest - bufferValues.yPredTestByTest),2.0);
           pdv.first = f1.Sum() + f2.Sum();
           pdv.second = bufferValues.coeffsTest;
          }
  
        return pdv;
       }
  
     /**
      Calculate the symmetric stability external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmertic stability external criterion and calculated model coefficients
      */
     PairDVXd          symStability(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                    BufferValues& bufferValues)
       {
        PairDVXd pdv1,pdv2,pdsum;
  
        pdv1 = stability(xTrain, xTest, yTrain, yTest, bufferValues);
        pdv2 = stability(xTrain, xTest, yTrain, yTest, bufferValues, true);
  
        pdsum.first=pdv1.first+pdv2.first;
        pdsum.second = pdv1.second;
  
        return pdsum;
       }
  
     /**
      Calculate the unbiased outputs external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the unbiased outputs external criterion and calculated model coefficients
      */
     PairDVXd          unbiasedOutputs(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                       BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector f;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        if(bufferValues.yPredTestByTrain.Size() == 0)
           bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
        if(bufferValues.yPredTestByTest.Size() == 0)
           bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
        f = MathPow((bufferValues.yPredTestByTrain - bufferValues.yPredTestByTest),2.0);
        pdv.first = f.Sum();
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the symmetric unbiased outputs external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmetric unbiased outputs external criterion and calculated model coefficients
      */
     PairDVXd          symUnbiasedOutputs(matrix &xTrain,  matrix &xTest,  vector &yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector f1,f2;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
        if(bufferValues.yPredTrainByTrain.Size() == 0)
           bufferValues.yPredTrainByTrain = xTrain.MatMul(bufferValues.coeffsTrain);
        if(bufferValues.yPredTrainByTest.Size() == 0)
           bufferValues.yPredTrainByTest = xTrain.MatMul(bufferValues.coeffsTest);
        if(bufferValues.yPredTestByTrain.Size() == 0)
           bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
        if(bufferValues.yPredTestByTest.Size() == 0)
           bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
        f1 = MathPow((bufferValues.yPredTrainByTrain - bufferValues.yPredTrainByTest),2.0);
        f2 = MathPow((bufferValues.yPredTestByTrain - bufferValues.yPredTestByTest),2.0);
        pdv.first = f1.Sum() + f2.Sum();
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the unbiased coefficients external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the unbiased coefficients external criterion and calculated model coefficients
      */
     PairDVXd          unbiasedCoeffs(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector f1;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        f1 = MathPow((bufferValues.coeffsTrain - bufferValues.coeffsTest),2.0);
        pdv.first = f1.Sum();
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the absolute noise immunity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the absolute noise immunity external criterion and calculated model coefficients
      */
     PairDVXd          absoluteNoiseImmunity(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        vector yPredTestByAll,f1,f2;
        PairDVXd pdv;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        if(bufferValues.coeffsAll.Size() == 0)
          {
           matrix dataX(xTrain.Rows() + xTest.Rows(), xTrain.Cols());
  
           for(ulong i = 0; i<xTrain.Rows(); i++)
              dataX.Row(xTrain.Row(i),i);
  
           for(ulong i = 0; i<xTest.Rows(); i++)
              dataX.Row(xTest.Row(i),i+xTrain.Rows());
  
           vector dataY(yTrain.Size() + yTest.Size());
  
           for(ulong i=0; i<yTrain.Size(); i++)
              dataY[i] = yTrain[i];
  
           for(ulong i=0; i<yTest.Size(); i++)
              dataY[i+yTrain.Size()] = yTest[i];
  
           bufferValues.coeffsAll = findBestCoeffs(dataX, dataY);
          }
  
        if(bufferValues.yPredTestByTrain.Size() == 0)
           bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
        if(bufferValues.yPredTestByTest.Size() == 0)
           bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
        yPredTestByAll = xTest.MatMul(bufferValues.coeffsAll);
  
        f1 =  yPredTestByAll - bufferValues.yPredTestByTrain;
        f2 = bufferValues.yPredTestByTest - yPredTestByAll;
  
        pdv.first = f1.Dot(f2);
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the symmetric absolute noise immunity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmetric absolute noise immunity external criterion and calculated model coefficients
      */
     PairDVXd          symAbsoluteNoiseImmunity(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector yPredAllByTrain, yPredAllByTest, yPredAllByAll,f1,f2;
        matrix dataX(xTrain.Rows() + xTest.Rows(), xTrain.Cols());
  
        for(ulong i = 0; i<xTrain.Rows(); i++)
           dataX.Row(xTrain.Row(i),i);
  
        for(ulong i = 0; i<xTest.Rows(); i++)
           dataX.Row(xTest.Row(i),i+xTrain.Rows());
  
        vector dataY(yTrain.Size() + yTest.Size());
  
        for(ulong i=0; i<yTrain.Size(); i++)
           dataY[i] = yTrain[i];
  
        for(ulong i=0; i<yTest.Size(); i++)
           dataY[i+yTrain.Size()] = yTest[i];
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        if(bufferValues.coeffsAll.Size() == 0)
           bufferValues.coeffsAll = findBestCoeffs(dataX, dataY);
  
        yPredAllByTrain = dataX.MatMul(bufferValues.coeffsTrain);
        yPredAllByTest = dataX.MatMul(bufferValues.coeffsTest);
        yPredAllByAll = dataX.MatMul(bufferValues.coeffsAll);
  
        f1 = yPredAllByAll - yPredAllByTrain;
        f2 = yPredAllByTest - yPredAllByAll;
  
        pdv.first = f1.Dot(f2);
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
  
       }
  
     /**
      Get k models from the given ones with the best values of the external criterion
     param combinations Vector of the trained models
     param data Object containing parts of a split dataset used in model training. 在系列规则中使用参数
  参数 func 是一个函数，它使用输入变量列索引的给定组合，从原始数据中构造新的训练数据集X（train）和测试数据集X（test），然后返回这两个数据集。Parameter is used in sequential criterion
     param k Number of best models
     return Vector containing k best models
      */
     virtual void      getBestCombinations(CVector &combinations, CVector &bestCombo,SplittedData& data, MatFunc func, int k)
       {
        double proxys[];
        int best[];
  
        ArrayResize(best,combinations.size());
        ArrayResize(proxys,combinations.size());
  
        for(int i = 0 ; i<combinations.size(); i++)
          {
           proxys[i] = combinations[i].evaluation();
           best[i] = i;
          }
  
        MathQuickSortAscending(proxys,best,0,combinations.size()-1);
  
        for(int i = 0; i<int(MathMin(MathAbs(k),combinations.size())); i++)
           bestCombo.push_back(combinations[best[i]]);
  
       }
     /**
      Calculate the value of the selected external criterion for the given data.
      For the individual criterion this method only calls the getResult() method
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     return The value of the external criterion and calculated model coefficients
      */
     virtual PairDVXd  calculate(matrix& xTrain,  matrix& xTest,
                                 vector& yTrain,  vector& yTest)
       {
        BufferValues tempValues;
        return getResult(xTrain, xTest, yTrain, yTest, criterionType, tempValues);
       }
  
  public:
     ///  Construct a new Criterion object
                       Criterion() {};
  
     /**
      Construct a new Criterion object
     param _criterionType Selected external criterion type
     param _solver Selected method for linear equations solving
      */
                       Criterion(CriterionType _criterionType)
       {
        criterionType = _criterionType;
        solver = balanced;
       }
  
    };
  

gmdh_internal.mqh最后部分的两个函数：

validateInputData() - 函数用于确保传递给类的方法或其他独立函数的值是正确且符合要求的。

**
 *  Validate input parameters values
 *
 * param testSize Fraction of the input data that should be placed into the second part
 * param pAverage The number of best models based of which the external criterion for each level will be calculated
 * param threads The number of threads used for calculations. Set -1 to use max possible threads
 * param verbose 1 if the printing detailed infomation about training process is needed, otherwise 0
 * param limit The minimum value by which the external criterion should be improved in order to continue training
 * param kBest The number of best models based of which new models of the next level will be constructed
 * return Method exit status
 */
int validateInputData(double testSize=0.0, int pAverage=0, double limit=0.0, int kBest=0)
  {
   int errorCode = 0;
//
   if(testSize <= 0 || testSize >= 1)
     {
      Print("testsize value must be in the (0, 1) range");
      errorCode |= 1;
     }
   if(pAverage && pAverage < 1)
     {
      Print("p_average value must be a positive integer");
      errorCode |= 4;
     }
   if(limit && limit < 0)
     {
      Print("limit value must be non-negative");
      errorCode |= 8;
     }
   if(kBest && kBest < 1)
     {
      Print("k_best value must be a positive integer");
      errorCode |= 16;
     }

   return errorCode;
  }

timeSeriesTransformation() - 是一个实用函数，它接受一个向量作为输入，并根据所传入的lags参数将其转换为包含输入和目标的数据结构。

/**
 *  Convert the time series vector to the 2D matrix format required to work with GMDH algorithms
 *
 * param timeSeries Vector of time series data
 * param lags The lags (length) of subsets of time series into which the original time series should be divided
 * return Transformed time series data
 */
PairMVXd timeSeriesTransformation(vector& timeSeries, int lags)
  {
   PairMVXd p;

   string errorMsg = "";
   if(timeSeries.Size() == 0)
      errorMsg = "time_series value is empty";
   else
      if(lags <= 0)
         errorMsg = "lags value must be a positive integer";
      else
         if(lags >= int(timeSeries.Size()))
            errorMsg = "lags value can't be greater than  time_series  size";
   if(errorMsg != "")
      return p;

   ulong last = timeSeries.Size() - ulong(lags);
   vector yTimeSeries(last,slice,timeSeries,ulong(lags));
   matrix xTimeSeries(last, ulong(lags));
   vector vect;
   for(ulong i = 0; i < last; ++i)
     {
      vect.Init(ulong(lags),slice,timeSeries,i,i+ulong(lags-1));
      xTimeSeries.Row(vect,i);
     }

   p.first = xTimeSeries;
   p.second = yTimeSeries;

   return p;
  }

在这里，“lags”指的是先导序列值的数量，用于预测算法计算后续值。

gmdh_internal.mqh介绍完了。我们接着看第二个头文件gmdh.mqh。

首先是splitData()函数。

/**
 *  Divide the input data into 2 parts
 *
 * param x Matrix of input data containing predictive variables
 * param y Vector of the taget values for the corresponding x data
 * param testSize Fraction of the input data that should be placed into the second part
 * param shuffle True if data should be shuffled before splitting into 2 parts, otherwise false
 * param randomSeed Seed number for the random generator to get the same division every time
 * return SplittedData object containing 4 elements of data: train x, train y, test x, test y
 */
SplittedData splitData(matrix& x,  vector& y, double testSize = 0.2, bool shuffle = false, int randomSeed = 0)
  {
   SplittedData data;

   if(validateInputData(testSize))
      return data;
   
   string errorMsg = "";
   if(x.Rows() != y.Size())
      errorMsg = " x rows number and y size must be equal";
   else
      if(round(x.Rows() * testSize) == 0 || round(x.Rows() * testSize) == x.Rows())
         errorMsg = "Result contains an empty array. Change the arrays size or the  value for correct splitting";
   if(errorMsg != "")
     {
      Print(__FUNCTION__," ",errorMsg);
      return data;
     }


   if(!shuffle)
      data = GmdhModel::internalSplitData(x, y, testSize);
   else
     {
      if(randomSeed == 0)
         randomSeed = int(GetTickCount64());
      MathSrand(uint(randomSeed));

      int shuffled_rows_indexes[],shuffled[];
      MathSequence(0,int(x.Rows()-1),1,shuffled_rows_indexes);
      MathSample(shuffled_rows_indexes,int(shuffled_rows_indexes.Size()),shuffled);

      int testItemsNumber = (int)round(x.Rows() * testSize);


      matrix Train,Test;
      vector train,test;

      Train.Resize(x.Rows()-ulong(testItemsNumber),x.Cols());
      Test.Resize(ulong(testItemsNumber),x.Cols());

      train.Resize(x.Rows()-ulong(testItemsNumber));
      test.Resize(ulong(testItemsNumber));

      for(ulong i = 0; i<Train.Rows(); i++)
        {
         Train.Row(x.Row(shuffled[i]),i);
         train[i] = y[shuffled[i]];
        }

      for(ulong i = 0; i<Test.Rows(); i++)
        {
         Test.Row(x.Row(shuffled[Train.Rows()+i]),i);
         test[i] = y[shuffled[Train.Rows()+i]];
        }

      data.xTrain = Train;
      data.xTest = Test;
      data.yTrain = train;
      data.yTest = test;
     }

   return data;
  }  

它接收一个矩阵和一个向量作为输入，分别代表变量和目标。其中，“testSize”参数定义了用作测试集的数据的比例。“shuffle”控制是否启用数据集的随机乱序，“randomSeed”则指定了在打乱过程中使用的随机数生成器的种子。

接下来是“GmdhModel”类，它定义了GMDH算法的一般逻辑。

//+------------------------------------------------------------------+
//| Class implementing the general logic of GMDH algorithms          |
//+------------------------------------------------------------------+

class  GmdhModel
  {
protected:

   string            modelName; // model name
   int               level; // Current number of the algorithm training level
   int               inputColsNumber; // The number of predictive variables in the original data
   double            lastLevelEvaluation; // The external criterion value of the previous training level
   double            currentLevelEvaluation; // The external criterion value of the current training level
   bool              training_complete; // flag indicator successful completion of model training
   CVector2d         bestCombinations; // Storage for the best models of previous levels

   /**
    *struct for generating vector sequence
    */
   struct unique
     {
   private:
      int            current;

      int            run(void)
        {
         return ++current;
        }

   public:
                     unique(void)
        {
         current = -1;
        }

      vector         generate(ulong t)
        {
         ulong s=0;
         vector ret(t);

         while(s<t)
            ret[s++] = run();

         return ret;
        }
     };

   /**
    *  Find all combinations of k elements from n
    *
    * param n Number of all elements
    * param k Number of required elements
    * return Vector of all combinations of k elements from n
    */
   void              nChooseK(int n, int k, vector &combos[])
     {
      if(n<=0 || k<=0 || n<k)
        {
         Print(__FUNCTION__," invalid parameters for n and or k", "n ",n , " k ", k);
         return;
        }

      unique q;

      vector comb = q.generate(ulong(k));

      ArrayResize(combos,combos.Size()+1,100);

      long first, last;

      first = 0;
      last = long(k);
      combos[combos.Size()-1]=comb;

      while(comb[first]!= double(n - k))
        {
         long mt = last;
         while(comb[--mt] == double(n - (last - mt)));
         comb[mt]++;
         while(++mt != last)
            comb[mt] = comb[mt-1]+double(1);
         ArrayResize(combos,combos.Size()+1,100);
         combos[combos.Size()-1]=comb;
        }

      for(uint i = 0; i<combos.Size(); i++)
        {
         combos[i].Resize(combos[i].Size()+1);
         combos[i][combos[i].Size()-1] = n;
        }

      return;
     }

   /**
    *  Get the mean value of extrnal criterion of the k best models
    *
    * param sortedCombinations Sorted vector of current level models
    * param k The numebr of the best models
    * return Calculated mean value of extrnal criterion of the k best models
    */
   double            getMeanCriterionValue(CVector &sortedCombinations, int k)
     {
      k = MathMin(k, sortedCombinations.size());

      double crreval=0;

      for(int i = 0; i<k; i++)
         crreval +=sortedCombinations[i].evaluation();
      if(k)
         return crreval/double(k);
      else
        {
         Print(__FUNCTION__, " Zero divide error ");
         return 0.0;
        }
     }

   /**
    *  Get the sign of the polynomial variable coefficient
    *
    * param coeff Selected coefficient
    * param isFirstCoeff True if the selected coefficient will be the first in the polynomial representation, otherwise false
    * return String containing the sign of the coefficient
    */
   string            getPolynomialCoeffSign(double coeff, bool isFirstCoeff)
     {
      return ((coeff >= 0) ? ((isFirstCoeff) ? " " : " + ") : " - ");
     }

   /**
    *  Get the rounded value of the polynomial variable coefficient without sign
    *
    * param coeff Selected coefficient
    * param isLastCoeff True if the selected coefficient will be the last one in the polynomial representation, otherwise false
    * return String containing the rounded value of the coefficient without sign
    */
   string            getPolynomialCoeffValue(double coeff, bool isLastCoeff)
     {
      string stringCoeff = StringFormat("%e",MathAbs(coeff));
      return ((stringCoeff != "1" || isLastCoeff) ? stringCoeff : "");
     }

   /**
    *  Train given subset of models and calculate external criterion for them
    *
    * param data Data used for training and evaulating models
    * param criterion Selected external criterion
    * param beginCoeffsVec Iterator indicating the beginning of a subset of models
    * param endCoeffsVec Iterator indicating the end of a subset of models
    * param leftTasks The number of remaining untrained models at the entire level
    * param verbose 1 if the printing detailed infomation about training process is needed, otherwise 0
    */
   bool              polynomialsEvaluation(SplittedData& data,  Criterion& criterion,  CVector &combos, uint beginCoeffsVec,
                                           uint endCoeffsVec)
     {
      vector cmb,ytrain,ytest;
      matrix x1,x2;
      for(uint i = beginCoeffsVec; i<endCoeffsVec; i++)
        {
         cmb = combos[i].combination();
         x1 = xDataForCombination(data.xTrain,cmb);
         x2 = xDataForCombination(data.xTest,cmb);
         ytrain = data.yTrain;
         ytest = data.yTest;
         PairDVXd pd = criterion.calculate(x1,x2,ytrain,ytest);

         if(pd.second.HasNan()>0)
            {
             Print(__FUNCTION__," No solution found for coefficient at ", i, "\n xTrain \n", x1, "\n xTest \n", x2, "\n yTrain \n", ytrain, "\n yTest \n", ytest);
             combos[i].setEvaluation(DBL_MAX);
             combos[i].setBestCoeffs(vector::Ones(3));
            }
         else
            {
             combos[i].setEvaluation(pd.first);
             combos[i].setBestCoeffs(pd.second);
            } 
        }

      return true;
     }

   /**
   *  Determine the need to continue training and prepare the algorithm for the next level
   *
   * param kBest The number of best models based of which new models of the next level will be constructed
   * param pAverage The number of best models based of which the external criterion for each level will be calculated
   * param combinations Trained models of the current level
   * param criterion Selected external criterion
   * param data Data used for training and evaulating models
   * param limit The minimum value by which the external criterion should be improved in order to continue training
   * return True if the algorithm needs to continue training, otherwise fasle
   */
   bool              nextLevelCondition(int kBest, int pAverage, CVector &combinations,
                                        Criterion& criterion, SplittedData& data, double limit)
     {
      MatFunc fun = NULL;
      CVector bestcombinations;
      criterion.getBestCombinations(combinations,bestcombinations,data, fun, kBest);
      currentLevelEvaluation = getMeanCriterionValue(bestcombinations, pAverage);

      if(lastLevelEvaluation - currentLevelEvaluation > limit)
        {
         lastLevelEvaluation = currentLevelEvaluation;
         if(preparations(data,bestcombinations))
           {
            ++level;
            return true;
           }
        }
      removeExtraCombinations();
      return false;

     }

   /**
    *  Fit the algorithm to find the best solution
    *
    * param x Matrix of input data containing predictive variables
    * param y Vector of the taget values for the corresponding x data
    * param criterion Selected external criterion
    * param kBest The number of best models based of which new models of the next level will be constructed
    * param testSize Fraction of the input data that should be used to evaluate models at each level
    * param pAverage The number of best models based of which the external criterion for each level will be calculated
    * param limit The minimum value by which the external criterion should be improved in order to continue training
    * return A pointer to the algorithm object for which the training was performed
    */
   bool              gmdhFit(matrix& x,  vector& y,  Criterion& criterion, int kBest,
                             double testSize, int pAverage, double limit)
     {
      if(x.Rows() != y.Size())
        {
         Print("X rows number and y size must be equal");
         return false;
        }

      level = 1; // reset last training
      inputColsNumber = int(x.Cols());
      lastLevelEvaluation = DBL_MAX;

      SplittedData data = internalSplitData(x, y, testSize, true) ;
      training_complete = false;
      bool goToTheNextLevel;
      CVector evaluationCoeffsVec;
      do
        {
         vector combinations[];
         generateCombinations(int(data.xTrain.Cols() - 1),combinations);
         
         if(combinations.Size()<1)
           {
            Print(__FUNCTION__," Training aborted");
            return training_complete;
           }  

         evaluationCoeffsVec.clear();

         int currLevelEvaluation = 0;
         for(int it = 0; it < int(combinations.Size()); ++it, ++currLevelEvaluation)
           {
            Combination ncomb(combinations[it]);
            evaluationCoeffsVec.push_back(ncomb);
           }

         if(!polynomialsEvaluation(data,criterion,evaluationCoeffsVec,0,uint(currLevelEvaluation)))
           {
            Print(__FUNCTION__," Training aborted");
            return training_complete;
           }

         goToTheNextLevel = nextLevelCondition(kBest, pAverage, evaluationCoeffsVec, criterion, data, limit); // checking the results of the current level for improvement
        }
      while(goToTheNextLevel);

      training_complete = true;

      return true;
     }

   /**
    *  Get new model structures for the new level of training
    *
    * param n_cols The number of existing predictive variables at the current training level
    * return Vector of new model structures
    */
   virtual void      generateCombinations(int n_cols,vector &out[])
     {
      return;
     }


   ///  Removed the saved models that are no longer needed
   virtual void      removeExtraCombinations(void)
     {
      return;
     }

   /**
    *  Prepare data for the next training level
    *
    * param data Data used for training and evaulating models at the current level
    * param _bestCombinations Vector of the k best models of the current level
    * return True if the training process can be continued, otherwise false
    */
   virtual bool      preparations(SplittedData& data, CVector &_bestCombinations)
     {
      return false;
     }

   /**
    *  Get the data constructed according to the model structure from the original data
    *
    * param x Training data at the current level
    * param comb Vector containing the indexes of the x matrix columns that should be used in the model
    * return Constructed data
    */
   virtual matrix    xDataForCombination(matrix& x,  vector& comb)
     {
      return matrix::Zeros(10,10);
     }

   /**
    *  Get the designation of polynomial equation
    *
    * param levelIndex The number of the level counting from 0
    * param combIndex The number of polynomial in the level counting from 0
    * return The designation of polynomial equation
    */
   virtual string    getPolynomialPrefix(int levelIndex, int combIndex)
     {
      return NULL;
     }

   /**
    *  Get the string representation of the polynomial variable
    *
    * param levelIndex The number of the level counting from 0
    * param coeffIndex The number of the coefficient related to the selected variable in the polynomial counting from 0
    * param coeffsNumber The number of coefficients in the polynomial
    * param bestColsIndexes Indexes of the data columns used to construct polynomial of the model
    * return The string representation of the polynomial variable
    */
   virtual string    getPolynomialVariable(int levelIndex, int coeffIndex, int coeffsNumber,
                                           vector& bestColsIndexes)
     {
      return NULL;
     }

   /*
    *  Transform model data to JSON format for further saving
    *
    * return JSON value of model data
    */
   virtual CJAVal    toJSON(void)
     {
      CJAVal json_obj_model;

      json_obj_model["modelName"] = getModelName();
      json_obj_model["inputColsNumber"] = inputColsNumber;
      json_obj_model["bestCombinations"] = CJAVal(jtARRAY,"");


      for(int i = 0; i<bestCombinations.size(); i++)
        {

         CJAVal Array(jtARRAY,"");

         for(int k = 0; k<bestCombinations[i].size(); k++)
           {
            CJAVal collection;
            collection["combination"] = CJAVal(jtARRAY,"");
            collection["bestCoeffs"] = CJAVal(jtARRAY,"");
            vector combination = bestCombinations[i][k].combination();
            vector bestcoeff = bestCombinations[i][k].bestCoeffs();
            for(ulong j=0; j<combination.Size(); j++)
               collection["combination"].Add(int(combination[j]));
            for(ulong j=0; j<bestcoeff.Size(); j++)
               collection["bestCoeffs"].Add(bestcoeff[j],-15);
            Array.Add(collection);
           }

         json_obj_model["bestCombinations"].Add(Array);

        }

      return json_obj_model;

     }

   /**
    *  Set up model from JSON format model data
    *
    * param jsonModel Model data in JSON format
    * return Method exit status
    */
   virtual bool      fromJSON(CJAVal &jsonModel)
     {
      modelName = jsonModel["modelName"].ToStr();
      bestCombinations.clear();
      inputColsNumber = int(jsonModel["inputColsNumber"].ToInt());

      for(int i = 0; i<jsonModel["bestCombinations"].Size(); i++)
        {
         CVector member;
         for(int j = 0; j<jsonModel["bestCombinations"][i].Size(); j++)
           {
            Combination cb;
            vector c(ulong(jsonModel["bestCombinations"][i][j]["combination"].Size()));
            vector cf(ulong(jsonModel["bestCombinations"][i][j]["bestCoeffs"].Size()));
            for(int k = 0; k<jsonModel["bestCombinations"][i][j]["combination"].Size(); k++)
               c[k] = jsonModel["bestCombinations"][i][j]["combination"][k].ToDbl();
            for(int k = 0; k<jsonModel["bestCombinations"][i][j]["bestCoeffs"].Size(); k++)
               cf[k] = jsonModel["bestCombinations"][i][j]["bestCoeffs"][k].ToDbl();
            cb.setBestCoeffs(cf);
            cb.setCombination(c);
            member.push_back(cb);
           }
         bestCombinations.push_back(member);
        }
      return true;
     }



   /**
    *  Compare the number of required and actual columns of the input matrix
    *
    * param x Given matrix of input data
    */
   bool              checkMatrixColsNumber(matrix& x)
     {
      if(ulong(inputColsNumber) != x.Cols())
        {
         Print("Matrix  must have " + string(inputColsNumber) + " columns because there were " + string(inputColsNumber) + " columns in the training  matrix");
         return false;
        }

      return true;
     }
     
     

public:
   ///  Construct a new Gmdh Model object
                     GmdhModel() : level(1), lastLevelEvaluation(0) {}

   /**
   *  Get full class name
   *
   * return String containing the name of the model class
   */
   string            getModelName(void)
     {
      return modelName;
     }
   /**
     *Get number of inputs required for model
     */
    int getNumInputs(void)
     {
      return inputColsNumber;
     }

   /**
    *  Save model data into regular file
    *
    * param path Path to regular file
    */
   bool              save(string file_name)
     {

      CFileTxt modelFile;

      if(modelFile.Open(file_name,FILE_WRITE|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print("failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         CJAVal js=toJSON();
         if(modelFile.WriteString(js.Serialize())==0)
           {
            Print("failed write to ",file_name,". Error -",::GetLastError());
            return false;
           }
        }

      return true;
     }

   /**
    *  Load model data from regular file
    *
    * param path Path to regular file
    */
   bool               load(string file_name)
     {
      training_complete = false;
      CFileTxt modelFile;
      CJAVal js;

      if(modelFile.Open(file_name,FILE_READ|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print("failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         training_complete = fromJSON(js);
        }
      return training_complete;
     }
   /**
    *  Divide the input data into 2 parts without shuffling
    *
    * param x Matrix of input data containing predictive variables
    * param y Vector of the taget values for the corresponding x data
    * param testSize Fraction of the input data that should be placed into the second part
    * param addOnesCol True if it is needed to add a column of ones to the x data, otherwise false
    * return SplittedData object containing 4 elements of data: train x, train y, test x, test y
    */
   static SplittedData internalSplitData(matrix& x,  vector& y, double testSize, bool addOnesCol = false)
     {
      SplittedData data;
      ulong testItemsNumber = ulong(round(double(x.Rows()) * testSize));
      matrix Train,Test;
      vector train,test;

      if(addOnesCol)
        {
         Train.Resize(x.Rows() - testItemsNumber, x.Cols() + 1);
         Test.Resize(testItemsNumber, x.Cols() + 1);

         for(ulong i = 0; i<Train.Rows(); i++)
            Train.Row(x.Row(i),i);

         Train.Col(vector::Ones(Train.Rows()),x.Cols());

         for(ulong i = 0; i<Test.Rows(); i++)
            Test.Row(x.Row(Train.Rows()+i),i);

         Test.Col(vector::Ones(Test.Rows()),x.Cols());

        }
      else
        {
         Train.Resize(x.Rows() - testItemsNumber, x.Cols());
         Test.Resize(testItemsNumber, x.Cols());

         for(ulong i = 0; i<Train.Rows(); i++)
            Train.Row(x.Row(i),i);

         for(ulong i = 0; i<Test.Rows(); i++)
            Test.Row(x.Row(Train.Rows()+i),i);
        }

      train.Init(y.Size() - testItemsNumber,slice,y,0,y.Size() - testItemsNumber - 1);
      test.Init(testItemsNumber,slice,y,y.Size() - testItemsNumber);

      data.yTrain = train;
      data.yTest = test;

      data.xTrain = Train;
      data.xTest = Test;

      return data;
     }

   /**
    *  Get long-term forecast for the time series
    *
    * param x One row of the test time series data
    * param lags The number of lags (steps) to make a forecast for
    * return Vector containing long-term forecast
    */
   virtual vector    predict(vector& x, int lags)
     {
      return vector::Zeros(1);
     }

   /**
    *  Get the String representation of the best polynomial
    *
    * return String representation of the best polynomial
    */
   string            getBestPolynomial(void)
     {
      string polynomialStr = "";
      int ind = 0;
      for(int i = 0; i < bestCombinations.size(); ++i)
        {
         for(int j = 0; j < bestCombinations[i].size(); ++j)
           {
            vector bestColsIndexes = bestCombinations[i][j].combination();
            vector bestCoeffs = bestCombinations[i][j].bestCoeffs();
            polynomialStr += getPolynomialPrefix(i, j);
            bool isFirstCoeff = true;
            for(int k = 0; k < int(bestCoeffs.Size()); ++k)
              {
               if(bestCoeffs[k])
                 {
                  polynomialStr += getPolynomialCoeffSign(bestCoeffs[k], isFirstCoeff);
                  string coeffValuelStr = getPolynomialCoeffValue(bestCoeffs[k], (k == (bestCoeffs.Size() - 1)));
                  polynomialStr += coeffValuelStr;
                  if(coeffValuelStr != "" && k != bestCoeffs.Size() - 1)
                     polynomialStr += "*";
                  polynomialStr += getPolynomialVariable(i, k, int(bestCoeffs.Size()), bestColsIndexes);
                  isFirstCoeff = false;
                 }
              }
            if(i < bestCombinations.size() - 1 || j < (bestCombinations[i].size() - 1))
               polynomialStr += "\n";
           }//j
         if(i < bestCombinations.size() - 1 && bestCombinations[i].size() > 1)
            polynomialStr += "\n";
        }//i
      return polynomialStr;
     }

                    ~GmdhModel()
     {
      for(int i = 0; i<bestCombinations.size(); i++)
         bestCombinations[i].clear();

      bestCombinations.clear();
     }
  };


//+------------------------------------------------------------------+

这是用于派生其他GMDH类型的基类。它提供了用于训练或构建模型以及随后使用该模型进行预测的方法。“save”和“load”方法允许用户将模型保存到文件中并从文件中加载出来以供后续使用。模型以JSON格式存储到一个文本文件中，文件所在目录为所有MetaTrader终端共用的目录。

最后一个头文件mia.mqh包含了“MIA”类的定义。

//+------------------------------------------------------------------+
//| Class implementing multilayered iterative algorithm MIA          |
//+------------------------------------------------------------------+
class MIA : public GmdhModel
  {
protected:
   PolynomialType    polynomialType; // Selected polynomial type

   void              generateCombinations(int n_cols,vector &out[])  override
     {
      GmdhModel::nChooseK(n_cols,2,out);
      return;
     }
   /**
   *  Get predictions for the input data
   *
   * param x Test data of the regression task or one-step time series forecast
   * return Vector containing prediction values
   */
   virtual vector    calculatePrediction(vector& x)
     {
      if(x.Size()<ulong(inputColsNumber))
         return vector::Zeros(ulong(inputColsNumber));

      matrix modifiedX(1,x.Size()+ 1);

      modifiedX.Row(x,0);

      modifiedX[0][x.Size()] = 1.0;

      for(int i = 0; i < bestCombinations.size(); ++i)
        {
         matrix xNew(1, ulong(bestCombinations[i].size()) + 1);
         for(int j = 0; j < bestCombinations[i].size(); ++j)
           {
            vector comb = bestCombinations[i][j].combination();
            matrix xx(1,comb.Size());
            for(ulong i = 0; i<xx.Cols(); ++i)
               xx[0][i] = modifiedX[0][ulong(comb[i])];
            matrix ply = getPolynomialX(xx);
            vector c,b;
            c = bestCombinations[i][j].bestCoeffs();
            b = ply.MatMul(c);
            xNew.Col(b,ulong(j));
           }
         vector n  = vector::Ones(xNew.Rows());
         xNew.Col(n,xNew.Cols() - 1);
         modifiedX = xNew;
        }

      return modifiedX.Col(0);

     }

   /**
    *  Construct vector of the new variable values according to the selected polynomial type
    *
    * param x Matrix of input variables values for the selected polynomial type
    * return Construct vector of the new variable values
    */
   matrix            getPolynomialX(matrix& x)
     {
      matrix polyX = x;
      if((polynomialType == linear_cov))
        {
         polyX.Resize(x.Rows(), 4);
         polyX.Col(x.Col(0)*x.Col(1),2);
         polyX.Col(x.Col(2),3);
        }
      else
         if((polynomialType == quadratic))
           {
            polyX.Resize(x.Rows(), 6);
            polyX.Col(x.Col(0)*x.Col(1),2) ;
            polyX.Col(x.Col(0)*x.Col(0),3);
            polyX.Col(x.Col(1)*x.Col(1),4);
            polyX.Col(x.Col(2),5) ;
           }

      return polyX;
     }

   /**
    *  Transform data in the current training level by constructing new variables using selected polynomial type
    *
    * param data Data used to train models at the current level
    * param bestCombinations Vector of the k best models of the current level
    */
   virtual void      transformDataForNextLevel(SplittedData& data,  CVector &bestCombs)
     {
      matrix xTrainNew(data.xTrain.Rows(), ulong(bestCombs.size()) + 1);
      matrix xTestNew(data.xTest.Rows(), ulong(bestCombs.size()) + 1);

      for(int i = 0; i < bestCombs.size(); ++i)
        {
         vector comb = bestCombs[i].combination();

         matrix train(xTrainNew.Rows(),comb.Size()),test(xTrainNew.Rows(),comb.Size());

         for(ulong k = 0; k<comb.Size(); k++)
           {
            train.Col(data.xTrain.Col(ulong(comb[k])),k);
            test.Col(data.xTest.Col(ulong(comb[k])),k);
           }

         matrix polyTest,polyTrain;
         vector bcoeff = bestCombs[i].bestCoeffs();
         polyTest = getPolynomialX(test);
         polyTrain = getPolynomialX(train);

         xTrainNew.Col(polyTrain.MatMul(bcoeff),i);
         xTestNew.Col(polyTest.MatMul(bcoeff),i);
        }

      xTrainNew.Col(vector::Ones(xTrainNew.Rows()),xTrainNew.Cols() - 1);
      xTestNew.Col(vector::Ones(xTestNew.Rows()),xTestNew.Cols() - 1);

      data.xTrain = xTrainNew;
      data.xTest =  xTestNew;
     }

   virtual void      removeExtraCombinations(void) override
     {

      CVector2d realBestCombinations(bestCombinations.size());
      CVector n;
      n.push_back(bestCombinations[level-2][0]);
      realBestCombinations.setAt(realBestCombinations.size() - 1,n);

      vector comb(1);
      for(int i = realBestCombinations.size() - 1; i > 0; --i)
        {
         double usedCombinationsIndexes[],unique[];
         int indexs[];
         int prevsize = 0;
         for(int j = 0; j < realBestCombinations[i].size(); ++j)
           {
            comb = realBestCombinations[i][j].combination();
            ArrayResize(usedCombinationsIndexes,prevsize+int(comb.Size()-1),100);
            for(ulong k = 0; k < comb.Size() - 1; ++k)
               usedCombinationsIndexes[ulong(prevsize)+k] = comb[k];
            prevsize = int(usedCombinationsIndexes.Size());
           }
         MathUnique(usedCombinationsIndexes,unique);
         ArraySort(unique);

         for(uint it = 0; it<unique.Size(); ++it)
            realBestCombinations[i - 1].push_back(bestCombinations[i - 1][int(unique[it])]);

         for(int j = 0; j < realBestCombinations[i].size(); ++j)
           {
            comb = realBestCombinations[i][j].combination();
            for(ulong k = 0; k < comb.Size() - 1; ++k)
               comb[k] = ArrayBsearch(unique,comb[k]);
            comb[comb.Size() - 1] = double(unique.Size());
            realBestCombinations[i][j].setCombination(comb);
           }

         ZeroMemory(usedCombinationsIndexes);
         ZeroMemory(unique);
         ZeroMemory(indexs);
        }

      bestCombinations = realBestCombinations;
     }
   virtual bool      preparations(SplittedData& data, CVector &_bestCombinations) override
     {
      bestCombinations.push_back(_bestCombinations);
      transformDataForNextLevel(data, bestCombinations[level - 1]);
      return true;
     }
   virtual matrix    xDataForCombination(matrix& x,  vector& comb)  override
     {
      matrix xx(x.Rows(),comb.Size());

      for(ulong i = 0; i<xx.Cols(); ++i)
         xx.Col(x.Col(ulong(comb[i])),i);

      return getPolynomialX(xx);
     }

   string            getPolynomialPrefix(int levelIndex, int combIndex)  override
     {
      return ((levelIndex < bestCombinations.size() - 1) ?
              "f" + string(levelIndex + 1) + "_" + string(combIndex + 1) : "y") + " =";
     }
   string            getPolynomialVariable(int levelIndex, int coeffIndex, int coeffsNumber,
                                           vector &bestColsIndexes)  override
     {
      if(levelIndex == 0)
        {
         if(coeffIndex < 2)
            return "x" + string(int(bestColsIndexes[coeffIndex]) + 1);
         else
            if(coeffIndex == 2 && coeffsNumber > 3)
               return "x" + string(int(bestColsIndexes[0]) + 1) + "*x" + string(int(bestColsIndexes[1]) + 1);
            else
               if(coeffIndex < 5 && coeffsNumber > 4)
                  return "x" + string(int(bestColsIndexes[coeffIndex - 3]) + 1) + "^2";
        }
      else
        {
         if(coeffIndex < 2)
            return "f" + string(levelIndex) + "_" + string(int(bestColsIndexes[coeffIndex]) + 1);
         else
            if(coeffIndex == 2 && coeffsNumber > 3)
               return "f" + string(levelIndex) + "_" + string(int(bestColsIndexes[0]) + 1) +
                      "*f" + string(levelIndex) + "_" + string(int(bestColsIndexes[1]) + 1);
            else
               if(coeffIndex < 5 && coeffsNumber > 4)
                  return "f" + string(levelIndex) + "_" + string(int(bestColsIndexes[coeffIndex - 3]) + 1) + "^2";
        }
      return "";
     }


   CJAVal            toJSON(void)  override
     {
      CJAVal json_obj_model = GmdhModel::toJSON();

      json_obj_model["polynomialType"] = int(polynomialType);
      return json_obj_model;

     }

   bool              fromJSON(CJAVal &jsonModel) override
     {
      bool parsed = GmdhModel::fromJSON(jsonModel);

      if(!parsed)
         return false;

      polynomialType = PolynomialType(jsonModel["polynomialType"].ToInt());

      return true;
     }

public:
   //+------------------------------------------------------------------+
   //| Constructor                                                      |
   //+------------------------------------------------------------------+

                     MIA(void)
     {
      modelName = "MIA";
     }

   //+------------------------------------------------------------------+
   //| model a time series                                              |
   //+------------------------------------------------------------------+

   virtual bool      fit(vector &time_series,int lags,double testsize=0.5,PolynomialType _polynomialType=linear_cov,CriterionType criterion=stab,int kBest = 10,int pAverage = 1,double limit = 0.0)
     {

      if(lags < 3)
        {
         Print(__FUNCTION__," lags must be >= 3");
         return false;
        }

      PairMVXd transformed = timeSeriesTransformation(time_series,lags);

      SplittedData splited = splitData(transformed.first,transformed.second,testsize);

      Criterion criter(criterion);

      if(kBest < 3)
        {
         Print(__FUNCTION__," kBest value must be an integer >= 3");
         return false;
        }

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      polynomialType = _polynomialType;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

   //+------------------------------------------------------------------+
   //| model a multivariable data set  of inputs and targets            |
   //+------------------------------------------------------------------+

   virtual bool      fit(matrix &vars,vector &targets,double testsize=0.5,PolynomialType _polynomialType=linear_cov,CriterionType criterion=stab,int kBest = 10,int pAverage = 1,double limit = 0.0)
     {

      if(vars.Cols() < 3)
        {
         Print(__FUNCTION__," columns in vars must be >= 3");
         return false;
        }

      if(vars.Rows() != targets.Size())
        {
         Print(__FUNCTION__, " vars dimensions donot correspond with targets");
         return false;
        }

      SplittedData splited = splitData(vars,targets,testsize);

      Criterion criter(criterion);

      if(kBest < 3)
        {
         Print(__FUNCTION__," kBest value must be an integer >= 3");
         return false;
        }

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      polynomialType = _polynomialType;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

   virtual vector     predict(vector& x, int lags)  override
     {
      if(lags <= 0)
        {
         Print(__FUNCTION__," lags value must be a positive integer");
         return vector::Zeros(1);
        }

      if(!training_complete)
        {
         Print(__FUNCTION__," model was not successfully trained");
         return vector::Zeros(1);
        }

      vector expandedX = vector::Zeros(x.Size() + ulong(lags));
      for(ulong i = 0; i<x.Size(); i++)
         expandedX[i]=x[i];

      for(int i = 0; i < lags; ++i)
        {
         vector vect(x.Size(),slice,expandedX,ulong(i),x.Size()+ulong(i)-1);
         vector res = calculatePrediction(vect);
         expandedX[x.Size() + i] = res[0];
        }

      vector vect(ulong(lags),slice,expandedX,x.Size());
      return vect;
     }



  };
//+------------------------------------------------------------------+

它继承自“GmdhModel”，以实现多层迭代算法。“MIA”具有两个“fit()”方法的重载版本，可用于对给定数据集进行建模。这两个方法通过其第一个和第二个参数进行区分。当仅使用历史值对时间序列进行建模时，会使用下面列出的“fit()”方法。

fit(vector &time_series,int lags,double testsize=0.5,PolynomialType _polynomialType=linear_cov,CriterionType criterion=stab,int kBest = 10,int pAverage = 1,double limit = 0.0)

而另一个方法（即另一个“fit()”重载版本）在建模包含因变量和自变量的数据集时非常有用。两个方法的参数在下一表中给出：

数据类型	参数名称	说明
vector	time_series	代表vector动态数组中的一个时间序列
integer	lags	代表用于模型预测的延迟数
矩阵	vars	包含预测变量的输入数据矩阵
vector	targets	vars中对应行成员的目标值动态数组（vector）
CriterionType	criterion	指定模型构建过程中使用的外部标准的枚举变量
integer	kBest	它定义了最佳局部模型的数量，这些模型将作为后续层构建新输入的基础
PolynomialType	_polynomialType	在训练过程中，从现有变量中构造新变量时所选用的多项式类型
double	testSize	用于评估模型的输入数据的比例
int	pAverage	在计算停止训练的条件时考虑的最佳局部模型的数量
double	limit	为了继续训练，外部标准需要提高的最小值

一旦模型训练完成，就可以通过调用“predict()”方法来进行预测。该方法需要一个输入向量（vector）和一个指定所需预测数量的整数值。成功执行后，该方法会返回一个包含计算出的预测结果向量（vector）。否则，会返回一个零向量。在接下来的部分，我们将看几个简单的例子，以便更好地了解如何使用刚刚描述的代码。

示例

我们将通过三个以脚本形式实现的例子来进行说明。这些例子展示了MIA如何在不同的场景中进行应用。第一个例子介绍如何构建时间序列模型。它可以使用序列中一定数量的前序值来确定后续项。这个例子包含在名为MIA_Test.mq5的脚本中，其代码如下所示。

//+------------------------------------------------------------------+
//|                                                     MIA_Test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\mia.mqh>

input int NumLags = 3;
input int NumPredictions = 6;
input CriterionType critType = stab;
input PolynomialType polyType = linear_cov;
input double DataSplitSize = 0.33;
input int NumBest = 10;
input int pAverge = 1;
input double critLimit = 0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---time series we want to model
   vector tms = {1,2,3,4,5,6,7,8,9,10,11,12};
//---
   if(NumPredictions<1)
     {
      Alert("Invalid setting for NumPredictions, has to be larger than 0");
      return;
     }
//---instantiate MIA object
   MIA mia;
//---fit the series according to user defined hyper parameters
   if(!mia.fit(tms,NumLags,DataSplitSize,polyType,critType,NumBest,pAverge,critLimit))
      return;
//---generate filename based on user defined parameter settings
   string modelname = mia.getModelName()+"_"+EnumToString(critType)+"_"+string(DataSplitSize)+"_"+string(pAverge)+"_"+string(critLimit);
//---save the trained model
   mia.save(modelname+".json");
//---inputs from original series to be used for making predictions
   vector in(ulong(NumLags),slice,tms,tms.Size()-ulong(NumLags));
//---predictions made from the model
   vector out = mia.predict(in,NumPredictions);
//---output result of prediction
   Print(modelname, " predictions ", out);
//---output the polynomial that defines the model
   Print(mia.getBestPolynomial());
  }
//+------------------------------------------------------------------+

运行脚本时，用户可以更改模型的各个方面。“NumLags”指定用于计算下一项的前序序列值的数量。“NumPredictions”表示在指定序列之外要进行的预测数量。其它用户可调参数是对应于传递给“fit()”方法的参数。当模型成功构建后，它会被保存到文件中。预测结果以及与模型对应的最终多项式会被输出到终端的“Experts”（专家）标签页上。使用默认设置运行脚本的结果如下所示。所显示的多项式代表了描述给定时间序列的最佳数学模型。考虑到序列的简单性，显然没有必要搞得太复杂。然而，从预测结果来看，该模型仍然捕捉到了序列的总体趋势。

PS      0       22:37:31.246    MIA_Test (USDCHF,D1)    MIA_stab_0.33_1_0.0 predictions [13.00000000000001,14.00000000000002,15.00000000000004,16.00000000000005,17.0000000000001,18.0000000000001]
OG      0       22:37:31.246    MIA_Test (USDCHF,D1)    y = - 9.340179e-01*x1 + 1.934018e+00*x2 + 3.865363e-16*x1*x2 + 1.065982e+00

第二次运行脚本。将 NumLags 增加到 4。让我们看看这会对模型产生什么影响。

请注意，增加了一个额外的预测变量后，给模型带来了多少复杂度。以及这对预测结果产生的影响。尽管模型预测结果没有明显改善，但现在这个多项式已经扩展到了好几行。

22:37:42.921    MIA_Test (USDCHF,D1)    MIA_stab_0.33_1_0.0 predictions [13.00000000000001,14.00000000000002,15.00000000000005,16.00000000000007,17.00000000000011,18.00000000000015]
ML      0       22:37:42.921    MIA_Test (USDCHF,D1)    f1_1 = - 1.666667e-01*x2 + 1.166667e+00*x4 + 8.797938e-16*x2*x4 + 6.666667e-01
CO      0       22:37:42.921    MIA_Test (USDCHF,D1)    f1_2 = - 6.916614e-15*x3 + 1.000000e+00*x4 + 1.006270e-15*x3*x4 + 1.000000e+00
NN      0       22:37:42.921    MIA_Test (USDCHF,D1)    f1_3 = - 5.000000e-01*x1 + 1.500000e+00*x3 + 1.001110e-15*x1*x3 + 1.000000e+00
QR      0       22:37:42.921    MIA_Test (USDCHF,D1)    f2_1 = 5.000000e-01*f1_1 + 5.000000e-01*f1_3 - 5.518760e-16*f1_1*f1_3 - 1.729874e-14
HR      0       22:37:42.921    MIA_Test (USDCHF,D1)    f2_2 = 5.000000e-01*f1_1 + 5.000000e-01*f1_2 - 1.838023e-16*f1_1*f1_2 - 8.624525e-15
JK      0       22:37:42.921    MIA_Test (USDCHF,D1)    y = 5.000000e-01*f2_1 + 5.000000e-01*f2_2 - 2.963544e-16*f2_1*f2_2 - 1.003117e-14

在我们的最后一个示例中，我们来看一个不同的场景，我们想要通过自变量来建模输出。在这个示例中，我们尝试训练模型将3个输入值一起加入。The code for this example is in MIA_Multivariable_test.mq5.

//+------------------------------------------------------------------+
//|                                       MIA_miavariable_test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\mia.mqh>

input CriterionType critType = stab;
input PolynomialType polyType = linear_cov;
input double DataSplitSize = 0.33;
input int NumBest = 10;
input int pAverge = 1;
input double critLimit = 0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---simple independent and dependent data sets we want to model
   matrix independent = {{1,2,3},{3,2,1},{1,4,2},{1,1,3},{5,3,1},{3,1,9}};
   vector dependent = {6,6,7,5,9,13};
//---declare MIA object     
   MIA mia;   
//---train the model based on chosen hyper parameters
   if(!mia.fit(independent,dependent,DataSplitSize,polyType,critType,NumBest,pAverge,critLimit))
      return;
//---construct filename for generated model
   string modelname = mia.getModelName()+"_"+EnumToString(critType)+"_"+string(DataSplitSize)+"_"+string(pAverge)+"_"+string(critLimit)+"_multivars";
//---save the model
   mia.save(modelname+".json");
//---input data to be used as input for making predictions
   matrix unseen = {{1,2,4},{1,5,3},{9,1,3}};
//---make predictions and output to the terminal
  for(ulong row = 0; row<unseen.Rows(); row++)
     {
       vector in = unseen.Row(row);
       Print("inputs ", in , " prediction ", mia.predict(in,1));
     }  
//---output the polynomial that defines the model
   Print(mia.getBestPolynomial()); 
  }
//+------------------------------------------------------------------+

预测变量存储在矩阵"vars"中。每一行对应于向量“targets”中的一个目标值。与前面的示例一样，我们可以选择设置模型的各种训练参数。使用默认设置进行训练的结果非常糟糕，如下所示。

RE      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      inputs [1,2,4] prediction [5.999999999999997]
JQ      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      inputs [1,5,3] prediction [7.5]
QI      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      inputs [9,1,3] prediction [13.1]
QK      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      y = 1.900000e+00*x1 + 1.450000e+00*x2 - 9.500000e-01*x1*x2 + 3.100000e+00

通过调整训练参数，模型可以被改进优化。使用如下的参数我们得到了最好的结果。

使用这些设置，模型最终能够对一组“未见过的”输入变量做出准确预测。尽管如此，就像第一个例子中的一样，生成的多项式仍然过于复杂。

DM      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      inputs [1,2,4] prediction [6.999999999999998]
JI      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      inputs [1,5,3] prediction [8.999999999999998]
CD      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      inputs [9,1,3] prediction [13.00000000000001]
OO      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f1_1 = 1.071429e-01*x1 + 6.428571e-01*x2 + 4.392857e+00
IQ      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f1_2 = 6.086957e-01*x2 - 8.695652e-02*x3 + 4.826087e+00
PS      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f1_3 = - 1.250000e+00*x1 - 1.500000e+00*x3 + 1.125000e+01
LO      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f2_1 = 1.555556e+00*f1_1 - 6.666667e-01*f1_3 + 6.666667e-01
HN      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f2_2 = 1.620805e+00*f1_2 - 7.382550e-01*f1_3 + 7.046980e-01
PP      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f2_3 = 3.019608e+00*f1_1 - 2.029412e+00*f1_2 + 5.882353e-02
JM      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f3_1 = 1.000000e+00*f2_1 - 3.731079e-15*f2_3 + 1.155175e-14
NO      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f3_2 = 8.342665e-01*f2_2 + 1.713326e-01*f2_3 - 3.359462e-02
FD      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      y = 1.000000e+00*f3_1 + 3.122149e-16*f3_2 - 1.899249e-15

从上面简单的例子中可以清楚地看出，多层迭代算法对于基本数据集可能是过于复杂了。生成的多项式可能会变得非常复杂。此类模型存在对训练数据过拟合的风险。算法最终可能会捕捉到数据中的噪声或异常值，从而导致在新样本上的泛化性能较差。一般来说，多层迭代算法（MIA）和自组织数据挖掘算法（GMDH）的性能高度依赖于输入数据的质量和特性。噪声数据或不完整数据可能会对模型的准确性和稳定性产生不利影响，可能导致预测结果不可靠。最后，虽然训练过程相对简单，但仍然需要进行一定程度的众多参数调整才能获得最佳结果。这并不是完全自动的。

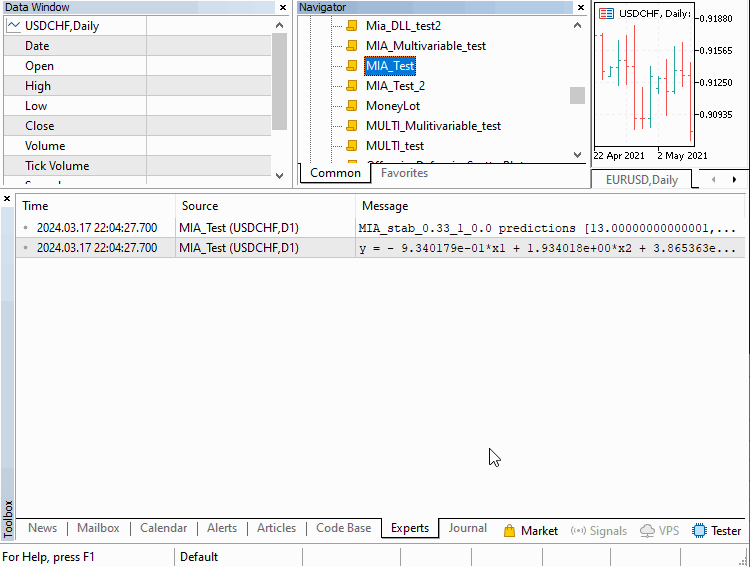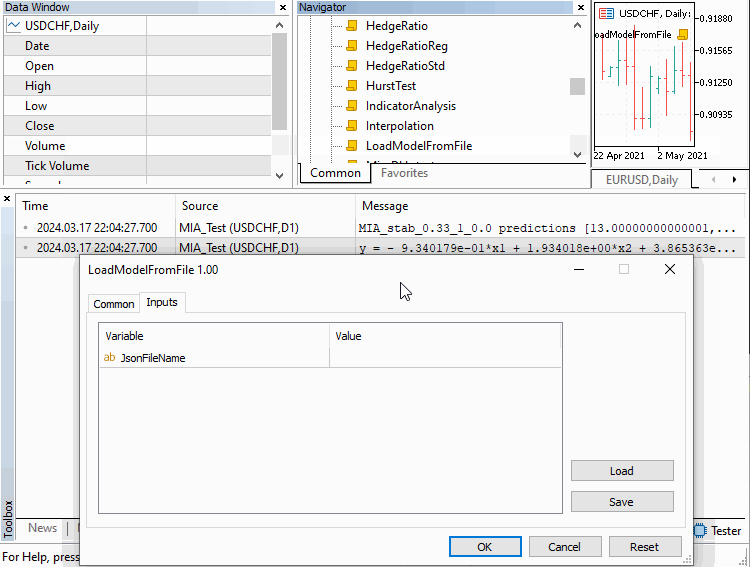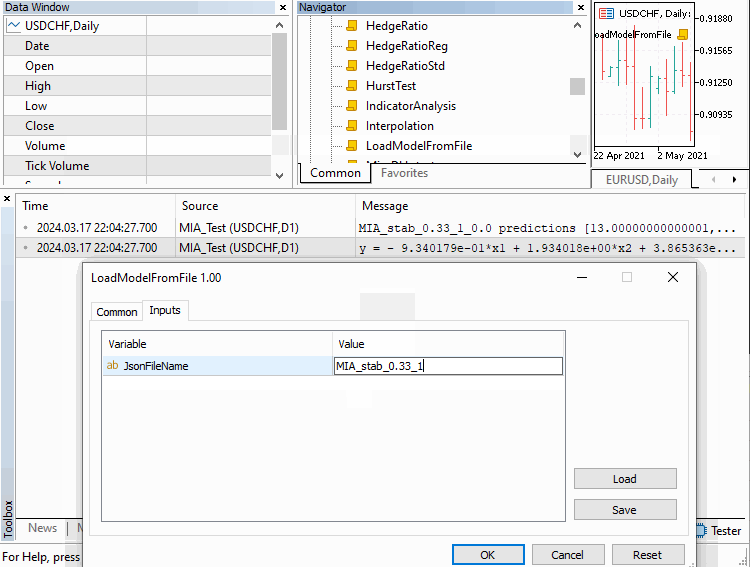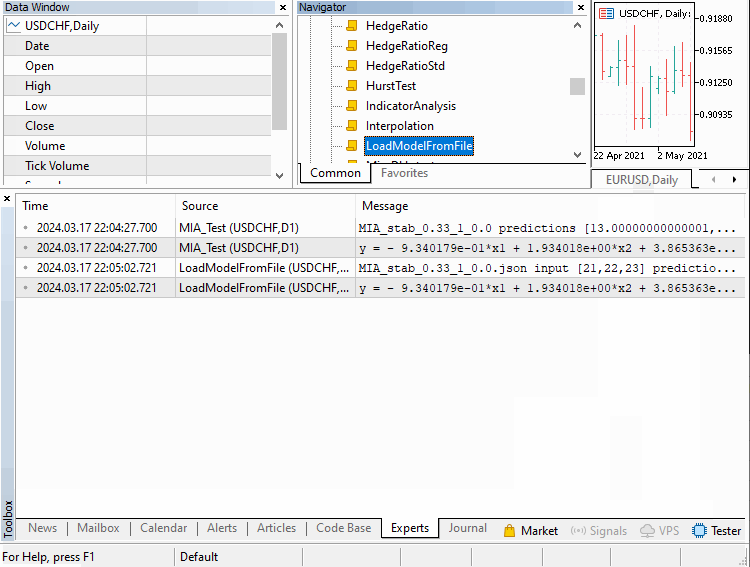
在我们的最后一个例子中，有一个脚本可以从文件中加载模型并使用它进行预测。这个例子在“LoadModelFromFile.mq5”中给出。

//+------------------------------------------------------------------+
//|                                            LoadModelFromFile.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\mia.mqh>
//--- input parameters
input string   JsonFileName="";

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---declaration of MIA instance
    MIA mia;
//---load the model from file  
    if(!mia.load(JsonFileName))
      return;
//---get the number of required inputs for the loaded model     
    int numlags = mia.getNumInputs();
//---generate arbitrary inputs to make a prediction with  
    vector inputs(ulong(numlags),arange,21.0,1.0);
//---make prediction and output results to terminal    
    Print(JsonFileName," input ", inputs," prediction ", mia.predict(inputs,1));
//---output the model's polynomial    
    Print(mia.getBestPolynomial()); 
  }
//+------------------------------------------------------------------+

以下图表说明了脚本的工作原理以及成功运行后的结果。

结论

在MQL5中实现GMDH多层迭代算法为交易者提供了一个机会，让他们能够在自己的策略中应用这一算法。该算法提供了一个动态框架，使用户能够不断适应和完善其市场分析策略。然而，尽管它应用前景广阔，但用户仍需审慎地应对其局限性。用户应注意GMDH算法对计算资源的要求，尤其是在处理大型数据集或高维数据集时。由于该算法的迭代性质，它需要进行多次计算以确定最佳模型结构，在此过程中会消耗大量时间和资源。

鉴于这些考虑因素，我们提醒用户在使用GMDH多层迭代算法时，要对其优势和局限性有细致入微的理解。虽然它提供了一个强大的动态市场分析工具，但因谨慎地考虑它的复杂性，以有效发挥其全部潜力。在对应用场景和算法复杂性深思熟虑后，交易者可以利用GMDH算法丰富其交易策略，并从市场数据中获取有价值的见解。

所有MQL5代码都附在文末。

文件	说明
Mql5\include\VectorMatrixTools.mqh	定义用于操作和处理向量与矩阵的函数的头文件（translation）
Mql5\include\JAson.mqh	包含用于解析和生成JSON对象时所使用的自定义类型的定义。
Mql5\include\GMDH\gmdh_internal.mqh	包含gmdh库中使用的自定义类型定义的头文件
Mql5\include\GMDH\gmdh.mqh	定义基类GmdhModel的头文件
Mql5\include\GMDH\mia.mqh	包含实现多层迭代算法的MIA类。
Mql5\script\MIA_Test.mq5	展示如何通过创建一个简单时间序列模型来使用MIA类的脚本
Mql5\script\MIA_Multivarible_test.mq5	展示如果通过使用MIA类来创建一个对变量数据集模型的脚本
Mql5\script\LoadModelFromFile.mq5	展示如何从json文件中加载一个模型的脚本