Algoritmos de otimização populacionais: algoritmo genético binário (Binary Genetic Algorithm, BGA). Parte II

Conteúdo:

1. Introdução
2. Descrição do algoritmo
3. Resultados dos testes

1. Introdução

No artigo anterior, apresentamos todos os conceitos e métodos básicos importantes, utilizados não apenas em algoritmos genéticos, mas, de alguma forma, em quaisquer algoritmos populacionais de otimização. Agora, com base nesses conhecimentos, podemos examinar detalhadamente o principal assunto deste "dossiê" o algoritmo genético binário (BGA). Começando com informações gerais, passamos ao código desta, em todos os sentidos, notável estratégia de busca, e finalizando com os resultados dos testes.

O algoritmo genético (GA) pertence aos algoritmos evolutivos, que incluem várias abordagens, como algoritmos genéticos, programação genética, estratégias evolutivas e outros. Eles são baseados nas ideias de evolução e hereditariedade, onde as soluções são representadas em forma de população, e operadores genéticos, como cruzamento e mutação, são aplicados para criar novas gerações de soluções.

Os algoritmos genéticos utilizam os princípios da seleção natural e genética para resolver problemas de otimização. O algoritmo genético binário (BGA) abordado no artigo foi o primeiro de todos os tipos de algoritmos genéticos. Assim, o BGA pertence à classe dos algoritmos evolutivos e é uma variante específica do algoritmo genético que utiliza a representação binária dos dados.

Os trabalhos sobre a criação de algoritmos genéticos começaram ainda na metade do século 20. Um dos pioneiros é John Holland, que em 1975 publicou o livro "Sistemas Adaptativos em Inteligência Artificial" (Adaptation in Natural and Artificial Systems), onde apresentou pela primeira vez o algoritmo genético como uma abordagem completa para resolver problemas de otimização.

O desenvolvimento do algoritmo genético binário foi inspirado por vários fatores e ideias. Os principais são:

• Seleção natural e princípios da evolução: O BGA é baseado nos princípios da seleção natural e evolução, propostos por Charles Darwin. A ideia é que na população existe uma diversidade de soluções, e aquelas que estão melhor adaptadas ao ambiente têm mais chances de sobreviver e transmitir suas características para a próxima geração.
• Genética e hereditariedade: O BGA também utiliza conceitos de genética, como gene, cromossomo e hereditariedade. As soluções no BGA são representadas como cadeias binárias, onde grupos individuais de bits representam genes específicos, e um gene, por sua vez, representa um parâmetro a ser otimizado. Os operadores genéticos, como cruzamento e mutação, são aplicados às cadeias binárias para criar novas gerações de soluções.

No geral, o desenvolvimento do BGA foi o resultado da combinação de ideias das áreas de algoritmos evolutivos, genética e otimização. Ele foi criado para resolver problemas de otimização, utilizando os princípios da seleção natural e genética, e seu desenvolvimento continua até os dias de hoje, com a criação de um grande número de variantes de GA, bem como o amplo uso de ideias e abordagens em algoritmos genéticos como parte de híbridos, incluindo algoritmos muito complexos e sofisticados.

O algoritmo genético binário, BGA, utiliza a representação binária dos dados. Isso significa que cada indivíduo (solução) é representado como uma sequência de bits (0 e 1). Operadores genéticos, como cruzamento e mutação, são aplicados às sequências de bits para criar novas gerações de soluções.

Fato interessante: os algoritmos genéticos, incluindo o BGA, podem ser usados para criar e melhorar a inteligência artificial. Por exemplo, eles podem ser aplicados para a evolução de redes neurais, permitindo a criação de modelos de aprendizado de máquina mais eficazes.

Os algoritmos genéticos em geral, e o BGA em particular, representam uma ferramenta poderosa para resolver problemas complexos de otimização, onde métodos tradicionais podem ser insuficientemente eficazes devido à ausência de uma solução analítica. No MetaTrader 5, é utilizado um GA binário, e por isso é duplamente interessante estudar os princípios de funcionamento deste notável algoritmo.

2. Descrição do algoritmo

O algoritmo genético binário inclui os seguintes passos:

1. Inicialização da população: criar uma população inicial, composta por cromossomos com valores binários aleatórios.
2. Avaliação da adaptabilidade: avaliar a adaptação de cada indivíduo (cromossomo) na população descendente.
3. Seleção: escolher os pais para criar a prole usando o método da roleta.
4. Cruzamento: dividir os cromossomos parentais em segmentos e criar novos cromossomos descendentes com segmentos de ambos os pais.
5. Inversão: dividir o cromossomo do descendente em um ponto escolhido aleatoriamente e trocar as posições dos segmentos obtidos.
   
6. Mutação: alterar bits nos genes da prole aleatoriamente com uma probabilidade de mutação determinada.
7. Avaliação da adaptabilidade da prole: avaliar a adaptabilidade de cada novo descendente.
8. Formação de uma nova população: colocar a população de descendentes no final da população geral e ordenar pelo valor de adaptação.
9. Critério de parada: repetir o processo a partir do passo 3 até atingir o critério de parada.

Para garantir que o BGA trabalhe apenas com números positivos, para simplificar as operações com sequências binárias e aumentar a velocidade dos cálculos, usaremos a distância entre os valores "max" e "min" dos parâmetros otimizáveis. Os valores positivos obtidos dessa forma serão representados em código binário de Gray e dispostos sequencialmente em um único array de caracteres do cromossomo, conforme mostrado na figura 1. Vale destacar que os pontos de quebra dos cromossomos ao executar o método de cruzamento são colocados em locais aleatórios do cromossomo e não necessariamente nos pontos de junção dos genes; os pontos de quebra podem estar dentro do espaço do gene.

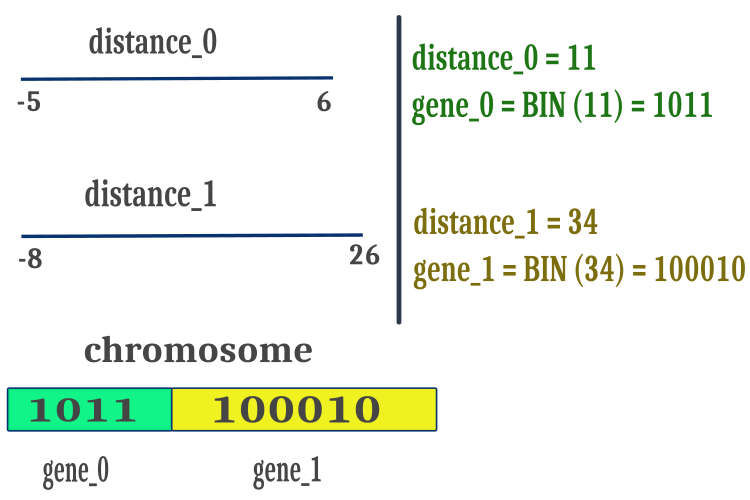
Figura 1. Disposição dos atributos do indivíduo (parâmetros otimizáveis) no cromossomo.

Há um número significativo de parâmetros externos no algoritmo genético, portanto, é sensato considerá-los com mais detalhes. Por padrão, os parâmetros praticamente correspondem totalmente às recomendações de muitos autores de publicações científicas. Eles foram verificados por mim e selecionados de forma a garantir a máxima eficiência na maioria dos tipos de tarefas. No entanto, a divergência desses parâmetros em qualquer direção pode levar à obtenção de 100% de convergência em testes com 10 ou até 50 parâmetros otimizáveis em funções específicas, mas ao mesmo tempo reduzir significativamente a eficácia em outras tarefas. Portanto, os parâmetros padrão são ótimos para uso na maioria dos casos praticamente relevantes.

• Population_P (tamanho da população = 50): o parâmetro define o número de indivíduos descendentes em cada geração da população. Esse tamanho de população é usado na maioria dos algoritmos considerados nos testes e garante um equilíbrio entre a diversidade de soluções e a velocidade de convergência.
  

• ParentPopulation_P (tamanho da população parental = 50): o parâmetro define o número de indivíduos parentais selecionados para reprodução e criação da próxima geração. A diminuição desse parâmetro melhora a convergência em funções suaves (aumenta a precisão), enquanto o aumento melhora em funções discretas (aumenta a diversidade do material genético).
  

• CrossoverProbab_P (probabilidade de cruzamento = 1.0): o parâmetro define a probabilidade de realizar a operação de cruzamento entre dois indivíduos parentais selecionados. Uma alta probabilidade de cruzamento aumenta as possibilidades combinatórias do algoritmo, enquanto a diminuição do valor aumenta a velocidade de convergência, mas aumenta a chance de estagnação.
  

• CrossoverPoints_P (número de pontos de cruzamento = 3): o parâmetro define o número de pontos onde ocorre o cruzamento entre os cromossomos parentais. O aumento dos pontos leva a uma mistura mais intensa dos parâmetros entre si e, no limite, se aproxima do comportamento aleatório do algoritmo.
  

• MutationProbab_P (probabilidade de mutação = 0.001): o parâmetro define a probabilidade de mutação de cada bit no genótipo do cromossomo. A mutação permite fazer alterações aleatórias no material genético e adicionar novas soluções à população. Uma probabilidade baixa aumenta a velocidade de convergência do algoritmo, mas diminui a diversidade, enquanto uma probabilidade muito alta leva à perda de informações úteis.

• InversionProbab_P (probabilidade de inversão = 0.7): o parâmetro define a probabilidade de realizar a operação de inversão no cromossomo. Uma alta probabilidade de inversão aumenta a diversidade do material genético, mas uma probabilidade muito alta leva ao comportamento aleatório do algoritmo.

• DoubleDigitsInChromo_P (número de dígitos decimais no gene): o parâmetro define o número de casas decimais do número real (parâmetro otimizável) representado em formato binário no cromossomo. O aumento desse valor leva ao aumento da complexidade dos cálculos e ao aumento do tempo de otimização (sem aplicar o formato binário diretamente na solução do problema, não faz sentido definir mais de 16 na saída, ao converter para double, os dígitos serão perdidos).

Passamos à análise do código.

Na inicialização dos agentes, é necessário determinar o número de bits na representação binária do parâmetro otimizável. Suponha que precisamos considerar cinco casas decimais, o que corresponde a um determinado comprimento do código de Gray. No entanto, esse código pode codificar um número que excede o necessário. Portanto, precisamos determinar o número máximo em ponto flutuante que pode ser codificado em formato binário. Posteriormente, podemos escalar o número codificado para o intervalo requerido do parâmetro otimizável na saída. Para a parte fracionária do número em ponto flutuante, utilizamos o número especificado de dígitos (indicado nos parâmetros), e para a parte inteira, quantos forem necessários em formato binário.

Por exemplo, se o parâmetro de entrada da função "digitsInGrayCode" for 3, a função retornará o valor máximo do tipo "ulong" usando o código de Gray para 3 bits, ou seja, 7 (111 no sistema binário).

Para alcançar esse objetivo determinar o número máximo possível que pode ser codificado com um determinado número de bits para as partes fracionária e inteira do número em ponto flutuante usaremos a função "GetMaxDecimalFromGray".

//——————————————————————————————————————————————————————————————————————————————
//Calculation of the maximum possible ulong number using the Gray code for a given number of bits
ulong GetMaxDecimalFromGray (int digitsInGrayCode)
{
  ulong maxValue = 1;

  for (int i = 1; i < digitsInGrayCode; i++)
  {
    maxValue <<= 1;
    maxValue |= 1;
  }

  return maxValue;
}
//——————————————————————————————————————————————————————————————————————————————

Para representar cada gene no cromossomo (posição do gene no cromossomo), usaremos a estrutura "S_BinaryGene", que contém campos e métodos para trabalhar com genes em formato binário:

• "gene": array de caracteres representando o gene.
• "integPart": array de caracteres da parte inteira do gene.
• "fractPart": array de caracteres da parte fracionária do gene.
• "integGrayDigits": número de dígitos no código de Gray para a parte inteira do gene.
• "fractGrayDigits": número de dígitos no código de Gray para a parte fracionária do gene.
• "length": comprimento total do gene.
• "minDoubleRange": valor mínimo do intervalo dos números em ponto flutuante.
• "maxDoubleRange": valor máximo do intervalo dos números em ponto flutuante.
• "maxDoubleNumber": número máximo em ponto flutuante que pode ser representado usando o gene.
• "doubleFract": valor para converter a parte fracionária do gene em número em ponto flutuante.

Métodos da estrutura:

• "Init": inicializa os campos da estrutura. Aceita valores mínimos e máximos do intervalo de números em ponto flutuante, bem como o número de dígitos na parte fracionária do gene. Dentro do método, são calculados os valores para o número máximo em ponto flutuante, partes codificantes do gene usando o código de Gray.
  

• "ToDouble": converte o gene em número em ponto flutuante. Aceita um array de caracteres do código de Gray "chromo" (cromossomo) e o índice de início do gene "indChr". O método lê a seção do cromossomo e converte o gene lido em valor decimal, depois o escala para o intervalo especificado de números em ponto flutuante.

• "Scale": executa a escala do valor de entrada "In" do intervalo "InMIN" e "InMAX" para o intervalo de saída "OutMIN" e "OutMAX". Este é um método auxiliar usado em "ToDouble".

//——————————————————————————————————————————————————————————————————————————————
struct S_BinaryGene
{
  char   gene      [];
  char   integPart [];
  char   fractPart [];

  uint   integGrayDigits;
  uint   fractGrayDigits;
  uint   length;

  double minDoubleRange;
  double maxDoubleRange;
  double maxDoubleNumber;
  double doubleFract;

  //----------------------------------------------------------------------------
  void Init (double min, double max, int doubleDigitsInChromo)
  {
    doubleFract = pow (0.1, doubleDigitsInChromo);
    
    minDoubleRange = min;
    maxDoubleRange = max - min;

    ulong decInfr = 0;

    for (int i = 0; i < doubleDigitsInChromo; i++)
    {
      decInfr += 9 * (ulong)pow (10, i);
    }
    
    //----------------------------------------
    DecimalToGray (decInfr, fractPart);
    
    ulong maxDecInFr = GetMaxDecimalFromGray (ArraySize (fractPart));
    double maxDoubFr = maxDecInFr * doubleFract;
    
    
    //----------------------------------------
    DecimalToGray ((ulong)maxDoubleRange, integPart);
    
    ulong  maxDecInInteg = GetMaxDecimalFromGray (ArraySize (integPart));
    double maxDoubInteg  = (double)maxDecInInteg + maxDoubFr;

    maxDoubleNumber = maxDoubInteg;

    ArrayResize (gene, 0, 1000);
    integGrayDigits = ArraySize (integPart);
    fractGrayDigits = ArraySize (fractPart);
    length          = integGrayDigits + fractGrayDigits;

    ArrayCopy (gene, integPart, 0,                0, WHOLE_ARRAY);
    ArrayCopy (gene, fractPart, ArraySize (gene), 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  double ToDouble (const char &chromo [], const int indChr)
  {
    double d;
    if(integGrayDigits > 0)d = (double)GrayToDecimal(chromo, indChr, indChr + integGrayDigits - 1);
    else                   d = 0.0;

    d +=(double)GrayToDecimal(chromo, indChr + integGrayDigits, indChr + integGrayDigits + fractGrayDigits - 1) * doubleFract;

    return minDoubleRange + Scale(d, 0.0, maxDoubleNumber, 0.0, maxDoubleRange);
  }

  //----------------------------------------------------------------------------
  double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX)
  {
    if (OutMIN == OutMAX) return (OutMIN);
    if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0));
    else
    {
      if (In < InMIN) return OutMIN;
      if (In > InMAX) return OutMAX;

      return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
    }
  }
};
//——————————————————————————————————————————————————————————————————————————————

Para descrever um agente, precisamos da estrutura "S_Agent", que representa o agente e contém, além do cromossomo, os seguintes dados:

• "c": array de valores das coordenadas do agente em ponto flutuante. 
• "f": valor da adaptabilidade do agente.
• "genes": array de estruturas "S_BinaryGene", descrevendo a posição de cada gene no cromossomo e as regras para converter o código binário em número em ponto flutuante.
• "chromosome": array de caracteres do cromossomo do agente.
• "calculated": valor lógico indicando se os valores do agente foram calculados (campo presente, mas não utilizado no código).

Métodos da estrutura:

• "Init": inicializa os campos da estrutura. Aceita a quantidade de coordenadas "coords", arrays "min" e "max" com os valores mínimos e máximos para cada parâmetro otimizável, bem como "doubleDigitsInChromo" o número de dígitos da parte fracionária do número em ponto flutuante no gene. O método cria e inicializa os genes para cada coordenada, além de definir o valor inicial de adaptabilidade e a flag "calculated".

• "ExtractGenes": extrai os valores dos genes do cromossomo e os salva no array "c", utilizando o método "ToDouble" da estrutura "S_BinaryGene" para converter os genes do cromossomo em números em ponto flutuante.

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (const int coords, const double &min [], const double &max [], int doubleDigitsInChromo)
  {
    ArrayResize(c, coords);
    f = -DBL_MAX;

    ArrayResize(genes, coords);
    ArrayResize(chromosome, 0, 1000);

    for(int i = 0; i < coords; i++)
    {
      genes [i].Init(min [i], max [i], doubleDigitsInChromo);
      ArrayCopy(chromosome, genes [i].gene, ArraySize(chromosome), 0, WHOLE_ARRAY);
    }

    calculated = false;
  }

  void ExtractGenes ()
  {
    uint pos = 0;

    for (int i = 0; i < ArraySize (genes); i++)
    {
      c [i] = genes [i].ToDouble (chromosome, pos);
      pos  += genes [i].length;

    }
  }

  double c []; //coordinates
  double f;    //fitness

  S_BinaryGene genes [];
  char chromosome    [];
  bool calculated;
};
//——————————————————————————————————————————————————————————————————————————————

Em seguida, o código apresenta a definição da estrutura "S_Roulette", que representa um segmento da roleta.

Campos da estrutura:

• "start": valor do ponto inicial do segmento da roleta.
• "end": valor do ponto final do segmento da roleta.

//——————————————————————————————————————————————————————————————————————————————
struct S_Roulette
{
  double start;
  double end;
};
//——————————————————————————————————————————————————————————————————————————————

Declaramos a classe "C_AO_BGA", implementando o algoritmo genético:

• "cB": array de valores das melhores coordenadas.
• "fB": valor da adaptabilidade das melhores coordenadas.
• "a": array de estruturas "S_Agent", representando os agentes.
• "rangeMax": array de valores máximos do intervalo de busca.
• "rangeMin": array de valores mínimos do intervalo de busca.
• "rangeStep": array de valores representando o passo de busca.

Métodos da classe:

• "Init": inicializa os campos da classe. Aceita os parâmetros: quantidade de coordenadas "coordsP", tamanho da população "popSizeP", tamanho da população parental "parentPopSizeP", probabilidade de cruzamento "crossoverProbabP", número de pontos de cruzamento "crossoverPointsP", probabilidade de mutação "mutationProbabP", probabilidade de inversão "inversionProbabP", número de dígitos decimais no gene "doubleDigitsInChromoP". O método inicializa variáveis internas e arrays necessários para a operação do algoritmo genético.

• "Moving": método principal do algoritmo genético, executa operações com a população, como cruzamento, mutação, inversão e avaliação de adaptabilidade.

• "Revision": método que revisa a população, ordenando os agentes e selecionando os melhores.

Campos e métodos privados da classe são utilizados para a implementação interna do algoritmo genético, incluindo operações com a roleta, escalonamento de valores, ordenação e outras operações.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BGA
{
  //----------------------------------------------------------------------------
  public: double  cB [];  //best coordinates
  public: double  fB;     //FF of the best coordinates
  public: S_Agent a  [];  //agent

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,               //coordinates number
                     const int    popSizeP,              //population size
                     const int    parentPopSizeP,        //parent population size
                     const double crossoverProbabP,      //crossover probability
                     const int    crossoverPointsP,      //crossover points
                     const double mutationProbabP,       //mutation probability
                     const double inversionProbabP,      //inversion probability
                     const int    doubleDigitsInChromoP);//number of decimal places in the gene

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;               //coordinates number
  private: int    popSize;              //population size
  private: int    parentPopSize;        //parent population size
  private: double crossoverProbab;      //crossover probability
  private: int    crossoverPoints;      //crossover points
  private: double mutationProbab;       //mutation probability
  private: double inversionProbab;      //inversion probability
  private: int    doubleDigitsInChromo; //number of decimal places in the gene
  private: bool   revision;

  private: S_Agent    parents    [];  //parents
  private: int        ind        [];  //temporary array for sorting the population
  private: double     val        [];  //temporary array for sorting the population
  private: S_Agent    pTemp      [];  //temporary array for sorting the population
  private: char       tempChrome [];  //temporary chromosome for inversion surgery
  private: uint       lengthChrome;   //length of the chromosome (the length of the string of characters according to the Gray code)
  private: int        pCount;         //indices of chromosome break points
  private: uint       poRND      [];  //temporal indices of chromosome break points
  private: uint       points     [];  //final indices of chromosome break points
  private: S_Roulette roulette   [];  //roulette

  private: void   PreCalcRoulette ();
  private: int    SpinRoulette    ();
  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: void   Sorting   (S_Agent &p [], int size);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX);
};
//——————————————————————————————————————————————————————————————————————————————

Em seguida, o código apresenta a implementação do método "Init" da classe "C_AO_BGA". Este método inicializa os campos da classe e arrays necessários para a operação do algoritmo genético.

Parâmetros de entrada do método:

• "coordsP": quantidade de coordenadas.
• "popSizeP": tamanho da população.
• "parentPopSizeP": tamanho da população parental.
• "crossoverProbabP": probabilidade de cruzamento.
• "crossoverPointsP": número de pontos de cruzamento.
• "mutationProbabP": probabilidade de mutação.
• "inversionProbabP": probabilidade de inversão.
• "doubleDigitsInChromoP": número de dígitos decimais no gene.

O método "Init" é usado para inicializar os campos da classe e arrays antes de executar o algoritmo genético. Ele define os valores dos campos da classe, verifica e corrige os valores de alguns parâmetros, além de redimensionar arrays, alocando memória para eles.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::Init (const int    coordsP,               //coordinates number
                     const int    popSizeP,              //population size
                     const int    parentPopSizeP,        //parent population size
                     const double crossoverProbabP,      //crossover probability
                     const int    crossoverPointsP,      //crossover points
                     const double mutationProbabP,       //mutation probability
                     const double inversionProbabP,      //inversion probability
                     const int    doubleDigitsInChromoP) //number of decimal places in the gene
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords               = coordsP;
  popSize              = popSizeP;
  parentPopSize        = parentPopSizeP;
  crossoverProbab      = crossoverProbabP;
  crossoverPoints      = crossoverPointsP;
  pCount               = crossoverPointsP;
  mutationProbab       = mutationProbabP;
  inversionProbab      = inversionProbabP;
  doubleDigitsInChromo = doubleDigitsInChromoP;

  if (crossoverPoints < 1) crossoverPoints = 1;
  if (pCount < 1) pCount = 1;

  ArrayResize (poRND,  pCount);
  ArrayResize (points, pCount + 2);

  ArrayResize (ind,   parentPopSize + popSize);
  ArrayResize (val,   parentPopSize + popSize);
  ArrayResize (pTemp, parentPopSize + popSize);
  ArrayResize (a,     popSize);

  ArrayResize (parents,  parentPopSize + popSize);
  ArrayResize (roulette, parentPopSize);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//——————————————————————————————————————————————————————————————————————————————

Todas as principais operações com o material genético dos agentes são executadas pelo método "Moving" da classe "C_AO_BGA". O método "Moving" executa um passo do algoritmo genético, incluindo a seleção de indivíduos parentais, cruzamento, inversão e mutação dos cromossomos, bem como a aplicação de operações aos genes e coordenadas dos indivíduos.

O método é logicamente dividido em várias partes:

1. "if (!revision)" se "revision" for "false", a inicialização dos indivíduos da população é realizada:

• O método "Init" é chamado para inicializar o indivíduo com os parâmetros dados.
• Um cromossomo aleatório é gerado preenchendo cada gene com um valor aleatório de 0 ou 1.
• O método "ExtractGenes" é chamado para extrair os genes do cromossomo.
• As coordenadas do indivíduo "c" são ajustadas para o intervalo usando a função "SeInDiSp".
• O valor de adaptabilidade de cada indivíduo "f" é definido como "-DBL_MAX".
• "lengthChrome = ArraySize(a[0].chromosome)" a duração do cromossomo do indivíduo é determinada (todos os indivíduos têm a mesma duração).
• "ArrayResize(tempChrome, lengthChrome)" o tamanho do array temporário "tempChrome" é ajustado para "lengthChrome".

2. Para cada indivíduo na população:

• O cálculo preliminar da roleta de seleção dos indivíduos parentais é realizado usando o método "PreCalcRoulette".
• A seleção do indivíduo parental é realizada usando o método "SpinRoulette".
• O cromossomo do indivíduo parental selecionado é copiado para o cromossomo do indivíduo atual.
• A operação de cruzamento é realizada com a probabilidade "crossoverProbab".
• Um segundo indivíduo parental é selecionado.
• Os pontos de quebra do cromossomo são determinados.
• O cruzamento dos cromossomos dos indivíduos parentais é realizado.
• A operação de inversão é realizada com a probabilidade "inversionProbab".
• Um ponto de quebra aleatório do cromossomo é determinado.
• As partes do cromossomo são trocadas.
• A operação de mutação é realizada para cada gene do cromossomo com a probabilidade "mutationProbab".
• O método "ExtractGenes" é chamado para extrair os genes do cromossomo.
• As coordenadas do indivíduo "c" são ajustadas para o intervalo usando a função "SeInDiSp".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      a [i].Init (coords, rangeMin, rangeMax, doubleDigitsInChromo);

      int r = 0;

      for (int len = 0; len < ArraySize (a [i].chromosome); len++)
      {
        r  = MathRand (); //[0,32767]

        if (r > 16384) a [i].chromosome [len] = 1;
        else           a [i].chromosome [len] = 0;
      }

      a [i].ExtractGenes ();

      for (int c = 0; c < coords; c++) a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      a [i].f = -DBL_MAX;
      a [i].calculated = true;
    }

    lengthChrome = ArraySize (a [0].chromosome);
    ArrayResize (tempChrome, lengthChrome);

    for (int i = 0; i < parentPopSize + popSize; i++)
    {
      parents [i].Init (coords, rangeMin, rangeMax, doubleDigitsInChromo);
      parents [i].f = -DBL_MAX;
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  int    pos       = 0;
  double r         = 0;
  uint   p1        = 0;
  uint   p2        = 0;
  uint   p3        = 0;
  uint   temp      = 0;

  for (int i = 0; i < popSize; i++)
  {
    PreCalcRoulette ();

    //selection, select and copy the parent to the child------------------------
    pos = SpinRoulette ();

    ArrayCopy (a [i].chromosome, parents [pos].chromosome, 0, 0, WHOLE_ARRAY);

    //crossover-----------------------------------------------------------------
    r = RNDfromCI (0.0, 1.0);

    if (r < crossoverProbab)
    {
      //choose a second parent to breed with------------------------------------
      pos = SpinRoulette ();

      //determination of chromosome break points--------------------------------
      for (int p = 0; p < pCount; p++)
      {
        poRND [p] = (int)RNDfromCI (0.0, lengthChrome);
        if (poRND [p] >= lengthChrome) poRND [p] = lengthChrome - 1;
      }
      ArraySort (poRND);
      ArrayCopy (points, poRND, 1, 0, WHOLE_ARRAY);
      points [0] = 0;
      points [pCount + 1] = lengthChrome - 1;

      r = RNDfromCI (0.0, 1.0);

      int startPoint = r > 0.5 ? 0 : 1;

      for (int p = startPoint; p < pCount + 2; p += 2)
      {
        if (p < pCount + 1)
        {
          for (uint len = points [p]; len < points [p + 1]; len++) a [i].chromosome [len] = parents [pos].chromosome [len];
        }
      }
    }

    //perform an inversion------------------------------------------------------
    //(break the chromosome, swap the received parts, connect them together)
    r = RNDfromCI (0.0, 1.0);

    if (r < inversionProbab)
    {
      p1 = (int)RNDfromCI (0.0, lengthChrome);
      if (p1 >= lengthChrome) p1 = lengthChrome - 1;

      //copying the second part to the beginning of the temporary array
      for (uint len = p1; len < lengthChrome; len++) tempChrome [len - p1] = a [i].chromosome [len];

      //copying the first part to the end of the temporary array
      for (uint len = 0; len < p1; len++)       tempChrome [lengthChrome - p1 + len] = a [i].chromosome [len];

      //copying a temporary array back
      for (uint len = 0; len < lengthChrome; len++)   a [i].chromosome [len] = tempChrome [len];
    }

    //perform mutation---------------------------------------------------------
    for (uint len = 0; len < lengthChrome; len++)
    {
      r = RNDfromCI (0.0, 1.0);
      if (r < mutationProbab) a [i].chromosome [len] = a [i].chromosome [len] == 1 ? 0 : 1;
    }

    a [i].ExtractGenes ();

    for (int c = 0; c < coords; c++) a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

    a [i].calculated = true;
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "Revision" realiza a revisão da população, ordena os indivíduos pelo valor de sua função de adaptabilidade e atualiza a adaptabilidade da melhor solução "fB" e as coordenadas da melhor solução "cB". Antes de ordenar a população, a população descendente é copiada para o final da população geral.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::Revision ()
{
  //----------------------------------------------------------------------------
  for (int i = parentPopSize; i < parentPopSize + popSize; i++)
  {
    parents [i] = a [i - parentPopSize];
  }

  Sorting (parents, parentPopSize + popSize);

  if (parents [0].f > fB)
  {
    fB = parents [0].f;
    ArrayCopy (cB, parents [0].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————

O código de pré-calculação da roleta representa o método "PreCalcRoulette". Este método calcula previamente os valores dos intervalos para a roleta de seleção de indivíduos com base em sua função de adaptabilidade.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::PreCalcRoulette ()
{
  roulette [0].start = parents [0].f;
  roulette [0].end   = roulette [0].start + (parents [0].f - parents [parentPopSize - 1].f);

  for (int s = 1; s < parentPopSize; s++)
  {
    if (s != parentPopSize - 1)
    {
      roulette [s].start = roulette [s - 1].end;
      roulette [s].end   = roulette [s].start + (parents [s].f - parents [parentPopSize - 1].f);
    }
    else
    {
      roulette [s].start = roulette [s - 1].end;
      roulette [s].end   = roulette [s].start + (parents [s - 1].f - parents [s].f) * 0.1;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "SpinRoulette" é usado para impor a probabilidade de escolher a posição do pai.

//——————————————————————————————————————————————————————————————————————————————
int C_AO_BGA::SpinRoulette ()
{
  double r = RNDfromCI (roulette [0].start, roulette [parentPopSize - 1].end);

  for (int s = 0; s < parentPopSize; s++)
  {
    if (roulette [s].start <= r && r < roulette [s].end) return s;
  }

  return 0;
}
//——————————————————————————————————————————————————————————————————————————————

3. Resultados dos testes

Impressão do funcionamento do algoritmo genético binário (BGA) no ambiente de teste:

C_AO_BGA:50:50:1.0:3:0.001:0.7:3
=============================
5 Hilly's; Func runs: 10000; result: 0.9999191151339382
25 Hilly's; Func runs: 10000; result: 0.994841435673127
500 Hilly's; Func runs: 10000; result: 0.5048331764136147
=============================
5 Forest's; Func runs: 10000; result: 1.0
25 Forest's; Func runs: 10000; result: 0.9997457419655973
500 Forest's; Func runs: 10000; result: 0.32054251149158375
=============================
5 Megacity's; Func runs: 10000; result: 0.9066666666666668
25 Megacity's; Func runs: 10000; result: 0.9640000000000001
500 Megacity's; Func runs: 10000; result: 0.23034999999999997
=============================
All score: 6.92090 (76.90%)

A visualização do processo de otimização do BGA demonstra claramente a alta convergência do algoritmo. É interessante notar que, no processo de otimização, uma parte da população permanece distante do extremo global, o que indica a exploração de novas áreas desconhecidas do espaço de busca, mantendo a diversidade de soluções na população. No entanto, o algoritmo enfrenta certas dificuldades ao trabalhar com a função discreta "Megacity", que é problemática para a maioria dos algoritmos. Apesar de certa dispersão nos resultados ao trabalhar com essa função complexa, o BGA se destaca significativamente melhor que outros algoritmos.

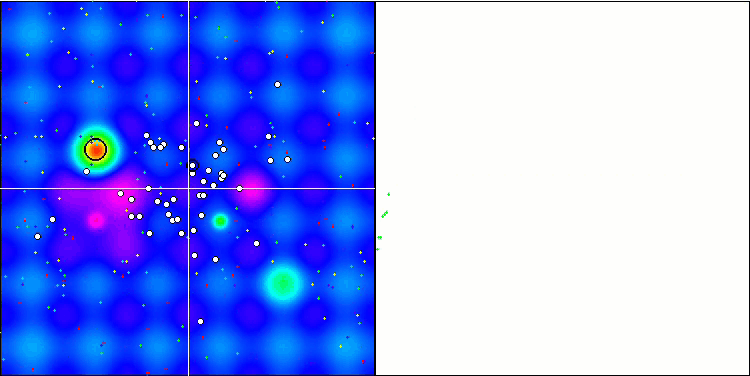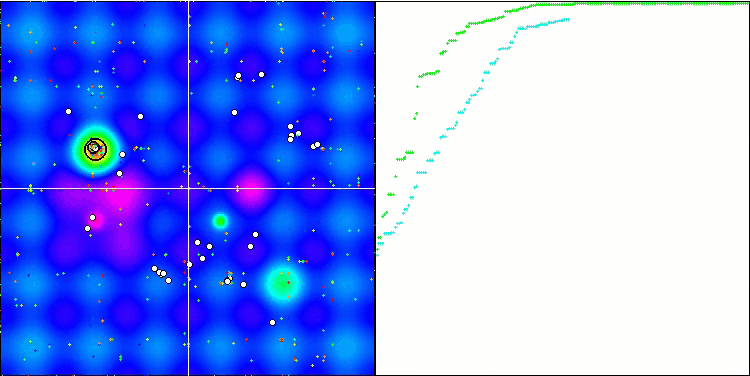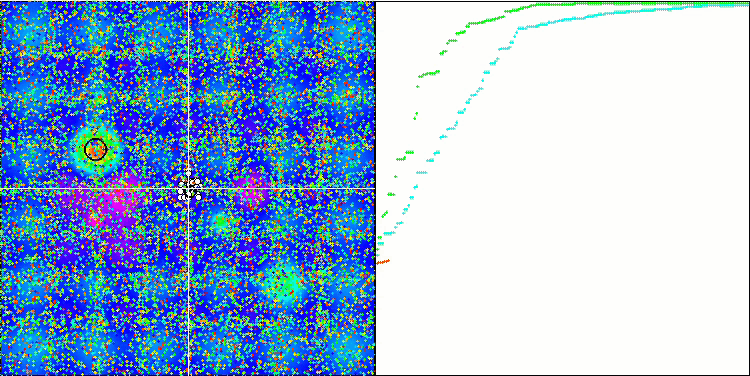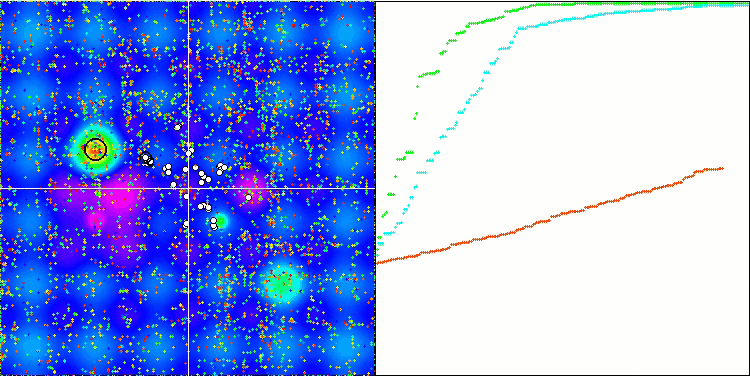
BGA na função de teste Hilly.

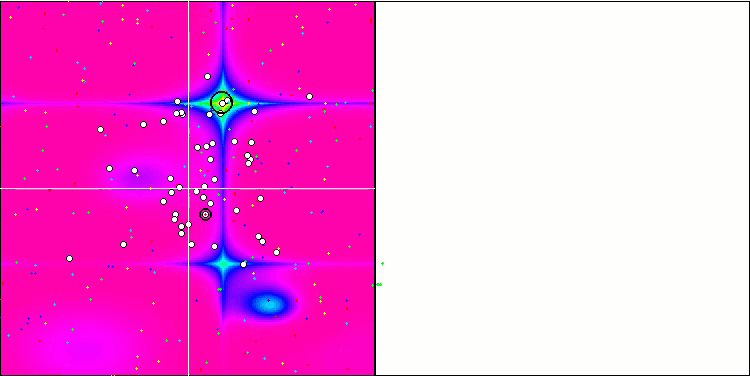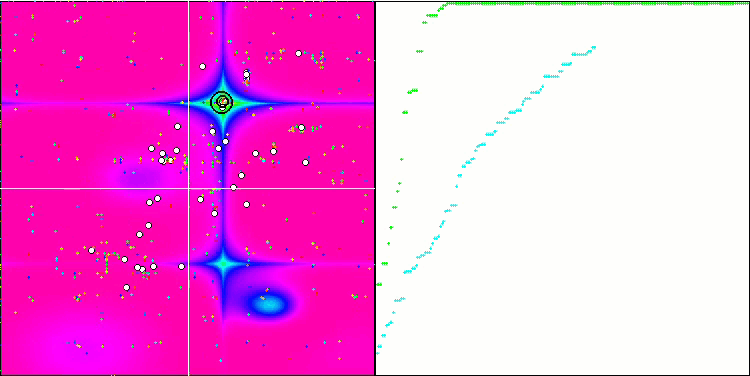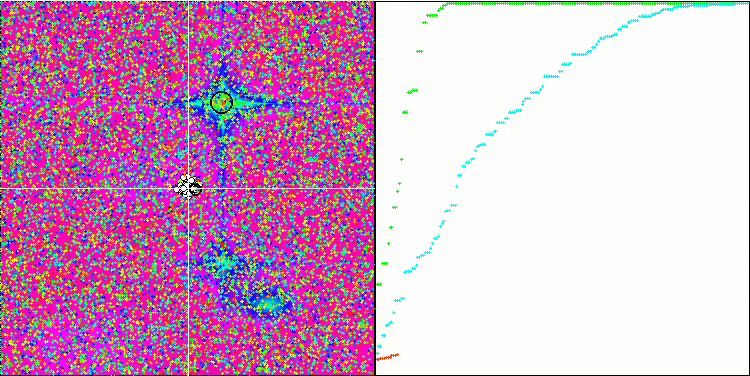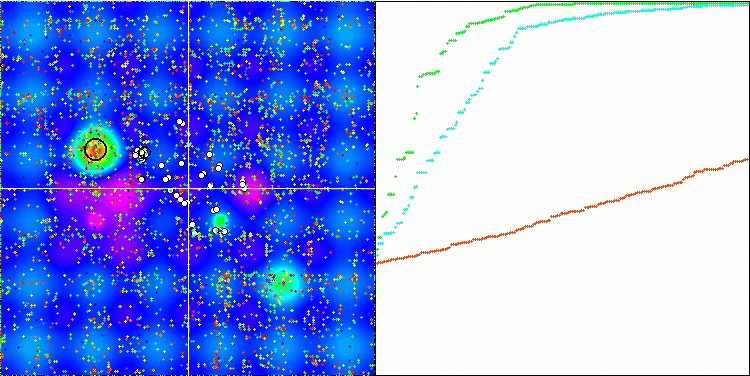
BGA na função de teste Forest.

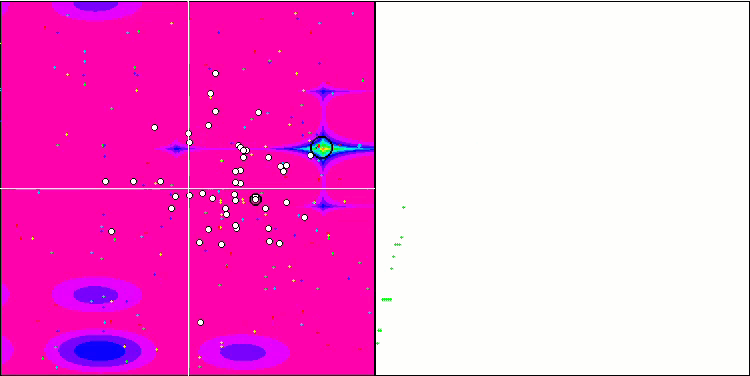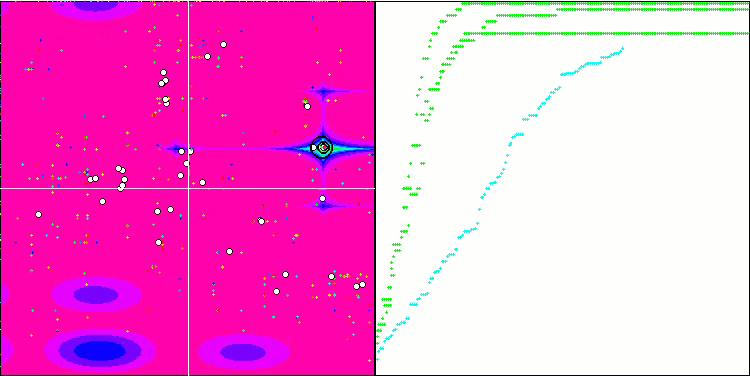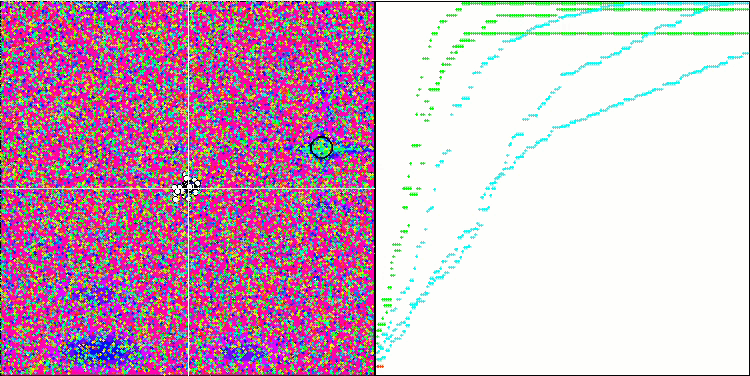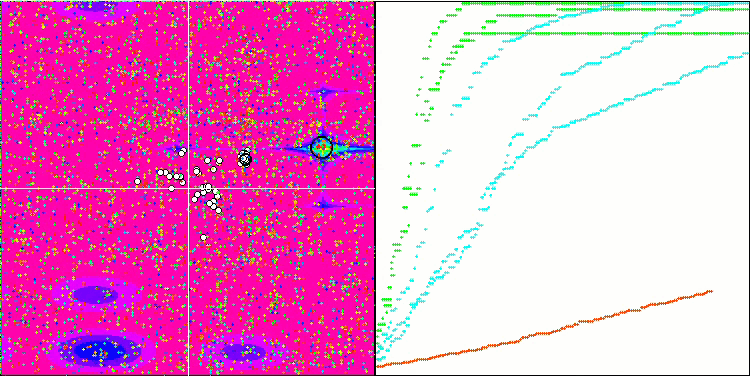
BGA na função de teste Megacity.

O BGA ocupou o primeiro lugar na tabela de classificação, demonstrando os melhores resultados na maioria dos testes para todas as três funções de teste. Os resultados do BGA foram especialmente impressionantes na função discreta Megacity, superando outros algoritmos.

№ AO Description Hilly Hilly final Forest Forest final Megacity (discrete) Megacity final Final result % of MAX 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 1 BGA binary genetic algorithm 0,99992 0,99484 0,50483 2,49959 1,00000 0,99975 0,32054 2,32029 0,90667 0,96400 0,23035 2,10102 6,921 76,90 2 (P+O)ES (P+O) evolution strategies 0,99934 0,91895 0,56297 2,48127 1,00000 0,93522 0,39179 2,32701 0,83167 0,64433 0,21155 1,68755 6,496 72,18 3 SDSm stochastic diffusion search M 0,93066 0,85445 0,39476 2,17988 0,99983 0,89244 0,19619 2,08846 0,72333 0,61100 0,10670 1,44103 5,709 63,44 4 SIA simulated isotropic annealing 0,95784 0,84264 0,41465 2,21513 0,98239 0,79586 0,20507 1,98332 0,68667 0,49300 0,09053 1,27020 5,469 60,76 5 DE differential evolution 0,95044 0,61674 0,30308 1,87026 0,95317 0,78896 0,16652 1,90865 0,78667 0,36033 0,02953 1,17653 4,955 55,06 6 HS harmony search 0,86509 0,68782 0,32527 1,87818 0,99999 0,68002 0,09590 1,77592 0,62000 0,42267 0,05458 1,09725 4,751 52,79 7 SSG saplings sowing and growing 0,77839 0,64925 0,39543 1,82308 0,85973 0,62467 0,17429 1,65869 0,64667 0,44133 0,10598 1,19398 4,676 51,95 8 (PO)ES (PO) evolution strategies 0,79025 0,62647 0,42935 1,84606 0,87616 0,60943 0,19591 1,68151 0,59000 0,37933 0,11322 1,08255 4,610 51,22 9 ACOm ant colony optimization M 0,88190 0,66127 0,30377 1,84693 0,85873 0,58680 0,15051 1,59604 0,59667 0,37333 0,02472 0,99472 4,438 49,31 10 BFO-GA bacterial foraging optimization ga 0,89150 0,55111 0,31529 1,75790 0,96982 0,39612 0,06305 1,42899 0,72667 0,27500 0,03525 1,03692 4,224 46,93 11 MEC mind evolutionary computation 0,69533 0,53376 0,32661 1,55569 0,72464 0,33036 0,07198 1,12698 0,52500 0,22000 0,04198 0,78698 3,470 38,55 12 IWO invasive weed optimization 0,72679 0,52256 0,33123 1,58058 0,70756 0,33955 0,07484 1,12196 0,42333 0,23067 0,04617 0,70017 3,403 37,81 13 Micro-AIS micro artificial immune system 0,79547 0,51922 0,30861 1,62330 0,72956 0,36879 0,09398 1,19233 0,37667 0,15867 0,02802 0,56335 3,379 37,54 14 COAm cuckoo optimization algorithm M 0,75820 0,48652 0,31369 1,55841 0,74054 0,28051 0,05599 1,07704 0,50500 0,17467 0,03380 0,71347 3,349 37,21 15 SDOm spiral dynamics optimization M 0,74601 0,44623 0,29687 1,48912 0,70204 0,34678 0,10944 1,15826 0,42833 0,16767 0,03663 0,63263 3,280 36,44 16 NMm Nelder-Mead method M 0,73807 0,50598 0,31342 1,55747 0,63674 0,28302 0,08221 1,00197 0,44667 0,18667 0,04028 0,67362 3,233 35,92 17 FAm firefly algorithm M 0,58634 0,47228 0,32276 1,38138 0,68467 0,37439 0,10908 1,16814 0,28667 0,16467 0,04722 0,49855 3,048 33,87 18 GSA gravitational search algorithm 0,64757 0,49197 0,30062 1,44016 0,53962 0,36353 0,09945 1,00260 0,32667 0,12200 0,01917 0,46783 2,911 32,34 19 BFO bacterial foraging optimization 0,61171 0,43270 0,31318 1,35759 0,54410 0,21511 0,05676 0,81597 0,42167 0,13800 0,03195 0,59162 2,765 30,72 20 ABC artificial bee colony 0,63377 0,42402 0,30892 1,36671 0,55103 0,21874 0,05623 0,82600 0,34000 0,14200 0,03102 0,51302 2,706 30,06 21 BA bat algorithm 0,59761 0,45911 0,35242 1,40915 0,40321 0,19313 0,07175 0,66810 0,21000 0,10100 0,03517 0,34617 2,423 26,93 22 SA simulated annealing 0,55787 0,42177 0,31549 1,29513 0,34998 0,15259 0,05023 0,55280 0,31167 0,10033 0,02883 0,44083 2,289 25,43 23 IWDm intelligent water drops M 0,54501 0,37897 0,30124 1,22522 0,46104 0,14704 0,04369 0,65177 0,25833 0,09700 0,02308 0,37842 2,255 25,06 24 PSO particle swarm optimisation 0,59726 0,36923 0,29928 1,26577 0,37237 0,16324 0,07010 0,60572 0,25667 0,08000 0,02157 0,35823 2,230 24,77 25 MA monkey algorithm 0,59107 0,42681 0,31816 1,33604 0,31138 0,14069 0,06612 0,51819 0,22833 0,08567 0,02790 0,34190 2,196 24,40 26 SFL shuffled frog-leaping 0,53925 0,35816 0,29809 1,19551 0,37141 0,11427 0,04051 0,52618 0,27167 0,08667 0,02402 0,38235 2,104 23,38 27 FSS fish school search 0,55669 0,39992 0,31172 1,26833 0,31009 0,11889 0,04569 0,47467 0,21167 0,07633 0,02488 0,31288 2,056 22,84 28 RND random 0,52033 0,36068 0,30133 1,18234 0,31335 0,11787 0,04354 0,47476 0,25333 0,07933 0,02382 0,35648 2,014 22,37 29 GWO grey wolf optimizer 0,59169 0,36561 0,29595 1,25326 0,24499 0,09047 0,03612 0,37158 0,27667 0,08567 0,02170 0,38403 2,009 22,32 30 CSS charged system search 0,44252 0,35454 0,35201 1,14907 0,24140 0,11345 0,06814 0,42299 0,18333 0,06300 0,02322 0,26955 1,842 20,46 31 EM electroMagnetism-like algorithm 0,46250 0,34594 0,32285 1,13129 0,21245 0,09783 0,10057 0,41085 0,15667 0,06033 0,02712 0,24412 1,786 19,85

Considerações finais

Neste artigo, examinamos a versão clássica do BGA, um caso específico da classe geral dos algoritmos genéticos (GA), e todas as conclusões se referem a ele. Apesar da antiga ideia de representar soluções de forma binária, a abordagem utilizando código binário permanece relevante até hoje. Ela integra dimensões espaciais independentes do problema de otimização em uma única entidade, codificando informações em um único cromossomo, algo que é difícil de realizar com a codificação tradicional em ponto flutuante, destacando assim este algoritmo entre outros algoritmos de otimização.

Embora eu entenda perfeitamente a matemática e a lógica da estratégia BGA, ainda fico maravilhado com o que acontece com o cromossomo. É como comparar isso a um caleidoscópio mágico. Quando giramos o caleidoscópio, diversas formas e cores se combinam em padrões únicos, criando uma imagem impressionante. Da mesma forma, o operador de cruzamento no BGA corta aleatoriamente o cromossomo em várias partes, incluindo áreas internas dos parâmetros. Essas partes são então reunidas, semelhante à mistura de fragmentos do caleidoscópio. Esse processo permite combinar as melhores características de diferentes soluções e criar uma nova combinação mais otimizada. Como no caso do caleidoscópio, os resultados do cruzamento no BGA podem ser surpreendentes e inesperados, transformando cromossomos simples em verdadeiros "diamantes" de soluções ótimas.

Estou confiante de que a informação nas duas partes do artigo sobre métodos e ferramentas usadas em algoritmos genéticos ajudará você a expandir seu conhecimento e alcançar novos patamares em seu trabalho e pesquisas. Na natureza, na engenharia e na mente humana, a força da evolução se manifesta continuamente, e o BGA é um dos muitos algoritmos incríveis que nos ajudam a alcançar novos patamares e conquistas.

O BGA resolve eficientemente diversas tarefas, seja em superfícies suaves, problemas discretos ou até mesmo problemas de grande dimensionalidade, inclusive utilizando uma abordagem estocástica, abrindo novas possibilidades onde as soluções analíticas são limitadas.

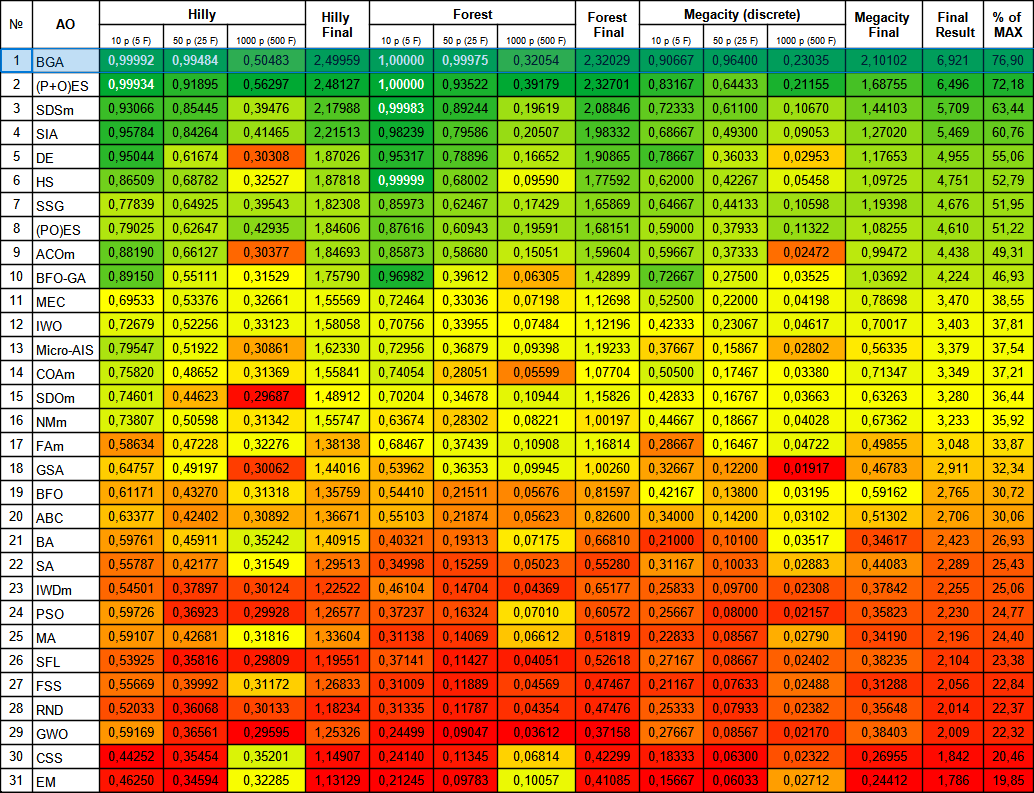
Figura 2. Graduação de cores dos algoritmos nos testes correspondentes. Resultados iguais ou superiores a 0.99 são destacados em branco.

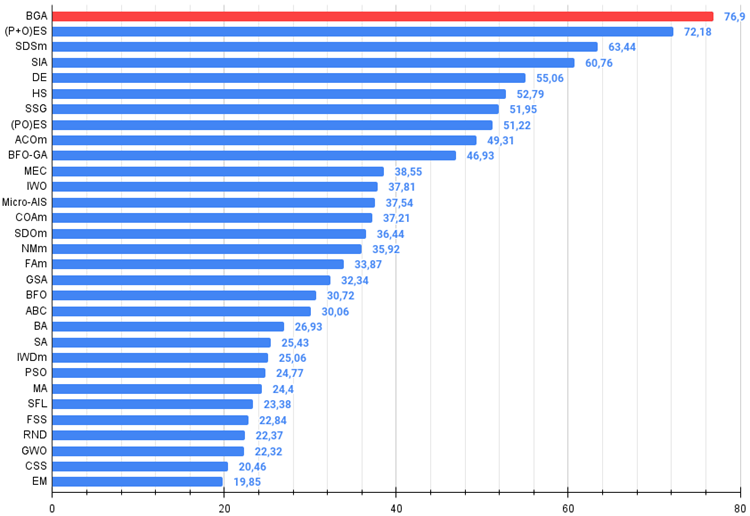
Figura 3. Histograma dos resultados dos testes dos algoritmos (na escala de 0 a 100, quanto maior, melhor,

onde 100 é o resultado teórico máximo possível, o script para cálculo da tabela de classificação está no arquivo).

Vantagens e desvantagens do algoritmo genético binário (BGA), referem-se exclusivamente à implementação apresentada:

Vantagens:

1. Alta eficiência na resolução de diversas tarefas.
2. Resistência a ficar preso em soluções locais.
3. Altos resultados tanto em funções suaves quanto em funções discretas complexas.
4. Alta convergência.

Desvantagens:

1. Grande quantidade de parâmetros externos.
   
2. Implementação do algoritmo bastante complexa.
   
3. Alta complexidade computacional.
   

Um arquivo com versões atualizadas e atuais dos códigos dos algoritmos descritos em artigos anteriores está anexado ao artigo. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitas modificações foram feitas para melhorar as capacidades de busca. As conclusões e julgamentos apresentados nos artigos são baseados nos resultados dos experimentos realizados.