使用 Python 的深度学习 GRU 模型到使用 EA 的 ONNX，以及 GRU 与 LSTM 模型的比较

概述

这是 使用 Python、MetaTrader5 Python 包和 ONNX 模型文件进行深度学习预测和下单 一文的延续，但您可以在没有读过前一篇文章的情况下继续这篇文章。一切都会得到解释，我们将使用到的所有内容都包含在本文中。在本节中，我们将指导您完成整个过程，最终创建一个用于交易和后续测试的专家顾问 (EA)。

机器学习是人工智能 (AI) 的一个子集，专注于开发算法和统计模型，使计算机无需明确编程即可执行任务。机器学习的主要目标是使计算机能够从数据中学习并随着时间的推移提高其性能。

模型如何运作

让我们使用机器学习模型操作和应用的基本原理。虽然对于已经有统计建模或机器学习经验的人来说这似乎很简单，但请放心，我们将很快转向开发复杂而强大的模型。

我们首先将关注一个称为决策树的模型。虽然有更复杂的模型可以提供更高的预测准确性，但决策树由于其简单性和在构建数据科学领域一些最先进的模型中发挥的基本作用，成为一个可访问的切入点。

为了简化问题，让我们从决策树最基本的形式开始。

在此我们仅将房屋分为两类。每栋符合条件的房屋的预期价格来自同一类别房屋的历史平均价格。

它使用数据来确定将房屋分为这两组的最佳方法，然后确定每组的预期价格。这一关键步骤，即模型从数据中捕获模式，被称为拟合或训练模型。用于此目的的数据集称为训练数据。

模型拟合的复杂性，包括数据分割决策，已经足够复杂，稍后将更详细地介绍。一旦模型拟合完毕，就可以运用于新数据来预测更多房屋的价格。

改进决策树

下面显示的两个决策树中，哪一个更有可能在调整房地产训练数据的过程中出现？

左边的决策树（决策树 1）可能更符合现实，因为它反映了卧室数量与较高的房屋销售价格之间的相关性。然而，其主要缺点是它没有考虑到影响房价的许多其他因素，如浴室数量、地块大小、位置等。

为了考虑更广泛的因素，人们可以使用具有额外“分裂”的树，称为“更深”的树。例如，考虑每个房屋总地块面积的决策树可能如下所示：

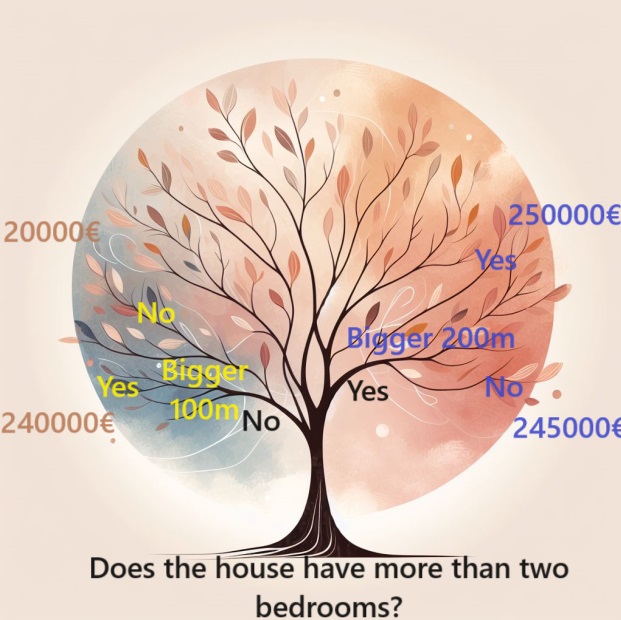
要估算房屋的价格，请遵循决策树的分支，始终选择与房屋具体特征相匹配的路径。房屋的预测价格位于树的末端。做出预测的这个特定点称为“叶子”。

这些叶子的划分和值受到数据的影响，提示您查看正在使用的数据集。

使用 Pandas 处理数据

在任何机器学习项目的初始阶段，您都需要熟悉数据集。由此可见 Pandas 库是不可或缺的。数据科学家通常使用 Pandas 作为检查和处理数据的主要工具。在代码中，通常把它缩写为“pd”

import pandas as pd

选择建模数据

数据集有大量的变量，很难理解甚至清晰地呈现。我们如何将大量数据组织成更易于管理的形式，以便更好地理解它？

我们的第一种方法是根据直觉选择变量子集。接下来，我们将引入能够自动对变量进行优先排序的统计技术。

为了确定要选择的变量或列，我们首先需要检查数据集中所有列的完整列表。

我们使用这种方式导入了这些数据：

mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_H1, start_date, end_date)

建立模型

为了创建模型，最好的资源是 scikit-learn 库，在代码中通常缩写为 sklearn。Scikit-learn 是建模通常存储在 DataFrames 中的数据类型的首选。

以下是创建和使用模型的关键步骤：

• 定义：确定您想要创建的模型类型。它是决策树吗，或者你会选择不同的模型？您还可以为所选模型类型定义特定参数。
• 自定义：此阶段是建模的核心，您的模型从提供的数据中学习和捕获模式。它包括在数据集上训练模型。
• 预测：听起来很简单，这一步就是使用训练好的模型对新的或未见过的数据进行预测。该模型概括了它所学到的做出有根据的预测的知识。
• 评估：评估模型预测的准确性。这一关键步骤将模型的输出与实际结果进行比较，以便您评估其性能和可靠性。

使用scikit-learn，这些步骤提供了一个结构化的框架，用于有效地构建、训练和评估针对 DataFrames 中常见的不同数据量身定制的模型。

门控循环单元（GRU）

维基百科说到：

门控循环单元（GRU）是循环神经网络中的一种门控机制，由 Kyunghyun Cho 于 2014 年提出。GRU 类似于具有门控机制的长短期记忆（LSTM）来输入或忘记某些特征，但缺少上下文向量或输出门，因此参数比 LSTM 少。 GRU 在复调音乐建模、语音信号建模和自然语言处理等特定任务上的表现与 LSTM 相似。 GRU 表明，门控总体上确实有帮助，而 Bengio 的团队并没有就这两个门控单元哪一个更好得出具体的结论。

GRU 是门控循环单元 (Gated Recurrent Unit) 的缩写，代表类似于 LSTM（长短期记忆，Long Short-Term Memory）的循环神经网络 (RNN，recurrent neural network) 架构的变体。

与 LSTM 非常相似，GRU 是为对顺序数据进行建模而设计的，能够跨时间选择性地保留或省略信息。值得注意的是，GRU 相对于 LSTM 拥有精简的架构，参数更少。这一特性提高了训练的便利性和计算效率。

GRU 和 LSTM 的主要区别在于它们对记忆单元状态的处理。在 LSTM 中，记忆单元状态与隐藏状态不同，并通过三个门进行更新：输入门、输出门和遗忘门。相反，GRU 用“候选激活向量”取代记忆单元状态，通过两个门进行更新：重置门和更新门。

总之，GRU 成为序列数据建模中 LSTM 的首选替代方案，特别是在存在计算约束或需要更简单架构的情况下。

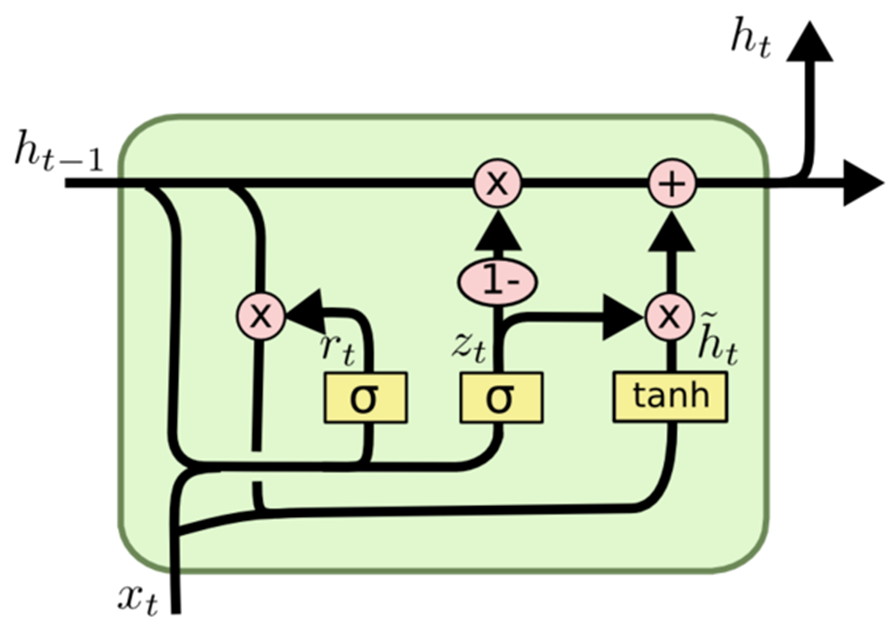
GRU 如何运行：

与其他循环神经网络架构类似，GRU 逐个元素地处理序列数据，并根据当前输入和前一个隐藏状态调整其隐藏状态。在每个时间步骤中，GRU 都会计算一个“候选激活向量”，融合来自输入和先前隐藏状态的信息。然后，该向量会更新后续时间步骤的隐藏状态。

候选激活向量是使用两个门来计算的：重置门和更新门。重置门决定了对先前隐藏状态的遗忘程度，而更新门则影响候选激活向量与新隐藏状态的整合。

这就是我们将在本文中选择的模型（GRU）。

model.add(Dense(128, activation='relu', input_shape=(inp_history_size,1), kernel_regularizer=l2(k_reg)))
model.add(Dropout(0.05))
model.add(Dense(256, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dropout(0.05))
model.add(Dense(128, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dropout(0.05))
model.add(Dense(64, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dropout(0.05))
model.add(Dense(1, activation='linear'))

首先，我们选择特征中的输入和目标变量

if 'Close' in data.columns:
    data['target'] = data['Close']
else:
    data['target'] = data.iloc[:, 0]

# Extract OHLC columns
x_features = data[[0]]
# Target variable
y_target = data['target']

我们将数据放入训练集和测试集中

x_train, x_test, y_train, y_test = train_test_split(x_features, y_target, test_size=0.2, shuffle=False)

这里的测试集大小是 20%，通常，测试集大小选择小于 30%（以避免过度拟合）

顺序模型初始化：

model = Sequential()

此行创建了一个空的顺序模型，允许您逐步添加层级。

添加密集层：

model.add(Dense(128, activation='relu', input_shape=(X_train.shape[1],), kernel_regularizer=l2(k_reg)))
model.add(Dense(256, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(128, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(64, activation='relu', kernel_regularizer=l2(k_reg)))

密集层是神经网络中的全连接层。

括号中的数字表示每层的神经元数量。因此，第一层由 128 个神经元组成，第二层由 256 个神经元组成，第三层由 128 个神经元组成，第四层由 64 个神经元组成。

激活函数“relu”（整流线性单元）用于在每一层后引入非线性，这有助于模型学习复杂的模式。

参数 input_shape 仅在第一层指定，定义输入数据的形状。在这种情况下，它对应于输入数据中的特征数量。

kernel_regularizer=l2(k_reg) 将 L2 正则化应用于层的权重，并通过惩罚较大的权重值来帮助防止过度拟合。

输出层：

model.add(Dense(1, activation='linear'))

• 最后一层由一个神经元组成，这是回归任务（预测连续值）的典型代表。
• 使用“linear”激活函数，这意味着输出是输入的线性组合，无需进一步变换。
• 总之，该模型由几个密集层组成，这些层具有校正的线性单元激活函数，后面是线性输出层。对于正则化，对权重应用了 L2 正则化。这种架构通常用于目标是预测数值的回归任务。

我们现在编译模型

# Compile the model[]
model.compile(optimizer='adam', loss='mean_squared_error')

优化器：

优化器是训练过程的关键组成部分。它决定了在训练过程中如何更新模型的权重以最小化损失函数。'adam' 是一种流行的优化算法，以其在训练神经网络的效率而闻名。它单独调整每个参数的学习率，因此适用于各种问题。

损失函数：

损失参数定义了模型在训练期间试图最小化的目标。在这种情况下，使用“mean_squared_error”作为损失函数。均方误差 (MSE) 是回归问题的常见选择，其目标是最小化预测值和实际值之间的均方差。它适用于输出为连续值的问题。MAE 计算预测值和实际值之间的绝对差的平均值。

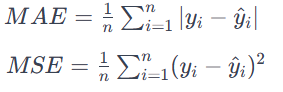
所有错误，无论其方向如何，都具有相同的重要性。较低的 MAE 也意味着模型性能更好。

总而言之，model.compile 语句可以配置神经网络模型进行训练。它指定用于在训练期间更新权重的优化器（“adam”）和应最小化模型的损失函数（“mean_squared_error”）。此编译步骤是用数据训练模型的必要初步阶段。

我们训练之前定义的神经网络模型。

# Train the model
model.fit(X_train_scaled, y_train, epochs=int(epoch), batch_size=256, validation_split=0.2, verbose=1)

训练数据：

X_train_scaled：这是用于训练的输入特征数据，可能经过缩放或预处理以确保数值稳定性。

y_train：这些是训练数据的对应目标值或标签。

训练配置：

epochs=int(epoch) :该参数指定整个训练数据集通过神经网络向前和向后传递的次数。

int(epoch) 指定 epoch 的数量由变量 epoch 决定。

batch_size=256 :在每个时期，训练数据被分成几批，每处理完一批数据就会更新模型的权重。这里，每个批次由 256 个数据点组成。

验证数据：

validation_split=0.2 :该参数指定 20％ 的训练数据作为验证集。在训练期间会监控该集合上模型的性能，但不会用于更新权重。

详细程度：
verbose=1 :此参数控制训练输出的详细程度。值为 1 表示训练进度显示在控制台中。

在训练过程中，模型学习根据提供的输入数据（X_train_scaled）和目标值（y_train）调整其权重来做出预测。验证分割有助于评估模型在未见过的数据上的性能，并根据详细程度设置显示训练进度。

推出线性单元

当我们研究神经元网络时，我们从基本的构建块开始：单个神经元。从图表上看，当配置单个输入时，神经元（也称为单元）看起来像这样：

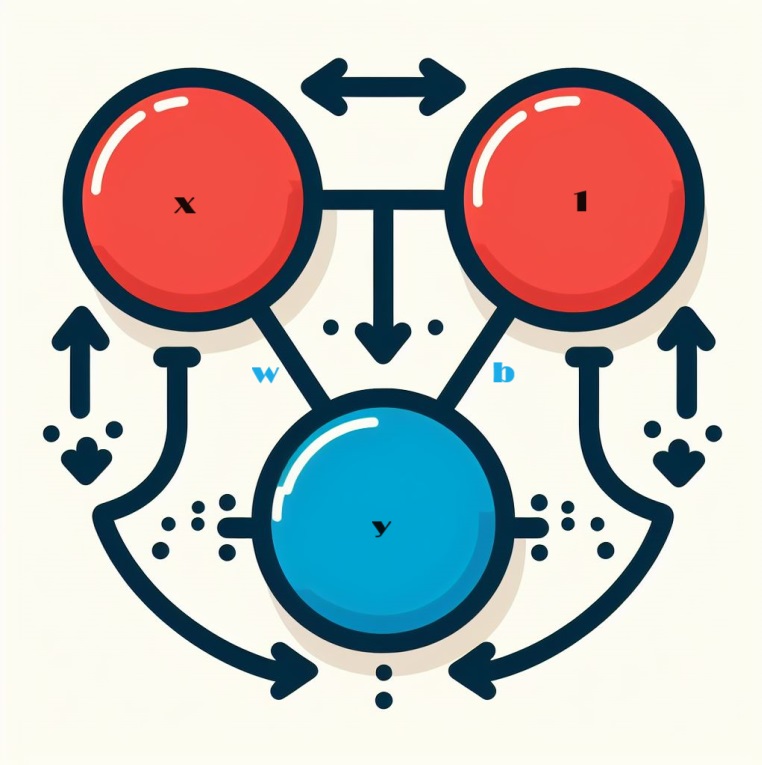
揭秘线性单位机制

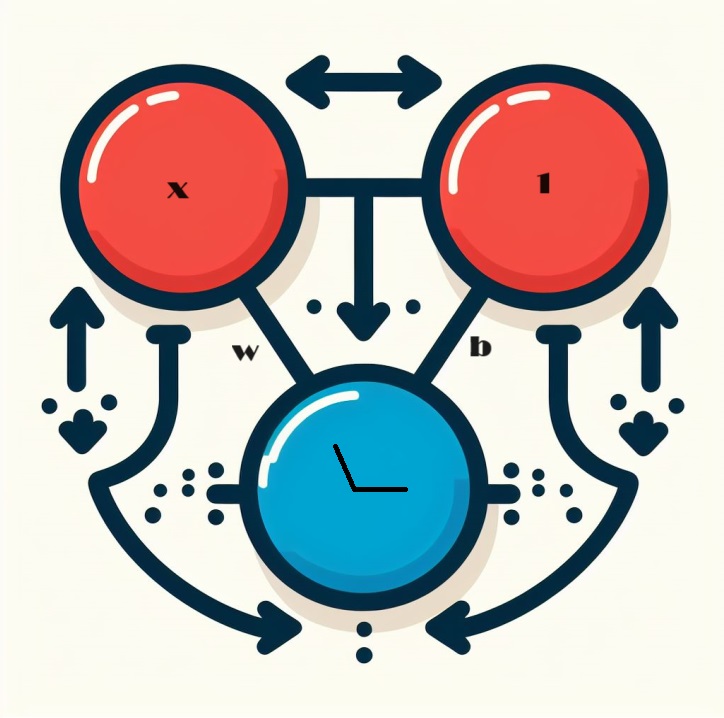
让我们来探索神经网络核心组件的复杂性：单个神经元。可视化后，具有单个输入 x 的神经元表示如下：

标记为 x 的输入与神经元形成连接，这个连接有一个标记为 w 的权重。当信息通过此连接时，该值会乘以分配给该连接的权重。对于输入 x 的情况，最终到达神经元的是 w * x 的乘积。通过调整这些权重，神经网络可以随着时间的推移而“学习”。

现在我们引入 b，一种特殊形式的权重，称为偏差。与其他权重不同，偏差没有与之相关的输入数据。相反，将值 1 插入到图中以确保到达神经元的值只是 b（因为 1 * b 等于 b）。通过引入偏差，神经元能够独立于输入改变其输出。

Y = X*W + b*1

拥抱多种输入

如果我们想纳入更多因素呢？请不要担心，因为解决方案非常简单。通过扩展我们的模型，我们可以无缝地向神经元添加额外的输入连接，每个输入连接对应一个特定的特征。

为了获得输出，我们执行了一个简单的过程。每个输入都乘以适当的连接权重，结果被很好地合并。结果是一个整体表示，神经元巧妙地处理了多个输入，使模型更加细致，反映了不同特征的复杂相互作用。这种方法使我们的神经网络能够捕获更广泛的信息，增强其全面识别模式的能力。

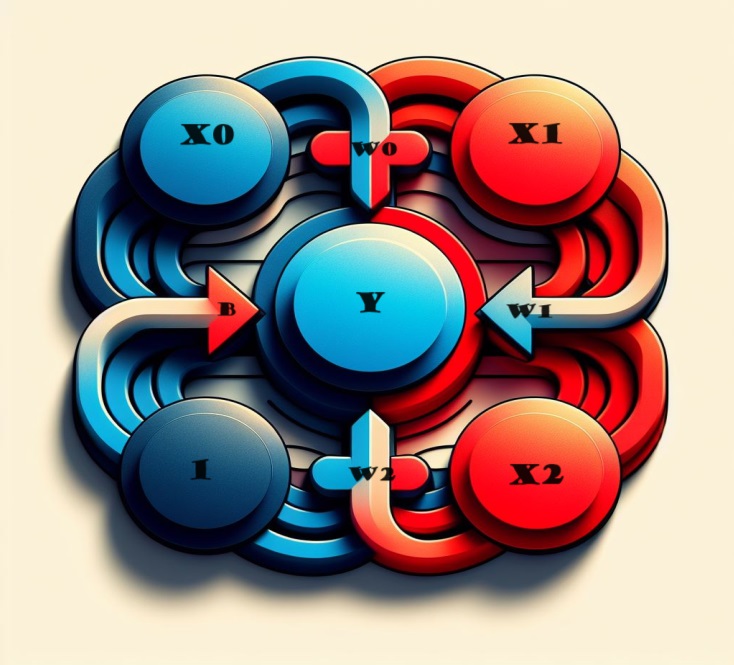
从数学角度来表达，这个神经元的操作可以用以下公式简洁地描述：

y = w 0 ⋅ x 0 + w 1 ⋅ x 1 + w 2 ⋅ x 2 + b = y=w0​⋅x0​+w1​⋅x1​+w2​⋅x2​+b

在这个等式中：

• y 表示神经元的输出。
• w0,w1,w2 ​ 表示与各个输入 x 0 、 x 1 、 x 2 相关的权重 ​。
• b 代表偏差项。

这个线性单元配备了两个输入，具有在三维空间中模拟平面的能力。随着输入数量超过两个，该单元变得擅长拟合超平面 - 复杂地捕捉多个输入特征之间关系的多维曲面。这种灵活性使神经网络能够导航和理解数据中超出简单线性关系的复杂模式。

Keras 中的线性单位

通过“keras.Sequential()”可以无缝地在 Keras 中构建神经网络。该实用程序通过堆叠层来组装神经网络，为模型创建提供了一种简单的方法。这些层封装了网络架构的本质，其中，“密集”层对于构建类似于之前探索的模型尤为重要。

model = Sequential()

在接下来的文章中，我们将更深入地研究密集层的复杂性，揭示其在构建健壮和富有表现力的神经网络架构中的能力和作用。

深度神经网络

通过集成隐藏层来增强网络的深度和表达能力。这些隐藏层在揭示数据中复杂的关系方面发挥着关键作用，使你的神经网络能够辨别和捕捉复杂的模式。通过战略性地添加隐藏层来提高模型的复杂性，从而使其能够学习和表示细微差别的特征，以进行更全面和准确的预测。

探索复杂神经网络的构建

我们现在开始了构建神经网络的旅程，该网络能够掌握表征深度神经网络能力的复杂关系。

我们方法的核心是模块化的概念，这是一种将基本功能单元拼凑成复杂网络的策略。在之前深入研究了线性单元如何计算线性函数之后，我们的重点现在转向了这些单个单元的融合和自适应。通过战略性地组合和修改这些基础组件，我们释放了建模和理解复杂数据集中固有的更复杂和多方面关系的潜力。这是构建神经网络的门户，神经网络可以熟练地导航和理解定义深度学习领域的细微差别模式。

揭开层的面纱

在神经网络的复杂架构中，神经元被系统地组织成层。出现的一个值得注意的配置是密集层 - 共享一组公共输入的线性单元的合并。

这种安排有助于形成一个强大而相互连接的结构，使该层内的神经元能够共同处理和解释信息。当我们深入研究层的复杂性时，密集层作为一个基础结构脱颖而出，说明了神经元如何协同促进网络理解和学习数据中复杂关系的能力。

 

Keras 中的不同层

在 Keras 领域中，“层”包含一个非常多功能的实体。本质上，它表现为任何形式的数据转换。以卷积层和循环层为例的许多层利用神经元来变形数据，其主要特征是它们形成的复杂连接模式。相反，其他层服务于从特征工程到基本算术的各种目的，展示了可以在神经网络的模块化框架内协调的广泛变换。层的多样性突显了神经网络架构丰富多彩的适应性和扩展性。

使用激活函数增强神经网络

令人惊讶的是，没有任何介入元件的两个致密层的结合不会超过单独致密层的功效。孤立的密集层将我们限制在线性结构的领域内，无法超越线和平面的边界。为了摆脱这种线性，我们引入了一个关键元素：非线性。这一关键因素体现在激活函数中。

激活函数作为变革的力量，将非线性注入神经网络。它们提供了超越线性约束的基本工具，使模型能够识别数据中复杂的模式和关系。本质上，激活函数是推动神经网络进入复杂领域的催化剂，释放了它们捕捉不同数据集中固有细微差别特征的能力。

当我们将整流函数与线性单元合并时，结果是一个强大的实体，称为整流线性单元或ReLU。因此，在普通用语中，整流函数通常被称为“ReLU 函数”。将 ReLU 激活应用于线性单元将输出转换为max（0，w*x+b），该描述可以用下图说明：

密集网络的战略分层

借助新发现的非线性，让我们探索层堆叠的效力，以及它如何使我们能够协调复杂的数据转换。

揭示神经网络中的隐藏层

在输出层之前，中间的层通常被称为“隐藏层”，因为它们的输出不被直接观察。

观察最终（输出）层采用线性单元的形式，没有任何激活函数。这种架构选择与回归性质的任务相一致，其目标是预测数值。然而，分类等任务可能需要在输出层加入激活函数，以更好地满足手头特定任务的要求。

构建序列模型

迄今为止所使用的顺序模型以顺序的方式无缝链接一系列层 - 从初始层到最后一层。在这个结构编排中，第一层作为输入的接收者，而最后一层最终生成所需的输出。此顺序组装反映了上图所示的模型：

model = keras.Sequential([
    # the hidden ReLU layers
    layers.Dense(units=4, activation='relu', input_shape=[2]),
    layers.Dense(units=3, activation='relu'),
    # the linear output layer 
    layers.Dense(units=1),
])

通过将所有层一起显示在列表中（类似于 [层，层，层，...]）来确保分层的凝聚力，而不是单独列出它们。要将激活函数无缝地合并到层中，只需在激活参数中指定其名称。这种简化的方法确保了神经网络架构的简洁和有组织的表示。

选择密集层中的单元数

关于层中单元数量的决定。密集层（例如，layers.Density（units=4，…））取决于问题的独特特征以及您希望在数据中揭示的模式的复杂性。请考虑以下因素：

问题复杂性：

• 对于数据中关系不太复杂的简单问题，较小数量的单位（如4个）可能是一个合适的起点。
• 在更复杂的情况下，以微妙和多方面的关系为特征，选择更多的单位通常是有益的。

数据大小：

• 数据集大小起着重要作用；较大的数据集可以容纳更多的单元供模型学习。
• 较小的数据集需要采取更谨慎的方法来防止过拟合和模型学习噪声的可能性。

模型容量：

• 单元的数量会影响模型捕捉复杂模式的能力，增加通常会增强表现力。
• 建议谨慎避免过度参数化，特别是在处理有限数据时，因为这可能会导致过度拟合。

实验：

• 尝试不同的配置，从适量的单元开始，训练模型，并根据性能指标和观察结果进行改进。
• 交叉验证等技术提供了对模型在各种数据子集上的泛化性能的见解。

记住，单元的选择并不是普遍固定的，可能需要一些试错。监控模型在验证集上的性能并迭代调整架构是模型开发过程中有价值的一部分。

我们选择这个：

model = Sequential()
model.add(Dense(128, activation='relu', input_shape=(X_train.shape[1],), kernel_regularizer=l2(k_reg)))
model.add(Dense(256, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(128, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(64, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(1, activation='linear'))

第一层（输入层）：

Units (128):第一层的单元数量相对较多（128），这使得模型能够捕获输入数据中的多样化和复杂模式。这对于在网络的初始阶段提取复杂的特征非常有利。 Activation ('relu'):整流线性单元 (ReLU) 激活引入了非线性，使模型能够从复杂的关系和模式中学习。 Regularization (L2):L2 正则化项（kernel_regularizer=l2(k_reg)）通过惩罚层中的大权重来帮助防止过度拟合。

第二层和第三层：

Units (256 and 128):在后续层中维持更多单元（256 和 128）可以继续允许模型捕获和处理复杂信息。单位数量的逐渐减少有助于创建特征的层次结构。 Activation ('relu'):ReLU 激活持续存在，促进每一层的非线性。 Regularization (L2):跨层一致应用 L2 正则化有助于防止过度拟合。

第四层： 

Units (64):单位的减少进一步细化了特征的表示，有助于提炼重要信息，同时保持复杂性和简单性之间的平衡。 Activation ('relu'):ReLU 激活持久，确保非线性特性的保留。 Regularization (L2):正则化项始终用于保证稳定性。

第五层（输出层）：

Units (1):具有单个单元的最后一层非常适合目标是预测连续数值的回归任务。 Activation ('linear'):线性激活适用于回归，允许模型直接输出预测值而无需任何额外的变换。

总体而言，所选择的架构似乎是为回归任务量身定制的，在表达能力和正则化之间实现了精心的平衡，以防止过度拟合。单元数量的逐渐减少有利于提取分层特征。这种设计表明了对任务复杂性的全面理解，并努力构建一个可以很好地推广到看不见的数据的模型。

总之，隐藏层中单元数量的逐渐减少，以及每层的具体选择，表明了一种旨在捕获输入数据的层次和抽象表示的设计。该架构似乎在模型复杂性与避免过拟合的需要之间取得了平衡，单元的选择与手头回归任务的性质相一致。具体数字可能是根据模型在验证数据上的性能通过实验和调整确定的。

编译模型

# Compile the model[]
model.compile(optimizer='adam', loss='mean_squared_error')

我们已经深入研究了使用密集层堆栈构建完全连接的网络。在创建的初始阶段，网络的权重是随机设置的，这意味着网络缺乏任何先验知识。现在，我们的重点转移到训练神经网络的过程上，揭示这些网络如何学习的本质。

按照机器学习的惯例，我们从一组精心策划的训练数据开始。该数据集中的每个示例都包括特征（输入）和预期目标（输出）。训练网络的关键在于调整其权重，以熟练地将输入特征转化为对目标输出的准确预测。

网络成功训练完成此类任务意味着其权重在一定程度上封装了这些特征与目标之间的关系，如训练数据所示。

除了训练数据之外，还有两个关键因素发挥作用：

1. 衡量网络预测有效性的“损失函数”。
2. “优化器”的任务是指导网络如何迭代调整其权重以提高性能。

随着我们进一步深入训练过程，了解这些组件的复杂性对于培养神经网络对未知数据进行泛化和准确预测的能力至关重要。

损失函数

虽然我们已经介绍了网络的架构设计，但指导网络解决其应解决的具体问题的关键方面仍有待探索。这一责任落在损失函数上。

本质上，损失函数量化了目标真实值与模型预测值之间的差异。它是评估模型预测与实际结果的一致性的标准。

回归问题中经常使用的损失函数是平均绝对误差（MAE）。在每个预测的上下文中，表示为y_pred，MAE通过计算绝对差abs（y_true-y_pred）来评估与真实目标 y_true 的差异。

整个数据集的累积 MAE 损失计算为所有这些绝对差异的平均值。该指标全面衡量了预测误差的平均幅度，指导模型尽量减少预测与真实目标之间的整体差异。

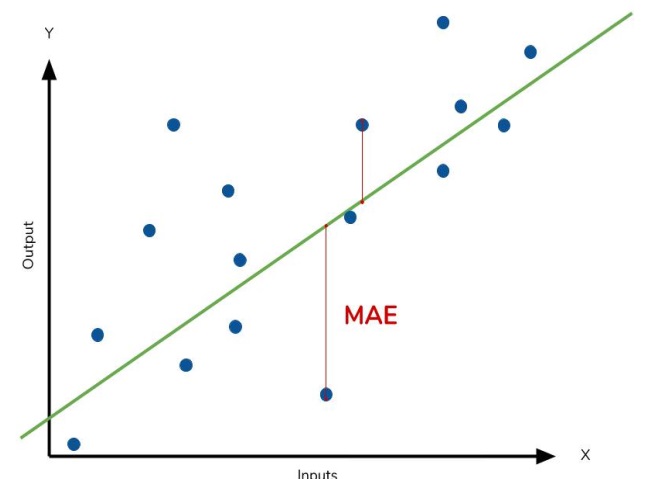
平均绝对误差表示拟合曲线和实际数据点之间的平均距离。

除了 MAE 之外，回归问题中常见的替代损失函数包括均方误差 (MSE) 和 Huber 损失，这两者都可以在 Keras 中访问。

在整个训练过程中，该模型依赖于损失函数作为导航指南，以确定其权重的最佳值，目标是尽可能低的损失。本质上，损失函数传达了网络的目标，引导它学习和细化其参数，以提高预测精度。

优化器 - 随机梯度下降

在定义了网络要解决的问题后，下一个关键步骤是概述如何解决它。这一责任由优化器承担，优化器是一种专门用于微调权重以最小化损失的算法。

在深度学习领域，大多数优化算法都属于随机梯度下降的范畴。这些是递增训练网络的迭代算法。每个训练步骤都遵循以下顺序：

1. 抽样一些训练数据并将其输入到网络中以生成预测。
2. 通过将预测值与真实值进行比较来评估损失。
3. 沿减少损失的方向调整重量。

迭代地重复该过程，直到达到所需的损失减少水平，或者直到进一步减少变得不切实际。本质上，优化器通过复杂的权重调整来引导网络，使其朝着最小化损失和提高预测准确性的配置方向发展。

在每次迭代中采样的每组训练数据称为小批量，通常简称为“批量”（batch）。另一方面，对训练数据的全面扫描被称为一个时期 (epoch)。指定的 epoch 数决定了网络处理每个训练示例的次数。

学习率和批量大小

该生产线在每批产品的方向上只进行了适度的调整，而不是彻底检修。这些变化的幅度取决于学习率。较小的学习率意味着网络在权重稳定到最佳值之前需要接触更多的小批量。

学习率和小批量的大小是影响 SGD 训练轨迹的两个最重要的参数。驾驭它们之间的相互作用可能是微妙的，而且最佳选择并不总是显而易见的。

值得庆幸的是，对于大多数任务而言，详尽搜索最佳超参数并不是获得令人满意的结果的必要条件。Adam 是一种具有自适应学习率的 SGD 算法，无需进行大量的参数调整。它的自调优特性使其成为适用于各种问题的优秀通用优化器。

对于这个例子，我们选择 ADAM 作为 SGD，MSE 作为损失。

model.compile(optimizer='adam', loss='mean_squared_error')

当拟合时，

# Train the model
model.fit(X_train_scaled, y_train, epochs=int(epoch), batch_size=256, validation_split=0.2, verbose=1)

我们将看到这样的情况：

44241/44241 [==============================] - 247s 6ms/step - loss: 0.0021 - val_loss: 8.0975e-04
Epoch 2/30
44241/44241 [==============================] - 247s 6ms/step - loss: 2.3062e-04 - val_loss: 0.0010
Epoch 3/30
44241/44241 [==============================] - 288s 7ms/step - loss: 2.3019e-04 - val_loss: 8.5903e-04
Epoch 4/30
44241/44241 [==============================] - 248s 6ms/step - loss: 2.3003e-04 - val_loss: 7.6378e-04
Epoch 5/30
44241/44241 [==============================] - 257s 6ms/step - loss: 2.2993e-04 - val_loss: 9.5630e-04
Epoch 6/30
44241/44241 [==============================] - 247s 6ms/step - loss: 2.2988e-04 - val_loss: 7.3110e-04
Epoch 7/30
44241/44241 [==============================] - 224s 5ms/step - loss: 2.2985e-04 - val_loss: 8.7191e-04

过度拟合和欠拟合

在模型训练的各个阶段，Keras 都会记录训练和验证损失。我们将深入解读这些学习曲线，并探索如何利用它们来增强模型开发。具体来说，我们将分析学习曲线以识别欠拟合和过度拟合的迹象，并探索一些解决这些问题的策略。

解释学习曲线：

当考虑训练数据中的信息时，它可以分为两个部分：信号和噪声。该信号代表了泛化的部分，有助于我们的模型对新数据进行预测。另一方面，噪声包括来自真实世界数据的随机波动和不利于模型预测能力的非信息模式。识别和理解这一区别至关重要。

在模型训练过程中，我们的目标是选择权重或参数，以尽量减少训练集的损失。然而，为了全面评估模型的性能，必须在一组新的数据（验证数据）上对其进行评估。

有效地解释这些曲线（在绘制它们时）对于成功训练深度学习模型至关重要。

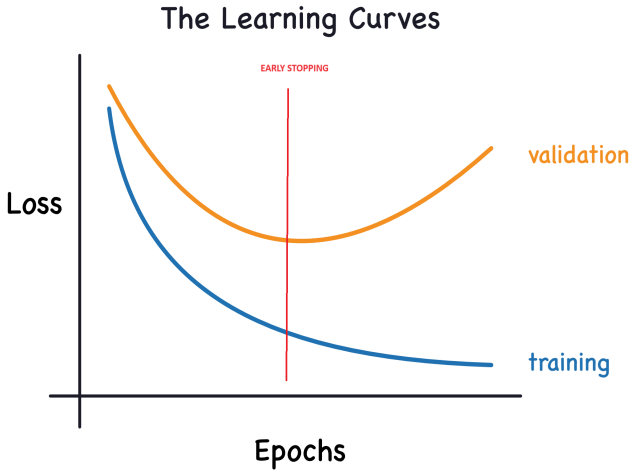
现在，当模型获取信号或噪声时，训练损失就会减少。然而，只有当模型学习信号时，验证损失才会减少，因为从训练集中获取的任何噪声都无法推广到新数据。因此，当模型学习信号时，两条曲线都呈下降趋势，而学习噪声会在它们之间产生差距。这个差距的大小表明了模型所获得的噪声程度。

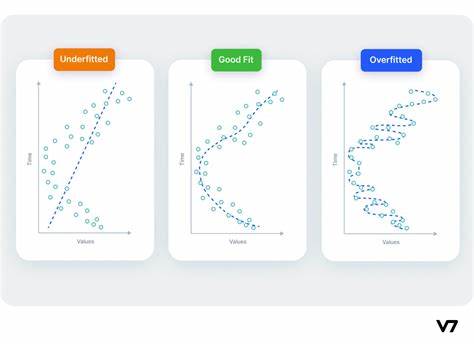
在理想情况下，我们的目标是建立学习所有信号而不学习任何噪声的模型。然而，实现这一理想状态实际上是不可能的。相反，我们进行了权衡。我们可以鼓励模型以获取更多噪声为代价来学习更多信号。只要这种权衡对我们有利，验证损失就会继续减少。然而，当权衡变得不利时，成本超过了收益，验证损失开始增加。

这种权衡突显了模型训练中的两个潜在挑战：信号不足或噪声过多。当模型没有学习到足够的信号导致损失无法最小化时，就会出现训练集欠拟合的情况。另一方面，当模型吸收了太多噪音导致损失无法最小化时，就会发生训练集过度拟合。训练深度学习模型的关键在于发现这两种场景之间的最佳平衡。

另一张图现在看起来像这样：

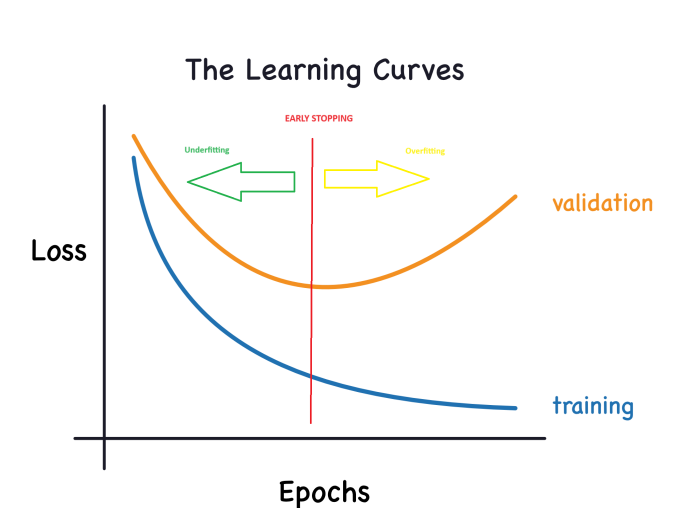
模型容量：

模型的容量表示其掌握和理解复杂模式的能力。在神经网络的背景下，这主要受到神经元数量及其相互联系的影响。如果您的网络似乎没有充分捕捉数据的复杂性（拟合不足），请考虑提高其容量。

网络的容量可以通过拓宽（在现有层中添加更多单元）或深化（合并更多层）来增加。更广泛的网络擅长学习更多的线性关系，而更深层的网络倾向于捕捉更多的非线性模式。两者之间的选择取决于数据集的性质。

早期停止：

如前所述，当模型在训练期间过度加入噪音时，验证损失可能会开始上升。为了解决这个问题，我们可以实施早期停止技术，即一旦发现验证损失不再减少，就立即停止训练过程。这种主动干预有助于防止过度拟合并确保模型很好地推广到新数据。

一旦我们观察到验证损失的上升，我们就可以将权重重置为最小值出现的点。这个预防步骤可确保模型不会持续学习噪声，从而避免过度拟合。

实施早期停止训练还可以降低在网络彻底掌握信号之前过早停止训练过程的风险。除了防止因训练时间过长而导致的过度拟合之外，早期停止还可以防止因训练时间不足而导致的欠拟合。只需将您的训练 epoch 配置为足够大的数量（超过要求），早期停止将根据验证损失趋势管理终止。

整合早期停止：

在 Keras 中，将早期停止纳入我们的训练是通过回调实现的。回调本质上是在网络训练过程中定期执行的函数。具体来说，早期停止回调是在每个 epoch 之后触发的。虽然 Keras 为方便起见提供了一系列预定义回调，但它也允许创建自定义回调以满足特定要求。

这是我们的选择：

from tensorflow import keras
from tensorflow.keras import layers, callbacks

early_stopping = callbacks.EarlyStopping(
    min_delta=0.001, # minimium amount of change to count as an improvement
    patience=20, # how many epochs to wait before stopping
    restore_best_weights=True,
)

# Train the model
model.fit(X_train_scaled, y_train, epochs=int(epoch), batch_size=256, validation_split=0.2,callbacks=[early_stopping], verbose=1)

我们还添加了更多单元和一个隐藏层（经过调整后，模型在 .py 中变得更加复杂）

model.add(Dense(128, activation='relu', input_shape=(X_train.shape[1],), kernel_regularizer=l2(k_reg)))
model.add(Dense(256, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(128, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(64, activation='relu', kernel_regularizer=l2(k_reg)))
model.add(Dense(1, activation='linear'))

这些参数传达了如下指令：“如果在过去 20 个 epoch 内验证损失没有至少 0.001 的改善，则停止训练并保留迄今为止确定的表现最佳的模型。”确定验证损失是否由于过度拟合或仅仅是随机批次变化而增加有时会很困难。指定的参数使我们能够建立一定的公差，指导系统何时停止训练过程。

我们最初将 epoch 的数量设置为 300，希望能够尽早终止训练过程。

处理缺失值

各种情况都可能导致数据集中出现缺失值。

使用 scikit-learn 等机器学习库时，尝试使用包含缺失值的数据构建模型通常会导致错误。因此，您必须采用以下策略之一来解决此问题。

三种方法

1. 精简解决方案（drop nan）：消除具有缺失值的列一种简单的方法是丢弃包含缺失值的列

df2 = df2.dropna()

然而，除非丢弃列中的大部分值丢失，否则选择这种方法会导致模型无法访问大量潜在有价值的信息。为了说明起见，设想一个包含 10,000 行的数据集，其中一个关键列只有一个缺失的条目。采用这一策略将需要移除整个列。

2）改进的替代方案：插补

插补涉及用特定的数值填充缺失的值。例如，我们可以选择在每列中填写平均值。

尽管在大多数情况下估算值可能并不完全准确，但与完全丢弃行相比，这种方法通常会产生更准确的模型。

3）推进插补技术

插补是传统方法，通常被证明是有效的。然而，估算值可能会系统地偏离其真实值（数据集中不可用）。或者，具有缺失值的行可能表现出不同的特征。在这种情况下，改进模型以考虑缺失值的原创性可以提高预测准确性。

在这种方法中，我们继续如前所述对缺失值进行插补。此外，对于初始数据集中缺少条目的每一列，我们都会引入一个新列，指示输入条目的位置。

虽然这种技术在某些情况下可以显著提高结果，但其有效性可能会有所不同，在某些情况中，它可能不会产生任何改善。

输出 ONNX 模型

1 加载数据。

现在我们对为训练模型而创建的.py 文件有了基本的了解，让我们继续训练它。 

我们应该在这里写下我们的路径：

# get rates
eurusd_rates = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_H1, start_date, end_date)

# create dataframe
df = pd.DataFrame(eurusd_rates)

代码最终如下所示（GRU_create_model.py）：

训练时，我们得到了以下结果：

Mean Squared Error: 0.0031695919830203693

Mean Absolute Error: 0.05063149001883482

R2 Score: 0.9263800140852619
Baseline MSE: 0.0430534174061265
Baseline MAE: 0.18048216851868318
Baseline R2 Score: 0.0

正如这篇论文所述：  使用深度循环神经网络进行外汇汇率预测，GRU 和 LTSM 的结果相似。 

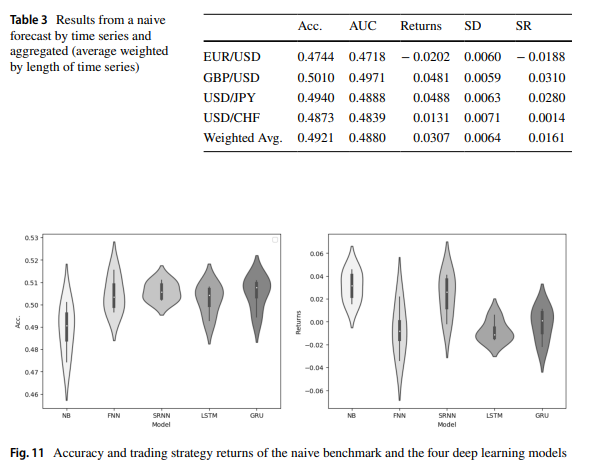
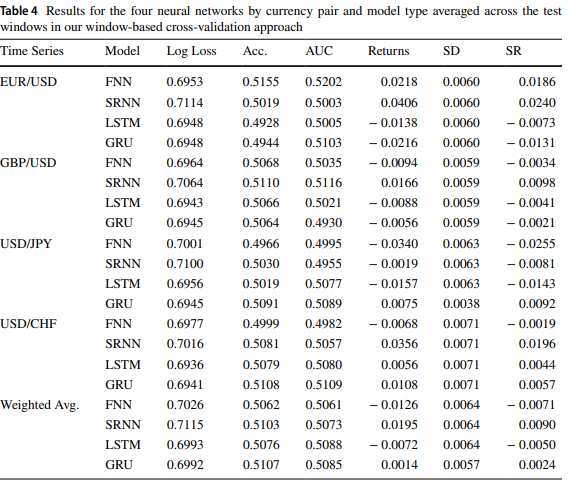
一旦我们运行了 ONNX_GRU.py，我们将在包含训练 python 文件（ONNX_GRU.py）的同一文件夹中获得一个 ONNX 模型。此 ONNX 模型应保存在 MQL5 文件文件夹中，以便从 EA 调用它。

这就是将 EA 添加到文章中的方式。

现在我们可以使用策略测试器或交易来测试该模型。

比较 GRU 与 LSTM

LSTM 单元维持一种单元状态，它既可以读取也可以写入。它包含四个门，根据输入和单元格状态值，控制向单元格状态读取、写入和从单元格状态输出值的过程。初始门指示隐藏状态应该忘记的信息。后续门负责识别要写入的单元状态段。第三道门决定了要记录的内容。最后，最后一个门从单元状态中检索信息以生成输出。

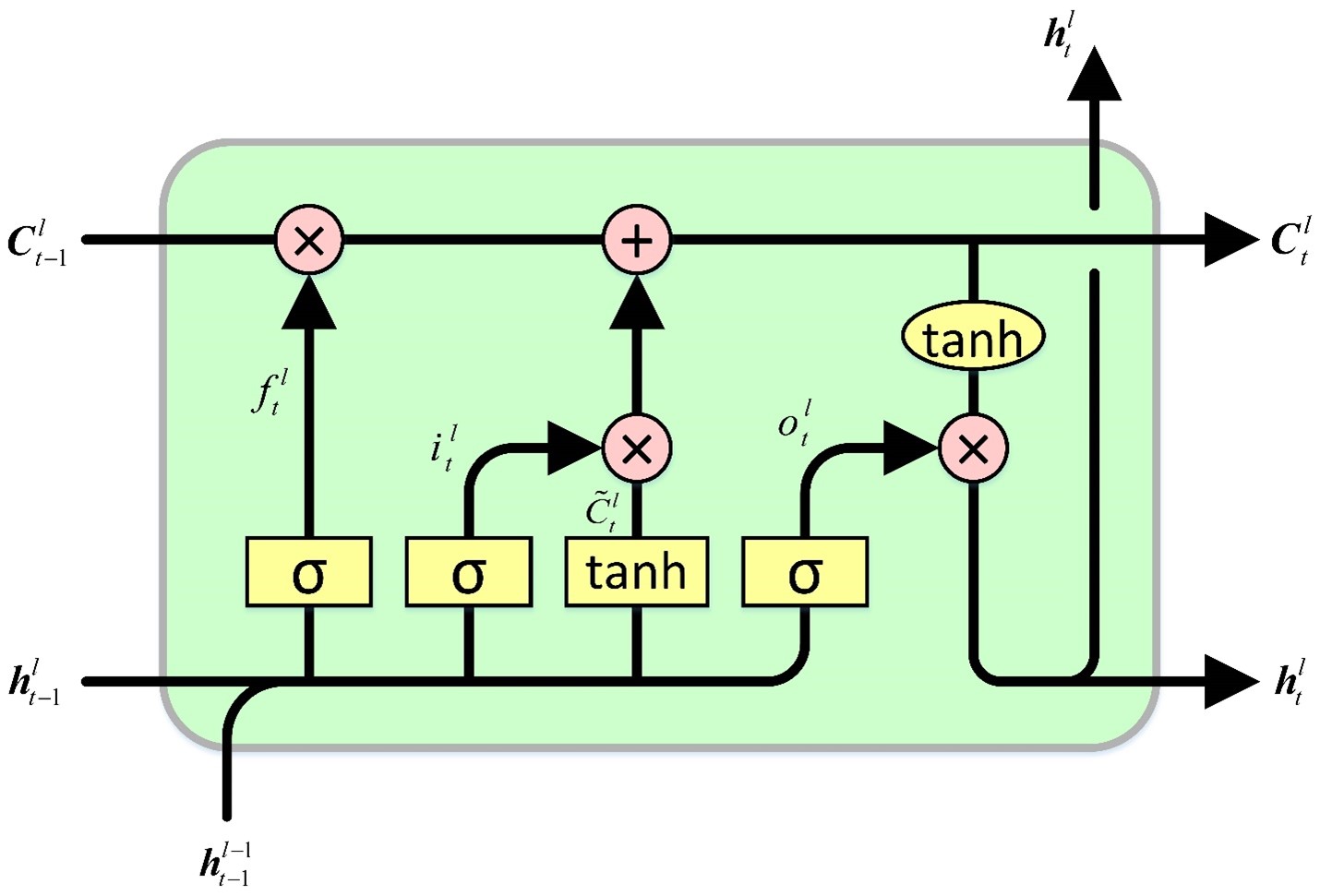
GRU 单元与 LSTM 单元有相似之处，但也存在一些显著的区别。首先，它缺乏隐藏状态，因为 LSTM 单元设计中隐藏状态的功能是由单元状态假设的。随后，决定单元状态忘记什么以及写入单元状态的哪个部分的过程被合并到一个单一的门中。然后，只有已擦除的单元格状态部分才会被刻写。最后，整个单元状态用作输出，偏离 LSTM 单元，LSTM 单元选择性地从单元状态读取以生成输出。与 LSTM 相比，这些整体修改使设计更简单，参数更少。然而，参数的减少可能会导致表达能力的降低。

实验比较

GRU

# Split the data into training and testing sets
x_train, x_test, y_train, y_test = train_test_split(x_features, y_target, test_size=0.2, shuffle=False)


# Standardize the features StandardScaler()
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(x_train)
X_test_scaled = scaler.transform(x_test)

scaler_y = StandardScaler()
y_train_scaled = scaler_y.fit_transform(np.array(y_train).reshape(-1, 1))
y_test_scaled = scaler_y.transform(np.array(y_test).reshape(-1, 1))

# Define parameters

learning_rate = 0.001
dropout_rate = 0.5
batch_size = 1024
layer_1 = 256
epochs = 1000
k_reg = 0.001
patience = 10
factor = 0.5
n_splits = 5  # Number of K-fold Splits
window_size = days  # Adjust this according to your needs

def create_windows(data, window_size):
    return [data[i:i + window_size] for i in range(len(data) - window_size + 1)]

custom_optimizer = Adam(learning_rate=learning_rate)
reduce_lr = ReduceLROnPlateau(monitor='val_loss', factor=factor, patience=patience, min_lr=1e-26)

def build_model(input_shape, k_reg):
    model = Sequential()
    
    layer_sizes = [ 512,1024,512, 256, 128, 64]
    model.add(Dense(layer_1, kernel_regularizer=l2(k_reg), input_shape=input_shape))
    for size in layer_sizes:
        model.add(Dense(size, kernel_regularizer=l2(k_reg)))
        model.add(BatchNormalization())
        model.add(Activation('relu'))
        model.add(Dropout(dropout_rate))

    model.add(Dense(1, activation='linear'))
    model.add(BatchNormalization())
    model.compile(optimizer=custom_optimizer, loss='mse', metrics=[rmse()])
    
    return model



# Define EarlyStopping callback
early_stopping = EarlyStopping(monitor='val_loss', patience=patience, restore_best_weights=True)

# KFold Cross Validation
kfold = KFold(n_splits=n_splits, shuffle=True, random_state=42)
history = []
loss_per_epoch = []
val_loss_per_epoch = []

for train, val in kfold.split(X_train_scaled, y_train_scaled):
    x_train_fold, x_val_fold = X_train_scaled[train], X_train_scaled[val]
    y_train_fold, y_val_fold = y_train_scaled[train], y_train_scaled[val]
    
    # Flatten the input data
    x_train_fold_flat = x_train_fold.flatten()
    x_val_fold_flat = x_val_fold.flatten()

    # Create windows for training and validation
    x_train_windows = create_windows(x_train_fold_flat, window_size)
    x_val_windows = create_windows(x_val_fold_flat, window_size)

    # Rebuild the model
    model = build_model((window_size, 1), k_reg)

    # Create a new optimizer
    custom_optimizer = Adam(learning_rate=learning_rate)
    
    # Recompile the model
    model.compile(optimizer=custom_optimizer, loss='mse', metrics=[rmse()])
    
    hist = model.fit(
        np.array(x_train_windows), y_train_fold[window_size - 1:],
        epochs=epochs,
        validation_data=(np.array(x_val_windows), y_val_fold[window_size - 1:]),
        batch_size=batch_size,
        callbacks=[reduce_lr, early_stopping]
    )
    history.append(hist)
    loss_per_epoch.append(hist.history['loss'])
    val_loss_per_epoch.append(hist.history['val_loss'])




mean_loss_per_epoch = [np.mean(loss) for loss in loss_per_epoch]
val_mean_loss_per_epoch = [np.mean(val_loss) for val_loss in val_loss_per_epoch]

print("mean_loss_per_epoch", mean_loss_per_epoch)
print("unique_min_val_loss_per_epoch", val_loss_per_epoch)

# Create a DataFrame to display the mean loss values
epoch_df = pd.DataFrame({
    'Epoch': range(1, len(mean_loss_per_epoch) + 1),
    'Train Loss': mean_loss_per_epoch,
    'Validation Loss': val_loss_per_epoch
})

LSTM

model = Sequential()
model.add(Conv1D(filters=256, kernel_size=2, activation='relu',padding = 'same',input_shape=(inp_history_size,1)))
model.add(MaxPooling1D(pool_size=2))
model.add(LSTM(100, return_sequences = True))
model.add(Dropout(0.3))
model.add(LSTM(100, return_sequences = False))
model.add(Dropout(0.3))
model.add(Dense(units=1, activation = 'sigmoid'))
model.compile(optimizer='adam', loss= 'mse' , metrics = [rmse()])

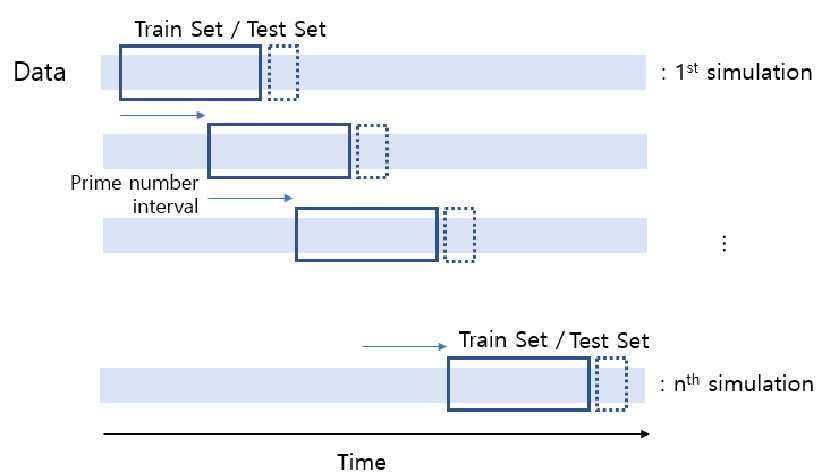
我为您留下了一个 .py 用于比较 LSTM 和 GRU 以及一个 cross validation.py。

还留下了一个 GRU simple .py 来制作 ONNX 模型

利用 GRU 的简单模型，我们可以得到 2024 年 1 月的结果

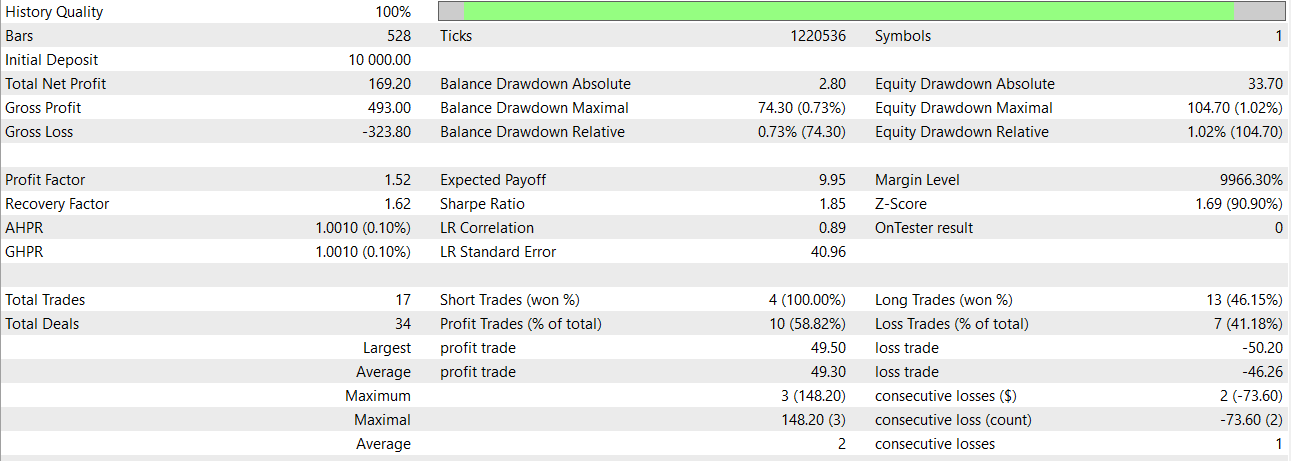
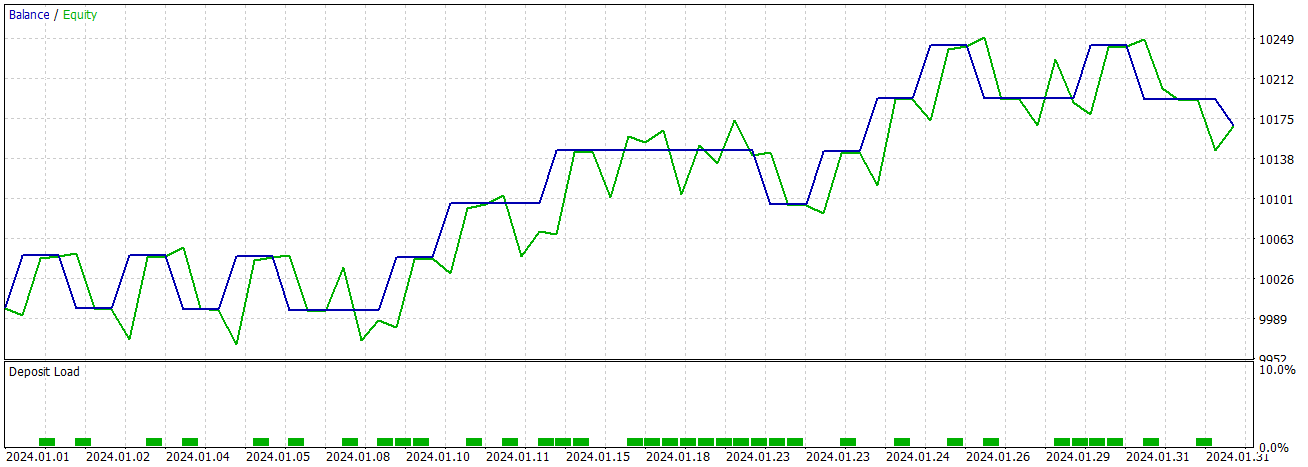
结论和未来工作

这种比较对于确定使用哪种模型至关重要，或者我们甚至可以考虑以堆叠或叠加的方式使用这两种模型。这种方法允许我们从我们使用的模型中提取基本信息，尽管批处理大小和层配置存在固有差异。如果像我认为的那样，它们以类似的结果恢复，GRU会快得多。

作为未来工作的一部分，探索针对每种单元类型量身定制的不同内核和循环初始化器，以提高潜在的性能，这将是有益的。

使用 ONNX 模型进行交易的一个好方法是将两者集成在同一个 EA 中，请阅读本文：如何在 mql5 中集成 ONNX 模型的一个例子。

结论

像 GRU 这样的模型能够获得良好的结果，并且看起来很强大。我希望你们喜欢这篇文章，就像我喜欢创作它一样。我们还看到了 GRU 和 LSTM 模型之间的比较，我们可以使用该 .py 代码来知道何时停止 epoch（考虑到输入的数据数量）。

免责声明

过去的业绩并不预示未来的结果。