Redes neurais em trading: Framework de previsão cruzada de domínio de séries temporais (TimeFound)

Introdução

A previsão de séries temporais já se tornou há muito tempo uma ferramenta indispensável para o analista financeiro. Se você já tentou ao menos uma vez prever para onde irão as cotações das ações ou como a volatilidade de um índice financeiro vai mudar, sabe muito bem que isso se assemelha a ler o futuro na borra de café. Ainda assim, sem esse tipo de adivinhação, nenhum fundo sério simplesmente sobrevive.

No passado, os modelos estatísticos clássicos eram amplamente utilizados: ARIMA, suavização exponencial. E, convenhamos, até a regressão linear com frequência trazia bons resultados. Os argumentos de que o modelo deveria ser mais simples soavam convincentes, até que as redes neurais profundas entraram em cena. Hoje, elas não apenas dão resultados, como colhem uma verdadeira safra, impressionando pela precisão e pela velocidade no processamento de terabytes de dados históricos.

No entanto, como qualquer arma poderosa, os modelos profundos têm seus efeitos colaterais. Para o aprendizado, eles exigem uma verdadeira mina de dados rotulados para uma tarefa específica. Sem isso, o grande irmão rede neural simplesmente não funciona. Mas o que fazer se você tem à disposição apenas um fragmento estreito do histórico ou se o mercado acabou de começar a ser negociado? Como prever os preços de um token recém-lançado, cujos dados o contador no terminal da corretora ainda nem teve tempo de acumular? É aí que entra em cena o conceito de Zero-Shot Forecasting, a garantia de que o modelo vai se mostrar eficaz onde os métodos clássicos são totalmente impotentes.

Pesquisadores de séries temporais traçaram analogias com grandes modelos de linguagem (Large Language Models). Os famosos LLM trabalham com texto de forma excelente: traduzem, escrevem poemas, respondem a perguntas. Então por que não transferir essas ideias para a previsão de tendências de preços? Assim surgiu o boom dos chamados Foundation Models para séries temporais. Imagine: um único modelo universal, e para ele não faz diferença se está prevendo o preço de ações, o volume de consumo de eletricidade ou o nível de desemprego. O principal é treiná-lo corretamente em um conjunto de dados diversificado.

Inspirados por essa abordagem fundamental, os autores do trabalho "TimeFound: A Foundation Model for Time Series Forecasting" apresentaram como base para a previsão de séries temporais um novo framework baseado na arquitetura Transformer, o TimeFound. Eles pegaram as melhores ideias do mundo de NLP e as adaptaram para a previsão de séries temporais.

O framework TimeFound é construído segundo o esquema clássico Codificador – Decodificador. O codificador estuda a série histórica de dados e extrai dela o contexto. O decodificador, por sua vez, projeta o futuro, preservando as relações de causa e efeito.

No núcleo do modelo está uma nova abordagem para o patching de séries temporais. Esquecemos o tamanho fixo da janela. Os autores do framework propõem dividir a sequência imediatamente em vários patches de diferentes tamanhos. Imagine que você está estudando o comportamento das ações de uma empresa: as oscilações mensais parecem monótonas, enquanto as intradiárias são marcadas por saltos bruscos. Multi-resolution patching permite capturar ambas as escalas: tanto a tendência de longo prazo quanto o ruído da volatilidade.

Para o pré-treinamento, os autores do framework reuniram um enorme dataset multidomínio. Toda essa diversidade é necessária para que o modelo aprenda a capturar padrões universais. Quanto mais dados, mais rico é o vocabulário de padrões aprendido pelo modelo.

O objetivo do aprendizado é simples, a tarefa de previsão autorregressiva. Na entrada é fornecido um conjunto de dados históricos, e o modelo aprende a prever os valores seguintes passo a passo. No entanto, neste caso, o passo da previsão pode diferir do passo dos dados históricos. Isso ocorre porque o modelo retorna os resultados na forma de patches. E um patch pode incluir vários passos do sistema analisado.

Algoritmo TimeFound

TimeFound é um modelo universal desenvolvido como base para a construção de sistemas de previsão em diversos domínios, incluindo, mas não se limitando, aos mercados financeiros. A arquitetura do modelo é construída no formato Codificador-Decodificador com um princípio modular de processamento de dados. Nela, o papel central é desempenhado pela normalização, patching multinível, mecanismo de atenção com posicionamento relativo e aprendizado conjunto utilizando erros pontuais e quantílicos de previsão.

O algoritmo do framework começa com uma preparação cuidadosa da série temporal bruta, pois sem uma base confiável qualquer previsão corre o risco de ser instável. Primeiro, os dados são levados a uma forma comparável, normalizando cada série com a normalização clássica, subtraindo de cada ponto o valor médio de toda a sequência e dividindo pelo seu desvio padrão. Graças a essa técnica, o modelo não se perde quando um movimento de mercado parece uma pequena senoide em comparação com um crescimento colossal do consumo de eletricidade e, ao contrário, consegue perceber até flutuações sutis quando elas são realmente importantes.

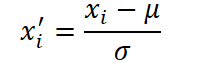
onde μ e σ são a média e o desvio padrão da série X. Isso equaliza a escala dos dados sem perda da estrutura temporal.

Assim que a escala é ajustada, chega o momento de dividir a série em fragmentos ou patches. Nas soluções clássicas, todos os patches são iguais, mas sabemos que em uma mesma série temporal podem estar escondidos tanto picos rápidos quanto tendências lentas. Por esse motivo, os autores do framework TimeFound propõem o patching multiescalar. No primeiro nível, são formados patches de escala mínima. Eles são em maior quantidade. Com o aumento do nível, o tamanho do patch também aumenta, com uma redução proporcional da sua quantidade. Os autores do framework, em seu trabalho, utilizaram patches cujo tamanho é uma potência de 2.

Cada patch desse tipo armazena em si um fragmento da narrativa temporal, seja um pico de volatilidade de curta duração ou uma queda prolongada.

Em seguida, aos patches formados é adicionada uma mascaragem binária, indicando onde estão os dados reais e onde há apenas preenchimento até um tamanho uniforme. E cada fragmento desse da série temporal passa por seu próprio perceptron de duas camadas com conexões residuais. Esses MLP-projetores traduzem patches de diferentes comprimentos para um espaço latente d-dimensional unificado, onde cada vetor reflete a essência do comportamento local da série analisada.

No entanto, ainda não está tudo pronto. Como já foi dito anteriormente, no processo de patching multiescalar, em cada nível é formada uma quantidade diferente de objetos, pequenos blocos existem em número muito maior do que os grandes. Para uni-los em um todo único, os autores do framework propõem duplicar (replicar) as representações dos patches maiores o número necessário de vezes, para alinhar sua quantidade com o número dos patches mais pequenos. Como resultado, em cada passo temporal surge uma representação estéreo multicanal, na qual os vetores de todas as escalas são fundidos. Depois disso, seus atributos são combinados em uma única matriz latente. É ela que entra no bloco de atenção, garantindo a interação entre escalas.

A base do modelo é composta por um Codificador–Decodificador com atenção modificada. O codificador estuda cuidadosamente a sequência obtida, aplicando atenção bidirecional (bi-directional). Isso significa que cada posição pode consultar todas as outras sobre como os eventos se desenvolveram antes e depois dela e, com base nas respostas ponderadas, formar uma representação mais profunda. Ao mesmo tempo, o mecanismo de atenção se apoia no posicionamento relativo dos patches, o modelo percebe que um fragmento recente (por exemplo, três patches atrás) é mais importante do que um distante (digamos, vinte patches atrás) e distribui os pesos de acordo.

Quando o codificador conclui seu trabalho, seus resultados são transmitidos ao decodificador, que já não tem o direito de olhar para frente de fato, apoiando-se apenas nos dados históricos. O mecanismo de atenção não permite que o modelo espreite o futuro além do que a agregação das previsões já realizadas possibilita e, por isso, cada nova previsão é precisa e honesta. Um elo importante aqui é o Cross-Attention. O decodificador, ao formar a representação do próximo patch, volta a recorrer aos ricos vetores de contexto do codificador, extraindo deles informações sobre as tendências recentemente observadas.

Na saída do decodificador, obtemos o vetor de previsão do patch subsequente, uma descrição compacta dos eventos anteriores e dos sinais-chave. Esse vetor é transmitido para o módulo de transformação, implementado na forma de um MLP de duas camadas MLP com conexão residual. Nele, a representação latente é desdobrada novamente nos valores habituais da série temporal e imediatamente é formado um bloco de pontos futuros. Essa saída em lote de previsões acelera o funcionamento do modelo e é especialmente eficaz em horizontes de longo prazo.

Durante o treinamento, os autores do framework não se limitam apenas à busca pela convergência média aos valores corretos. Juntamente com o erro padrão MSE, que penaliza a diferença quadrática entre os valores previstos e os reais, eles utilizam a função de perda quantílica, forçando o modelo a fornecer uma estimativa de incerteza. Para cada passo temporal, ele aprende, além dos valores médios, a fornecer também, por exemplo, os percentis 10, 50 e 90. A função de perda conjunta, que acumula MSE e Quantile Loss, forma um equilíbrio entre a precisão da previsão e a largura do intervalo de confiança.

Dessa forma, todo o algoritmo TimeFound representa um pipeline único e bem elaborado. Ele combina o poder dos transformers com a flexibilidade do patching multiescalar e a sensibilidade à incerteza, o que torna o modelo capaz de trabalhar com qualquer série temporal.

Para o pré-treinamento do TimeFound, os autores do framework formaram um dataset amplo e heterogêneo, abrangendo séries temporais reais e sintéticas em diversos domínios. Foram coletadas séries publicamente disponíveis com diferentes frequências, de 5 minutos até dados anuais. Utilizaram-se dados dos mercados financeiros (preços de ações, futuros de moedas), consumo de energia, temperaturas e volumes de vendas. Em seguida, sua diversidade foi ampliada por meio de gerações sintéticas. Isso permite que o TimeFound forme representações universais de séries temporais, garantindo alta capacidade de generalização sem a necessidade de retreinamento em novas tarefas.

A visualização original do framework TimeFound é apresentada abaixo.

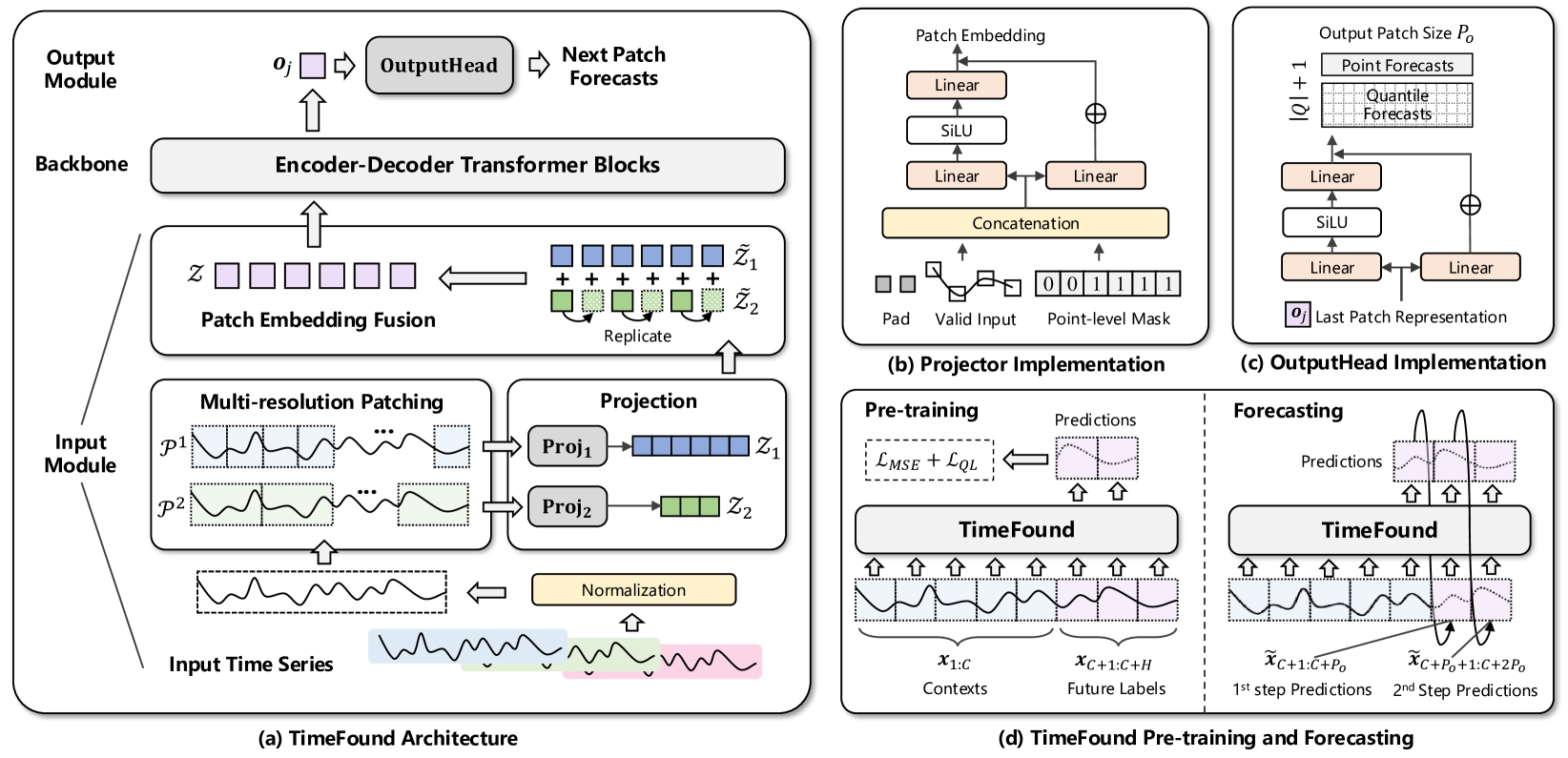
Implementação com MQL5

Após a análise dos aspectos teóricos do framework TimeFound, passamos à parte prática do nosso artigo, na qual implementamos, com recursos do MQL5, nossa própria visão das abordagens propostas pelos autores do framework. Porém, antes de mergulhar nos detalhes do código, é importante ter uma compreensão clara da sequência de tarefas e de suas inter-relações. Nosso caminho começa com a preparação dos dados brutos, e é exatamente aqui que reside a chave para a qualidade de toda a previsão subsequente.

Para a normalização dos dados da série temporal analisada, não vamos reinventar a roda, utilizaremos um bloco pronto de normalização em lote. Esse módulo varre automaticamente o buffer acumulado de preços, calcula a média e a variância a cada passo e, em tempo real, equaliza a distribuição dos dados, livrando o modelo de saltos bruscos quando há mudança no cenário de mercado. Graças a essa normalização deslizante, preservamos a dinâmica dos padrões importantes, mas removemos a dispersão que atrapalha o treinamento e a previsão estáveis.

Quando os dados estão alinhados em uma escala única, chega o momento de resolver a tarefa realmente importante, o patching multiescalar. No abordagem clássica sequencial-replicativa, primeiro dividiríamos a série em fragmentos de diferentes tamanhos, depois igualaríamos a quantidade de blocos pequenos por meio de uma simples cópia dos vetores grandes e somente após isso, lentamente, colaríamos tudo de volta. Esse método é compreensível, mas inaceitável devido às latências. A cada nova vela, perde-se um tempo precioso com a replicação, e os embeddings finais das escalas maiores são duplicados várias vezes, perdendo sua unicidade.

Em nossa implementação, agiremos de forma diferente. Utilizaremos o conceito de convolução multi-janela. Imagine que, em vez de três procedimentos separados, executamos três kernels de uma camada convolucional em paralelo, cada um com seu próprio tamanho de janela. Graças ao padding zero e à sobreposição, os filtros convolucionais com o mesmo passo percorrem cuidadosamente toda a extensão da série temporal analisada, formando simultaneamente três matrizes de atributos de mesmo comprimento.

Essa abordagem nos proporciona vários efeitos vantajosos. Em primeiro lugar, todos os cálculos são realizados simultaneamente, não há necessidade de esperar que os patches pequenos sejam processados para depois serem complementados com dados dos grandes. Em segundo lugar, graças à janela deslizante com passo uniforme, cada novo valor da série participa das três transformações, e não temos problemas de alinhamento. Os tensores de saída já ficam organizados segundo um único índice temporal. Em terceiro lugar, devido à sobreposição, a janela dos filtros maiores captura segmentos vizinhos, o que permite fixar melhor tendências lentas e oscilações suavizadas, e não apenas blocos rígidos.

Ao mesmo tempo, não precisamos replicar ou interpolar nada manualmente, o algoritmo mantém a mesma quantidade de elementos e uma representação homogênea para cada passo temporal.

Como resultado, obtemos um recorte instantâneo e compacto do cenário de mercado com o nível de detalhamento necessário, pronto para projeção no espaço latente do projetor MLP.

É justamente esse patching multiescalar paralelo que se torna o coração do módulo de pré-processamento, ele preserva a unicidade dos embeddings de cada escala, elimina a replicação excessiva e permite que o seu robô tome decisões mais rápidas e precisas, reagindo simultaneamente a micro-picos e a tendências de longo prazo.

Em seguida, passamos à transformação dos embeddings obtidos em atributos altamente informativos. Após a convolução multi-janela, em cada passo temporal já existe uma quantidade definida de canais na forma de embeddings. Porém, para um modelo profundo isso não é suficiente. É necessário adicionar uma camada de não linearidade e conexões treináveis para obter uma representação realmente expressiva. No original, os autores do TimeFound propõem um MLP de duas camadas MLP com o padrão de conexões residuais. Entretanto, em nossa implementação, utilizamos um bloco Feed-Forward multi-head pronto Feed-Forward do framework StockFormer.

Imagine que você tenha três fluxos de atributos de diferentes escalas, e cada um deles precise ser elevado a um padrão único de qualidade. Nosso bloco divide esses fluxos em cabeças independentes, cada uma processada em paralelo com seus próprios pesos e vieses. Em seguida, todos os resultados são novamente combinados em um único vetor. Graças às conexões residuais, a informação dos embeddings primários é preservada e suavemente misturada com a saída da camada, o que melhora a convergência e torna o modelo mais resistente ao ruído nos dados.

Dentro desse bloco Feed-Forward, cada cabeça representa um MLP de duas camadas MLP com não linearidade entre as camadas. Os resultados do MLP são somados aos dados de entrada e normalizados. Dessa forma, o vetor final em cada passo de tempo representa uma síntese de padrões locais e atributos globais, pronto para ser enviado ao próximo módulo.

Essa abordagem nos permite manter a proximidade conceitual com a arquitetura original do TimeFound, mas utilizando um componente comprovado e otimizado do StockFormer, o que economiza tempo de desenvolvimento e garante alta performance em tempo real.

Ao concluir a preparação dos atributos multiescalares, passamos à sua agregação, e aqui a simples técnica de soma dá lugar a um mecanismo mais flexível, a sequência de convolução e max-pooling. Imagine que você tenha três canais de embeddings, e cada um deles contribua de forma diferente para a compreensão do que está acontecendo. Se somarmos esses canais elemento a elemento, todos receberão o mesmo peso, independentemente de quão relevantes sejam, nesse trecho, os picos de curto prazo ou as tendências de longo prazo. Em vez disso, executamos uma convolução, na qual filtros treináveis analisam os valores de diferentes escalas e destacam as combinações mais informativas.

Durante a passagem da camada convolucional pelo tensor de três canais, cada filtro enxerga simultaneamente todas as escalas e procura nelas padrões característicos. Na saída, obtemos um conjunto de novos atributos, cada um refletindo a combinação de sinais locais e globais. E é exatamente aqui que entra o max-pooling, deslizando sobre os mapas de atributos obtidos, ele preserva apenas as respostas mais fortes, ignorando o ruído e as flutuações irrelevantes. Assim, se no mesmo intervalo temporal o micro nível capturou um pico brusco de volume e o macro nível um crescimento estável, o pooling garante que ambos os sinais sejam devidamente representados no vetor final.

Como resultado dessa combinação de convolução e max-pooling, eliminamos a necessidade de definir manualmente pesos para cada escala. O próprio modelo aprende a enfatizar o conjunto de atributos mais relevante para a previsão atual. Esse mecanismo adaptativo não apenas aumenta a precisão do resultado, como também torna o algoritmo mais resistente a saltos e ruídos de mercado, pois sinais fracos ou raros são suavizados, enquanto picos importantes, ao contrário, são reforçados e chegam às etapas do codificador e do decodificador sem perdas.

A abordagem descrita acima é implementada no âmbito do objeto CNeuronTimeFoundPatching, cuja estrutura é apresentada abaixo.

class CNeuronTimeFoundPatching   :  public CNeuronConvOCL
  {
protected:
   CNeuronTransposeOCL              cToVarSeq;
   CNeuronMultiWindowsConvWPadOCL   cProjecting;
   CNeuronTransposeVRCOCL           cToVarProjSeq;
   CNeuronMultiWindowsConvWPadOCL   cPatchingProj;
   CNeuronMHFeedForward             cPatchsFeedForward;
   CNeuronConvOCL                   cPatchingAgr;
   CNeuronProofOCL                  cProof;
   CNeuronTransposeOCL              cToPatchVarEmb;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)  override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL)  override;

public:
                     CNeuronTimeFoundPatching(void) {};
                    ~CNeuronTimeFoundPatching(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint count, uint patchs, uint variables,
                          uint embedding_size, uint patch_filters,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual int       Type(void)  override const {  return defNeuronTimeFoundPatching; }
   //---
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
  };

Todos os módulos internos do CNeuronTimeFoundPatching vivem uma vida independente desde o início do programa. Eles são declarados estaticamente e inicializados juntamente com o carregamento da biblioteca. Portanto, não precisamos criá-los no construtor nem nos preocupar com a limpeza no destrutor, esses métodos permanecem vazios, e toda a magia de gerenciamento da arquitetura do objeto fica a cargo de um único método universal Init.

Nos parâmetros do método de inicialização, recebemos uma série de constantes que determinam a arquitetura dos objetos internos.

bool CNeuronTimeFoundPatching::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                    uint count, uint patchs, uint variables,
                                    uint embedding_size, uint patch_filters,
                                    ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   uint inside_emb = MathMax((embedding_size + 2) / 6, 8);
   if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, 3 * inside_emb, 3 * inside_emb,
                            embedding_size, patchs * variables, 1, optimization_type, batch))
      return false;
   SetActivationFunction(SoftPlus);

Vale destacar que, ao construir esse objeto, nós tomamos emprestadas as melhores ideias do framework Mantis. Em vez de tamanhos de patches rigidamente definidos, nossa classe recebe como entrada apenas o número de segmentos para o nível mais fino e o tamanho desejado do token de saída. Isso oferece flexibilidade, permitindo alterar rapidamente a granularidade do patching sem modificar o código.

Mas fomos além. O Mantis utilizava uma única convolução para gerar canais de atributos, enquanto nós implementamos uma convolução multi-janela, que cria imediatamente vários níveis de observação do sinal original. Quando chega o momento da inicialização, nossa tarefa é calcular o tamanho interno do vetor de token para cada nível de detalhamento. O usuário pode definir qualquer comprimento de token na saída do objeto. Porém, ele nem sempre será divisível pelo número de níveis sem resto. É aqui que entra em cena a classe convolucional pai, ela ajusta cuidadosamente o número de canais até o tamanho especificado, aplicando seus filtros otimizados e garantindo uma representação de atributos coerente e uniforme.

Como anteriormente, na entrada do objeto esperamos receber um tensor bidimensional de descrição de uma série temporal multimodal, onde cada linha é uma descrição detalhada de um passo temporal. Porém, para que nosso pipeline de patching possa perceber atributos individuais como sequências unitárias independentes, primeiro transponemos a matriz dos dados brutos.

Essa técnica simples, mas importante, garante que todas as operações subsequentes trabalhem segundo o princípio rigoroso de um atributo — uma história, e não misturem sinais de diferentes fontes. É dessa forma que preservamos a integridade e a legibilidade de cada série temporal.

int index = 0;
  if(!cToVarSeq.Init(0, index, OpenCL, count, variables, optimization, iBatch))
     return false;  

Em seguida, chega a vez da convolução multi-janela. Executamos simultaneamente três filtros com tamanhos de janela de 3, 7 e 8 barras e passo 1. Graças ao padding zero, o comprimento das séries de saída permanece o mesmo, mas cada valor agora é enriquecido com o conhecimento de seus vizinhos mais próximos e do seu contexto.

index++;
  {
   int windows[] = {3, 5, 7};
   if(!cProjecting.Init(0, index, OpenCL, windows, 1, inside_emb, count, variables,
                        optimization, iBatch))
      return false;
   cProjecting.SetActivationFunction(SoftPlus);
  }

Nesta etapa, formamos com sucesso os atributos básicos para a análise posterior. Agora, temos a tarefa de estruturar esses dados para enviá-los aos blocos seguintes do modelo, ou seja, realizar o patching. Mas antes de segmentar a série temporal em partes, é necessário executar uma importante operação técnica, reorganizar os últimos eixos no tensor quadridimensional obtido.

O tensor formado na etapa anterior possui a forma [Variável × Comprimento da série × Quantidade de canais × Quantidade de atributos], onde cada passo temporal é descrito por um vetor de três canais, obtidos de diferentes escalas de convolução. No entanto, para um trabalho mais conveniente com sequências unitárias, que serão segmentadas de forma independente, precisamos levar os dados à forma [Variável × Quantidade de canais × Quantidade de atributos × Comprimento da série]. Isso permite tratar cada característica como uma sequência temporal separada e, posteriormente, cortá-la em segmentos de comprimento fixo, os patches.

index++;
if(!cToVarProjSeq.Init(0, index, OpenCL, variables, count, 3 * inside_emb, optimization, iBatch))
   return false;

Essa representação é especialmente conveniente no contexto financeiro, cada canal, enriquecido pela convolução multi-janela, passa agora a atuar como um indicador de mercado independente, cuja dinâmica pode ser analisada no âmbito do patching.

Em seguida, avançamos para a etapa-chave, o patching multiescalar, que constitui a base da nossa arquitetura de pré-processamento de séries temporais. Aqui implementamos um conceito inspirado não tanto em abordagens clássicas, mas na prática real da análise de dados de mercado de alta frequência, onde tanto a profundidade de cobertura quanto a rapidez de reação são importantes.

Em vez de segmentar a sequência em patches de forma rígida e unidimensional, utilizamos uma camada de convolução multi-janela, que permite trabalhar simultaneamente em várias escalas. Isso dá ao modelo a capacidade de observar o mercado a partir de diferentes distâncias temporais, como um analista que acompanha ao mesmo tempo velas de 1 minuto, gráficos horários e o gráfico diário.

index++;
  {
   uint step = (count + patchs) / (patchs + 1);
   uint windows[] = {step, 3 * step / 2, 2 * step};
   if(!cPatchingProj.Init(0, index, OpenCL, windows, step, patch_filters, patchs,
                          3 * inside_emb * variables, optimization, iBatch))
      return false;
   cPatchingProj.SetActivationFunction(SoftPlus);
  }

Os tamanhos das janelas de convolução, nesse caso, são determinados automaticamente, eles dependem do comprimento da sequência temporal analisada e da quantidade de patches definida pelo usuário. Em escalas mais altas, esse valor é ampliado com sobreposição, para garantir a conectividade e a continuidade das informações entre os patches.

Na etapa seguinte, os patches previamente extraídos entram no módulo FeedForward multi-head. Isso não é apenas uma formalidade, é aqui que começa o verdadeiro trabalho de compreensão. Cada patch, obtido em diferentes escalas, agora se transforma em um embedding completo, ou seja, em uma representação compacta e rica, que codifica as principais características do fragmento correspondente da série temporal. O resultado do módulo é um conjunto de vetores compactos, porém expressivos, cada um dos quais pode ser considerado a quintessência do respectivo fragmento temporal.

index++;
if(!cPatchsFeedForward.Init(0, index, OpenCL, 3 * patch_filters, 6 * patch_filters, patchs,
                            3 * inside_emb * variables, 3, optimization, iBatch))
   return false;
index++;

Depois de obtermos embeddings expressivos de cada patch em todas as escalas, chega o momento da agregação dos dados. Afinal, para que o modelo consiga formar uma representação integral do contexto de mercado atual, ele precisa unir informações de diferentes níveis de detalhamento em um único vetor de atributos.

Para resolver essa tarefa, utilizamos a combinação de convolução e max-pooling. A camada convolucional permite identificar dependências locais entre embeddings de diferentes escalas. Ela atua como um analista que procura combinações características de padrões curtos e longos, por exemplo, volatilidade de curto prazo sobre o pano de fundo de uma tendência estável de longo prazo. Tais combinações frequentemente se mostram decisivas na tomada de decisões de trading, especialmente em trechos complexos do mercado.

Em seguida, os dados passam pelo max-pooling, que destaca os atributos mais fortes e expressivos em cada região do tensor resultante. Como resultado, obtemos um único vetor agregado de atributos. Trata-se de uma representação compacta, porém rica, de todo o histórico de entrada, processado em múltiplas escalas.

index++;
if(!cPatchingAgr.Init(0, index, OpenCL, 3 * patch_filters, 3 * patch_filters, patch_filters,
                      patchs, 3 * inside_emb * variables, optimization, iBatch))
   return false;
cPatchingAgr.SetActivationFunction(SoftPlus);
index++;
if(!cProof.Init(0, index, OpenCL, patch_filters, patch_filters, 3 * patchs * inside_emb * variables,
                optimization, iBatch))
   return false;

Mas antes de encaminhar os tokens obtidos para as próximas etapas da arquitetura, precisamos realizar mais um passo importante, transpor o tensor resultante, retornando o eixo do tempo para a primeira posição.

   index++;
   if(!cToPatchVarEmb.Init(0, index, OpenCL, variables * 3 * inside_emb, patchs, optimization, iBatch))
      return false;
//---
   return true;
  }

Por que isso é necessário? Tudo se deve ao fato de que, nas etapas anteriores, em particular na formação dos embeddings e na agregação dos patches, os dados foram representados em um formato no qual o foco principal estava nos patches e nos atributos. Essa ordem dos eixos é conveniente para o processamento local, mas não é adequada para mecanismos sensíveis ao tempo.

Ao retornar o eixo do tempo para o início, nós efetivamente organizamos os tokens obtidos em ordem cronológica. Cada token passa a ser percebido como um momento no tempo, saturado de informações provenientes de vários níveis de escala. Isso dá ao modelo a capacidade de perceber os dados como uma sequência temporal completa, e não como um conjunto abstrato de atributos.

É exatamente nessa forma que o tensor é enviado para as próximas etapas de processamento, onde já entram em jogo as dependências temporais, a análise de contexto e a geração de previsões. Essa ordem permite preservar a relação causal-temporal nos dados, sem a qual qualquer tentativa de modelar o mercado financeiro perde o sentido.

Apesar da aparente complexidade da arquitetura interna do objeto, a implementação dos algoritmos de propagação para frente e propagação reversa permanece extremamente direta. A lógica dos cálculos é organizada de forma etapa por etapa e sequencial, sem laços aninhados ou ramificações confusas. Acredito que compreender a estrutura desses métodos não apresentará dificuldades. Por esse motivo, optamos conscientemente por não nos deter em uma análise detalhada deles no âmbito deste artigo. Para todos que desejarem se aprofundar na implementação técnica do objeto CNeuronTimeFoundPatching, o código-fonte completo, incluindo todos os seus métodos, estará disponível em anexo ao artigo.

Aos poucos, nos aproximamos de limites razoáveis para o formato de um artigo. O volume de material já é suficientemente grande. No entanto, como você entende, nosso trabalho ainda está longe de estar concluído. Apenas lançamos as bases e implementamos o módulo crítico de pré-processamento de dados, que forma o alicerce de toda a análise subsequente.

Vamos fazer uma breve pausa, respirar um pouco e, já no próximo artigo, continuar o caminho, implementando passo a passo os demais componentes do framework analisado.

Conclusão

Neste artigo, nos familiarizamos com os aspectos teóricos do TimeFound, um framework capaz de transformar a estrutura caótica dos dados de séries temporais em um padrão formalizado e previsível.

Iniciamos a implementação da nossa própria visão das abordagens propostas pelos autores do framework. A atenção principal foi dedicada ao módulo de pré-processamento de dados, pois é exatamente ele que determina o quão precisa e expressiva será a forma como o modelo percebe a estrutura do sinal de entrada.

À frente, há um trabalho não menos interessante, no qual iremos mergulhar no próximo artigo.

Links

• TimeFound: A Foundation Model for Time Series Forecasting
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert	EA coletor de exemplos
2	ResearchRealORL.mq5	Expert	EA coletor de exemplos pelo método Real-ORL
3	StudyEncoder.mq5	Expert	EA de treinamento do Codificador do ambiente
4	Study.mq5	Expert	EA de treinamento offline dos modelos
5	StudyOnline.mq5	Expert	EA de treinamento online dos modelos
6	Test.mq5	Expert	EA para teste do modelo
7	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema e da arquitetura dos modelos
8	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação da rede neural
9	NeuroNet.cl	Biblioteca	Biblioteca de código de programas OpenCL