Processos gaussianos em aprendizado de máquina: modelo de regressão em MQL5

Introdução

Os processos gaussianos (PG) são uma ferramenta de modelagem bayesiana amplamente utilizada em aprendizado de máquina para tarefas de regressão e classificação. Ao contrário de muitos modelos tradicionais, que fornecem apenas previsões pontuais, os PG formam uma distribuição de probabilidade completa para os valores previstos. Isso permite não apenas obter previsões pontuais, mas também avaliar a incerteza associada a elas por meio de intervalos de confiança. Essa é uma característica distintiva da abordagem bayesiana, na qual o conhecimento a priori é combinado com os dados observados para obter uma distribuição preditiva.

Os PG pertencem à classe dos métodos baseados em kernel, que utilizam funções de covariância (ou kernels) para modelar as dependências entre os dados. A possibilidade de combinar diferentes kernels, por exemplo, por meio de soma ou multiplicação, proporciona certa flexibilidade na descrição das possíveis funções preditivas. Cada kernel possui seus próprios hiperparâmetros, que devem ser otimizados para alcançar a máxima precisão do modelo.

Neste artigo, vamos destrinchar em detalhes o processo de previsão utilizando um modelo de regressão baseado em processos gaussianos, demonstrando de forma clara como os PG permitem não apenas construir previsões precisas, mas também avaliar de maneira abrangente a incerteza associada a elas.

O que é um processo gaussiano

Do ponto de vista probabilístico, um processo gaussiano é um processo aleatório que descreve uma distribuição de probabilidades sobre funções. Ao contrário da distribuição normal comum, que descreve uma única variável aleatória, o PG define um conjunto infinito de variáveis aleatórias, sendo que qualquer subconjunto finito delas obedece a uma distribuição normal multivariada.

No aprendizado de máquina, os PG pertencem aos modelos não paramétricos, que não exigem uma forma de função previamente definida, como linear ou polinomial, por exemplo, ao contrário da regressão clássica. Em vez disso, o PG modela uma função latente f(x), que se supõe refletir as dependências reais nos dados. No entanto, a própria função f(x) não é observável diretamente; temos acesso apenas aos seus valores com ruído em pontos x específicos. A base do modelo de PG é a suposição de que a distribuição dessa função desconhecida f(x) é normal:

f (x)~ N( μ, Σ),

onde:

• f(x) é a função oculta (latente), cujos valores nos pontos observados queremos modelar,
•  μ é o vetor de valores médios, dependente da função média a priori, que frequentemente é assumida como zero por simplicidade,
•  Σ é a matriz de covariância, cujos elementos são determinados pela função de covariância (ou kernel) K(x, x'), que define o grau de correlação entre os pontos x e x'.

A ideia central dos PG consiste em modelar a distribuição de funções por meio da estrutura de covariância definida pelo kernel, que, por sua vez, determina diferentes propriedades das funções, como sua suavidade, periodicidade, não estacionariedade, etc.

O objetivo principal dos PG é reconstruir a função latente f(x) com base em um conjunto finito de dados D=(X,y), onde X é o conjunto de características e y são as observações com ruído.

Abordagem bayesiana nos PG

Os processos gaussianos utilizam a abordagem bayesiana para inferência estatística, combinando conhecimento a priori com dados observados para construir previsões probabilísticas. Isso diferencia os PG de muitos outros métodos de aprendizado de máquina, como redes neurais ou SVM, pois permite não apenas prever valores, mas também avaliar sua incerteza. A base dessa abordagem é o teorema de Bayes:

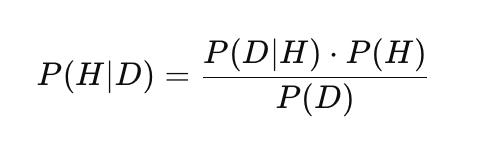
onde:

• P(H) é a probabilidade a priori, isto é, a probabilidade inicial da hipótese H, refletindo o conhecimento ou suposições prévias antes da observação dos dados,
• P(D|H) é a verossimilhança, a probabilidade de observar os dados D se a hipótese H for verdadeira,
• P(H|D) é a probabilidade a posteriori, a probabilidade da hipótese H após a observação dos dados D,
• P(D) é a probabilidade marginal dos dados, a constante de normalização que garante a correção da distribuição a posteriori.

No contexto dos PG, a abordagem bayesiana é aplicada da seguinte forma. A hipótese H é interpretada como uma distribuição sobre as funções f(x), a partir das quais nosso conjunto de dados poderia ter sido gerado, enquanto os dados D correspondem ao conjunto de treinamento (X, y).

Dessa forma, o teorema de Bayes nos PG assume a forma:

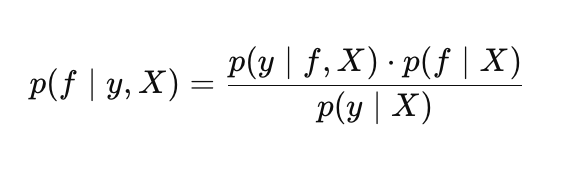
onde:

• p(f |X) é a distribuição a priori sobre as funções f,
• p(y |f, X) é a verossimilhança,
• p(f |y, X) é a distribuição a posteriori sobre as funções f,
• p(y |X) é a verossimilhança marginal (evidence), utilizada para a otimização dos hiperparâmetros do processo gaussiano.

Nos PG, como tanto a distribuição a priori das funções quanto a verossimilhança são gaussianas, a distribuição a posteriori também é um processo gaussiano, porém já com funções de média e covariância atualizadas, que incorporam a informação extraída dos dados. Isso ocorre graças à propriedade matemática de conjugação das distribuições gaussianas, o que torna relativamente simples a derivação das fórmulas de previsão.

Distribuição a priori

A distribuição a priori descreve nossas suposições iniciais sobre as funções possíveis antes de observarmos os dados. Essencialmente, a distribuição a priori é um conjunto de funções candidatas, dentre as quais o PG selecionará as mais adequadas com base nos dados de treinamento. O kernel desempenha um papel fundamental ao definir as propriedades dessas funções. Existem diversos tipos de kernels, cada um adequado a diferentes tipos de dados, por exemplo:

RBF (kernel gaussiano): modela funções suaves e não lineares:

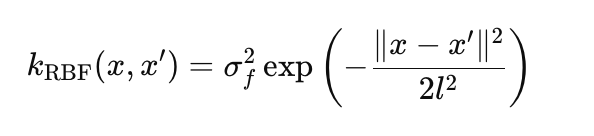
onde:

• σ_f é a amplitude, que define a escala das variações (no código params.rbf.sigma_f),
• l é o comprimento de escala (length scale), que controla a taxa de decaimento da correlação (params.rbf.length),
• ∥x−x′∥ é a distância euclidiana entre os pontos x e x'.

Kernel linear: modela dependências lineares:

• x*x' é o produto escalar de dois vetores,
• σ_l é a escala da tendência linear (params.linear.sigma_l)

Kernel periódico: captura padrões cíclicos:

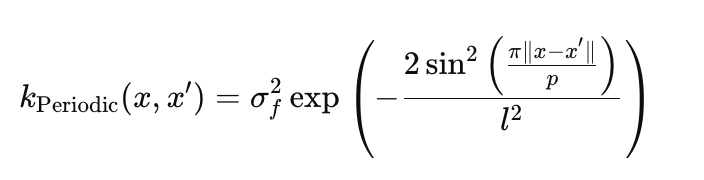
• σ_f é a amplitude, define a escala das oscilações (params.periodic.sigma_f),
• l é o comprimento de escala, controla a suavidade das oscilações (params.periodic.length),
• p é o período, define a frequência de repetição (params.periodic.period).

Para uma demonstração visual da distribuição a priori, consideremos amostras das funções f(x) geradas usando diferentes kernels. Na fig.1 são mostradas amostras da distribuição a priori com kernel RBF. As trajetórias representam funções não lineares suaves, que variam de acordo com os parâmetros do kernel.

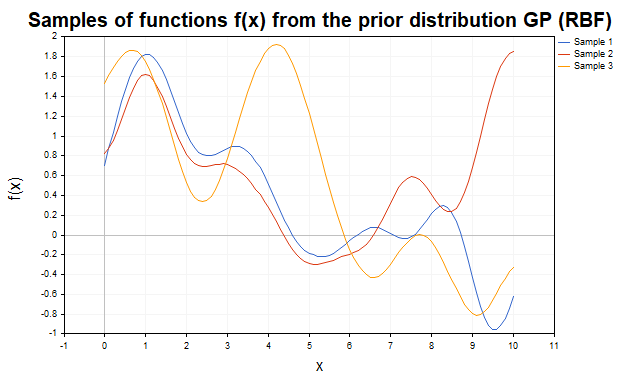
Fig.1 Amostras de funções f da distribuição a priori de PG (kernel RBF)

Na (fig.2) são mostradas amostras da distribuição a priori com kernel linear. As trajetórias representam linhas retas com diferentes inclinações, o que reflete a capacidade do kernel de modelar tendências lineares.

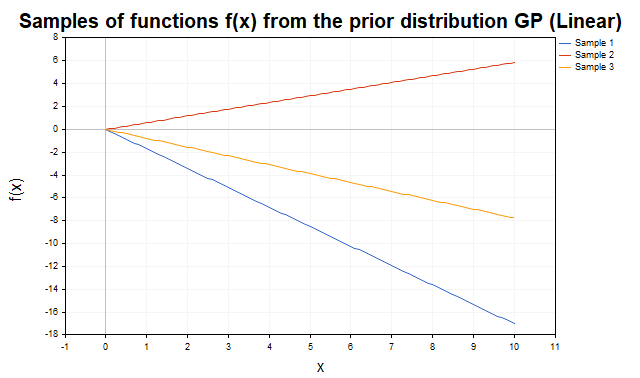
Fig.2 Amostras de funções f da distribuição a priori de PG (kernel linear)

A fig.3 demonstra amostras com kernel periódico. As trajetórias representam funções cíclicas com período p, o que torna esse kernel ideal para modelar componentes periódicas.

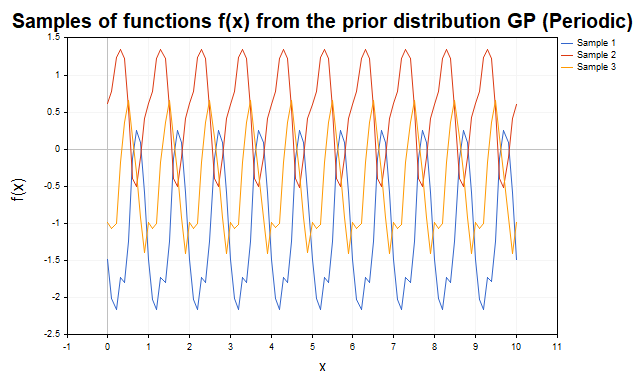
Fig.3 Amostras de funções f da distribuição a priori de PG (kernel periódico)

Na fig.4 são mostradas as trajetórias do bem conhecido processo de Wiener com função de covariância K(x,x') = min(x, x'). 

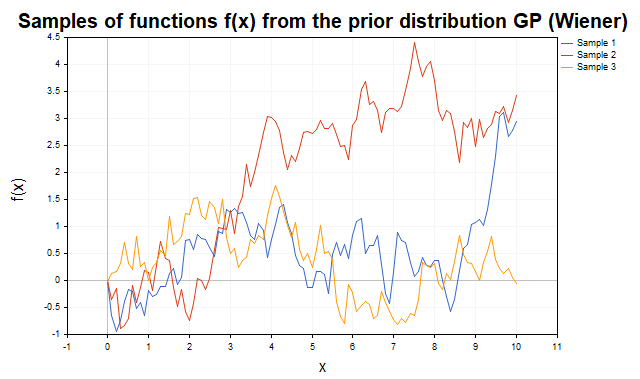
Fig.4 Amostras de funções f da distribuição a priori de PG com função de covariância do processo de Wiener

A flexibilidade dos PG é alcançada pela possibilidade de combinar kernels, por meio de soma ou multiplicação, o que permite modelar funções com propriedades variadas, como a combinação de tendências lineares e não lineares, oscilações periódicas, etc. As amostras foram geradas utilizando o script SamplesPrior.

Verossimilhança

Nos processos gaussianos, a verossimilhança p(y |f, X) descreve a probabilidade de observar os dados y dado uma função específica f da distribuição a priori e os dados X. Ela desempenha um papel fundamental na inferência bayesiana, conectando a distribuição a priori sobre funções com os dados observados. Para um conjunto de dados, a verossimilhança é definida por uma distribuição normal multivariada:

onde:

• f(x) é o vetor de valores da função latente nos pontos X,
• σy^2 é a variância do ruído,
• ∥y−f(x)∥^2 é o quadrado da norma euclidiana da diferença entre os dados observados e os valores da função f.

Essa fórmula mostra que a verossimilhança é tanto maior quanto mais próximos os valores da função f estiverem dos dados observados y.

Distribuição a posteriori

A distribuição a posteriori é o resultado da atualização bayesiana da distribuição a priori levando em conta os dados observados e a verossimilhança. Ela descreve a probabilidade dos valores da função latente f(x) em novos pontos de teste X. Essa distribuição é caracterizada por uma média atualizada μ, que representa a previsão, e por uma matriz de covariância Σ*, que descreve a incerteza das previsões.

Dessa forma, a distribuição a priori define um conjunto de funções, a verossimilhança as "pondera" com base nos dados, e a distribuição a posteriori fornece a função mais provável com uma estimativa de incerteza.

Regressão por PG com verossimilhança gaussiana

Os processos gaussianos, em combinação com o ruído gaussiano das observações, permitem resolver o problema de regressão de forma analítica, utilizando métodos de álgebra linear. Isso simplifica significativamente os cálculos e elimina a necessidade de aplicar métodos numéricos complexos. Os PG são adequados para modelar tanto dados com ruído quanto dados sem ruído.  Consideremos primeiro o caso idealizado, quando os valores alvo y são valores verdadeiros da função sem ruído, isto é, quando y = f(x), o cenário de interpolação.

Caso sem ruído: interpolação

Suponhamos que temos um conjunto de dados D = {(xn, yn) : n = 1 : N}, onde yn = f(xn), isto é, uma observação exata e sem ruído da função f avaliada no ponto xn. Nossa tarefa é prever os valores da função f para um conjunto de teste X de dimensão N*×d.

Para os pontos de treinamento X e os pontos de teste X*, a distribuição a priori conjunta dos valores da função f e f* é uma distribuição normal multivariada:

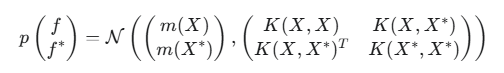
onde:

• f é o vetor dos valores verdadeiros da função latente nos pontos de treinamento,
• f* é o vetor dos valores verdadeiros da função latente nos pontos de teste,
• m(X) é o vetor dos valores médios da função para os pontos de treinamento, vetor nulo para simplificação,
• m(X*) é o vetor dos valores médios da função para os pontos de teste, vetor nulo para simplificação,
• K(X,X) é a matriz de covariância N×N entre todos os pares de pontos de treinamento,
• K(X,X*) é a matriz de covariância N×N* entre os pontos de treinamento e de teste,
• K(X*,X*) é a matriz de covariância N*×N* entre todos os pares de pontos de teste,
• N é o número de pontos de dados de entrada,
• N* é o número de pontos de dados de teste,
• d é a dimensionalidade dos dados de entrada, isto é, o número de características.

Como as observações y neste caso correspondem exatamente a f, y = f, ou seja, a verossimilhança é uma função delta, podemos passar diretamente para a distribuição condicional de f* dado y. Em virtude das propriedades das distribuições condicionais da distribuição normal multivariada, a distribuição a posteriori de f* condicionada aos dados observados y assume a forma:

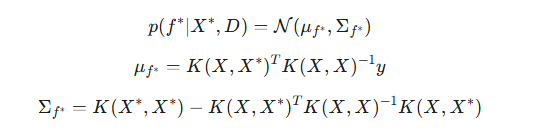
onde:

• μf* é a média a posteriori, a melhor previsão dos valores da função latente f nos novos pontos de teste, com base nos dados de treinamento,
• Σf* é a matriz de covariância a posteriori para os pontos de teste. Ela expressa quantitativamente a incerteza na previsão da função latente f.

Caso com ruído: regressão

Em problemas reais, os dados y geralmente contêm ruído imprevisível: y = f(X) + ϵ, onde ϵ ∼ N(0, σ^2) é um ruído gaussiano. Nesse caso, os PG não interpolam exatamente os dados de treinamento, isto é, não passam estritamente por cada ponto, mas, em vez disso, os suavizam, levando em conta o nível de ruído assumido. A distribuição a posteriori para dados com ruído é modificada pela adição da variância do ruído aos elementos diagonais da matriz de covariância dos dados de treinamento:

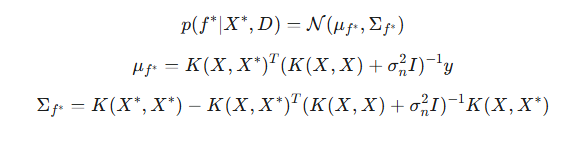
O parâmetro de ruído σ é um hiperparâmetro do modelo e é otimizado juntamente com os parâmetros do kernel. 

Um ponto muito importante: com a adição de ruído, passamos a ter a possibilidade de prever intervalos de confiança não apenas para a função latente f, mas também para novas observações y. Diferentemente do caso sem ruído, no qual as distribuições preditivas para f e y coincidiam, agora essas distribuições são distintas. A principal diferença reside em suas matrizes de covariância. A covariância Σf reflete a incerteza da própria função latente nos pontos de teste. A covariância Σy inclui a incerteza da função latente, acrescida da variância do ruído das observações.

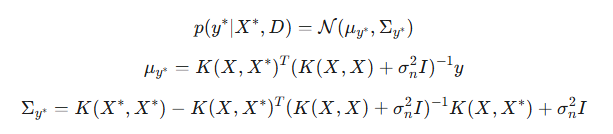
• μy é a média a posteriori para a nova observação y. Ela coincide com μf*, pois o valor esperado do ruído é igual a zero,
• Σy é a covariância a posteriori para a nova observação y.  

Portanto, se estivermos interessados em intervalos de confiança para novas observações y, e não para novos valores da função latente f, devemos utilizar essa fórmula.

Para demonstrar visualmente como os processos gaussianos se adaptam aos dados, consideremos a visualização de amostras das funções f geradas a partir da distribuição a posteriori no caso sem ruído. Na fig.5 são apresentadas três funções f construídas após a observação de cinco pontos de treinamento, utilizando o kernel RBF.

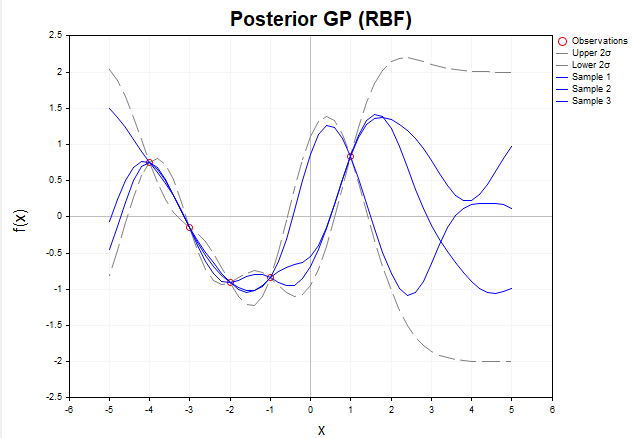
Fig.5 Amostras de funções f da distribuição a posteriori (kernel RBF, sem ruído)

Antes da observação de quaisquer dados, a distribuição a priori definida pelo PG descreve um conjunto infinito de funções. Após a adição dos dados de treinamento, a distribuição a posteriori restringe esse conjunto, deixando apenas as funções que passam exatamente pelos pontos observados. Em outras palavras, ela se concentra exclusivamente nas funções que interpolam os dados com precisão. 

Nos pontos de treinamento X, a variância, isto é, os elementos diagonais da matriz de covariância a posteriori Σ*, é igual a zero, o que significa ausência total de incerteza nesses pontos: todas as funções amostradas da distribuição a posteriori passam garantidamente exatamente pelos pontos de treinamento. Fora dos pontos de treinamento, as funções podem variar, refletindo a incerteza do modelo nas regiões onde não há dados. No entanto, seu comportamento ainda é determinado pela estrutura do kernel escolhido, neste caso, o RBF.

Agora, consideremos o gráfico das amostras das funções f da distribuição a posteriori quando os dados observados y contêm ruído gaussiano. (fig.6)

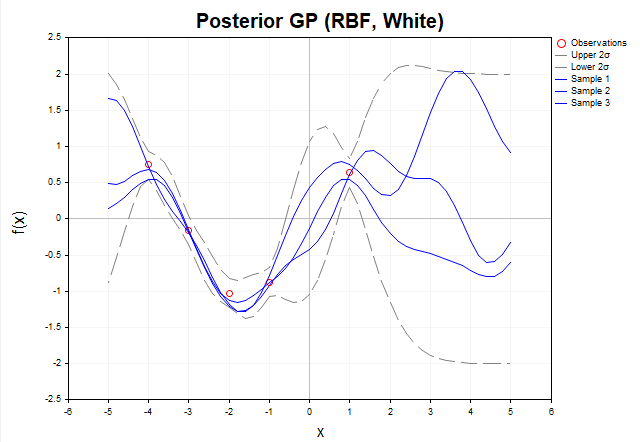
Fig. 6 Amostras de funções f da distribuição a posteriori (kernel RBF, com ruído)

Na presença de ruído, as funções a posteriori não são obrigadas a passar exatamente pelos dados observados y. Isso significa que o conjunto de funções possíveis que podem explicar os dados se torna mais amplo, pois elas podem se desviar dos valores observados dentro dos limites do ruído. As linhas tracejadas cinzas indicam os intervalos de confiança de 2 sigma, que abrangem cerca de 95% da probabilidade da distribuição posterior de f. Em regiões distantes dos dados de treinamento, a incerteza aumenta, e os intervalos de confiança se tornam significativamente mais largos, demonstrando a menor confiabilidade do modelo nessas áreas. É importante destacar que as linhas tracejadas cinzas indicam os intervalos de confiança especificamente para a função latente f, e não para novas observações y*. 

Otimização dos hiperparâmetros do processo gaussiano

A eficácia do modelo de processos gaussianos depende em grande medida da escolha ótima de seus hiperparâmetros, o que permite ao modelo se ajustar aos dados, maximizando sua capacidade de explicar as dependências observadas. Esses hiperparâmetros incluem os parâmetros do kernel e a variância do ruído. Nos PG, a otimização é realizada por meio da minimização do logaritmo negativo da verossimilhança marginal (NLML):

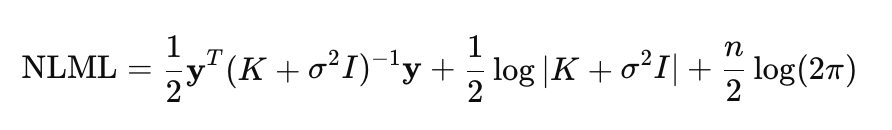
O cálculo direto de (K+σ^2I)^−1 y é computacionalmente custoso para valores grandes de n, pois exige a inversão de uma matriz de dimensão n×n. Por isso, para tornar os cálculos mais eficientes e numericamente estáveis, utiliza-se a decomposição de Cholesky. Considerando essa decomposição, a fórmula do NLML é reescrita como:

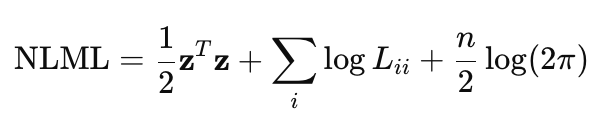
• z é o vetor obtido ao resolver o sistema de equações lineares utilizando a decomposição de Cholesky, z = L^−1*y,
• L é a matriz triangular inferior proveniente da decomposição de Cholesky K+σ^2*I = LL^T.

Essa fórmula está implementada na função NegativeLogMarginalLikelihood.

//+------------------------------------------------------------------+
//| Вычисление отрицательного логарифмического правдоподобия         |
//+------------------------------------------------------------------+
double NegativeLogMarginalLikelihood(const matrix &x, const matrix &y, int &kernel_list[], KernelParams &params)
{
   int n = (int)x.Rows();

   //--- Вычисляем ковариационную матрицу K
   matrix K = ComputeKernelMatrix(x, x, kernel_list, params);
   
   //--- Добавляем дисперсию белого шума, если выбран KERNEL_WHITE 
    double white_noise_variance = 0.0;
    for (int i = 0; i < ArraySize(kernel_list); i++)
    {
        if (kernel_list[i] == KERNEL_WHITE)
        {
            white_noise_variance = params.white.sigma * params.white.sigma;
            break; 
        }
    }
   // Добавление небольшого джиттера предотвращает проблемы,
   // если матрица K оказывается сингулярной или близкой к сингулярной 
   // из-за особенностей вычислений или выбранного ядра
    double jitter = 1e-6;
    K += matrix::Identity(n, n) * (white_noise_variance + jitter);
     
   // ---Выполняем разложение Холецкого: K + sigma^2*I = L * L^T
   matrix L;
   if (!K.Cholesky(L))
   {
      Print("Ошибка: Разложение Холецкого не удалось");
      return DBL_MAX;
   }

  //--- Решаем линейную систему L * z = y для нахождения z = L^(-1) * y
   vector z = L.LstSq(y.Col(0));
   if (z.Size() == 0)
   {
      Print("Ошибка: Не удалось решить систему L * z = y");
      return DBL_MAX;
   }

   //--- Вычисляем первое слагаемое в формуле NLML : 
   // 1/2 * y^T * (K + sigma^2*I)^-1 * y = 1/2 * z^T * z
    double data_term = 0.5 * z @ z; // Скалярное произведение z^T * z   

   //--- Вычисляем второе слагаемое: 1/2 * log|K + sigma^2*I| = sum(log(L_ii))
   vector diag = L.Diag();
   double log_det = 0.0;
   for (int i = 0; i < n; i++)
      log_det += MathLog(diag[i]); // суммируем логарифмы диагональных элементов L
  
   //--- Вычисляем третье слагаемое: n/2 * log(2π)
   double const_term = 0.5 * n * MathLog(2 * M_PI);

   return data_term + log_det + const_term;
   
}

A matriz de covariância K é calculada por meio da função ComputeKernelMatrix, que soma as contribuições de todos os kernels selecionados, por exemplo, RBF, Linear, Periodic, etc.

//+------------------------------------------------------------------+
//| Вычисление ковариационной матрицы                                |
//+------------------------------------------------------------------+
matrix ComputeKernelMatrix(const matrix &X1, const matrix &X2, int &kernel_list[], KernelParams &params)
{
   matrix K  = matrix::Zeros(X1.Rows(), X2.Rows());
   for (int i = 0; i < ArraySize(kernel_list); i++)
   {
      switch (kernel_list[i])
      {
         case KERNEL_RBF:
            K += RBF_kernel(X1, X2, params.rbf.sigma_f, params.rbf.length);
            break;
         case KERNEL_LINEAR:
            K += Linear_kernel(X1, X2, params.linear.sigma_l);
            break;
         case KERNEL_PERIODIC:
            K += Periodic_kernel(X1, X2, params.periodic.sigma_f, params.periodic.length, params.periodic.period);
            break;
         case KERNEL_WHITE:
            // WhiteKernel добавляется отдельно в виде sigma^2 * I
            break;
      }
   }
   return K;
}

O NLML é utilizado como função objetivo para a otimização dos hiperparâmetros na função OptimizeGP. A otimização é realizada por meio do método BLEIC da biblioteca ALGLIB. 

//+------------------------------------------------------------------+
//| Оптимизация гиперпараметров гауссовского процесса                |
//+------------------------------------------------------------------+
KernelParams OptimizeGP(int &kernel_list[], matrix &x_train, matrix &y_train)
{
   double w[]; //Массив начальных значений гиперпараметров
   double s[]; //Массив масштабов для гиперпараметров, используемых для нормализации в оптимизации
   double bndl[], bndu[]; // Массивы нижних и верхних границ для каждого гиперпараметра    
   CObject Obj;
   CNDimensional_GP ffunc(kernel_list, x_train, y_train);// Объект класса, реализующего целевую функцию NLML
   CNDimensional_Rep frep; // Объект для хранения отчета об оптимизации 
   
   // Инициализация параметров
   InitializeKernelParams(kernel_list, w, s, bndl, bndu);
   /*
   Подсчитывается общее количество параметров (num_params) в зависимости от типов ядер в kernel_list.
   Задает начальные значения параметров w,масштаб и границы для параметров  
   */

   CMinBLEICStateShell state;
   CMinBLEICReportShell rep; //Объект для хранения результатов оптимизации.

   double epsg = 0;  //Точность по градиенту (0 означает, что остановка по градиенту отключена)
   double epsf = 0.0001; //Точность по значению функции 
   double epsw = 0; // точность по параметрам 
   double diffstep = 0.0001; // Шаг для численного вычисления производных.
   double epso = 0.00001; // Параметры для внешних и внутренних условий сходимости в BLEIC
   double epsi = 0.00001;

   CAlglib::MinBLEICCreateF(w, diffstep, state); // Создает объект оптимизации BLEIC с начальными параметрами w и шагом для численных производных diffstep
   CAlglib::MinBLEICSetBC(state, bndl, bndu); //Устанавливает границы параметров (bndl, bndu).
   CAlglib::MinBLEICSetScale(state, s); //Устанавливает масштабы параметров (s).
   CAlglib::MinBLEICSetInnerCond(state, epsg, epsf, epsw); 
   CAlglib::MinBLEICSetOuterCond(state, epso, epsi);
   CAlglib::MinBLEICOptimize(state, ffunc, frep, 0, Obj);
   CAlglib::MinBLEICResults(state, w, rep);
   Print("TerminationType =", rep.GetTerminationType()); // Код завершения оптимизации
   /*
                * -8    internal integrity control  detected  infinite or
                        NAN   values   in   function/gradient.   Abnormal
                        termination signalled.
                * -3   inconsistent constraints. Feasible point is
                       either nonexistent or too hard to find. Try to
                       restart optimizer with better initial approximation
                *  1   relative function improvement is no more than EpsF.
                *  2   scaled step is no more than EpsX.
                *  4   scaled gradient norm is no more than EpsG.
                *  5   MaxIts steps was taken
                *  8   terminated by user who called minbleicrequesttermination().
                       X contains point which was "current accepted"  when
                       termination request was submitted.   
   */
   Print("IterationsCount =", rep.GetInnerIterationsCount()); // Количество итераций

   Print("Parameters:");
   PrintKernelParams(w, kernel_list); // Выводит оптимизированные параметры в журнал
   Print("NLML = ", ffunc.GetNLML()); // финальное значение NLML для оптимальных параметров

   KernelParams optimized_params;    
   CRowDouble parameters = w;   
   //определяем правильное распределение параметров по ядрам
   ExtractKernelParams(parameters, kernel_list, optimized_params); 

   return optimized_params;
}

Regressão por PG em MQL5

Para ilustrar as capacidades do modelo de regressão baseado em processos gaussianos, consideremos um exemplo utilizando dados sintéticos. A implementação é apresentada no script GP_Regressor, que demonstra o processo de criação, treinamento e teste do modelo.

A geração dos dados é realizada por meio da função Dataset, que forma as matrizes de dados sintéticos para treinamento e teste. O dataset consiste em 100 pontos uniformemente distribuídos no intervalo [−5,5] e representa a função y=sin(x)+0.5x com adição de ruído gaussiano. Essa abordagem permite simular dados reais que contêm tanto uma tendência linear quanto uma componente periódica, levando em conta a incerteza.

Para construir o modelo de regressão, é necessário definir a lista de kernels que compõem a função de covariância. Cada kernel contribui de forma única para a matriz de covariância K, determinando o tipo de dependências que o modelo é capaz de capturar. A configuração da lista de kernels é realizada pela função SetKernelList, que forma o array kernel_list com base no parâmetro de entrada kernel_combination, do tipo enum KernelCombination. As seguintes combinações são suportadas:

• COMBINATION_1: [RBF, Linear, White] (3 kernels),
• COMBINATION_2: [RBF, Linear, Periodic, White] (4 kernels),
• COMBINATION_3: [RBF, White] (2 kernels).

A flexibilidade na escolha das combinações de kernels permite adaptar o modelo a diferentes tipos de dados, sejam eles tendências lineares, oscilações periódicas ou dependências não lineares complexas.
Após a seleção dos kernels, é realizada a otimização dos hiperparâmetros do modelo por meio da função OptimizeGP. Essa função minimiza o logaritmo negativo da verossimilhança marginal (NLML), retornando a estrutura KernelParams, que contém os parâmetros ótimos para cada kernel, como a amplitude (σ_f), o comprimento de escala (l) ou o período (p).

Após a obtenção dos parâmetros ótimos, passamos à etapa de previsão utilizando a função Predict.

//+------------------------------------------------------------------------+
//| Предсказание гауссовского апостериорного распределения для новых точек |    
//+------------------------------------------------------------------------+
GPPredictionResult Predict(const matrix &x_train, const matrix &y_train, const matrix &x_test, 
             int &kernel_list[], KernelParams &params)
{
  GPPredictionResult result; 

   //  Вычисляет ковариационную матрицу K для обучающих точек
   matrix K = ComputeKernelMatrix(x_train, x_train, kernel_list, params); 
   // Получаем дисперсию шума наблюдений
    double observation_noise_variance = 0.0;
    for (int i = 0; i < ArraySize(kernel_list); i++)
    {
        if (kernel_list[i] == KERNEL_WHITE)
        {
            observation_noise_variance = params.white.sigma * params.white.sigma;
            break;
        }
    }
   
   // Формируем матрицу шума для обучающих данных: K + sigma_n^2 * I
   matrix K_noisy_train = K + matrix::Identity((int)x_train.Rows(), (int)x_train.Rows()) * observation_noise_variance;  
   // Вычисляет кросс-ковариационную матрицу K* между обучающими и тестовыми точками   
   matrix K_star = ComputeKernelMatrix(x_train, x_test, kernel_list, params);
   // Вычисление апостериорного среднего
   matrix inv_term = K_noisy_train.Inv(); 
   result.mu_f_star = K_star.Transpose() @ (inv_term @ y_train); // Совпадает с mu_y_star
     
   // Вычисление апостериорной ковариационной матрицы для скрытой функции (Sigma_f_star)
    matrix K_star_star = ComputeKernelMatrix(x_test, x_test, kernel_list, params);
    result.Sigma_f_star = K_star_star - K_star.Transpose() @ (inv_term @ K_star);
    
   // Вычисление апостериорной ковариационной матрицы для нового наблюдения (Sigma_y_star)
   // Sigma_y_star = Sigma_f_star + sigma_n^2 * I
    result.Sigma_y_star = result.Sigma_f_star + matrix::Identity((int)x_test.Rows(), (int)x_test.Rows()) * observation_noise_variance;

    return result;
   
}

A função Predict é um elemento central da implementação do modelo de PG, pois não apenas retorna os valores previstos, mas também fornece informações completas sobre a distribuição a posteriori nos pontos de teste. A função retorna a estrutura GPPredictionResult, que contém:

• média a posteriori para a função latente f (μf = μy*),
• matriz de covariância a posteriori Σf para a função latente f,
• matriz de covariância a posteriori Σy para novos valores observados y. Essa matriz inclui tanto a incerteza da função latente quanto a variância do ruído das observações (σ^2), que é determinada durante a otimização do parâmetro do kernel WhiteKernel.

Agora, vamos analisar os resultados de previsão para diferentes combinações de kernels. Inicialmente, tentemos prever nossa função utilizando apenas o kernel RBF, assumindo que há ruído nos dados (fig.7).

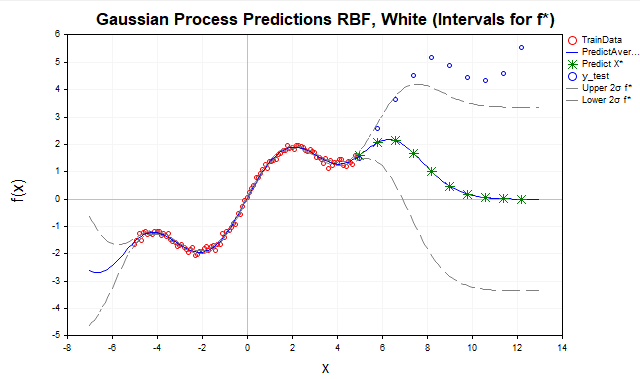
Fig.7 Previsão com kernel RBF

• Pontos vermelhos são os dados de treinamento (TrainData),
• Linha azul é a média prevista,
• Estrelas verdes são as previsões para os pontos de teste (X*),
• Pontos azuis são os dados de teste fora do intervalo de treinamento,
• Linhas tracejadas cinzas são os intervalos de confiança (± 2 sigma para f ou y).

Aqui observamos que, à medida que os pontos de teste se afastam do intervalo dos dados de treinamento [-5,5], as previsões tendem à média a priori do PG, que geralmente é assumida como zero. Isso ocorre porque, longe dos dados de treinamento, as covariâncias K, entre novos pontos x e os pontos de treinamento x, para o kernel RBF, decaem exponencialmente até zero. Portanto, o kernel RBF é mais adequado para interpolação dos dados, mas sua aplicação para extrapolação é limitada devido ao rápido decaimento das correlações.

 Para melhorar a extrapolação, adicionemos um kernel linear (fig.8).

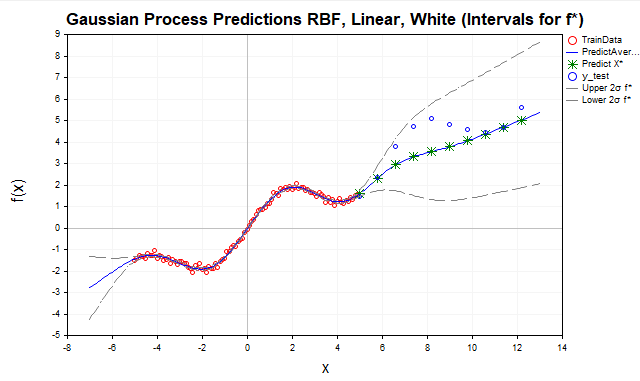
Fig.8 Previsão com soma de kernels RBF e linear, intervalos para f

O kernel linear modela dependências lineares, o que o torna adequado para extrapolação, especialmente se os dados apresentarem uma tendência linear ou quase linear, como no nosso exemplo com a função y=sin(x)+0.5x. A inclusão do kernel linear permitiu melhorar as previsões fora do intervalo dos dados de treinamento, capturando a componente linear (0.5x). No entanto, como pode ser observado no gráfico, o modelo ainda não reflete completamente a estrutura dos dados, deixando de captar sua componente periódica.

Para modelar oscilações sazonais ou cíclicas, como sin(x) em nossos dados, utiliza-se o kernel periódico (fig.9).

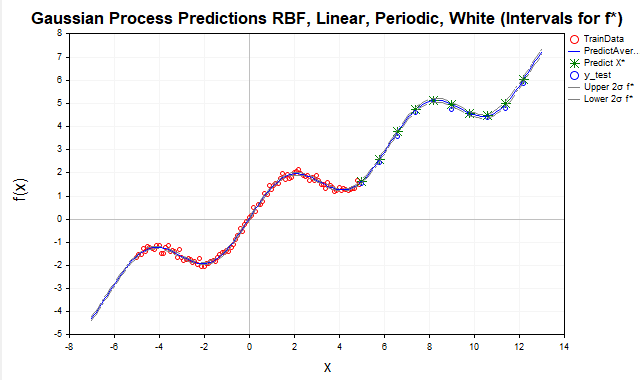
Fig.9 Previsão com soma de kernels RBF, periódico e linear, intervalos para f

Após a adição do kernel periódico, o modelo alcançou um prognóstico praticamente ideal, pois conseguiu captar todas as dependências essenciais presentes nos dados. Como resultado, os intervalos de confiança para f, a função latente, praticamente se fundem com a média a posteriori. Para os valores observados y, por outro lado, os intervalos de confiança são significativamente mais amplos, o que é esperado, pois levam em conta a variância do ruído das observações, como mostrado na fig.10.

Fig.10 Previsão com soma de kernels RBF, periódico e linear, intervalos para y

Observação importante sobre as previsões em PG. Sem a consideração adequada da variância do ruído, é possível interpretar erroneamente os intervalos de confiança para f(x) como intervalos preditivos para y. Para obter intervalos preditivos corretos para y*, é necessário incluir explicitamente a variância do ruído na matriz de covariância, o que foi implementado na função Predict.

Considerações finais

Nesta artigo, examinamos detalhadamente os fundamentos dos processos gaussianos a partir do exemplo de um problema de regressão. Estudamos os principais componentes dos PG: a distribuição a priori, a verossimilhança e a distribuição a posteriori, que fornecem previsões probabilísticas completas com avaliação quantitativa da incerteza. Implementamos as principais funções de kernel, como RBF, Linear e Periodic, embora, naturalmente, existam muitas outras.

Foi dada atenção especial à otimização dos hiperparâmetros, que é de importância crítica para a adaptação dos PG a dados específicos. Demonstramos que essa otimização é realizada por meio da minimização do logaritmo negativo da verossimilhança marginal (NLML), na qual, para aumentar a eficiência computacional e a estabilidade numérica, é aplicada a decomposição de Cholesky. No modelo implementado, o método de otimização utilizado foi o método gradiente BLEIC da biblioteca ALGLIB.

Este artigo está focado nos princípios básicos dos PG, e uma série de tópicos avançados ficou fora de seu escopo. Entre eles estão, por exemplo, o uso de expressões analíticas para os gradientes do NLML, o que pode aumentar significativamente a eficiência da otimização, bem como a utilização de aproximações esparsas, que são de importância crítica para o processamento de grandes volumes de dados. Essas direções abrem perspectivas para pesquisas futuras sobre o modelo de PG.

#	Nome	Tipo	Descrição
1	GP_Samples_Prior.mq5	Script	Demonstração de amostras da distribuição a priori
2	GP_Samples_Posterior.mq5	Script	Demonstração de amostras da distribuição a posteriori
3	GP_Regressor	Script	Construção do modelo de regressão