Redes neurais em trading: Aprendizado contextual com memória (MacroHFT)

Introdução

Os mercados financeiros atraem um número enorme de investidores, graças à sua ampla acessibilidade e potencial de alta lucratividade. Entre todos os ativos disponíveis, as criptomoedas se destacam por sua volatilidade extrema, o que abre oportunidades únicas para obter lucros significativos em curtos períodos. Um benefício adicional é o funcionamento ininterrupto 24/7, que permite aos traders reagirem rapidamente às mudanças de mercado. No entanto, essa alta volatilidade traz não apenas vantagens, mas também riscos relevantes, exigindo estratégias de gestão mais sofisticadas.

Para maximizar o lucro nos mercados de criptomoedas, a negociação de alta frequência (HFT) está sendo cada vez mais utilizada — uma forma de trading algorítmico baseada na execução ultrarrápida de ordens. HFT já ocupa posição de liderança nos mercados financeiros tradicionais e, mais recentemente, vem sendo ativamente aplicada no setor de criptoativos. A negociação de alta frequência se destaca não só pela velocidade de execução, mas também pela capacidade de processar grandes volumes de dados em tempo real, tornando-se indispensável diante da alta dinâmica dos mercados de criptomoedas.

Os métodos de aprendizado por reforço (RL) estão ganhando popularidade no setor financeiro, pois permitem lidar com tarefas complexas de tomada de decisão sequencial. RL-algoritmos conseguem processar dados multidimensionais, levar em conta múltiplos parâmetros e se adaptar a condições variáveis. No entanto, apesar dos avanços no trading de baixa frequência, algoritmos eficazes para mercados de criptomoedas em alta frequência ainda estão em desenvolvimento. Os mercados cripto se caracterizam por sua alta volatilidade, instabilidade e pela necessidade de considerar horizontes de negociação de longo prazo ao mesmo tempo em que se reage rapidamente aos eventos.

Os algoritmos HFT existentes para criptomoedas enfrentam uma série de problemas que limitam sua eficácia. Em primeiro lugar, o mercado muitas vezes é tratado como um sistema estacionário único, e muitos algoritmos se limitam à análise de tendências, ignorando a volatilidade. Essa abordagem dificulta a gestão de riscos e reduz a precisão das previsões. Em segundo lugar, muitas estratégias tendem ao sobreajuste devido ao foco excessivo em um conjunto restrito de características do mercado. Isso compromete sua capacidade de adaptação a novas condições de mercado. Por fim, as políticas de negociação individuais dos agentes geralmente carecem de flexibilidade suficiente para reagir rapidamente a mudanças bruscas, o que é especialmente crítico em mercados com dados de alta frequência.

Uma das soluções propostas para esses problemas foi apresentada no trabalho "MacroHFT: Memory Augmented Context-aware Reinforcement Learning On High Frequency Trading". Seus autores propuseram o framework MacroHFT, uma abordagem inovadora baseada em aprendizado por reforço dependente de contexto. Este framework foi desenvolvido especificamente para negociação de alta frequência com criptomoedas no timeframe de 1 minuto. MacroHFT utiliza informações macroeconômicas e outros dados contextuais para melhorar a qualidade das decisões tomadas. O processo inclui duas etapas principais. Na primeira etapa, o mercado é classificado com base em indicadores de tendência e volatilidade. Para cada categoria de condições de mercado, são treinados subagentes especializados, que ajustam suas estratégias conforme a situação atual. Esses subagentes garantem flexibilidade e a capacidade de considerar as particularidades locais do mercado.

Na segunda etapa, é criado um hiperagente que integra as estratégias dos subagentes e otimiza seu uso de acordo com a dinâmica do mercado. O hiperagente conta com um módulo de memória, que considera a experiência recente e permite desenvolver estratégias de negociação estáveis e adaptativas. Isso assegura alta resiliência do sistema diante de mudanças bruscas nas condições do mercado e ajuda a minimizar os riscos.

Algoritmo MacroHFT

O framework MacroHFT é uma plataforma inovadora para trading algorítmico, desenvolvida especialmente para os mercados de criptomoedas, com sua alta volatilidade e mudanças rápidas. No núcleo do funcionamento do framework estão os métodos de aprendizado por reforço, que permitem criar algoritmos adaptativos, capazes de analisar as condições do mercado e prever suas alterações. A principal ideia está na integração de subagentes especializados — cada um otimizado para um cenário de mercado específico — e de um hiperagente, que coordena seu funcionamento, garantindo coerência e ótimo desempenho do sistema como um todo.

Em um cenário de alta volatilidade e constantes mudanças nas condições de mercado, o uso de um único agente de aprendizado por reforço (RL) mostra-se pouco eficaz. Isso ocorre porque as condições de mercado podem mudar muito rapidamente e de maneira imprevisível, e um único algoritmo não consegue se adaptar a cada nova situação com a agilidade necessária. Para resolver esse problema, os autores do framework MacroHFT propuseram a criação de diversos subagentes especializados, cada um treinado em determinadas condições de mercado. Isso permite a construção de um sistema mais flexível e adaptativo.

A ideia principal está na segmentação e classificação dos dados de mercado com base em dois parâmetros-chave: tendência e volatilidade. Para realizar a análise, os dados de mercado são divididos em blocos de comprimento fixo. Esses blocos são usados tanto para o treinamento quanto para os testes. Em seguida, são atribuídos rótulos a cada bloco, que ajudam a determinar a qual tipo de condição de mercado ele pertence, o que facilita o processo de treinamento dos subagentes.

O processo de rotulação dos dados é dividido em duas etapas:

1. Definição dos rótulos de tendência. Para identificar a tendência do mercado, os dados de cada bloco são passados por um filtro de baixas frequências. Isso permite eliminar o ruído e destacar a direção principal do movimento do preço. Depois disso, é aplicada uma regressão linear: a inclinação da linha resultante serve como indicador de tendência. Com base nisso, as tendências são classificadas como positivas (mercado de alta), neutras (lateral) ou negativas (mercado de baixa).
2. Definição dos rótulos de volatilidade. Para avaliar o nível de volatilidade, calcula-se o valor médio das variações de preço dentro de cada bloco. Os valores obtidos são classificados em três categorias: alta volatilidade, média e baixa. A classificação é baseada na distribuição dos dados e na aplicação de quantis para definir os limites entre as categorias.

Dessa forma, cada bloco de dados recebe dois rótulos: de tendência e de volatilidade. Todos os dados são divididos em seis categorias, que correspondem às combinações dos tipos de tendência (alta, lateral, baixa) e níveis de volatilidade (alta, média, baixa). Isso permite criar seis subconjuntos de dados para treinamento, cada um voltado ao treinamento de subagentes sob condições específicas de mercado. Após isso, a mesma rotulação é aplicada aos dados de teste, usando os valores-limite calculados com base no conjunto de treinamento. Essa abordagem garante uma avaliação justa da performance de cada subagente.

Cada subagente é treinado em um dos seis subconjuntos de dados. Zatem, seu desempenho é avaliado em um conjunto de teste correspondente à sua categoria. Isso permite criar subagentes especializados, cada um otimizado para operar sob determinadas condições de mercado. Por exemplo, um subagente será mais eficaz em um mercado de alta com alta volatilidade, enquanto outro atuará melhor em um mercado de baixa com baixa volatilidade. Essa estrutura modular permite que o sistema se adapte com flexibilidade às condições mutáveis e melhore sua eficácia.

Para o treinamento dos subagentes, os autores do framework propõem o uso do método Double Deep Q-Network (DDQN) com uma arquitetura dual que leva em conta os indicadores de mercado, as características contextuais e a posição do trader. Esses dados são processados por camadas separadas da rede neural, sendo posteriormente combinados em uma representação conjunta. Essa representação é adaptada por meio do bloco Adaptive Layer Norm, que permite considerar as condições específicas do mercado, garantindo flexibilidade e precisão na tomada de decisão.

MacroHFT prevê a criação de seis subagentes, cada um especializado em uma condição de mercado específica. As estratégias finais são integradas por um hiperagente, que garante a eficácia e adaptabilidade do sistema em um mercado de criptomoedas em constante mudança.

O hiperagente consolida os resultados dos subagentes para formar uma política flexível e eficaz, capaz de se adaptar dinamicamente às mudanças de mercado. Ele combina as decisões dos subagentes por meio de uma metapolítica baseada em um modelo de pesos SoftMax. Essa abordagem minimiza o risco de depender excessivamente de um único subagente e leva em conta as decisões de todos os componentes do sistema.

Uma das principais vantagens do hiperagente é o uso de indicadores técnicos de tendência e volatilidade para decisões rápidas. Com isso, ele pode reagir prontamente a mudanças nas condições do mercado. No entanto, os métodos tradicionais de treinamento baseados em MDP de alto nível enfrentam dificuldades: alta variabilidade nas recompensas e mudanças extremas raras no mercado. Para lidar com esses desafios, o hiperagente conta com um módulo de memória.

O módulo de memória é implementado como uma tabela de tamanho limitado, onde são armazenados vetores-chave de estados e ações. As novas experiências são adicionadas à memória com base no cálculo de seu valor por meio de uma avaliação Q de um passo. Quando a tabela atinge sua capacidade, os registros antigos são removidos, mantendo os dados mais atuais. Durante a inferência, o hiperagente encontra os registros mais relevantes calculando a distância L2 entre o estado atual e as chaves armazenadas. O valor final é calculado como uma soma ponderada dos dados contidos na memória.

O módulo de memória também é utilizado para aprimorar a avaliação das ações do hiperagente. Isso é feito por meio da modificação da função de perda, que adiciona um novo componente com o objetivo de alinhar as estimativas da memória com as previsões atuais do hiperagente. Essa abordagem permite o treinamento de estratégias de negociação mais estáveis, capazes de reagir de forma eficaz a mudanças repentinas nas condições de mercado.

MacroHFT se destaca por uma arquitetura bem elaborada, que o torna uma ferramenta versátil para operar em diferentes mercados. Embora tenha sido desenvolvido principalmente para atuar com criptomoedas, suas abordagens e algoritmos podem ser adaptados para uso em outros mercados financeiros, incluindo o mercado de ações ou de commodities.

A visualização original do framework MacroHFT é apresentada abaixo.

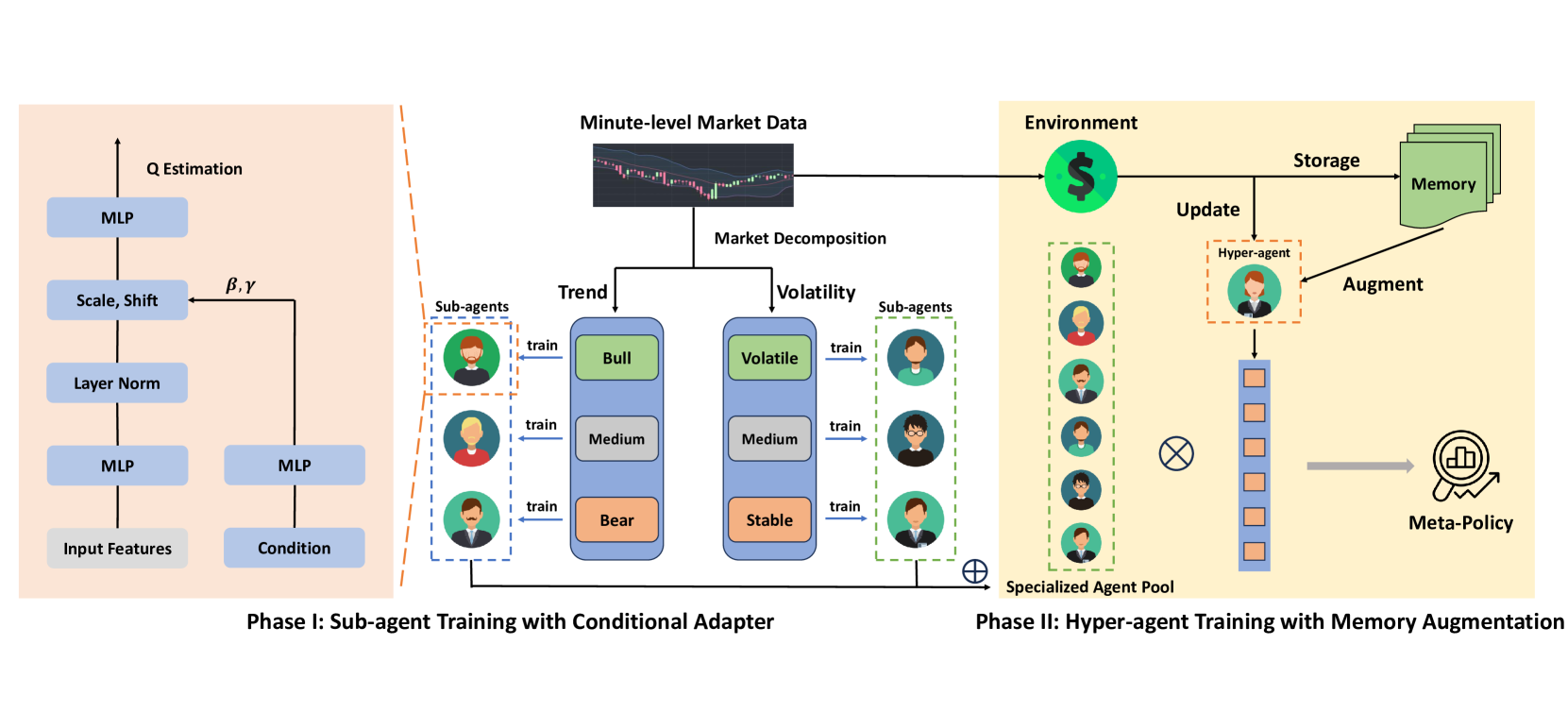
Implementação com MQL5

Após analisarmos os aspectos teóricos do framework MacroHFT, passamos agora à parte prática do nosso artigo, na qual implementamos nossa própria visão das abordagens propostas utilizando MQL5.

Na implementação apresentada, mantemos o conceito principal da construção hierárquica do modelo, mas realizamos mudanças significativas na arquitetura dos componentes e no processo de treinamento. Em primeiro lugar, optamos por abandonar a divisão manual do conjunto de treinamento e teste em blocos com rótulos de tendência e nível de volatilidade. Em segundo lugar, o processo de treinamento do modelo não é separado em duas etapas distintas. Em vez disso, implementamos um treinamento simultâneo do hiperagente e dos subagentes dentro de um único processo iterativo. Supomos que, durante o processo de aprendizado, o hiperagente seja capaz de classificar por conta própria os estados do ambiente e distribuir as funções entre os agentes.

Abandonamos o uso de uma tabela para estruturar a memória do hiperagente, substituindo-a por um objeto três camadas de memória, desenvolvido durante os trabalhos com o framework FinCon. Além disso, decidimos integrar o agente-analista criado anteriormente, com uma arquitetura mais robusta e desenvolvida, para implementar de forma eficiente a funcionalidade dos subagentes. Dessa forma, iniciamos nosso trabalho de implementação dos componentes do framework MacroHFT pela criação do hiperagente.

Construção do Hiperagente

Na descrição funcional do Hiperagente apresentada pelos autores do framework MacroHFT, é informado que ele analisa o estado atual do ambiente, o compara com os objetos presentes na memória e retorna uma distribuição probabilística da classificação do estado analisado. Essa classificação pode se referir à tendência ou à volatilidade do movimento do mercado. A distribuição probabilística obtida é utilizada para calcular a contribuição de cada subagente na decisão final de executar uma operação de trading, a qual é realizada por meio da ponderação das decisões dos subagentes com base em sua compatibilidade com as condições atuais de mercado. Essa abordagem permite adaptar a decisão geral de acordo com os fatores predominantes.

Em outras palavras, precisamos criar um componente de classificação do estado analisado do ambiente, que leve em consideração o contexto dos estados anteriores armazenados na memória. Isso é alcançado por meio da análise da sequência de mudanças nos parâmetros de mercado e sua correlação com a situação atual. Os estados anteriores ajudam a identificar tendências de longo prazo e padrões ocultos, permitindo decisões mais fundamentadas ao classificar o estado atual do mercado.

Esse hiperagente será criado dentro do objeto CNeuronMacroHFTHyperAgent, cuja estrutura é apresentada a seguir.

class CNeuronMacroHFTHyperAgent  :  public CNeuronSoftMaxOCL
  {
protected:
   CNeuronMemoryDistil  cMemory;
   CNeuronRMAT          cStatePrepare;
   CNeuronTransposeOCL  cTranspose;
   CNeuronConvOCL       cScale;
   CNeuronBaseOCL       cMLP[2];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMacroHFTHyperAgent(void) {};
                    ~CNeuronMacroHFTHyperAgent(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint layers, uint agents, uint stack_size,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMacroHFTHyperAgent; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual bool      Clear(void) override;
  };

Como classe base, é utilizada a implementação da camada SoftMax. Essa função foi proposta pelos autores do framework para o cálculo da distribuição probabilística. Ela desempenha um papel fundamental na definição da contribuição de cada subagente para a decisão final, garantindo precisão e adaptabilidade ao modelo.

A estrutura do hiperagente apresenta um conjunto padrão de métodos virtuais e alguns objetos internos, que servem como base para a construção do algoritmo de análise do estado atual do ambiente. Exploraremos mais a fundo suas funcionalidades durante a implementação dos métodos da classe do hiperagente.

Todos os objetos internos são declarados como estáticos, o que nos permite deixar o construtor e o destrutor da classe vazios. A inicialização dos objetos declarados e herdados é realizada no método Init. Esse método recebe como parâmetros um conjunto de constantes que definem de forma clara a arquitetura do objeto a ser criado.

bool CNeuronMacroHFTHyperAgent::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                     uint window, uint window_key, uint units_count,
                                     uint heads, uint layers, uint agents, uint stack_size,
                                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronSoftMaxOCL::Init(numOutputs, myIndex, open_cl, agents, optimization_type, batch))
      return false;
   SetHeads(1);
//---
   int index = 0;

No corpo do método, como de costume, começamos chamando o método de mesmo nome da classe base. Neste caso, trata-se da camada da função SoftMax. Esperamos que o tamanho do vetor de resultados seja igual ao número de subagentes utilizados. Esse valor é obtido da aplicação chamadora, através dos parâmetros do método.

Em seguida, passamos à inicialização dos objetos internos. E o primeiro a ser inicializado é o módulo de memória.

   int index = 0;
   if(!cMemory.Init(0, 0, OpenCL, window, window_key, units_count, heads, stack_size,
                                                                optimization, iBatch))
      return false;

A busca por dependências nos dados do estado analisado do ambiente será realizada por meio de um transformador com codificação relativa.

   index++;
   if(!cStatePrepare.Init(0, index, OpenCL, window, window_key, units_count, heads, layers,
                                                                     optimization, iBatch))
      return false;

O próximo passo é a projeção do estado analisado do ambiente para um subespaço com dimensionalidade igual ao número de subagentes. Isso exige a criação de um mecanismo de projeção eficiente, que preserve todas as características essenciais dos dados. À primeira vista, pode-se utilizar uma camada totalmente conectada ou uma camada convolucional padrão. No entanto, considerando a especificidade de uma série temporal multimodal, é importante manter a estrutura das sequências unitárias, que contêm informações valiosas. Esses dados podem ser perdidos em caso de agregação excessiva.

Acima, utilizamos um transformador com codificação relativa para analisar as dependências entre os passos temporais. Agora, é necessário complementar esse processo, preservando os detalhes das sequências unitárias individuais. Para isso, primeiro realizamos a transposição dos dados, o que facilita o processamento posterior dessas sequências.

   index++;
   if(!cTranspose.Init(0, index, OpenCL, units_count, window, optimization, iBatch))
      return false;

Em seguida, aplicamos uma camada convolucional, que permite extrair características espaciais e temporais das sequências unitárias, melhorando sua interpretação. A não linearidade da operação é obtida com o uso da tangente hiperbólica como função de ativação.

   index++;
   if(!cScale.Init(4 * agents, index, OpenCL, 3, 1, 1, units_count - 2, window, optimization, iBatch))
      return false;
   cScale.SetActivationFunction(TANH);

Depois dessa etapa, ocorre o momento crítico de compressão dos dados. Para reduzir a dimensionalidade, utiliza-se uma arquitetura MLP de duas camadas. A primeira camada é responsável pela redução inicial do volume de dados, eliminando correlações redundantes e ruídos. Aqui, usamos a função de ativação LReLU, que evita que as transformações se tornem lineares demais. A segunda camada finaliza o processo de compressão, otimizando os dados para as próximas análises.

   index++;
   if(!cMLP[0].Init(agents, index, OpenCL, 4 * agents, optimization, iBatch))
      return false;
   cMLP[0].SetActivationFunction(LReLU);
   index++;
   if(!cMLP[1].Init(0, index, OpenCL, agents, optimization, iBatch))
      return false;
   cMLP[0].SetActivationFunction(None);
//---
   return true;
  }

Essa abordagem garante um equilíbrio entre a preservação de informações úteis e a simplificação do modelo, o que é fundamental para o desempenho eficiente do hiperagente em um ambiente de trading de alta frequência.

Os dados obtidos serão então projetados para o domínio das probabilidades por meio dos métodos da classe base, que já foram inicializados anteriormente. Assim, neste ponto, podemos retornar um resultado lógico para o programa chamador e encerrar a execução do método de inicialização.

Após finalizar a inicialização do objeto, passamos à construção do algoritmo de propagação para frente dentro do método feedForward. Aqui, tudo ocorre de forma bastante direta e linear.

bool CNeuronMacroHFTHyperAgent::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cMemory.FeedForward(NeuronOCL))
      return false;

Nos parâmetros do método, recebemos um ponteiro para o objeto de dados brutos, que contém o tensor multimodal descrevendo o estado analisado do ambiente. Esse ponteiro é imediatamente passado para o método homônimo do módulo de memória. Nessa etapa, a descrição estática do estado do ambiente é enriquecida com informações sobre a dinâmica recente, permitindo criar uma representação mais completa e atualizada para a análise posterior. A integração desses dados proporciona um rastreamento mais preciso das mudanças que ocorrem no sistema e contribui para o aumento da eficácia dos algoritmos de processamento.

Os dados processados na etapa anterior são encaminhados para o bloco de atenção, onde são determinadas as interdependências entre pontos temporais distintos da série temporal analisada. Isso permite identificar correlações ocultas e aumentar a precisão na previsão da dinâmica dos movimentos de preço.

   if(!cStatePrepare.FeedForward(cMemory.AsObject()))
      return false;

Em seguida, passamos para a compressão dos dados. Aqui, primeiramente transpomos os resultados da análise realizada acima.

   if(!cTranspose.FeedForward(cStatePrepare.AsObject()))
      return false;

Depois, comprimimos os dados das sequências unitárias individuais utilizando uma camada convolucional, o que nos permite preservar a informação sobre sua estrutura.

   if(!cScale.FeedForward(cTranspose.AsObject()))
      return false;

Em seguida, projetamos o estado analisado do ambiente para um subespaço de tamanho definido, utilizando uma MLP.

   if(!cMLP[0].FeedForward(cScale.AsObject()))
      return false;
   if(!cMLP[1].FeedForward(cMLP[0].AsObject()))
      return false;

Agora, é necessário transferir os valores obtidos para o domínio das probabilidades. Para isso, utilizaremos os recursos da classe base SoftMax. Basta chamar o método homônimo da classe base, passando a ele os resultados do processamento anterior.

   return CNeuronSoftMaxOCL::feedForward(cMLP[1].AsObject());
  }

Em seguida, retornamos o resultado lógico da execução das operações para o programa chamador e finalizamos a execução do método.

Como você pôde observar, acima foi apresentado um algoritmo linear de funcionamento do hiperagente. Os algoritmos dos métodos de propagação reversa apresentam uma estrutura linear semelhante. Eles são relativamente simples para estudo autônomo.

Com isso, propomos encerrar a análise dos princípios de funcionamento do hiperagente. O código completo da classe apresentada, incluindo todos os seus métodos, está disponível em anexo. Você pode consultá-lo para um estudo mais aprofundado e aplicação prática. Agora seguimos adiante. O próximo passo será integrar os agentes em um framework unificado.

Construção do framework MacroHFT

Neste ponto, já temos objetos separados dos subagentes e do hiperagente. Chegou a hora de reuni-los em uma estrutura única e coesa, onde serão desenvolvidos os algoritmos de intercâmbio de dados entre os componentes do modelo. Essa tarefa será realizada dentro do objeto CNeuronMacroHFT, que será responsável por otimizar os processos de tratamento de dados. A estrutura do novo objeto é apresentada a seguir.

class CNeuronMacroHFT   :  public CNeuronBaseOCL
  {
protected:
   CNeuronTransposeOCL  cTranspose;
   CNeuronFinConAgent   caAgetnts[6];
   CNeuronMacroHFTHyperAgent  cHyperAgent;
   CNeuronBaseOCL       cConcatenated;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMacroHFT(void) {};
                    ~CNeuronMacroHFT(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint layers, uint stack_size, uint nactions,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMacroHFT; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual bool      Clear(void) override;
  }; 

A estrutura do novo objeto traz o conjunto habitual de métodos virtuais sobrescrevíveis, o que assegura flexibilidade na implementação de sua funcionalidade. Entre os objetos internos, destaca-se o hiperagente, que desempenha o papel central na gestão do sistema, e um array com seis subagentes, cada um responsável pelo processamento de aspectos específicos dos dados. A descrição detalhada das funcionalidades dos objetos internos e da lógica de suas interações será abordada durante o desenvolvimento dos métodos do novo objeto.

Todos os objetos internos são declarados como estáticos. Isso nos permite deixar o construtor e o destrutor da classe vazios. A inicialização dos objetos declarados e herdados é realizada no método Init. Nos parâmetros desse método, recebemos um conjunto de constantes que fornecem uma descrição clara da arquitetura do objeto a ser criado.

bool CNeuronMacroHFT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                           uint window, uint window_key, uint units_count,
                           uint heads, uint layers, uint stack_size, uint nactions,
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, nactions, optimization_type, batch))
      return false;

No corpo do método, como de costume, começamos chamando o método de mesmo nome da classe base, onde já está implementado o processo de inicialização dos objetos herdados e das interfaces. Neste caso, trata-se de uma camada totalmente conectada, da qual precisaremos apenas das interfaces básicas para a interação com os demais objetos do modelo. Na saída do nosso novo objeto, esperamos obter o tensor final de ações da modelo, de acordo com as condições de mercado analisadas. Por isso, nos parâmetros do método da classe base, indicamos a dimensionalidade do espaço de ações do nosso Agente.

Na organização do trabalho dos subagentes apresentada pelos autores, foi proposto dividi-los com base em tendência e volatilidade do mercado. Já nós optamos por usar uma divisão baseada no ângulo de visão do mercado. Nossos subagentes receberão diferentes projeções dos dados de mercado analisados. Para formar essas projeções, utilizamos uma camada de transposição dos dados.

   int index = 0;
   if(!cTranspose.Init(0, index, OpenCL, units_count, window, optimization, iBatch))
      return false;

Em seguida, realizamos a inicialização dos subagentes. A primeira metade dos subagentes analisa os dados brutos conforme recebidos do programa externo, enquanto a segunda metade analisa a versão transposta desses dados. Para executar esse processo de inicialização, organizamos dois ciclos sequenciais com o número necessário de iterações.

   uint half = (caAgetnts.Size() + 1) / 2;
   for(uint i = 0; i < half; i++)
     {
      index++;
      if(!caAgetnts[i].Init(0, index, OpenCL, window, window_key, units_count, heads,
                            stack_size, nactions, optimization, iBatch))
         return false;
     }
   for(uint i = half; i < caAgetnts.Size(); i++)
     {
      index++;
      if(!caAgetnts[i].Init(0, index, OpenCL, units_count, window_key, window, heads,
                            stack_size, nactions, optimization, iBatch))
         return false;
     }

Depois, inicializamos o objeto do hiperagente. Ele também analisa os dados brutos em sua forma original.

   index++;
   if(!cHyperAgent.Init(0, index, OpenCL, window, window_key, units_count, heads, layers,
                        caAgetnts.Size(), stack_size, optimization, iBatch))
      return false;

A seguir, conforme o algoritmo do framework MacroHFT, devemos realizar a soma ponderada dos resultados dos subagentes. Esses pesos são gerados pelo hiperagente. Essa operação é facilmente realizada por meio da multiplicação da matriz de resultados dos subagentes pelo vetor de pesos recebido do hiperagente. No entanto, no nosso caso, os resultados dos subagentes estão armazenados em objetos distintos. Assim, criamos um objeto para concatenar os vetores necessários em uma única matriz.

   index++;
   if(!cConcatenated.Init(0, index, OpenCL, caAgetnts.Size()*nactions, optimization, iBatch))
      return false;
//---
   return true;
  }

A multiplicação propriamente dita das matrizes será feita durante o processo de propagação para frente. Por ora, retornamos o resultado lógico da execução das operações para o programa chamador e encerramos o método de inicialização.

Nosso próximo passo será a construção do algoritmo de propagação para frente dentro do método feedForward. Como antes, nos parâmetros do método recebemos um ponteiro para o objeto de dados brutos, que imediatamente transpomos.

bool CNeuronMacroHFT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;

Em seguida, metade dos subagentes trabalha com a representação original do estado analisado do ambiente, enquanto a outra metade utiliza a projeção transposta.

   uint total = caAgetnts.Size();
   uint half = (total + 1) / 2;
   for(uint i = 0; i < half; i++)
      if(!caAgetnts[i].FeedForward(NeuronOCL))
         return false;

   for(uint i = half; i < total; i++)
      if(!caAgetnts[i].FeedForward(cTranspose.AsObject()))
         return false;

Nesse momento, o nosso hiperagente também analisa os dados brutos.

   if(!cHyperAgent.FeedForward(NeuronOCL))
      return false;

Agora precisamos reunir as informações de todos os subagentes em uma única matriz.

   if(!Concat(caAgetnts[0].getOutput(), caAgetnts[1].getOutput(), caAgetnts[2].getOutput(),
              caAgetnts[3].getOutput(), cConcatenated.getPrevOutput(), Neurons(), Neurons(),
              Neurons(), Neurons(), 1) ||
      !Concat(cConcatenated.getPrevOutput(), caAgetnts[4].getOutput(), caAgetnts[5].getOutput(),
              cConcatenated.getOutput(), 4 * Neurons(), Neurons(), Neurons(), 1))
      return false;

Na saída, obtemos uma matriz em que cada linha representa os resultados da execução de um subagente. Para calcular corretamente a soma ponderada, devemos multiplicar o vetor de pesos por essa matriz resultante.

   if(!MatMul(cHyperAgent.getOutput(), cConcatenated.getOutput(), Output, 1, total, Neurons(), 1))
      return false;
//---
   return true;
  }

Os resultados da multiplicação são gravados no buffer de interfaces externas, herdadas da classe base, e encerramos a execução do método, retornando previamente o resultado lógico da operação ao programa chamador.

Vale destacar que, apesar das modificações estruturais que implementamos, o algoritmo de propagação para frente manteve integralmente a ideia original dos autores do framework MacroHFT. No entanto, o mesmo não se pode dizer do processo de treinamento que desenvolvemos, sobre o qual falaremos a seguir.

Como foi mencionado anteriormente, os autores do framework dividiram o conjunto de treinamento em blocos distintos, com base na tendência e na volatilidade do mercado. Cada subagente era treinado em um subconjunto específico. Já nós planejamos treinar todos os agentes simultaneamente. É exatamente esse processo que será implementado nos métodos de propagação reversa da nossa classe.

Começamos a implementação dos processos de propagação reversa desenvolvendo o algoritmo de distribuição dos gradientes do erro entre os objetos internos da classe e os dados brutos, de acordo com sua influência no resultado do modelo. Esse trabalho é realizado dentro do método calcInputGradients.

bool CNeuronMacroHFT::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

Nos parâmetros do método, recebemos um ponteiro para o mesmo objeto de dados brutos utilizado na propagação para frente. Só que desta vez, precisamos transmitir a ele o gradiente de erro correspondente. E já no corpo do método, verificamos a validade do ponteiro recebido, pois caso contrário, não poderíamos registrar as informações em um objeto inexistente. E, nesse caso, todas as operações seguintes perderiam o sentido.

Como você sabe, o fluxo de informação na distribuição do gradiente de erro segue o caminho inverso ao da propagação para frente. E, se a propagação para frente foi encerrada com a operação de multiplicação da matriz de resultados pelo vetor de pesos, a propagação reversa começa distribuindo o gradiente de erro por essa mesma operação.

   uint total = caAgetnts.Size();
   if(!MatMulGrad(cHyperAgent.getOutput(), cHyperAgent.getGradient(), cConcatenated.getOutput(),
                                 cConcatenated.getGradient(), Gradient, 1, total, Neurons(), 1))
      return false;

Aqui é importante observar que essa operação divide o gradiente de erro em dois fluxos informacionais. Um deles é o fluxo informacional do hiperagente. Por meio dele, podemos imediatamente transmitir o erro para o nível dos dados brutos.

   if(!NeuronOCL.calcHiddenGradients(cHyperAgent.AsObject()))
      return false;

O segundo fluxo informacional está relacionado aos subagentes. Durante a distribuição do gradiente de erro por meio da operação de multiplicação matricial, obtivemos os valores de erro no nível do objeto concatenado. Acredito que aqui é evidente que o maior erro foi atribuído ao subagente que teve maior influência no resultado da execução do modelo. Isso nos permite fazer a distribuição de papéis entre os subagentes durante o processo de treinamento, com base na classificação dos estados do ambiente analisados pelo hiperagente.

Agora precisamos distribuir os valores obtidos entre os respectivos subagentes. Para isso, realizamos operações de desconcatenação dos dados.

   if(!DeConcat(cConcatenated.getPrevOutput(), caAgetnts[4].getGradient(), caAgetnts[5].getGradient(),
                cConcatenated.getGradient(), 4 * Neurons(), Neurons(), Neurons(), 1) ||
      !DeConcat(caAgetnts[0].getGradient(), caAgetnts[1].getGradient(), caAgetnts[2].getGradient(),
                caAgetnts[3].getGradient(), cConcatenated.getPrevOutput(), Neurons(), Neurons(),
                Neurons(), Neurons(), 1))
      return false;

Em seguida, podemos transmitir o gradiente de erro para o nível dos dados brutos pelas rotas de cada subagente individual. Mas aqui devemos prestar atenção a dois pontos. Primeiro, o buffer de gradientes do objeto de dados brutos já contém informações recebidas do hiperagente. E precisamos preservá-las. Para isso, como de costume, utilizamos a substituição dos ponteiros para os buffers de dados, trocando o buffer de gradientes de erro do objeto de dados brutos por outro que esteja livre.

   CBufferFloat *temp = NeuronOCL.getGradient();
   if(!temp ||
      !NeuronOCL.SetGradient(cTranspose.getPrevOutput(), false))
      return false;

Além disso, nem todos os nossos subagentes trabalham diretamente com o objeto de dados brutos. Metade deles analisa os dados transpostos. Portanto, isso precisa ser considerado durante a distribuição dos gradientes de erro. Assim como na propagação para frente, organizamos dois ciclos sequenciais. No primeiro, trabalhamos com os subagentes de interação direta. Aqui, baixamos o gradiente de erro até o nível dos dados brutos e somamos os dados obtidos com os já acumulados.

   uint half = (total + 1) / 2;
   for(uint i = 0; i < half; i++)
     {
      if(!NeuronOCL.calcHiddenGradients(caAgetnts[i].AsObject()))
         return false;
      if(!SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1))
         return false;
     }

O segundo ciclo é semelhante ao primeiro, mas adiciona-se a etapa de transmissão do gradiente de erro através da camada de transposição de dados. Aqui é processada a segunda metade dos subagentes.

   for(uint i = half; i < total; i++)
     {
      if(!cTranspose.calcHiddenGradients(caAgetnts[i].AsObject()) ||
         !NeuronOCL.calcHiddenGradients(cTranspose.AsObject()))
         return false;
      if(!SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1))
         return false;
     }

Após a conclusão bem-sucedida de todas as iterações desses ciclos, restauramos os ponteiros dos buffers de dados para o estado original. E finalizamos a execução do método, retornando previamente o resultado lógico da operação ao programa chamador.

Com isso, encerramos a análise dos algoritmos de construção dos métodos do nosso novo objeto de organização do funcionamento do framework MacroHFT. O código completo da classe apresentada e de todos os seus métodos está disponível em anexo.

Estamos quase no limite do formato deste artigo, mas nosso trabalho ainda não está concluído. Proponho uma breve pausa, e daremos continuidade a esse trabalho na próxima parte. Lá, realizaremos a avaliação das abordagens implementadas com base em dados históricos reais.

Considerações finais

Neste artigo, conhecemos o framework MacroHFT, que representa uma solução promissora para a negociação de alta frequência nos mercados de criptomoedas. Este framework leva em consideração os contextos macroeconômicos e as particularidades da dinâmica local do mercado. Isso o torna uma ferramenta poderosa para traders profissionais que buscam maximizar seus lucros em condições de mercado complexas e instáveis.

Na parte prática, implementamos nossa própria visão dos principais componentes do framework analisado, utilizando recursos do MQL5. E na próxima parte, daremos continuidade ao trabalho iniciado, concluindo-o com a verificação obrigatória da eficácia das abordagens implementadas com base em dados históricos reais.

Referências

• MacroHFT: Memory Augmented Context-aware Reinforcement Learning On High Frequency Trading
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA para coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para coleta de exemplos com o método Real-ORL
3	Study.mq5	Expert Advisor	EA para treinamento de modelos
4	Test.mq5	Expert Advisor	EA para teste de modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura para descrição do estado do sistema e da arquitetura dos modelos
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca com código do programa em OpenCL