
Técnicas do MQL5 Wizard que você deve conhecer (Parte 37): Regressão por Processo Gaussiano com Núcleos Lineares e de Matérn
Introdução
Continuamos esta série sobre as diferentes formas de implementar classes de componentes-chave de Expert Advisors montados pelo assistente, considerando 2 núcleos de Processo Gaussiano. O núcleo linear e o núcleo de Matérn. O primeiro é tão simples que não possui nem página na Wikipédia, no entanto o segundo possui uma página de referência aqui.
Se formos recapitular o que cobrimos sobre Núcleos de Processo Gaussiano (GPs), eles são modelos não paramétricos capazes de mapear relações complexas entre conjuntos de dados (tipicamente em forma de vetores) sem qualquer conhecimento funcional ou prévio sobre o par de conjuntos envolvidos. Isso os torna ideais para lidar com situações em que os conjuntos de dados envolvidos são não lineares ou até mesmo ruidosos. Essa flexibilidade, além disso, os torna bastante adequados para séries temporais financeiras que podem ser frequentemente voláteis, já que os GPs tendem a fornecer saídas mais refinadas. Eles oferecem uma estimativa de previsão mais um intervalo de confiança. Os GPs ajudam a determinar a similaridade entre dois conjuntos de dados e, como existem múltiplos tipos de núcleos a se usar na Regressão por Processo Gaussiano, é sempre essencial identificar o núcleo apropriado ou estar ciente das limitações do núcleo escolhido, especialmente em casos onde os núcleos são usados para extrapolar uma previsão.
Abaixo está uma tabela resumo que cobre os núcleos apresentados até agora nesta série e algumas de suas características:
| Tipo de Núcleo | Ideal para Capturar | Explicação: |
|---|---|---|
| Núcleo Linear | Tendências | Captura tendências lineares ao longo do tempo; ideal para ativos que mostram movimentos de preço ascendentes ou descendentes no longo prazo. Simples e computacionalmente eficiente, mas assume uma relação linear. |
| Núcleo de Função de Base Radial (RBF) | Tendências e Volatilidade | Melhor para capturar tendências suaves e de longo prazo com mudanças graduais de preço. Fornece estimativas suaves e é bom para padrões contínuos. No entanto, tem dificuldades com transições abruptas ou volatilidade extrema. |
| Núcleo de Matérn | Tendências, Volatilidade, Ciclos | Pode capturar tendências mais ásperas, menos suaves e mudanças súbitas de volatilidade. O parâmetro ν controla a suavidade, então valores menores de ν capturam mais volatilidade, enquanto valores maiores suavizam as tendências. |
Dependendo da série temporal que se deseja extrapolar, o núcleo apropriado deve ser selecionado com base em seus pontos fortes. Séries temporais financeiras frequentemente apresentam comportamento periódico ou cíclico, e núcleos como o de Matérn, que introduzimos abaixo, podem ajudar a mapear essas relações. Além disso, a quantificação da incerteza, como vimos com a Função de Base Radial neste artigo inicial, pode ser uma grande vantagem quando traders enfrentam mercados laterais ou com movimentos erráticos. Núcleos como o RBF não fornecem apenas estimativas pontuais, mas também intervalos de confiança, que podem ser benéficos nessas situações. Isso porque o intervalo de confiança pode ajudar a filtrar sinais fracos ao mesmo tempo em que destaca pontos de inflexão importantes em ambientes incertos.
Conjuntos de dados com reversão à média também podem ser tratados por núcleos especiais como o de Ornstein-Uhlenbeck, que podemos abordar em um artigo futuro. Outro aspecto interessante que poderíamos explorar no futuro é que os GPs permitem composição de núcleos, onde múltiplos núcleos, como a combinação de um núcleo linear e um RBF, podem ser utilizados para modelar relações mais complexas entre conjuntos de dados. Isso poderia incluir emparelhamentos como padrões de ação de preço de curto prazo e tendências de longo prazo, onde um modelo é capaz de definir pontos de saída de posições abertas em momentos ideais, ao mesmo tempo que aproveita qualquer movimento subjacente de longo prazo que um ativo possa estar apresentando.
Há diversas outras vantagens e usos para os GPs como tratamento e redução de ruído, adaptação a mudanças de regime e muito mais. Como traders, entretanto, queremos capitalizar esses benefícios, então vamos observar um núcleo linear muito básico.
Núcleo Linear
O principal uso dos núcleos lineares é mapear relações lineares simples entre conjuntos de dados em um processo gaussiano. Por exemplo, considere um par muito simples de conjuntos de dados: o custo de envio de um contêiner da China para os EUA e o preço do ETF de transporte marítimo BOAT. Sob circunstâncias normais, esperaríamos que altos custos de envio refletissem o poder de precificação das empresas de transporte, de forma que seus lucros e, portanto, suas receitas refletiriam isso, levando à valorização de suas ações. Nesse cenário, um trader interessado em comprar ações de empresas de transporte ao longo do tempo ou mesmo apenas os ETFs, estaria interessado em modelar os preços esperados das ações e os custos atuais de envio, com um núcleo linear.
É relativamente simples e nada complexa, o que faz com que exija os menores recursos computacionais entre todos os núcleos. Ela também requer apenas um único parâmetro constante c em sua fórmula. Essa fórmula é mostrada abaixo:
![]()
Onde:
- x e x′ são vetores de entrada
- x⊤x′ é o produto escalar do vetor x transposto com x′
- c é uma constante
A exigência de apenas esse único parâmetro c a torna rápida e muito eficiente para grandes conjuntos de dados. Seu papel é basicamente quádruplo: Primeiro, ela auxilia na ajuste de viés, ou seja, no caso de o conjunto de dados ou o gráfico não passar pela origem, a constante fornece um deslocamento que move o hiperplano, permitindo que o núcleo represente melhor o modelo subjacente. Sem essa constante, o núcleo assumiria que todos os pontos de dados estão centralizados na origem. Essa constante não é otimizável por si só, mas pode ser ajustada em etapas de validação cruzada predefinidas.
Em segundo lugar, a constante permite uma separação mais personalizada entre duas classes de conjuntos de dados, ao controlar esse intervalo de margem. Isso é particularmente importante quando esse núcleo é usado com Máquinas de Vetores de Suporte (SVM), e também em situações com grandes conjuntos de dados que não são facilmente linearmente separáveis. Em terceiro, essa constante permite homogeneidade não linear, que pode estar presente em determinados conjuntos de dados. Sem essa constante, se todas as entradas forem escaladas por um fator, a saída do núcleo será escalada pelo mesmo fator. Agora, embora alguns conjuntos de dados apresentem essas características, nem todos são assim. Por isso, a adição dessa constante c insere um viés inerente e garante que o modelo não assuma automaticamente linearidade.
Por fim, argumenta-se que ela fornece estabilidade numérica aos produtos escalares que poderiam resultar em valores muito pequenos, distorcendo a matriz do núcleo. Caso os vetores de entrada tenham valores muito pequenos, o produto escalar sem a constante também seria muito pequeno, o que afetaria o processo de otimização. A constante, portanto, fornece alguma estabilidade para uma melhor otimização.
O núcleo linear tem sido aplicado em extrapolação e previsão de tendências, pois, como veremos abaixo, ele consegue extrapolar tendências além dos dados observados. Assim, especialmente em casos onde se discute a taxa de valorização linear de um ativo ao longo do tempo, o núcleo linear pode ser útil. Além disso, o peso das características proveniente do produto escalar torna o modelo de núcleo linear mais interpretável. A interpretabilidade é útil quando se tem um vetor de dados de entrada e é necessário saber a importância relativa de cada ponto de dado nesse vetor. Para ilustrar isso, imagine que você tem um núcleo que usa para prever o preço de casas. Esse núcleo possui um vetor de entrada com 4 dados: a área da casa (em pés quadrados), o número de quartos, a renda média da região e o ano em que a casa foi construída. O preço previsto pelo nosso núcleo seria dado pela fórmula abaixo:
Onde:
- b é a constante que adicionamos ao produto escalar do vetor, cuja função já destacamos acima (referida como c)
- w1 a w4 são os pesos otimizados durante o treinamento
- x1 a x4 são os dados de entrada mencionados acima
Após o treinamento, você obteria valores para w1 a w4, e com essa configuração simples de núcleo linear, quanto maior o peso, mais importante é a característica ou ponto de dado para o próximo preço do imóvel. O mesmo vale se, por exemplo, w4 for o menor peso, o que indicaria que x4 (ano em que o imóvel foi comprado) é o menos relevante para o preço futuro. O uso do núcleo linear neste contexto, no entanto, não é o foco aqui, e sim seu uso com Regressão por Processo Gaussiano. Isso significa que, se alguém quiser inferir a importância das características, não poderá fazê-lo da forma simples que mostramos acima, pois a saída do produto escalar acima é um escalar, enquanto em nossa aplicação é uma matriz. As alternativas, porém, para obter uma noção da importância relativa dos dados de entrada incluem: determinação automática de relevância, análise de sensibilidade (onde certas entradas são ajustadas e seu impacto na previsão é observado), e verossimilhança marginal e hiperparâmetros (em que a magnitude dos hiperparâmetros, como na normalização em lote, pode indicar a relevância dos dados de entrada).
Implementamos o núcleo linear, para uso em Regressão por Processo Gaussiano, em MQL5 da seguinte maneira:
//+------------------------------------------------------------------+ // Linear Kernel Function //+------------------------------------------------------------------+ matrix CSignalGauss::Linear_Kernel(vector &Rows, vector &Cols) { matrix _linear, _c; _linear.Init(Rows.Size(), Cols.Size()); _c.Init(Rows.Size(), Cols.Size()); for(int i = 0; i < int(Rows.Size()); i++) { for(int ii = 0; ii < int(Cols.Size()); ii++) { _linear[i][ii] = Rows[i] * Cols[ii]; } } _c.Fill(m_constant); _linear += _c; return(_linear); }
As entradas aqui são 2 vetores, como já indicado na fórmula, com um deles rotulado como ‘Rows’, para indicar a transposição desse vetor antes da aplicação no produto escalar. Portanto, núcleos lineares, apesar de simples, além das vantagens que já mencionamos, servem como base de comparação de modelos com outros núcleos mais complexos, pois são os mais fáceis de configurar e testar. Ao começar com eles, é possível escalar gradualmente, dependendo se a complexidade adicional de outros núcleos é realmente necessária. Isso é particularmente importante porque, à medida que os núcleos se tornam mais complexos, os custos computacionais também aumentam, o que é crítico ao lidar com grandes conjuntos de dados. Núcleos lineares, apesar disso, capturam dependências de longo prazo, podem ser combinados com outros núcleos para definir relações mais complexas, e podem atuar como uma forma de regularização em casos onde os conjuntos de dados comparados possuem forte relação linear.
Núcleo de Matérn
O núcleo de Matérn também é uma função de covariância comum usada em Processos Gaussianos por conta de sua suavidade ajustável e capacidade de capturar dependências entre dados. Sua suavidade é controlada pelo parâmetro de entrada ν (pronunciado “niu”). Esse parâmetro consegue ajustar a suavidade de forma que o núcleo de Matérn possa se comportar como o núcleo exponencial irregular quando ν = ½, ou como o núcleo RBF quando esse parâmetro tende a ∞. Sua fórmula, baseada nos princípios fundamentais, é dada por:
Onde:
- ∥x−x′∥ é a distância Euclidiana entre dois pontos
- ν é o parâmetro de controle da suavidade
- l é o parâmetro de escala de comprimento (semelhante ao do núcleo RBF)
- Γ(ν) é a função gama
- Kν é a função de Bessel modificada de segunda espécie
As funções gama e Bessel são um pouco complexas, e não entraremos em detalhes, mas para os nossos propósitos estamos utilizando ν = 3/2, o que faz com que nosso núcleo fique quase no meio do caminho entre um núcleo exponencial e um núcleo RBF. Quando fazemos isso, a fórmula do núcleo de Matérn se simplifica para:
Onde:
- As representações são semelhantes à primeira fórmula compartilhada acima.
Casos especiais:
- Para ν = 1/2, o núcleo de Matérn se torna o Núcleo Exponencial.
- Para ν → ∞, ele se torna o núcleo RBF.
A suavidade deste núcleo é muito sensível ao parâmetro ν, e normalmente ele é definido como 1/2, 3/2 ou 5/2. Cada um desses valores representa um grau diferente de suavidade, sendo que valores maiores implicam maior suavidade.
Quando ν é 1/2, o núcleo é equivalente ao núcleo exponencial, como mencionado anteriormente, o que o torna adequado para modelar conjuntos de dados com mudanças abruptas ou descontinuidades frequentes. Do ponto de vista de um trader, isso geralmente aponta para ativos altamente voláteis ou pares de moedas do mercado forex. Essa configuração do núcleo assume um processo irregular e, portanto, tende a produzir resultados menos suaves e, possivelmente, mais responsivos a mudanças imediatas. Quando ν é 3/2, que é a configuração adotada neste artigo ao testar o Expert Advisor montado pelo assistente, sua suavidade é considerada intermediária. É uma solução de compromisso, pois consegue lidar tanto com dados levemente voláteis quanto com conjuntos de dados que apresentam tendência moderada. Esse tipo de configuração, pode-se argumentar, torna o núcleo adequado para identificar pontos de reversão em uma série temporal ou pontos de oscilação no mercado. A configuração 5/2 e quaisquer valores superiores tornam o núcleo mais adequado para ambientes com tendência, especialmente quando a taxa de mudança está em questão.
Portanto, dados ruidosos ou conjuntos de dados com saltos ou descontinuidades são melhor atendidos por valores menores de ν, enquanto dados mais graduais e com mudanças suaves funcionam melhor com valores maiores de ν. Como observação adicional, a diferenciabilidade — ou o número de vezes que a função do núcleo pode ser diferenciada — aumenta com o parâmetro ν. Isso, por sua vez, está correlacionado ao uso de recursos computacionais, já que valores maiores de ν consomem mais processamento. Implementamos o núcleo de Matérn em MQL5 da seguinte forma:
//+------------------------------------------------------------------+ // Matern Kernel Function //+------------------------------------------------------------------+ matrix CSignalGauss::Matern_Kernel(vector &Rows,vector &Cols) { matrix _matern; _matern.Init(Rows.Size(), Cols.Size()); for(int i = 0; i < int(Rows.Size()); i++) { for(int ii = 0; ii < int(Cols.Size()); ii++) { _matern[i][ii] = (1.0 + (sqrt(3.0) * fabs(Rows[i] - Cols[ii]) / m_next)) * exp(-1.0 * sqrt(3.0) * fabs(Rows[i] - Cols[ii]) / m_next); } } return(_matern); }
Quando comparado aos núcleos lineares, portanto, os núcleos de Matérn são mais flexíveis e mais adequados para capturar relações complexas e não lineares entre os dados. Ao modelar muitos fenômenos e dados do mundo real, ele claramente apresenta uma vantagem sobre os núcleos lineares, pois como vimos acima, pequenos ajustes no parâmetro ν o tornam capaz de lidar não apenas com dados tendenciais, mas também com dados voláteis e descontínuos.
Classe de Sinal
Criamos uma classe de sinal personalizada que reúne os dois núcleos como duas opções de implementação dentro da classe de sinal. Nossa função get output também é reprogramada para considerar a escolha do núcleo a partir da entrada do Expert Advisor. A nova função é a seguinte:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalGauss::GetOutput(double BasisMean, vector &Output) { ... matrix _k_s; matrix _k_ss; _k_s.Init(_next_time.Size(), _past_time.Size()); _k_ss.Init(_next_time.Size(), _next_time.Size()); if(m_kernel == KERNEL_LINEAR) { _k_s = Linear_Kernel(_next_time, _past_time); _k_ss = Linear_Kernel(_next_time, _next_time); } else if(m_kernel == KERNEL_MATERN) { _k_s = Matern_Kernel(_next_time, _past_time); _k_ss = Matern_Kernel(_next_time, _next_time); } ... }
As etapas envolvidas na interpolação das próximas variações de preço, uma vez que o núcleo apropriado foi selecionado, são idênticas às que abordamos neste artigo anterior. O processamento das condições de compra (long) e venda (short) também não são muito diferentes, e seus códigos são compartilhados aqui para fins de completude:
//+------------------------------------------------------------------+ //| "Voting" that price will grow. | //+------------------------------------------------------------------+ int CSignalGauss::LongCondition(void) { int result = 0; vector _o; GetOutput(0.0, _o); if(_o[_o.Size()-1] > _o[0]) { result = int(round(100.0 * ((_o[_o.Size()-1] - _o[0])/(_o.Max() - _o.Min())))); } //printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0); return(result); } //+------------------------------------------------------------------+ //| "Voting" that price will fall. | //+------------------------------------------------------------------+ int CSignalGauss::ShortCondition(void) { int result = 0; vector _o; GetOutput(0.0, _o); if(_o[_o.Size()-1] < _o[0]) { result = int(round(100.0 * ((_o[0] - _o[_o.Size()-1])/(_o.Max() - _o.Min())))); } //printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0); return(result); }
As condições, como no artigo mencionado, são baseadas em se a variação prevista do preço será positiva ou negativa. Essas variações são então normalizadas para estar na faixa de 0 a 100 inteiros, como se espera de todas as instâncias de classe de sinal personalizadas. A montagem desse arquivo de sinal em um Expert Advisor por meio do assistente MQL5 é abordada em artigos separados aqui e aqui para leitores iniciantes.
Relatórios do Testador de Estratégia
Realizamos algumas otimizações, no par GBPJPY, no período diário para o ano de 2023, com o núcleo linear e com o núcleo de Matérn. Os resultados de cada um, que demonstram apenas a usabilidade do Expert Advisor (sem indicar performance futura), são mostrados abaixo:
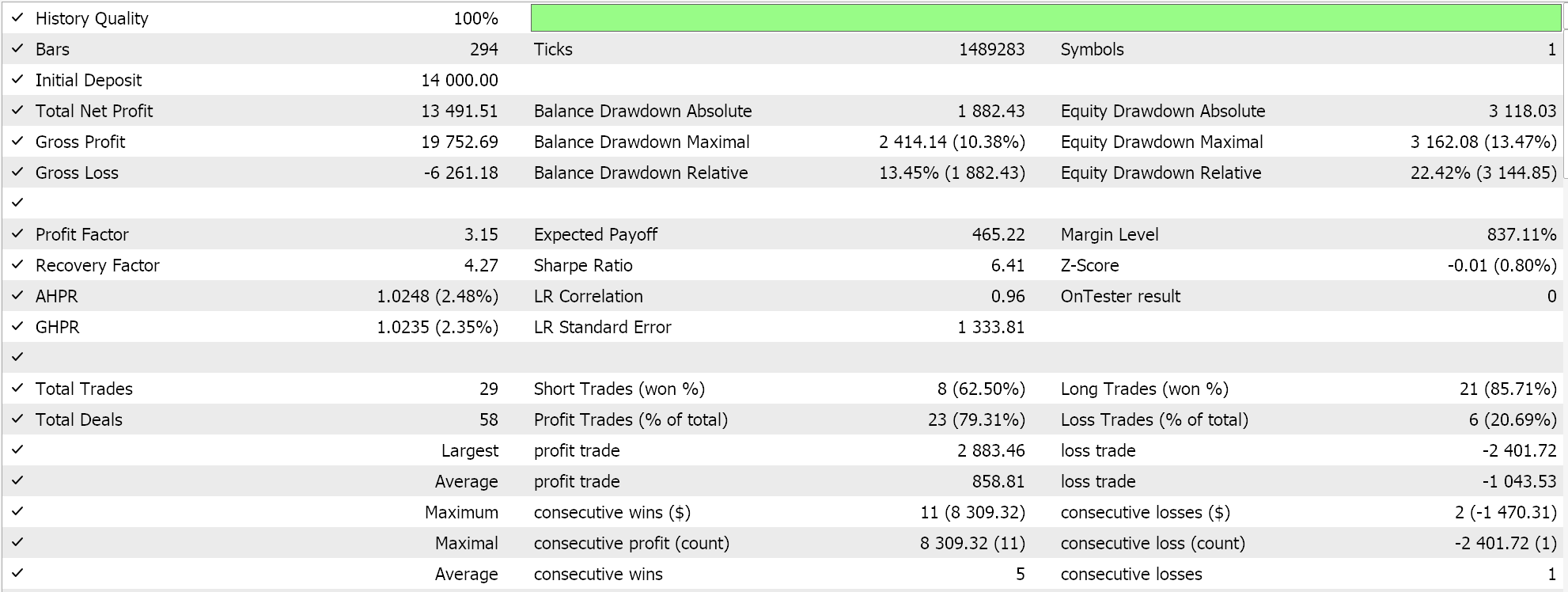
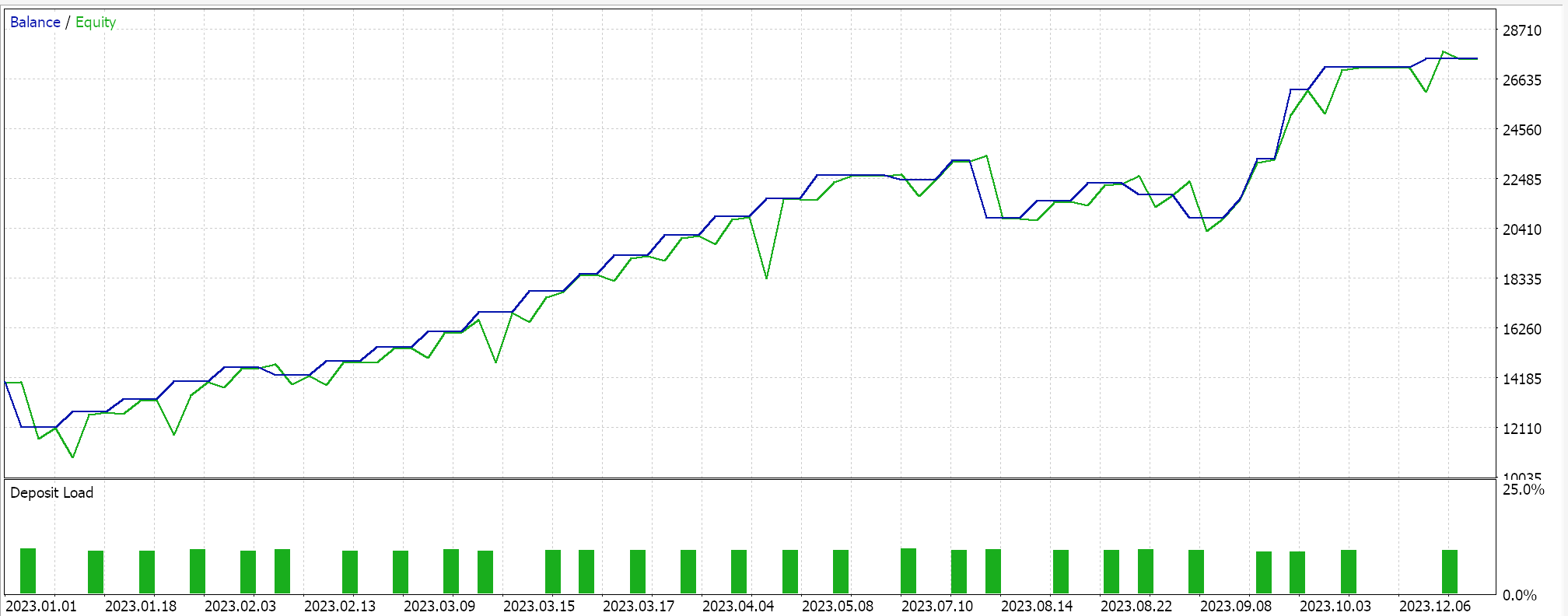
E os resultados para o núcleo de Matérn são:
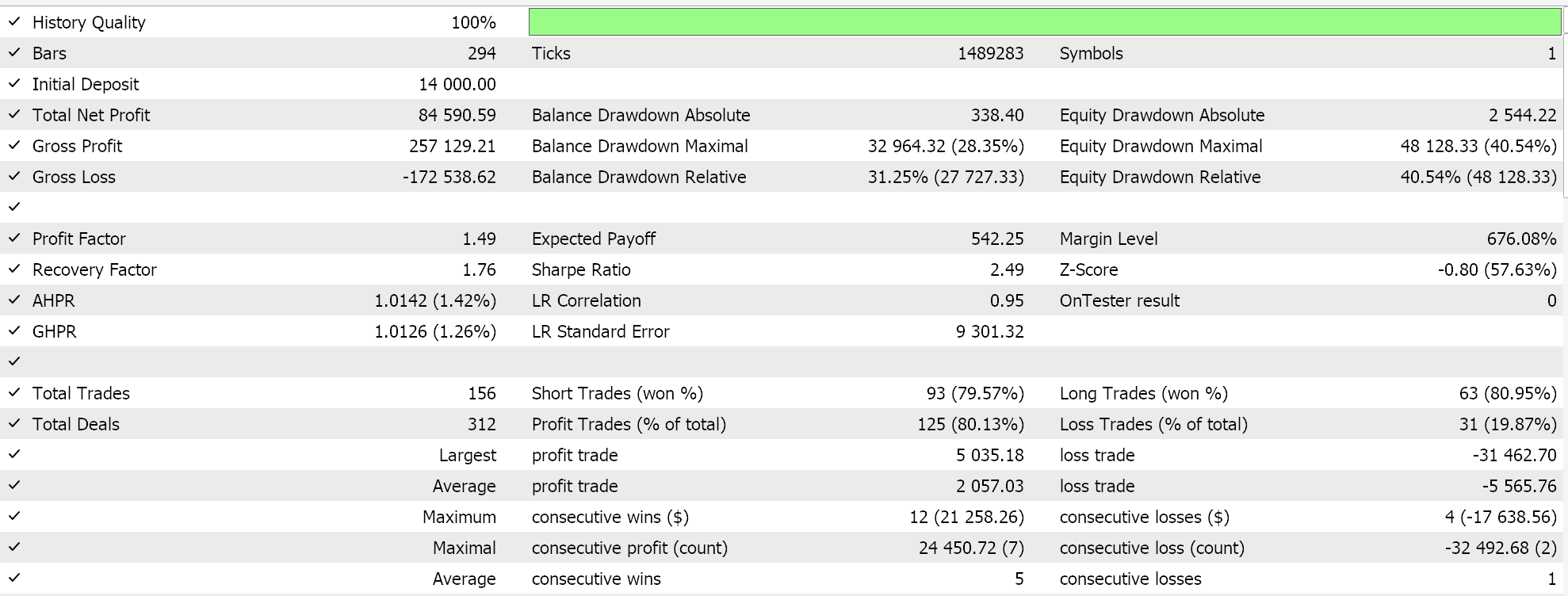
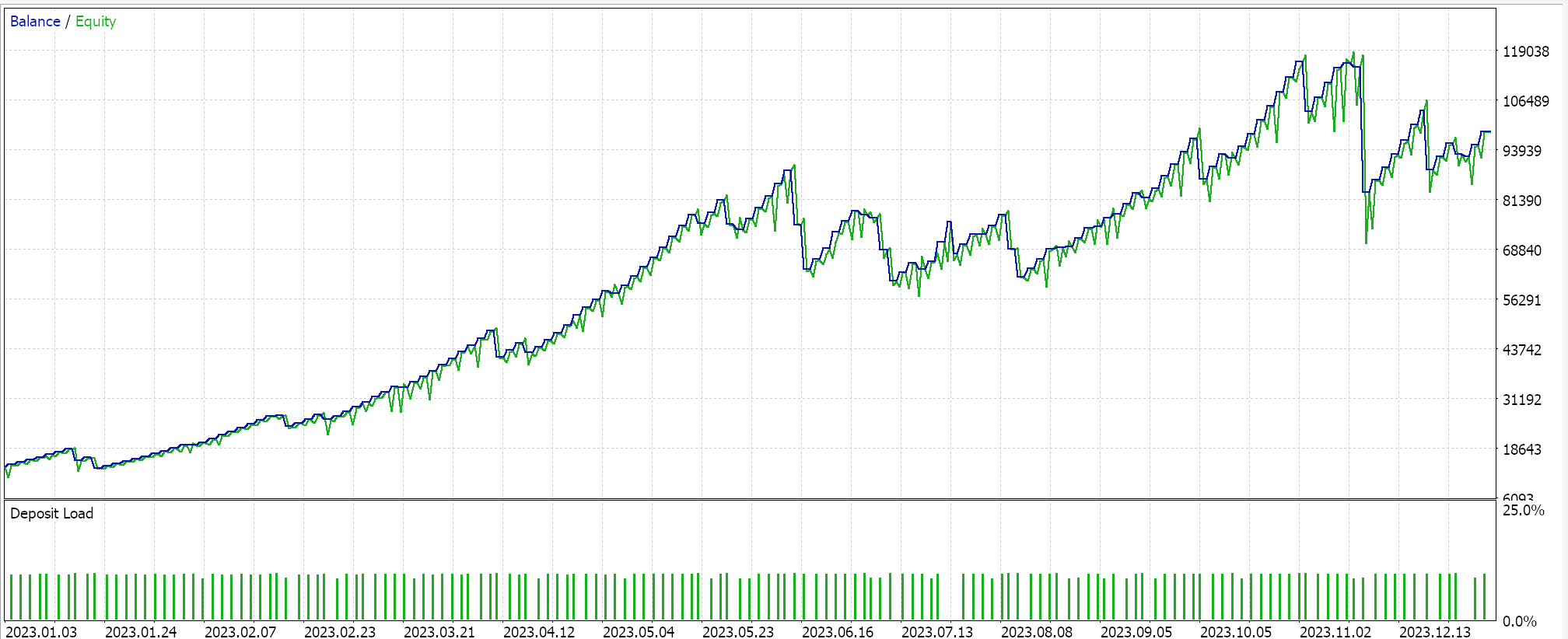
Uma implementação alternativa de ambos os núcleos também pode ser feita com uma classe personalizada de gerenciamento de capital. Essa, assim como a de sinal, pode ser montada no assistente MQL5, com a diferença de que apenas uma instância personalizada de gerenciamento de capital é selecionada. Para usar a regressão por processo gaussiano, como fizemos com a classe de sinal, idealmente teríamos uma classe âncora comum referenciada tanto pela classe de sinal quanto pela de gerenciamento de capital. Isso minimizaria duplicações de código de funções que realizam tarefas muito semelhantes nas duas classes personalizadas.
No entanto, na classe de gerenciamento de capital, temos algumas mudanças sutis no tipo de dado fornecido aos núcleos do processo gaussiano. Enquanto usávamos as variações de preços de fechamento como conjunto de entrada para a classe de sinal, para a classe de gerenciamento de capital usamos variações no indicador ATR como entradas para nosso núcleo. A saída do núcleo é treinada para prever a próxima variação no ATR. Essa classe personalizada é também uma adaptação da classe comum de otimização de tamanho de posição que, para quem não conhece, é construída para reduzir o tamanho da posição caso o Expert Advisor acumule uma sequência de perdas. A proporção de redução nos lotes é proporcional à sequência de perdas acumuladas. Adotamos essa classe e fazemos algumas alterações que determinam quando a redução dos lotes ocorre.
Com nossas modificações, só reduzimos os lotes se o Expert Advisor tiver prejuízos e houver uma projeção de aumento do ATR entre os valores previstos. O número desses valores previstos é definido pelo parâmetro ‘m_next’, como discutido no artigo já citado que introduziu a Regressão por Processo Gaussiano nesta série. Essas alterações, juntamente com a maior parte do código original para otimizar o tamanho da posição, são compartilhadas abaixo:
//+------------------------------------------------------------------+ //| Optimizing lot size for open. | //+------------------------------------------------------------------+ double CMoneyGAUSS::Optimize(int Type, double lots) { double lot = lots; //--- calculate number of losses orders without a break if(m_decrease_factor > 0) { //--- select history for access HistorySelect(0, TimeCurrent()); //--- int orders = HistoryDealsTotal(); // total history deals int losses = 0; // number of consequent losing orders //-- int size = 0; matrix series; series.Init(fmin(m_series_size, orders), 2); series.Fill(0.0); //-- CDealInfo deal; //--- for(int i = orders - 1; i >= 0; i--) { deal.Ticket(HistoryDealGetTicket(i)); if(deal.Ticket() == 0) { Print("CMoneySizeOptimized::Optimize: HistoryDealGetTicket failed, no trade history"); break; } //--- check symbol if(deal.Symbol() != m_symbol.Name()) continue; //--- check profit double profit = deal.Profit(); //-- series[size][0] = profit; size++; //-- if(size >= m_series_size) break; if(profit < 0.0) losses++; } //-- double _cond = 0.0; //-- vector _o; GetOutput(0.0, _o); //--- //decrease lots on rising ATR if(_o[_o.Size()-1] > _o[0]) lot = NormalizeDouble(lot - lot * losses / m_decrease_factor, 2); } //--- normalize and check limits double stepvol = m_symbol.LotsStep(); lot = stepvol * NormalizeDouble(lot / stepvol, 0); //--- double minvol = m_symbol.LotsMin(); if(lot < minvol) lot = minvol; //--- double maxvol = m_symbol.LotsMax(); if(lot > maxvol) lot = maxvol; //--- return(lot); }
Uma abordagem semelhante também pode ser usada ao criar uma classe de trailing personalizada que utiliza núcleos do processo gaussiano, como demonstramos acima. Há uma variedade de indicadores a serem escolhidos, além do fácil acesso a preços proporcionado pelos tipos de dados em vetores e matrizes.
Conclusão
Para concluir, continuamos nossa exploração da Regressão por Processo Gaussiano considerando outro conjunto de núcleos que podem ser usados com essa forma de regressão na previsão de séries temporais financeiras. O núcleo linear e o núcleo de Matérn são quase opostos, não apenas nos tipos de conjuntos de dados para os quais são mais adequados, mas também em sua flexibilidade. Enquanto o núcleo linear só pode lidar com um tipo específico de conjunto de dados, muitas vezes é prático começar a modelagem com ele, especialmente em casos onde a amostra de dados pode ser pequena no início do estudo. Com o tempo, à medida que o conjunto de dados aumenta e os dados se tornam mais complexos ou até ruidosos, um núcleo mais robusto como o de Matérn pode ser utilizado — não apenas para lidar com dados ruidosos, lacunas ou descontinuidades, mas também com conjuntos de dados muito suaves. Isso porque a capacidade de ajuste de seu parâmetro de entrada ν permite que ele assuma diferentes papéis dependendo dos desafios apresentados pelo conjunto de dados — e é por isso que ele é, provavelmente, mais adequado para a maioria dos ambientes de dados.
Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/15767
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Negociação algorítmica baseada em padrões de reversão 3D
Negociação algorítmica baseada em padrões de reversão 3D
 ADAM Populacional (estimativa adaptativa de momentos)
ADAM Populacional (estimativa adaptativa de momentos)
 Otimização de portfólio em Forex: Síntese de VaR e teoria de Markowitz
Otimização de portfólio em Forex: Síntese de VaR e teoria de Markowitz
 Redes neurais em trading: Conjunto de agentes com uso de mecanismos de atenção (MASAAT)
Redes neurais em trading: Conjunto de agentes com uso de mecanismos de atenção (MASAAT)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
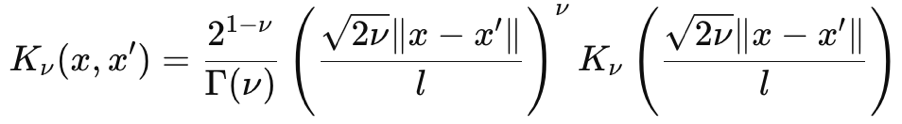
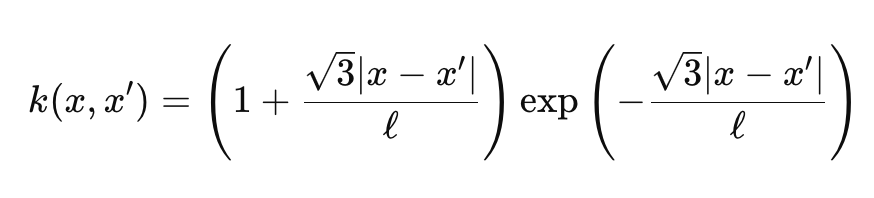
Estou recebendo um erro crítico.
índice fora do intervalo em 'MoneyWZ_37.mqh' (197,17)
em relação à linha
series[size][0] = profit;
índice fora do intervalo em 'MoneyWZ_37.mqh' (197,17)
relacionado à linha
series[size][0] = profit;
Hi,
Acabei de fazer alterações no código anexado e o reenviei para publicação.