
Redes neuronales en el trading: Detección de objetos con reconocimiento de escena (HyperDet3D)
Introducción
En los últimos años, la detección de objetos ha atraído una gran atención por parte de los investigadores. Basado en las representaciones y la convolución de volumen, PointNet se centra en la geometría local, analizando con elegancia la nube de puntos sin procesar, lo que le ha permitido ser ampliamente utilizada como línea troncal en diversos modelos de detección de objetos.
Sin embargo, los atributos de objetos similares resultan ambiguos, lo que reduce la calidad del rendimiento del modelo. Como consecuencia, el alcance del modelo se ve limitado o su arquitectura tiene que ser complicada. Los autores del artículo "HyperDet3D: Learning a Scene-conditioned 3D Object Detector" descubrieron que la información a nivel de escenario ofrece un conocimiento a priori para eliminar la ambigüedad en la interpretación de los atributos de los objetos. Esto elimina los resultados ilógicos de la detección de objetos en el aspecto de la comprensión a nivel de escena.
En el trabajo mencionado, se propuso el algoritmo HyperDet3D para la detección de objetos 3D en nubes de puntos, que usa una estructura basada en hiper-redes. HyperDet3D aprende la información de la escena e incorpora el conocimiento de la esta a los parámetros de la red. Esto permite que el detector de objetos 3D se ajuste dinámicamente a los distintos datos de entrada. En concreto, el conocimiento específico de la escena puede descomponerse en dos niveles: la información independiente de la escena y la información específica de la escena.
Para el conocimiento independiente de la escena, los autores del método proponen aprender incorporaciones que son utilizadas por la hiper-red y actualizadas iterativamente junto con el análisis sintáctico de diferentes escenas iniciales durante el entrenamiento del modelo. Este conocimiento independiente de una escena suele abstraerse de las características de las escenas de entrenamiento y puede ser utilizado por el detector durante su funcionamiento.
Además, como los detectores convencionales conservan el mismo conjunto de parámetros al reconocer objetos en distintas escenas, los autores de HyperDet3D proponen incluir información específica de la escena que adapte el detector a una escena determinada durante su funcionamiento. Para ello, se analiza en qué medida la escena actual coincide con la representación global (o en qué medida se distinguen), utilizando como consulta datos de origen específicos.
Este artículo propone la estructura de un nuevo módulo de «atención multicabeza condicionada por la escena» (Multi-head Scene-Conditioned Attention — MSA). El MSA permite agregar el conocimiento a priori obtenido con las características de los objetos candidatos, lo cual permite una detección de objetos más eficaz.
1. El algoritmo HyperDet3D
El modelo HyperDet3D incluye 3 componentes principales:
- El Codificador troncal;
- La capa del Decodificador de objetos;
- La cabeza de detección.
La nube de puntos de entrada inicial es procesada en primer lugar por una línea troncal que reduce la muestra de los puntos hasta convertirlos en candidatos a objetos iniciales y extrae sus características de forma aproximada usando arquitecturas jerárquicas. Los autores del método proponen utilizar PointNet++ como línea troncal.
A continuación, las capas de descodificación de objetos refinan las características potenciales incorporando conocimientos a priori condicionados por la escena a la representación a nivel de objeto, mientras que la cabeza detectora vuelve a trazar rectángulos delimitadores a partir de las ubicaciones y características refinadas de estos candidatos a objeto.
Para dotar a HyperDet3D de conciencia sobre la metainformación al nivel de la escena, los autores del método introducen una HyperNetwork, que es una red neuronal utilizada para parametrizar los parámetros entrenados de la red primaria. A diferencia de las redes neuronales profundas convencionales, que mantienen un nivel fijo durante el funcionamiento, las hiper-redes ofrecen flexibilidad en los parámetros aprendidos cambiándolos según los datos de entrada.
El HyperDet3D aplica una hiper-red basada en escenas para integrar el conocimiento previo en los parámetros de la capa del Descodificador del Transformer. Esto permite adaptar de forma dinámica la red de detección a una gran variedad de escenas de origen. El concepto clave consiste en utilizar hiper-redes condicionadas por la escena para enriquecer la representación del objeto 𝒐 partiendo de un conjunto de candidatos a objetos generados por el Codificador formador de sistemas utilizando un conocimiento a priori parametrizado por 𝑾.
Los parámetros se generan mediante hiper-redes condicionadas por la escena que pueden dividirse en específicas de la escena e independientes de la escena.
Para obtener un conocimiento independiente de la escena, los autores del método proponen entrenar un conjunto de n vectores de incorporación independientes de la escena 𝒁a, que luego son absorbidos por la hiper-red. A la salida de la hiper-red obtenemos la matriz de coeficientes de peso 𝑾a, que parametriza el conocimiento independiente de la escena.
A medida que las propiedades de los objetos se refinan de forma iterativa a través de una serie de capas de descodificación, estas pueden combinarse de forma coherente con los resultados de una hiper-red independiente de la escena que abstrae el conocimiento a priori sobre diferentes escenas 3D. De este modo, HyperDet3D no solo mantiene un conocimiento común de la escena en todos los niveles del descodificador, sino que también ahorra recursos computacionales compartiendo conocimientos con ricas jerarquías de características.
Para obtener conocimientos sobre escenas concretas, el modelo aprende un conjunto de incorporaciones 𝒁s similares a 𝒁a, solo que en este caso 𝒁s debe contener información específica de cada escena. Este efecto se logra usando un bloque de atención cruzada en el que la incorporación de la escena analizada se compara con las incorporaciones aprendidas de 𝒁s. Así, utilizando el mecanismo de atención, el modelo mide lo bien que 𝒁s se corresponde con la escena analizada (o lo diferentes que son) en el espacio de incorporación.
A continuación le presentamos la visualización del método HyperDet3D realizada por el autor.
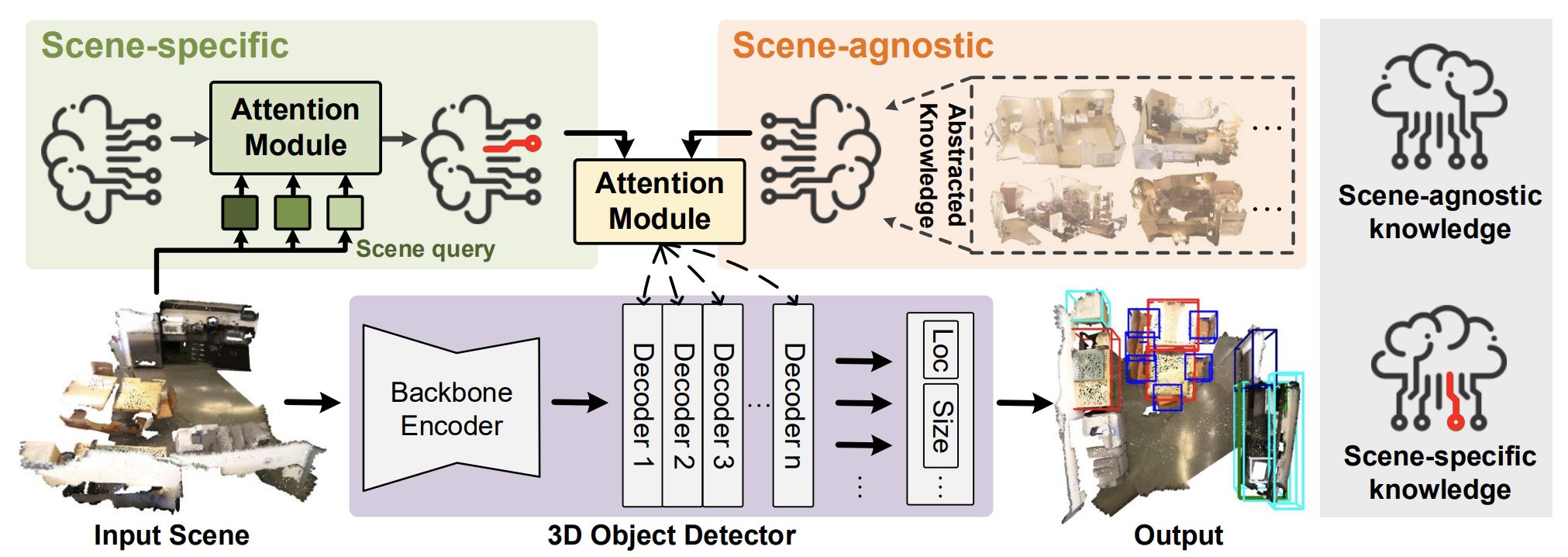
2. Implementación con MQL5
Tras familiarizarnos con los aspectos teóricos del método HyperDet3D, comenzaremos la parte práctica de nuestro trabajo, donde aplicaremos nuestra visión de los enfoques propuestos.
Diremos de entrada que hoy tenemos bastante trabajo. Por consiguiente, dividiremos la aplicación en varios bloques lógicos. Venga, manos a la obra.
2.1 Módulo de conocimientos específicos
En primer lugar, crearemos un módulo para aprender los conocimientos específicos de la escena. Como ya mencionamos en la parte teórica del artículo, para emparejar la escena analizada e incrustar conocimientos específicos de la escena se utiliza un algoritmo de atención cruzada. Como consecuencia, nuestra nueva clase CNeuronSceneSpecific la crearemos heredando del bloque de atención cruzada CNeuronMLCrossAttentionMLKV. A continuación, le mostramos la estructura de la nueva clase,
class CNeuronSceneSpecific : public CNeuronMLCrossAttentionMLKV { protected: CNeuronBaseOCL cOne; CNeuronBaseOCL cSceneSpecificKnowledge; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context) override { return feedForward(NeuronOCL); } //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override { return calcInputGradients(NeuronOCL); } virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context) override { return updateInputWeights(NeuronOCL); } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronSceneSpecific(void) {}; ~CNeuronSceneSpecific(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint units_count_kv, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronSceneSpecific; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Debemos señalar una diferencia fundamental entre nuestra nueva clase y su antecesora. Para que la clase padre funcione correctamente, necesitaremos dos fuentes de datos: los datos analizados y el contexto. En nuestra nueva clase, en cambio, el contexto serán los datos concretos de la escena aprendidos procedentes de la muestra de entrenamiento. Los estudiaremos en dos capas internas: cOne y cSceneSpecificKnowledge. En esencia, se tratará de un MLP de dos capas que toma "1" como entrada y generará un tensor de conocimiento específico de la escena. No resulta difícil adivinar que este tensor será estático durante el funcionamiento del modelo, pero durante el aprendizaje, podremos "escribir" en él la información necesaria.
Siguiendo la lógica anterior, excluiremos los punteros al contexto externo de los métodos de nuestra nueva clase.
Todos los objetos internos de nuestra clase se declararán estáticamente, lo cual nos permitirá dejar vacíos el constructor y el destructor de la clase. La inicialización del objeto se realizará en el método Init, en cuyos parámetros obtendremos las constantes básicas de la arquitectura del objeto a crear. La funcionalidad de los parámetros utilizados será similar al método homónimo de la clase padre.
bool CNeuronSceneSpecific::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint units_count_kv, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronMLCrossAttentionMLKV::Init(numOutputs, myIndex, open_cl, window, window_key, heads, 16, heads_kv, units_count, units_count_kv, layers, layers_to_one_kv, optimization_type, batch)) return false;
En el cuerpo del método llamaremos directamente al método de inicialización de la clase padre, al que transmitiremos todos los parámetros recibidos. Este método comprobará los parámetros recibidos e inicializará los objetos heredados.
A continuación, todo lo que tendremos que hacer es inicializar el MLP de conocimientos específicos anteriormente mencionado.
Obsérvese que la primera capa solo contendrá un elemento constante, mientras que la segunda capa nos generará un conjunto de vectores de incorporación de conocimientos específicos sobre el estado de la escena. Para cada incorporación, especificaremos un tamaño de vector de 16 elementos. El número de estas incorporaciones se especifica en los parámetros del método y dependerá de la complejidad del entorno estudiado.
if(!cOne.Init(16 * units_count_kv, 0, OpenCL, 1, optimization, iBatch)) return false; CBufferFloat *out = cOne.getOutput(); if(!out.BufferInit(1, 1) || !out.BufferWrite()) return false; if(!cSceneSpecificKnowledge.Init(0, 1, OpenCL, 16 * units_count_kv, optimization, iBatch)) return false; //--- return true; }
Antes de que el método finalice, retornaremos el resultado lógico de las operaciones al programa que realiza la llamada.
El método para inicializar nuestra nueva clase será bastante corto y conciso, y no contiene nada sorprendente, porque la funcionalidad principal se ha implementado previamente en el método de la clase padre. Sin embargo, esto no solo se aplicará al método de inicialización: podemos observar una imagen similar en el algoritmo del método feedForward, en cuyos parámetros obtendremos el puntero al objeto de datos de origen.
bool CNeuronSceneSpecific::feedForward(CNeuronBaseOCL *NeuronOCL) { if(bTrain && !cSceneSpecificKnowledge.FeedForward(cOne.AsObject())) return false;
En el cuerpo del método, primero tendremos que generar una matriz de representaciones de escenas dependientes del contexto aprendidas. Pero realizaremos esta operación solo durante el proceso de entrenamiento del modelo, cuando el tensor resultante también se modifica durante el ajuste de los parámetros de nuestro MLP. Durante el funcionamiento del modelo, los datos entrenados son estáticos y no necesitaremos volver a generarlos: solo estaremos utilizando información almacenada previamente.
A continuación, todo lo que deberemos hacer es llamar al método de pasada directa de la clase padre, a la que transmitiremos como contexto nuestro conocimiento específico de las representaciones de la escena.
if(!CNeuronMLCrossAttentionMLKV::feedForward(NeuronOCL, cSceneSpecificKnowledge.getOutput())) return false; //--- return true; }
Los métodos de pasada inversa también se construirán de forma similar, así que le sugiero que los estudie por su cuenta para no aumentar excesivamente el tamaño del artículo. Permítame recordarle que el código completo de la clase presentada y todos sus métodos se pueden encontrar en el archivo adjunto.
2.2 Construimos el bloque MSA
Ahora construiremos un bloque de atención multicabeza condicionado por la escena, así que tendrá sentido que heredemos la funcionalidad básica de uno de los bloques de atención implementados anteriormente. A continuación le mostramos la estructura de la nueva clase CNeuronMLMHSceneConditionAttention.
class CNeuronMLMHSceneConditionAttention : public CNeuronMLMHAttentionMLKV { protected: CLayer cSceneAgnostic; CLayer cSceneSpecific; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronMLMHSceneConditionAttention(void) {}; ~CNeuronMLMHSceneConditionAttention(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch) override; //--- virtual int Type(void) override const { return defNeuronMLMHSceneConditionAttention; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
En la estructura presentada anteriormente, podemos observar la declaración de dos nuevos objetos de la clase CLayer. Uno de ellos contendrá representaciones de escenas dependientes del contexto, mientras que la segunda supondrá información general sobre los objetos, independientemente de la escena.
Sin embargo, debemos decir de entrada que la presencia de 2 objetos no limitará la creación de las capas neuronales anidadas de identificación de objetos. En este caso, los objetos CLayer se utilizarán como arrays dinámicos, mientras que el número de capas neuronales internas lo determinará el usuario al inicializar un nuevo objeto.
Ya hemos declarado todos los objetos internos estáticamente, lo que nos permitirá dejar el constructor y el destructor de la clase "vacíos". La inicialización de todos los objetos internos y heredados se realizará en el método Init, como de costumbre.
bool CNeuronMLMHSceneConditionAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
En los parámetros del método obtendremos las constantes básicas que definirán la arquitectura del objeto a crear. Y en el cuerpo del método llamaremos directamente al método antecesor homónimo. Sin embargo, en este caso no estaremos utilizando el método de la clase padre directa, sino de la capa básica completamente conectada CNeuronBaseOCL. Esto se debe a diferencias significativas en la estructura y el tamaño de los objetos heredados.
Tras ejecutar con éxito las operaciones del método de inicialización del ancestro, guardaremos las constantes de arquitectura de nuestra nueva clase.
iWindow = fmax(window, 1); iWindowKey = fmax(window_key, 1); iUnits = fmax(units_count, 1); iHeads = fmax(heads, 1); iLayers = fmax(layers, 1); iHeadsKV = fmax(heads_kv, 1); iLayersToOneKV = fmax(layers_to_one_kv, 1);
Y calcularemos las dimensionalidades de los objetos internos.
uint num_q = iWindowKey * iHeads * iUnits; //Size of Q tensor uint num_kv = 2 * iWindowKey * iHeadsKV * iUnits; //Size of KV tensor uint q_weights = (iWindow * iHeads) * iWindowKey; //Size of weights' matrix of Q tenzor uint kv_weights = 2 * (iWindow * iHeadsKV) * iWindowKey; //Size of weights' matrix of KV tenzor uint scores = iUnits * iUnits * iHeads; //Size of Score tensor uint mh_out = iWindowKey * iHeads * iUnits; //Size of multi-heads self-attention uint out = iWindow * iUnits; //Size of out tensore uint w0 = (iWindowKey * iHeads + 1) * iWindow; //Size W0 tensor uint ff_1 = 4 * (iWindow + 1) * iWindow; //Size of weights' matrix 1-st feed forward layer uint ff_2 = (4 * iWindow + 1) * iWindow; //Size of weights' matrix 2-nd feed forward layer
Luego añadiremos dos variables locales adicionales para almacenar temporalmente punteros a los objetos de la capa neuronal.
CNeuronBaseOCL *base = NULL; CNeuronSceneSpecific *ss = NULL;
Y con esto concluiremos el trabajo preparatorio. A continuación, organizaremos un ciclo con un número de iteraciones igual al número de capas interiores especificado por el usuario en los parámetros del método. En cada iteración de este ciclo, crearemos los objetos de la capa interior. En consecuencia, tras completar totalmente un número determinado de iteraciones del ciclo, habremos creado un conjunto completo de objetos necesarios para el funcionamiento normal del número requerido de capas neuronales internas.
for(uint i = 0; i < iLayers; i++) { CBufferFloat *temp = NULL; for(int d = 0; d < 2; d++) { //--- Initilize Q tensor temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_q, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Tensors.Add(temp)) return false;
En el cuerpo del ciclo, crearemos directamente otro ciclo anidado de 2 iteraciones. En el cuerpo del ciclo anidado, almacenaremos los búferes de datos para registrar los datos del flujo principal de información de pasada directa y los gradientes de error de pasada inversa correspondientes. Precisamente el ciclo de dos iteraciones nos permitirá crear una arquitectura en espejo para las pasadas directa y inversa.
Y aquí primero crearemos un búfer para escribir las entidades Query generadas. Y, a continuación, crearemos un búfer para registrar la matriz de coeficientes de peso de generación de esta entidad.
//--- Initilize Q weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(q_weights, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false;
Fíjese: antes siempre rellenábamos la matriz de coeficientes de peso con valores aleatorios que se ajustaban durante el entrenamiento del modelo, pero ahora hemos creado un búfer con valores cero. Esto se debe a que hemos introducido una arquitectura de hiper-red que generará esta matriz considerando la escena analizada.
Repetiremos las mismas operaciones para generar los búferes de datos de las entidades Key y Value, solo que aquí añadiremos la posibilidad de utilizar un único tensor para múltiples capas internas. Por consiguiente, antes de crear búferes de datos, comprobaremos la viabilidad de dichas operaciones.
if(i % iLayersToOneKV == 0) { //--- Initilize KV tensor temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_kv, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!KV_Tensors.Add(temp)) return false; //--- Initilize KV weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(kv_weights, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!KV_Weights.Add(temp)) return false; }
A continuación, añadiremos un búfer para registrar los coeficientes de dependencia.
//--- Initialize scores temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(scores, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!S_Tensors.Add(temp)) return false;
Y los resultados de la atención multicabeza.
//--- Initialize multi-heads attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(mh_out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!AO_Tensors.Add(temp)) return false;
Al igual que antes, los resultados de la atención multicabeza se escalarán al tamaño de los datos de origen. Luego escribiremos el resultado de esta operación en el búfer de datos correspondiente.
//--- Initialize attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false;
Y añadiremos los búferes de la operación del bloque FeedForward.
//--- Initialize Feed Forward 1 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(4 * out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; //--- Initialize Feed Forward 2 if(i == iLayers - 1) { if(!FF_Tensors.Add(d == 0 ? Output : Gradient)) return false; continue; } temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; }
Aquí, al igual que sucede en el método análogo de la clase padre, para la última capa interna a la salida del bloque FeedForward no crearemos los nuevos búferes de datos, sino que escribiremos los punteros a los búferes correspondientes de nuestra capa heredada de la capa básica totalmente conectada. Estos búferes se utilizarán para intercambiar datos entre las capas del modelo. Y escribiremos datos en ellos inmediatamente en el flujo de operaciones, eliminando la transferencia innecesaria de datos de las capas internas a las interfaces externas.
Tras inicializar los búferes de almacenamiento de datos de los flujos de información de pasada directa y inversa, tendremos que inicializar las matrices de coeficientes de peso. Sin embargo, para generar entidades Query, Key y Value adaptadas al estado de la escena analizada usaremos 2 hiper-redes: una de conocimiento a priori de las entidades y otra de conocimiento dependiente del contexto del estado de la escena. Por lo tanto, tendremos que inicializar estas hiper-redes.
Y aquí hay varias opciones de aplicación. Como ya sabe, las entidades Key y Value, a diferencia de Query, no pueden generarse en cada capa interna. Por lo tanto, las hemos separado en un tensor independiente. Y podemos crear hiper-redes separadas para generar las matrices de pesos correspondientes. Sin embargo, este enfoque no será el mejor en términos de rendimiento. Al fin y al cabo, en esta variante aumentará el número de operaciones consecutivas. Así que hemos decidido generarlas en paralelo dentro de un único hipermodelo unificado, y luego distribuir la salida resultante a los búferes de datos correspondientes.
Pero aquí tenemos que tener en cuenta que las entidades Key y Value no se generan en cada capa interna. Por ello, si no necesitemos generar las entidades especificadas, simplemente utilizaremos un modelo con un tensor de resultados más pequeño.
Suena lógico. Pasemos a la aplicación. Primero dividiremos el flujo de operaciones en 2 direcciones dependiendo de la necesidad de generar el tensor Key-Value. Ambos flujos de operaciones tendrá el mismo algoritmo. La única diferencia será el tamaño del tensor resultante.
if(i % iLayersToOneKV == 0) { //--- Initilize Scene-Specific layers ss = new CNeuronSceneSpecific(); if(!ss) return false; if(!ss.Init((q_weights + kv_weights), cSceneSpecific.Total(), OpenCL, iWindow, iWindowKey, 4, 2, iUnits, 100, 2, 2, optimization, iBatch)) return false; if(!cSceneSpecific.Add(ss)) return false;
Primero trabajaremos con el modelo de representación dependiente del contexto. Aquí crearemos e inicializaremos el objeto dinámico del módulo de conocimiento específico que implementamos anteriormente. Y el puntero al objeto creado en un array del modelo cSceneSpecific sensible al contexto.
Sin embargo, aquí conviene señalar un matiz. Luego construiremos la clase del módulo de conocimiento específico basado en el bloque de atención cruzada que recibe el estado de la escena analizada como datos de entrada. Y retornaremos el tensor de tamaño correspondiente, pero enriquecido con conocimiento del modelo dependiente del contexto. El problema aquí es que lo más probable es que el tamaño del tensor de datos original no coincida con el tamaño de la matriz de coeficientes de peso que necesitamos. Por lo tanto, añadiremos una capa completamente conectada para escalar los datos en consecuencia.
base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(0, cSceneSpecific.Total(), OpenCL, (q_weights + kv_weights), optimization, iBatch)) return false; base.SetActivationFunction(TANH); if(!cSceneSpecific.Add(base)) return false;
Esta capa de escalado obtendrá una tangente hiperbólica como capa de activación, cuya región de valores estará en el rango [-1, 1]. Así, nuestro conocimiento dependiente del contexto sobre el estado de la escena actuará como una especie de bandera que indicará la posible presencia de tal o cual objeto en la escena analizada.
Para el modelo de conocimiento a priori independiente de la escena, utilizaremos un MLP de dos capas similar al descrito anteriormente para preservar las incorporaciones dependientes del contexto.
//--- Initilize Scene-Agnostic layers base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init((q_weights + kv_weights), cSceneAgnostic.Total(), OpenCL, 1, optimization, iBatch)) return false; temp = base.getOutput(); if(!temp.BufferInit(1, 1) || !temp.BufferWrite()) return false; if(!cSceneAgnostic.Add(base)) return false; base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(0, cSceneAgnostic.Total(), OpenCL, (q_weights + kv_weights), optimization, iBatch)) return false; if(!cSceneAgnostic.Add(base)) return false; }
Si no es necesario generar un tensor Key-Value, crearemos objetos similares pero de menor tamaño.
else { //--- Initilize Scene-Specific layers ss = new CNeuronSceneSpecific(); if(!ss) return false; if(!ss.Init(q_weights, cSceneSpecific.Total(), OpenCL, iWindow, iWindowKey, 4, 2, iUnits, 100, 2, 2, optimization, iBatch)) return false; if(!cSceneSpecific.Add(ss)) return false; base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(0, cSceneSpecific.Total(), OpenCL, q_weights, optimization, iBatch)) return false; base.SetActivationFunction(TANH); if(!cSceneSpecific.Add(base)) return false; //--- Initilize Scene-Agnostic layers base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(q_weights, cSceneAgnostic.Total(), OpenCL, 1, optimization, iBatch)) return false; temp = base.getOutput(); if(!temp.BufferInit(1, 1) || !temp.BufferWrite()) return false; if(!cSceneAgnostic.Add(base)) return false; base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(0, cSceneAgnostic.Total(), OpenCL, q_weights, optimization, iBatch)) return false; if(!cSceneAgnostic.Add(base)) return false; }
Para la capa de datos de escalado de los resultados de la atención multicabeza y el bloque FeedForward, utilizaremos matrices de parámetros de entrenamiento ordinarias inicializadas con parámetros aleatorios.
//--- Initilize Weights0 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(w0)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < w0; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- Initilize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_1)) return false; for(uint w = 0; w < ff_1; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_2)) return false; k = (float)(1 / sqrt(4 * iWindow + 1)); for(uint w = 0; w < ff_2; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
Y añadiremos búferes de momentos que utilizaremos en el proceso de optimización de las matrices de parámetros de entrenamiento creadas. El número de búferes de momentos se determinará con la ayuda del método de optimización de parámetros especificado.
//--- for(int d = 0; d < (optimization == SGD ? 1 : 2); d++) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? w0 : iWindow), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- Initilize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? ff_1 : 4 * iWindow), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? ff_2 : iWindow), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; } }
Una vez inicializados con éxito todos los objetos especificados, pasaremos a la siguiente iteración del ciclo, en la que crearemos objetos similares para la siguiente capa interior.
Al final del método de inicialización, inicializaremos el búfer auxiliar de almacenamiento temporal de datos y devolveremos el resultado lógico de las operaciones al programa que realiza la llamada.
if(!Temp.BufferInit(MathMax((num_q + num_kv)*iWindow, out), 0)) return false; if(!Temp.BufferCreate(OpenCL)) return false; //--- SetOpenCL(OpenCL); //--- return true; }
Una estructura compleja y un gran número de objetos dificultarán la comprensión del algoritmo que estamos construyendo. Además, deberemos supervisar cuidadosamente el flujo de información y la transferencia de datos entre objetos durante la aplicación de los métodos de pasada directa y inversa. Y empezaremos construyendo el método feedForward.
bool CNeuronMLMHSceneConditionAttention::feedForward(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *ss = NULL, *sa = NULL; CBufferFloat *q_weights = NULL, *kv_weights = NULL, *q = NULL, *kv = NULL;
En los parámetros del método, obtendremos el puntero al objeto de datos de origen. Sin embargo, no organizaremos la comprobación de la pertinencia del índice resultante. Al fin y al cabo, no tenemos previsto abordar directamente el objeto de datos de origen en esta fase. Sin embargo, realizaremos un pequeño trabajo preparatorio en el que crearemos variables locales para almacenar temporalmente punteros a diversos objetos. Y luego crearemos un ciclo de iterar las capas internas de nuestro bloque.
for(uint i = 0; i < iLayers; i++) { //--- Scene-Specific ss = cSceneSpecific[i * 2]; if(!ss.FeedForward(NeuronOCL)) return false; ss = cSceneSpecific[i * 2 + 1]; if(!ss.FeedForward(cSceneSpecific[i * 2])) return false;
Dentro del ciclo, primero generaremos los pesos para crear las entidades Query, Key y Value utilizando las hiper-redes previamente construidas.
En primer lugar, generaremos una matriz de parámetros dependientes del contexto a partir de la descripción del estado de la escena recibida del programa que realiza la llamada. Como ya hemos descrito anteriormente, tras producirse el enriquecimiento con los conocimientos dependientes del contexto, escalaremos el tensor de descripción del estado de la escena al tamaño de la matriz de parámetros requerida.
Aquí también generaremos una matriz de parámetros independiente de la escena.
//--- Scene-Agnostic sa = cSceneAgnostic[i * 2 + 1]; if(bTrain && !sa.FeedForward(cSceneAgnostic[i * 2])) return false;
Obsérvese que la operación de generación de la matriz de parámetros independientes de la escena solo la realizaremos durante el entrenamiento del modelo. La matriz permanecerá estática durante el funcionamiento, y no será necesario volver a generarla en cada pasada.
A continuación, tendremos que realizar la multiplicación elemento a elemento de las dos matrices. Como resultado obtendremos la matriz necesaria de parámetros de peso, que distribuiremos a los búferes de datos previamente creados. Y decimos precisamente «distribuir», ya que generaremos una matriz de pesos que dividiremos en 2 partes. Una se utilizará para formar las entidades Query. La segunda se usará para las entidades Key y Value. Pero recordamos que estos últimos no se forman en cada pasada. Por lo tanto, deberemos organizar la ramificación del flujo de operaciones según la necesidad de formar el tensor Key-Value.
Antes, sin embargo, realizaremos un poco de trabajo preparatorio. Para ello, trasladaremos el puntero al objeto de datos de origen de la capa interna actual a una variable local.
CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(6 * i - 4));
Aquí almacenaremos el puntero al objeto de datos de origen precisamente de la capa interna. Esto significa que pasaremos a la variable el puntero recibido del programa externo solo para la primera capa interna. En los demás casos, utilizaremos los resultados de la capa interior anterior.
Y almacenaremos en las variables locales a los búferes de datos de los parámetros de peso y el propio tensor de valores de la entidad Query, que utilizaremos en cualquiera de las 2 opciones descritas anteriormente.
q_weights = QKV_Weights[i * 2]; q = QKV_Tensors[i * 2];
En caso de que sea necesario formar el tensor Key-Value, primero realizaremos la multiplicación elemento a elemento de las dos matrices de coeficientes de peso formadas anteriormente. El resultado de la operación se escribirá en el búfer de almacenamiento temporal de datos.
if(i % iLayersToOneKV == 0) { if(IsStopped() || !ElementMult(ss.getOutput(), sa.getOutput(), GetPointer(Temp))) return false;
Guardaremos los punteros a los búferes de coeficientes de peso y entidades Key-Value en las variables locales.
kv_weights = KV_Weights[(i / iLayersToOneKV) * 2]; kv = KV_Tensors[(i / iLayersToOneKV) * 2];
Y luego distribuiremos el tensor de parámetros de peso total entre los dos búferes de datos.
if(IsStopped() || !DeConcat(q_weights, kv_weights, GetPointer(Temp), iHeads, 2 * iHeadsKV, iWindow * iWindowKey)) return false; if(IsStopped() || !MatMul(inputs, kv_weights, kv, iUnits, iWindow, 2 * iHeadsKV * iWindowKey, 1)) return false; }
A continuación, formaremos el tensor de entidades Key-Value mediante la multiplicación matricial del tensor de datos de origen de la capa interna actual por la matriz de coeficientes de peso resultante.
Si no haya necesidad de formar un tensor de entidad Key-Value, solo realizaremos la operación de multiplicación elemento a elemento de las dos matrices de parámetros con los resultados registrados en el búfer de datos correspondiente. Al fin y al cabo, en este caso nuestras hiper-redes solo formarán la matriz de coeficientes de peso de la entidad Query.
else { if(IsStopped() || !ElementMult(ss.getOutput(), sa.getOutput(), q_weights)) return false; }
La formación del tensor de valores de la entidad Query se realizará en cualquiera de los dos casos. Por lo tanto, efectuaremos esta operación ya en el flujo general.
if(IsStopped() || !MatMul(inputs, q_weights, q, iUnits, iWindow, iHeads * iWindowKey, 1)) return false;
Esta etapa completará la aplicación de las hiper-redes en el algoritmo de atención. Lo que seguirá es el ya conocido mecanismo de Self-Attention. En primer lugar, definiremos los resultados de la atención multicabeza.
//--- Score calculation and Multi-heads attention calculation CBufferFloat *temp = S_Tensors[i * 2]; CBufferFloat *out = AO_Tensors[i * 2]; if(IsStopped() || !AttentionOut(q, kv, temp, out)) return false;
A continuación, reduciremos la dimensionalidad del tensor de resultados obtenido.
//--- Attention out calculation temp = FF_Tensors[i * 6]; if(IsStopped() || !ConvolutionForward(FF_Weights[i * (optimization == SGD ? 6 : 9)], out, temp, iWindowKey * iHeads, iWindow, None)) return false;
Después, sumaremos los resultados del bloque de Self-Attention con los datos originales y normalizaremos el tensor obtenido.
//--- Sum and normilize attention if(IsStopped() || !SumAndNormilize(temp, inputs, temp, iWindow, true)) return false;
A continuación, los datos pasarán por el bloque FeedForward.
//--- Feed Forward inputs = temp; temp = FF_Tensors[i * 6 + 1]; if(IsStopped() || !ConvolutionForward(FF_Weights[i * (optimization == SGD ? 6 : 9) + 1], inputs, temp, iWindow, 4 * iWindow, LReLU)) return false; out = FF_Tensors[i * 6 + 2]; if(IsStopped() || !ConvolutionForward(FF_Weights[i * (optimization == SGD ? 6 : 9) + 2], temp, out, 4 * iWindow, iWindow, activation)) return false;
Luego se sumarán y normalizarán los datos.
//--- Sum and normilize out if(IsStopped() || !SumAndNormilize(out, inputs, out, iWindow, true)) return false; } //--- result return true; }
Repetiremos las operaciones para todas las capas interiores. Y tras la enumeración completa de todas las iteraciones del ciclo, devolveremos el resultado lógico de las operaciones del método al programa que realiza la llamada.
Llegados a este punto, es de esperar que haya usted resuelto el "rompecabezas" que supone el funcionamiento del algoritmo de nuestra clase. Pero también hay un matiz a considerar en la distribución del gradiente de error durante la pasada inversa, cuyo algoritmo implementamos en el método calcInputGradients.
bool CNeuronMLMHSceneConditionAttention::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer) == POINTER_INVALID) return false;
En los parámetros del método, como es habitual, obtendremos el puntero al objeto de la capa anterior al que vamos a pasar el gradiente de error según la influencia de los datos iniciales en el resultado final. Y en el cuerpo del método comprobaremos inmediatamente la relevancia del puntero recibido. Después crearemos varias variables locales para almacenar temporalmente los punteros a los objetos.
CBufferFloat *out_grad = Gradient; CBufferFloat *kv_g = KV_Tensors[KV_Tensors.Total() - 1]; CNeuronBaseOCL *ss = NULL, *sa = NULL;
Y organizaremos un ciclo para volver a pasar por las capas interiores.
for(int i = int(iLayers - 1); (i >= 0 && !IsStopped()); i--) { if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0) kv_g = KV_Tensors[(i / iLayersToOneKV) * 2 + 1];
Como ya sabemos, el algoritmo de distribución del gradiente de error es idéntico al de pasada directa, pero todas las operaciones se realizan en orden inverso. Por eso organizaremos un ciclo de iteración inversa en las capas internas de nuestro bloque.
Permítame recordarles que la segunda mitad de las operaciones del método de pasada directa repetirá por entero el bloque análogo de la clase padre. Por lo tanto, trasladaremos la primera mitad de nuestro método de distribución del gradiente de error desde el método análogo de la clase padre.
Primero distribuiremos el gradiente de error a través del bloque FeedForward.
//--- Passing gradient through feed forward layers if(IsStopped() || !ConvolutionInputGradients(FF_Weights[i * (optimization == SGD ? 6 : 9) + 2], out_grad, FF_Tensors[i * 6 + 1], FF_Tensors[i * 6 + 4], 4 * iWindow, iWindow, None)) return false; CBufferFloat *temp = FF_Tensors[i * 6 + 3]; if(IsStopped() || !ConvolutionInputGradients(FF_Weights[i * (optimization == SGD ? 6 : 9) + 1], FF_Tensors[i * 6 + 4], FF_Tensors[i * 6], temp, iWindow, 4 * iWindow, LReLU)) return false;
A continuación, sumaremos el gradiente de error de los dos flujos de información.
//--- Sum and normilize gradients if(IsStopped() || !SumAndNormilize(out_grad, temp, temp, iWindow, false)) return false;
Luego transmitiremos el gradiente de error por el bloque Multi-Head Self-Attention.
//--- Sum and normilize gradients if(IsStopped() || !SumAndNormilize(out_grad, temp, temp, iWindow, false)) return false; out_grad = temp; //--- Split gradient to multi-heads if(IsStopped() || !ConvolutionInputGradients(FF_Weights[i * (optimization == SGD ? 6 : 9)], out_grad, AO_Tensors[i * 2], AO_Tensors[i * 2 + 1], iWindowKey * iHeads, iWindow, None)) return false; //--- Passing gradient to query, key and value sa = cSceneAgnostic[i * 2 + 1]; ss = cSceneSpecific[i * 2 + 1]; if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0) { if(IsStopped() || !AttentionInsideGradients(QKV_Tensors[i * 2], QKV_Tensors[i * 2 + 1], KV_Tensors[(i / iLayersToOneKV) * 2], kv_g, S_Tensors[i * 2], AO_Tensors[i * 2 + 1])) return false; } else { if(IsStopped() || !AttentionInsideGradients(QKV_Tensors[i * 2], QKV_Tensors[i * 2 + 1], KV_Tensors[i / iLayersToOneKV * 2], GetPointer(Temp), S_Tensors[i * 2], AO_Tensors[i * 2 + 1])) return false; if(IsStopped() || !SumAndNormilize(kv_g, GetPointer(Temp), kv_g, iWindowKey, false, 0, 0, 0, 1)) return false; }
Aquí cabe destacar la distribución del gradiente de error en el tensor de entidades Key-Value. El matiz a considerar reside en la recopilación de los gradientes de error de todas las capas internas que se ven afectadas por un determinado tensor. El algoritmo se describe con más detalle en el artículo dedicado a la descripción de la clase padre.
A continuación, distribuiremos el gradiente de error al nivel de los datos de origen en el flujo de información principal.
CBufferFloat *inp = NULL; if(i == 0) { inp = prevLayer.getOutput(); temp = prevLayer.getGradient(); } else { temp = FF_Tensors.At(i * 6 - 1); inp = FF_Tensors.At(i * 6 - 4); } if(IsStopped() || !MatMulGrad(inp, temp, QKV_Weights[i * 2], QKV_Weights[i * 2 + 1], QKV_Tensors[i * 2 + 1], iUnits, iWindow, iHeads * iWindowKey, 1)) return false; //--- Sum and normilize gradients if(IsStopped() || !SumAndNormilize(out_grad, temp, temp, iWindow, false, 0, 0, 0, 1)) return false;
Y también transmitiremos el gradiente de error a las hiper-redes según su impacto en el resultado global del modelo.
//--- if((i % iLayersToOneKV) == 0) { if(IsStopped() || !MatMulGrad(inp, GetPointer(Temp), KV_Weights[i / iLayersToOneKV * 2], KV_Weights[i / iLayersToOneKV * 2 + 1], KV_Tensors[i / iLayersToOneKV * 2 + 1], iUnits, iWindow, 2 * iHeadsKV * iWindowKey, 1)) return false; if(IsStopped() || !SumAndNormilize(GetPointer(Temp), temp, temp, iWindow, false, 0, 0, 0, 1)) return false; if(!Concat(QKV_Weights[i * 2 + 1], KV_Weights[i / iLayersToOneKV * 2 + 1], ss.getGradient(), iHeads, 2 * iHeadsKV, iWindow * iWindowKey)) return false; if(!ElementMultGrad(ss.getOutput(), ss.getGradient(), sa.getOutput(), sa.getGradient(), ss.getGradient(), ss.Activation(), sa.Activation())) return false; } else { if(!ElementMultGrad(ss.getOutput(), ss.getGradient(), sa.getOutput(), sa.getGradient(), QKV_Weights[i * 2 + 1], ss.Activation(), sa.Activation())) return false; } if(i > 0) out_grad = temp; }
Después de eso, pasaremos a la siguiente iteración de nuestro ciclo de capa interna.
Nótese que en el ciclo del flujo principal de operaciones, solo transmitiremos el gradiente de error hasta el nivel de la hiper-red, pero no lo llevaremos más allá. Y aquí hay algunos momentos que debemos tener en cuenta. En primer lugar, nuestra hiper-red de conocimiento a priori independiente del estado de la escena consta solo de dos capas. La primera es estática y siempre contendrá un "1" en la salida, mientras que la segunda contendrá los parámetros a entrenar y retornará el resultado. En el flujo principal de operaciones, transmitiremos el gradiente de error a la última de ellas. Transmitir el gradiente de error hasta el nivel de la primera no tendrá sentido. Obviamente, se trata de un caso especial. Y con más capas en el hipermodelo, tendríamos que crear un algoritmo para transferir gradientes de error hasta todos los elementos con parámetros de aprendizaje.
El segundo momento se refiere a la construcción del algoritmo para el funcionamiento de un hipermodelo sensible al contexto y dependiente de la escena. En esta implementación, todos los parámetros se generarán a partir de la descripción inicial de la escena que transmite el programa que realiza la llamada. En consecuencia, también deberemos transmitir el gradiente de error completo al nivel especificado. Para no perturbar el flujo general de información, hemos decidido sacar la distribución del gradiente de este modelo a un ciclo separado. Pero, nuevamente, este es nuestro caso particular. Si tuviéramos una fuente diferente de descripción de la escena (por ejemplo, el resultado de la capa interior anterior), también deberíamos pasar el gradiente de error a la capa correspondiente.
Pero volvamos al algoritmo de nuestro método de distribución del gradiente de error. Tras ejecutar el ciclo de iteración inversa de las capas internas, escribiremos los valores de la influencia de los datos de entrada sobre el resultado del modelo en el flujo principal de operaciones en el búfer de gradiente de error de la capa anterior. Y ahora tendremos que añadir aquí el gradiente de error de las hiper-redes. Para ello, primero almacenaremos el puntero al objeto de búfer de gradiente de la capa anterior en una variable local. Y transmitiremos temporalmente al objeto de capa el puntero a nuestro búfer auxiliar de datos.
CBufferFloat *inp_grad = prevLayer.getGradient(); if(!prevLayer.SetGradient(GetPointer(Temp), false)) return false;
Ahora podremos pasar el gradiente de error al nivel de la capa anterior sin temor a perder los datos almacenados previamente. Luego organizaremos un ciclo de enumeración de objetos de nuestra hiper-red dependiente del contexto, en cuyo cuerpo haremos descender el gradiente de error al nivel de la capa de datos de origen. Y en cada iteración, añadiremos el resultado actual al gradiente acumulado anteriormente.
for(int i = int(iLayers - 2); (i >= 0 && !IsStopped()); i -= 2) { ss = cSceneSpecific[i]; if(IsStopped() || !ss.calcHiddenGradients(cSceneSpecific[i + 1])) return false; if(IsStopped() || !prevLayer.calcHiddenGradients(ss, NULL)) return false; if(IsStopped() || !SumAndNormilize(prevLayer.getGradient(), inp_grad, inp_grad, iWindow, false, 0, 0, 0, 1)) return false; }
Y tras ejecutar con éxito las operaciones del ciclo devolveremos al objeto de la capa anterior el puntero a su búfer con el gradiente de error ya acumulado de todos los flujos de información.
if(!prevLayer.SetGradient(inp_grad, false)) return false; //--- return true; }
El gradiente de error estará totalmente distribuido, así que retornaremos al programa que realiza la llamada el resultado lógico de las operaciones de nuestro método de distribución del gradiente de error. Le sugiero que se familiarice con el método de actualización de los parámetros del modelo. Encontrará el código completo de esta clase y todos sus métodos en el archivo adjunto.
2.3 Construcción del algoritmo HyperDet3D holístico
Más arriba hemos construido los bloques individuales del algoritmo HyperDet3D analizado. Ahora es el momento de reunirlo todo en una estructura coherente. Debemos decir que, por un lado, esto es bastante sencillo. Por otra parte, es un proceso no carente de matices.
Como parte de este experimento, hemos decidido utilizar el algoritmo Pointformer comentado en el artículo anterior, en el que sustituimos el bloque de atención global por un módulo MSA. No es una operación complicada. Además, hemos dejado los parámetros de todos los métodos sin cambios, incluido el método de inicialización de la clase, salvo que declararemos todos los objetos de la clase CNeuronPointFormer estáticamente. Y ahora no podremos heredar con un cambio de tipo de objetos individuales. Así que crearemos una copia de la clase en la que cambiaremos el tipo de objetos que necesitamos. A continuación, le mostramos la estructura de la nueva clase,
class CNeuronHyperDet : public CNeuronPointNet2OCL { protected: CNeuronMLMHSparseAttention caLocalAttention[2]; CNeuronMLCrossAttentionMLKV caLocalGlobalAttention[2]; CNeuronMLMHSceneConditionAttention caGlobalAttention[2]; CNeuronLearnabledPE caLocalPE[2]; CNeuronLearnabledPE caGlobalPE[2]; CNeuronBaseOCL cConcatenate; CNeuronConvOCL cScale; //--- CBufferFloat *cbTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override ; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronHyperDet(void) {}; ~CNeuronHyperDet(void) { delete cbTemp; } //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint output, bool use_tnets, ENUM_OPTIMIZATION optimization_type, uint batch) override; //--- virtual int Type(void) override const { return defNeuronHyperDet; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
No nos detendremos en los algoritmos de los métodos de esta clase, ya que todos los métodos se crean copiando directamente los métodos correspondientes de la clase CNeuronPointFormer.
La arquitectura de los modelos y todos los programas para interactuar con el entorno y entrenar a los modelos también los hemos tomado prestados del artículo anterior. Por lo tanto, no nos detendremos en ellos. Pues bien, en el archivo adjunto le presentamos el código completo de todos los programas utilizados en la elaboración de este artículo.
3. Simulación
Hoy hemos realizado un extenso trabajo para poner en práctica nuestra visión de los enfoques propuestos por los autores del método HyperDet3D. Ahora es momento de pasar a la parte final de nuestro artículo. Aquí realizaremos el entrenamiento y las pruebas de los modelos que usan los enfoques propuestos.
Al igual que antes, para entrenar los modelos utilizaremos los datos históricos reales del instrumento EURUSD para todo el año 2023 con el marco temporal H1. Los parámetros de todos los indicadores analizados se han usado por defecto. El proceso de aprendizaje también será totalmente coherente con el algoritmo descrito en el artículo anterior. Por consiguiente, solo nos centraremos en los resultados de las pruebas de la política de Actor entrenado, que se presentan a continuación.
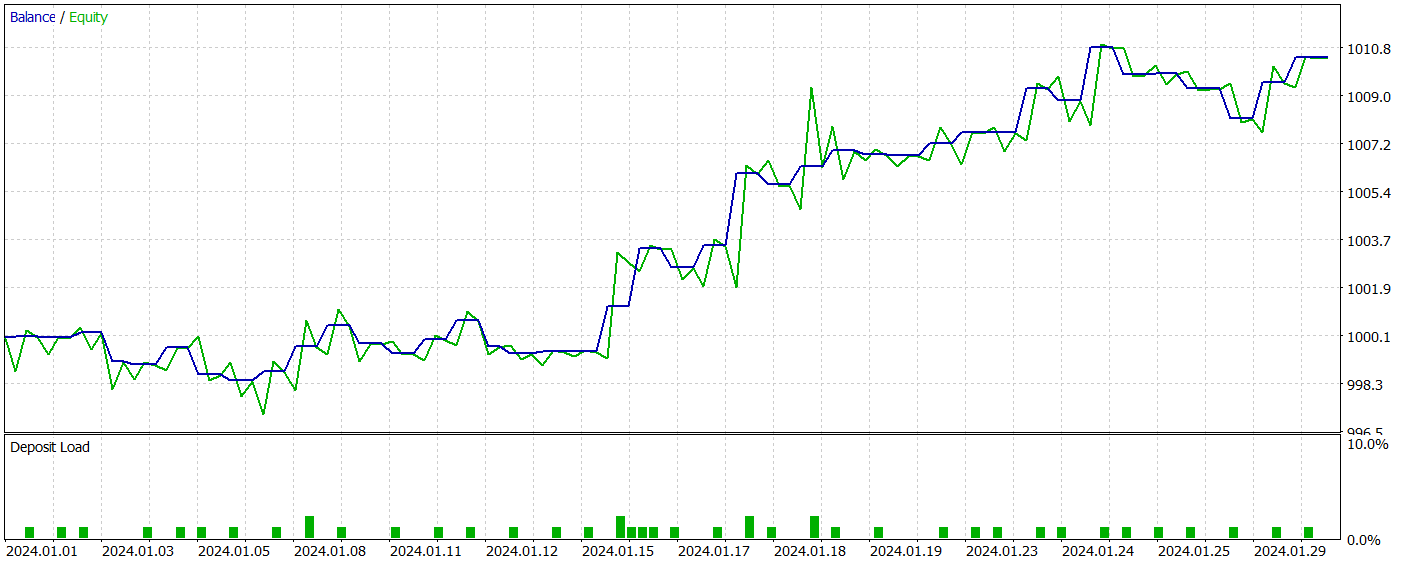
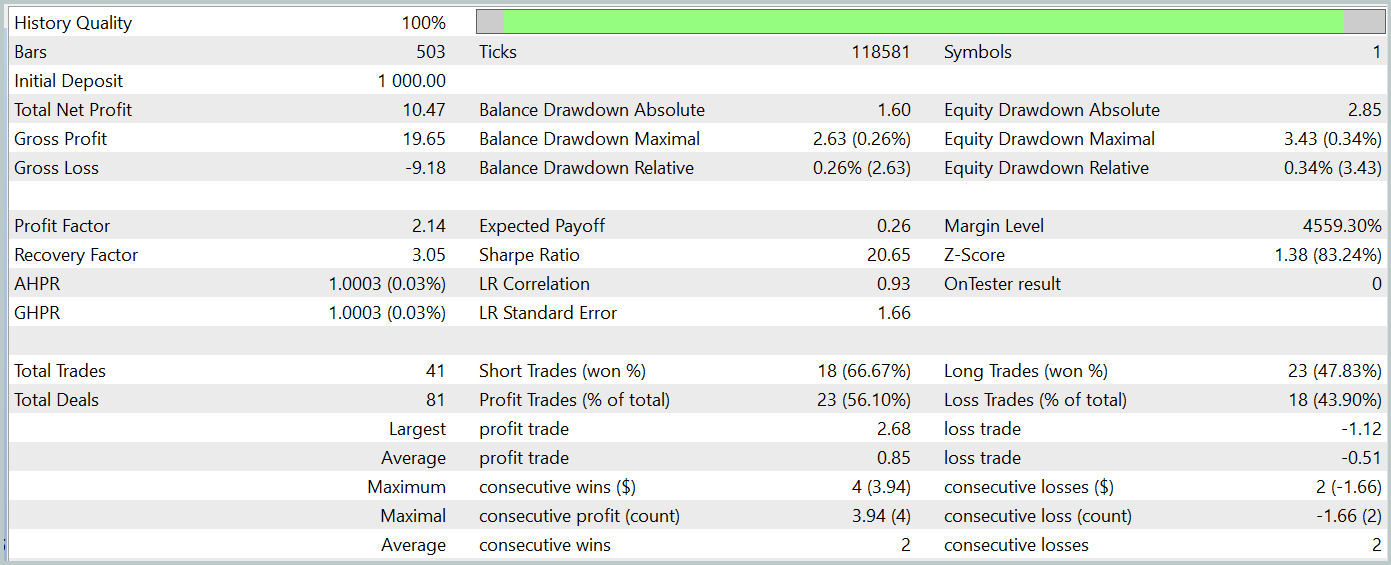
El modelo entrenado se ha probado con datos históricos de enero de 2024 que no formaban parte de la muestra de entrenamiento. Y durante el periodo de prueba, el modelo ha realizado 41 transacciones, el 56% de las cuales se cerraron con beneficios. Así, la transacción rentable máxima supera a la pérdida máxima en 2,4 veces, mientras que la transacción rentable media supera al mismo indicador de transacciones deficitarias en un 67%. Todo ello ha permitido fijar el factor de beneficio en el nivel de 2,14, mientras que el ratio de Sharpe ha alcanzado la marca de 20,65.
En general, durante el periodo de prueba el modelo ha obtenido un 1% de beneficios, mientras que la reducción máxima de la RV no ha superado el 0,34%. Y la reducción del balance ha sido aún menor. En el gráfico, podemos ver un crecimiento bastante uniforme del balance, y la carga del depósito no supera el 1-2%.
La impresión general de los resultados obtenidos es buena: el modelo tiene potencial, pero el corto periodo de las pruebas y el reducido número de transacciones realizadas no nos permiten hablar de la estabilidad del modelo a largo plazo. Antes de usar el modelo en el trabajo real, todavía tenemos que entrenarlo con un conjunto más largo de datos históricos y realizar pruebas exhaustivas.
Conclusión
En este artículo, hemos presentado el método HyperDet3D, que utiliza hiper-redes basadas en escenas para integrar el conocimiento a priori en la arquitectura del Transformer. Esto permite adaptar eficazmente el modelo a diferentes escenas para la tarea de detección de objetos, lo cual mejora la calidad del reconocimiento al ajustar dinámicamente los parámetros del detector según la información de la escena, haciendo que el sistema resulte más versátil y potente.
En la parte práctica de nuestro trabajo, hemos implementado nuestra visión de los enfoques propuestos utilizando herramientas MQL5 y los hemos implementado en la estructura de nuestro modelo. Las pruebas realizadas demuestran el potencial del modelo. Sin embargo, aún nos queda trabajo por hacer antes de que pueda aplicarse en los mercados financieros.
Enlaces
Programas utilizados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 5 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 6 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15859
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Del básico al intermedio: Unión (I)
Del básico al intermedio: Unión (I)
 Uso conjunto de PSAR, Heiken Ashi y Deep Learning para el trading
Uso conjunto de PSAR, Heiken Ashi y Deep Learning para el trading
 Del básico al intermedio: Unión (II)
Del básico al intermedio: Unión (II)
 Algoritmo de tiro con arco - Archery Algorithm (AA)
Algoritmo de tiro con arco - Archery Algorithm (AA)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso