
Population optimization algorithms
"Nothing at all takes place in the universe
in which some rule of maximum or minimum does not appear"
Leonhard Euler, 18th century
Contents:
- Historical perspective
- OA classification
- Convergence and rate of convergence. Convergence stability. Optimization algorithm scalability
- Test functions, construction of a complex OA evaluation criterion
- Test stand
- Simple OA using RNG
- Results
1. Historical perspective
Optimization algorithms are algorithms that allow finding extreme points in a function domain, at which the function reaches its minimum or maximum value.
The ancient Greek pundits of antiquity already knew that:
— Of all the shapes with a given perimeter, the circle has the largest area.
— Of all polygons with a given number of sides and a given perimeter, a regular polygon has the largest area.
— Of all three-dimensional figures having a given area, the sphere has the largest volume.
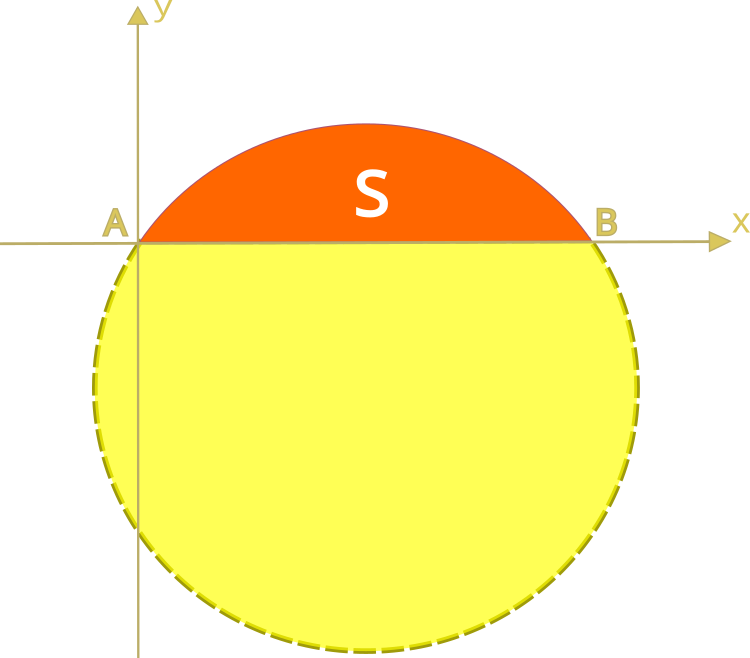
The first problem having variational solutions was proposed around the same time as well. According to the legend, this happened around 825 BC. Dido, the sister of the king of the Phoenician city of Tyre, has moved to the southern coast of the Mediterranean Sea and asked a local tribe for a piece of land that could be covered with a bull hide. The locals gave her a hide. The resourceful girl cut it into narrow belts and tied them making a rope. With this rope, she covered the territory off the coast and founded the city of Carthage there.
The problem lies in finding the most efficient curve, covering the maximum surface area, among closed plane curves of a given length. The maximum area in this problem is represented by the area circumsribed by a semicircle.
Now let's skip a huge chunk of history, including the ancient culture of the Mediterranean, oppression of the Inquisition and quackery of the Middle Ages, up to the Renaissance with its free flight of thought and new theories. In June 1696, Johann Bernoulli publishes the following text for the readers of Acta Eruditorum: "I, Johann Bernoulli, address the most brilliant mathematicians in the world. Nothing is more attractive to intelligent people than an honest, challenging problem, whose possible solution will bestow fame and remain as a lasting monument. Following the example set by Pascal, Fermat, etc., I hope to gain the gratitude of the whole scientific community by placing before the finest mathematicians of our time a problem which will test their methods and the strength of their intellect. If someone communicates to me the solution of the proposed problem, I shall publicly declare him worthy of praise".
Johann Bernulli's brachistochrone problem:
"Given two points A and B in a vertical plane, what is the curve traced out by a point acted on only by gravity, which starts at A and reaches B in the shortest time". Remarkably, Galileo tried to solve a similar problem back in 1638, long before the Bernoulli's publication. The answer: the fastest path of all, from one point to another, is not the shortest path, as it seems at first glance, not a straight line, but a curve — a cycloid that determines the curvature of the curve at each point.
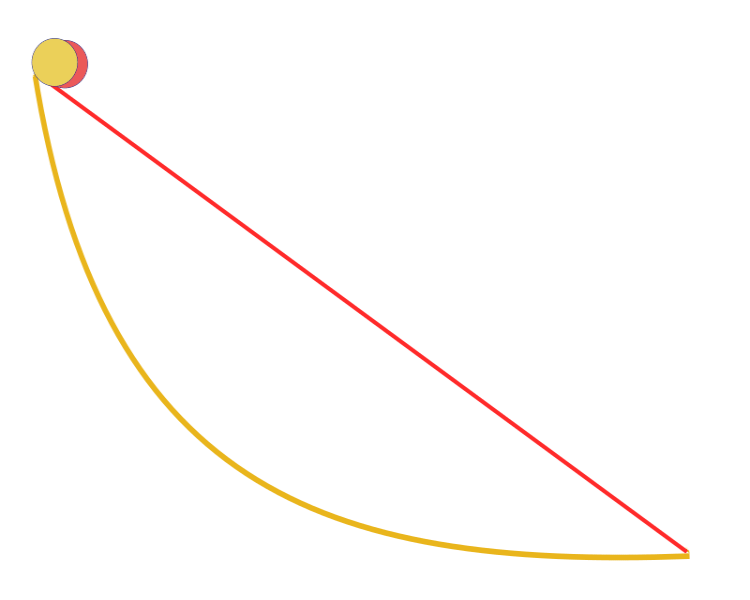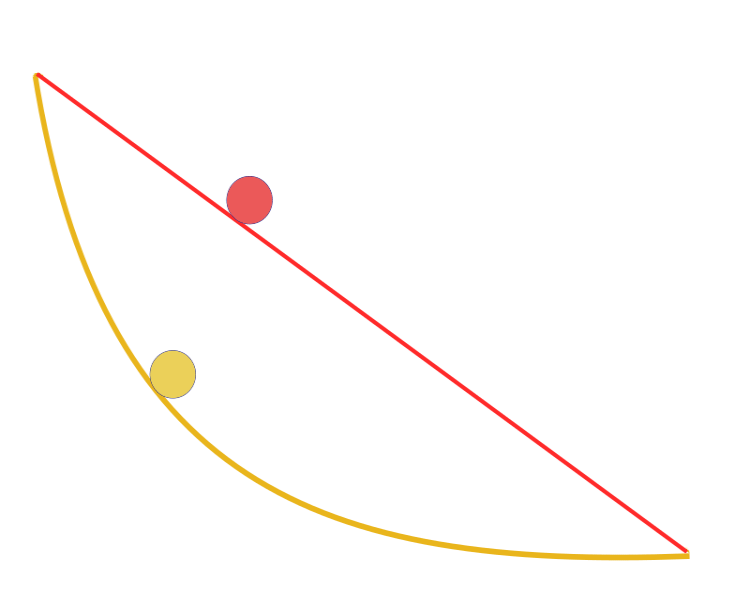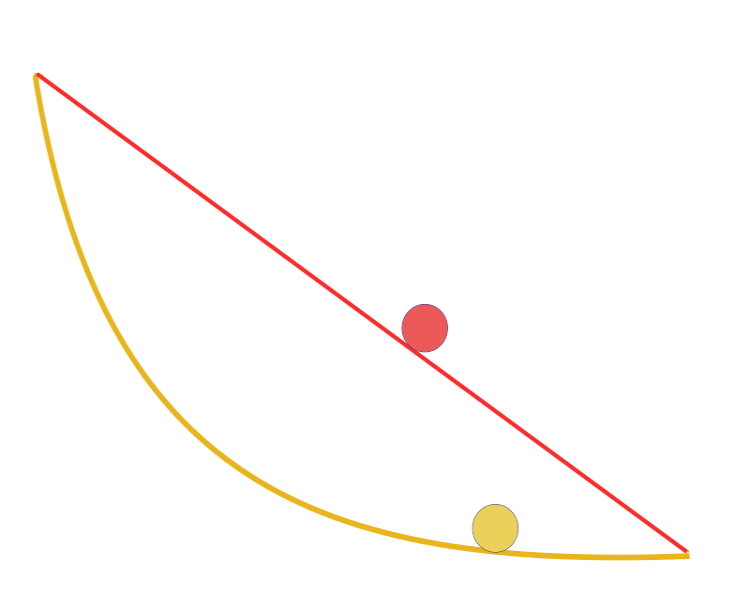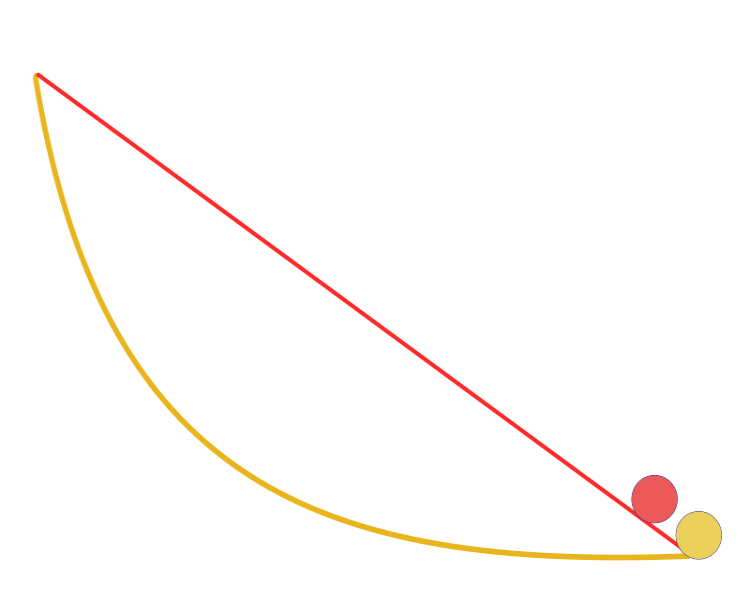
Brachistochrone curve
All other solutions, including Newton's (which were not revealed at the time), are based on finding the gradient at each point. The method behind the solution proposed by Isaac Newton forms the basis of the variational calculation. The methods of the variational calculation are usually applied in solving problems, in which the optimality criteria are presented in the form of functionals and whose solutions are unknown functions. Such problems usually arise in the static optimization of processes with distributed parameters or in dynamic optimization problems.
First-order extremum conditions in the variational calculation were obtained by Leonard Euler and Joseph Lagrange (the Euler-Lagrange equations). These equations are widely used in optimization problems and, together with the stationary-action principle, are applied in calculations of trajectories in mechanics. Soon, however, it became clear that the solutions of these equations do not always give a real extremum, which means that sufficient conditions guaranteeing its finding are required. The work was continued and second-order extremum conditions were derived by Legendre and Jacobi, and then by the student of the latter - Hesse. The question of the existence of a solution in the variational calculation was first raised by Weierstrass in the second half of the 19th century.
By the second half of the 18th century, the search for optimal solutions to the problems formed the mathematical foundations and principles of optimization. Unfortunately, optimization methods actually had little use in many areas of science and technology until the second half of the 20th century, since the practical use of mathematical methods required huge computing resources. The advent of new computing technologies in the modern world has finally made it possible to implement complex optimization methods giving rise to a great variety of available algorithms.
The 1980s saw the start of the intensive development of the class of stochastic optimization algorithms, which were the result of modeling borrowed from nature.
2. OA classification
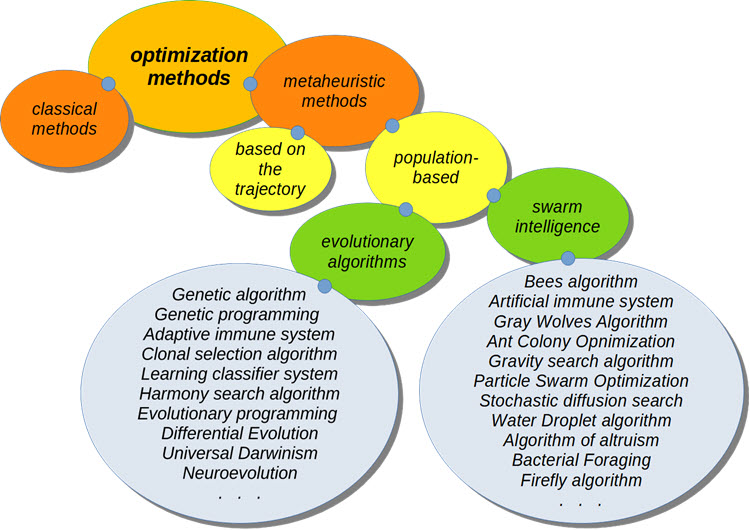
Classification AO
When optimizing trading systems, the most exciting things are metaheuristic optimization algorithms. They do not require knowledge of the formula of the function being optimized. Their convergence to the global optimum has not been proven, but it has been experimentally established that in most cases they give a fairly good solution and this is sufficient for a number of problems.
A lot of OAs appeared as models borrowed from nature. Such models are also called behavioral, swarming or population, such as the behavior of birds in a flock (the particle swarm algorithm) or the principles of the ant colony behavior (ant algorithm).
Population algorithms involve the simultaneous handling of several options for solving the optimization problem and represent an alternative to classical algorithms based on motion trajectories whose search area has only one candidate evolving when solving the problem.
3. Convergence and rate of convergence. Convergence stability. Optimization algorithm scalability
Efficiency, speed, convergence, as well as the effects of the problem conditions and algorithm parameters require careful analysis for each algorithmic implementation and for each class of optimization problems.
3.1) Convergence and rate of convergence
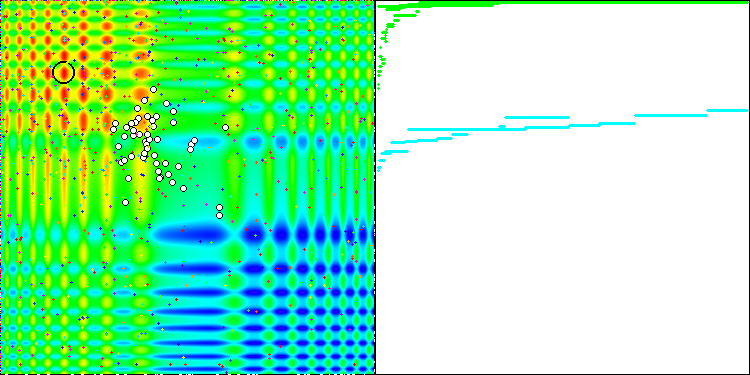
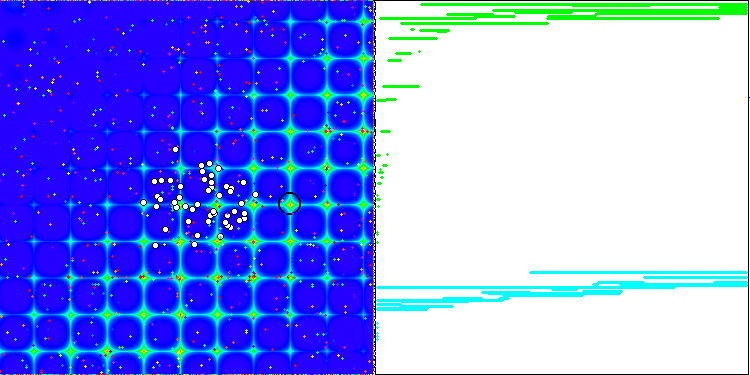
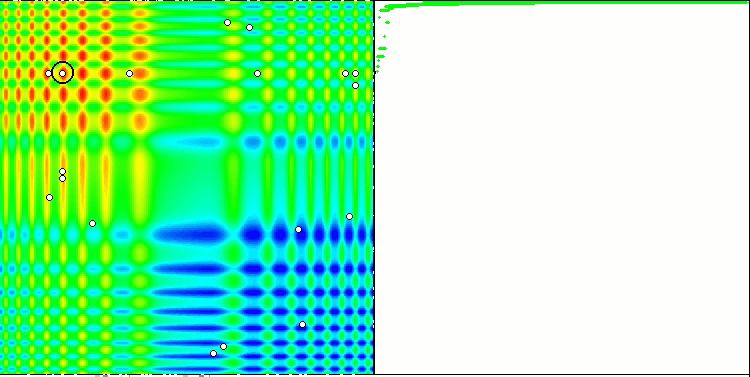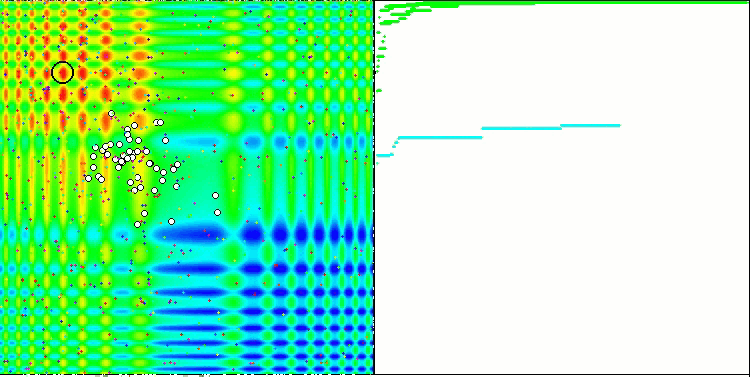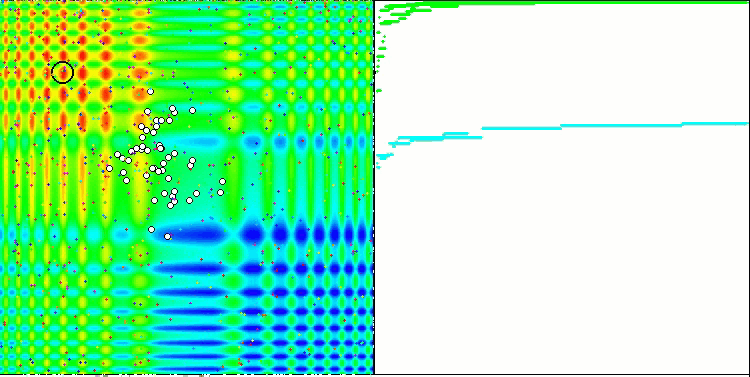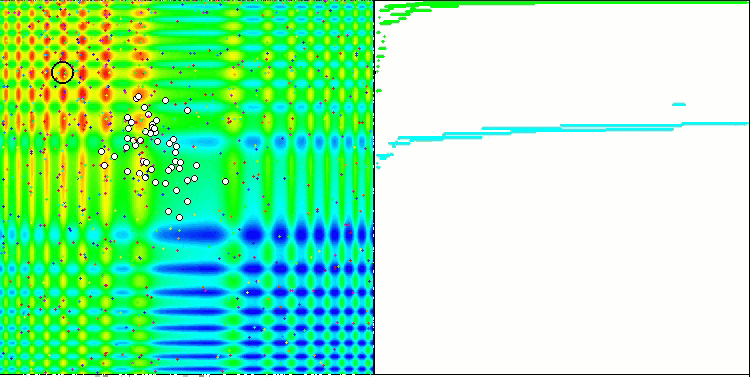
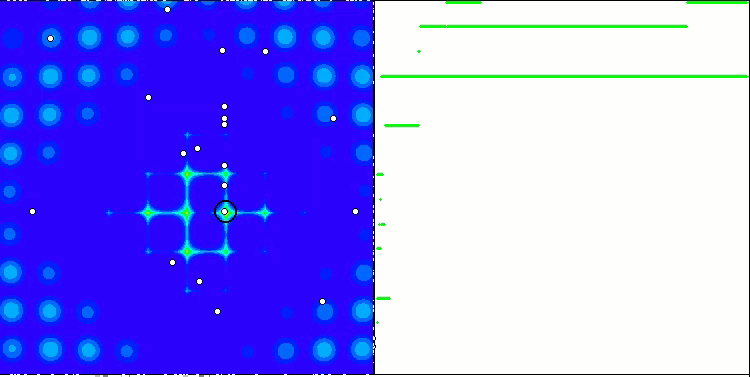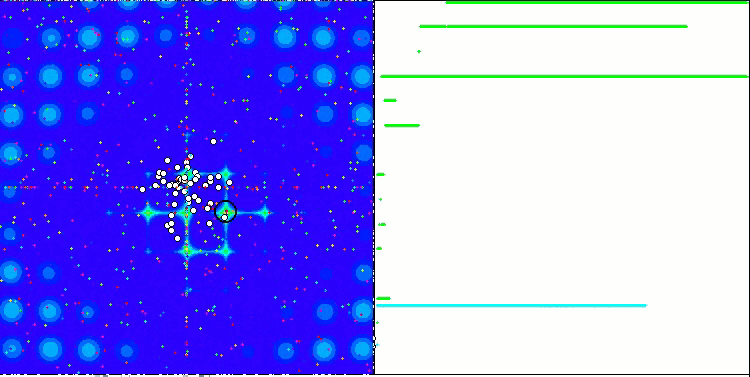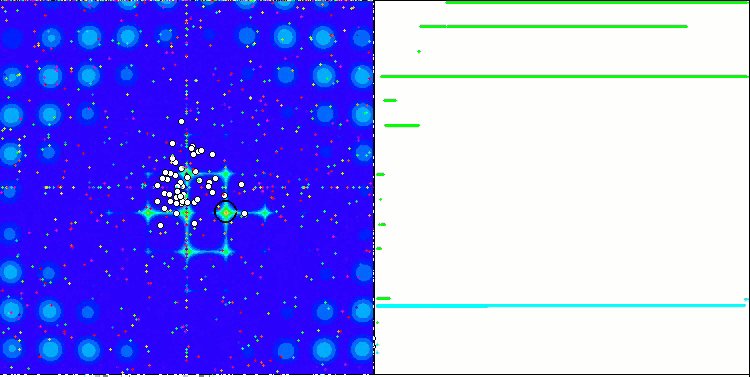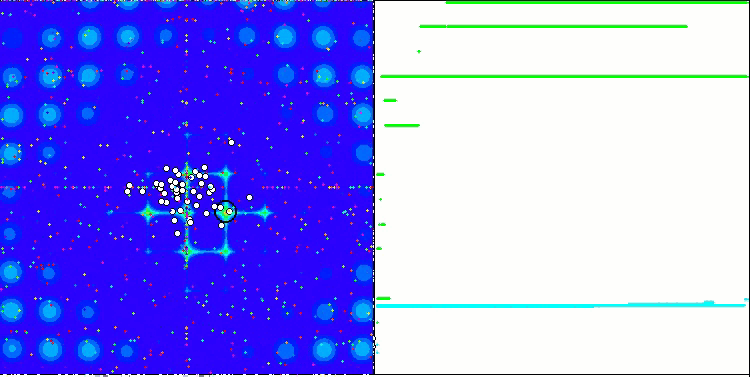
The property of an iterative algorithm to reach the optimum of the objective function or to come close enough to it in a finite number of steps. On the right side of the screenshots above, we see an iteratively constructed graph of the results yielded by the calculated test function. Based on these two images, we can conclude that the convergence is affected by the complexity of the function surface. The more complex it is, the more difficult it is to find the global extremum.
The rate of the algorithms' convergence is one of the most important indicators of the quality of an optimization algorithm and is one of the main characteristics of optimization methods. When we hear that one algorithm is faster than another, in most cases this means the rate of convergence. The closer the result is to the global extremum and the faster it is obtained (meaning the earlier iterations of the algorithm), the higher this parameter. Note that the rate of convergence of methods usually does not exceed the quadratic one. In rare cases, the method may have a cubic rate of convergence.
3.2) Convergence stability
The number of iterations required to achieve the result depends not only on the search ability of the algorithm itself, but also on the function under study. If the function is characterized by a high complexity of the surface (the presence of sharp bends, discreteness, discontinuities), then the algorithm may turn out to be unstable and unable to provide acceptable accuracy at all. In addition, the stability of convergence can be understood as the repeatability of optimization results when several consecutive tests are carried out. If the results have high discrepancies in values, then the stability of the algorithm is low.
3.3) Optimization algorithm scalability
Optimization algorithm scalability is the ability to maintain convergence with an increase in the dimension of the problem. In other words, with an increase in the number of variables of the optimized function, convergence should remain at a level acceptable for practical purposes. Population algorithms of search optimization have undeniable advantages in comparison with classical algorithms, especially when solving high dimension and poorly formalized problems. Under these conditions, population algorithms can provide a high probability of localizing the global extremum of the function being optimized.
In the case of a smooth and unimodal optimized function, population algorithms are generally less efficient than any classical gradient method. Also, the disadvantages of population algorithms include a strong dependence of their efficiency on the degrees of freedom (the number of tuning parameters), which are quite numerous in most algorithms.
4. Test functions, construction of a complex OA evaluation criterion
There is no generally accepted methodology for testing and comparing optimization algorithms. However, there are many test functions proposed by researchers in different years. We will use the functions that I created before positng the first article. These functions can be found in the terminal folder \MQL5\Experts\Examples\Math 3D\Functions.mqh and \MQL5\Experts\Examples\Math 3D Morpher\Functions.mqh. These functions meet all the complexity criteria for OA testing. Additionally, the Forest and Megacity functions have been developed to provide a more comprehensive study of the OA search capabilities.
Skin test function:
![]()
The function is smooth throughout its domain and has many local max/min values that differ insignificantly (convergence traps), which cause algorithms that do not reach the global extremum to get stuck.
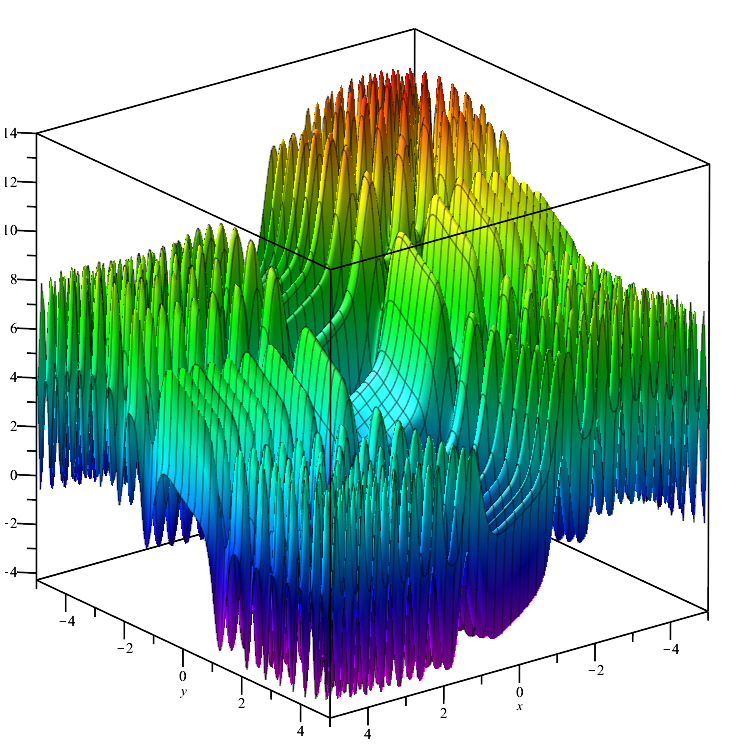
Skin
Forest test function:
![]()
The function represents several maximums that do not have a differential at their points. Therefore, it may tun out to be difficult for optimization algorithms, the robustness of which is critically dependent on the smoothness of the function under study.
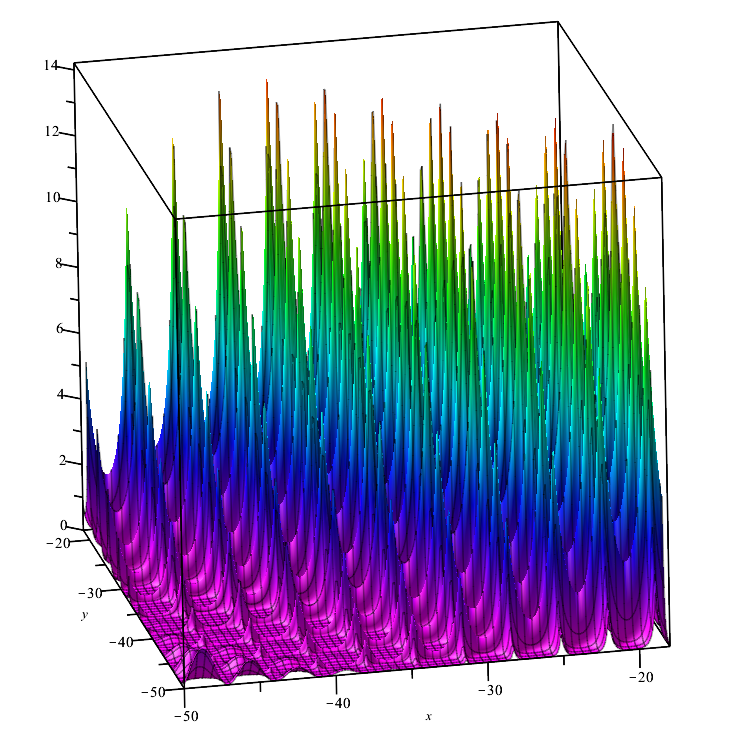
Forest
Megacity test function:
![]()
A discrete function that forms "areas" (where changing the variables does not lead to a significant change in the value of the function). Therefore, it poses a difficulty for algorithms that require a gradient.
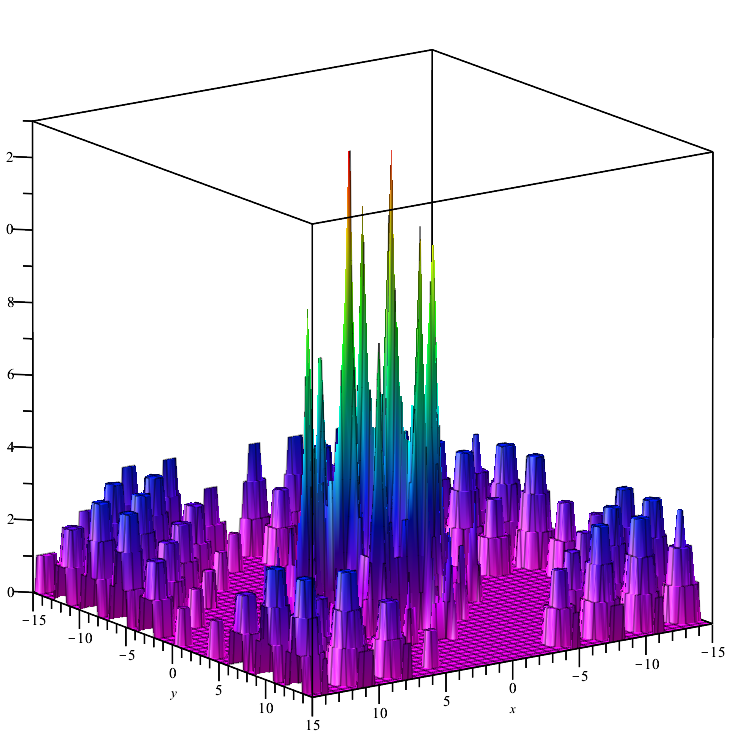
Megacity
5. Test stand
For a comprehensive comparison of optimization algorithms, an attempt was made to create a general evaluation criterion. The complexity of this idea lies in the fact that it is not clear how to compare algorithms, because each of them is good in its own way for the corresponding class of problems. For example, one algorithm converges quickly but does not scale well, while another scales well but is unstable.
- Convergence: To study convergence, we use three functions presented above. Their maximum and minimum are converted to a range from 0.0 (worst result) to 1.0 (best result), which will allow us to evaluate the ability of algorithms to ensure convergence on different types of problems.
- Convergence rate: The best results of the algorithm are measured at the 1000th and 10,000th run of the tested function. Thus, we can see how fast the OA converges. The faster the convergence, the more curved the convergence graph will be towards the maximum.
- Stability: Make five optimization runs for each of the functions and calculate the average value in the range from 0.0 to 1.0. This is necessary because the results of some algorithms can vary greatly from run to run. The higher the convergence in each of the five tests, the higher the stability.
- Scalability: Some OAs can only show practical results on functions with a small number of variables, for example, no more than two, and some are not even able to work with more than one variable. In addition, there are algorithms capable of working with functions with a thousand variables. Such optimization algorithms can be used as OA for neural networks.
For the convenience of using test functions, let's write a parent class and an enumerator that will allow us to select an object of the child class of the corresponding test function in the future:
//—————————————————————————————————————————————————————————————————————————————— class C_Function { public: //==================================================================== double CalcFunc (double &args [], //function arguments int amount) //amount of runs functions { double x, y; double sum = 0.0; for (int i = 0; i < amount; i++) { x = args [i * 2]; y = args [i * 2 + 1]; sum += Core (x, y); } sum /= amount; return sum; } double GetMinArg () { return minArg;} double GetMaxArg () { return maxArg;} double GetMinFun () { return minFun;} double GetMaxFun () { return maxFun;} string GetNamFun () { return fuName;} protected: //================================================================== void SetMinArg (double min) { minArg = min;} void SetMaxArg (double max) { maxArg = max;} void SetMinFun (double min) { minFun = min;} void SetMaxFun (double max) { maxFun = max;} void SetNamFun (string nam) { fuName = nam;} private: //==================================================================== virtual double Core (double x, double y) { return 0.0;} double minArg; double maxArg; double minFun; double maxFun; string fuName; }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— enum EFunc { Skin, Forest, Megacity, }; C_Function *SelectFunction (EFunc f) { C_Function *func; switch (f) { case Skin: func = new C_Skin (); return (GetPointer (func)); case Forest: func = new C_Forest (); return (GetPointer (func)); case Megacity: func = new C_Megacity (); return (GetPointer (func)); default: func = new C_Skin (); return (GetPointer (func)); } } //——————————————————————————————————————————————————————————————————————————————
Then the child classes will look like this:
//—————————————————————————————————————————————————————————————————————————————— class C_Skin : public C_Function { public: //=================================================================== C_Skin () { SetNamFun ("Skin"); SetMinArg (-5.0); SetMaxArg (5.0); SetMinFun (-4.3182); //[x=3.07021;y=3.315935] 1 point SetMaxFun (14.0606); //[x=-3.315699;y=-3.072485] 1 point } private: //=================================================================== double Core (double x, double y) { double a1=2*x*x; double a2=2*y*y; double b1=MathCos(a1)-1.1; b1=b1*b1; double c1=MathSin(0.5*x)-1.2; c1=c1*c1; double d1=MathCos(a2)-1.1; d1=d1*d1; double e1=MathSin(0.5*y)-1.2; e1=e1*e1; double res=b1+c1-d1+e1; return(res); } }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— class C_Forest : public C_Function { public: //=================================================================== C_Forest () { SetNamFun ("Forest"); SetMinArg (-50.0); SetMaxArg (-18.0); SetMinFun (0.0); //many points SetMaxFun (15.95123239744); //[x=-25.132741228718345;y=-32.55751918948773] 1 point } private: //=================================================================== double Core (double x, double y) { double a = MathSin (MathSqrt (MathAbs (x - 1.13) + MathAbs (y - 2.0))); double b = MathCos (MathSqrt (MathAbs (MathSin (x))) + MathSqrt (MathAbs (MathSin (y - 2.0)))); double f = a + b; double res = MathPow (f, 4); if (res < 0.0) res = 0.0; return (res); } }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— class C_Megacity : public C_Function { public: //=================================================================== C_Megacity () { SetNamFun ("Megacity"); SetMinArg (-15.0); SetMaxArg (15.0); SetMinFun (0.0); //many points SetMaxFun (15.0); //[x=`3.16;y=1.990] 1 point } private: //=================================================================== double Core (double x, double y) { double a = MathSin (MathSqrt (MathAbs (x - 1.13) + MathAbs (y - 2.0))); double b = MathCos (MathSqrt (MathAbs (MathSin (x))) + MathSqrt (MathAbs (MathSin (y - 2.0)))); double f = a + b; double res = floor (MathPow (f, 4)); return (res); } }; //——————————————————————————————————————————————————————————————————————————————
To check the validity of the OA testing results obtained on the test stand, we can use a script that enumerates the X and Y functions with the Step step size. Take care when choosing the step, as a very small step size will cause the calculation to take too long. For example, the Skin function has the range of arguments [-5;5]. With the step of 0.00001 along the X axis, it will be (5-(-5))/0.00001=1'000'000 (million) steps, the same number along the Y axis, respectively, the total number of runs of the test function to calculate the value in each of the points will be equal to 1'000'000 х 1'000'000= 1'000'000'000'000 (10^12, trillion).
It is necessary to understand how difficult the task is for OA, since it is required to find the maximum in just 10,000 steps (approximately this value is used in the MetaTrader 5 optimizer). Please note that this calculation is made for a function with two variables, and the maximum number of variables that will be used in tests is 1000.
Keep in mind the following: the algorithm tests in this and subsequent articles use the step of 0.0! or the minimum possible one for a specific implementation of the corresponding OA.
//—————————————————————————————————————————————————————————————————————————————— input EFunc Function = Skin; input double Step = 0.01; //—————————————————————————————————————————————————————————————————————————————— void OnStart () { C_Function *TestFunc = SelectFunction (Function); double argMin = TestFunc.GetMinArg (); double argMax = TestFunc.GetMaxArg (); double maxFuncValue = 0; double xMaxFunc = 0.0; double yMaxFunc = 0.0; double minFuncValue = 0; double xMinFunc = 0.0; double yMinFunc = 0.0; double fValue = 0.0; double arg [2]; arg [0] = argMin; arg [1] = argMin; long cnt = 0; while (arg [1] <= argMax && !IsStopped ()) { arg [0] = argMin; while (arg [0] <= argMax && !IsStopped ()) { cnt++; fValue = TestFunc.CalcFunc (arg, 1); if (fValue > maxFuncValue) { maxFuncValue = fValue; xMaxFunc = arg [0]; yMaxFunc = arg [1]; } if (fValue < minFuncValue) { minFuncValue = fValue; xMinFunc = arg [0]; yMinFunc = arg [1]; } arg [0] += Step; if (cnt == 1) { maxFuncValue = fValue; minFuncValue = fValue; } } arg [1] += Step; } Print ("======", TestFunc.GetNamFun (), ", launch counter: ", cnt); Print ("MaxFuncValue: ", DoubleToString (maxFuncValue, 16), " X: ", DoubleToString (xMaxFunc, 16), " Y: ", DoubleToString (yMaxFunc, 16)); Print ("MinFuncValue: ", DoubleToString (minFuncValue, 16), " X: ", DoubleToString (xMinFunc, 16), " Y: ", DoubleToString (yMinFunc, 16)); delete TestFunc; } //——————————————————————————————————————————————————————————————————————————————
Let's write a test stand:
#include <Canvas\Canvas.mqh> #include <\Math\Functions.mqh> #include "AO_RND.mqh" //—————————————————————————————————————————————————————————————————————————————— input int Population_P = 50; input double ArgumentStep_P = 0.0; input int Test1FuncRuns_P = 1; input int Test2FuncRuns_P = 20; input int Test3FuncRuns_P = 500; input int Measur1FuncValue_P = 1000; input int Measur2FuncValue_P = 10000; input int NumberRepetTest_P = 5; input int RenderSleepMsc_P = 0; //—————————————————————————————————————————————————————————————————————————————— int WidthMonitor = 750; //monitor screen width int HeighMonitor = 375; //monitor screen height int WidthScrFunc = 375 - 2; //test function screen width int HeighScrFunc = 375 - 2; //test function screen height CCanvas Canvas; //drawing table C_AO_RND AO; //AO object C_Skin SkiF; C_Forest ForF; C_Megacity ChiF; struct S_CLR { color clr []; }; S_CLR FunctScrin []; //two-dimensional matrix of colors double ScoreAll = 0.0; //—————————————————————————————————————————————————————————————————————————————— void OnStart () { //creating a table ----------------------------------------------------------- string canvasName = "AO_Test_Func_Canvas"; if (!Canvas.CreateBitmapLabel (canvasName, 5, 30, WidthMonitor, HeighMonitor, COLOR_FORMAT_ARGB_RAW)) { Print ("Error creating Canvas: ", GetLastError ()); return; } ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false); ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true); ArrayResize (FunctScrin, HeighScrFunc); for (int i = 0; i < HeighScrFunc; i++) { ArrayResize (FunctScrin [i].clr, HeighScrFunc); } //============================================================================ //Test Skin################################################################### Print ("============================="); CanvasErase (); FuncTests (SkiF, Test1FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrLime); FuncTests (SkiF, Test2FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrAqua); FuncTests (SkiF, Test3FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrOrangeRed); //Test Forest################################################################# Print ("============================="); CanvasErase (); FuncTests (ForF, Test1FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrLime); FuncTests (ForF, Test2FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrAqua); FuncTests (ForF, Test3FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrOrangeRed); //Test Megacity############################################################# Print ("============================="); CanvasErase (); FuncTests (ChiF, Test1FuncRuns_P, ChiF.GetMinFun (), ChiF.GetMaxFun (), 3.16, 1.990, clrLime); FuncTests (ChiF, Test2FuncRuns_P, ChiF.GetMinFun (), ChiF.GetMaxFun (), 3.16, 1.990, clrAqua); FuncTests (ChiF, Test3FuncRuns_P, ChiF.GetMinFun (), ChiF.GetMaxFun (), 3.16, 1.990, clrOrangeRed); Print ("All score for C_AO_RND: ", ScoreAll / 18.0); } //—————————————————————————————————————————————————————————————————————————————— void CanvasErase () { Canvas.Erase (XRGB (0, 0, 0)); Canvas.FillRectangle (1, 1, HeighMonitor - 2, HeighMonitor - 2, COLOR2RGB (clrWhite)); Canvas.FillRectangle (HeighMonitor + 1, 1, WidthMonitor - 2, HeighMonitor - 2, COLOR2RGB (clrWhite)); } //—————————————————————————————————————————————————————————————————————————————— void FuncTests (C_Function &f, int funcCount, double minFuncVal, double maxFuncVal, double xBest, double yBest, color clrConv) { DrawFunctionGraph (f.GetMinArg (), f.GetMaxArg (), minFuncVal, maxFuncVal, f); SendGraphToCanvas (1, 1); int x = (int)Scale (xBest, f.GetMinArg (), f.GetMaxArg (), 0, WidthScrFunc - 1, false); int y = (int)Scale (yBest, f.GetMinArg (), f.GetMaxArg (), 0, HeighScrFunc - 1, false); Canvas.Circle (x + 1, y + 1, 10, COLOR2RGB (clrBlack)); Canvas.Circle (x + 1, y + 1, 11, COLOR2RGB (clrBlack)); Canvas.Update (); Sleep (1000); int xConv = 0.0; int yConv = 0.0; int EpochCmidl = 0; int EpochCount = 0; double aveMid = 0.0; double aveEnd = 0.0; //---------------------------------------------------------------------------- for (int test = 0; test < NumberRepetTest_P; test++) { InitAO (funcCount * 2, f.GetMaxArg (), f.GetMinArg (), ArgumentStep_P); EpochCmidl = Measur1FuncValue_P / (ArraySize (AO.S_Colony)); EpochCount = Measur2FuncValue_P / (ArraySize (AO.S_Colony)); // Optimization------------------------------------------------------------- AO.F_EpochReset (); for (int epochCNT = 1; epochCNT <= EpochCount && !IsStopped (); epochCNT++) { AO.F_Preparation (); for (int set = 0; set < ArraySize (AO.S_Colony); set++) { AO.A_FFcol [set] = f.CalcFunc (AO.S_Colony [set].args, funcCount); } AO.F_Sorting (); if (epochCNT == EpochCmidl) aveMid += AO.A_FFpop [0]; SendGraphToCanvas (1, 1); //draw a population on canvas for (int i = 0; i < ArraySize (AO.S_Population); i++) { if (i > 0) PointDr (AO.S_Population [i].args, f.GetMinArg (), f.GetMaxArg (), clrWhite, 1, 1, funcCount); } PointDr (AO.S_Population [0].args, f.GetMinArg (), f.GetMaxArg (), clrBlack, 1, 1, funcCount); Canvas.Circle (x + 1, y + 1, 10, COLOR2RGB (clrBlack)); Canvas.Circle (x + 1, y + 1, 11, COLOR2RGB (clrBlack)); xConv = (int)Scale (epochCNT, 1, EpochCount, 2, WidthScrFunc - 2, false); yConv = (int)Scale (AO.A_FFpop [0], minFuncVal, maxFuncVal, 1, HeighScrFunc - 2, true); Canvas.FillCircle (xConv + HeighMonitor + 1, yConv + 1, 1, COLOR2RGB (clrConv)); Canvas.Update (); Sleep (RenderSleepMsc_P); } aveEnd += AO.A_FFpop [0]; Sleep (1000); } aveMid /= (double)NumberRepetTest_P; aveEnd /= (double)NumberRepetTest_P; double score1 = Scale (aveMid, minFuncVal, maxFuncVal, 0.0, 1.0, false); double score2 = Scale (aveEnd, minFuncVal, maxFuncVal, 0.0, 1.0, false); ScoreAll += score1 + score2; Print (funcCount, " ", f.GetNamFun (), "'s; Func runs ", Measur1FuncValue_P, " result: ", aveMid, "; Func runs ", Measur2FuncValue_P, " result: ", aveEnd); Print ("Score1: ", DoubleToString (score1, 5), "; Score2: ", DoubleToString (score2, 5)); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— void InitAO (const int params, //amount of the optimized arguments const double max, //maximum of the optimized argument const double min, //minimum of the optimized argument const double step) //step of the optimized argument { AO.F_Init (params, Population_P); for (int idx = 0; idx < params; idx++) { AO.A_RangeMax [idx] = max; AO.A_RangeMin [idx] = min; AO.A_RangeStep [idx] = step; } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— void PointDr (double &args [], double Min, double Max, color clr, int shiftX, int shiftY, int count) { double x = 0.0; double y = 0.0; double xAve = 0.0; double yAve = 0.0; int width = 0; int height = 0; color clrF = clrNONE; for (int i = 0; i < count; i++) { xAve += args [i * 2]; yAve += args [i * 2 + 1]; x = args [i * 2]; y = args [i * 2 + 1]; width = (int)Scale (x, Min, Max, 0, WidthScrFunc - 1, false); height = (int)Scale (y, Min, Max, 0, HeighScrFunc - 1, false); clrF = DoubleToColor (i, 0, count - 1, 0, 360); Canvas.FillCircle (width + shiftX, height + shiftY, 1, COLOR2RGB (clrF)); } xAve /= (double)count; yAve /= (double)count; width = (int)Scale (xAve, Min, Max, 0, WidthScrFunc - 1, false); height = (int)Scale (yAve, Min, Max, 0, HeighScrFunc - 1, false); Canvas.FillCircle (width + shiftX, height + shiftY, 3, COLOR2RGB (clrBlack)); Canvas.FillCircle (width + shiftX, height + shiftY, 2, COLOR2RGB (clr)); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— void SendGraphToCanvas (int shiftX, int shiftY) { for (int w = 0; w < HeighScrFunc; w++) { for (int h = 0; h < HeighScrFunc; h++) { Canvas.PixelSet (w + shiftX, h + shiftY, COLOR2RGB (FunctScrin [w].clr [h])); } } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— void DrawFunctionGraph (double min, double max, double fMin, double fMax, C_Function &f) { double ar [2]; double fV; for (int w = 0; w < HeighScrFunc; w++) { ar [0] = Scale (w, 0, HeighScrFunc, min, max, false); for (int h = 0; h < HeighScrFunc; h++) { ar [1] = Scale (h, 0, HeighScrFunc, min, max, false); fV = f.CalcFunc (ar, 1); FunctScrin [w].clr [h] = DoubleToColor (fV, fMin, fMax, 0, 250); } } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— //Scaling a number from a range to a specified range double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers = false) { if (OutMIN == OutMAX) return (OutMIN); if (InMIN == InMAX) return ((OutMIN + OutMAX) / 2.0); else { if (Revers) { if (In < InMIN) return (OutMAX); if (In > InMAX) return (OutMIN); return (((InMAX - In) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN); } else { if (In < InMIN) return (OutMIN); if (In > InMAX) return (OutMAX); return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN); } } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— color DoubleToColor (const double in, //input value const double inMin, //minimum of input values const double inMax, //maximum of input values const int loH, //lower bound of HSL range values const int upH) //upper bound of HSL range values { int h = (int)Scale (in, inMin, inMax, loH, upH, true); return HSLtoRGB (h, 1.0, 0.5); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— color HSLtoRGB (const int h, //0 ... 360 const double s, //0.0 ... 1.0 const double l) //0.0 ... 1.0 { int r; int g; int b; if (s == 0.0) { r = g = b = (unsigned char)(l * 255); return StringToColor ((string)r + "," + (string)g + "," + (string)b); } else { double v1, v2; double hue = (double)h / 360.0; v2 = (l < 0.5) ? (l * (1.0 + s)) : ((l + s) - (l * s)); v1 = 2.0 * l - v2; r = (unsigned char)(255 * HueToRGB (v1, v2, hue + (1.0 / 3.0))); g = (unsigned char)(255 * HueToRGB (v1, v2, hue)); b = (unsigned char)(255 * HueToRGB (v1, v2, hue - (1.0 / 3.0))); return StringToColor ((string)r + "," + (string)g + "," + (string)b); } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— double HueToRGB (double v1, double v2, double vH) { if (vH < 0) vH += 1; if (vH > 1) vH -= 1; if ((6 * vH) < 1) return (v1 + (v2 - v1) * 6 * vH); if ((2 * vH) < 1) return v2; if ((3 * vH) < 2) return (v1 + (v2 - v1) * ((2.0f / 3) - vH) * 6); return v1; } //——————————————————————————————————————————————————————————————————————————————
To convert a double number from a range to a color, the algorithm of converting HSL to RGB was used (the color system of MetaTrader 5).
The test stand displays an image on the graph. It is divided in half.
- The test function is displayed on the left side. Its three-dimensional graph is projected onto a plane, where red means the maximum, while blue means the minimum. Display the position of the points in the population (the color corresponds to the ordinal number of the test function with the number of variables 40 and 1000, coloring is not performed for a function with two variables), the points whose coordinates are averaged are marked in white, while the best one is marked in black.
- The convergence graph is displayed on the right side, tests with 2 variables are marked in green, tests with 40 variables are blue, while tests featuring 1000 variables are red. Each of the tests is carried out five times (5 graphs of convergence of each color). Here we can observe how much the convergence of OA deteriorates with an increase in the number of variables.
6. Simple OA using RNG
Let's implement the simplest search strategy as a test example. It has no practical value, but it will be in some way a standard for comparing optimization algorithms. The strategy generates a new set of function variables in a 50/50 random choice: either copy the variable from a randomly selected parent set from the population or generate a variable from the min/max range. After receiving the values of the test functions, the resulting new set of variables is copied to the second half of the population and is sorted. Thus, new sets constantly replace one half of the population, while the best sets are concentrated in the other.
Below is an OA code based on RNG:
//+————————————————————————————————————————————————————————————————————————————+ class C_AO_RND { public: //|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| struct ArrColony { double args []; }; //---------------------------------------------------------------------------- double A_RangeStep []; //Step ranges of genes double A_RangeMin []; //Min ranges of genes double A_RangeMax []; //Max ranges of genes ArrColony S_Population []; //Population ArrColony S_Colony []; //Colony double A_FFpop []; //Values of fitness of individuals in population double A_FFcol []; //Values of fitness of individuals in colony //---------------------------------------------------------------------------- // Initialization of algorithm void F_Init (int argCount, //Number of arguments int populationSize) //Population size { MathSrand ((int)GetMicrosecondCount ()); //reset of the generator p_argCount = argCount; p_sizeOfPop = populationSize; p_sizeOfCol = populationSize / 2; p_dwelling = false; f_arrayInitResize (A_RangeStep, argCount, 0.0); f_arrayInitResize (A_RangeMin, argCount, 0.0); f_arrayInitResize (A_RangeMax, argCount, 0.0); ArrayResize (S_Population, p_sizeOfPop); ArrayResize (s_populTemp, p_sizeOfPop); for (int i = 0; i < p_sizeOfPop; i++) { f_arrayInitResize (S_Population [i].args, argCount, 0.0); f_arrayInitResize (s_populTemp [i].args, argCount, 0.0); } ArrayResize (S_Colony, p_sizeOfCol); for (int i = 0; i < p_sizeOfCol; i++) { f_arrayInitResize (S_Colony [i].args, argCount, 0.0); } f_arrayInitResize (A_FFpop, p_sizeOfPop, -DBL_MAX); f_arrayInitResize (A_FFcol, p_sizeOfCol, -DBL_MAX); f_arrayInitResize (a_indexes, p_sizeOfPop, 0); f_arrayInitResize (a_valueOnIndexes, p_sizeOfPop, 0.0); } //---------------------------------------------------------------------------- void F_EpochReset () //Reset of epoch, allows to begin evolution again without initial initialization of variables { p_dwelling = false; ArrayInitialize (A_FFpop, -DBL_MAX); ArrayInitialize (A_FFcol, -DBL_MAX); } //---------------------------------------------------------------------------- void F_Preparation (); //Preparation //---------------------------------------------------------------------------- void F_Sorting (); //The settling of a colony in population and the subsequent sorting of population private: //||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| //---------------------------------------------------------------------------- void F_PopulSorting (); //---------------------------------------------------------------------------- ArrColony s_populTemp []; //Temporal population int a_indexes []; //Indexes of chromosomes double a_valueOnIndexes []; //VFF of the appropriate indexes of chromosomes //---------------------------------------------------------------------------- template <typename T1> void f_arrayInitResize (T1 &arr [], const int size, const T1 value) { ArrayResize (arr, size); ArrayInitialize (arr, value); } //---------------------------------------------------------------------------- double f_seInDiSp (double In, double InMin, double InMax, double step); double f_RNDfromCI (double min, double max); double f_scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX); //---Constants---------------------------------------------------------------- int p_argCount; //Quantity of arguments in a set of arguments int p_sizeOfCol; //Quantity of set in a colony int p_sizeOfPop; //Quantity of set in population bool p_dwelling; //Flag of the first settling of a colony in population }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— void C_AO_RND::F_Preparation () { //if starts of algorithm weren't yet - generate a colony with random arguments if (!p_dwelling) { for (int person = 0; person < p_sizeOfCol; person++) { for (int arg = 0; arg < p_argCount; arg++) { S_Colony [person].args [arg] = f_seInDiSp (f_RNDfromCI (A_RangeMin [arg], A_RangeMax [arg]), A_RangeMin [arg], A_RangeMax [arg], A_RangeStep [arg]); } } p_dwelling = true; } //generation of a colony using with copying arguments from parent sets-------- else { int parentAdress = 0; double rnd = 0.0; double argVal = 0.0; for (int setArg = 0; setArg < p_sizeOfCol; setArg++) { //get a random address of the parent set parentAdress = (int)f_RNDfromCI (0, p_sizeOfPop - 1); for (int arg = 0; arg < p_argCount; arg++) { if (A_RangeMin [arg] == A_RangeMax [arg]) continue; rnd = f_RNDfromCI (0.0, 1.0); if (rnd < 0.5) { S_Colony [setArg].args [arg] = S_Population [parentAdress].args [arg]; } else { argVal = f_RNDfromCI (A_RangeMin [arg], A_RangeMax [arg]); argVal = f_seInDiSp (argVal, A_RangeMin [arg], A_RangeMax [arg], A_RangeStep [arg]); S_Colony [setArg].args [arg] = argVal; } } } } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— void C_AO_RND::F_Sorting () { for (int person = 0; person < p_sizeOfCol; person++) { ArrayCopy (S_Population [person + p_sizeOfCol].args, S_Colony [person].args, 0, 0, WHOLE_ARRAY); } ArrayCopy (A_FFpop, A_FFcol, p_sizeOfCol, 0, WHOLE_ARRAY); F_PopulSorting (); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Ranging of population. void C_AO_RND::F_PopulSorting () { //---------------------------------------------------------------------------- int cnt = 1, i = 0, u = 0; int t0 = 0; double t1 = 0.0; //---------------------------------------------------------------------------- // We will put indexes in the temporary array for (i = 0; i < p_sizeOfPop; i++) { a_indexes [i] = i; a_valueOnIndexes [i] = A_FFpop [i]; } while (cnt > 0) { cnt = 0; for (i = 0; i < p_sizeOfPop - 1; i++) { if (a_valueOnIndexes [i] < a_valueOnIndexes [i + 1]) { //----------------------- t0 = a_indexes [i + 1]; t1 = a_valueOnIndexes [i + 1]; a_indexes [i + 1] = a_indexes [i]; a_valueOnIndexes [i + 1] = a_valueOnIndexes [i]; a_indexes [i] = t0; a_valueOnIndexes [i] = t1; //----------------------- cnt++; } } } // On the received indexes create the sorted temporary population for (u = 0; u < p_sizeOfPop; u++) ArrayCopy (s_populTemp [u].args, S_Population [a_indexes [u]].args, 0, 0, WHOLE_ARRAY); // Copy the sorted array back for (u = 0; u < p_sizeOfPop; u++) ArrayCopy (S_Population [u].args, s_populTemp [u].args, 0, 0, WHOLE_ARRAY); ArrayCopy (A_FFpop, a_valueOnIndexes, 0, 0, WHOLE_ARRAY); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Choice in discrete space double C_AO_RND::f_seInDiSp (double in, double inMin, double inMax, double step) { if (in <= inMin) return (inMin); if (in >= inMax) return (inMax); if (step == 0.0) return (in); else return (inMin + step * (double)MathRound ((in - inMin) / step)); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Random number generator in the custom interval. double C_AO_RND::f_RNDfromCI (double min, double max) { if (min == max) return (min); double Min, Max; if (min > max) { Min = max; Max = min; } else { Min = min; Max = max; } return (double(Min + ((Max - Min) * (double)MathRand () / 32767.0))); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— double C_AO_RND::f_scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX) { if (OutMIN == OutMAX) return (OutMIN); if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0)); else { if (In < InMIN) return (OutMIN); if (In > InMAX) return (OutMAX); return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN); } } //——————————————————————————————————————————————————————————————————————————————
7. Results
| AO | Runs | Skin | Forest | Megacity (discrete) | Final result | ||||||
| 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | |||
| RND | 1000 | 0.98744 | 0.61852 | 0.49408 | 0.89582 | 0.19645 | 0.14042 | 0.77333 | 0.19000 | 0.14283 | 0.51254 |
| 10,000 | 0.99977 | 0.69448 | 0.50188 | 0.98181 | 0.24433 | 0.14042 | 0.88000 | 0.20133 | 0.14283 | ||
After testing on the test stand, the results of the RND OA turned out to be quite unexpected. The algorithm is able to find the optimum of functions of two variables with very high accuracy, while in case of Forest and Megacity, the results are noticeably worse. On the other hand, my assumptions about weak search properties for functions with many variables was confirmed. The results are very mediocre at 40 arguments already. The final cumulative value is 0.51254.
In subsequent articles, I will analyze and test well-known and widely used optimization algorithms and continue filling in the results table making up the OA rating.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/8122
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Developing a trading Expert Advisor from scratch (Part 24): Providing system robustness (I)
Developing a trading Expert Advisor from scratch (Part 24): Providing system robustness (I)
 Neural networks made easy (Part 23): Building a tool for Transfer Learning
Neural networks made easy (Part 23): Building a tool for Transfer Learning
 Developing a trading Expert Advisor from scratch (Part 25): Providing system robustness (II)
Developing a trading Expert Advisor from scratch (Part 25): Providing system robustness (II)
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Thank you for your reply.
Is there a fast method for binary variables/predictors (total around 5k) with gene length up to 10 letters (or whatever it's called?)?
I don't have the answer yet, I will look for it together with the reader in future articles)))
There is a lot of research work to be done.
I don't have the answer, I will look for it together with the reader in future articles)))
There is a lot of research work to be done.
If you need to calculate something - I am ready to share the power, for the sake of science! :)
If you need something to calculate - I'm ready to share the power, for the sake of science! :)
oh, the offer is very helpful, thanks).
The classification tree does not represent all existing optimisation methods to date. In addition, only population-based algorithms will be considered.