两样本Kolmogorov-Smirnov检验作为时间序列非平稳性的指标

概述

当开始分析金融时间序列时，研究人员经常会遇到数据非平稳性的问题。货币汇率、股票和期货等时间序列通常都是非平稳的。为了使这些序列达到平稳状态，通常使用价格对数的一阶差分Ln(Xn/Xn-1)来处理数据，以便进行后续的工作。

但是这样的修改后的时间序列能否平稳呢？接下来，我将尝试回答这个问题，但首先让我们回顾一下什么是平稳性。在没有正式定义的情况下，平稳性可以描述为时间序列的统计特性（如数学期望和方差）随时间保持恒定。如果除了这些特性外，还假设分布函数随时间保持恒定，那么该过程就被称为狭义平稳性。

在本研究中，我将使用经验分布函数来检验金融时间序列的狭义平稳性。概率论和数理统计作为前者的一个特定部分，都是基于平稳性假设的。分析平稳过程的方法有很多，包括回归分析、自相关分析、光谱分析方法以及使用神经网络等。然而，将这些方法应用于非平稳数据可能会导致显著的预测误差。

对于交易者来说，平稳性问题与用于计算各种指标数据量的选择密切相关。在平稳过程的情况下，可用的数据越多，所有统计特性的计算就越准确。然而，在分析非平稳过程时，很难确定最佳数据量。数据量过大可能包含已过时且不再影响当前情况的信息。如果数据量太少，则由于代表性不足，我们将无法充分评估过程的统计特性。

随机过程最完整的特性是其分布律（概率函数）。因此，构建一个能够跟踪时间序列分布函数随时间变化的指标是一项重要任务。这个指标反过来将作为重新衡量用于计算标准技术指标数据量的信号。在数学统计学中，检验随机变量的分布函数是否随时间发生变化的问题被称为“检验同质性假设”。

同质性假说

样本数据的同质性是通过同质性检验来衡量的。目前已经开发出了大量类似的标准，可以分为以下几种：

• 两样本柯尔莫哥洛夫-斯米尔诺夫（Kolmogorov-Smirnov）检验，

• 安德森（Anderson）同质性检验，

• 皮尔森卡方（Pearson chi-square）同质性检验。

所谓同质性假设，即两个在随机变量X和Y上获得的数据样本(x1,x2,x3,...xn)和(y1,y2,y3,...ym)遵循相同的分布律，或者换句话说，这两个样本是从同一个总体中抽取的。形式上，这个假设可以写为H0：F(x) = G(y)。备择假设是两个样本属于不同的总体，但不具体指定是哪两个总体，H1：F(x) ≠ G(y)。

• Fn（x）和Gm（y）分别是随机x和y变量的经验累积分布函数。

• n, m – 计算数据量

两样本Kolmogorov-Smirnov检验

Kolmogorov-Smirnov两样本检验是一种统计检验，用于验证两个样本是否来自同一连续分布的假设。该准则基于两个独立样本的经验分布函数的比较。

两样本Kolmogorov-Smirnov检验在统计分析中被广泛用于检验分布相等性的假设，这在生物统计学、计量经济学和其他需要通过统计学比较两个不同样本的研究领域中非常有用。当可用数据不足以支持更复杂的参数方法时，这一点尤为重要。

于是产生了一个问题：应该用什么来衡量两个经验分布函数之间的差异？斯米尔诺夫提出了以下统计量：

Dn,m = sup | Fn(x) - Gm(y) |

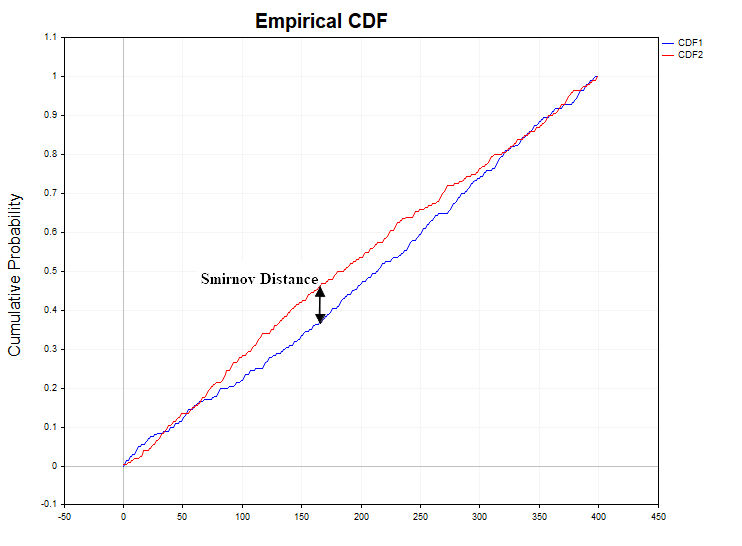
这个统计量代表两个分布函数差的绝对值的精确上限（最大值）。如果随机变量的分布规律在不同样本之间保持一致，那么我们可以预计Dn，m的统计量值偏低。反过来，如果这一统计值过高，表明数据的同质性假设可能不成立。在实际进行统计假设检验时，我们并不直接使用D统计量，而是使用其稍作修改后的版本。

λ = D * ( sqrt(k) + 0,12 + 0,11/sqrt(k) )，

其中 k = (m*n/(m+n))。当参数 k 趋于无穷大时，λ统计量的分布会收敛到柯尔莫哥洛夫（Kolmogorov）分布函数：                                                  

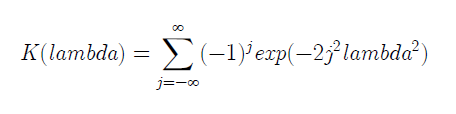
当n等于m时，有时候可使用更简化的方程来计算λ：

λ = D *sqrt(n/2)

接下来，在获得某些统计值后，使用样本数据对同质性假设进行检验。

统计假设检验如下：

• 设定原假设（null hypothesis，样本是同质的）和备择假设（alternative hypothesis，样本是异质的），

• 采用α显著性水平（通常使用的标准值为0.1、0.05和0.01），

• u（α）临界值是根据Kolmogorov分布计算的（例如，如果α为0.05，u（α） 为1.3581），

• 计算λ统计量的样本值，

• 如果λ＜u（α），则认为原假设成立，

• 如果λ＞u（α），在α显著性水平上，由于与原观测数据相矛盾，因此认为原假设不成立。

从逻辑上来讲以另一种方式结束也是有可能的。不是计算u(α)临界值，而是计算概率P值（PValue）= 1 - K(λ)，并将其与指定的α显著性水平进行比较。如果α ≥ P值，则认为原假设不成立，因为我们认为发生了一个与随机性概念不兼容的小概率的事件，因此应认为样本是不同质的。

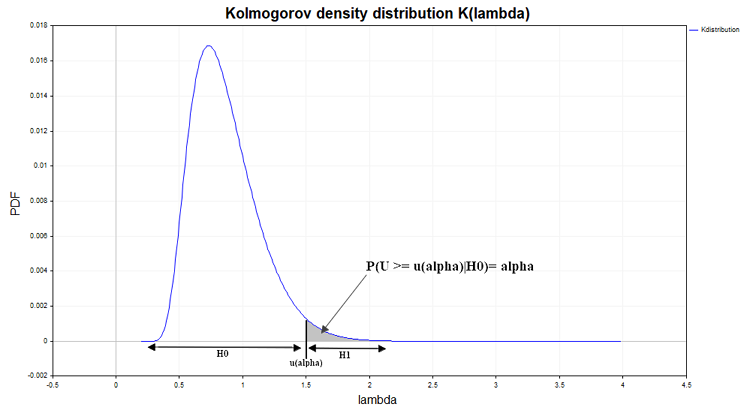
该图展示了在原假设成立的条件下，计算得出Kolmogorov分布函数的导数，也就是概率密度函数。如果根据样本数据计算得出的斯米尔诺夫距离（Smirnov Distance）的概率密度函数与柯尔莫哥洛夫（Kolmogorov）函数存在差异，这可能表明数据间存在异质性。

双样本柯尔莫哥洛夫-斯米尔诺夫（Kolmogorov-Smirnov）检验不应与单样本检验相混淆。在 前者中，我们比较的是两个经验分布函数（empirical distribution functions），而后者则比较的是经验分布函数和假设分布函数（hypothetical distribution functions）。

有一个非常重要的点是，经验分布函数必须使用未分组的观测数据来计算，因为Kolmogorov分布函数是在这一假设下计算得出的。同样要强调的重要一点是，双样本Kolmogorov-Smirnov检验并不依赖于特定类型的分布函数。在分析金融时间序列时，由于很难得出观测数据属于哪一种假设分布类型的结论，因此这一准则对于分析师来说很有价值。在不对观测数据可能属于的假设分布类型做任何推测的情况下，我们可以仅基于经验分布函数来检验同质性假设。对于时间序列分析，斯米尔诺夫准则可以视为过程平稳性的一个指标。毕竟，根据平稳性的定义，当一个过程的概率分布函数不随时间变化时，该过程被认为是平稳的。

简单计算方法解析

假设我们有两个装满弹珠的大袋子。一个袋子里的弹珠来自一个国家，而另一个袋子里的弹珠来自另一个国家。我们的任务是找出这两个袋子里的弹珠是否相同或不同。

1. 弹珠分类. 首先，我们把弹珠从两个袋子里倒出来，按照每个弹珠的大小排列——从最小到最大。

2. 比较弹珠. 接下来，我们开始查看第一个袋子里的每个弹珠，并在第二个袋子里寻找相同大小的弹珠。我们测量两行中相似弹珠之间的距离。在这里，“距离”指的是当我们查看弹珠在行中的位置时，它们之间相隔多远。
   
   我们假设从第一个袋子中取出一个弹珠，它在所在行中排第五位。如果第二个袋子中有一个大小相近的弹珠在其行中排第二十位，那么这两个弹珠之间的距离就是15个位置（20 - 5 = 15）。这个数值反映了在两个不同袋子（或两个数据样本）中，相似弹珠在各自排序中的位置差距。
   
   在柯尔莫哥洛夫-斯米尔诺夫（Kolmogorov-Smirnov）统计检验中，我们比较所有弹珠的这种“距离”，并寻找其中的最大值。如果这个最大距离大于某个特定值（该值取决于袋子中弹珠的数量），这可能表明袋子中的弹珠在某些属性上存在差异。
   

3. 找出最大的区别. 我们正在寻找两行弹珠之间差异（“距离”）最大的位置。例如，如果在某个位置上，弹珠的大小非常接近，而在另一个位置上，它们的大小差异很大，我们就会标记这个位置。

4. 评估差异。如果弹珠之间的最大距离非常远，这可能意味着袋子里的弹珠确实不同。如果整行中所有的弹珠都彼此相当接近，那么它们可能确实来自同一个地方。

因此，如果两行弹珠之间的差异很大，我们就说这两袋弹珠是不同的。如果差异很小，那么弹珠很可能是一样的。这有助于我们理解来自两个不同地方的弹珠是否可以被认定是相同的。

使用两样本Kolmogorov-Smirnov检验的数据分析

在继续分析基于实际计算的D Smirnov距离之前，我们首先需要研究这个统计量在具有相关增量和独立增量的平稳过程模型上的表现。为此，我将生成1000个时间序列样本（Samples），每个样本具有给定的分布函数，并且每个序列包含1440个数据点。之后，我将计算这些样本之间的D Smirnov距离，检查在多少百分比的情况下认定原假设不成立，并且构建这些距离的经验概率密度函数，以便与Kolmogorov密度函数进行比较。下图显示了从正态分布和均匀分布中获得的N=1440数据样本的Smirnov距离序列。       

                               
                               

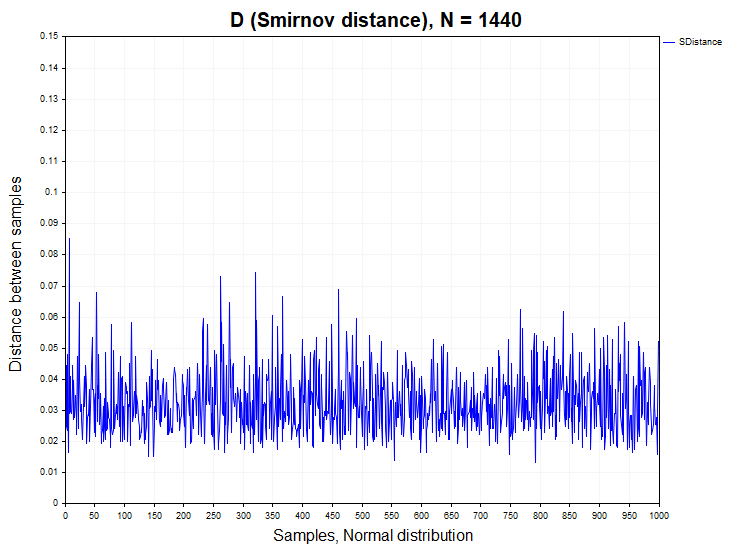
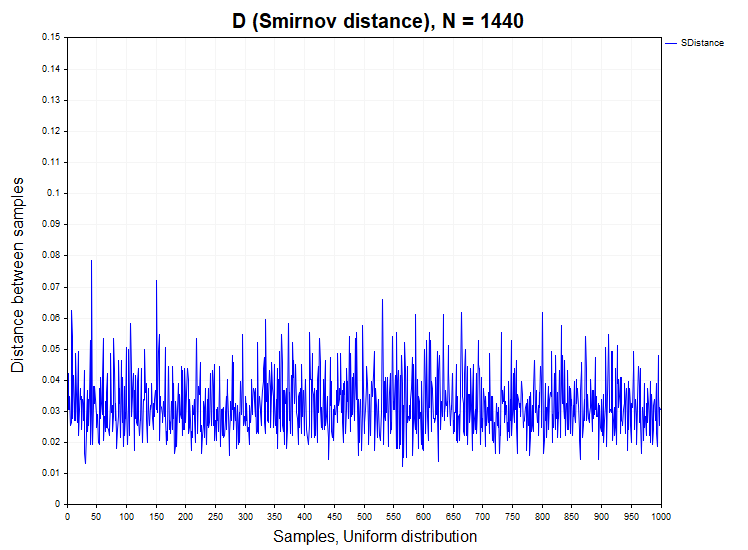
对于来自正态分布和均匀分布的样本，在第一类错误（α=0.05）的可接受范围内，在1000个样本中，认定同质性假设不成立的情况不会超过50个。H1/ Samples = 50/1000 = 0.05. 以下是正态分布和均匀分布的Smirnov距离的样本概率密度图。

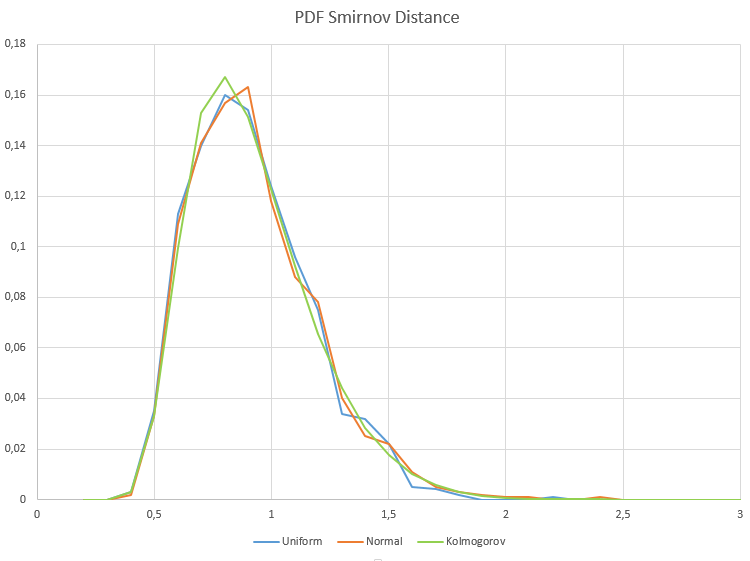
X轴显示λ值。

由此可以看出，对于均匀分布和正态分布的数据样本，其Smirnov距离的样本分布与它们应该收敛到的Kolmogorov分布是完全匹配的，这一前提是原假设成立。

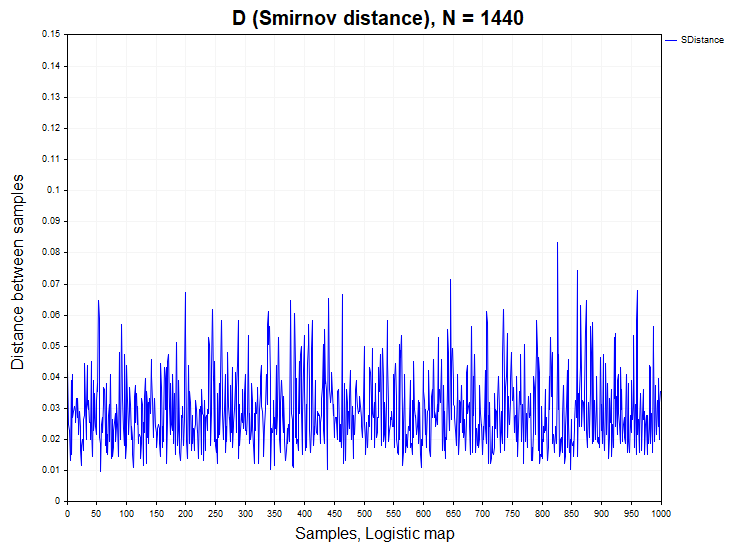
我们刚刚处理的正态分布和均匀分布正是平稳独立过程的实例。作为平稳但相关的一个过程，我将以离散非线性方程为例，该方程在确定性混沌领域经常被用作示例——即逻辑映射（logistic map）：

Xn= R*Xn-1 *(1 – Xn-1), X0 = (0;1), R = 4

当参数R=4时，这是一个一维非线性动力系统，它展现出的混沌行为，几乎与白噪声无法区分。由该方程生成的时间序列自相关函数在0附近波动。然而，在这个过程中存在着非线性依赖关系，检查这种依赖关系如何影响Smirnov距离的分布是一件很有趣的事情。这绝不是一个无关紧要的问题，因为许多人认为在金融数据中存在非线性依赖关系，因此我将这个方程纳入到了分析之中。

当然，分析需要一个具有线性依赖关系的模型，这种依赖关系在真实数据中也可能存在。因此，平稳相关过程的第二个模型将是一阶线性自回归模型：

ARt = 0.5 * ARt-1 + et

• et – 具有0均值和单位方差的随机变量，高斯白噪声

在这种情况下，自回归过程也就是高斯过程，尽管它已经是相关的。

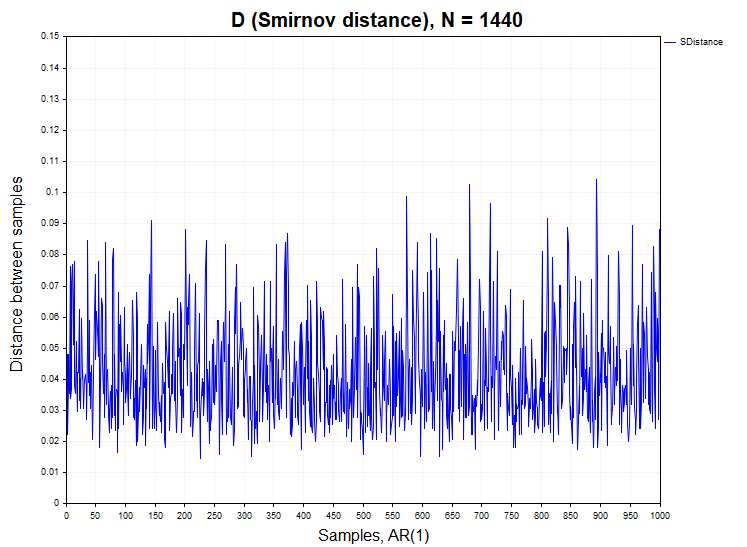
在具有相关增量的过程中，认定同质性假设不成立的情况略有不同。对于逻辑映射，第一类错误的允许值略有超出，为0.058（H1/样本数=58/1000），而对于一阶自回归，这一错误已经接近0.25（H1/样本数=250/1000），即比原假设的允许水平高出了五倍。

我们得出了一个非常有趣的结果。根据两样本Kolmogorov-Smirnov检验，我们竟然应该将逻辑映射和AR(1)都识别为非均匀（非平稳）过程。然而，事实并非如此。为什么会这样？原来，只有当观测数据在统计上独立时，平稳分布的Smirnov距离的概率密度函数才仅仅取决于所研究过程的分布类型。由于逻辑映射和自回归都是具有相关增量的过程，因此在这种情况下，Smirnov距离的概率密度将与Kolmogorov分布不同。反过来意味着，两样本Kolmogorov-Smirnov检验不仅可以作为异质性（过程的非平稳性）的指标，还可以作为数据依赖性（线性或非线性）存在的指标。

让我们继续分析真实数据。举一个例子，我使用了欧元对美元（EURUSD）和黄金对美元（XAUUSD）的分钟线数据。

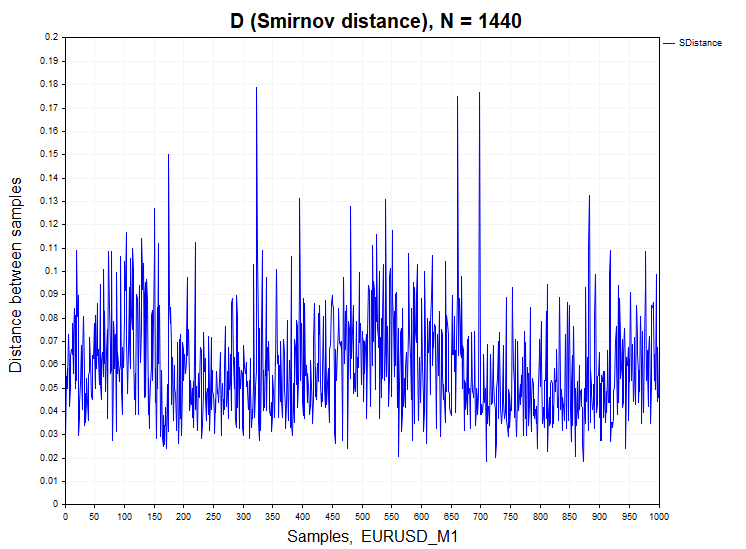
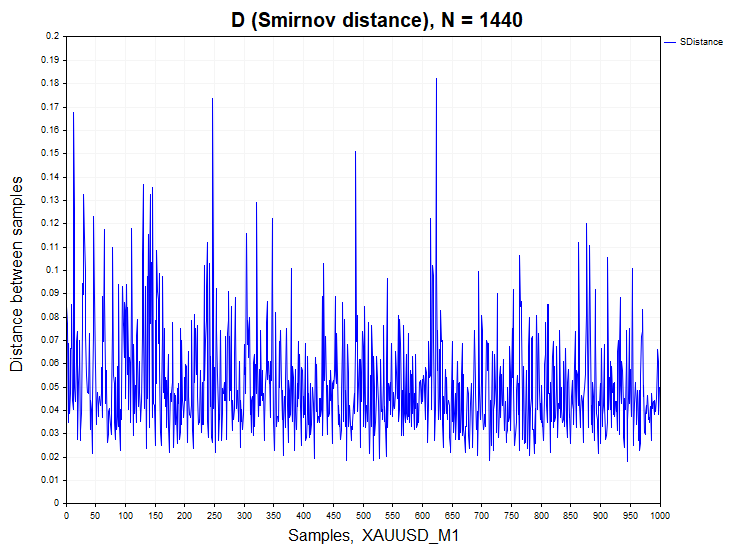
对于分钟数据，原假设的偏离百分比与平稳过程存在显著差异。具体而言，XAUUSD的H1/样本数=466/1000=0.46，EURUSD的H1/样本数=640/1000=0.64。为了更清晰地说明这一点，下面给出了真实数据以及自回归和逻辑映射等依赖过程的Smirnov距离样本概率密度函数的图形。

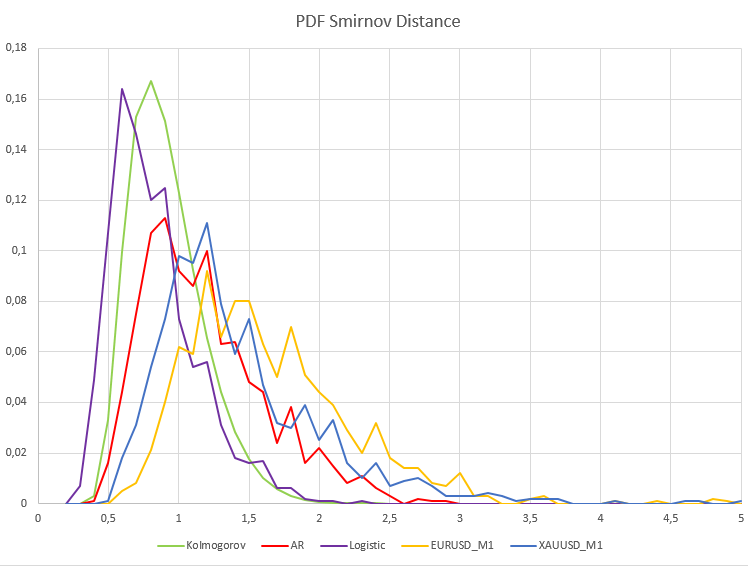
我们可以看到，无论是对于平稳依赖过程，还是对于真实的欧元对美元一分钟（EURUSD_M1）和黄金对美元一分钟（XAUUSD_M1）报价，这里都出现了截然不同的画面。这些过程的Smirnov距离样本概率密度与Kolmogorov分布存在着显著的差异。在这种情况下，逻辑映射和一阶自回归过程不收敛于Kolmogorov分布，仅仅是因为这些数据中存在统计依赖性。

关于金融工具的价格，即使尝试使用一阶差分将其转化为平稳形式，但是它们仍然具有非平稳性。从对平稳依赖过程的分析中我们可以看出，如此大的原假设偏离值很可能受到实际报价中可能存在的某些依赖性的影响。在我看来，无法评估这种影响中有多少是由于数据依赖性造成的，又有多少纯粹是由于金融工具时间序列中的非平稳因素造成的。但主要影响仍然与数据的异质性以及价格增量概率分布函数的不断变化有关。

为了清楚地了解两个异质性样本的Smirnov距离的概率密度可能呈现何种形式，我们将进行另一项实验，在该实验中，我们将比较来自两个属于不同群体的正态分布样本的数据。这两个分布在数学期望和离散度上会有所不同——一个是N(0,1) ，另一个是N(0.1,1.2)。显然，两样本Kolmogorov-Smirnov检验通常应该推翻同质性的原假设。在这里，如果备择假设为真却又接受了原假设，很明显就是一个错误。 

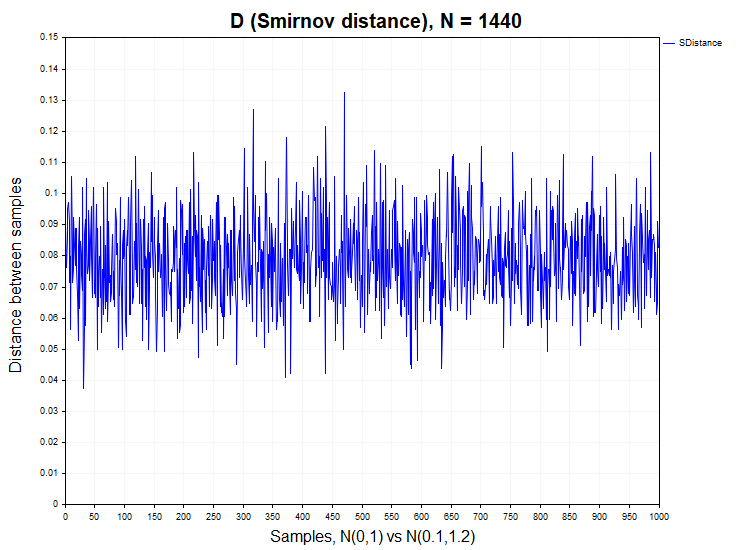
在这种情况下，我们认定原假设不成立的比例为0.98（H1/样本数 = 980/1000）。下列图表显示了实际报价、两个非均匀正态分布模型以及柯尔莫哥洛夫分布的斯米尔诺夫距离分布的概率密度函数。

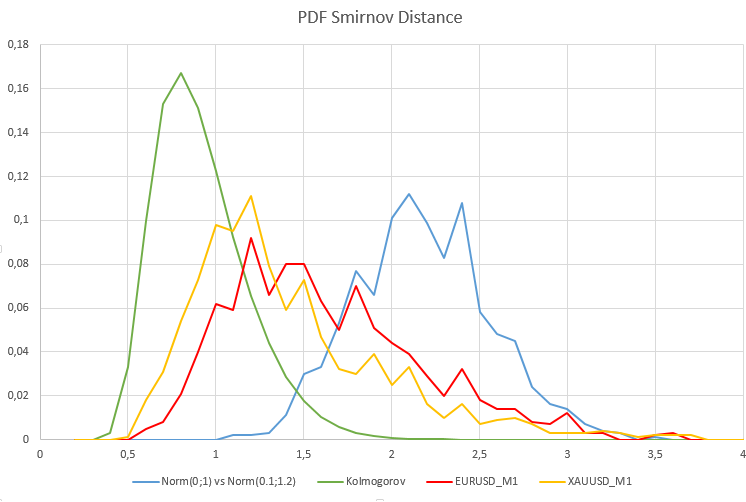
正如预期的那样，在两个正态样本具有异质性模型的情况下，Smirnov距离的概率密度函数与Kolmogorov分布之间存在着显著的差异。值得注意的是，两样本Kolmogorov-Smirnov检验对分布参数的微小变化都非常敏感。 

iSmirnovDistance指标

与上述分析不同，iSmirnovDistance 指标仅基于两个相邻交易日中各自包含的数据量进行计算，而不允许这些数据与其他交易时段重叠。该指标本身应在每日时间周期上运行，所有计算均基于同一交易品种的5分钟数据。对于货币价格，这相当于每天有287个数据点。如果其中任何一天的数据点不足以用于计算（我设定了270个数据点作为下限），则将该天的指标值设置为0。

因此，在每个交易日开始时，我们都会收到基于前两个交易日数据计算得出的Smirnov统计量值。这个指标实际上只有一个可以优化的参数——α显著性水平。在这一版中，我采用了标准值0.05。指标窗口中的蓝色虚线显示了显著性水平α=0.05时的Smirnov距离u(α)，即对于原假设的距离。它是用上述公式计算得到的：λ = D*sqrt(n/2)。已知Kolmogorov分布的λ临界值等于1.3581（参见Kolmogorov分布函数表）以及5分钟时间周期的数据量为287，我们可以找到相应的距离D = λ/sqrt(n/2) = 1.3581/sqrt(287/2) = 0.1133。如果实际计算值超过了该数值，表明数据分布的结构发生了质的变化。指标值低于蓝色虚线的可以被认为是同质的。

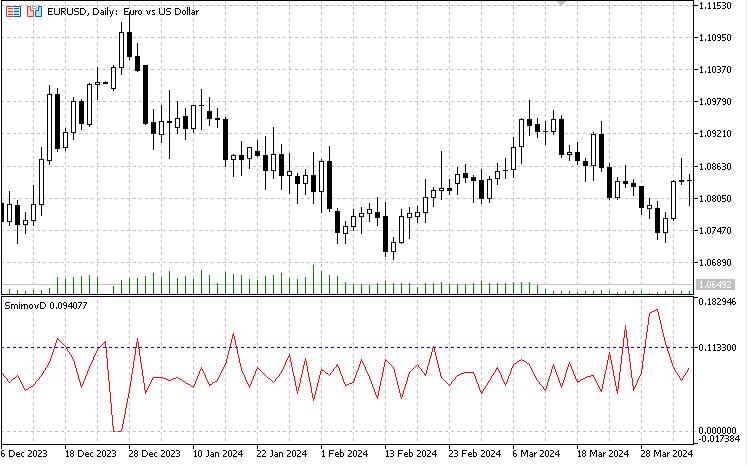
值得一提的是，计算Smirnov距离所使用的时间周期同样至关重要。我们可以看出，对于分钟数据，序列存在显著的非平稳性，而对于5分钟时间周期，序列则更为平稳，同质性假设被推翻的频率也显著降低。这在一定程度上归因于数据量的差异——M1有1440个数据点，而M5仅有287个。随着数据量从287逐渐增加到1440，原假设被推翻的频率也会上升。然而，在M1图表中，同质性假设被推翻的情况更为常见。 

结论

这篇文章旨在回答关于金融交易时间序列分析中的几个重要问题：

• 第一个问题是对数价格增量时间序列是否可以被视为具有平稳性。 在我看来，通过数值计算已经得到了令人信服的答案——不，至少对于分钟时间周期来说是不可能的。至于五分钟时间周期，与分钟相比，其序列看起来更为平稳，但仍然表现出非平稳性。

• 本次研究尝试回答的第二个问题是第一个问题的逻辑延伸——计算特定指标需要多少数据量？在我看来，iSmirnovDistance指标提供了以下解释——进行计算时，需要选取在两次推翻同质性原假设的时间段内的数据量。在原假设被推翻之前，需要分析的数据量逐渐增加。在推翻原假设后，先前的数据被废弃，重新开始计算数据量。因此，需要分析的数据量不是一个固定值。这是一个随时间不断变化的值，是基于非平稳随机过程性质而应有的情况。