
Redes neuronales en el trading: Un método complejo de predicción de trayectorias (Traj-LLM)
Introducción
La previsión de los movimientos futuros de precios en los mercados financieros desempeña un papel fundamental en los procesos de toma de decisiones de los operadores. Los pronósticos de alta calidad permiten a los comerciantes tomar decisiones más informadas y minimizar los riesgos. Sin embargo, pronosticar las trayectorias futuras de los precios enfrenta numerosos desafíos debido a la naturaleza caótica y estocástica de los mercados. Incluso los modelos de previsión más avanzados a menudo no logran tener en cuenta adecuadamente todos los factores que influyen en la dinámica del mercado, como cambios repentinos en el comportamiento de los participantes o eventos externos inesperados.
En los últimos años, el desarrollo de la inteligencia artificial, especialmente en el campo de los grandes modelos lingüísticos (Large Language Models, LLMs), ha abierto nuevas vías para resolver diversas tareas complejas. Las LLMs han demostrado notables capacidades para procesar información compleja y modelar escenarios de formas que se asemejan al razonamiento humano. Estos modelos se aplican con éxito en diversos campos, desde el procesamiento del lenguaje natural a la previsión de series temporales, lo que los convierte en herramientas prometedoras para analizar y predecir los movimientos del mercado.
Me gustaría presentarles el algoritmo Traj-LLM, descrito en el artículo «Traj-LLM: A New Exploration for Empowering Trajectory Prediction with Pre-trained Large Language Models». Traj-LLM fue desarrollado para resolver tareas en el campo de la predicción de trayectorias de vehículos autónomos. Los autores proponen utilizar LLMs para mejorar la precisión y adaptabilidad de la previsión de trayectorias futuras de los participantes en el tráfico.
Además, Traj-LLM combina la potencia de los grandes modelos lingüísticos con enfoques innovadores para modelar las dependencias temporales y las interacciones entre objetos, lo que permite realizar predicciones de trayectoria más precisas incluso en condiciones complejas y dinámicas. Este modelo no sólo mejora la precisión de las previsiones, sino que también ofrece nuevas formas de analizar y comprender posibles escenarios futuros. Esperamos que el empleo de la metodología propuesta por los autores sea eficaz para abordar nuestras tareas y mejore la calidad de nuestras previsiones sobre la evolución futura de los precios.
1. Algoritmo Traj-LLM
La arquitectura Traj-LLM consta de cuatro componentes integrales:
- Codificación conjunta contextual dispersa.
- Modelización de interacciones de alto nivel.
- Aprendizaje probabilístico en función del carril.
- Decodificador multimodal de Laplace.
Los autores del método Traj-LLM sugieren utilizar las capacidades de LLM para la predicción de trayectorias, eliminando la necesidad de ingeniería explícita de características en tiempo real. La codificación conjunta contextual dispersa transforma inicialmente las características del agente y de la escena en una forma interpretable por los LLM. A continuación, estas representaciones se introducen en los LLMs preentrenados para gestionar el modelado de interacción de alto nivel. Para imitar funciones cognitivas similares a las humanas y mejorar aún más la comprensión de escenas en Traj-LLM, se introduce el aprendizaje probabilístico consciente del carril a través de un módulo Mamba. Por último, se emplea el descodificador multimodal de Laplace para generar predicciones fiables.
El primer paso en Traj-LLM es la codificación de los datos espacio-temporales en bruto de la escena, como los estados de los agentes y la información del carril. Para cada una de ellas, se utiliza un modelo de incrustación compuesto por una capa recurrente y MLP para extraer características multidimensionales. Los tensores resultantes hi y fl se pasan a un submódulo Fusion, facilitando el intercambio de información compleja entre estados de agentes y carriles en zonas localizadas. Este proceso utiliza un mecanismo de incrustación de tokens para alinearse con la arquitectura LLM.
En concreto, el proceso de fusión emplea un mecanismo de Self-Attention (Autoatención) multicabezal para fusionar características de Agente-Agente. Además, la fusión de las funciones Agente-Carril y Carril-Agente incluye la actualización de las vistas de Agente y Carril mediante un mecanismo de atención cruzada multicabezal con conexiones de salto. Formalmente, este proceso puede representarse del siguiente modo:

Después, hi y fl se combinan para formar codificaciones conjuntas contextuales dispersas gi, capturando intuitivamente dependencias relevantes para los campos receptivos locales de entidades vectorizadas. Este enfoque de codificación está diseñado para permitir a las LLM interpretar eficazmente los datos de trayectoria, ampliando así las capacidades de las LLM.
Las transiciones de trayectorias siguen patrones regidos por restricciones de alto nivel derivadas de diversos elementos de la escena. Para estudiar estas interacciones, los autores exploran las capacidades de las LLM para modelar las dependencias inherentes a las tareas de predicción de trayectorias. A pesar de las similitudes entre los datos de trayectorias y los textos en lenguaje natural, el uso directo de LLMs para procesar codificaciones conjuntas contextuales dispersas se considera ineficiente. Porque los LLMs preentrenados están optimizados principalmente para datos de texto. Una propuesta alternativa es un reentrenamiento exhaustivo de todos los LLMs. Este proceso requiere importantes recursos informáticos, lo que lo hace poco viable. Otra solución más eficaz es utilizar el método Parameter-Efficient Fine-Tuning (PEFT) para afinar los LLMs preentrenados.
Los autores de Traj-LLM utilizan parámetros de arquitecturas de transformadores NLP preentrenadas, en particular GPT-2, para el modelado de interacciones de alto nivel. Proponen congelar todos los parámetros preentrenados e introducir otros nuevos entrenables mediante una técnica de adaptación de bajo rango (LoRA). LoRA se aplica a las entidades Query y Key del mecanismo de atención LLM.
Así, las codificaciones conjuntas contextuales dispersas g<i se introducen en un LLM formado por una serie de bloques Transformer preentrenados y mejorados con LoRA. Este procedimiento produce representaciones de interacción de alto nivel zi.
![]()
Las salidas del LLM preentrenado se transforman mediante un MLP para que coincidan con las dimensiones de gi, lo que da como resultado estados de interacción finales de alto nivel si.
La mayoría de los conductores experimentados se centran en un número limitado de segmentos de carril relevantes que influyen significativamente en sus acciones futuras. Para reproducir esta función cognitiva similar a la humana y mejorar aún más la comprensión de la escena en Traj-LLM, los autores del método utilizan el aprendizaje probabilístico consciente del carril para evaluar continuamente la probabilidad de alinear los estados de movimiento con los segmentos del carril. El modelo alinea la trayectoria del agente objetivo con la información del carril en cada paso temporal t∈{1,...,tf} utilizando una capa Mamba. Actuando como un modelo de espacio de estados estructurado selectivo (SSM), Mamba refina y generaliza la información relevante. Esto es similar a la forma en que los conductores humanos procesan selectivamente las señales ambientales cruciales, como los carriles potenciales, para tomar sus decisiones.
En la arquitectura propuesta, la capa Mamba incluye un bloque Mamba, normalización de triple capa y una red feed-forward en función de la posición. El bloque Mamba primero expande la dimensionalidad mediante proyecciones lineales, creando representaciones distintas para dos flujos de datos paralelos. Una rama se somete a convolución y activación SiLU para capturar las dependencias de carril. En su núcleo, el bloque Mamba incorpora un modelo selectivo de espacio de estados con parámetros discretizados, basado en los datos de entrada. Para mejorar la estabilidad, se añaden la normalización de instancias y las conexiones residuales, lo que da lugar a representaciones latentes.
Posteriormente, una red FeedForward en función de la posición mejora el modelado de las evaluaciones alineadas en el carril en la dimensión oculta. Una vez más, se aplican la normalización de instancias y las conexiones residuales para producir vectores de entrenamiento sensibles al carril, que se pasan a una capa MLP.
Como ya se ha dicho, los conductores experimentados se centran en los segmentos clave del carril para tomar decisiones eficientes. Por lo tanto, los mejores carriles candidatos se seleccionan cuidadosamente y se combinan en un conjunto ℳ.
El aprendizaje probabilístico en función del carril se modela como una tarea de clasificación, utilizando la pérdida de entropía cruzada binaria ℒlane (carril) para optimizar la estimación de la probabilidad.
A continuación se presenta la visualización de los autores del método Traj-LLM.
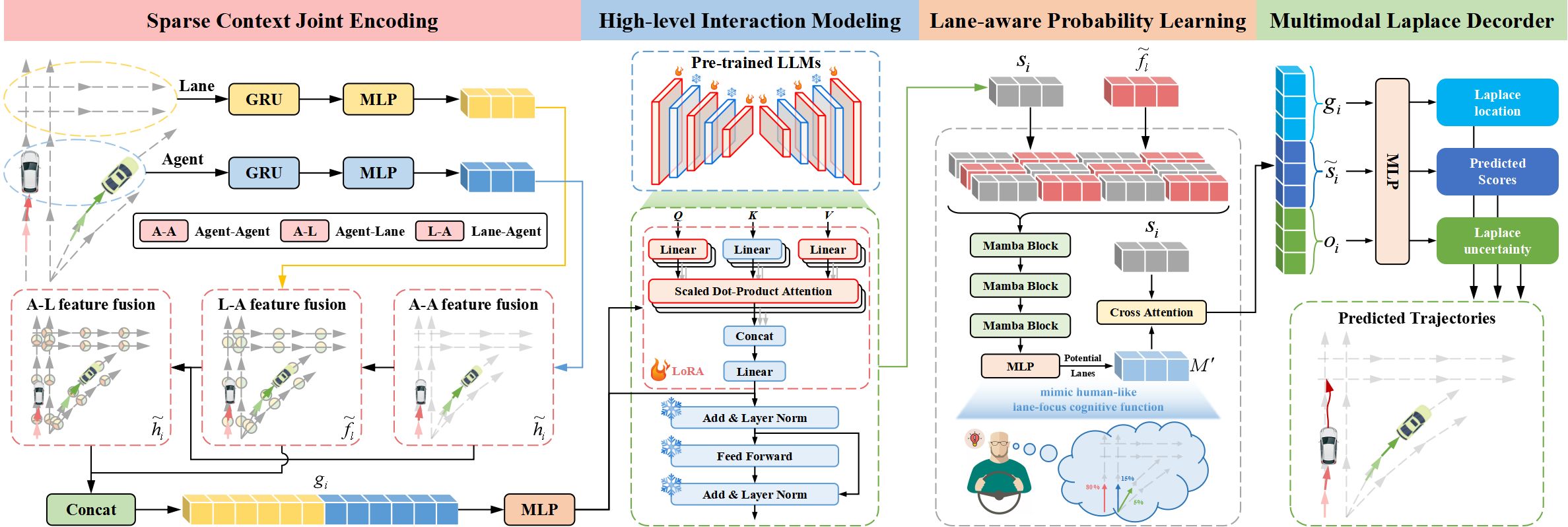
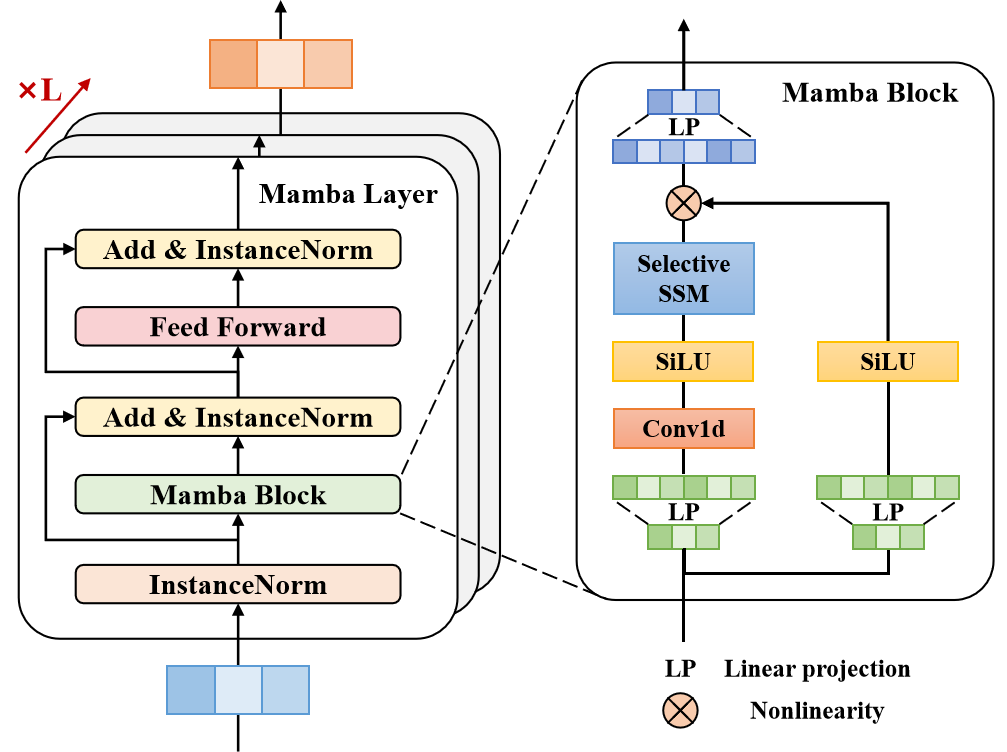
2. Implementación en MQL5
Tras considerar los aspectos teóricos del método Traj-LLM, pasamos a la parte práctica de nuestro artículo, en la que implementamos nuestra visión de los enfoques propuestos utilizando MQL5. El algoritmo Traj-LLM es un marco complejo que integra múltiples componentes arquitectónicos, algunos de los cuales ya hemos encontrado en trabajos anteriores. Así, podemos utilizar módulos existentes al construir el algoritmo. Sin embargo, serán necesarias modificaciones adicionales.
2.1 Ajuste del algoritmo de bloques LSTM
Veamos la visualización del método Traj-LLM presentada anteriormente. Los datos de entrada brutos pasan primero por el bloque de codificación conjunta contextual dispersa, que comprende una capa recurrente y MLP. Nuestra biblioteca ya incluye la capa recurrente CNeuronLSTMOCL. Sin embargo, procesa los datos de entrada como una representación única y unificada del estado del medio ambiente. En cambio, los autores del método proponen una codificación independiente de los agentes individuales y de los estados de los carriles. Por lo tanto, debemos organizar una codificación independiente para cada canal de datos. Bien, podríamos instanciar un objeto CNeuronLSTMOCL separado para cada canal. Sin embargo, esto provocaría un aumento incontrolable de los objetos internos y del procesamiento secuencial, lo que afectaría negativamente al rendimiento del modelo.
Una segunda solución es modificar la clase de capa recurrente CNeuronLSTMOCL existente. Esto requiere cambios en el lado del programa OpenCL. El paso feed-forward de nuestra capa recurrente se implementa en el kernel LSTM_FeedForward. Para implementar operaciones dentro de secuencias univariantes, no realizaremos cambios en los parámetros externos del núcleo. Para organizar el procesamiento paralelo de datos de secuencias univariantes individuales, añadiremos una dimensión más al espacio de tareas.
__kernel void LSTM_FeedForward(__global const float *inputs, int inputs_size, __global const float *weights, __global float *concatenated, __global float *memory, __global float *output) { uint id = (uint)get_global_id(0); uint total = (uint)get_global_size(0); uint id2 = (uint)get_local_id(1); uint idv = (uint)get_global_id(2); uint total_v = (uint)get_global_size(2);
Permítanme recordarles que el funcionamiento del bloque LSTM se basa en cuatro entidades, cuyos valores son calculados por capas internas:
- Forget Gate - responsable de descartar la información irrelevante
- Input Gate - responsable de incorporar nueva información
- Output Gate - responsable de generar la señal de salida
- New Content - que representan los valores candidatos para actualizar el estado de la célula
El algoritmo para calcular estas entidades es uniforme y sigue la estructura de una capa completamente conectada. La única diferencia radica en las funciones de activación aplicadas en cada etapa. Por lo tanto, en nuestra implementación, hemos diseñado el cálculo de estas entidades para que se procesen en subprocesos paralelos dentro de un grupo de trabajo. Para permitir el intercambio de datos entre subprocesos, utilizamos una matriz asignada en la memoria local.
__local float Temp[4];
A continuación definimos las constantes de desplazamiento en los buffers de datos globales.
float sum = 0; uint shift_in = idv * inputs_size; uint shift_out = idv * total; uint shift = (inputs_size + total + 1) * (id2 + id);
Por favor, preste atención a los siguientes puntos. Implementamos el proceso de trabajo del bloque recurrente con canales independientes. Sin embargo, según la lógica de construcción del algoritmo Traj-LLM, todos los canales de información independientes contienen datos comparables, ya se trate de información sobre el estado de varios agentes o de las vías de tráfico existentes. Por lo tanto, es bastante lógico utilizar una matriz de pesos para codificar la información de diferentes canales de datos, lo que nos permitirá obtener incrustaciones comparables en la salida.
De esta forma, el identificador del canal afecta el desplazamiento en los buffers de origen y de resultados. Pero no afecta el cambio en la matriz de peso.
A continuación, creamos un bucle para calcular la suma ponderada del estado oculto.
for(uint i = 0; i < total; i += 4) { if(total - i > 4) sum += dot((float4)(output[shift_out + i], output[shift_out + i + 1], output[shift_out + i + 2], output[shift_out + i + 3]), (float4)(weights[shift + i], weights[shift + i + 1], weights[shift + i + 2], weights[shift + i + 3])); else for(uint k = i; k < total; k++) sum += output[shift_out + k] * weights[shift + k]; }
Y añadimos la influencia de los datos de entrada.
shift += total; for(uint i = 0; i < inputs_size; i += 4) { if(total - i > 4) sum += dot((float4)(inputs[shift_in + i], inputs[shift_in + i + 1], inputs[shift_in + i + 2], inputs[shift_in + i + 3]), (float4)(weights[shift + i], weights[shift + i + 1], weights[shift + i + 2], weights[shift + i + 3])); else for(uint k = i; k < total; k++) sum += inputs[shift_in + k] * weights[shift + k]; } sum += weights[shift + inputs_size];
Aplicamos la función de activación correspondiente al valor obtenido.
if(isnan(sum) || isinf(sum)) sum = 0; if(id2 < 3) sum = Activation(sum, 1); else sum = Activation(sum, 0);
Después de esto, guardamos los resultados de las operaciones y sincronizamos los hilos del grupo de trabajo.
Temp[id2] = sum; concatenated[4 * shift_out + id2 * total + id] = sum; //--- barrier(CLK_LOCAL_MEM_FENCE);
Ahora sólo necesitamos calcular el resultado del trabajo del bloque LSTM que es simultáneamente el estado oculto de una celda dada.
if(id2 == 0) { float mem = memory[shift_out + id + total_v * total] = memory[shift_out + id]; float fg = Temp[0]; float ig = Temp[1]; float og = Temp[2]; float nc = Temp[3]; //--- memory[shift_out + id] = mem = mem * fg + ig * nc; output[shift_out + id] = og * Activation(mem, 0); } }
Los resultados de las operaciones se guardan en los elementos correspondientes de las memorias intermedias de datos globales.
Hicimos modificaciones similares en los núcleos de paso de retropropagación. Los más significativos se produjeron en el núcleo LSTM_HiddenGradient. Como en el núcleo feed-forward, no cambiamos la composición de los parámetros externos y sólo ajustamos el espacio de tareas.
__kernel void LSTM_HiddenGradient(__global float *concatenated_gradient, __global float *inputs_gradient, __global float *weights_gradient, __global float *hidden_state, __global float *inputs, __global float *weights, __global float *output, const int hidden_size, const int inputs_size) { uint id = get_global_id(0); uint total = get_global_size(0); uint idv = (uint)get_global_id(1); uint total_v = (uint)get_global_size(1);
Todos los canales independientes trabajan con una matriz de pesos. Por lo tanto, para los coeficientes de ponderación tenemos que recoger los gradientes de error de todos los canales independientes. Cada canal de datos opera en su propio hilo, que combinaremos en grupos de trabajo. Para intercambiar datos entre subprocesos, utilizaremos una matriz en la memoria local.
__local float Temp[LOCAL_ARRAY_SIZE]; uint ls = min(total_v, (uint)LOCAL_ARRAY_SIZE);
A continuación definimos desplazamientos en los buffers de datos.
uint shift_in = idv * inputs_size; uint shift_out = idv * total; uint weights_step = hidden_size + inputs_size + 1;
Creamos un bucle sobre el buffer concatenado de los datos de entrada. Primero simplemente actualizamos el estado oculto.
for(int i = id; i < (hidden_size + inputs_size); i += total) { float inp = 0; if(i < hidden_size) { inp = hidden_state[shift_out + i]; hidden_state[shift_out + i] = output[shift_out + i]; }
Y luego determinamos el gradiente de error en el nivel de entrada.
else { inp = inputs[shift_in + i - hidden_size]; float grad = 0; for(uint g = 0; g < 3 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; grad += temp * (1 - temp) * weights[i + g * weights_step]; } for(uint g = 3 * hidden_size; g < 4 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; grad += temp * (1 - pow(temp, 2.0f)) * weights[i + g * weights_step]; } inputs_gradient[shift_in + i - hidden_size] = grad; }
Aquí también calculamos el gradiente de error a nivel de peso. Primero, restablecemos los valores de la matriz local.
for(uint g = 0; g < 3 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; if(idv < ls) Temp[idv % ls] = 0; barrier(CLK_LOCAL_MEM_FENCE);
Asegúrese de sincronizar el trabajo de los hilos del grupo de trabajo.
A continuación, recopilamos el gradiente de error total de todos los canales de datos. En el primer paso, guardamos valores individuales en una matriz local.
for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += temp * (1 - temp) * inp; barrier(CLK_LOCAL_MEM_FENCE); }
Suponemos que habrá un número relativamente pequeño de canales independientes en los datos analizados. Por lo tanto, recopilamos la suma de los valores de la matriz en un hilo y luego guardamos el valor resultante en el búfer de datos global.
if(idv == 0) { temp = Temp[0]; for(int v = 1; v < ls; v++) temp += Temp[v]; weights_gradient[i + g * weights_step] = temp; } barrier(CLK_LOCAL_MEM_FENCE); }
Del mismo modo, recogemos el gradiente de error para los pesos de New Content.
for(uint g = 3 * hidden_size; g < 4 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; if(idv < ls) Temp[idv % ls] = 0; barrier(CLK_LOCAL_MEM_FENCE); for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += temp * (1 - pow(temp, 2.0f)) * inp; barrier(CLK_LOCAL_MEM_FENCE); } if(idv == 0) { temp = Temp[0]; for(int v = 1; v < ls; v++) temp += Temp[v]; weights_gradient[i + g * weights_step] = temp; } barrier(CLK_LOCAL_MEM_FENCE); } }
Nótese aquí que durante la ejecución de las operaciones del bucle principal, perdimos de vista los factores de ponderación del sesgo bayesiano. Para calcular los gradientes de error correspondientes, implementamos operaciones adicionales de acuerdo con el esquema anterior.
for(int i = id; i < 4 * hidden_size; i += total) { if(idv < ls) Temp[idv % ls] = 0; barrier(CLK_LOCAL_MEM_FENCE); float temp = concatenated_gradient[4 * shift_out + (i + 1) * hidden_size]; if(i < 3 * hidden_size) { for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += temp * (1 - temp); barrier(CLK_LOCAL_MEM_FENCE); } } else { for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += 1 - pow(temp, 2.0f); barrier(CLK_LOCAL_MEM_FENCE); } } if(idv == 0) { temp = Temp[0]; for(int v = 1; v < ls; v++) temp += Temp[v]; weights_gradient[(i + 1) * weights_step] = temp; } barrier(CLK_LOCAL_MEM_FENCE); } }
Se debe prestar especial atención a los puntos de sincronización de hilos. Su número debe ser mínimamente suficiente para garantizar el correcto funcionamiento del algoritmo. Los puntos de sincronización excesivos degradarán el rendimiento y ralentizarán las operaciones. Además, los puntos de sincronización ubicados incorrectamente, donde no todos los subprocesos los alcanzan, pueden provocar que el programa deje de responder.
Con esto, concluimos nuestra revisión de los ajustes de código de OpenCL necesarios para organizar las operaciones de bloque de LSTM bajo canales de datos independientes. En cuanto a las ediciones específicas del programa principal, le animo a que las explore por su cuenta. El código completo de la clase CNeuronLSTMOCL actualizada y todos sus métodos se proporciona en el archivo adjunto.
2.2 Construcción del bloque Mamba
El siguiente paso en nuestro trabajo preparatorio es la construcción del bloque Mamba. El nombre de este bloque recuerda intencionadamente al método que comentamos en el artículo anterior. Los autores de Traj-LLM amplían el uso de modelos de espacio de estados (SSM) y proponen una arquitectura de bloques que puede compararse a un Codificador de transformadores. Pero en este caso, Self-Attention se sustituye por la arquitectura Mamba.
Para implementar el algoritmo propuesto, crearemos una nueva clase CNeuronMambaBlockOCL, cuya estructura se presenta a continuación.
class CNeuronMambaBlockOCL : public CNeuronBaseOCL { protected: uint iWindow; CNeuronMambaOCL cMamba; CNeuronBaseOCL cMambaResidual; CNeuronConvOCL cFF[2]; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronMambaBlockOCL(void) {}; ~CNeuronMambaBlockOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronMambaBlockOCL; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
La funcionalidad básica se heredará de la clase base de capa totalmente conectada CNeuronBaseOCL. Anularemos la lista familiar de métodos virtuales.
Dentro de la estructura de nuestra nueva clase, podemos destacar los objetos internos, cuya funcionalidad exploraremos paso a paso a medida que avancemos con la implementación de métodos. Todos los objetos se declaran estáticamente. Esto nos permite dejar el constructor y el destructor de la clase "vacíos". La inicialización de todos los objetos y variables internas será manejada dentro del método Init.
Como se mencionó anteriormente, el bloque Mamba, por su arquitectura, se asemeja a un Transformer codificador. Este parecido también es evidente en los parámetros del método de inicialización, que proporcionan una definición clara y estructurada de la arquitectura interna del bloque.
bool CNeuronMambaBlockOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
Dentro del cuerpo del método, llamamos al método del mismo nombre de la clase padre, que ya contiene un bloque mínimamente necesario para la validación de parámetros y la inicialización de todos los objetos heredados.
Una vez ejecutado con éxito el método de inicialización de la clase padre, guardamos el tamaño de la ventana de análisis de datos en una variable local para su uso posterior.
iWindow = window;
A continuación pasamos a inicializar los objetos internos. Primero inicializamos la capa de espacio de estados Mamba.
if(!cMamba.Init(0, 0, OpenCL, window, window_key, units_count, optimization, iBatch)) return false;
Le sigue una capa totalmente conectada, cuyo búfer pretendemos utilizar para almacenar los resultados normalizados del análisis selectivo del espacio de estados con conexión residual.
if(!cMambaResidual.Init(0, 1, OpenCL, window * units_count, optimization, iBatch)) return false; cMambaResidual.SetActivationFunction(None);
Después añadimos un bloque FeedForward.
if(!cFF[0].Init(0, 2, OpenCL, window, window, 4 * window, units_count, 1, optimization, iBatch)) return false; cFF[0].SetActivationFunction(LReLU); if(!cFF[1].Init(0, 2, OpenCL, 4 * window, 4 * window, window, units_count, 1, optimization, iBatch)) return false; cFF[1].SetActivationFunction(None);
A continuación, organizamos la sustitución de punteros por búferes de datos para eliminar las operaciones de copia innecesarias.
SetActivationFunction(None); SetGradient(cFF[1].getGradient(), true); //--- return true; }
Tenga en cuenta que aquí solo estamos reemplazando el puntero al búfer de gradiente de error. Esto se debe al hecho de que durante el paso de avance, antes de transferir los resultados a la salida de la capa, se organizará una conexión residual adicional y una normalización de los resultados obtenidos.
No olvides monitorear los resultados de las operaciones en cada paso. Al final del método devolvemos el resultado lógico de las operaciones realizadas al programa que lo llamó.
Después de inicializar el objeto de la clase, pasamos a construir el algoritmo de paso feed-forward, que se implementa en el método FeedForward. Es bastante sencillo.
bool CNeuronMambaBlockOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cMamba.FeedForward(NeuronOCL)) return false;
En los parámetros del método, recibimos un puntero al objeto de la capa anterior, que nos pasa los datos de entrada. Y en el cuerpo del método, pasamos inmediatamente el puntero recibido al modelo selectivo del espacio de estados.
Después de completar con éxito las operaciones del método de paso directo de la capa interna, sumamos los resultados obtenidos y los datos originales, seguido de la normalización de los valores.
if(!SumAndNormilize(cMamba.getOutput(), NeuronOCL.getOutput(), cMambaResidual.getOutput(), iWindow, true)) return false;
A continuación viene el bloque FeedForward.
if(!cFF[0].FeedForward(cMambaResidual.AsObject())) return false; if(!cFF[1].FeedForward(cFF[0].AsObject())) return false;
Organizamos la conexión residual con la posterior normalización de los datos.
if(!SumAndNormilize(cMambaResidual.getOutput(), cFF[1].getOutput(), getOutput(), iWindow, true)) return false; //--- return true; }
Los métodos de retropropagación también tienen un algoritmo bastante sencillo, y sugiero dejarlos para un estudio independiente. Permítanme recordarles que en el archivo adjunto encontrarán el código completo de esta clase y todos sus métodos.
Con esto completamos el trabajo preparatorio y pasamos a construir el algoritmo general del método Traj-LLM.
2.3 Ensamblaje de bloques individuales en un algoritmo coherente
Arriba hemos hecho el trabajo preparatorio y hemos complementado nuestra biblioteca con los «bloques de construcción» que nos faltaban y que utilizaremos para construir el algoritmo Traj-LLM dentro de la clase CNeuronTrajLLMOCL. La estructura de la nueva clase se muestra a continuación.
class CNeuronTrajLLMOCL : public CNeuronBaseOCL { protected: //--- State Encoder CNeuronLSTMOCL cStateRNN; CNeuronConvOCL cStateMLP[2]; //--- Variables Encoder CNeuronTransposeOCL cTranspose; CNeuronLSTMOCL cVariablesRNN; CNeuronConvOCL cVariablesMLP[2]; //--- Context Encoder CNeuronLearnabledPE cStatePE; CNeuronLearnabledPE cVariablesPE; CNeuronMLMHAttentionMLKV cStateToState; CNeuronMLCrossAttentionMLKV cVariableToState; CNeuronMLCrossAttentionMLKV cStateToVariable; CNeuronBaseOCL cContext; CNeuronConvOCL cContextMLP[2]; //--- CNeuronMLMHAttentionMLKV cHighLevelInteraction; CNeuronMambaBlockOCL caMamba[3]; CNeuronMLCrossAttentionMLKV cLaneAware; CNeuronConvOCL caForecastMLP[2]; CNeuronTransposeOCL cTransposeOut; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronTrajLLMOCL(void) {}; ~CNeuronTrajLLMOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronTrajLLMOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Como se puede ver, en la estructura de clases anulamos los mismos métodos virtuales. Sin embargo, esta clase se distingue por un número significativamente mayor de objetos internos, lo cual es bastante esperado para una arquitectura tan compleja. El propósito de estos objetos declarados quedará claro a medida que avancemos con la implementación de los métodos de clase.
Todos los objetos internos de la clase se declaran como estáticos. En consecuencia, el constructor y el destructor permanecen vacíos. La inicialización de todos los objetos declarados se realiza en el método Init.
En los parámetros del método recibimos las constantes principales que se utilizarán para inicializar los objetos anidados. Aquí vemos los nombres de los parámetros que ya nos resultan familiares. Sin embargo, tenga en cuenta que algunos de ellos pueden tener diferentes funcionalidades para objetos internos individuales.
bool CNeuronTrajLLMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * forecast, optimization_type, batch)) return false;
Siguiendo una tradición ya establecida, el primer paso dentro del método Init es llamar al método de la clase padre del mismo nombre. Como sabes, este método ya realiza la validación de parámetros básicos y la inicialización de todos los objetos heredados. Después de la ejecución exitosa del método de la clase padre, procedemos a inicializar los objetos internos declarados.
Basándonos en la experiencia adquirida en la construcción de modelos anteriores, asumimos que la entrada del modelo es una matriz que describe la situación actual del mercado. Cada fila de esta matriz contiene un conjunto de parámetros que caracterizan una vela de mercado individual, incluidos los valores correspondientes de los indicadores analizados.
Según el algoritmo Traj-LLM, los datos de entrada obtenidos se pasan primero al bloque Sparse Context Encoder, que incluye un codificador de agente y un codificador de carril. En nuestro caso, estos corresponden a codificadores de estados ambientales (datos de barras individuales) y trayectorias históricas de parámetros analizados (indicadores).
El codificador de estados se construirá a partir de un bloque recurrente para analizar barras individuales y dos capas convolucionales posteriores, que implementarán la operación MLP dentro de canales de información independientes.
//--- State Encoder if(!cStateRNN.Init(0, 0, OpenCL, window_key, units_count, optimization, iBatch) || !cStateRNN.SetInputs(window)) return false; if(!cStateMLP[0].Init(0, 1, OpenCL, window_key, window_key, 4 * window_key, units_count, optimization, iBatch)) return false; cStateMLP[0].SetActivationFunction(LReLU); if(!cStateMLP[1].Init(0, 2, OpenCL, 4 * window_key, 4 * window_key, window_key, units_count, optimization, iBatch)) return false;
Los parámetros del método incluyen las constantes principales utilizadas para inicializar objetos incrustados. Aquí vemos nombres de parámetros familiares, pero es importante tener en cuenta que algunos de ellos pueden cumplir funciones diferentes para objetos internos específicos.
//--- Variables Encoder if(!cTranspose.Init(0, 3, OpenCL, units_count, window, optimization, iBatch)) return false; if(!cVariablesRNN.Init(0, 4, OpenCL, window_key, window, optimization, iBatch) || !cVariablesRNN.SetInputs(units_count)) return false; if(!cVariablesMLP[0].Init(0, 5, OpenCL, window_key, window_key, 4 * window_key, window, optimization, iBatch)) return false; cVariablesMLP[0].SetActivationFunction(LReLU); if(!cVariablesMLP[1].Init(0, 6, OpenCL, 4 * window_key, 4 * window_key, window_key, window, optimization, iBatch)) return false;
Es importante señalar que, según el algoritmo Traj-LLM, posteriormente se realiza un análisis conjunto de Agentes y Carriles. Por lo tanto, la salida de los codificadores produce vectores que representan elementos individuales de las secuencias (estados ambientales o trayectorias históricas de indicadores analizados) de dimensiones idénticas. Al mismo tiempo, se permiten diferencias en las longitudes de las secuencias, ya que el número de estados ambientales analizados a menudo no es igual al número de parámetros analizados que describen esos estados.
Siguiendo el siguiente paso del algoritmo Traj-LLM, las salidas de los codificadores se pasan al bloque Fusion, donde se lleva a cabo un análisis exhaustivo de las interdependencias entre los elementos individuales de la secuencia mediante los mecanismos Self-Attention y Cross-Attention. Sin embargo, es bien sabido que para mejorar la eficiencia de los mecanismos de atención, se deben agregar etiquetas de codificación posicional a los elementos de secuencia. Para lograr esta funcionalidad, introduciremos dos capas de codificación posicional entrenables.
//--- Position Encoder if(!cStatePE.Init(0, 7, OpenCL, cStateMLP[1].Neurons(), optimization, iBatch)) return false; if(!cVariablesPE.Init(0, 8, OpenCL, cVariablesMLP[1].Neurons(), optimization, iBatch)) return false;
Y sólo entonces analizamos las dependencias entre estados individuales en el bloque Self-Attention.
//--- Context if(!cStateToState.Init(0, 9, OpenCL, window_key, window_key, heads, heads / 2, units_count, 2, 1, optimization, iBatch)) return false;
Luego realizamos un análisis de dependencia cruzada en los siguientes 2 bloques Cross-Attention.
if(!cStateToVariable.Init(0, 10, OpenCL, window_key, window_key, heads, window_key, heads / 2, units_count, window, 2, 1, optimization, iBatch)) return false; if(!cVariableToState.Init(0, 11, OpenCL, window_key, window_key, heads, window_key, heads / 2, window, units_count, 2, 1, optimization, iBatch)) return false;
Las representaciones enriquecidas de estados y trayectorias se concatenan en un solo tensor.
if(!cContext.Init(0, 12, OpenCL, window_key * (units_count + window), optimization, iBatch)) return false;
Después, los datos pasan por otro MLP.
if(!cContextMLP[0].Init(0, 13, OpenCL, window_key, window_key, 4 * window_key, window + units_count, optimization, iBatch)) return false; cContextMLP[0].SetActivationFunction(LReLU); if(!cContextMLP[1].Init(0, 14, OpenCL, 4 * window_key, 4 * window_key, window_key, window + units_count, optimization, iBatch)) return false;
A continuación viene el bloque de modelado de interacciones de alto nivel. Aquí los autores del método Traj-LLM utilizan un modelo de lenguaje preentrenado, que nosotros sustituiremos por un bloque Transformer.
if(!cHighLevelInteraction.Init(0, 15, OpenCL, window_key, window_key, heads, heads / 2, window + units_count, 4, 2, optimization, iBatch)) return false;
A continuación viene el bloque cognitivo de aprendizaje de las probabilidades de movimiento posterior, teniendo en cuenta los carriles de tráfico existentes. Aquí utilizamos 3 bloques Mamba consecutivos que tienen las mismas arquitecturas.
for(int i = 0; i < int(caMamba.Size()); i++) { if(!caMamba[i].Init(0, 16 + i, OpenCL, window_key, 2 * window_key, window + units_count, optimization, iBatch)) return false; }
Los valores obtenidos se comparan con las trayectorias históricas en el bloque Cross-Attention.
if(!cLaneAware.Init(0, 19, OpenCL, window_key, window_key, heads, window_key, heads / 2, window, window + units_count, 2, 1, optimization, iBatch)) return false;
Y, por último, utilizamos MLP para predecir trayectorias posteriores de canales de datos independientes.
if(!caForecastMLP[0].Init(0, 20, OpenCL, window_key, window_key, 4 * forecast, window, optimization, iBatch)) return false; caForecastMLP[0].SetActivationFunction(LReLU); if(!caForecastMLP[1].Init(0, 21, OpenCL, 4 * forecast, 4 * forecast, forecast, window, optimization, iBatch)) return false; caForecastMLP[1].SetActivationFunction(TANH); if(!cTransposeOut.Init(0, 22, OpenCL, window, forecast, optimization, iBatch)) return false;
Tenga en cuenta que el tensor de trayectoria previsto se transpone para llevar la información a la representación de los datos originales.
SetOutput(cTransposeOut.getOutput(), true); SetGradient(cTransposeOut.getGradient(), true); SetActivationFunction((ENUM_ACTIVATION)caForecastMLP[1].Activation()); //--- return true; }
También utilizamos sustitución de puntero de búfer de datos para evitar operaciones de copia innecesarias. Después de eso, devolvemos el resultado lógico de las operaciones del método al programa que lo llama.
Una vez completado el trabajo sobre el método de inicialización de la clase, pasamos a construir el algoritmo de paso feed-forward, que implementamos en el método FeedForward.
bool CNeuronTrajLLMOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- State Encoder if(!cStateRNN.FeedForward(NeuronOCL)) return false; if(!cStateMLP[0].FeedForward(cStateRNN.AsObject())) return false; if(!cStateMLP[1].FeedForward(cStateMLP[0].AsObject())) return false;
En los parámetros del método recibimos un puntero a un objeto con los datos iniciales, que pasamos inmediatamente por el bloque codificador de estado.
A continuación, transponemos los datos originales y codificamos las trayectorias históricas de los parámetros analizados que describen el estado del entorno.
//--- Variables Encoder if(!cTranspose.FeedForward(NeuronOCL)) return false; if(!cVariablesRNN.FeedForward(cTranspose.AsObject())) return false; if(!cVariablesMLP[0].FeedForward(cVariablesRNN.AsObject())) return false; if(!cVariablesMLP[1].FeedForward(cVariablesMLP[0].AsObject())) return false;
Añadimos codificación posicional a los datos obtenidos.
//--- Position Encoder if(!cStatePE.FeedForward(cStateMLP[1].AsObject())) return false; if(!cVariablesPE.FeedForward(cVariablesMLP[1].AsObject())) return false;
Después enriquecemos los datos con el contexto de las interdependencias.
//--- Context if(!cStateToState.FeedForward(cStatePE.AsObject())) return false; if(!cStateToVariable.FeedForward(cStateToState.AsObject(), cVariablesPE.getOutput())) return false; if(!cVariableToState.FeedForward(cVariablesPE.AsObject(), cStateToVariable.getOutput())) return false;
Los datos enriquecidos se concatenan en un único tensor.
if(!Concat(cStateToVariable.getOutput(), cVariableToState.getOutput(), cContext.getOutput(), cStateToVariable.Neurons(), cVariableToState.Neurons(), 1)) return false;
Y luego es procesado por un MLP.
if(!cContextMLP[0].FeedForward(cContext.AsObject())) return false; if(!cContextMLP[1].FeedForward(cContextMLP[0].AsObject())) return false;
A continuación viene el bloque del análisis de dependencias de alto nivel.
//--- Lane aware if(!cHighLevelInteraction.FeedForward(cContextMLP[1].AsObject())) return false;
Y el modelo de espacio de estados.
if(!caMamba[0].FeedForward(cHighLevelInteraction.AsObject())) return false; for(int i = 1; i < int(caMamba.Size()); i++) { if(!caMamba[i].FeedForward(caMamba[i - 1].AsObject())) return false; }
A continuación, comparamos las trayectorias históricas con los resultados de nuestro análisis.
if(!cLaneAware.FeedForward(cVariablesPE.AsObject(), caMamba[caMamba.Size() - 1].getOutput())) return false;
Y a partir de los datos obtenidos, hacemos una previsión del cambio más probable en los parámetros analizados.
//--- Forecast if(!caForecastMLP[0].FeedForward(cLaneAware.AsObject())) return false; if(!caForecastMLP[1].FeedForward(caForecastMLP[0].AsObject())) return false;
Después transponemos los valores predichos a la representación de los datos de entrada.
if(!cTransposeOut.FeedForward(caForecastMLP[1].AsObject())) return false; //--- return true; }
Por último, el método devuelve al programa de llamada un valor booleano que indica el éxito o el fracaso de las operaciones realizadas.
La siguiente etapa de nuestro trabajo implica construir algoritmos de retropropagación. Aquí, debemos implementar la distribución de gradientes de error en todos los objetos de acuerdo con su influencia en la salida final, así como el ajuste posterior de los parámetros entrenables destinados a minimizar el error.
Si bien actualizar los parámetros es relativamente sencillo (dado que todos los parámetros entrenables están contenidos dentro de los objetos internos (anidados) y, por lo tanto, es suficiente llamar secuencialmente a los métodos de actualización de parámetros de estos objetos internos), distribuir los gradientes de error presenta un desafío mucho más complejo e intrincado.
La distribución de los gradientes de error se lleva a cabo en total acuerdo con el algoritmo del paso de avance, pero en orden inverso. Y aquí, hay que tener en cuenta que nuestro pase de avance no es tan "avanzado", si me permiten el juego de palabras. Se pueden identificar varios flujos de información paralelos en el paso hacia adelante. Y ahora debemos recopilar los gradientes de error de todos estos flujos.
El algoritmo de distribución del gradiente de error se implementará en el método calcInputGradients. Los parámetros de este método incluyen un puntero al objeto capa anterior, al que debemos pasar el gradiente de error, distribuido en función de la influencia de los datos de entrada iniciales sobre la salida final del modelo. Al principio del método, comprobamos inmediatamente la validez del puntero recibido, ya que si el puntero no es correcto, todo el proceso posterior carece de sentido.
bool CNeuronTrajLLMOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Es importante recordar que en el momento en que se invoca este método, el gradiente de error de la capa actual ya se ha almacenado en su búfer de gradiente. Este valor se escribió durante la ejecución del método correspondiente en la capa posterior de nuestro modelo. Además, gracias al mecanismo de sustitución de punteros que organizamos anteriormente, este mismo gradiente de error también está presente en el búfer de nuestra capa interna que transpone los resultados de la predicción. Así, comenzamos el proceso de distribución del gradiente haciendo pasar este gradiente por el MLP encargado de predecir el movimiento futuro.
//--- Forecast if(!caForecastMLP[1].calcHiddenGradients(cTransposeOut.AsObject())) return false; if(!caForecastMLP[0].calcHiddenGradients(caForecastMLP[1].AsObject())) return false;
Una vez completado esto, propagamos el gradiente de error a la capa que alinea las trayectorias históricas de los parámetros analizados con los resultados del análisis cognitivo.
//--- Lane aware if(!cLaneAware.calcHiddenGradients(caForecastMLP[0].AsObject())) return false;
Aquí es fundamental tener en cuenta que el bloque de atención cruzada coincide con datos de dos flujos de información separados. En consecuencia, debemos distribuir el gradiente de error en estos dos flujos, proporcionalmente a su influencia en el resultado final del modelo.
if(!cVariablesPE.calcHiddenGradients(cLaneAware.AsObject(), caMamba[caMamba.Size() - 1].getOutput(), caMamba[caMamba.Size() - 1].getGradient(), (ENUM_ACTIVATION)caMamba[caMamba.Size() - 1].Activation())) return false;
A continuación, pasamos el gradiente de error a través del modelo de espacio de estados.
for(int i = int(caMamba.Size()) - 2; i >= 0; i--) if(!caMamba[i].calcHiddenGradients(caMamba[i + 1].AsObject())) return false;
A continuación, a través del bloque de análisis de dependencias de alto nivel.
if(!cHighLevelInteraction.calcHiddenGradients(caMamba[0].AsObject())) return false;
Usando el contexto MLP, empujamos el gradiente de error un nivel más profundo, al buffer de datos concatenados de estados y trayectorias.
if(!cContextMLP[1].calcHiddenGradients(cHighLevelInteraction.AsObject())) return false; if(!cContextMLP[0].calcHiddenGradients(cContextMLP[1].AsObject())) return false; if(!cContext.calcHiddenGradients(cContextMLP[0].AsObject())) return false;
Y ahora viene la parte más intrincada y crucial. Aquí es necesaria la máxima atención para no pasar por alto ningún detalle.
En este punto, necesitamos dividir el gradiente del búfer concatenado en dos flujos separados. No hay nada complicado en ello. Simplemente podemos ejecutar el método de desconcatenación, especificando los buffers de datos apropiados. En nuestro caso, se trata de las dos capas de atención cruzada: de trayectorias a estados y de estados a trayectorias. Sin embargo, el desafío está en el siguiente paso. Una vez que comenzamos a pasar el gradiente de error a través del bloque de atención cruzada de trayectorias a estados, este bloque también generará un gradiente que debe pasarse a la capa de atención cruzada de estados a trayectorias. Así, para asegurarnos de que no perdemos ninguna parte de la información del gradiente durante este proceso de varios pasos, debemos guardarla en un búfer temporal. Pero dentro de esta clase, hemos creado muchos objetos incluso sin buffers auxiliares. Y entre estos objetos, muchos simplemente esperan su turno. Entonces, usémoslos para el almacenamiento temporal de información. Utilicemos la capa de codificación posicional asociada al bloque de atención cruzada de estados a trayectorias como soporte temporal de este gradiente parcial.
if(!DeConcat(cStatePE.getGradient(), cVariableToState.getGradient(), cContext.getGradient(), cStateToVariable.Neurons(), cVariableToState.Neurons(), 1)) return false;
Además, recordamos que el búfer de gradiente de la capa de codificación posicional para trayectorias ya contiene gradientes de error útiles. Para evitar perder esta valiosa información, la transferimos temporalmente al buffer de gradiente del MLP dentro del codificador correspondiente.
if(!SumAndNormilize(cVariablesPE.getGradient(), cVariablesPE.getGradient(), cVariablesMLP[1].getGradient(), 1, false)) return false;
Una vez que hemos asegurado la preservación de toda la información de gradiente necesaria, procedemos a distribuir el gradiente de error a través del bloque de atención cruzada alineando trayectorias con estados.
if(!cVariablesPE.calcHiddenGradients(cVariableToState.AsObject(), cStateToVariable.getOutput(), cStateToVariable.getGradient(), (ENUM_ACTIVATION)cStateToVariable.Activation())) return false;
Ahora, podemos sumar los gradientes de error a nivel del bloque de atención cruzada alineando estados a trayectorias, acumulándolos de ambos vapores.
if(!SumAndNormilize(cStateToVariable.getGradient(), cStatePE.getGradient(), cStateToVariable.getGradient(), 1, false, 0, 0, 0, 1)) return false;
Sin embargo, en el siguiente paso, tenemos que volver a pasar el gradiente de error a la capa de codificación posicional de trayectorias, por tercera vez. Por lo tanto, primero agregamos los gradientes de error existentes en ambos flujos de datos.
if(!SumAndNormilize(cVariablesPE.getGradient(), cVariablesMLP[1].getGradient(), cVariablesMLP[1].getGradient(), 1, false, 0, 0, 0, 1)) return false;
Sólo después de esta agregación, invocamos el método de distribución de gradiente del bloque de atención cruzada alineando los estados a las trayectorias.
if(!cStateToState.calcHiddenGradients(cStateToVariable.AsObject(), cVariablesPE.getOutput(), cVariablesPE.getGradient(), (ENUM_ACTIVATION)cVariablesPE.Activation())) return false;
En este punto, podemos finalmente sumar todos los gradientes de error en la capa de codificación posicional para trayectorias, combinándolos desde tres fuentes diferentes.
if(!SumAndNormilize(cVariablesPE.getGradient(), cVariablesMLP[1].getGradient(), cVariablesPE.getGradient(), 1, false, 0, 0, 0, 1)) return false;
A continuación, propagamos el gradiente de error a la capa de codificación posicional de los estados.
if(!cStatePE.calcHiddenGradients(cStateToState.AsObject())) return false;
Cabe señalar que las capas de codificación posicional operan en dos flujos de datos independientes y paralelos, y debemos propagar los gradientes de error respectivos hasta los codificadores apropiados en cada flujo:
//--- Position Encoder if(!cStateMLP[1].calcHiddenGradients(cStatePE.AsObject())) return false; if(!cVariablesMLP[1].calcHiddenGradients(cVariablesPE.AsObject())) return false;
A continuación, pasamos los gradientes de error a través de dos codificadores paralelos, cada uno de los cuales trabaja en el mismo tensor de entrada de datos sin procesar. Aquí nos encontramos con la necesidad de fusionar los gradientes de error de estos dos flujos paralelos en un único búfer de gradiente. Nuevamente necesitamos un buffer de datos auxiliar, que no creamos. Además, en esta etapa, todos nuestros objetos internos ya están llenos de datos esenciales que no podemos sobrescribir.
Sin embargo, hay un matiz sutil pero crítico. La capa de transposición de datos, que utilizamos para reorganizar los datos de entrada sin procesar antes de la codificación de la trayectoria, no contiene parámetros entrenables. Su búfer de gradiente de error solo se utiliza para pasar datos a la capa anterior. Además, el tamaño de este buffer se adapta perfectamente a nuestras necesidades, ya que estamos tratando con los mismos datos pero en un orden diferente. Maravilloso. Propagamos el gradiente de error a través del bloque de codificación de trayectoria.
//--- Variables Encoder if(!cVariablesMLP[0].calcHiddenGradients(cVariablesMLP[1].AsObject())) return false; if(!cVariablesRNN.calcHiddenGradients(cVariablesMLP[0].AsObject())) return false; if(!cTranspose.calcHiddenGradients(cVariablesRNN.AsObject())) return false; if(!NeuronOCL.FeedForward(cTranspose.AsObject())) return false;
Y transferimos el gradiente de error obtenido al buffer de la capa de transposición de datos.
if(!SumAndNormilize(NeuronOCL.getGradient(), NeuronOCL.getGradient(), cTranspose.getGradient(), 1, false)) return false;
De manera similar, pasamos el gradiente de error a través del codificador de estado.
//--- State Encoder if(!cStateMLP[0].calcHiddenGradients(cStateMLP[1].AsObject())) return false; if(!cStateRNN.calcHiddenGradients(cStateMLP[0].AsObject())) return false; if(!NeuronOCL.calcHiddenGradients(cStateRNN.AsObject())) return false;
Luego, sumamos los gradientes de error de ambas corrientes.
if(!SumAndNormilize(cTranspose.getGradient(), NeuronOCL.getGradient(), NeuronOCL.getGradient(), 1, false, 0, 0, 0, 1)) return false; //--- return true; }
Finalmente, devolvemos el resultado lógico de todas las operaciones al programa que las realiza, indicando éxito o fracaso.
Con esto concluye la descripción de los algoritmos de la clase CNeuronTrajLLMOCL. Puedes encontrar el código completo de esta clase y todos sus métodos en el archivo adjunto.
2.4 Arquitectura del modelo
Ahora podemos integrar sin problemas esta clase en nuestro modelo para evaluar la eficiencia práctica del enfoque propuesto utilizando datos históricos reales. El algoritmo Traj-LLM está diseñado específicamente para predecir trayectorias futuras. Utilizamos métodos similares en el Codificador de Estado Ambiental (Environmental State Encoder, ESE).
Tenga en cuenta que nuestra interpretación de la aplicación práctica de Traj-LLM se ha implementado dentro de un bloque compuesto unificado. Esto nos permite mantener una estructura de modelo externo limpia y sencilla sin sacrificar la funcionalidad.
Como es habitual, se introducen en la entrada del modelo datos brutos, sin procesar, que describen la situación actual del mercado.
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } //--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
El tratamiento primario de los datos se realiza en la capa de normalización por lotes.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
A continuación, los datos se transfieren inmediatamente a nuestro nuevo bloque Traj-LLM. Es difícil llamar a una solución arquitectónica tan compleja una capa neuronal.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTrajLLMOCL; descr.window = BarDescr; //window descr.window_out = EmbeddingSize; //Inside Dimension descr.count = HistoryBars; //Units prev_count = descr.layers = NForecast; //Forecast descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
A la salida del bloque ya tenemos valores predichos, a los que añadimos los parámetros estadísticos de los valores originales.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
Luego alineamos los resultados en el dominio de la frecuencia.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
La arquitectura de los demás modelos se mantuvo sin cambios. Así como el código de todos los programas utilizados. Podrás estudiarlos en el código adjunto a continuación. Estamos pasando a la siguiente etapa de nuestro trabajo.
3. Pruebas
Hemos completado un trabajo sustancial implementando el enfoque Traj-LLM en MQL5. Y ahora es el momento de evaluar los resultados prácticos. Nuestro objetivo es entrenar los modelos con datos históricos reales y evaluar su desempeño en conjuntos de datos nunca antes vistos.
Como se mencionó anteriormente, los cambios en la arquitectura del modelo no afectaron la estructura de los datos de entrada ni el formato de sus salidas. Esto nos permite confiar en conjuntos de datos de entrenamiento previamente compilados para fines de preentrenamiento.
En la primera etapa, entrenamos al codificador de estado ambiental para pronosticar los próximos movimientos de precios. El entrenamiento continúa hasta que el error de predicción se estabilice en un nivel aceptable. En particular, no actualizamos ni modificamos el conjunto de datos de entrenamiento durante esta fase. En esta etapa, el modelo demostró resultados prometedores. Demostró una buena capacidad para identificar las próximas tendencias de precios.
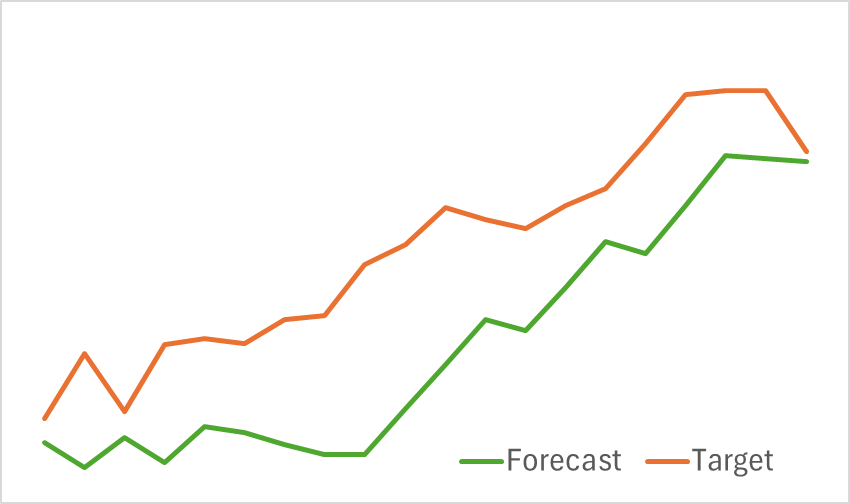
En la segunda fase, realizamos un entrenamiento iterativo de la política de comportamiento de Actores y de la función de recompensas Críticas. La formación del modelo Crítico cumple una función de apoyo. Proporcionaba ajustes a las acciones del Actor. Sin embargo, nuestro objetivo principal es desarrollar una política rentable para el Actor. Para garantizar una evaluación fiable de las acciones del Actor, durante esta fase actualizamos periódicamente el conjunto de datos de entrenamiento. Tras varias iteraciones, desarrollamos con éxito una política capaz de generar beneficios en el conjunto de datos de prueba.
Permítanme recordarles que todos los modelos se entrenan utilizando datos históricos del símbolo EURUSD para 2023, marco temporal H1. Las pruebas se realizan con datos de enero de 2024, manteniendo inalterados todos los demás parámetros.
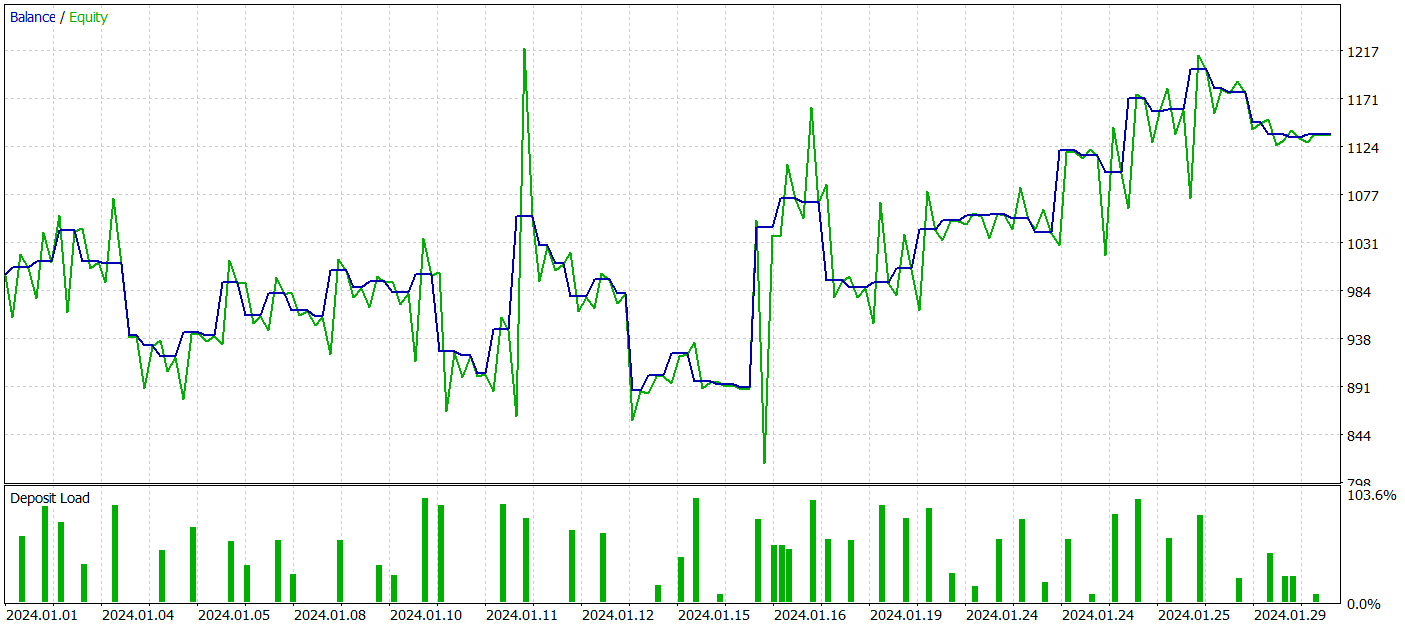
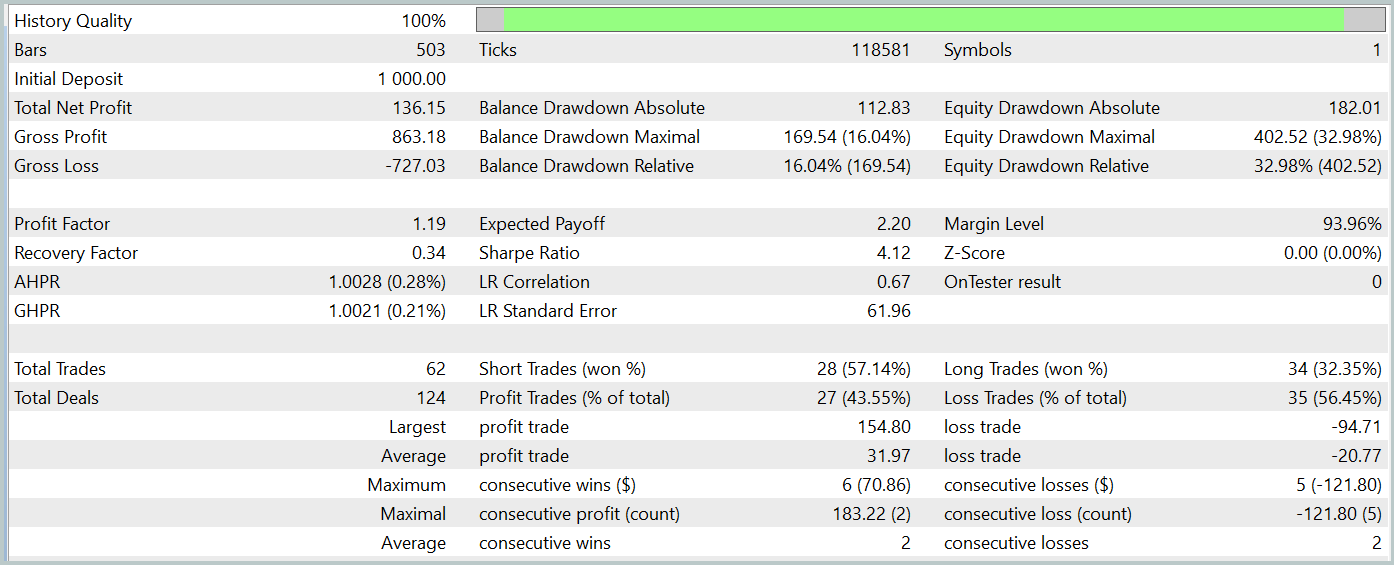
Durante el periodo de prueba, nuestro modelo ejecutó 62 operaciones y 27 de ellas (43,55%) se cerraron con beneficios. Sin embargo, debido a que las operaciones rentables máximas y medias son más de la mitad de las variables de las operaciones perdedoras, en conjunto se obtuvo un beneficio del 13,6% durante el periodo de prueba. Y el factor de beneficio estaba en 1,19. Sin embargo, un motivo de preocupación importante es la reducción de los fondos propios, que alcanzó casi el 33%. Está claro que, en su forma actual, el modelo aún no es adecuado para el comercio en el mundo real y requiere nuevas mejoras.
Conclusión
En este artículo, exploramos el nuevo método Traj-LLM, cuyos autores proponen una perspectiva novedosa en la aplicación de grandes modelos lingüísticos (LLM). Este método demuestra cómo las capacidades de LLM pueden adaptarse para predecir valores futuros de diversas series temporales, permitiendo así predicciones más precisas y adaptables en condiciones de incertidumbre y caos.
En la sección práctica, implementamos nuestra propia interpretación del enfoque propuesto y lo probamos con datos históricos reales. Aunque los resultados aún no son perfectos, son prometedores e indican un potencial de desarrollo.
Referencias
- Traj-LLM: A New Exploration for Empowering Trajectory Prediction with Pre-trained Large Language Models
- Otros artículos de esta serie
Programas utilizados en el artículo
| # | Emitido a | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor Experto | Ejemplo de colección (EA) |
| 2 | ResearchRealORL.mq5 | Asesor Experto | EA para la recogida de ejemplos mediante el método Real-ORL |
| 3 | Study.mq5 | Asesor Experto | Entrenamiento de modelos (EA) |
| 4 | StudyEncoder.mq5 | Asesor Experto | Entrenamiento de codificadores (EA) |
| 5 | Test.mq5 | Asesor Experto | Prueba de modelos (EA) |
| 6 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema |
| 7 | NeuroNet.mqh | Biblioteca de clases | Una biblioteca de clases para crear una red neuronal |
| 8 | NeuroNet.cl | Código base | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15595
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Algoritmo de Algas Artificiales (Artificial Algae Algorithm, AAA)
Algoritmo de Algas Artificiales (Artificial Algae Algorithm, AAA)
 Redes neuronales en el trading: Análisis de nubes de puntos (PointNet)
Redes neuronales en el trading: Análisis de nubes de puntos (PointNet)
 Optimización de la quimiotaxis bacteriana - Bacterial Chemotaxis Optimisation (BCO)
Optimización de la quimiotaxis bacteriana - Bacterial Chemotaxis Optimisation (BCO)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso