Ciclos y Forex
440
1
Introducción
La ciclicidad es uno de los principales factores de nuestro mundo. Los ciclos permiten a las personas organizar sus vidas. Conociendo el orden cíclico, podemos predecir el futuro. Por ejemplo, puedo afirmar con seguridad que 2025 comienza el 1 de enero.
Los ciclos del mercado de divisas pueden estar relacionados con diversos factores: noticias económicas, hora del día, días de la semana, meses del año y estaciones. El estudio de estos ciclos puede ayudar al operador a predecir la evolución futura de los precios y a tomar decisiones más informadas.
Los ciclos pueden encontrarse en lugares insospechados. Incluso el interés por los ciclos y las ondas en Forex es de naturaleza cíclica:
- Artículo «La implementación del análisis automático de las Ondas de Elliott en MQL5» - 2011
- Artículo «Ondas de Wolfe» - 2017
- Artículo «La estacionalidad en el mercado de divisas y oportunidades para aprovecharla» - 2023
- Artículo «Filtrado de estacionalidad y período de tiempo para modelos de Deep Learning ONNX con Python para EA» - 2024.
Como puede ver, los artículos se publicaron una vez cada 6 años. Sólo el último artículo rompió este ciclo. Pero, ¿quizás haya alguna otra explicación para esta desviación?
Intentemos encontrar respuestas a dos preguntas. ¿Existen ciclos en el movimiento de precios? Y si existen ¿Cómo pueden utilizarse en el comercio?
Buscando ciclos
En el trading, los ciclos pueden asociarse con tendencias o patrones recurrentes del mercado. Por ejemplo, el precio puede fluctuar dentro de un canal determinado. Y tal comportamiento puede continuar por mucho tiempo.
Podemos utilizar análisis espectral, polinomios trigonométricos, periodogramas, función de autocorrelación y algoritmos de detección de ciclos para extraer el componente cíclico de una serie temporal.
También podemos utilizar una media móvil simple (Simple Moving Average, SMA) para encontrar el ciclo. Este método es el más simple y visual. Supongamos que tenemos una serie temporal que es un ciclo con periodo N. Si aplicamos a esta serie un SMA con el mismo periodo, obtendremos un nivel medio, alrededor del cual se producen las oscilaciones. El uso de SMA con otros periodos permite obtener procesos oscilatorios distintos del original. Pero a pesar de estas diferencias, utilizando tales medias es posible restablecer los parámetros del ciclo original.
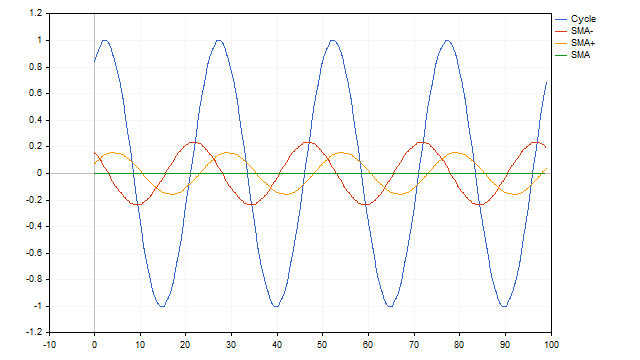
Algunas series de tiempo pueden ser una suma de ciclos con diferentes períodos. En este caso, los promedios móviles también funcionarán bien. El algoritmo es bastante simple. Primero, restamos los valores del promedio con el período más grande de la serie original. Restamos los valores del siguiente promedio de los restos resultantes y continuamos esta operación hasta que nos quedemos sólo con ceros. Necesitamos más SMA.
Las medias móviles también se adaptan con la misma facilidad al modelo de series temporales de ciclo + tendencia. En este caso, la SMA actuará como detector de ciclo y tendencia al mismo tiempo.
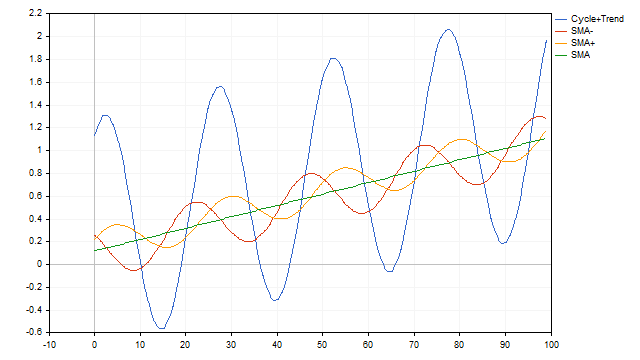
Hasta ahora, hemos aplicado una media móvil a una serie temporal determinista: las ecuaciones de ciclo y tendencia estaban rígidamente definidas y no cambiaban con el tiempo. Agreguemos algo de aleatoriedad a la serie temporal original y veamos cómo SMA maneja esta situación. Tomaremos la amplitud del ciclo como 100%. Supongamos que la amplitud puede cambiar aleatoriamente dentro del 10% en cualquier dirección. La velocidad de la tendencia puede variar del 0 al 1%. Y agreguemosle un 10% de ruido blanco. SMA también consigue afrontar esta tarea con éxito.
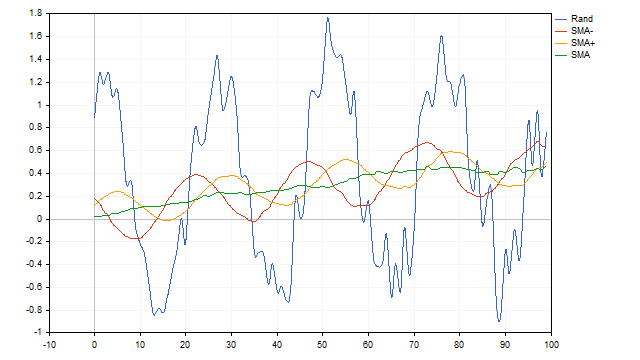
Parece que hemos encontrado el indicador perfecto. Desafortunadamente, las desventajas de la SMA pueden ser mayores que sus ventajas. La media móvil no podrá ordenar ciclos que consten únicamente de medias ondas positivas o negativas. Además, este indicador tiene baja resolución. En términos simples, no será posible aislar una señal útil si el ruido excede un cierto límite.
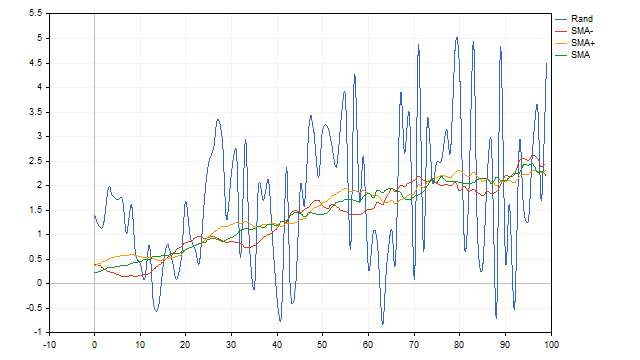
Otro pequeño inconveniente es que antes de utilizar SMA es recomendable saber de antemano qué ciclo necesitamos seleccionar. Aquí nos enfrentamos a dos preguntas:
- ¿Existe un ciclo en la serie temporal que estamos estudiando?
- Si existe un ciclo, ¿cómo podemos conocer sus parámetros?
Para responder a estas preguntas podemos utilizar el mapeo de puntos.
Mira este gráfico. ¿Puedes decirme qué muestra?
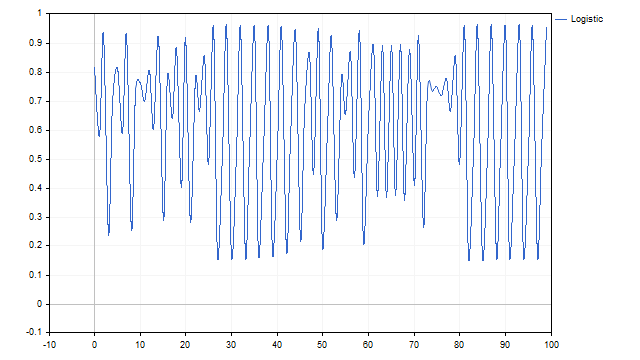
Es posible que este sea un gráfico de la suma de varios ciclos. O puede que sea parte de El plan maestro de los Daleks.
Entonces, tenemos una serie de tiempo unidimensional con valores Z[i]. En base a esto, construiré un gráfico bidimensional, y las coordenadas de cada punto de este gráfico se establecerán de acuerdo a la siguiente regla (indexando como en series de tiempo):
X[i] = Z[i];
Y[i] = Z[i-1].
El objetivo de esta transformación es mostrar la relación entre dos valores adyacentes de la serie temporal original. Por ejemplo, este oscuro gráfico proporciona la siguiente visualización.
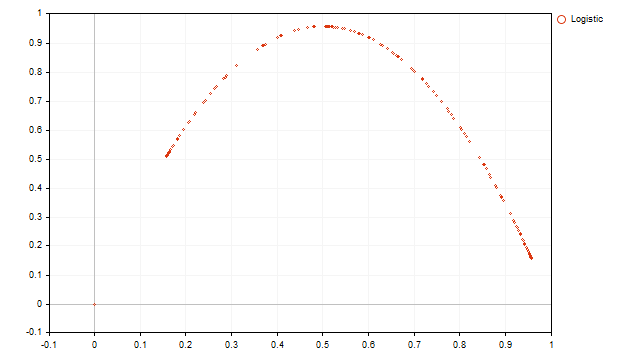
Podemos ver una parábola normal. Conociendo las propiedades de la parábola, podemos formular la ecuación de la serie temporal original:
Para hallar los coeficientes de las ecuaciones, podemos utilizar el método de los mínimos cuadrados. Como resultado, obtendremos un mapa logístico, que se utilizó para generar los valores de la serie temporal original.
El método del diagrama de puntos puede aplicarse a cualquier serie temporal, pero no siempre ofrece una representación clara y precisa de la misma.
Por ejemplo, examinemos el generador de números pseudoaleatorios. Su gráfico se ve así:
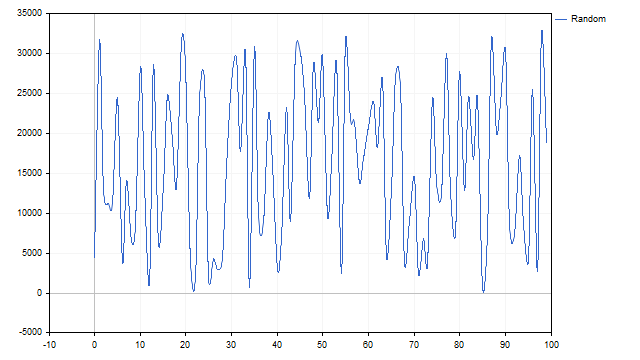
Se ve claramente la adición de varios ciclos. Ahora lo resolveremos todo. Construya una representación de puntos de los valores obtenidos.
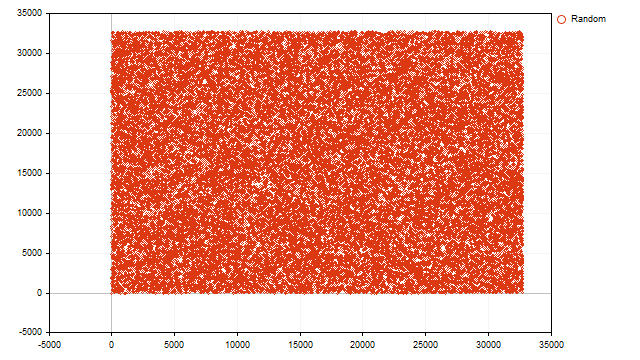
Todos los puntos llenan uniformemente todo el plano. De esto podemos concluir que el valor actual del generador de números pseudoaleatorios no depende del anterior y todas las coincidencias son aleatorias.
La visualización de un proceso cíclico parece cíclica:
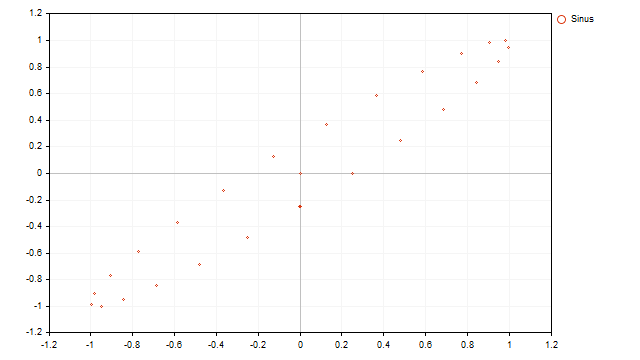
Ahora veamos cómo se ve la representación punteada de los precios reales:
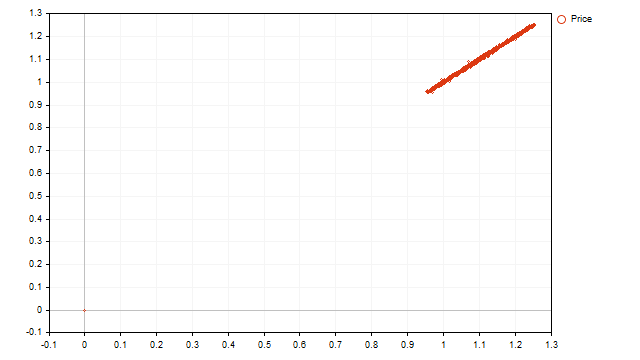
Vemos una tendencia lineal creciente y sin ciclos. Sin embargo, es demasiado pronto para que caigamos en la desesperación. Observando esta imagen podemos sacar las siguientes conclusiones:
- La tendencia es el factor principal que determina el movimiento de los precios;
- La fuerza de la tendencia es suficientemente grande y puede enmascarar procesos cíclicos.
La conclusión es obvia: necesitamos más formas de identificar ciclos.
Ciclos y aleatoriedad
En 1927, Eugen Slutsky publicó el artículo "Adición de causas aleatorias como fuente de procesos cíclicos" (Addition of random causes as a source of cyclic processes). En este trabajo demostró brillantemente que los procesos cíclicos y ondulatorios pueden surgir como resultado de la interacción (por ejemplo, la adición) de variables aleatorias.
Probemos cómo funciona esta teoría en series de tiempo financieras. Tomaremos los precios de diferentes símbolos como variable aleatoria inicial. En este caso, haremos lo siguiente: para el par actual, tomaremos el precio de la barra actual, para todos los símbolos subsiguientes, tomaremos el precio de 1 barra atrás. Entonces, la ecuación para la variable aleatoria será aproximadamente la siguiente:
Por tanto, la variable aleatoria resultante dependerá de un gran número de valores de precios anteriores de diferentes símbolos. Fortalezcamos esta dependencia construyendo un promedio móvil basado en estos valores.
Hay procesos ondulatorios. ¿Pero nos gustaría saber si son cíclicos? Y si hay un ciclo ¿cuáles son sus parámetros?
Para responder a estas preguntas, podemos utilizar diferencias finitas. La primera diferencia se obtiene restando el valor anterior de la serie temporal al actual:
La segunda diferencia finita se obtiene restando las primeras diferencias.
Esta diferencia es interesante porque, si se cumplen ciertas condiciones, puede indicar la naturaleza cíclica del proceso. Supongamos que estamos ante algún tipo de ciclo. Sea a el valor inicial del ángulo y s su paso de cambio. Luego los últimos tres puntos de la serie temporal se pueden establecer como:
Utiliza identidades trigonométricas para hallar la segunda diferencia de estos valores:
Esta es la ecuación para el oscilador armónico discreto. Tenga en cuenta que aquí oscilador significa un sistema oscilante, no un indicador.
No es fácil trasladar esta ecuación a los precios. En el lado izquierdo de la ecuación, podemos usar cualquier valor real tal como está, pero en el lado derecho, tendremos que hacer algunos cambios.
Para aislar las fluctuaciones, primero necesitamos encontrar el nivel alrededor del cual ocurren. Lo llamaremos MA. Entonces la ecuación se verá así:
En el lado izquierdo, las MA se absorberán mutuamente, pero en el lado derecho, permanecerán.
Hay varias formas de calcular este nivel. Por ejemplo, primero podemos eliminar la tendencia de la serie temporal original o encontrar el promedio de todos los valores de la serie. Ambos métodos tienen un inconveniente común: dependen en gran medida de datos históricos y responden débilmente a los cambios actuales en el mercado. Para librarme de este inconveniente, utilizaré el algoritmo de cálculo indicadores adaptativos. En este caso, el nivel MA se ajustará a la situación actual del mercado. Como resultado, obtendremos un indicador que nos permitirá rastrear el nivel alrededor del cual fluctúa la media móvil. Para el ejemplo utilicé SMA, pero en la práctica puedes utilizar cualquier promedio de precios.
Desafortunadamente, el oscilador armónico tiene una serie de desventajas que deben tenerse en cuenta al utilizarlo. Funciona bien con señales sinusoidales. Pero incluso una mezcla de sinusoides puede causar dificultades: el oscilador simplemente no podrá seleccionar el ciclo más importante.
La mayoría de las deficiencias se pueden solucionar con la ayuda de la segunda diferencia. En apariencia sigue siendo lo mismo. Pero podemos cambiar la distancia entre los miembros de esta diferencia. Por ejemplo, tengo un gráfico con el marco temporal H1 abierto. Supongo que puede haber un ciclo diario en el movimiento de precios (el período es 24). Luego usaré la segunda diferencia que queda de la siguiente manera:
Si hay un ciclo o ciclos en el movimiento del precio, entonces la segunda diferencia será cero. La aparición de estos ciclos no es importante. Lo principal es que se repitan más o menos correctamente. Además, la segunda diferencia puede afrontar fácilmente la tendencia. El único requisito es que la duración de esta tendencia no sea inferior al doble del período.
¿Cómo se puede aplicar este método en la práctica? Supongamos que hay un ciclo estable en el movimiento de precios con algunas desviaciones aleatorias. Entonces, si encontramos la suma de varios (en mi caso 24) últimos valores de diferencias, entonces los errores aleatorios se compensan entre sí. Es decir, si el ciclo y/o tendencia es estable, la suma de las diferencias fluctuará alrededor de cero. Si hay alguna perturbación en el mercado (el comienzo de una nueva tendencia, el lanzamiento de un nuevo ciclo o el final de uno antiguo), la suma de las diferencias comenzará a desviarse significativamente. Además, estas desviaciones pueden parecer cíclicas. De esto podemos concluir que las perturbaciones del ciclo pueden ser de naturaleza cíclica. Es como un mercado de Schrödinger.
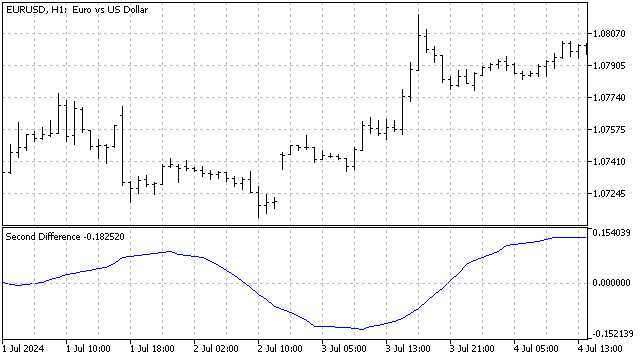
En general, el uso de diferencias finitas puede ser muy útil en el análisis de mercados. They can be used as is, combined with each other and paired with other indicators. Como resultado, podrá obtener nuevas herramientas interesantes para estudiar los movimientos de precios.
Otras diferencias
No es necesario utilizar diferencias clásicas al analizar series de tiempo. Podemos construir diferencias según nuestras tareas. Para ello, podemos utilizar los principios aplicados en la construcción de ondículas.
Tomemos un número que represente la onda inicial. La opción más sencilla y obvia es tomar 1. Ponemos 0 a la derecha e izquierda de este número. Obtendremos una cadena como esta: "0, 1, 0". Ahora, comenzando desde el segundo número, vamos de izquierda a derecha y restamos el número izquierdo del derecho.
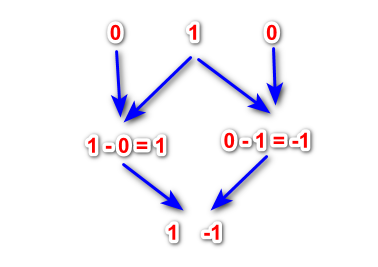
De esta manera obtenemos una ondícula de nivel 1. Coloque ceros a la izquierda y a la derecha de las proporciones resultantes y realice las restas nuevamente. Esta operación puede continuar hasta alcanzar el nivel de la ondícula deseado. Estas diferencias tienen algunas propiedades de las ondículas clásicas y pueden utilizarse en el análisis de series temporales financieras.
Se puede utilizar cualquier grupo de números como onda inicial, por ejemplo 1, 2, 1 o 1, 1, 1. En este caso, las proporciones de la onda original no deberían ser simétricas con respecto al centro de la onda. No pasará nada malo si la onda original se representa como 3, 2, 1. También podemos utilizar números negativos.
Dado que la suma de las relaciones de todas las diferencias obtenidas es igual a 0, representan inmediatamente osciladores listos para usar.
La desventaja de tales diferencias es que ni siquiera podemos imaginar cuál será el resultado al utilizar una determinada onda inicial.
La principal ventaja de tales diferencias es que con su ayuda podemos restaurar la señal original. Por ejemplo, conocemos los valores de la 1ª y 2ª diferencia. Si restamos la 1ª diferencia al valor actual de la serie temporal, obtendremos el valor anterior de la serie. Conociendo estos dos valores y la 2ª diferencia, obtenemos el siguiente valor de la serie, y así sucesivamente.
Esta propiedad nos permite buscar áreas similares en la historia. Si las diferencias entre los distintos niveles son aproximadamente iguales entre sí, entonces tenemos movimientos de precios similares.
Conclusión
Es importante recordar que el mercado no suele seguir ciclos predecibles. Incluso si observamos algún tipo de ciclo, siempre existe el riesgo de que el patrón cambie. Hay ondas, pero su comportamiento requiere un estudio más profundo. De cualquier manera, comprender los ciclos del mercado puede ser una herramienta útil en el arsenal de cualquier comerciante. Al explorar los ciclos, podemos encontrar nuevas formas y medios para el análisis técnico.
Se adjuntan al artículo los siguientes programas:
| Nombre | Tipo | Características |
|---|---|---|
| Dot Mapping | Script | Tipos de visualización
Una vez que el script completa su trabajo, las imágenes se guardan en la carpeta "Files". |
| Slutsky cycles | Indicador | Maneja todos los símbolos disponibles en "Observación del mercado" |
| Slutsky MA | Indicador |
|
| Second Difference | Indicador |
|
| scr Wavelet | Script | Muestra las relaciones ondículas
|
| Wavelet | Indicador | Utiliza las ondículas como oscilador
|
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15614
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
Redes neuronales en el trading: Segmentación de datos basada en expresiones de referencia
El enfoque cuantitativo en la gestión de riesgos: Aplicación de un modelo VaR para la optimización de portafolios multidivisa con Python y MetaTrader 5
Métodos de William Gann (Parte III): ¿Funciona la astrología?
Optimización de la quimiotaxis bacteriana - Bacterial Chemotaxis Optimisation (BCO)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso