非平稳过程和伪回归

内容

• 概述
• 回归分析中的非平稳性
• 对回归模型的参数进行统计假设检验
• 回归模型的无效说明
• 结论

概述

作为应用数理统计的一部分，回归分析是研究随机变量之间依存关系时处理经验数据的最常见方法之一。相关分析能让我们找出两个随机变量之间是否存在关联，而回归分析则能找出这种关联呈现的形式。在回归分析中，分为配对回归和多元回归。在本研究中，为了简化问题，我将使用广为人知的配对线性回归模型：

                                                Yt = b0 + b1Xt + et                                 (1)

• Yt - 因变量 （响应）；
• Xt - 自变量 （解释变量）；
• b0, b1 模型参数； t - time (0,1,2,...n) n - 观测数据量：
• et - 随机分量，通常指高斯白噪声。

在这里，我们标出了索引t，以强调我们正在处理的是一个时间序列，而随机变量的排列顺序对我们来说很重要。

回归分析的任务包括以下几点：

• 评估所选回归模型的参数（在线性情况下，使用普通最小二乘法）
• 对模型参数进行统计假设检验
• 为获得的参数估计值构建置信区间

如果分析发现该模型在统计上具有显著性，则认为其适用于预测因变量。但是，在应用回归分析时，尤其是时间序列分析时，我们应该始终牢记，对所研究的随机序列施加的平稳性要求存在局限性。平稳性要求假设随机变量的分布函数随时间保持不变，因此，该随机变量的数学期望和方差也保持不变。尝试将回归分析应用于非平稳过程，可能会导致得出研究变量之间存在显著关系的错误结论。在这种情况下，标准的统计检验（如F统计量和t统计量）将失效，并且将错误的依赖关系当真的风险将大大增加。

回归分析中的非平稳性

在本文中，我将使用蒙特卡洛模拟来展示当违反平稳性假设时或错误设定平稳情况下的回归模型时，虚假回归是如何发生的。为此，我将使用标准的MQL5统计库来生成随机数，并计算正态分布和t分布的临界值，同时还将使用图形库来绘制所得到的结果。使用矩阵代数方法可以极大地简化回归模型的计算。例如，使用最小二乘法在矩阵形式下求解回归模型参数的方程可以写为：

(2) 

• X - 自变量值矩阵；
• Y - 因变量列向量；
• b - 从样本中评估未知参数的列向量。

在MQL5中，向量b（在我们配对线性回归的情况下，它将包含两个元素——b0和b1）可以通过计算X矩阵的伪逆矩阵PInv()，并将其与Y向量相乘从而得到：

pinv = x.PInv(); 

Coeff = pinv.MatMul(Y);  //基于OLS的线性回归参数向量

这是计算的简化版本。我们可以按照方程式逐步计算：

xt = x.Transpose();

xtm = xt.MatMul(x);
inv = xtm.Inv();      
invt = inv.MatMul(xt);
Coeff_B = invt.MatMul(Y); // vector of regression parameters using OLS

结果将会是相同的。

为了建模，我们需要一个随机游走模型作为非平稳过程的示例。我们将为因变量Y和自变量X构建这个模型。之后，对Y关于X进行回归，并评估诸如R方（决定系数）这样的指标，计算t统计量，并分析回归模型的残差以判断是否存在相关性依赖。                                            

 Yt = Yt-1 + zt                           (3)

  Xt = Xt-1 + vt                           (4)

zt and vt  - 两个独立生成高斯“白噪声”的过程，其数学期望为零且单位方差为N（0,1）；

图1呈现了这种过程的两种可能轨迹

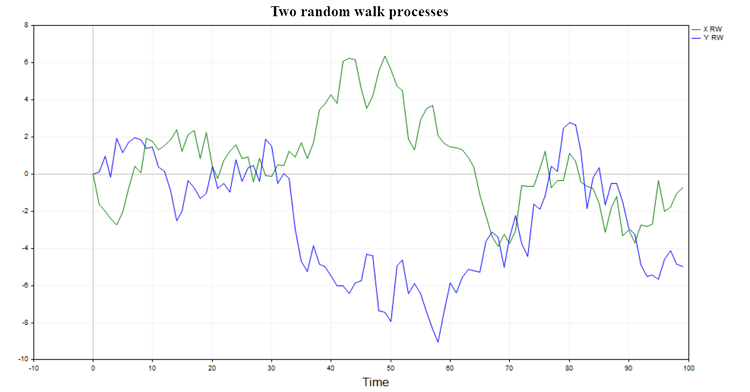
Fig. 1. 两次随机游走

这样的过程不具备记忆性，且彼此之间没有任何关联，因此预测两个随机游走之间基本上是独立的，对于两个随机游走之间存在联系的假设通常会被否决（由所选显著性水平决定的小部分情况除外）。

图2展现了一个可能的回归示例：

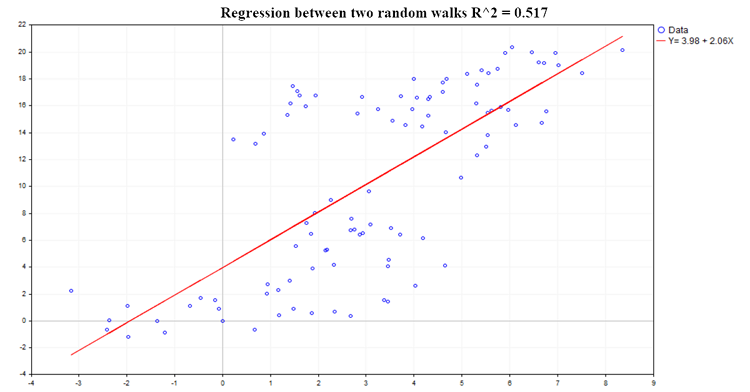
Fig. 2. 两次随机游走之间的回归，R2=0.517

决定系数（R²）使用以下方程式计算： 

R^2 = 1 - SSE/TSS                              (5)

• SSE - 方差之和；
• RSS - 回归平方和；
• TSS - 平方总和 = RSS+SSE;

计算所有主要回归特征的代码：

      pinv = x.PInv();
      Coeff = pinv.MatMul(Y);  // vector of linear regression parameters using OLS
      yRegression = x.MatMul(Coeff);  // y regression
      res = Y-yRegression;   //  regression residuals, y - y regression
      yMean = Y.Mean();
      reg_yMean = yRegression-yMean;  // y regression - mean y
      reg_yMeanT = reg_yMean.Transpose();
      RSS = reg_yMeanT.MatMul(reg_yMean);  // Sum( y regression - y mean )^2 , sum of squares due to regression
      resT = res.Transpose();
      SSE = resT.MatMul(res);  // Sum(y - regression y)^2
      TSS = RSS[0,0]+SSE[0,0];  // Total sum of squares
      RSquare = 1-SSE[0,0]/TSS;  // R-square determination ratio
      R2_data[s] = RSquare;

      Vres = SSE[0,0]/(T-2);           // residuals variance estimate
      SEb1 = MathSqrt(Vres/SX);        // estimate of the standard deviation of the b1 ratio deviation of the regression Y = b0 + b1*X;
      t_stat[s] = (Coeff[1,0]-0)/SEb1; // find the t-statistic for the b1 ratio under the hypothesis that b1 = 0;

R²的取值范围从0到1。在配对线性回归的情况下，R²等于X和Y之间共同相关系数的平方。当X不影响Y时，R²接近于0；而当因变量Y完全由自变量X解释时，R²则趋近于1在我们研究的两个独立随机游走的回归案例中，从逻辑上讲R²的预测值会分布在0附近。为了验证这一点，我们将使用蒙特卡洛方法模拟1000对各有100个观测值的随机游走，并随后计算每对随机游走的R²值，从而构建R²的分布。我们得到了如下图的分布（图3）：

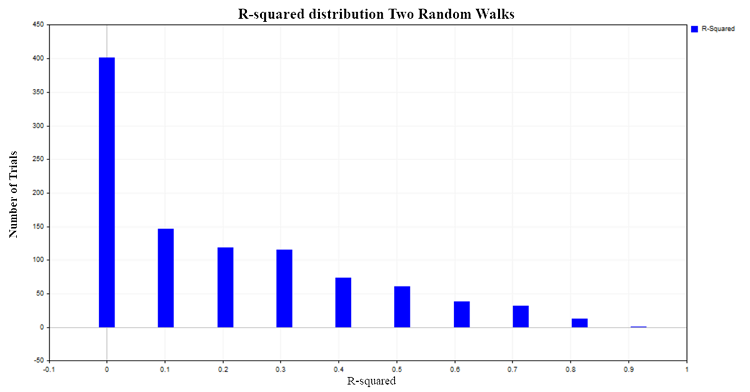
Fig. 3. 两次随机游走的R2分布

决定系数（R²）的值大于0.2的情况大约占比50%，这表明那些原本互不相关的量之间似乎存在某种关系。为了进行比较，我们来获取两个独立平稳过程的R²分布。对于这样的过程，一个合适的模型是高斯白噪声模型。

                    Yt =  et                                   (6) 

 et  -  Gaussian white noise N(0,1)

让我们生成1000对平稳随机过程，每对包含100个观测值。结果我们得到了R²在0附近的预期分布，如图4所示：

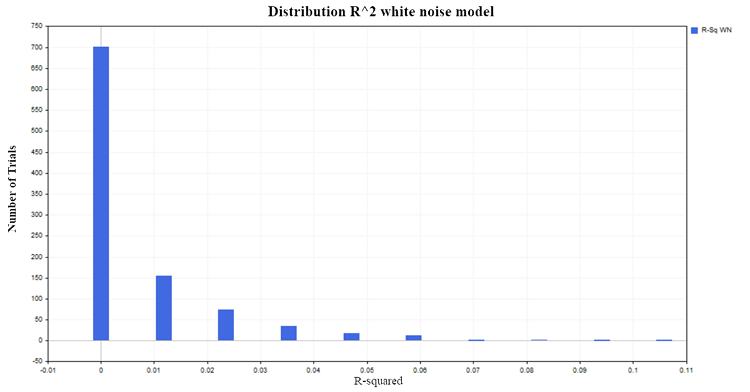
Fig. 4. R2分布，白噪声模型

让我们回到两个随机游走的情况，并观察用于评估线性回归模型中参数显著性的t统计量的行为。

对回归模型的参数进行统计假设检验

从样本中计算出的回归系数本身就是随机变量，因此有必要检查这些样本特征的显著性。在检验b1回归参数的显著性时，我们提出零假设（H0），即自变量X不影响因变量Y。换句话说，H0(i) : b1 = 0，即b1参数与0无显著差异。备择假设（H1）则表明参数b1与0有显著差异。即，H1(i): b1 ≠ 0，因此自变量X影响因变量Y。

为了检验这一假设，使用t统计量：

                                               t = bi /SEi                                      (7)

SEi - 双估计参数的标准偏差 

这个统计量服从自由度为(n-p)的t分布，记作a/2 (n-p) 。

• n - 回归模型中用于计算的数据量（在我们的例子中n的值为100）；
• p - 评估参数的数量（在我们的配对回归中，数量为2个）；
• a - 显著性水平(1,5,10%)。

对于我们的实验，我选择了5%的显著性水平。如果t统计量的绝对值超过了t分布（Student's distribution）的临界值{|t| > t0.025 (98) =1.9844}，我们就可以得出结论，回归参数b不等于零1 ，因此，解释变量X和因变量Y之间存在关系。由于我选择了5%的显著性水平，在全部进行的测试中，我们预期只有大约5%的情况下会错误地拒绝原假设。但是，根据模拟结果，大约75%的情况下t统计量过于频繁地拒绝了零假设（误判，因为实际上并不存在依赖关系）（图5）：

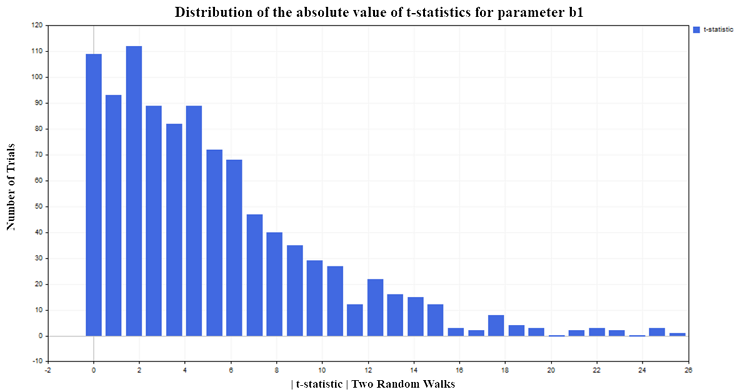
Fig.5. b1参数t统计量绝对值的分布

我还想说明以下趋势。样本中的观测值越多，拒绝零假设的可能性就越大。于是出现了一个看似矛盾的情况：样本越大，自变量X对因变量Y的影响就越大，变量之间的关联性就越强。当然，这实际上并不是矛盾，而是简单地将回归分析应用到了它不适用的过程中。我们发现，当将回归分析应用于非平稳时间序列的分析时，标准t统计量会失效。这种情况被称为伪回归。

回归模型的无效说明

但非平稳性只是标准统计检验失效的一个原因。即使两个序列是平稳的，但如果回归模型的设定被推翻，这些检验也可能会失效。也就是说，如果变量之间的函数依赖关系有误（例如应该是线性关系而不是非线性关系）。或者，如果模型中省略了Y变量实际依赖的X自变量，而错误地使用了完全无关的变量来替代。为了澄清这一点，让我们构建两个独立的X和Y的平稳过程。作为示例，我将使用一阶自回归模型AR(1)：

Yt = A*Yt-1 + zt                           (8)

 Xt = B*Xt-1 + vt                          (9)

• zt和vtz是两个独立生成的高斯“白噪声”过程，具有零数学期望和 N(0,1) 单位方差；
• A 和 B 是AR(1)模型的参数，其绝对值必须严格小于1以满足平稳性条件。

让我们再次在与两个随机游走模型相同的条件下（每个过程100个数据点，测试次数1000次），构建Y对X的回归（例如，使用AR(1)参数 A=0.5, B=0.5）。结果，我们得到了回归参数b1的t统计量，如下（图6）分布：:

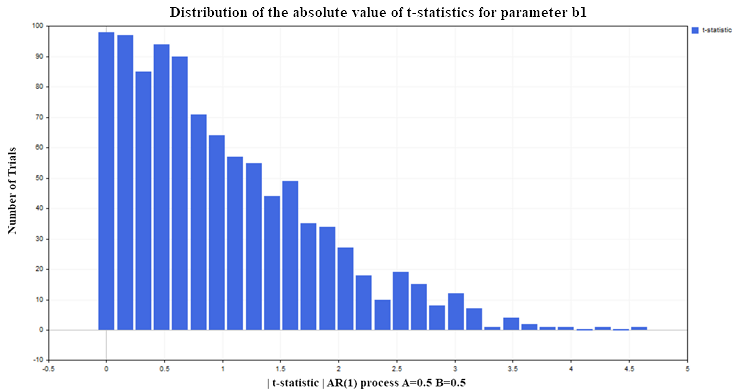
Fig. 6. b1参数t统计量绝对值的分布

我们可以看到，在这里拒绝零假设的情况要比非平稳情况下好得多。在可接受的5%水平下，只有大约12-13%的错误拒绝率（自由度为98的t分布临界值为1.9844）。对于平稳过程，这个百分比不会随着样本量的增加而增加，而是保持在同一水平。这次，t统计量失效不是因为变量非平稳，而是因为回归模型的设定不正确。尽管我们选择了正确的依赖形式（线性），但我们假设Y变量不依赖于同一变量的滞后值，而是依赖于与Y变量无关的X变量的值。如果我们在回归模型中保留X变量，并添加Y的滞后值，那么回归参数的统计性质将得到改善，在设定的显著性水平（我们的情况为5%）下t变量将减少给出错误结论的几率。在实践中，为了理解回归模型是否是伪回归或设定不正确，应该进行残差分析。 

                                         Residuals =  Yt - Yreg_t                       (10)

• Yt - Y因变量的实际值；
• Yreg_t  - 计算回归值

如果模型残差中存在显著的自相关，这通常表明回归模型可能会存在设定错误或伪回归。 

以下是计算自相关函数（ACF）和99%置信区间的代码示例

////////////////////////// ACF计算 /////////////////////////////////////////

   avgres = res.Mean();  // mean of residuals
   ArrayResize(acov,K);
   ArrayResize(acf,K);
   ArrayResize(se,K);
   ArrayResize(se2,K);

   for(i=0; i<K; i++)
     {
      ArrayResize(c,T-i);
      for(j=0; j<T-i; j++)
        {
         c[j] = (res[j,0]-avgres)*(res[j+i,0]-avgres);
        }
      acov[i] = double(MathSum(c)/T);  // Auto covariance
      acf [i] = acov [i]/acov [0];  // Auto correlation
      se[i] =   MathQuantileNormal(0.995,0,1,err)/MathSqrt(T);    // 99% confidence intervals for ACF //
      se2[i] = -MathQuantileNormal(0.995,0,1,err)/MathSqrt(T);
     }

图7展示了两个随机游走模型的回归残差自相关函数（ACF）的图形。同时，还展示了使用方程SE = MathQuantileNormal(0.995,0,1,err)/MathSqrt(T)计算得出的ACF99%置信区间的边界，其中T为回归模型中的观测值数量。

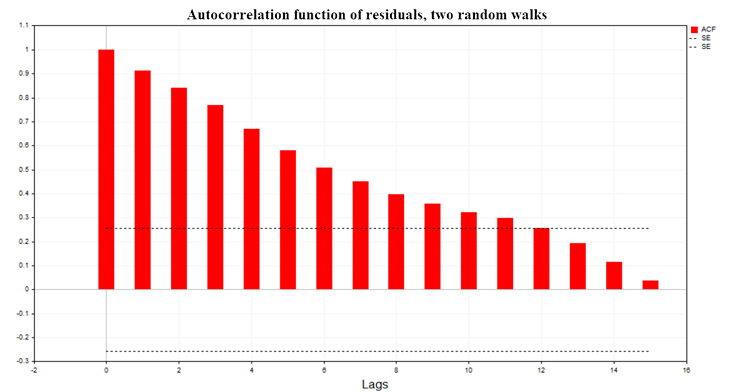
Fig. 7. 残差自相关函数，两个随机游走

图8显示了参数A=0.5, В=0.5的两个AR（1）过程模型的回归残差的ACF图

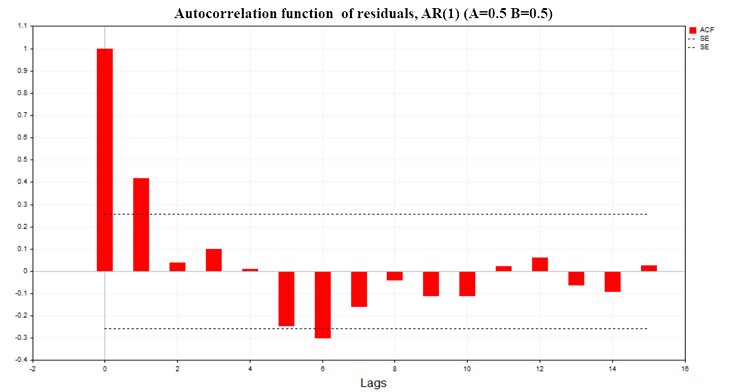
Fig. 8. 残差自相关函数，AR(1) A=0.5 B=0.5

从图中我们可以看出，回归模型的残差存在显著的自相关性。因此，我们要处理的是一个定义错误的回归模型，甚至可能是虚假回归。德宾-沃森（Durbin-Watson，简称DW）检验也是基于残差的自相关函数构建的。它用于检验回归模型残差的一阶滞后自相关性。 

                                            DW = 2*(1-ACF(1))                         (11)

在虚假回归中，这一统计数据接近于零。

结论

本文我主要想探讨的是统计方法，特别是回归分析方法的适用范围限制，并展示违反这些限制导致的后果。如果仅仅进行形式上的计算，得到的“显著”性的统计结果，由此很容易推断出关于两个随机过程之间存在关联性的错误结论。

从上述所有内容中可以得出结论： 

• 在构建回归模型之前，首先必须对模型中的所有变量进行平稳性检验。
• 如果某个变量是非平稳的，应将其转化为平稳形式（通常通过取一阶差分），然后尝试使用这个修改后的变量构建模型。
• 构建模型后，需要检查残差是否存在自相关依赖。
• 如果残差的自相关函数值没有超出99%置信区间，那么我们可以继续使用t统计量来评估回归模型参数的重要性。
• 如果参数显著，那么我们就可以开始使用构建的模型来预测Y因变量。

为了重现上述所有结果，请在脚本开头根据想要获取结果的具体模型，选择变量M的值为1、0或0.5。之后，在脚本的最底部，取消注释负责显示每个具体模型某些统计数据的代码块。同样在包含的Math.mqh文件中，为了在图上显示频率，请将计算经验概率密度函数（MathProbabilityDensityEmpirical）注释掉。

 5432  //  for(int i=0; i<count; i++)
 5433 //    pdf[i]*=coef;