神经网络实践：割线

概述

亲爱的读者朋友们，欢迎你们阅读一个不会被当作系列文章处理的话题。

虽然很多人可能会认为，最好就人工智能这一主题发布一系列文章，但我无法想象如何才能做到这一点。大多数人不了解神经网络的真正目的，因此也不了解所谓的人工智能。

因此，我们不在这里详细讨论这个话题。相反，我们将重点关注其他方面。因此，您可以按照任何顺序阅读我关于这一主题的文章，重点阅读与您相关的材料。我们将尽可能广泛地探讨神经网络和人工智能这一主题。这里的主要目的不是创建一个面向市场或特定任务的系统，而是解释和展示计算机程序如何能够做到媒体所展示的、令许多人着迷的事情，让他们相信神经网络或人工智能可以具有某种程度的意识。

我认为神经网络和人工智能是有区别的，当然，这只是我的看法。在这些文章中，你会发现人工智能和神经网络并没有什么特别之处。它只是一个经过深思熟虑的程序，旨在实现一个特定的目标。不过，我们还是不要操之过急。首先，我们必须通过不同的阶段来了解一切是如何运作的。除了 MQL5，我们不会使用任何其他软件。

对我来说，这将是一项个人挑战。我只是想告诉大家，只要有正确的概念和对事物实际运作方式的理解，你就可以使用任何语言来创建本文将展示的内容。因此，我祝愿大家阅读愉快，并希望这些文章能引起你们的兴趣，丰富你们对这一主题的认识。

线性回归

正如理论部分已经解释的那样，在使用神经网络时，我们需要使用线性回归和导数。为什么呢？原因是线性回归是现存最简单的公式之一。事实上，线性回归只是一个仿射函数。然而，当我们谈论神经网络时，我们对直接线性回归的影响并不感兴趣。我们感兴趣的是生成这条直线的方程。我们感兴趣的不是创建出的线，而是公式。

为了理解这一点，让我们创建一个小指标，如下代码中所示。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. CCanvas canvas;
09. //+------------------------------------------------------------------+
10. void Func_01(const int x, const int y)
11. {
12.     int A[] {
13.                 -100,  150,
14.                  -80,   50,
15.                   30,  -80,
16.                  100, -120
17.             };
18. 
19.     canvas.LineVertical(x, y - 200, y + 200, ColorToARGB(clrRoyalBlue, 255));
20.     canvas.LineHorizontal(x - 200, x + 200, y, ColorToARGB(clrRoyalBlue, 255));
21. 
22.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
23.         canvas.FillCircle(x + A[c1++], y + A[c1++], 5, ColorToARGB(clrRed, 255));
24. }
25. //+------------------------------------------------------------------+
26. int OnInit()
27. {    
28.     int px, py;
29.     
30.     px = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
31.     py = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
32. 
33.     canvas.CreateBitmapLabel("BL", 0, 0, px, py, COLOR_FORMAT_ARGB_NORMALIZE);
34.     canvas.Erase(ColorToARGB(clrWhite, 255));
35.         
36.     Func_01(px / 2, py / 2);
37. 
38.     canvas.Update(true);
39.     
40.     return INIT_SUCCEEDED;
41. }
42. //+------------------------------------------------------------------+
43. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
44. {
45.     return rates_total;
46. }
47. //+------------------------------------------------------------------+
48. void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
49. {
50. }
51. //+------------------------------------------------------------------+
52. void OnDeinit(const int reason)
53. {
54.     canvas.Destroy();
55. }
56. //+------------------------------------------------------------------+

执行该代码后，屏幕上会出现以下内容。

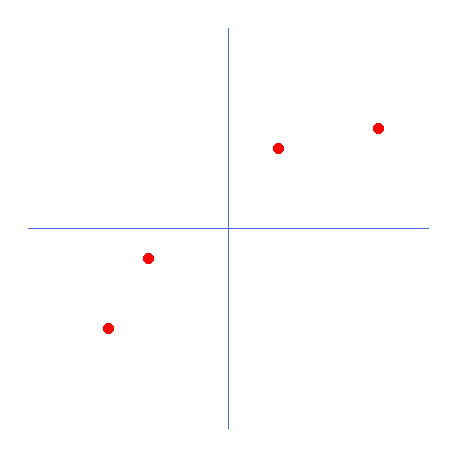
我们应该从这里开始理解，为什么在使用神经网络时要使用线性回归和导数。红点代表神经网络中的信息，也就是说，人工智能已经过训练，包含以红点显示的信息。蓝线为坐标轴。问题是，什么数学公式能最好地描述这组数据？换句话说，如果我们要概括上图中描述的概念，哪一个数学公式最能代表这幅图呢？从点的分布来看，可以说这是一条直线。那么我们可以考虑线性方程，它是一个仿射函数。该方程如下所示。

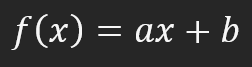
这样，该函数用于创建一条直线。现在让我们回到主要问题上来。我们应该使用 A 和 B 的什么值来以最佳方式创建直线呢？好吧，很多人可能会说，你需要通过反复试验来寻找它们。不过，我们还是把事情简单化吧。为此，我们假设 B 等于零。也就是说，直线将穿过坐标轴的原点。首先，为了简单起见，我们将这样做，以理解神经网络中使用的数学。

在这种情况下，我们只需要找到常数 A 的值。现在出现了另一个问题：我们如何找到 A 的这个值？你可以放任何一个，但根据使用的值，公式不会真正优化。即使我们的神经网络中存储了如此少量的知识，也不值得失去它。因此，我们不（或不能）使用任何含义。我们需要找到 A 的最佳值。

这就是机器开始学习的地方。这就是机器学习（ML）的由来。许多人在使用这一术语时并不理解其含义。这个想法正是：创建一个最能代表网络中知识点的数学方程。手动执行此操作是最困难的任务之一。然而，通过数学运算，我们可以迫使机器为我们生成一个方程。这就是所谓的机器学习系统。这个想法是以某种方式让计算机自动生成一个数学方程。

现在，你已经开始了解机器是如何学习的了。这只是一种方法，还有其他方法。但是，现在我们将重点介绍这种特殊的方法。我们已经有一个具体的任务需要完成。我们必须计算如何在上述仿射方程中找到常数 A 的最佳值。

你可以认为我们可以创建一个循环，迭代给定范围内的所有值。这实际上是可行的，但计算效率不高。考虑一下：在这个例子中，我们只需要一个变量，常数 A。因为我们认为常数 B 的值等于零。然而，在实际应用中，常数 B 很可能不为零。因此，这种遍历数值范围的方法并不适用于所有情况。我们需要构建一个能够适应所有情况的东西，即使我们必须改变常数 B 的值。

那么，我们该如何解决这个问题呢？为了让大家更容易理解，我们将对这一方法稍作修改，以便更直观地展示将要使用的数学知识。新代码如下所示：

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. #define _ToRadians(A) (A * (M_PI / 180.0))
09. #define _SizeLine 200
10. //+------------------------------------------------------------------+
11. CCanvas canvas;
12. //+------------------------------------------------------------------+
13. struct st_00
14. {
15.     int     x,
16.             y;
17.     double  Angle;
18. }global;
19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[] {
23.                   -100,  150,
24.                    -80,   50,
25.                     30,  -80,
26.                    100, -120
27.             };
28. 
29.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
30.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
31. 
32.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
33.         canvas.FillCircle(global.x + A[c1++], global.y + A[c1++], 5, ColorToARGB(clrRed, 255));
34. }
35. //+------------------------------------------------------------------+
36. void NewAngle(const char direct, const double step = 1)
37. {
38.     canvas.Erase(ColorToARGB(clrWhite, 255));
39.     Func_01();
40. 
41.     global.Angle = (MathAbs(global.Angle + (step * direct)) <= 90 ? global.Angle + (step * direct) : global.Angle);
42.     canvas.TextOut(global.x + 250, global.y, StringFormat("%.2f", global.Angle), ColorToARGB(clrBlack));
43.     canvas.Line(
44.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
45.                 global.y - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
46.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
47.                 global.y + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
48.                 ColorToARGB(clrForestGreen)
49.             );
50.     canvas.Update(true);
51. }
52. //+------------------------------------------------------------------+
53. int OnInit()
54. {    
55.     global.Angle = 0;
56.     global.x = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
57.     global.y = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
58. 
59.     canvas.CreateBitmapLabel("BL", 0, 0, global.x, global.y, COLOR_FORMAT_ARGB_NORMALIZE);
60.     global.x /= 2;
61.     global.y /= 2;
62.         
63.     NewAngle(0);
64. 
65.     canvas.Update(true);
66.     
67.     return INIT_SUCCEEDED;
68. }
69. //+------------------------------------------------------------------+
70. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
71. {
72.     return rates_total;
73. }
74. //+------------------------------------------------------------------+
75. void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
76. {
77.     switch (id)
78.     {
79.         case CHARTEVENT_KEYDOWN:
80.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_LEFT))
81.                 NewAngle(-1);
82.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_RIGHT))
83.                 NewAngle(1);
84.             break;
85.     }
86. }
87. //+------------------------------------------------------------------+
88. void OnDeinit(const int reason)
89. {
90.     canvas.Destroy();
91. }
92. //+------------------------------------------------------------------+

下图显示了我们得到的结果：

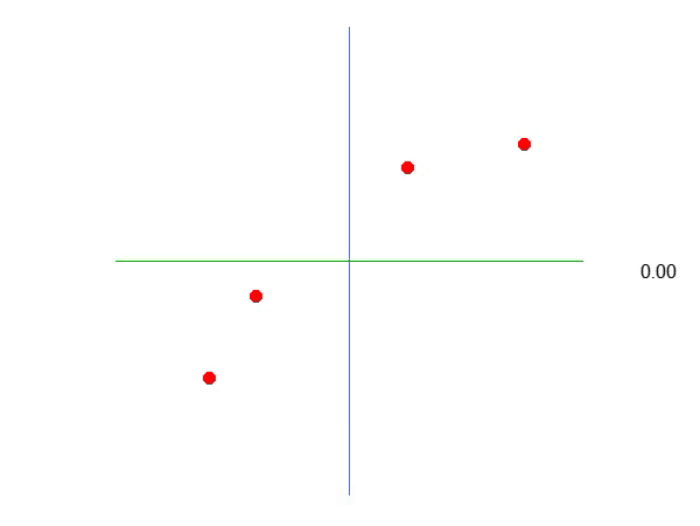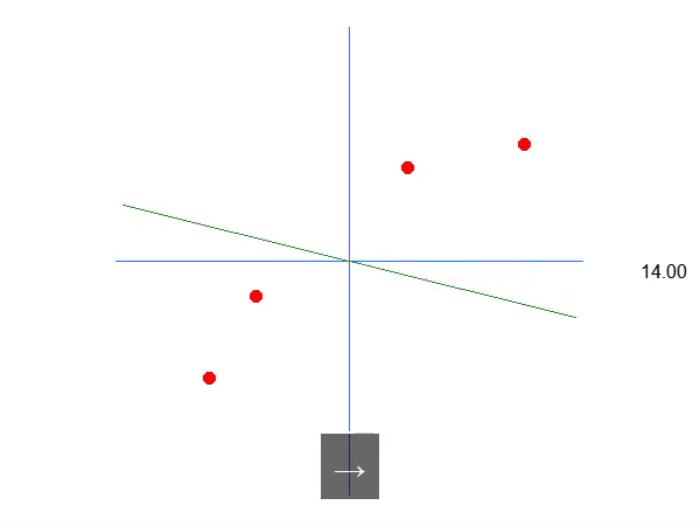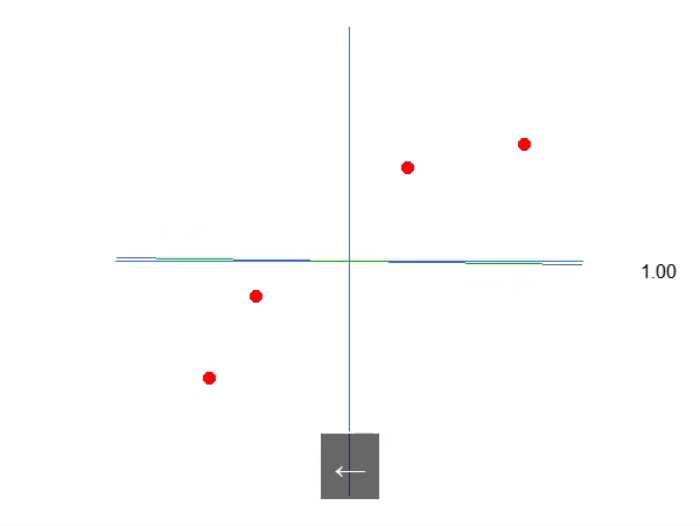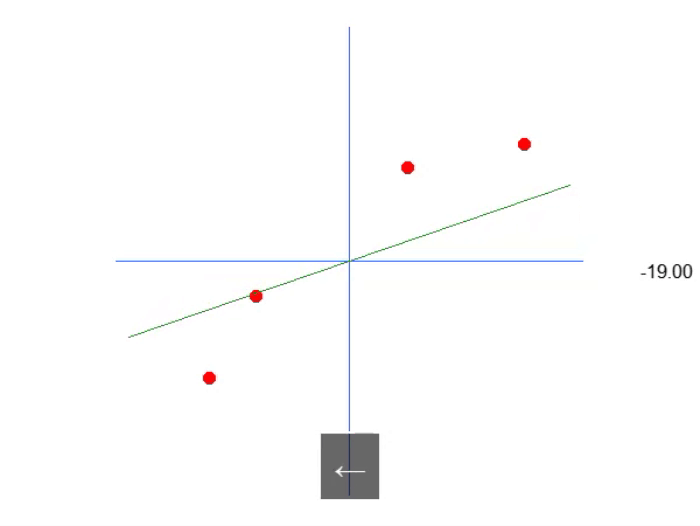
也就是说，我们可以构造一个仿射方程，通过改变常数 A 的值来创建一个可能的线性回归方程，试图保留现有的知识，即红点。在这种情况下，正确的方程如下所示。显示的角度是使用左箭头或右箭头获得的角度。

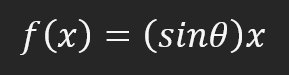
因此，我们可以假设所需的常数是角度的正弦，从而组成我们的方程。然而，情况并非如此。不是因为常数与角度无关（事实上，它是），而是因为你会认为你会使用正弦或余弦。这种方法不是表达想法的最佳通用方式。通常，仿射方程不是用三角函数表示的。这没有错，只是不寻常。在本文中，我们将了解如何利用角度来获得这一常数。不过，我得先解释一下别的事情。如果您稍微更改代码，如下面的代码所示，您可以看到它看起来更像动画中显示的直线的正确方程。因为常数会知道使用正确的术语。

35. //+------------------------------------------------------------------+
36. void NewAngle(const char direct, const double step = 1)
37. {
38.     canvas.Erase(ColorToARGB(clrWhite, 255));
39.     Func_01();
40. 
41.     global.Angle = (MathAbs(global.Angle + (step * direct)) < 90 ? global.Angle + (step * direct) : global.Angle);
42.     canvas.TextOut(global.x + _SizeLine + 50, global.y, StringFormat("%.2f", MathAbs(global.Angle)), ColorToARGB(clrBlack));
43.     canvas.TextOut(global.x, global.y + _SizeLine + 50, StringFormat("f(x) = %.2fx", -MathTan(_ToRadians(global.Angle))), ColorToARGB(clrBlack));
44.     canvas.Line(
45.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
46.                 global.y - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
47.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
48.                 global.y + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
49.                 ColorToARGB(clrForestGreen)
50.             );
51.     canvas.Update(true);
52. }
53. //+------------------------------------------------------------------+

代码执行的结果如下图所示。

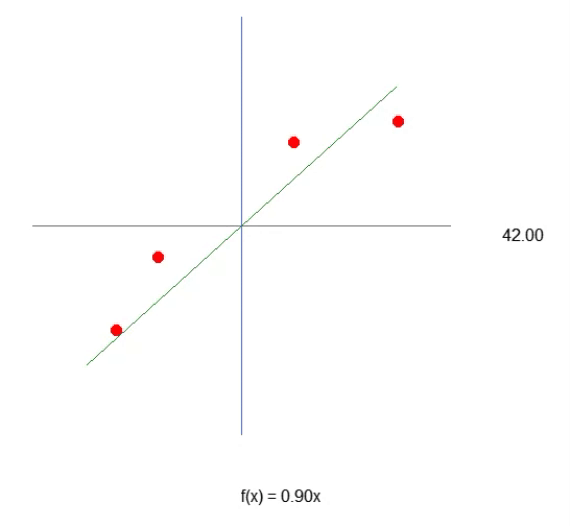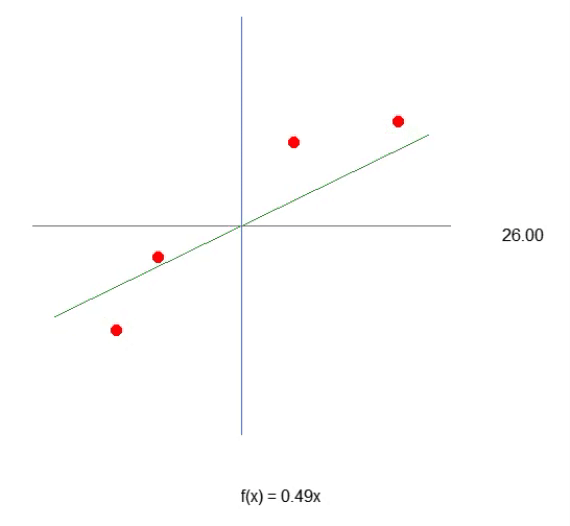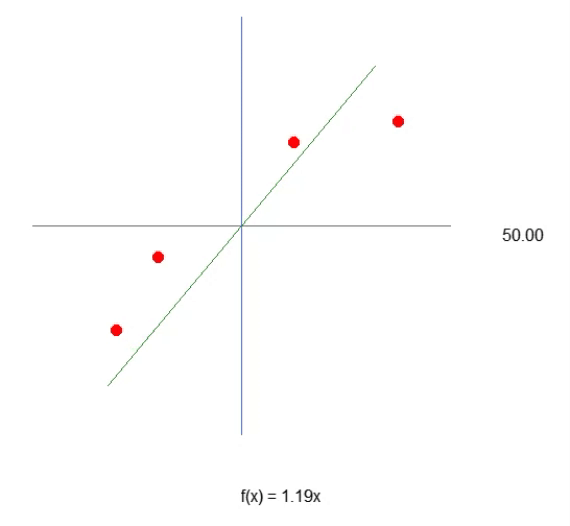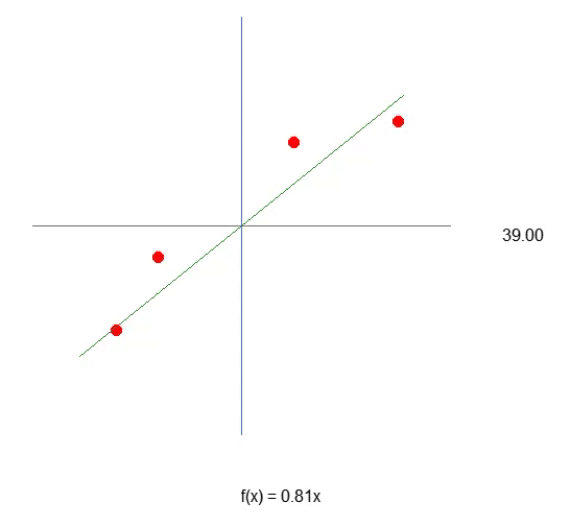
请注意，由于有了第 43 行，我们现在得到了非常接近直线方程的结果。您可以看到，为了创建公式，我们将使用角度的切线，而不是正弦或余弦。这只是为了生成最合适的值。然而，尽管我们设法列出了方程，但我们可以看到，要猜出直线斜率的最佳值，也就是系统的角度，并不那么容易。我们可以尝试手动完成，但这是一项非常困难的任务。尽管构建产生线性回归的方程非常复杂，但重要的是要记住，此时我们在这个系统中只处理一个变量。这就是我们需要找到的值，如上面的动画所示。

然而，如果我们正确使用数学，它将使我们能够找到最合适的斜角值。为此，我们需要在系统中使用导数。我们还需要了解为什么正切是最能表示方程中所用常数的三角函数。但是，亲爱的读者，为了更容易理解，让我们开始一个新的话题。

使用导数

这就是数学对许多人来说有点困惑的地方。但这不是绝望、恐惧或内心痛苦的原因。我们需要告诉我们的代码如何找到角度的最佳值，以便方程允许我们访问我们已经知道的值或尽可能接近它们。因此，该方程将具有非常接近理想值的常数。这将允许图上存在的知识以方程格式保存，在这种情况下，方程格式将是线性方程。

我们使用线性方程（通常类似于线性回归）的事实是，这类方程最容易计算必要的常数。这并不是因为它是在图表上表示数值的更好方法，而是因为它更易于计算。不过，在某些情况下，处理时间可能会很长。但这是另外一个问题。

要计算这样一个方程，我们需要一些数学资源。这是因为仿射函数是直线函数，不允许我们获得导数。导数是穿过给定点的直线，可以从任何方程中获得。许多人对这些解释感到困惑，但实际上，导数只是函数给定点的切线。切线绘制在属于通常在图形上创建曲线的方程的点上。由于仿射函数是一条切线，切线反映了未知部分乘以的常数的值，从而提供了该特定线的方程。因此，无法使用此原始方程绘制第二条切线。我们还需要其他东西。因此，我们用哪一点来求导并不重要。在仿射函数中创建导数是不可能的。

不过，有一种方法可以确保导数的创建。这正是我们今天要开始学习的内容。要了解我们如何做到这一点，你需要先了解什么是导数。然后，您将需要了解用于获取该导数的方法，并据此创建一个描述最小理想线的仿射函数。为此，我们将使用一个可以输出导数的函数。其中最简单的是二次函数。其计算公式如下：

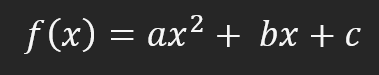
请注意，这个等式中有一个 2 次幂。仅凭这一事实，我们就能解释系统中导数的存在，但我们可以使用任何函数来构建曲线。甚至可以是对数函数。然而，如果我们考虑下一步需要做什么，那么对数函数就没有意义了。因此，为了使计算过程尽可能简单，我们将使用一元二次方程。这样，利用上述公式，我们可以得到如下图形。

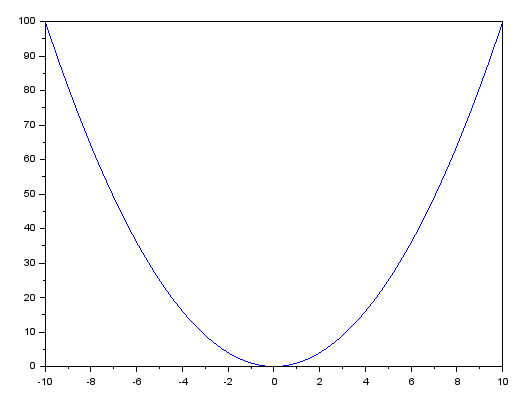
此图是通过将 A 的值设置为 1，将 B 和 C 的值设为0来实现的。然而，对我们来说真正重要的是在图表上可以看到的曲线。

现在请注意 - 这个解释对于理解我们将在程序中执行什么来找到我们需要的方程非常重要。

从上图中，我们将做出一些假设，了解这些假设非常重要。我们想知道 X 等于 4 时的导数值。为此，您需要画一条切线，该切线必须恰好经过 X 等于 4 的点。乍一看，这很简单：拿一把尺子，在等于 4 的坐标上标出一个点 X。然后我们将尝试构造一条与曲线上的一点相切的直线。但我们真的可以通过这样做来画一条切线吗？这不太可能！

我们更有可能创建一条不相切的线。因此，我们需要进行一些计算。这就是事情变得复杂的地方。但为了不使情况无端复杂化，我现阶段不会详细介绍计算本身。我假设读者知道二次方程导数的公式。对于那些不知道的人，我稍后会解释如何获得这个公式。现在对我们来说最重要的是获取导数方程的方法。最终结果并不重要，但从导数中得出的公式却很重要。那我们继续。

二次方程的导数可以用以下公式求出。

接下来，我将展示两种最常见的符号。你可以用右边的那个，也可以用左边的那个，没关系。现在我们对公式本身感兴趣，它等于 X 的 2 倍。这个公式给了我们一个值 8，在我们的例子中，它是 X 为 4 的点处的切线的值。如果你知道 8 的含义，就可以在 X 等于 4 的点上画一条切线。但是，如果您不知道该值的含义，则需要第二个公式来绘制正切图。 

如果你不明白为什么这个值是 8，看看下面的图片，我们希望 X 的导数是 4。为此，我们计算该位置的值，如下所示。

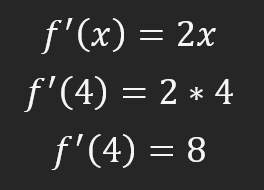
不过，在进行其他计算之前，我们先来弄清楚这个数值 8 意味着什么。这意味着，如果我们在 X 轴上移动一个位置，就需要在 Y 轴上移动八个位置。这样我们就能画出一条切线。除非亲眼所见，否则你可能不会相信。如果是这种情况，有一个公式可以让你写出切线的方程。这个方程是：

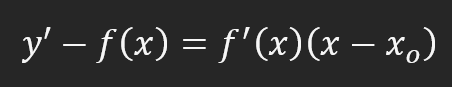
是的，这有点吓人，但它比看起来简单得多。不过，这个方程确实很特别。虽然导数最终将是一条切线，但它允许你创建导数的切线方程。但这只是我提到的一个有趣的事实，没什么好担心的。因此，由于我们已经知道了大多数值，我们可以进行适当的替换来找到切线方程的公式。这一刻可以在下面看到。

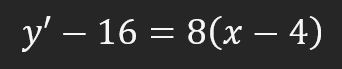
复杂性就在于此，但我们还是要弄清楚这些值的来源。数值 16 是原始方程的结果。换句话说，我们将导数中使用的 X 值（即 "4"）代入二次方程。数值 8 是计算函数导数的结果。同样，X 等于 4，这也适用于函数的导数。我们在这里看到的值 4 就是我们在所有其他方程中使用的 X 初始值。经过计算，我们得出切线的计算公式如下。

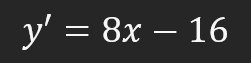
很好，现在我们可以根据上面的方程画出一条切线了。在下图中可以看到绘制的线条，它以红色突出显示。

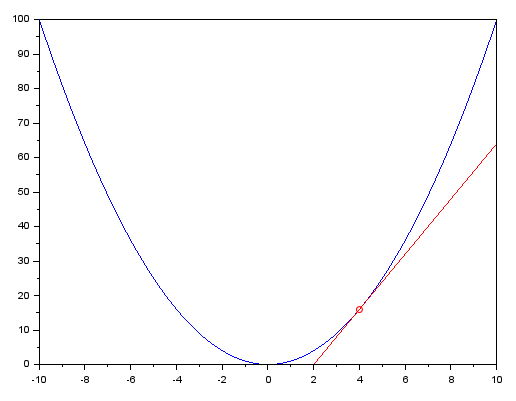
该图使用 SCILAB 程序绘制。对于那些想仔细看看的人来说，下面是 SCILAB 中用于生成它的代码。

x = [-10:.2:10];
y = x ^ 2;

plot(x, y, 'b-');
plot(4, 16, 'ro');

x = [2:.2:10];
y = 8 * x - 16;

plot(x, y, 'r-');

我添加这个是为了让你明白，这不仅仅是学习如何使用这个或那个程序。精通一门特定的语言并不能给你真正的资格。为了准确分析情况，我们经常不得不求助于各种程序。因此，继续教育非常重要。无论你认为自己有多优秀，总会有人在某个领域比你更有经验。所以，要不断学习。

现在我们已经掌握了所有必要的知识，但这条切线是什么意思？为什么它对那些使用神经网络的人如此重要？因为这条线告诉我们应该往哪里走。更确切地说，我们的程序应该移动到哪里来创建线性回归方程。

但这还不是全部：这条线解释了如何计算偏差。神经网络的 "魔力" 就在于这些计算。你看不出来吗？也许，你不明白这怎么可能。因此，要理解这一点，我们需要了解是什么驱动了导数计算。尽管我们在最后使用了切线，但计算并不是从切线开始的。它们产生于另一个三角函数。这正是该系统的神奇之处。这种 "魔力" 让我们能够为所有可能的、可接受的情况创建一个通用的解决方案，这就是神经系统的工作原理。因此，我们将把这个问题留到另一个话题中单独讨论。

割线

虽然大家在谈论神经网络时都只提到导数，但秘密并不在于导数或切线。秘密在于另一条直线上。这是一条割线。这就是为什么我不太愿意写神经网络这个主题的原因。实际上，人们要求我讨论这个话题。真实情况是，很多人都在谈论神经网络，但很少有人真正从数学的角度理解它们是如何工作的。编程容易，难的是数学。许多人认为，他们应该使用这样或那样的库，这样或那样的编程语言。但实际上，只要我们了解其数学部分的工作原理，我们就能使用任何语言。我无意对任何人说三道四，也无意暗示任何人的解释是错误的。每个人都有权按照自己的方式理解一切。不过，我的愿望是真正解释一切是如何运作的。我不希望你成为语言或库的另一个奴隶。我想让你从内部了解一切是如何运作的。因此，我决定撰写一系列文章来讨论这个话题。

导数的原理是找出切线的值。这是因为切线表示函数的斜率。换句话说，它是线性回归在神经网络中使用时的误差。因此，当切线开始达到零度角时，误差将接近零。换句话说，对数据库中已有的值进行线性回归的方程接近理想值。这就是在这种特殊情况下以及在这些特定值下发生的情况。

但是，当我们执行计算时，我们不使用切线。实际上，我们使用的是一条割线。采用哪种神经网络并不重要。如果需要计算，则使用的不是切线，而是割线。你可能会认为这要复杂得多，但如果你这么想，那么你就不知道导数的切线是如何实际获得的。或者，更糟糕的是，导数的公式是如何得到的。背公式没有什么特别的意义。最好的办法是理解为什么公式有这种格式而不是另一种格式。还记得上一主题中给出的计算结果吗？你知道它们是从哪里来的吗？如果不知道，请看下图：

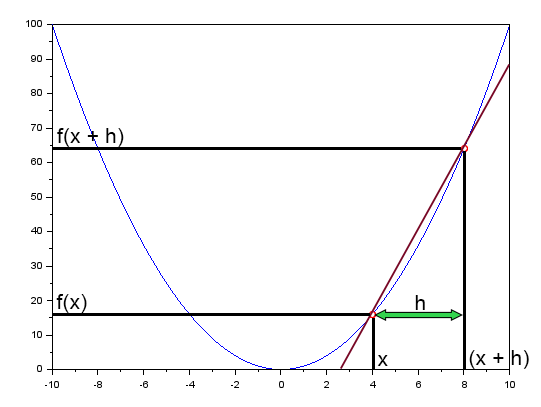
图中的红线是一条割线。如果你到目前为止一直很专注，现在我希望你加倍关注。这将比你能读到或听到的任何关于神经网络的东西都更重要。

这里我使用的 X 点与上一个主题中的相同，等于 4。我这样做是为了帮助你们更好地理解我的解释。

请注意，无论你怎么想或想象，都不可能生成切线。从图形上的曲线生成切线是不可能的.不过，如果使用割线，就可以得到切线。如何做呢？这一切都很简单。注意，f(x + h) 是 f(x) 移动了 h 的距离。那么，如果 h 趋于零，正割就会变成正切。而当 h 恰好为零时，图中所示的割线将与切线完全重合。因此，在这一点上，切线将给出函数在给定点的导数斜率。好吧，但我还是不明白。好了，亲爱的读者，让我们用一种不那么令人困惑的方式来表述上述内容，也许这样就能弄清情况了。

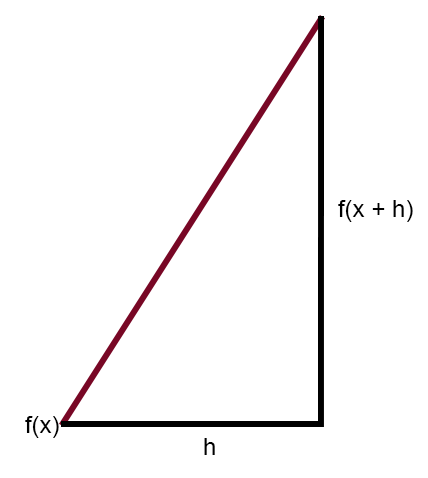
上图显示的内容与前一张相同。我想这将使使用割线的思路更加清晰。而且，为什么不像大家所说的那样，我们在使用神经网络时使用切线或导数，我们实际上使用的是割线，这样计算机就能生成正确的方程。

如果减小 h 值，就会开始接近 f(x)，但这个 h 值永远不会等于零。这就是我们要使用的神经网络。这可能是一个很小的数值；这个数值有多小取决于一件事，我们稍后会看到。这一刻被称为神经网络的疯狂。h 值越小，神经网络就越不疯狂，但 h 值越大，神经网络就越疯狂。为什么呢？原因在于收敛。在我们稍后考虑的计算过程中，可以注意到这种收敛倾向于值 h。这将导致最后得到的方程在这个收敛范围内趋于变化。因此，"h" 非常重要。解释看似复杂，但实际操作起来却简单得多。然而，我们还没有达到我们想要展示的地步。根据上面的图片，我们可以得出以下公式。

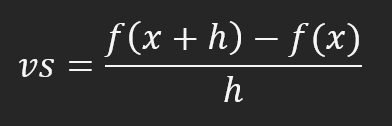
这个公式显示了切线与割线的距离。不过，实际使用的计算方法如下图所示。

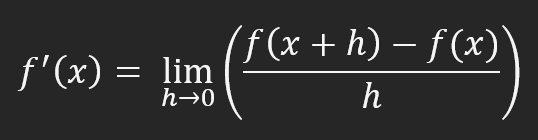
这个等式解释了神经网络的所有知识。这就是神经网络使用导数的原因。正是这个等式产生了许多人死记硬背的计算：导数公式。就是这些了。没有什么需要解释或讨论的了。我们只需要上面这个方程。这样，我就可以合上这篇文章，安静地过我的生活了。

最后的想法

但请等一等。你没有解释如何使用这个正割方程，也没有解释为什么它能解释一切。你说 "没有解释" 是什么意思？你在开玩笑吗？亲爱的读者，其实我刚刚开始介绍这个话题。我希望你们先静下心来研究这份材料。在下一篇关于神经网络的文章中，我们将探讨如何利用这里介绍的知识来列出正确的方程。