Distribuciones Estadísticas en MQL5: tomamos lo mejor de R y lo hacemos más rápido
Analizaremos las funciones para trabajar con las principales distribuciones estadísticas implementadas en el lenguaje R.
Se trata de las distribuciones de Cauchy, Weibull, normal, log-normal, logística, exponencial, uniforme, la distribución gamma, la distribución beta central y no central, la distribución chi-cuadrado, la distribución F de Fisher, la distribución t de Student, así como las distribuciones binomial discreta y binomial negativa, la geométrica, la hipergeométrica y la distribución de Poisson. Además, también existen funciones de cálculo de los momentos teóricos de las distribuciones, que permiten valorar el grado de correspondencia entre la distribución real y la modelada.
Hemos incluido en la biblioteca estándar MQL5 un gran número de funciones matemáticas de R. Además, hemos logrado que funcionen de 3 a 7 veces más rápido en comparación con las variantes originales en el lenguaje R. Asimismo, hemos detectado ciertos errores de implementación en algunas funciones en R.
Contenido
- Funciones para el cálculo de las características estadísticas de los elementos de la matriz
- Funciones para trabajar con distribuciones estadísticas
2.1. Distribución normal
- 2.1.1. MathProbabilityDensityNormal()
- 2.1.2. MathCumulativeDistributionNormal()
- 2.1.3. MathQuantileNormal()
- 2.1.4. MathRandomNormal()
- 2.1.5. MathMomentsNormal()
2.2. Distribución log-normal
- 2.2.1. MathProbabilityDensityLognormal()
- 2.2.2. MathCumulativeDistributionLognormal()
- 2.2.3. MathQuantileLognormal()
- 2.2.4. MathRandomLognormal()
- 2.2.5. MathMomentsLognormal()
2.3. Distribución beta
- 2.3.1. MathProbabilityDensityBeta()
- 2.3.2. MathCumulativeDistributionBeta()
- 2.3.3. MathQuantileBeta()
- 2.3.4. MathRandomBeta()
- 2.3.5. MathMomentsBeta()
2.4. Distribución beta no central
- 2.4.1. MathProbabilityDensityNoncentralBeta()
- 2.4.2. MathCumulativeDistributionNoncentralBeta()
- 2.4.3. MathQuantileNoncentralBeta()
- 2.4.4. MathRandomNoncentralBeta()
- 2.4.5. MathMomentsNoncentralBeta()
2.5. Distribución gamma
- 2.5.1. MathProbabilityDensityGamma()
- 2.5.2. MathCumulativeDistributionGamma()
- 2.5.3. MathQuantileGamma()
- 2.5.4. MathRandomGamma()
- 2.5.5. MathMomentsGamma()
2.6. Distribución chi-cuadrado
- 2.6.1. MathProbabilityDensityChiSquare()
- 2.6.2. MathCumulativeDistributionChiSquare()
- 2.6.3. MathQuantileChiSquare()
- 2.6.4. MathRandomChiSquare()
- 2.6.5. MathMomentsChiSquare()
2.7. Distribución chi-cuadrado no central
- 2.7.1. MathProbabilityDensityNoncentralChiSquare()
- 2.7.2. MathCumulativeDistributionNoncentralChiSquare()
- 2.7.3. MathQuantileNoncentralChiSquare()
- 2.7.4. MathRandomNoncentralChiSquare()
- 2.7.5. MathMomentsNoncentralChiSquare()
2.8. Distribución exponencial- 2.8.1. MathProbabilityDensityExponential()
- 2.8.2. MathCumulativeDistributionExponential()
- 2.8.3. MathQuantileExponential()
- 2.8.4. MathRandomExponential()
- 2.8.5. MathMomentsExponential()
2.9. Distribución F- 2.9.1. MathProbabilityDensityF()
- 2.9.2. MathCumulativeDistributionF()
- 2.9.3. MathQuantileF()
- 2.9.4. MathRandomF()
- 2.9.5. MathMomentsF()
2.10. Distribución F no central
- 2.10.1. MathProbabilityDensityNoncentralF()
- 2.10.2. MathCumulativeDistributionNoncentralF()
- 2.10.3. MathQuantileNoncentralF()
- 2.10.4. MathRandomNoncentralF()
- 2.10.5. MathMomentsNoncentralF()
2.11. Distribución T
- 2.11.1. MathProbabilityDensityT()
- 2.11.2. MathCumulativeDistributionT()
- 2.11.3. MathQuantileT()
- 2.11.4. MathRandomT()
- 2.11.5. MathMomentsT()
2.12 Distribución T no central
- 2.12.1. MathProbabilityDensityNoncentralT()
- 2.12.2. MathCumulativeDistributionNoncentralT()
- 2.12.3. MathQuantileNoncentralT()
- 2.12.4. MathRandomNoncentralT()
- 2.12.5. MathMomentsNoncentralT()
2.13. Distribución logística
- 2.13.1. MathProbabilityDensityLogistic()
- 2.13.2. MathCumulativeDistributionLogistic()
- 2.13.3. MathQuantileLogistic()
- 2.13.4. MathRandomLogistic()
- 2.13.5. MathMomentsLogistic()
2.14. Distribución de Cauchy
- 2.14.1. MathProbabilityDensityCauchy()
- 2.14.2. MathCumulativeDistributionCauchy()
- 2.14.3. MathQuantileCauchy()
- 2.14.4. MathRandomCauchy()
- 2.14.5. MathMomentsCauchy()
2.15. Distribución uniforme
- 2.15.1. MathProbabilityDensityUniform()
- 2.15.2. MathCumulativeDistributionUniform()
- 2.15.3. MathQuantileUniform()
- 2.15.4. MathRandomUniform()
- 2.15.5. MathMomentsUniform()
2.16. Distribución de Weibull
- 2.16.1. MathProbabilityDensityWeibull()
- 2.16.2. MathCumulativeDistributionWeibull()
- 2.16.3. MathQuantileWeibull()
- 2.16.4. MathRandomWeibull()
- 2.16.5. MathMomentsWeibull()
2.17. Distribución binomial
- 2.17.1. MathProbabilityDensityBinomial()
- 2.17.2. MathCumulativeDistributionBinomial()
- 2.17.3. MathQuantileBinomial()
- 2.17.4. MathRandomBinomial()
- 2.17.5. MathMomentsBinomial()
2.18. Distribución binomial negativa
- 2.18.1. MathProbabilityDensityNegativeBinomial()
- 2.18.2. MathCumulativeDistributionNegativeBinomial()
- 2.18.3. MathQuantileNegativeBinomial()
- 2.18.4. MathRandomNegativeBinomial()
- 2.18.5. MathMomentsNegativeBinomial()
2.19. Distribución geométrica
- 2.19.1. MathProbabilityDensityGeometric()
- 2.19.2. MathCumulativeDistributionGeometric()
- 2.19.3. MathQuantileGeometric()
- 2.19.4. MathRandomGeometric()
- 2.19.5. MathMomentsGeometric()
2.20. Distribución hipergeométrica
- 2.20.1. MathProbabilityDensityHypergeometric()
- 2.20.2. MathCumulativeDistributionHypergeometric()
- 2.20.3. MathQuantileHypergeometric()
- 2.20.4. MathRandomHypergeometric()
- 2.20.5. MathMomentsHypergeometric()
2.21. Distribución de Poisson
- 2.21.1. MathProbabilityDensityPoisson()
- 2.21.2. MathCumulativeDistributionPoisson()
- 2.21.3. MathQuantilePoisson()
- 2.21.4. MathRandomPoisson()
- 2.21.5. MathMomentsPoisson()
- Tablas de correspondencia con las funciones estadísticas del lenguaje R
- Ejemplo de uso de las funciones:
- Comparación de la velocidad de los cálculos
- Detectando los errores de cálculo en R
- Literatura
Introducción
El lenguaje R es una de las mejores herramientas de procesamiento y análisis estadístico de datos.
Gracias a su accesibilidad y al soporte de multitud de distribuciones estadísticas, ha obtenido una amplia difusión a la hora de analizar y procesar diferentes datos. El uso del aparato de la teoría de probabilidad y de la estadística matemática permite mirar de una forma nueva a los datos de los mercados financieros y abre nuevas posibilidades para la creación de estrategias comerciales. Con la aparición de la biblioteca estadística, estas posibilidades ahora están disponibles en el lenguaje MQL5.
La biblioteca estadística contiene funciones para el cálculo de las características estadísticas de los datos, así como funciones para trabajar con distribuciones estadísticas.
En este artículo estudiaremos las funciones principales de la biblioteca, así como ejemplos de su uso práctico.
1. Funciones para el cálculo de las características estadísticas de los elementos de la matriz
Este grupo de funciones realiza el cálculo de las características estadísticas (media, dispersión, coeficiente de asimetría, curtosis, mediana, desviación estándar y desviación media cuadrática) de los elementos de la matriz.
1.1. MathMean
La función calcula el valor medio (primer momento) de los elementos de la matriz. En caso de error, retorna NaN (no numérico). Análogo de mean() en R.
double MathMean( const double &array[] // [in] Matriz con los datos );
1.2. MathVariance
La función calcula la varianza (segundo momento) de los elementos de la matriz. En caso de error, retorna NaN. Análogo de var() en R.
double MathVariance( const double &array[] // [in] Matriz con los datos );
1.3. MathSkewness
La función calcula el coeficiente de asimetría (tercer momento) de los elementos de la matriz. En caso de error, retorna NaN. Análogo de skewness() en R (biblioteca e1071).
double MathSkewness( const double &array[] // [in] Matriz con los datos );
1.4. MathKurtosis
La función calcula la curtosis (cuarto momento) de los elementos de la matriz. En caso de error, retorna NaN. Análogo de kurtosis() en R (biblioteca e1071).
double MathKurtosis( const double &array[] // [in] Matriz con los datos );
1.5. MathMoments
La función calcula los primeros 4 momentos (media, varianza, coeficiente de asimetría, curtosis) de los elementos de la matriz. Retorna true, si los momentos se han calculado con éxito, si no, false.
bool MathMoments( const double &array[], // [in] Matriz con los datos double &mean, // [out] Variable para el valor medio (1 momento) double &variance, // [out] Variable para la varianza (2 momento) double &skewness, // [out] Variable para el coeficiente de asimetría (3 momento) double &kurtosis, // [out] Variable para la curtosis (4 momento) const int start=0, // [in] Índice inicial para el cálculo const int count=WHOLE_ARRAY // [in] Número de elementos para el cálculo );
1.6. MathMedian
La función calcula el valor mediano de los elementos de la matriz. En caso de error, retorna NaN. Análogo de median() en R.
double MathMedian( double &array[] // [in] Matriz con los datos );
1.7. MathStandardDeviation
La función calcula la desviación estándar de los elementos de la matriz. En caso de error, retorna NaN. Análogo de sd() en R.
double MathStandardDeviation( const double &array[] // [in] Matriz con los datos );
1.8. MathAverageDeviation
La función calcula la desviación media de los elementos de la matriz. En caso de error, retorna NaN. Análogo de aad() en R.
double MathAverageDeviation( const double &array[] // [in] Matriz con los datos );
En todas las funciones en la que se realiza el cálculo de la curtosis, se usa una curtosis excesiva con respecto a la distribución normal (excess kurtosis=kurtosis-3), es decir, la curtosis excesiva de una distribución normal es igual a cero.
Es positiva si el pico de la distribución cerca del valor esperado es agudo, y negativa, si el pico es plano.
2. Distribuciones estadísticas
Para trabajar con distribuciones estadísticas en la biblioteca estadística del lenguaje MQL5 hay 5 funciones:
- Cálculo de la densidad de la distribución (función MathProbabilityDensityX());
- Cálculo de la probabilidad (función MathCumulativeDistributionX());
La función de distribución de probabilidad es igual a la probabilidad de que una magnitud aleatoria entre en el intervalo (-inf; x]). - Cálculo de los cuantiles de las distribuciones (función MathQuantileX());
El cuantil x de una distribución corresponde a la entrada de una magnitud aleatoria en el intervalo (-inf, x] con una probabilidad "probability" especificada para los parámetros de distribución dados. - Generación de números aleatorios con una distribución establecida (función MathRandomX());
- Cálculo de los momentos teóricos de las distribuciones (función MathMomentsX());
2.1. Distribución normal
2.1.1. MathProbabilityDensityNormal
La función calcula el valor de la función de densidad de la probabilidad de la distribución normal con los parámetros mu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.double MathProbabilityDensityNormal( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Parámetro de distribución mean (esperanza matemática) const double sigma, // [in] Parámetro de distribución sigma (desviación media cuadrática) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución normal con los parámetros mu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityNormal( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Parámetro de distribución mean (esperanza matemática) const double sigma, // [in] Parámetro de distribución sigma (desviación media cuadrática) int &error_code // [out] Variable para el código de error );
La función calcula los valores de la función de densidad de la probabilidad de una distribución normal con los parámetros mu y sigma para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de dnorm() en R.
bool MathProbabilityDensityNormal( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Parámetro de distribución mean (esperanza matemática) const double sigma, // [in] Parámetro de distribución sigma (desviación media cuadrática) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula los valores de la función de densidad de la probabilidad de una distribución normal con los parámetros mu y sigma para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityNormal( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Parámetro de distribución mean (esperanza matemática) const double sigma, // [in] Parámetro de distribución sigma (desviación media cuadrática) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.1.2. MathCumulativeDistributionNormal
La función calcula el valor de la función de distribución normal de la probabilidad con los parámetros mu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionNormal( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Esperanza matemática const double sigma, // [in] Desviación media cuadrática const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución normal de la probabilidad con los parámetros mu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionNormal( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Esperanza matemática const double sigma, // [in] Desviación media cuadrática int &error_code // [out] Variable para el código de error );La función calcula el valor de la función de distribución normal de la probabilidad con los parámetros mu y sigma para la matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de pnorm() en R.
bool MathCumulativeDistributionNormal( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Esperanza matemática const double sigma, // [in] Desviación media cuadrática const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de distribución normal de la probabilidad con los parámetros mu y sigma para la matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionNormal( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Esperanza matemática const double sigma, // [in] Desviación media cuadrática double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.1.3. MathQuantileNormal
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución normal con los parámetros mu y sigma. En caso de error, retorna NaN.
double MathQuantileNormal( const double probability, // [in] Valor de la probabilidad de la magnitud aleatoria const double mu, // [in] Esperanza matemática const double sigma, // [in] Desviación media cuadrática const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución normal con los parámetros mu y sigma. En caso de error, retorna NaN.
double MathQuantileNormal( const double probability, // [in] Valor de la probabilidad de la magnitud aleatoria const double mu, // [in] Esperanza matemática const double sigma, // [in] Desviación media cuadrática int &error_code // [out] Variable para el código de error );Para la matriz de valores de la probabilidad "probability", la función calcula los valores de la función inversa de distribución normal con los parámetros mu y sigma. En caso de error, retorna false. Análogo de qnorm() en R.
bool MathQuantileNormal( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double mu, // [in] Esperanza matemática const double sigma, // [in] Desviación media cuadrática const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de la probabilidad "probability", la función calcula los valores de la función inversa de distribución normal con los parámetros mu y sigma. En caso de error, retorna false.
bool MathQuantileNormal( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double mu, // [in] Esperanza matemática const double sigma, // [in] Desviación media cuadrática double &result[] // [out] Matriz con los valores de los cuantiles );
2.1.4. MathRandomNormal
La función genera una magnitud pseudoaleatoria, distribuida según la ley normal con los parámetros mu y sigmа. En caso de error, retorna NaN.
double MathRandomNormal( const double mu, // [in] Esperanza matemática const double sigma, // [in] Desviación media cuadrática int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley normal con los parámetros mu y sigmа. En caso de error, retorna false. Análogo de rnorm() en R.
bool MathRandomNormal( const double mu, // [in] Esperanza matemática const double sigma, // [in] Desviación media cuadrática const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.1.5. MathMomentsNormal
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución normal. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsNormal( const double mu, // [in] Esperanza matemática const double sigma, // [in] Desviación media cuadrática double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.2. Distribución log-normal
2.2.1. MathProbabilityDensityLognormal
La función calcula el valor de la función de densidad de la probabilidad de la distribución log-normal con los parámetros mu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityLognormal( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Logaritmo de esperanza matemática (log mean) const double sigma, // [in] Logaritmo de desviación media cuadrática (log standard deviation) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución log-normal con los parámetros mu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityLognormal( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Logaritmo de esperanza matemática (log mean) const double sigma, // [in] Logaritmo de desviación media cuadrática (log standard deviation) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de una distribución log-normal con los parámetros mu y sigma para una matriz de magnitudes aleatorias x[]. En caso de error, retorna NaN. Análogo de dlnorm() en R.
bool MathProbabilityDensityLognormal( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Logaritmo de esperanza matemática (log mean) const double sigma, // [in] Logaritmo de desviación media cuadrática (log standard deviation) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de densidad de la probabilidad de una distribución log-normal con los parámetros mu y sigma para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityLognormal( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Logaritmo de esperanza matemática (log mean) const double sigma, // [in] Logaritmo de desviación media cuadrática (log standard deviation) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.2.2. MathCumulativeDistributionLognormal
La función calcula el valor de la función de distribución log-normal de la probabilidad con los parámetros mu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionLognormal( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Logaritmo de esperanza matemática (log mean) const double sigma, // [in] Logaritmo de desviación media cuadrática (log standard deviation) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución log-normal de la probabilidad con los parámetros mu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionLognormal( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Logaritmo de esperanza matemática (log mean) const double sigma, // [in] Logaritmo de desviación media cuadrática (log standard deviation) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución normal de la probabilidad con los parámetros mu y sigma para la matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de plnorm() en R.
bool MathCumulativeDistributionLognormal( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Logaritmo de esperanza matemática (log mean) const double sigma, // [in] Logaritmo de desviación media cuadrática (log standard deviation) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de distribución normal de la probabilidad con los parámetros mu y sigma para la matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionLognormal( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Logaritmo de esperanza matemática (log mean) const double sigma, // [in] Logaritmo de desviación media cuadrática (log standard deviation) double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.2.3. MathQuantileLognormal
La función calcula el valor de la función inversa de distribución log-normal con los parámetros mu y sigma para la probabilidad "probability". En caso de error, retorna NaN.
double MathQuantileLognormal( const double probability, // [in] Valor de la probabilidad de aparición de una magnitud aleatoria const double mu, // [in] Logaritmo de esperanza matemática (log mean) const double sigma, // [in] Logaritmo de desviación media cuadrática (log standard deviation) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función inversa de distribución log-normal con los parámetros mu y sigma para la probabilidad "probability". En caso de error, retorna NaN.
double MathQuantileLognormal( const double probability, // [in] Valor de la probabilidad de aparición de una magnitud aleatoria const double mu, // [in] Logaritmo de esperanza matemática (log mean) const double sigma, // [in] Logaritmo de desviación media cuadrática (log standard deviation) int &error_code // [out] Variable para el código de error );
Para la matriz de valores de la probabilidad probability[] , la función calcula los valores de la función inversa de distribución log-normal con los parámetros mu y sigma. En caso de error, retorna false. Análogo de qlnorm() en R.
bool MathQuantileLognormal( const double &probability[], // [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double mu, // [in] Logaritmo de esperanza matemática (log mean) const double sigma, // [in] Logaritmo de desviación media cuadrática (log standard deviation) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de la probabilidad probability[] , la función calcula los valores de la función inversa de distribución log-normal con los parámetros mu y sigma. En caso de error, retorna false.
bool MathQuantileLognormal( const double &probability[], // [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double mu, // [in] Logaritmo de esperanza matemática (log mean) const double sigma, // [in] Logaritmo de desviación media cuadrática (log standard deviation) double &result[] // [out] Matriz con los valores de los cuantiles );
2.2.4. MathRandomLognormal
La función genera una magnitud pseudoaleatoria, distribuida según la ley log-normal con los parámetros mu y sigmа. En caso de error, retorna NaN.
double MathRandomLognormal( const double mu, // [in] Logaritmo de esperanza matemática (log mean) const double sigma, // [in] Logaritmo de desviación media cuadrática (log standard deviation) int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley log-normal con los parámetros mu y sigmа. En caso de error, retorna false. Análogo de rlnorm() en R.
bool MathRandomLognormal( const double mu, // [in] Logaritmo de esperanza matemática (log mean) const double sigma, // [in] Logaritmo de desviación media cuadrática (log standard deviation) const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.2.5. MathMomentsLognormal
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución log-normal. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsLognormal( const double mu, // [in] Logaritmo de esperanza matemática (log mean) const double sigma, // [in] Logaritmo de desviación media cuadrática (log standard deviation) double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.3. Distribución beta
2.3.1. MathProbabilityDensityBeta
La función calcula el valor de la función de densidad de la probabilidad de la distribución beta con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityBeta( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución beta con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityBeta( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución beta con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de dbeta() en R.
bool MathProbabilityDensityBeta( const double &x[], // [in] Valor de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de densidad de la probabilidad de la distribución beta con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityBeta( const double &x[], // [in] Valor de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.3.2. MathCumulativeDistributionlBeta
La función calcula el valor de la función de distribución de la probabilidad de la distribución beta con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionBeta( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de la probabilidad de la distribución beta con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionBeta( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de la probabilidad de la distribución beta con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de pbeta() en R.
bool MathCumulativeDistributionBeta( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de distribución de la probabilidad de la distribución beta con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionBeta( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.3.3. MathQuantileBeta
Para la probabilidad "probability", la función calcula el valor de la función inversa de la distribución beta con los parámetros a y b. En caso de error, retorna NaN.
double MathQuantileBeta( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de la distribución beta con los parámetros a y b. En caso de error, retorna NaN.
double MathQuantileBeta( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) int &error_code // [out] Variable para el código de error );
Para la matriz de valores de la probabilidad probability[], la función calcula los valores de la función inversa de la distribución beta con los parámetros a y b. En caso de error, retorna false. Análogo de qbeta() en R.
bool MathQuantileBeta( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de la probabilidad probability[], la función calcula los valores de la función inversa de la distribución beta con los parámetros a y b. En caso de error, retorna false.
bool MathQuantileBeta( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) double &result[] // [out] Matriz con los valores de los cuantiles );
2.3.4. MathRandomBeta
La función genera una magnitud pseudoaleatoria, distribuida según la ley de la distribución beta con los parámetros a y b. En caso de error, retorna NaN.
double MathRandomBeta( const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de la distribución beta con los parámetros a y b. En caso de error, retorna false. Análogo de rbeta() en R.
bool MathRandomBeta( const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.3.5. MathMomentsBeta
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución beta. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsBeta( const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.4. Distribución beta no central
2.4.1. MathProbabilityDensityNoncentralBeta
La función calcula el valor de la función de densidad de la probabilidad de la distribución beta no central con los parámetros a, b y lambda para una magnitud aleatoria x. En caso de error, retorna NaN.double MathProbabilityDensityNoncentralBeta( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const double lambda, // [in] Parámetro de no-centralidad const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución beta no central con los parámetros a, b y lambda para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityNoncentralBeta( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const double lambda, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución beta no central con los parámetros a, b y lambda para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de dbeta() en R.
bool MathProbabilityDensityNoncentralBeta( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const double lambda, // [in] Parámetro de no-centralidad const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de densidad de la probabilidad de la distribución beta no central con los parámetros a, b y lambda para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityNoncentralBeta( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const double lambda, // [in] Parámetro de no-centralidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.4.2. MathCumulativeDistributionNoncentralBeta
La función calcula el valor de la función de distribución de la probabilidad de la distribución beta no-central con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionNoncentralBeta( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const double lambda, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de la probabilidad de la distribución beta no-central con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionNoncentralBeta( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const double lambda, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de la probabilidad de la distribución beta no-central con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de pbeta() en R.
bool MathCumulativeDistributionNoncentralBeta( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const double lambda, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de distribución de la probabilidad de la distribución beta no-central con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionNoncentralBeta( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const double lambda, // [in] Parámetro de no-centralidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.4.3. MathQuantileNoncentralBeta
La función calcula el valor de la función inversa de distribución de la probabilidad de la distribución beta no-central con los parámetros a, b y lambda para la probabilidad de aparición de un valor de la magnitud aleatoria "probability". En caso de error, retorna NaN.
double MathQuantileNoncentralBeta( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const double lambda, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función inversa de distribución de la probabilidad de la distribución beta no-central con los parámetros a, b y lambda para la probabilidad de aparición de un valor de la magnitud aleatoria "probability". En caso de error, retorna NaN.
double MathQuantileNoncentralBeta( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const double lambda, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor de la función inversa de la distribución de la probabilidad de la distribución beta no-central con los parámetros a y b. En caso de error, retorna false. Análogo de qbeta() en R.
bool MathQuantileNoncentralBeta( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const double lambda, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor de la función inversa de la distribución de la probabilidad de la distribución beta no-central con los parámetros a y b. En caso de error, retorna false.
bool MathQuantileNoncentralBeta( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const double lambda, // [in] Parámetro de no-centralidad double &result[] // [out] Matriz con los valores de los cuantiles );
2.4.4. MathRandomNoncentralBeta
La función genera una magnitud pseudoaleatoria, distribuida según la ley de la distribución beta no-central con los parámetros a, b y lambda. En caso de error, retorna NaN.
double MathRandomNoncentralBeta( const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const double lambda, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de la distribución beta no-central con los parámetros a, b y lambda. En caso de error, retorna false. Análogo de rbeta() en R.
bool MathRandomNoncentralBeta( const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const double lambda, // [in] Parámetro de no-centralidad const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.4.5. MathMomentsNoncentralBeta
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución beta no-central con los parámetros a, b y lambda. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
double MathMomentsNoncentralBeta( const double a, // [in] Primer parámetro de la distribución beta (shape1) const double b, // [in] Segundo parámetro de la distribución beta (shape2) const double lambda, // [in] Parámetro de no-centralidad double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.5. Distribución gamma
2.5.1. MathProbabilityDensityGamma
La función calcula el valor de la función de densidad de la probabilidad de la distribución gamma con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.double MathProbabilityDensityGamma( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución (shape) const double b, // [in] Segundo parámetro de la distribución (scale) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución gamma con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityGamma( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución (shape) const double b, // [in] Segundo parámetro de la distribución (scale) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución gamma con los parámetros a y b para una matriz de magnitudes aleatorias x[] En caso de error, retorna false. Análogo de dgamma() en R.
bool MathProbabilityDensityGamma( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución (shape) const double b, // [in] Segundo parámetro de la distribución (scale) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de densidad de la probabilidad de la distribución gamma con los parámetros a y b para una matriz de magnitudes aleatorias x[] En caso de error, retorna false.
bool MathProbabilityDensityGamma( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución (shape) const double b, // [in] Segundo parámetro de la distribución (scale) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.5.2. MathCumulativeDistributionGamma
La función calcula el valor de la función de la distribución gamma de la probabilidad con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionGamma( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución (shape) const double b, // [in] Segundo parámetro de la distribución (scale) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de la distribución gamma de la probabilidad con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionGamma( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución (shape) const double b, // [in] Segundo parámetro de la distribución (scale) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de la distribución gamma de la probabilidad con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de pgamma() en R.
bool MathCumulativeDistributionGamma( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución (shape) const double b, // [in] Segundo parámetro de la distribución (scale) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de la distribución gamma de la probabilidad con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionGamma( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución (shape) const double b, // [in] Segundo parámetro de la distribución (scale) double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.5.3. MathQuantileGamma
Para la probabilidad "probability", la función calcula el valor de la función inversa de la distribución gamma con los parámetros a y b. En caso de error, retorna NaN.
double MathQuantileGamma( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double a, // [in] Primer parámetro de la distribución (shape) const double b, // [in] Segundo parámetro de la distribución (scale) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de la distribución gamma con los parámetros a y b. En caso de error, retorna NaN.
double MathQuantileGamma( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double a, // [in] Primer parámetro de la distribución (shape) const double b, // [in] Segundo parámetro de la distribución (scale) int &error_code // [out] Variable para el código de error );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor de la función inversa de la distribución gamma con los parámetros a y b. En caso de error, retorna false. Análogo de qgamma() en R.
bool MathQuantileGamma( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución (shape) const double b, // [in] Segundo parámetro de la distribución (scale) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor de la función inversa de la distribución gamma con los parámetros a y b. En caso de error, retorna false.
bool MathQuantileGamma( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double a, // [in] Primer parámetro de la distribución (shape) const double b, // [in] Segundo parámetro de la distribución (scale) double &result[] // [out] Matriz con los valores de los cuantiles );
2.5.4. MathRandomGamma
La función genera una magnitud pseudoaleatoria, distribuida según la ley de la distribución gamma con los parámetros a y b. En caso de error, retorna NaN.
double MathRandomGamma( const double a, // [in] Primer parámetro de la distribución (shape) const double b, // [in] Segundo parámetro de la distribución (scale) int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de la distribución gamma con los parámetros a y b. En caso de error, retorna false. Análogo de rgamma() en R.
bool MathRandomGamma( const double a, // [in] Primer parámetro de la distribución (shape) const double b, // [in] Segundo parámetro de la distribución (scale) const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.5.5. MathMomentsGamma
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución gamma con los parámetros a y b. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsGamma( const double a, // [in] Primer parámetro de la distribución (shape) const double b, // [in] Segundo parámetro de la distribución (scale) double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.6. Distribución chi-cuadrado
2.6.1. MathProbabilityDensityChiSquare
La función calcula el valor de la función de densidad de la probabilidad de la distribución chi-cuadrado con el parámetro nu para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityChiSquare( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );La función calcula el valor de la función de densidad de la probabilidad de la distribución chi-cuadrado con el parámetro nu para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityChiSquare( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución chi-cuadrado con el parámetro nu para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de dchisq() en R.
bool MathProbabilityDensityChiSquare( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de densidad de la probabilidad de la distribución chi-cuadrado con el parámetro nu para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityChiSquare( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.6.2. MathCumulativeDistributionChiSquare
La función calcula el valor de la función de distribución de la probabilidad de chi-cuadrado con el parámetro nu para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionChiSquare( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de la probabilidad de chi-cuadrado con el parámetro nu para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionChiSquare( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de la probabilidad de chi-cuadrado con el parámetro nu para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de pchisq() en R.
bool MathCumulativeDistributionChiSquare( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de distribución de la probabilidad de chi-cuadrado con el parámetro nu para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionChiSquare( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.6.3. MathQuantileChiSquare
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución de la probabilidad chi-cuadrado. En caso de error, retorna NaN.
double MathQuantileChiSquare( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución de la probabilidad chi-cuadrado. En caso de error, retorna NaN.
double MathQuantileChiSquare( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) int &error_code // [out] Variable para el código de error );
Para la matriz de valores de probabilidad probability[], la función calcula el valor de la función inversa de distribución de la probabilidad chi-cuadrado. En caso de error, retorna false. Análogo de qchisq() en R.
bool MathQuantileChiSquare( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de probabilidad probability[], la función calcula el valor de la función inversa de distribución de la probabilidad chi-cuadrado. En caso de error, retorna false.
bool MathQuantileChiSquare( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) double &result[] // [out] Matriz con los valores de los cuantiles );
2.6.4. MathRandomChiSquare
La función genera una magnitud pseudoaleatoria, distribuida según la ley de la distribución chi-cuadrado con el parámetro nu. En caso de error, retorna NaN.
double MathRandomChiSquare( const double nu, // [in] Parámetro de distribución (número de grados de libertad) int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de la distribución chi-cuadrado con el parámetro nu. En caso de error, retorna false. Análogo de rchisq() en R.
bool MathRandomChiSquare( const double nu, // [in] Parámetro de distribución (número de grados de libertad) const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.6.5. MathMomentsChiSquare
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución chi-cuadrado con el parámetro nu. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsChiSquare( const double nu, // [in] Parámetro de distribución (número de grados de libertad) double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.7. Distribución chi-cuadrado no central
2.7.1. MathProbabilityDensityNoncentralChiSquare
La función calcula el valor de la función de densidad de la probabilidad de la distribución chi-cuadrado no-central con los parámetros nu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityNoncentralChiSquare( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución chi-cuadrado no-central con los parámetros nu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityNoncentralChiSquare( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución chi-cuadrado no-central con los parámetros nu y sigma para una matriz de magnitudes aleatorias x. En caso de error, retorna false. Análogo de dchisq() en R.
bool MathProbabilityDensityNoncentralChiSquare( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de densidad de la probabilidad de la distribución chi-cuadrado no-central con los parámetros nu y sigma para una matriz de magnitudes aleatorias x. En caso de error, retorna false.
bool MathProbabilityDensityNoncentralChiSquare( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.7.2. MathCumulativeDistributionNoncentralChiSquare
La función calcula el valor de la función de distribución de la probabilidad de la distribución chi-cuadrado no-central con los parámetros nu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionNoncentralChiSquare( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de la probabilidad de la distribución chi-cuadrado no-central con los parámetros nu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionNoncentralChiSquare( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de la probabilidad de la distribución chi-cuadrado no-central con los parámetros nu y sigma para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de pchisq() en R.
bool MathCumulativeDistributionNoncentralChiSquare( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de distribución de la probabilidad de la distribución chi-cuadrado no-central con los parámetros nu y sigma para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionNoncentralChiSquare( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.7.3. MathQuantileNoncentralChiSquare
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución chi-cuadrado no-central con los parámetros mu y sigma. En caso de error, retorna NaN.
double MathQuantileNoncentralChiSquare( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución chi-cuadrado no-central con los parámetros mu y sigma. En caso de error, retorna NaN.
double MathQuantileNoncentralChiSquare( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
Para la probabilidad probability[], la función calcula el valor de la función inversa de distribución chi-cuadrado no-central con los parámetros mu y sigma. En caso de error, retorna false. Análogo de qchisq() en R.
bool MathQuantileNoncentralChiSquare( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la probabilidad probability[], la función calcula el valor de la función inversa de distribución chi-cuadrado no-central con los parámetros mu y sigma. En caso de error, retorna false false.
bool MathQuantileNoncentralChiSquare( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad double &result[] // [out] Matriz con los valores de los cuantiles );
2.7.4. MathRandomNoncentralChiSquare
La función genera una magnitud pseudoaleatoria, distribuida según la ley de la distribución chi-cuadrado no-central con los parámetros nu y sigma. En caso de error, retorna NaN.
double MathRandomNoncentralChiSquare( const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de la distribución chi-cuadrado no-central con los parámetros nu y sigma. En caso de error, retorna false. Análogo de rchisq() en R.
bool MathRandomNoncentralChiSquare( const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.7.5. MathMomentsNoncentralChiSquare
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución chi-cuadrado no-central con los parámetros nu y sigma. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsNoncentralChiSquare( const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.8. Distribución exponencial
2.8.1. MathProbabilityDensityExponential
La función calcula el valor de la función de densidad de la probabilidad de la distribución exponencial con el parámetro mu para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityExponential( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Parámetro de distribución (esperanza matemática) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución exponencial con el parámetro mu para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityExponential( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Parámetro de distribución (esperanza matemática) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución exponencial con el parámetro mu para una matriz de magnitudes aleatorias x. En caso de error, retorna false. Análogo de dexp() en R.
bool MathProbabilityDensityExponential( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Parámetro de distribución (esperanza matemática const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de densidad de la probabilidad de la distribución exponencial con el parámetro mu para una matriz de magnitudes aleatorias x. En caso de error, retorna false.
bool MathProbabilityDensityExponential( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Parámetro de distribución (esperanza matemática) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.8.2. MathCumulativeDistributionExponential
La función calcula el valor de la función de distribución exponencial de la probabilidad con el parámetro mu para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionExponential( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Parámetro de distribución (esperanza matemática) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución exponencial de la probabilidad con el parámetro mu para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionExponential( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Parámetro de distribución (esperanza matemática) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución exponencial de la probabilidad con el parámetro mu para una magnitud aleatoria x. En caso de error, retorna false. Análogo de pexp() en R.
bool MathCumulativeDistributionExponential( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Parámetro de distribución (esperanza matemática const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de distribución exponencial de la probabilidad con el parámetro mu para una magnitud aleatoria x. En caso de error, retorna false.
bool MathCumulativeDistributionExponential( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Parámetro de distribución (esperanza matemática) double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.8.3. MathQuantileExponential
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución exponencial de probabilidad con el parámetro mu. En caso de error, retorna NaN.
double MathQuantileExponential( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double mu, // [in] Parámetro de distribución (esperanza matemática) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución exponencial de probabilidad con el parámetro mu. En caso de error, retorna NaN.
double MathQuantileExponential( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double mu, // [in] Parámetro de distribución (esperanza matemática) int &error_code // [out] Variable para el código de error );
Para la matriz de valores de probabilidad probability[], la función calcula el valor de la función inversa de distribución exponencial de la probabilidad con el parametro mu. En caso de error, retorna false. Análogo de qexp() en R.
bool MathQuantileExponential( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double mu, // [in] Parámetro de distribución (esperanza matemática) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de probabilidad probability[], la función calcula el valor de la función inversa de distribución exponencial de la probabilidad con el parametro mu. En caso de error, retorna false.
bool MathQuantileExponential( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double mu, // [in] Parámetro de distribución (esperanza matemática) double &result[] // [out] Matriz con los valores de los cuantiles );
2.8.4. MathRandomExponential
La función genera una magnitud pseudoaleatoria, distribuida según la ley de distribución exponencial con el parámetro mu. En caso de error, retorna NaN.
double MathRandomExponential( const double mu, // [in] Parámetro de distribución (esperanza matemática) int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de distribución exponencial con el parámetro mu. En caso de error, retorna false. Análogo de rexp() en R.
bool MathRandomExponential( const double mu, // [in] Parámetro de distribución (esperanza matemática) const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.8.5. MathMomentsExponential
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución exponencial con el parámetro mu. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsExponential( const double mu, // [in] Parámetro de distribución (esperanza matemática) double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.9. Distribución F
2.9.1. MathProbabilityDensityF
La función calcula el valor de la función de densidad de la probabilidad de la distribución F de Fisher con los parámetros nu1 y nu2 para la magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityF( const double x, // [in] Valor de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución F de Fisher con los parámetros nu1 y nu2 para la magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityF( const double x, // [in] Valor de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución F de Fisher con los parámetros nu1 y nu2 para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de df() en R.
bool MathProbabilityDensityF( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de densidad de la probabilidad de la distribución F de Fisher con los parámetros nu1 y nu2 para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityF( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.9.2. MathCumulativeDistributionF
La función calcula el valor de la función de distribución de la probabilidad según la ley de la distribución F de Fisher con los parámetros nu1 y nu2 para la magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionF( const double x, // [in] Valor de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de la probabilidad según la ley de la distribución F de Fisher con los parámetros nu1 y nu2 para la magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionF( const double x, // [in] Valor de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de la probabilidad según la ley de la distribución F de Fisher con los parámetros nu1 y nu2 para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de pf() en R.
bool MathCumulativeDistributionF( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de distribución de la probabilidad según la ley de la distribución F de Fisher con los parámetros nu1 y nu2 para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionF( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.9.3. MathQuantileF
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución F de probabilidad con los parámetros nu1 y nu2. En caso de error, retorna NaN.
double MathQuantileF( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución F de probabilidad con los parámetros nu1 y nu2. En caso de error, retorna NaN.
double MathQuantileF( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución F de probabilidad con los parámetros nu1 y nu2. En caso de error, retorna false. Análogo de qf() en R.
bool MathQuantileF( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución F de probabilidad con los parámetros nu1 y nu2. En caso de error, retorna false.
bool MathQuantileF( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) double &result[] // [out] Matriz con los valores de los cuantiles );
2.9.4. MathRandomF
La función genera una magnitud pseudoaleatoria, distribuida según la ley de la distribución F de Fisher con los parámetros nu1 y nu2. En caso de error, retorna NaN.
double MathRandomF( const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de la distribución F de Fisher con los parámetros nu1 y nu2. En caso de error, retorna false. Análogo de rf() en R.
bool MathRandomF( const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.9.5. MathMomentsF
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución F de Fisher con los parámetros nu1 y nu2. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsF( const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.10. Distribución F no-central
2.10.1. MathProbabilityDensityNoncentralF
La función calcula el valor de la función de densidad de la probabilidad de la distribución F de Fisher no-central con los parámetros nu1, nu2 y sigma para la magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityNoncentralF( const double x, // [in] Valor de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución F de Fisher no-central con los parámetros nu1, nu2 y sigma para la magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityNoncentralF( const double x, // [in] Valor de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución F de Fisher no-central con los parámetros nu1, nu2 y sigma para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de df() en R.
double MathProbabilityDensityNoncentralF( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de densidad de la probabilidad de la distribución F de Fisher no-central con los parámetros nu1, nu2 y sigma para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
double MathProbabilityDensityNoncentralF( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.10.2. MathCumulativeDistributionlNoncentralF
La función calcula el valor de la función de distribución de la probabilidad de la distribución F de Fisher no-central con los parámetros nu1, nu2 y sigma para la magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionNoncentralF( const double x, // [in] Valor de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de la probabilidad de la distribución F de Fisher no-central con los parámetros nu1, nu2 y sigma para la magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionNoncentralF( const double x, // [in] Valor de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de la probabilidad de la distribución F de Fisher no-central con los parámetros nu1, nu2 y sigma para la magnitud aleatoria x. En caso de error, retorna false. Análogo de pf() en R.
bool MathCumulativeDistributionNoncentralF( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de distribución de la probabilidad de la distribución F de Fisher no-central con los parámetros nu1, nu2 y sigma para la magnitud aleatoria x. En caso de error, retorna NaN.
bool MathCumulativeDistributionNoncentralF( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.10.3. MathQuantileNoncentralF
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución F de Fisher no-central con los parámetros nu1, nu2 y sigma. En caso de error, retorna NaN.
double MathQuantileNoncentralF( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución F de Fisher no-central con los parámetros nu1, nu2 y sigma. En caso de error, retorna NaN.
double MathQuantileNoncentralF( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución F de Fisher no-central con los parámetros nu1, nu2 y sigma. En caso de error, retorna false. Análogo de qf() en R.
bool MathQuantileNoncentralF( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución F de Fisher no-central con los parámetros nu1, nu2 y sigma. En caso de error, retorna false.
bool MathQuantileNoncentralF( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad double &result[] // [out] Matriz con los valores de los cuantiles );
2.10.4. MathRandomNoncentralF
La función genera una magnitud pseudoaleatoria, distribuida según la ley de la distribución F de Fisher no-central con los parámetros nu1, nu2 y sigma. En caso de error, retorna NaN.
double MathRandomNoncentralF( const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de la distribución F de Fisher no-central con los parámetros nu1, nu2 y sigma. En caso de error, retorna false. Análogo de rf() en R.
bool MathRandomNoncentralF( const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad double &result[] // [out] Matriz con los valores de los cuantiles );
2.10.5. MathMomentsNoncentralF
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución F de Fisher no-central con los parámetros nu1, nu2 y sigma. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsNoncentralF( const double nu1, // [in] Primer parámetro de distribución (número de grados de libertad) const double nu2, // [in] Segundo parámetro de distribución (número de grados de libertad) const double sigma, // [in] Parámetro de no-centralidad double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error )
2.11. Distribución T
2.11.1. MathProbabilityDensityT
La función calcula el valor de la función de densidad de la probabilidad de la distribución T de Student con el parámetro nu para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityT( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución T de Student con el parámetro nu para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityT( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución T de Student con el parámetro nu para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de dt() en R.
bool MathProbabilityDensityT( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de densidad de la probabilidad de la distribución T de Student con el parámetro nu para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityT( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.11.2. MathCumulativeDistributionT
La función calcula el valor de la función de distribución de Student con el parámetro nu para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionT( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de Student con el parámetro nu para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionT( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de Student con el parámetro nu para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de pt() en R.
bool MathCumulativeDistributionT( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de distribución de Student con el parámetro nu para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionT( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.11.3. MathQuantileT
Para la probabilidad "probability", la función calcula el valor de la función inversa de la distribución T de Student con el parámetro mu. En caso de error, retorna NaN.
double MathQuantileT( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de la distribución T de Student con el parámetro mu. En caso de error, retorna NaN.
double MathQuantileT( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) int &error_code // [out] Variable para el código de error );
Para la matriz de valores de probabilidad probability[], la función calcula el valor de la función inversa de la distribución T de Student con el parametro mu. En caso de error, retorna false. Análogo de qt() en R.
bool MathQuantileT( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de probabilidad probability[], la función calcula el valor de la función inversa de la distribución T de Student con el parametro mu. En caso de error, retorna false.
bool MathQuantileT( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) double &result[] // [out] Matriz con los valores de los cuantiles );
2.11.4. MathRandomT
La función genera una magnitud pseudoaleatoria, distribuida según la ley de la distribución T de Student con el parámetro nu. En caso de error, retorna NaN.
double MathRandomT( const double nu, // [in] Parámetro de distribución (número de grados de libertad) int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de la distribución T de Student con el parámetro nu. En caso de error, retorna false. Análogo de rt() en R.
bool MathRandomT( const double nu, // [in] Parámetro de distribución (número de grados de libertad) const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.11.5. MathMomentsT
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución T de Student con el parámetro nu. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
double MathMomentsT( const double nu, // [in] Parámetro de distribución (número de grados de libertad) double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.12. Distribución T no central
2.12.1. MathProbabilityDensityNoncentralT
La función calcula el valor de la densidad de la probabilidad de la distribución T de Student no-central con los parámetros nu y delta para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityNoncentralT( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double delta, // [in] Parámetro de no-centralidad const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución T de Student no-central con los parámetros nu y delta para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityNoncentralT( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double delta, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución T de Student no-central con los parámetros nu y delta para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de dt() en R.
bool MathProbabilityDensityNoncentralT( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double delta, // [in] Parámetro de no-centralidad const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de densidad de la probabilidad de la distribución T de Student no-central con los parámetros nu y delta para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityNoncentralT( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double delta, // [in] Parámetro de no-centralidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.12.2. MathCumulativeDistributionlNoncentralT
La función calcula el valor de la función de distribución de la probabilidad de la distribución T no-central con los parámetros nu y delta para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionNoncentralT( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double delta, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de la probabilidad de la distribución T no-central con los parámetros nu y delta para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionNoncentralT( const double x, // [in] Valor de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double delta, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de la probabilidad de la distribución T no-central con los parámetros nu y delta para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de pt() en R.
bool MathCumulativeDistributionNoncentralT( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double delta, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de distribución de la probabilidad de la distribución T no-central con los parámetros nu y delta para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionNoncentralT( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double delta, // [in] Parámetro de no-centralidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.12.3. MathQuantileNoncentralT
Para la probabilidad "probability", la función calcula el valor de la función inversa de la distribución T no-central con los parámetros nu y delta. En caso de error, retorna NaN.
double MathQuantileNoncentralT( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double delta, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de la distribución T no-central con los parámetros nu y delta. En caso de error, retorna NaN.
double MathQuantileNoncentralT( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double delta, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
Para la matriz de valores de probabilidad "probability", la función calcula el valor de la función inversa de la distribución T no-central con los parámetros nu y delta. En caso de error, retorna false. Análogo de qt() en R.
bool MathQuantileNoncentralT( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double delta, // [in] Parámetro de no-centralidad const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de probabilidad "probability", la función calcula el valor de la función inversa de la distribución T no-central con los parámetros nu y delta. En caso de error, retorna false.
bool MathQuantileNoncentralT( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double delta, // [in] Parámetro de no-centralidad double &result[] // [out] Matriz con los valores de los cuantiles );
2.12.4. MathRandomNoncentralT
La función genera una magnitud pseudoaleatoria, distribuida según la ley de la distribución T de Student no central con los parámetros nu y delta. En caso de error, retorna NaN.
double MathRandomNoncentralT( const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double delta, // [in] Parámetro de no-centralidad int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de la distribución T de Student no-central con los parámetros nu y delta. En caso de error, retorna false. Análogo de rt() en R.
bool MathRandomNoncentralT( const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double delta, // [in] Parámetro de no-centralidad const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.12.5. MathMomentsNoncentralT
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución T de Student no-central con los parámetros nu y delta. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
double MathMomentsNoncentralT( const double nu, // [in] Parámetro de distribución (número de grados de libertad) const double delta, // [in] Parámetro de no-centralidad double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.13. Distribución logística
2.13.1. MathProbabilityDensityLogistic
La función calcula el valor de la función de densidad de la probabilidad de la distribución logística con los parámetros mu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityLogistic( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Parámetro de distribución mean const double sigma, // [in] Parámetro de distribución scale const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución logística con los parámetros mu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityLogistic( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Parámetro de distribución mean const double sigma, // [in] Parámetro de distribución scale int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución logística con los parámetros mu y sigma para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de dlogis() en R.
bool MathProbabilityDensityLogistic( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Parámetro de distribución mean const double sigma, // [in] Parámetro de distribución scale const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de densidad de la probabilidad de la distribución logística con los parámetros mu y sigma para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityLogistic( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Parámetro de distribución mean const double sigma, // [in] Parámetro de distribución scale double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.13.2. MathCumulativeDistributionlLogistic
La función calcula el valor de la función de distribución logística de la probabilidad con los parámetros mu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionLogistic( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Parámetro de distribución mean const double sigma, // [in] Parámetro de distribución scale const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución logística de la probabilidad con los parámetros mu y sigma para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionLogistic( const double x, // [in] Valor de la magnitud aleatoria const double mu, // [in] Parámetro de distribución mean const double sigma, // [in] Parámetro de distribución scale int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución logística de la probabilidad con los parámetros mu y sigma para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de plogis() en R.
bool MathCumulativeDistributionLogistic( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Parámetro de distribución mean const double sigma, // [in] Parámetro de distribución scale const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de distribución logística de la probabilidad con los parámetros mu y sigma para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de plogis() en R.
bool MathCumulativeDistributionLogistic( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double mu, // [in] Parámetro de distribución mean const double sigma, // [in] Parámetro de distribución scale double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.13.3. MathQuantileLogistic
Para la probabilidad "probability", la función calcula el valor de la función inversa de la distribución logística con los parámetros mu y sigma. En caso de error, retorna NaN.
double MathQuantileLogistic( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double mu, // [in] Parámetro de distribución mean const double sigma, // [in] Parámetro de distribución scale const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de la distribución logística con los parámetros mu y sigma. En caso de error, retorna NaN.
double MathQuantileLogistic( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double mu, // [in] Parámetro de distribución mean const double sigma, // [in] Parámetro de distribución scale int &error_code // [out] Variable para el código de error );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor de la función inversa de distribución logística con los parámetros mu y sigma. En caso de error, retorna false. Análogo de qlogis() en R.
bool MathQuantileLogistic( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double mu, // [in] Parámetro de distribución mean const double sigma, // [in] Parámetro de distribución scale const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor de la función inversa de distribución logística con los parámetros mu y sigma. En caso de error, retorna false.
bool MathQuantileLogistic( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double mu, // [in] Parámetro de distribución mean const double sigma, // [in] Parámetro de distribución scale double &result[] // [out] Matriz con los valores de los cuantiles );
2.13.4. MathRandomLogistic
La función genera una magnitud pseudoaleatoria, distribuida según la ley de distribución logística con los parámetros mu y sigma. En caso de error, retorna NaN.
double MathRandomLogistic( const double mu, // [in] Parámetro de distribución mean const double sigma, // [in] Parámetro de distribución scale int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de distribución logística con los parámetros mu y sigma. En caso de error, retorna false. Análogo de rlogis() en R.
bool MathRandomLogistic( const double mu, // [in] Parámetro de distribución mean const double sigma, // [in] Parámetro de distribución scale const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.13.5. MathMomentsLogistic
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución logística con los parámetros mu y sigma. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsLogistic( const double mu, // [in] Parámetro de distribución mean const double sigma, // [in] Parámetro de distribución scale double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.14. Distribución de Cauchy
2.14.1. MathProbabilityDensityCauchy
La función calcula el valor de la función de densidad de la probabilidad de la distribución de Cauchy con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityCauchy( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Parámetro de distribución mean const double b, // [in] Parámetro de distribución scale const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución de Cauchy con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityCauchy( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Parámetro de distribución mean const double b, // [in] Parámetro de distribución scale int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución de Cauchy con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de dcauchy() en R.
bool MathProbabilityDensityCauchy( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Parámetro de distribución mean const double b, // [in] Parámetro de distribución scale const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de densidad de la probabilidad de la distribución de Cauchy con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityCauchy( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Parámetro de distribución mean const double b, // [in] Parámetro de distribución scale double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.14.2. MathCumulativeDistributionCauchy
La función calcula el valor de la función de densidad de la probabilidad de la distribución de Cauchy con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionCauchy( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Parámetro de distribución mean const double b, // [in] Parámetro de distribución scale const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución de Cauchy con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionCauchy( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Parámetro de distribución mean const double b, // [in] Parámetro de distribución scale int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de la probabilidad de Cauchy con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de pcauchy() en R.
bool MathCumulativeDistributionCauchy( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Parámetro de distribución mean const double b, // [in] Parámetro de distribución scale const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de distribución de la probabilidad de Cauchy con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionCauchy( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Parámetro de distribución mean const double b, // [in] Parámetro de distribución scale double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.14.3. MathQuantileCauchy
Para la probabilidad "probability", la función calcula el valor de la función inversa de la distribución de Cauchy con los parámetros a y b. En caso de error, retorna NaN.
double MathQuantileCauchy( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double a, // [in] Parámetro de distribución mean const double b, // [in] Parámetro de distribución scale const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de la distribución de Cauchy con los parámetros a y b. En caso de error, retorna NaN.
double MathQuantileCauchy( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double a, // [in] Parámetro de distribución mean const double b, // [in] Parámetro de distribución scale int &error_code // [out] Variable para el código de error );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor de la función inversa de la distribución de Cauchy con los parámetros a y b. En caso de error, retorna false. Análogo de qcauchy() en R.
bool MathQuantileCauchy( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double a, // [in] Parámetro de distribución mean const double b, // [in] Parámetro de distribución scale const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor de la función inversa de la distribución de Cauchy con los parámetros a y b. En caso de error, retorna false.
bool MathQuantileCauchy( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double a, // [in] Parámetro de distribución mean const double b, // [in] Parámetro de distribución scale double &result[] // [out] Matriz con los valores de los cuantiles );
2.14.4. MathRandomCauchy
La función genera una magnitud pseudoaleatoria, distribuida según la ley de la distribución de Cauchy con los parámetros a y b. En caso de error, retorna NaN.
double MathRandomCauchy( const double a, // [in] Parámetro de distribución mean const double b, // [in] Parámetro de distribución scale int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de la distribución de Cauchy con los parámetros a y b. En caso de error, retorna false. Análogo de rcauchy() en R.
double MathRandomCauchy( const double a, // [in] Parámetro de distribución mean const double b, // [in] Parámetro de distribución scale const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.14.5. MathMomentsCauchy
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución de Cauchy. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsCauchy( const double a, // [in] Parámetro de distribución mean const double b, // [in] Parámetro de distribución scale double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.15. Distribución uniforme
2.15.1. MathProbabilityDensityUniform
La función calcula el valor de la función de densidad de la probabilidad de la distribución uniforme con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityUniform( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Parámetro de distribución a (límite inferior) const double b, // [in] Parámetro de distribución b (límite superior) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución uniforme con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityUniform( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Parámetro de distribución a (límite inferior) const double b, // [in] Parámetro de distribución b (límite superior) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución uniforme con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de dunif() en R.
bool MathProbabilityDensityUniform( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Parámetro de distribución a (límite inferior) const double b, // [in] Parámetro de distribución b (límite superior) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de densidad de la probabilidad de la distribución uniforme con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityUniform( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Parámetro de distribución a (límite inferior) const double b, // [in] Parámetro de distribución b (límite superior) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.15.2. MathCumulativeDistributionUniform
La función calcula el valor de la función de distribución uniforme con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.double MathCumulativeDistributionUniform( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Parámetro de distribución a (límite inferior) const double b, // [in] Parámetro de distribución b (límite superior) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución uniforme con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionUniform( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Parámetro de distribución a (límite inferior) const double b, // [in] Parámetro de distribución b (límite superior) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución uniforme con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de punif() en R.
bool MathCumulativeDistributionUniform( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Parámetro de distribución a (límite inferior) const double b, // [in] Parámetro de distribución b (límite superior) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de distribución uniforme con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionUniform( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Parámetro de distribución a (límite inferior) const double b, // [in] Parámetro de distribución b (límite superior) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.15.3. MathQuantileUniform
Para la probabilidad "probability", la función calcula el valor de la función inversa de la distribución uniforme con los parámetros a y b. En caso de error, retorna NaN.
double MathQuantileUniform( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double a, // [in] Parámetro de distribución a (límite inferior) const double b, // [in] Parámetro de distribución b (límite superior) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de la distribución uniforme con los parámetros a y b. En caso de error, retorna NaN.
double MathQuantileUniform( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double a, // [in] Parámetro de distribución a (límite inferior) const double b, // [in] Parámetro de distribución b (límite superior) int &error_code // [out] Variable para el código de error );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor de la función inversa de la distribución uniforme con los parámetros a y b. En caso de error, retorna false. Análogo de qunif() en R.
bool MathQuantileUniform( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double a, // [in] Parámetro de distribución a (límite inferior) const double b, // [in] Parámetro de distribución b (límite superior) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor de la función inversa de la distribución uniforme con los parámetros a y b. En caso de error, retorna false.
bool MathQuantileUniform( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double a, // [in] Parámetro de distribución a (límite inferior) const double b, // [in] Parámetro de distribución b (límite superior) double &result[] // [out] Matriz con los valores de los cuantiles );
2.15.4. MathRandomUniform
La función genera una magnitud pseudoaleatoria, distribuida según la ley de la distribución uniforme con los parámetros a y b. En caso de error, retorna NaN.
double MathRandomUniform( const double a, // [in] Parámetro de distribución a (límite inferior) const double b, // [in] Parámetro de distribución b (límite superior) int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de la distribución uniforme con los parámetros a y b. En caso de error, retorna false. Análogo de runif() en R.
bool MathRandomUniform( const double a, // [in] Parámetro de distribución a (límite inferior) const double b, // [in] Parámetro de distribución b (límite superior) const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.15.5. MathMomentsUniform
La función calcula los valores numéricos teóricos de los 4 primeros momentos para la distribución uniforme. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsUniform( const double a, // [in] Parámetro de distribución a (límite inferior) const double b, // [in] Parámetro de distribución b (límite superior) double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.16. Distribución de Weibull
2.16.1. MathProbabilityDensityWeibull
La función calcula el valor de la función de densidad de la probabilidad de la distribución de Weibull con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityWeibull( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Parámetro de distribución (shape) const double b, // [in] Parámetro de distribución (scale) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución de Weibull con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityWeibull( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Parámetro de distribución (shape) const double b, // [in] Parámetro de distribución (scale) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de densidad de la probabilidad de la distribución de Weibull con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de dweibull() en R.
bool MathProbabilityDensityWeibull( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Parámetro de distribución (shape) const double b, // [in] Parámetro de distribución (scale) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de densidad de la probabilidad de la distribución de Weibull con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityWeibull( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Parámetro de distribución (shape) const double b, // [in] Parámetro de distribución (scale) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.16.2. MathCumulativeDistributionWeibull
La función calcula el valor de la función de la distribución de Weibull con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.double MathCumulativeDistributionWeibull( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Parámetro de distribución (shape) const double b, // [in] Parámetro de distribución (scale) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de la distribución de Weibull con los parámetros a y b para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionWeibull( const double x, // [in] Valor de la magnitud aleatoria const double a, // [in] Parámetro de distribución (shape) const double b, // [in] Parámetro de distribución (scale) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de la distribución de Weibull con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de pweibull() en R.
bool MathCumulativeDistributionWeibull( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Parámetro de distribución (shape) const double b, // [in] Parámetro de distribución (scale) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de la distribución de Weibull con los parámetros a y b para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionWeibull( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double a, // [in] Parámetro de distribución (shape) const double b, // [in] Parámetro de distribución (scale) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.16.3. MathQuantileWeibull
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución de Weibull con los parámetros a y b. En caso de error, retorna NaN.
double MathQuantileWeibull( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double a, // [in] Parámetro de distribución (shape) const double b, // [in] Parámetro de distribución (scale) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor de la función inversa de distribución de Weibull con los parámetros a y b. En caso de error, retorna NaN.
double MathQuantileWeibull( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double a, // [in] Parámetro de distribución (shape) const double b, // [in] Parámetro de distribución (scale) int &error_code // [out] Variable para el código de error );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor de la función inversa de la distribución de probabilidad de Weibull con los parámetros a y b. En caso de error, retorna false. Análogo de qweibull() en R.
bool MathQuantileWeibull( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double a, // [in] Parámetro de distribución (shape) const double b, // [in] Parámetro de distribución (scale) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor de la función inversa de la distribución de probabilidad de Weibull con los parámetros a y b. En caso de error, retorna false.
bool MathQuantileWeibull( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double a, // [in] Parámetro de distribución (shape) const double b, // [in] Parámetro de distribución (scale) double &result[] // [out] Matriz con los valores de los cuantiles );
2.16.4. MathRandomWeibull
La función genera una magnitud pseudoaleatoria, distribuida según la ley de la distribución de Weibull con los parámetros a y b. En caso de error, retorna NaN.
double MathRandomWeibull( const double a, // [in] Parámetro de distribución (shape) const double b, // [in] Parámetro de distribución (scale) int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de la distribución de Weibull con los parámetros a y b. En caso de error, retorna false. Análogo de rweibull() en R.
bool MathRandomWeibull( const double a, // [in] Parámetro de distribución (shape) const double b, // [in] Parámetro de distribución (scale) const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.16.5. MathMomentsWeibull
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución de Weibull. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsWeibull( const double a, // [in] Parámetro de distribución (shape) const double b, // [in] Parámetro de distribución (scale) double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.17. Distribución binomial
2.17.1. MathProbabilityDensityBinomial
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución binomial con los parámetros n y p para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityBinomial( const double x, // [in] Valor de la magnitud aleatoria (número entero) const double n, // [in] Parámetro de distribución (número de pruebas) const double p, // [in] Parámetro de distribución (probabilidad de éxito para cada prueba) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución binomial con los parámetros n y p para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityBinomial( const double x, // [in] Valor de la magnitud aleatoria (número entero) const double n, // [in] Parámetro de distribución (número de pruebas) const double p, // [in] Parámetro de distribución (probabilidad de éxito para cada prueba) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución binomial con los parámetros n y p para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de dbinom() en R.
bool MathProbabilityDensityBinomial( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double n, // [in] Parámetro de distribución (número de pruebas) const double p, // [in] Parámetro de distribución (probabilidad de éxito para cada prueba) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución binomial con los parámetros n y p para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityBinomial( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double n, // [in] Parámetro de distribución (número de pruebas) const double p, // [in] Parámetro de distribución (probabilidad de éxito para cada prueba) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.17.2. MathCumulativeDistributionBinomial
La función calcula el valor de la función de distribución para la ley binomial con los parámetros n y p para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionBinomial( const double x, // [in] Valor de la magnitud aleatoria (número entero) const double n, // [in] Parámetro de distribución (número de pruebas) const double p, // [in] Parámetro de distribución (probabilidad de éxito para cada prueba) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución para la ley binomial con los parámetros n y p para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionBinomial( const double x, // [in] Valor de la magnitud aleatoria (número entero) const double n, // [in] Parámetro de distribución (número de pruebas) const double p, // [in] Parámetro de distribución (probabilidad de éxito para cada prueba) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución para la ley binomial con los parámetros n y p para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de pbinom() en R.
bool MathCumulativeDistributionBinomial( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double n, // [in] Parámetro de distribución (número de pruebas) const double p, // [in] Parámetro de distribución (probabilidad de éxito para cada prueba) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de distribución para la ley binomial con los parámetros n y p para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionBinomial( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double n, // [in] Parámetro de distribución (número de pruebas) const double p, // [in] Parámetro de distribución (probabilidad de éxito para cada prueba) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.17.3. MathQuantileBinomial
Para la probabilidad "probability", la función calcula el valor inverso de la función de distribuición para la ley binomial con los parámetros n y p. En caso de error, retorna NaN.
double MathQuantileBinomial( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double n, // [in] Parámetro de distribución (número de pruebas) const double p, // [in] Parámetro de distribución (probabilidad de éxito para cada prueba) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor inverso de la función de distribuición para la ley binomial con los parámetros n y p. En caso de error, retorna NaN.
double MathQuantileBinomial( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double n, // [in] Parámetro de distribución (número de pruebas) const double p, // [in] Parámetro de distribución (probabilidad de éxito para cada prueba) int &error_code // [out] Variable para el código de error );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor inverso de la función de distribuición para la ley binomial con los parámetros n y p. En caso de error, retorna false. Análogo de qbinom() en R.
bool MathQuantileBinomial( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double n, // [in] Parámetro de distribución (número de pruebas) const double p, // [in] Parámetro de distribución (probabilidad de éxito para cada prueba) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor inverso de la función de distribuición para la ley binomial con los parámetros n y p. En caso de error, retorna false.
bool MathQuantileBinomial( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double n, // [in] Parámetro de distribución (número de pruebas) const double p, // [in] Parámetro de distribución (probabilidad de éxito para cada prueba) double &result[] // [out] Matriz con los valores de los cuantiles );
2.17.4. MathRandomBinomial
La función genera una magnitud pseudoaleatoria, distribuida según la ley de distribución binominal con los parámetros n y p. En caso de error, retorna NaN.
double MathRandomBinomial( const double n, // [in] Parámetro de distribución (número de pruebas) const double p, // [in] Parámetro de distribución (probabilidad de éxito para cada prueba) int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de distribución binominal con los parámetros n y p. En caso de error, retorna false. Análogo de rbinom() en R.
bool MathRandomBinomial( const double n, // [in] Parámetro de distribución (número de pruebas) const double p, // [in] Parámetro de distribución (probabilidad de éxito para cada prueba) const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.17.5. MathMomentsBinomial
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución binomial con los parámetros n y p. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsBinomial( const double n, // [in] Número de pruebas const double p, // [in] Probabilidad de éxito para cada prueba double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.18. Distribución binomial negativa
2.18.1. MathProbabilityDensityNegativeBinomial
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución binomial negativa con los parámetros r y p para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityNegativeBinomial( const double x, // [in] Valor de la magnitud aleatoria (número entero) const double r, // [in] Número de pruebas exitosas double p, // [in] Probabilidad de éxito const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución binomial negativa con los parámetros r y p para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityNegativeBinomial( const double x, // [in] Valor de la magnitud aleatoria (número entero) const double r, // [in] Número de pruebas exitosas double p, // [in] Probabilidad de éxito int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución binomial negativa con los parámetros r y p para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de dnbinom() en R.
bool MathProbabilityDensityNegativeBinomial( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double r, // [in] Número de pruebas exitosas double p, // [in] Probabilidad de éxito const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución binomial negativa con los parámetros r y p para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityNegativeBinomial( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double r, // [in] Número de pruebas exitosas double p, // [in] Probabilidad de éxito double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.18.2. MathCumulativeDistributionNegativeBinomial
La función calcula el valor de la función de distribución para la ley binomial negativa con los parámetros r y p para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionNegativeBinomial( const double x, // [in] Valor de la magnitud aleatoria (número entero) const double r, // [in] Número de pruebas exitosas double p, // [in] Probabilidad de éxito const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución para la ley binomial negativa con los parámetros r y p para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionNegativeBinomial( const double x, // [in] Valor de la magnitud aleatoria (número entero) const double r, // [in] Número de pruebas exitosas double p, // [in] Probabilidad de éxito int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución para la ley binomial negativa con los parámetros r y p para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de pnbinom() en R.
bool MathCumulativeDistributionNegativeBinomial( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double r, // [in] Número de pruebas exitosas double p, // [in] Probabilidad de éxito const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de distribución para la ley binomial negativa con los parámetros r y p para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionNegativeBinomial( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double r, // [in] Número de pruebas exitosas double p, // [in] Probabilidad de éxito double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.18.3. MathQuantileNegativeBinomial
Para la probabilidad "probability", la función calcula el valor inverso de la función de distribuición para la ley binomial negativa con los parámetros r y p. En caso de error, retorna NaN.
double MathQuantileNegativeBinomial( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double r, // [in] Número de pruebas exitosas double p, // [in] Probabilidad de éxito const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor inverso de la función de distribuición para la ley binomial negativa con los parámetros r y p. En caso de error, retorna NaN.
double MathQuantileNegativeBinomial( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double r, // [in] Número de pruebas exitosas double p, // [in] Probabilidad de éxito int &error_code // [out] Variable para el código de error );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor inverso de la función de distribuición para la ley binomial negativa con los parámetros r y p. En caso de error, retorna false. Análogo de qnbinom() en R.
bool MathQuantileNegativeBinomial( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double r, // [in] Número de pruebas exitosas double p, // [in] Probabilidad de éxito const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor inverso de la función de distribuición para la ley binomial negativa con los parámetros r y p. En caso de error, retorna false.
bool MathQuantileNegativeBinomial( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double r, // [in] Número de pruebas exitosas double p, // [in] Probabilidad de éxito double &result[] // [out] Matriz con los valores de los cuantiles );
2.18.4. MathRandomNegativeBinomial
La función genera una magnitud pseudoaleatoria, distribuida según la ley de distribución binominal negativa con los parámetros r y p. En caso de error, retorna NaN.
double MathRandomNegativeBinomial( const double r, // [in] Número de pruebas exitosas double p, // [in] Probabilidad de éxito int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de distribución binominal negativa con los parámetros r y p. En caso de error, retorna false. Análogo de rnbinom() en R.
bool MathRandomNegativeBinomial( const double r, // [in] Número de pruebas exitosas double p, // [in] Probabilidad de éxito const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.18.5. MathMomentsNegativeBinomial
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución binomial negativa con los parámetros r y p. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsNegativeBinomial( const double r, // [in] Número de pruebas exitosas double p, // [in] Probabilidad de éxito double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.19. Distribución geométrica
2.19.1. MathProbabilityDensityGeometric
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución geométrica con el parámetro p para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityGeometric( const double x, // [in] Valor de la magnitud aleatoria const double p, // [in] Parámetro de distribución (probabilidad de aparición de un evento en una prueba) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución geométrica con el parámetro p para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityGeometric( const double x, // [in] Valor de la magnitud aleatoria const double p, // [in] Parámetro de distribución (probabilidad de aparición de un evento en una prueba) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución geométrica con el parámetro p para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de dgeom() en R.
bool MathProbabilityDensityGeometric( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double p, // [in] Parámetro de distribución (probabilidad de aparición de un evento en una prueba) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución geométrica con el parámetro p para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityGeometric( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double p, // [in] Parámetro de distribución (probabilidad de aparición de un evento en una prueba) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.19.2. MathCumulativeDistributionGeometric
La función calcula el valor de la función de distribución para la ley geométrica con el parámetro p para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionGeometric( const double x, // [in] Valor de la magnitud aleatoria const double p, // [in] Parámetro de distribución (probabilidad de aparición de un evento en una prueba) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución para la ley geométrica con el parámetro p para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionGeometric( const double x, // [in] Valor de la magnitud aleatoria const double p, // [in] Parámetro de distribución (probabilidad de aparición de un evento en una prueba) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución para la ley geométrica con el parámetro p para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de pgeom() en R.
bool MathCumulativeDistributionGeometric( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double p, // [in] Parámetro de distribución (probabilidad de aparición de un evento en una prueba) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de distribución para la ley geométrica con el parámetro p para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionGeometric( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double p, // [in] Parámetro de distribución (probabilidad de aparición de un evento en una prueba) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.19.3. MathQuantileGeometric
Para la probabilidad "probability", la función calcula el valor inverso de la función de distribuición para la ley geométrica con el parámetro p. En caso de error, retorna NaN.
double MathQuantileGeometric( const double probability, // [in] Probabilidad de aparición de una magnitud aleatoria const double p, // [in] Parámetro de distribución (probabilidad de aparición de un evento en una prueba) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor inverso de la función de distribuición para la ley geométrica con el parámetro p. En caso de error, retorna NaN.
double MathQuantileGeometric( const double probability, // [in] Probabilidad de aparición de una magnitud aleatoria const double p, // [in] Parámetro de distribución (probabilidad de aparición de un evento en una prueba) int &error_code // [out] Variable para el código de error );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor inverso de la función de distribuición para la ley geométrica con el parámetro p. En caso de error, retorna false. Análogo de qgeom() en R.
bool MathQuantileGeometric( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double p, // [in] Parámetro de distribución (probabilidad de aparición de un evento en una prueba) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor inverso de la función de distribuición para la ley geométrica con el parámetro p. En caso de error, retorna false.
bool MathQuantileGeometric( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double p, // [in] Parámetro de distribución (probabilidad de aparición de un evento en una prueba) double &result[] // [out] Matriz con los valores de los cuantiles );
2.19.4. MathRandomGeometric
La función genera una magnitud pseudoaleatoria, distribuida según la ley de distribución geométrica con el parámetro p. En caso de error, retorna NaN.
double MathRandomGeometric( const double p, // [in] Parámetro de distribución (probabilidad de aparición de un evento en una prueba) int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de distribución geométrica con el parámetro p. En caso de error, retorna false. Análogo de rgeom() en R.
bool MathRandomGeometric( const double p, // [in] Parámetro de distribución (probabilidad de aparición de un evento en una prueba) const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.19.5. MathMomentsGeometric
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución geométrica con el parámetro p. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsGeometric( const double p, // [in] Parámetro de distribución (probabilidad de aparición de un evento en una prueba) double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.20. Distribución hipergeométrica
2.20.1. MathProbabilityDensityHypergeometric
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución hipergeométrica con los parámetros m, k y n para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityHypergeometric( const double x, // [in] Valor de la magnitud aleatoria (número entero) const double m, // [in] Número total de objetos (número entero) const double k, // [in] Número de objetos con la característica deseada (número entero) const double n, // [in] Número de objetos tomados (número entero) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución hipergeométrica con los parámetros m, k y n para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityHypergeometric( const double x, // [in] Valor de la magnitud aleatoria (número entero) const double m, // [in] Número total de objetos (número entero) const double k, // [in] Número de objetos con la característica deseada (número entero) const double n, // [in] Número de objetos tomados (número entero) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución hipergeométrica con los parámetros m, k y n para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de dhyper() en R.
bool MathProbabilityDensityHypergeometric( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double m, // [in] Número total de objetos (número entero) const double k, // [in] Número de objetos con la característica deseada (número entero) const double n, // [in] Número de objetos tomados (número entero) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución hipergeométrica con los parámetros m, k y n para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityHypergeometric( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double m, // [in] Número total de objetos (número entero) const double k, // [in] Número de objetos con la característica deseada (número entero) const double n, // [in] Número de objetos tomados (número entero) double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.20.2. MathCumulativeDistributionHypergeometric
La función calcula el valor de la función de distribución para la ley hipergeométrica con los parámetros m, k y n para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionHypergeometric( const double x, // [in] Valor de la magnitud aleatoria (número entero) const double m, // [in] Número total de objetos (número entero) const double k, // [in] Número de objetos con la característica deseada (número entero) const double n, // [in] Número de objetos tomados (número entero) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución para la ley hipergeométrica con los parámetros m, k y n para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionHypergeometric( const double x, // [in] Valor de la magnitud aleatoria (número entero) const double m, // [in] Número total de objetos (número entero) const double k, // [in] Número de objetos con la característica deseada (número entero) const double n, // [in] Número de objetos tomados (número entero) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución para la ley hipergeométrica con los parámetros m, k y n para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de phyper() en R.
bool MathCumulativeDistributionHypergeometric( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double m, // [in] Número total de objetos (número entero) const double k, // [in] Número de objetos con la característica deseada (número entero) const double n, // [in] Número de objetos tomados (número entero) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz para los valores de la función de distribución );
La función calcula el valor de la función de distribución para la ley hipergeométrica con los parámetros m, k y n para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionHypergeometric( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double m, // [in] Número total de objetos (número entero) const double k, // [in] Número de objetos con la característica deseada (número entero) const double n, // [in] Número de objetos tomados (número entero) double &result[] // [out] Matriz para los valores de la función de distribución );
2.20.3. MathQuantileHypergeometric
Para la probabilidad "probability", la función calcula el valor inverso de la función de distribuición para la ley hipergeométrica con los parámetros m, k y n. En caso de error, retorna NaN.
double MathQuantileHypergeometric( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double m, // [in] Número total de objetos (número entero) const double k, // [in] Número de objetos con la característica deseada (número entero) const double n, // [in] Número de objetos tomados (número entero) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor inverso de la función de distribuición para la ley hipergeométrica con los parámetros m, k y n. En caso de error, retorna NaN.
double MathQuantileHypergeometric( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double m, // [in] Número total de objetos (número entero) const double k, // [in] Número de objetos con la característica deseada (número entero) const double n, // [in] Número de objetos tomados (número entero) int &error_code // [out] Variable para el código de error );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor inverso de la función de distribuición para la ley hipergeométrica con los parámetros m, k y n. En caso de error, retorna false. Análogo de qhyper() en R.
bool MathQuantileHypergeometric( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double m, // [in] Número total de objetos (número entero) const double k, // [in] Número de objetos con la característica deseada (número entero) const double n, // [in] Número de objetos tomados (número entero) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor inverso de la función de distribuición para la ley hipergeométrica con los parámetros m, k y n. En caso de error, retorna false.
bool MathQuantileHypergeometric( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double m, // [in] Número total de objetos (número entero) const double k, // [in] Número de objetos con la característica deseada (número entero) const double n, // [in] Número de objetos tomados (número entero) double &result[] // [out] Matriz con los valores de los cuantiles );
2.20.4. MathRandomHypergeometric
La función genera una magnitud pseudoaleatoria, distribuida según la ley de distribución hipergeométrica con los parámetros m, n y k. En caso de error, retorna NaN.
double MathRandomHypergeometric( const double m, // [in] Número total de objetos (número entero) const double k, // [in] Número de objetos con la característica deseada (número entero) const double n, // [in] Número de objetos tomados (número entero) int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de distribución hipergeométrica con los parámetros m, n y k. En caso de error, retorna false. Análogo de rhyper() en R.
bool MathRandomHypergeometric( const double m, // [in] Número total de objetos (número entero) const double k, // [in] Número de objetos con la característica deseada (número entero) const double n, // [in] Número de objetos tomados (número entero) const int data_count, // [in] Número de datos necesarios double &result[] // [out] Matriz con los valores de las magnitudes pseudoaleatorias );
2.20.5. MathMomentsHypergeometric
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución hipergeométrica con los parámetros m, n y k. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsHypergeometric( const double m, // [in] Número total de objetos (número entero) const double k, // [in] Número de objetos con la característica deseada (número entero) const double n, // [in] Número de objetos tomados (número entero) double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
2.21. Distribución de Poisson
2.21.1. MathProbabilityDensityPoisson
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución de Poisson con el parámetro lambda para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityPoisson( const double x, // [in] Valor de la magnitud aleatoria const double lambda, // [in] Parámetro de distribución (mean) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución de Poisson con el parámetro lambda para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathProbabilityDensityPoisson( const double x, // [in] Valor de la magnitud aleatoria const double lambda, // [in] Parámetro de distribución (mean) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución de Poisson con el parámetro lambda para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de dpois() en R.
bool MathProbabilityDensityPoisson( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double lambda, // [in] Parámetro de distribución (mean) const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se retorna el logaritmo natural de densidad de probabilidad double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
La función calcula el valor de la función de masa de probabilidad (probability mass function) de la distribución de Poisson con el parámetro lambda para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathProbabilityDensityPoisson( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double lambda, // [in] Parámetro de distribución (mean) double &result[] // [out] Matriz para los valores de la función de densidad de probabilidad );
2.21.2. MathCumulativeDistributionPoisson
La función calcula el valor de la función de distribución de Poisson con el parámetro lambda para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionPoisson( const double x, // [in] Valor de la magnitud aleatoria const double lambda, // [in] Parámetro de distribución (mean) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de Poisson con el parámetro lambda para una magnitud aleatoria x. En caso de error, retorna NaN.
double MathCumulativeDistributionPoisson( const double x, // [in] Valor de la magnitud aleatoria const double lambda, // [in] Parámetro de distribución (mean) int &error_code // [out] Variable para el código de error );
La función calcula el valor de la función de distribución de Poisson con el parámetro lambda para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false. Análogo de ppois() en R.
bool MathCumulativeDistributionPoisson( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double lambda, // [in] Parámetro de distribución (mean) const bool tail, // [in] Bandera para calcular, si true, entonces se calcula la probabilidad de que la magnitud aleatoria no supere x const bool log_mode, // [in] Bandera para calcular el logaritmo del valor, si log_mode=true, entonces se calcula el logaritmo natural de probabilidad double &result[] // [out] Matriz para los valores de la función de probabilidad );
La función calcula el valor de la función de distribución de Poisson con el parámetro lambda para una matriz de magnitudes aleatorias x[]. En caso de error, retorna false.
bool MathCumulativeDistributionPoisson( const double &x[], // [in] Matriz con los valores de la magnitud aleatoria const double lambda, // [in] Parámetro de distribución (mean) double &result[] // [out] Matriz para los valores de la función de probabilidad );
2.21.3. MathQuantilePoisson
Para la probabilidad "probability", la función calcula el valor inverso de la función de distribuición de Poisson con el parámetro lambda. En caso de error, retorna NaN.
double MathQuantilePoisson( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double lambda, // [in] Parámetro de distribución (mean) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) int &error_code // [out] Variable para el código de error );
Para la probabilidad "probability", la función calcula el valor inverso de la función de distribuición de Poisson con el parámetro lambda. En caso de error, retorna NaN.
double MathQuantilePoisson( const double probability, // [in] Valor de probabilidad de la aparición de una magnitud aleatoria const double lambda, // [in] Parámetro de distribución (mean) int &error_code // [out] Variable para el código de error );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor inverso de la función de distribuición de Poisson con el parámetro lambda. En caso de error, retorna false. Análogo de qpois() en R.
double MathQuantilePoisson( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double lambda, // [in] Parámetro de distribución (mean) const bool tail, // [in] Bandera para calcular, si false, entonces el cálculo se realiza para la probabilidad 1.0-probability const bool log_mode, // [in] Bandera para calcular, si log_mode=true, entonces el cálculo se realiza para la probabilidad Exp(probability) double &result[] // [out] Matriz con los valores de los cuantiles );
Para la matriz de valores de la probabilidad probability[], la función calcula el valor inverso de la función de distribuición de Poisson con el parámetro lambda. En caso de error, retorna false.
double MathQuantilePoisson( const double &probability[],// [in] Matriz con los valores de probabilidad de la magnitud aleatoria const double lambda, // [in] Parámetro de distribución (mean) double &result[] // [out] Matriz con los valores de los cuantiles );
2.21.4. MathRandomPoisson
La función genera una magnitud pseudoaleatoria, distribuida según la ley de la distribución de Poisson con el parámetro lambda. En caso de error, retorna NaN.
double MathRandomPoisson( const double lambda, // [in] Parámetro de distribución (mean) int &error_code // [out] Variable para el código de error );
La función genera magnitudes pseudoaleatorias, distribuidas según la ley de la distribución de Poisson con el parámetro lambda. En caso de error, retorna false. Análogo de rpois() en R.
double MathRandomPoisson( const double lambda, // [in] Parámetro de distribución (mean) int &error_code // [out] Variable para el código de error );
2.21.5. MathMomentsPoisson
La función calcula los valores numéricos teóricos de los 4 primeros momentos de la distribución de Poisson con el parámetro lambda. Retorna true, si el cálculo de los momentos se realiza con éxito, de lo contrario, false.
bool MathMomentsPoisson( const double lambda, // [in] Parámetro de distribución (mean) double &mean, // [out] Variable para el valor medio double &variance, // [out] Variable para la varianza double &skewness, // [out] Variable para el coeficiente de asimetría double &kurtosis, // [out] Variable para la curtosis int &error_code // [out] Variable para el código de error );
3. Tabla de correspondencia con las funciones estadísticas del lenguaje R
Para mayor comodidad, en los recuadros 1-2 se muestran las funciones de la biblioteca estadística y las funciones que les corresponden del lenguaje R.
| № | Valor calculado | Funciones MQL5 | Función del lenguaje R |
|---|---|---|---|
| 1 | Media | MathMean | mean |
| 2 | Varianza | MathVariance | var |
| 3 | Coeficiente de asimetría | MathSkewness | skewness |
| 4 | Curtosis | MathKurtosis | kurtosis |
| 5 | Valor mediano | MathMedian | median |
| 6 | Desviación estándar | MathStandardDeviation | sd |
| 7 | Desviación media | MathAverageDeviation | aad |
Recuadro 1. Función para calcular las características estadísticas de los datos de la matriz
| № | Distribución | Función de densidad | Funciones MQL5 | Funciones del lenguaje R |
|---|---|---|---|---|
| 1 | Normal | 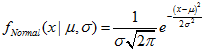 | MathProbabilityDensityNormal MathCumulativeDistributionNormal MathQuantileNormal MathRandomNormal | dnorm pnorm qnorm rnorm |
| 2 | Beta | | MathProbabilityDensityBeta MathCumulativeDistributionBeta MathQuantileBeta MathRandomBeta | dbeta pbeta qbeta rbeta |
| 3 | Binomial | | MathProbabilityDensityBinomial MathCumulativeDistributionBinomial MathQuantileBinomial MathRandomBinomial | dbinom pbinom qbinom rbinom |
| 4 | Cauchy | 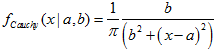 | MathProbabilityDensityCauchy MathCumulativeDistributionCauchy MathQuantileCauchy MathRandomCauchy | dcauchy pcauchy qcauchy rcauchy |
| 5 | Chi-cuadrado | 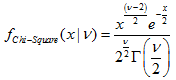 | MathProbabilityDensityChiSquare MathCumulativeDistributionChiSquare MathQuantileChiSquare MathRandomChiSquare | dchisq pchisq qchisq rchisq |
| 6 | Exponencial | | MathProbabilityDensityExponential MathCumulativeDistributionExponential MathQuantileExponential MathRandomExponential | dexp pexp qexp rexp |
| 7 | F de Fisher | 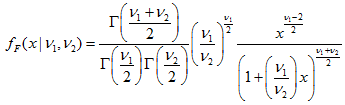 | MathProbabilityDensityF MathCumulativeDistributionF MathQuantileF MathRandomF | df pf qf rf |
| 8 | Gamma | | MathProbabilityDensityGamma MathCumulativeDistributionGamma MathQuantileGamma MathRandomGamma | dgamma pgamma qgamma rgamma |
| 9 | Geométrica | | MathProbabilityDensityGeometric MathCumulativeDistributionGeometric MathQuantileGeometric MathRandomGeometric | dgeom pgeom qgeom rgeom |
| 10 | Hipergeométrica | 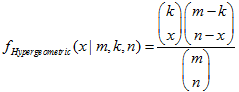 | MathProbabilityDensityHypergeometric MathCumulativeDistributionHypergeometric MathQuantileHypergeometric MathRandomHypergeometric | dhyper phyper qhyper rhyper |
| 11 | Logística | 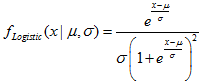 | MathProbabilityDensityLogistic MathCumulativeDistributionLogistic MathQuantileLogistic MathRandomLogistic | dlogis plogis qlogis rlogis |
| 12 | Log-normal | | MathProbabilityDensityLognormal MathCumulativeDistributionLognormal MathQuantileLognormal MathRandomLognormal | dlnorm plnorm qlnorm rlnorm |
| 13 | Binomial negativa | | MathProbabilityDensityNegativeBinomial MathCumulativeDistributionNegativeBinomial MathQuantileNegativeBinomial MathRandomNegativeBinomial | dnbinom pnbinom qnbinom rnbinom |
| 14 | Beta no central | 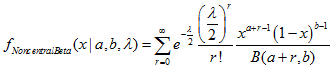 | MathProbabilityDensityNoncentralBeta MathCumulativeDistributionNoncentralBeta MathQuantileNoncentralBeta MathRandomNoncentralBeta | dbeta pbeta qbeta rbeta |
| 15 | Chi-cuadrado no central | 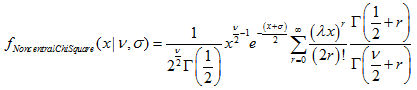 | MathProbabilityDensityNoncentralChiSquare MathCumulativeDistributionNoncentralChiSquare MathQuantileNoncentralChiSquare MathRandomNoncentralChiSquare | dchisq pchisq qchisq rchisq |
| 16 | F no central | 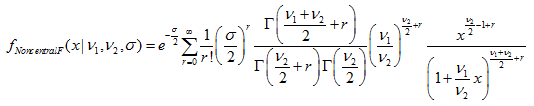 | MathProbabilityDensityNoncentralF() MathCumulativeDistributionNoncentralF() MathQuantileNoncentralF() MathRandomNoncentralF() | df pf qf rf |
| 17 | T de Student no central | 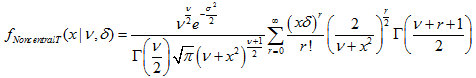 | MathProbabilityDensityNoncentralT MathCumulativeDistributionNoncentralT MathQuantileNoncentralT MathRandomNoncentralT | dt pt qt rt |
| 18 | Poisson | | MathProbabilityDensityPoisson MathCumulativeDistributionPoisson MathQuantilePoisson MathRandomPoisson | dpois ppois qpois rpois |
| 19 | T de Student | 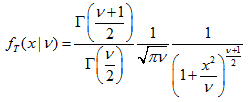 | MathProbabilityDensityT MathCumulativeDistributionT MathQuantileT MathRandomT | dt pt qt rt |
| 20 | Uniforme | | MathProbabilityDensityUniform MathCumulativeDistributionUniform MathQuantileUniform MathRandomUniform | dunif punif qunif runif |
| 21 | Weibull | 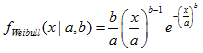 | MathProbabilityDensityWeibull MathCumulativeDistributionWeibull MathQuantileWeibull MathRandomWeibull | dweibull pweibull qweibull rweibull |
Recuadro 2. Funciones para trabajar con distribuciones estadísticas
En la biblioteca estadística MQL5 también hay funciones para calcular las funciones matemáticas en las matrices, la lista se muestra en el recuadro 3.
| Descripción | MQL5 | R |
|---|---|---|
| Forma una secuencia de valores | bool MathSequence(const double from,const double to,const double step,double &result[]) bool MathSequenceByCount(const double from,const double to,const int count,double &result[]) bool MathSequence(const int from,const int to,const int step,int &result[]) bool MathSequenceByCount(const int from,const int to,const int count,int &result[]) | seq() |
| Forma una secuencia que se repite | bool MathReplicate(const double &array[],const int count,double &result[]) bool MathReplicate(const int &array[],const int count,int &result[]) | rep() |
| Forma una matriz con el orden inverso de elementos | bool MathReverse(const double &array[],double &result[]) bool MathReverse(const int &array[],int &result[]) | rev(x) |
| Compara las matrices y retorna true si coinciden todos los elementos | bool MathIdentical(const double &array1[],const double &array2[]) bool MathIdentical(const int &array1[],const int &array2[]) | identical() |
| Forma una matriz solo con los valores no repetidos | bool MathUnique(const double &array[],double &result[]) bool MathUnique(const int &array[],int &result[]) | unique() |
| Forma una matriz de número entero con permutación de acuerdo con el orden de los elementos de la matriz después de la clasificación | bool MathOrder(const double &array[],int &result[]) bool MathOrder(const int &array[],int &result[]) | order() |
| Realiza un muestreo aleatorio de los elementos de la matriz. El argumento replace=true permite realizar la selección aleatoria de elementos con su posterior retorno al conjunto original. La matriz probabilities[] establece la probabilidad con la que se realiza la selección de los elementos. | bool MathSample(const double &array[],const int count,double &result[]) bool MathSample(const double &array[],const int count,const bool replace,double &result[]) bool MathSample(const double &array[],double &probabilities[],const int count,double &result[]) bool MathSample(const double &array[],double &probabilities[],const int count,const bool replace,double &result[]) bool MathSample(const int &array[],const int count,int &result[]) bool MathSample(const int &array[],const int count,const bool replace,int &result[]) bool MathSample(const int &array[],double &probabilities[],const int count,int &result[]) bool MathSample(const int &array[],double &probabilities[],const int count,const bool replace,int &result[]) | sample() |
| Retorna la suma de los elementos de la matriz | double MathSum(const double &array[]) | sum() |
| Retorna el producto de los elementos de la matriz | double MathProduct(const double &array[]) | prod() |
| Forma una matriz con la suma acumulada | bool MathCumulativeSum(const double &array[],double &result[]) bool MathCumulativeSum(double &array[]) | cumsum() |
| Forma una matriz con el producto acumulado | bool MathCumulativeProduct(const double &array[],double &result[]) bool MathCumulativeProduct(double &array[]) | cumprod() |
| Forma una matriz con los valores mínimos acumulados | bool MathCumulativeMin(const double &array[],double &result[]) bool MathCumulativeMin(double &array[]) | cummin() |
| Forma una matriz con los valores máximos acumulados | bool MathCumulativeMax(const double &array[],double &result[]) bool MathCumulativeMax(double &array[]) | cummax() |
| Forma una matriz con las diferencias de los elementos y[i]=x[i+lag]-x[i] | bool MathDifference(const double &array[],const int lag,double &result[]) bool MathDifference(const double &array[],const int lag,const int differences,double &result[]) bool MathDifference(const int &array[],const int lag,int &result[]) bool MathDifference(const int &array[],const int lag,const int differences,int &result[]) | diff() |
| Retorna el valor mínimo de los elementos de la matriz | double MathMin(const double &array[]) | min() |
| Retorna el valor máximo de los elementos de la matriz | double MathMax(const double &array[]) | max() |
| Calcula los valores máximos y mínimos de los elementos de la matriz | bool MathRange(const double &array[],double &min,double &max) | range() |
| Calcula el valor medio de los elementos de la matriz | double MathMean(const double &array[]) | mean() |
| Calcula la desviación estándar de los elementos de la matriz | double MathStandardDeviation(const double &array[]) | sd() |
| Calcula el valor mediano de los elementos de la matriz | double MathMedian(double &array[]) | median() |
| Calcula los rangos de los elementos de la matriz | bool MathRank(const int &array[],double &rank[]) bool MathRank(const double &array[],double &rank[]) | rank() |
| Calcula los coeficientes de correlación de Pearson, Spearman y Kendall | bool MathCorrelationPearson(const double &array1[],const double &array2[],double &r) bool MathCorrelationPearson(const int &array1[],const int &array2[],double &r) bool MathCorrelationSpearman(const double &array1[],const double &array2[],double &r) bool MathCorrelationSpearman(const int &array1[],const int &array2[],double &r) bool MathCorrelationKendall(const double &array1[],const double &array2[],double &tau) bool MathCorrelationKendall(const int &array1[],const int &array2[],double &tau) | corr() |
| Calcula los cuantiles de muestreo, correspondientes a las probabilidades indicadas | bool MathQuantile(const double &array[],const double &probs[],double &quantile[]) | qunatile() |
| Calcula Tukey's five number summary (minimum, lower-hinge, median, upper-hinge, maximum) para los elementos de la matriz | bool MathTukeySummary(const double &array[],const bool removeNAN,double &minimum,double &lower_hinge,double &median,double &upper_hinge,double &maximum) | fivenum() |
| Calcula los logaritmos de los elementos de la matriz (naturales y según la base establecida) | bool MathLog(const double &array[],double &result[]) bool MathLog(const double &array[],const double base,double &result[]) bool MathLog(double &array[]) bool MathLog(double &array[],const double base) | log() |
| Calcula los logaritmos de los elementos de la matriz conforme a la base 2 | bool MathLog2(const double &array[],double &result[]) bool MathLog2(double &array[]) | log2() |
| Calcula los logaritmos de los elementos de la matriz conforme a la base 10 | bool MathLog10(const double &array[],double &result[]) bool MathLog10(double &array[]) | log10() |
| Calcula el valor de la función log(1+x) para los elementos de la matriz | bool MathLog1p(const double &array[], double &result[]) bool MathLog1p(double &array[]) | log1p() |
| Calcula el valor de la función exp(x) para los elementos de la matriz | bool MathExp(const double &array[], double &result[]) bool MathExp(double &array[]) | exp() |
| Calcula el valor de la función exp(x)-1 para los elementos de la matriz | bool MathExpm1(const double &array[], double &result[]) bool MathExpm1(double &array[]) | expm1() |
| Calcula el valor de la función sin(x) para los elementos de la matriz | bool MathSin(const double &array[], double &result[]) bool MathSin(double &array[]) | sin() |
| Calcula el valor de la función cos(x) para los elementos de la matriz | bool MathCos(const double &array[], double &result[]) bool MathCos(double &array[]) | cos() |
| Calcula el valor de la función tan(x) para los elementos de la matriz | bool MathTan(const double &array[], double &result[]) bool MathTan(double &array[]) | tan() |
| Calcula el valor de la función arcsin(x) para los elementos de la matriz | bool MathArcsin(const double &array[], double &result[]) bool MathArcsin(double &array[]) | arcsin() |
| Calcula el valor de la función arccos(x) para los elementos de la matriz | bool MathArccos(const double &array[], double &result[]) bool MathArccos(double &array[]) | arccos() |
| Calcula el valor de la función arctan(x) para los elementos de la matriz | bool MathArctan(const double &array[], double &result[]) bool MathArctan(double &array[]) | arctan() |
| Calcula el valor de la función arctan(y/x) para los elementos de la matriz | bool MathArctan2(const double &array1[], const double &array2[], double &result[]) | arctan2() |
| Calcula el valor de la función sin(pi*x) para los elementos de la matriz | bool MathSinPi(const double &array[], double &result[]) bool MathSinPi(double &array[]) | sinpi() |
| Calcula el valor de la función cos(pi*x) para los elementos de la matriz | bool MathCosPi(const double &array[], double &result[]) bool MathCosPi(const double &array[]) | cospi() |
| Calcula el valor de la función tan(pi*x) para los elementos de la matriz | bool MathTanPi(const double &array[], double &result[]) bool MathTanPi(double &array[]) | tanpi() |
| Calcula el valor absoluto de los elementos de la matriz | bool MathAbs(const double &array[], double &result[]) bool MathAbs(double &array[]) | abs() |
| Calcula la raíz cuadrada para los elementos de la matriz | bool MathSqrt(const double &array[], double &result[]) bool MathSqrt(double &array[]) | sqrt() |
| Retorna el valor númerico entero superior más cercano para los elementos de la matriz | bool MathCeil(const double &array[], double &result[]) bool MathCeil(double &array[]) | ceil() |
| Retorna el valor númerico entero inferior más cercano para los elementos de la matriz | bool MathFloor(const double &array[], double &result[]) bool MathFloor(double &array[]) | floor() |
| Calcula la parte entera de los lementos de la matriz | bool MathTrunc(const double &array[], const int digits, double &result[]) bool MathTrunc(double &array[]) | trunc() |
| Calcula el valor redondeado de los elementos de la matriz | bool MathRound(const double &array[], const int digits, double &result[]) bool MathRound(double &array[],int digits) | round() |
| Para los elementos de la matriz se calcula un valor redondeado hasta el número indicado de dígitos en la mantisa | bool MathSignif(const double &array[], const int digits, double &result[]) bool MathSignif(double &array[], const int digits) | signinf() |
| Calcula el valor de la función sinh(x) para los elementos de la matriz | bool MathSinh(const double &array[],double &result[]) bool MathSinh(double &array[]) | sinh() |
| Calcula el valor de la función cosh(x) para los elementos de la matriz | bool MathCosh(const double &array[],double &result[]) bool MathCosh(double &array[]) | cosh() |
| Calcula el valor de la función tanh(x) para los elementos de la matriz | bool MathTanh(const double &array[],double &result[]) bool MathTanh(double &array[]) | tanh() |
| Calcula el valor de la función arcsinh(x) para los elementos de la matriz | bool MathArcsinh(const double &array[],double &result[]) bool MathArcsinh(double &array[]) | asinh() |
| Calcula el valor de la función arccosh(x) para los elementos de la matriz | bool MathArccosh(const double &array[],double &result[]) bool MathArccosh(double &array[]) | acosh() |
| Calcula el valor de la función arctan(x) para los elementos de la matriz | bool MathArctanh(const double &array[],double &result[]) bool MathArctanh(double &array[]) | atanh() |
| Calcula el resultado de la operación binaria NOT para los elementos de la matriz | bool MathBitwiseNot(const int &array[],int &result[]) bool MathBitwiseNot(int &array[]) | bitwNot() |
| Calcula el resultado de la operación binaria AND para las matrices indicadas | bool MathBitwiseAnd(const int &array1[],const int &array2[],int &result[]) | bitwAnd() |
| Calcula el resultado de la operación binaria OR para las matrices indicadas | bool MathBitwiseOr(const int &array1[],const int &array2[],int &result[]) | bitwOr() |
| Calcula el resultado de la operación binaria XOR para las matrices indicadas | bool MathBitwiseXor(const int &array1[],const int &array2[],int &result[]) | bitwXor() |
| Calcula el resultado de la operación binaria SHL para los elementos de la matriz | bool MathBitwiseShiftL(const int &array[],const int n,int &result[]) bool MathBitwiseShiftL(int &array[],const int n) | bitwShiftL() |
| Calcula el resultado de la operación binaria SHR para los elementos de la matriz | bool MathBitwiseShiftR(const int &array[],const int n,int &result[]) bool MathBitwiseShiftR(int &array[],const int n) | bitwShiftR() |
Recuadro 3. Funciones matemáticas de cálculo de valores en las matrices
4. Ejemplo de uso de las funciones:
Vamos a analizar el uso práctico de las funciones estadísticas usando como ejemplo la distribución normal.
Consideremos que tenemos que resolver las siguientes tareas:
- Calcular la probabilidad de que una magnitud aleatoria distribuida según la ley normal con los parámetros mu y sigma, entre en el intervalo [mu-sigma,mu+sigma].
- Encontrar el intervalo de valores de una magnitud aleatoria x, distribuido según la ley normal con los parámetros mu y sigma, simétrico con respecto a mu, y que corresponda al 95% a la probabilidad confiada.
- Generar 1000000 números aleatorios distribuidos según la ley normal con los parámetros mu y sigma, calcular el histograma de los valores obtenidos, los 4 primeros momentos y comparar con los valores teóricos.
Ejemplo de solución en el script NormalExample:
//+------------------------------------------------------------------+ //| NormalExample.mq5 | //| Copyright 2016, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" //--- incluimos las funciones para el cálculo de la distribución normal #include <Math\Stat\Normal.mqh> //+------------------------------------------------------------------+ //| CalculateHistogram | //+------------------------------------------------------------------+ void CalculateHistogram(double &data[],const int ncells=200,const string filename="normal.csv") { if(ArraySize(data)<=0) return; int n=ArraySize(data); //--- encontramos los valores máximo y mínimo de los datos en la matriz data double minv,maxv,range; minv=data[0]; maxv=data[0]; for(int i=1; i<n; i++) { minv=MathMin(minv,data[i]); maxv=MathMax(maxv,data[i]); } //--- calculamos el rango range=maxv-minv; // Print("Min=",minv," Max=",maxv," range=",range," size=",n); if(range==0) return; //--- matrices para el cálculo del histograma double x[]; double y[]; //--- establecemos los valores del histograma ArrayResize(x,ncells); ArrayResize(y,ncells); for(int i=0; i<ncells; i++) { x[i]=minv+i*range/(ncells-1); y[i]=0; } //--- calculamos el histograma for(int i=0; i<n; i++) { double v=(maxv-data[i])/range; int ind=int((v*(ncells-1))); y[ind]++; } //--- comprobamos el nombre del archivo if(filename=="") return; //--- abrimos el archivo para la escritura ResetLastError(); int filehandle=FileOpen(filename,FILE_WRITE|FILE_TXT|FILE_ANSI); //--- escribimos los datos en el archivo if(filehandle!=INVALID_HANDLE) { for(int i=0; i<ncells; i++) { string str=StringFormat("%6.20f;%6.20f",x[i],y[i]); FileWrite(filehandle,str); } FileClose(filehandle); PrintFormat("El histograma se ha guardado en el archivo %s",filename); } else PrintFormat("Error de llamada FileOpen, código del error=%d",GetLastError()); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- 1. Calculamos la probabilidad de que una magnitud aleatoria, //--- distribuida según la ley normal con los parámetros mu y sigma, entre en el intervalo [mu-sigma,mu+sigma] //--- establecemos los parámetros de distribución double mu=5.0; double sigma=1.0; //--- establecemos el intervalo double x1=mu-sigma; double x2=mu+sigma; //--- variables para el cálculo de la probabilidad double cdf1,cdf2,probability; //--- variables para el código de error int error_code1,error_code2; //--- calculamos los valores de la función de distribución cdf1=MathCumulativeDistributionNormal(x1,mu,sigma,error_code1); cdf2=MathCumulativeDistributionNormal(x2,mu,sigma,error_code2); //--- comprobamos el código de los errores if(error_code1==ERR_OK && error_code2==ERR_OK) { //--- calculamos la probabilidad probability=cdf2-cdf1; //--- mostramos el resultado PrintFormat("x1=%5.8f, x2=%5.8f, Probability=%5.8f",x1,x2,probability); } //--- 2. Encontramos el intervalo de valores de la magnitud aleatoria x, distribuido según la ley normal con los parámetros mu y sigma, //--- simétrico con respecto a mu, y que corresponda al 95% a la probabilidad confiada. //--- establecemos la probabilidad confiada probability=0.95; //--- establecemos la probabilidad en los límites del intervalo double p1=(1.0-probability)*0.5; double p2=probability+(1.0-probability)*0.5; //--- calculamos los límites del intervalo x1=MathQuantileNormal(p1,mu,sigma,error_code1); x2=MathQuantileNormal(p2,mu,sigma,error_code2); //--- comprobamos el código de los errores if(error_code1==ERR_OK && error_code2==ERR_OK) { //--- mostramos el resultado PrintFormat("x1=%5.8f, x2=%5.8f",x1,x2); } //--- 3. Generamos 1000000 números aleatorios, distribuidos según la ley normal con los parámetros mu y sigma, //--- calculamos el histograma de los valores obtenidos, los 4 primeros momentos y comparamos con los valores teóricos //--- establecemos el número de valores y preparamos la matriz int data_count=1000000; double data[]; ArrayResize(data,data_count); //--- generamos los valores aleatorios y los guardamos en la matriz for(int i=0; i<data_count; i++) { data[i]=MathRandomNormal(mu,sigma,error_code1); } //--- establecemos el índice del valor inicial y el número de datos para el cálculo int start=0; int count=data_count; //--- calculamos los 4 primeros momentos de los valores generados double mean=MathMean(data,start,count); double variance=MathVariance(data,start,count); double skewness=MathSkewness(data,start,count); double kurtosis=MathKurtosis(data,start,count); //--- variables para los momentos teóricos double normal_mean=0; double normal_variance=0; double normal_skewness=0; double normal_kurtosis=0; //--- mostramos los valores de los momentos calculados PrintFormat(" mean=%.10f, variance=%.10f skewness=%.10f kurtosis=%.10f",mean,variance,skewness,kurtosis); //--- calculamos los valores teóricos de los momentos y comparamos con los obtenidos if(MathMomentsNormal(mu,sigma,normal_mean,normal_variance,normal_skewness,normal_kurtosis,error_code1)) { PrintFormat("Normal mean=%.10f, Normal variance=%.10f Normal skewness=%.10f Normal kurtosis=%.10f",normal_mean,normal_variance,normal_skewness,normal_kurtosis); PrintFormat("delta mean=%.4f, delta variance=%.4f delta skewness=%.4f delta kurtosis=%.4f",mean-normal_mean,variance-normal_variance,skewness-normal_skewness,kurtosis-normal_kurtosis); } //--- calculamos el histograma de la distribución y lo guardamos en el archivo normal.csv int ncells=50; CalculateHistogram(data,ncells,"normal.csv"); }
Resultado del funcionamiento del script:
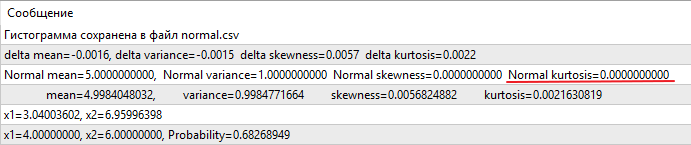
Fig 1. Resultado del funcionamiento del script TestNormal.mq5
Notemos que al calcular los valores del parámetro kurtosis, se usa excess kurtosis=kurtosis-3, es decir, para la distribución normal, es igual a 0.
El histograma calculado se guarda en el archivo normal.csv (fig. 2)
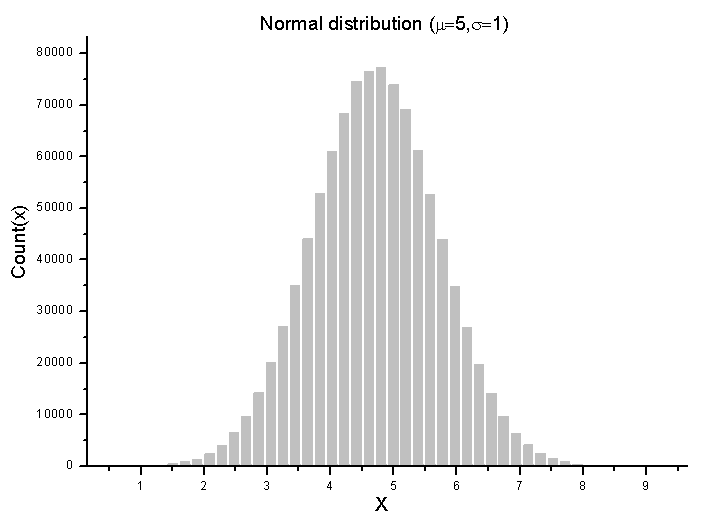
Fig. 2. Histograma de distribución de números aleatorios, generados según la distribución normal con los parámetros mu=5 y sigma=1
5. Comparación de la velocidad de los cálculos
Para comparar la velocidad de cálculo de las funciones estadísticas, se han preparado unos scripts para medir el tiempo de cálculo de las funciones de densidad (pdf), de las funciones de probabilidad (cdf), de las funciones de cálculo de los cuantiles y de las funciones de generación de números pseudoaleatorios.
Los cálculos se han realizado en una matriz de 51 valores, para las distribuciones continuas, el cálculo de las funciones se ha realizado en el rango de 0 a 1, para las discretas, de 0 a 50. La medición del tiempo de cálculo de las funciones estadísticas del lenguaje R se ha realizado con la ayuda de la biblioteca microbenchmark. El tiempo de cálculo de las funciones MQL5 se ha calculado con la ayuda de la función GetMicrosecondCount(). El script de cálculo TestStatBenchmark.mq5 se encuentra en la carpeta catálogo_de_datos_del_terminal\MQL5\Scripts\UnitTests\Stat. El script para R y los resultados de la medición de la velocidad de los cálculos se muestran en los Anexos.
Los cálculos se han realizado en un Intel Core i7-4790, CPU 3.6 Ghz, 16 GB RAM, Windows 10 x64.
Los resultados de la medición del tiempo de los cálculos (en microsegundos) se muestran en el recuadro 3.
| № | Distribución | Tiempo de cálculo en MQL5 del PDF (µs) | Tiempo de cálculo en R del PDF (µs) | PDF R/MQL5 | Tiempo de cálculo en MQL5 del CDF (µs) | Tiempo de cálculo en R del CDF (µs) | CDF R/MQL5 | Tiempo de cálculo en MQL5de los cuantiles (µs) | Tiempo de cálculo en Rde los cuantiles (µs) | Quantile R/MQL5 | Tiempo de generación en MQL5 de los números aleatorios (µs) | Tiempo de generación en R de los números aleatorios (µs) | Random R/MQL5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Binomial | 4.39 | 11.663 | 2.657 | 13.65 | 25.316 | 1.855 | 50.18 | 66.845 | 1.332 | 318.73 | 1816.463 | 5.699 |
| 2 | Beta | 1.74 | 17.352 | 9.972 | 4.76 | 15.076 | 3.167 | 48.72 | 129.992 | 2.668 | 688.81 | 1723.45 | 2.502 |
| 3 | Gamma | 1.31 | 8.251 | 6.347 | 8.09 | 14.792 | 1.828 | 50.83 | 64.286 | 1.265 | 142.84 | 1281.707 | 8.973 |
| 4 | Cauchy | 0.45 | 1.423 | 3.162 | 1.33 | 15.078 | 11.34 | 1.37 | 2.845 | 2.077 | 224.19 | 588.517 | 2.625 |
| 5 | Exponential | 0.85 | 3.13 | 3.682 | 0.77 | 2.845 | 3.695 | 0.53 | 2.276 | 4.294 | 143.18 | 389.406 | 2.72 |
| 6 | Uniform | 0.42 | 2.561 | 6.098 | 0.45 | 1.423 | 3.162 | 0.18 | 2.846 | 15.81 | 40.3 | 247.467 | 6.141 |
| 7 | Geometric | 2.3 | 5.121 | 2.227 | 2.12 | 4.552 | 2.147 | 0.81 | 5.407 | 6.675 | 278 | 1078.045 | 3.879 |
| 8 | Hypergeometric | 1.85 | 11.095 | 5.997 | 0.9 | 8.819 | 9.799 | 0.75 | 9.957 | 13.28 | 302.55 | 880.356 | 2.91 |
| 9 | Logistic | 1.27 | 4.267 | 3.36 | 1.11 | 4.267 | 3.844 | 0.71 | 3.13 | 4.408 | 178.65 | 626.632 | 3.508 |
| 10 | Weibull | 2.99 | 5.69 | 1.903 | 2.74 | 4.268 | 1.558 | 2.64 | 6.828 | 2.586 | 536.37 | 1558.472 | 2.906 |
| 11 | Poisson | 2.91 | 5.974 | 2.053 | 6.26 | 8.534 | 1.363 | 3.43 | 13.085 | 3.815 | 153.59 | 303.219 | 1.974 |
| 12 | F | 3.86 | 10.241 | 2.653 | 9.94 | 22.472 | 2.261 | 65.47 | 135.396 | 2.068 | 1249.22 | 1801.955 | 1.442 |
| 13 | Chi Square | 2.47 | 5.974 | 2.419 | 7.71 | 13.37 | 1.734 | 44.11 | 61.725 | 1.399 | 210.24 | 1235.059 | 5.875 |
| 14 | Noncentral ChiSquare | 8.05 | 14.223 | 1.767 | 45.61 | 209.068 | 4.584 | 220.66 | 10342.96 | 46.873 | 744.45 | 1997.653 | 2.683 |
| 15 | Noncentral F | 19.1 | 28.446 | 1.489 | 14.67 | 46.935 | 3.199 | 212.21 | 2561.991 | 12.073 | 1848.9 | 2912.141 | 1.575 |
| 16 | Noncentral Beta | 16.3 | 26.739 | 1.64 | 10.48 | 43.237 | 4.126 | 153.66 | 2290.915 | 14.909 | 2686.82 | 2839.893 | 1.057 |
| 17 | Negative Binomial | 6.13 | 11.094 | 1.81 | 12.21 | 19.627 | 1.607 | 14.05 | 60.019 | 4.272 | 1130.39 | 1936.498 | 1.713 |
| 18 | Normal | 1.15 | 4.267 | 3.71 | 0.81 | 3.983 | 4.917 | 0.7 | 2.277 | 3.253 | 293.7 | 696.321 | 2.371 |
| 19 | Lognormal | 1.99 | 5.406 | 2.717 | 3.19 | 8.819 | 2.765 | 3.18 | 6.259 | 1.968 | 479.75 | 1269.761 | 2.647 |
| 20 | T | 2.32 | 11.663 | 5.027 | 8.01 | 19.059 | 2.379 | 50.23 | 58.596 | 1.167 | 951.58 | 1425.92 | 1.498 |
| 21 | Noncentral T | 38.47 | 86.757 | 2.255 | 27.75 | 39.823 | 1.435 | 1339.51 | 1930.524 | 1.441 | 1550.27 | 1699.84 | 1.096 |
| <PDF R/MQL5> | 3.474 | <CDF R/MQL5> | 3.465 | <Quantile R/MQL5> | 7.03 | <Random R/MQL5> | 3.13 |
Recuadro 4. Tiempo de cálculo de las funciones estadísticas en R y MQL5 (en microsegundos)
Para R se han tomado los valores del tiempo mínimo, y para MQL5 se han tomado los valores medios (pdf_mean, cdf_mean, quantile_mean, random_mean).
En el recuadro 3 se puede ver que con estas condiciones, el cálculo de las funciones de la biblioteca estadística MQL5 se realizan varias veces más rápido que en R. De media, MQL5 calcula de 3 a 7 más rápido que R, incluso teniendo en cuenta que las versiones comparadas de las funciones R están en realidad escritas en C++.
En la práctica, el compilador del lenguaje MQL5 ha resultado bastante más rápido que las implementaciones С++ de las funciones en R, lo que muestra la alta calidad de nuestros desarrollos. Pasando los programas de R a MQL5 podemos obtener un serio incremento de la velocidad y no será necesario usar bibliotecas DLL ajenas.
6. Detectando los errores de cálculo en R
Durante la puesta a prueba de R, se ha detectado un error de cálculo de los cuantiles de la distribución T no-central.
Ejmplo:
> n <- 10 > k <- seq(0,1,by=1/n) > nt_pdf<-dt(k, 10,8, log = FALSE) > nt_cdf<-pt(k, 10,8, log = FALSE) > nt_quantile<-qt(nt_cdf, 10,8, log = FALSE) > nt_pdf [1] 4.927733e-15 1.130226e-14 2.641608e-14 6.281015e-14 1.516342e-13 3.708688e-13 9.166299e-13 [8] 2.283319e-12 5.716198e-12 1.433893e-11 3.593699e-11 > nt_cdf [1] 6.220961e-16 1.388760e-15 3.166372e-15 7.362630e-15 1.742915e-14 4.191776e-14 1.021850e-13 [8] 2.518433e-13 6.257956e-13 1.563360e-12 3.914610e-12 > k [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 > nt_quantile [1] -Inf -1.340781e+154 -1.340781e+154 -1.340781e+154 -1.340781e+154 -1.340781e+154 [7] -1.340781e+154 7.000000e-01 8.000000e-01 9.000000e-01 1.000000e+00
Para calcular la probabilidad de la distribución T de Student no-central en el lenguaje R, se usa el algoritmo AS 243, propuesto por Lenth [6]. La ventaja de este método es la rápida computación recursiva de los miembros de la una serie infinita con una función beta incompleta. Pero en el artículo [7] se ha demostrado que debido a un error de valoración de la precisión al sumar los miembros de la serie, este algoritmo produce errores (recuadro 2 en el artículo [7]), en especial para los valores grandes del parámetro delta de no-centralidad. Los autores del artículo [7] han propuesto un algoritmo corregido de cálculo recursivo de la probabilidad de la distribución T no-central.
En la biblioteca estadística MQL5 se usa el algoritmo correcto para el cálculo de la probabilidad, sugerido en el artículo [7], lo que da resultados precisos.
También conviene destacar que en el lenguaje R, el método de determinación de las densidades para las distribuciones Gamma, ChiSquare y Noncentral ChiSquare en el punto x=0 produce expresiones infinitas:
> dgamma(0,0.5,1) [1] Inf > dchisq(0,df=0.5,ncp=1) [1] Inf > dchisq(0,df=0.5,ncp=0) [1] Inf
De esta forma, en el lenguaje R, a la hora de determinar la densidad de la probabilidad en el punto x=0, se usan valores límite. A pesar de la infinitud en el punto x=0, en este caso no suceden divergencias durante la integración, y las integrales de la densidad
son finitas.
Al calcular las probabilidades (por ejemplo, para x=0.1) estas coinciden con los valores de Wolfram Alpha (Gamma, ChiSquare, NoncentralChiSquare).
> pgamma(0.1,0.5,1) [1] 0.3452792 > pchisq(0.1,df=0.5,ncp=0) [1] 0.5165553 > pchisq(0.1,df=0.5,ncp=1) [1] 0.3194965
En Wolfram Alpha (Mathematica) y Matlab se usa otro método de definición de la densidad en el punto x=0:
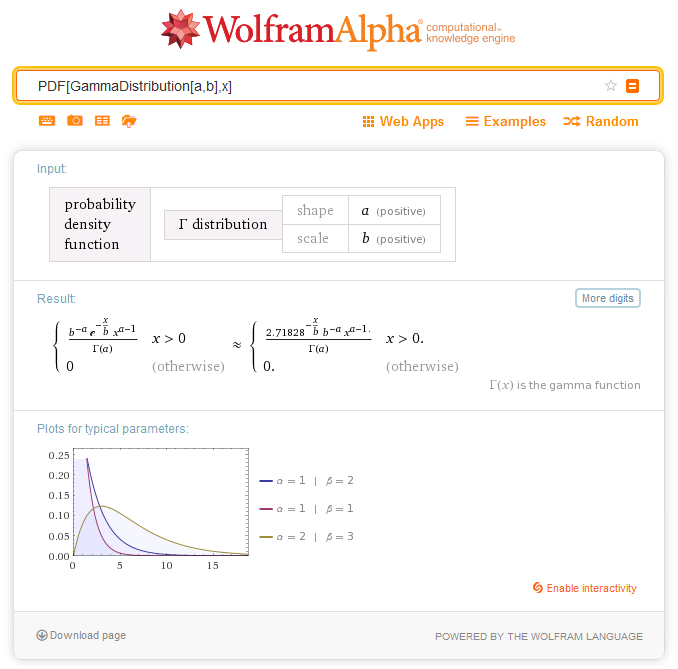
Fig. 3. Definición de la densidad de la probabilidad de la distribución Gamma en Wolfram Alpha
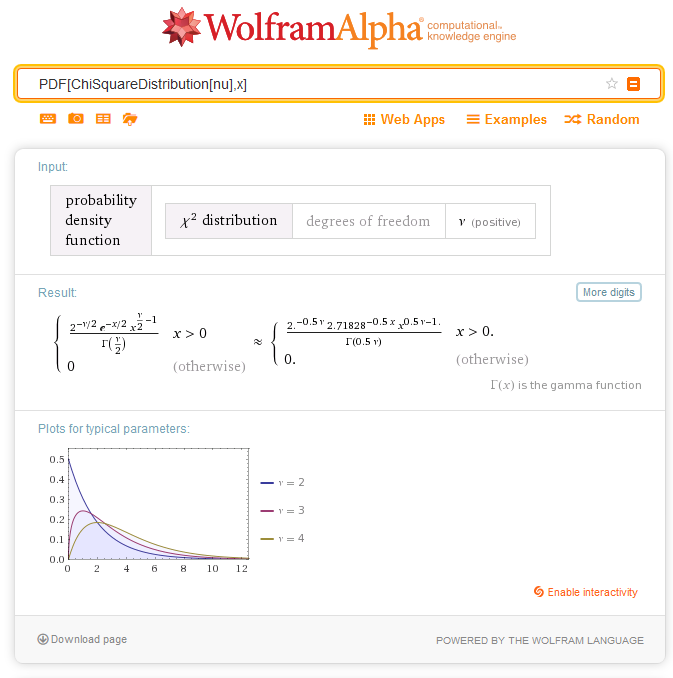
Fig. 4. Definición de la densidad de la probabilidad de la distribución ChiSquare en Wolfram Alpha
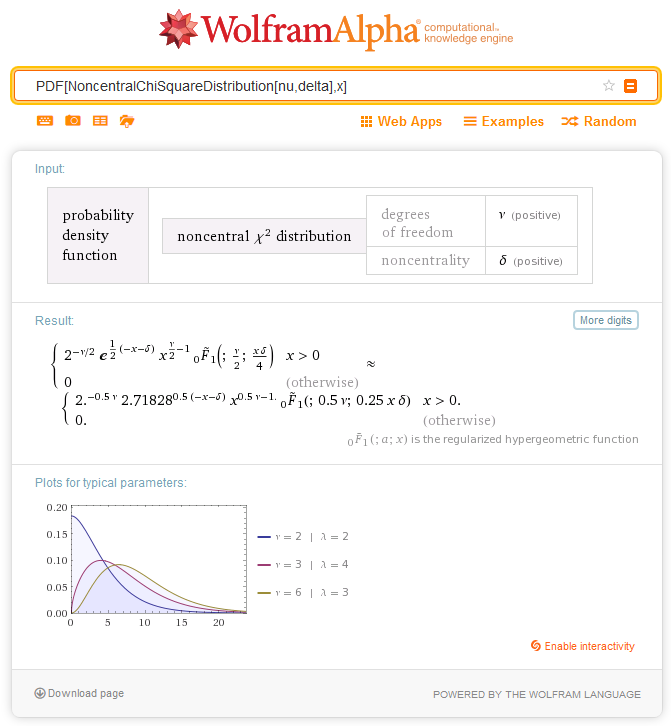
Fig. 5. Definición de la densidad de la probabilidad de la distribución Noncentral ChiSquare en Wolfram Alpha
En la biblioteca estadística del lenguaje MQL5, las densidades de datos de las distribuciones en el punto x=0 se consideran por defecto igual a cero.
Para estar seguro de la exactitud de los cálculos y darle la posibilidad a otros desarrolladores de comprobar la calidad de la biblioteca, hemos incluido varios unit test de los scripts en el paquete estándar. Podrá encontrarlos en el catálogo /Scripts/UnitTests/Stat.
Conclusión
En el artículo hemos visto las principales funciones de la biblioteca estadística del lenguaje MQL5.
Estas permiten realizar el cálculo de las características estadísticas de los datos y trabajar con las principales distribuciones estadísticas implementadas en el lenguaje R. Además, en la biblioteca también existen funciones de cálculo de los momentos teóricos de las distribuciones, que permiten valorar el grado de correspondencia entre la distribución real y la modelada.
Gracias a la alta productividad del nuevo compilador de 64 bits del lenguaje MQL5, los complejos cálculos matemáticos se realizan a una velocidad varias veces mayor que en el lenguaje R, lo que simplifica significativamente la realización de investigaciones.
Literatura
- The R Project for Statistical Computing..
- N. Balakrishnan, N. L. Johnson, S. Kotz. "Continuous Univariate Distributions: Volume 1.". Wiley-Interscience, 1994.
- N. Balakrishnan, N. L. Johnson, S. Kotz. "Continuous Univariate Distributions: Volume 1." Wiley-Interscience, 1994.
- N. L. Johnson, S. Kotz, A. W. Kemp "Univariate Discrete Distributions", Wiley-Interscience, 1994.
- Forbes C., Evans M., Hastings N., Peacock B., "Statistical Distributions", 4th Edition, John Wiley and Sons, 2011.
- Lenth, R.V., "Cumulative distribution function of the noncentral t distribution", Appled Statistics, vol. 38 (1989), 185–189.
- D. Benton, K. Krishnamoorthy, "Computing discrete mixtures of continuous distributions: noncentral chisquare, noncentral t and the distribution of the square of the sample multiple correlation coefficient", Computational Statistics & Data Analysis, 43, (2003), 249-267
Anexos. Resultados de las mediciones del tiempo del cálculo de las funciones estadísticas
En los anexos se adjunta un script para calcular el tiempo computación de las funciones estadísticas en el lenguaje R y los resultados de su funcionamiento, así como los resultados de la ejecución del script TestStatBenchmark.mq5.
Script en el lenguaje R:
n <- 50
k <- seq(0,n,by=1)
binomial_pdf <- microbenchmark(pdf<-dbinom(k, 50, 0.6, log = FALSE))
binomial_cdf <- microbenchmark(cdf<-pbinom(k, 50, 0.6, log = FALSE))
binomial_quantile <- microbenchmark(quantile<-qbinom(cdf, 50, 0.6, log = FALSE))
binomial_random <- microbenchmark(random<-rbinom(10000, 50, 0.6))
print(binomial_pdf)
print(binomial_cdf)
print(binomial_quantile)
print(binomial_random)
n <- 50
k <- seq(0,1,by=1/n)
beta_pdf <- microbenchmark(pdf<-dbeta(k, 2, 4, log = FALSE))
beta_cdf <- microbenchmark(cdf<-pbeta(k, 2, 4, log = FALSE))
beta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2, 4, log = FALSE))
beta_random <- microbenchmark(random<-rbeta(10000, 2, 4,))
print(beta_pdf)
print(beta_cdf)
print(beta_quantile)
print(beta_random)
n <- 50
k <- seq(0,1,by=1/n)
gamma_pdf <- microbenchmark(pdf<-dgamma(k, 1,1, log = FALSE))
gamma_cdf <- microbenchmark(cdf<-pgamma(k, 1,1, log = FALSE))
gamma_quantile <- microbenchmark(quantile<-qgamma(cdf, 1, 1, log = FALSE))
gamma_random <- microbenchmark(random<-rgamma(10000, 1,1))
print(gamma_pdf)
print(gamma_cdf)
print(gamma_quantile)
print(gamma_random)
n <- 50
k <- seq(0,1,by=1/n)
cauchy_pdf <- microbenchmark(pdf<-dcauchy(k, 2,1, log = FALSE))
cauchy_cdf <- microbenchmark(cdf<-pgamma(k, 2,1, log = FALSE))
cauchy_quantile <- microbenchmark(quantile<-qcauchy(cdf, 2, 1, log = FALSE))
cauchy_random <- microbenchmark(random<-rcauchy(10000, 2, 1))
print(cauchy_pdf)
print(cauchy_cdf)
print(cauchy_quantile)
print(cauchy_random)
n <- 50
k <- seq(0,1,by=1/n)
exponential_pdf <- microbenchmark(pdf<-dexp(k, 2, log = FALSE))
exponential_cdf <- microbenchmark(cdf<-pexp(k, 2, log = FALSE))
exponential_quantile <- microbenchmark(quantile<-qexp(cdf, 2, log = FALSE))
exponential_random <- microbenchmark(random<-rexp(10000, 2))
print(exponential_pdf)
print(exponential_cdf)
print(exponential_quantile)
print(exponential_random)
n <- 50
k <- seq(0,1,by=1/n)
uniform_pdf <- microbenchmark(pdf<-dunif(k, 0, 10, log = FALSE))
uniform_cdf <- microbenchmark(cdf<-punif(k, 0, 10, log = FALSE))
uniform_quantile <- microbenchmark(quantile<-qunif(cdf, 0, 10, log = FALSE))
uniform_random <- microbenchmark(random<-runif(10000, 0, 10))
print(uniform_pdf)
print(uniform_cdf)
print(uniform_quantile)
print(uniform_random)
n <- 50
k <- seq(0,n,by=1)
geometric_pdf <- microbenchmark(pdf<-dgeom(k, 0.3, log = FALSE))
geometric_cdf <- microbenchmark(cdf<-pgeom(k, 0.3, log = FALSE))
geometric_quantile <- microbenchmark(quantile<-qgeom(cdf, 0.3, log = FALSE))
geometric_random <- microbenchmark(random<-rgeom(10000, 0.3))
print(geometric_pdf)
print(geometric_cdf)
print(geometric_quantile)
print(geometric_random)
n <- 50
k <- seq(0,n,by=1)
hypergeometric_pdf <- microbenchmark(pdf<-dhyper(k, 12,38,11, log = FALSE))
hypergeometric_cdf <- microbenchmark(cdf<-phyper(k, 12,38,11, log = FALSE))
hypergeometric_quantile <- microbenchmark(quantile<-qhyper(cdf, 12,38,11, log = FALSE))
hypergeometric_random <- microbenchmark(random<-rhyper(10000, 12,38,11))
print(hypergeometric_pdf)
print(hypergeometric_cdf)
print(hypergeometric_quantile)
print(hypergeometric_random)
n <- 50
k <- seq(0,1,by=1/n)
logistic_pdf <- microbenchmark(pdf<-dlogis(k, 1,2, log = FALSE))
logistic_cdf <- microbenchmark(cdf<-plogis(k, 1,2, log = FALSE))
logistic_quantile <- microbenchmark(quantile<-qlogis(cdf, 1,2, log = FALSE))
logistic_random <- microbenchmark(random<-rlogis(10000, 1,2))
print(logistic_pdf)
print(logistic_cdf)
print(logistic_quantile)
print(logistic_random)
n <- 50
k <- seq(0,1,by=1/n)
weibull_pdf <- microbenchmark(pdf<-dweibull(k, 5,1, log = FALSE))
weibull_cdf <- microbenchmark(cdf<-pweibull(k, 5,1, log = FALSE))
weibull_quantile <- microbenchmark(quantile<-qweibull(cdf, 5,1, log = FALSE))
weibull_random <- microbenchmark(random<-rweibull(10000, 5,1))
print(weibull_pdf)
print(weibull_cdf)
print(weibull_quantile)
print(weibull_random)
n <- 50
k <- seq(0,n,by=1)
poisson_pdf <- microbenchmark(pdf<-dpois(k, 1, log = FALSE))
poisson_cdf <- microbenchmark(cdf<-ppois(k, 1, log = FALSE))
poisson_quantile <- microbenchmark(quantile<-qpois(cdf, 1, log = FALSE))
poisson_random <- microbenchmark(random<-rpois(10000, 1))
print(poisson_pdf)
print(poisson_cdf)
print(poisson_quantile)
print(poisson_random)
n <- 50
k <- seq(0,1,by=1/n)
f_pdf <- microbenchmark(pdf<-df(k, 10,20, log = FALSE))
f_cdf <- microbenchmark(cdf<-pf(k, 10,20, log = FALSE))
f_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,log = FALSE))
f_random <- microbenchmark(random<-rf(10000, 10,20))
print(f_pdf)
print(f_cdf)
print(f_quantile)
print(f_random)
n <- 50
k <- seq(0,1,by=1/n)
chisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,log = FALSE))
chisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2, log = FALSE))
chisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2, log = FALSE))
chisquare_random <- microbenchmark(random<-rchisq(10000, 2))
print(chisquare_pdf)
print(chisquare_cdf)
print(chisquare_quantile)
print(chisquare_random)
n <- 50
k <- seq(0,1,by=1/n)
nchisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,1, log = FALSE))
nchisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2,1,log = FALSE))
nchisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2,1, log = FALSE))
nchisquare_random <- microbenchmark(random<-rchisq(10000, 2,1))
print(nchisquare_pdf)
print(nchisquare_cdf)
print(nchisquare_quantile)
print(nchisquare_random)
n <- 50
k <- seq(0,1,by=1/n)
nf_pdf <- microbenchmark(pdf<-df(k, 10,20,2, log = FALSE))
nf_cdf <- microbenchmark(cdf<-pf(k, 10,20,2, log = FALSE))
nf_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,2, log = FALSE))
nf_random <- microbenchmark(random<-rf(10000, 10,20,2))
print(nf_pdf)
print(nf_cdf)
print(nf_quantile)
print(nf_random)
n <- 50
k <- seq(0,1,by=1/n)
nbeta_pdf <- microbenchmark(pdf<-dbeta(k, 2,4,1, log = FALSE))
nbeta_cdf <- microbenchmark(cdf<-pbeta(k, 2,4,1, log = FALSE))
nbeta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2,4,1, log = FALSE))
nbeta_random <- microbenchmark(random<-rbeta(10000, 2,4,1))
print(nbeta_pdf)
print(nbeta_cdf)
print(nbeta_quantile)
print(nbeta_random)
n <- 50
k <- seq(0,n,by=1)
nbinom_pdf <- microbenchmark(pdf<-dnbinom(k, 2, 0.5, log = FALSE))
nbinom_cdf <- microbenchmark(cdf<-pnbinom(k, 2, 0.5, log = FALSE))
nbinom_quantile <- microbenchmark(quantile<-qnbinom(cdf, 2, 0.5, log = FALSE))
nbinom_random <- microbenchmark(random<-rnbinom(10000, 2, 0.5))
print(nbinom_pdf)
print(nbinom_cdf)
print(nbinom_quantile)
print(nbinom_random)
n <- 50
k <- seq(0,1,by=1/n)
normal_pdf <- microbenchmark(pdf<-dnorm(k, 1, 1, log = FALSE))
normal_cdf <- microbenchmark(cdf<-pnorm(k, 1, 1, log = FALSE))
normal_quantile <- microbenchmark(quantile<-qnorm(cdf, 1,1, log = FALSE))
normal_random <- microbenchmark(random<-rnorm(10000, 1,1))
print(normal_pdf)
print(normal_cdf)
print(normal_quantile)
print(normal_random)
n <- 50
k <- seq(0,1,by=1/n)
lognormal_pdf <- microbenchmark(pdf<-dlnorm(k, 0.5,0.6, log = FALSE))
lognormal_cdf <- microbenchmark(cdf<-plnorm(k, 0.5,0.6, log = FALSE))
lognormal_quantile <- microbenchmark(quantile<-qlnorm(cdf, 0.5,0.6, log = FALSE))
lognormal_random <- microbenchmark(random<-rlnorm(10000, 0.5,0.6))
print(lognormal_pdf)
print(lognormal_cdf)
print(lognormal_quantile)
print(lognormal_random)
n <- 50
k <- seq(0,1,by=1/n)
t_pdf <- microbenchmark(pdf<-dt(k, 8, log = FALSE))
t_cdf <- microbenchmark(cdf<-pt(k, 8, log = FALSE))
t_quantile <- microbenchmark(quantile<-qt(cdf, 8, log = FALSE))
t_random <- microbenchmark(random<-rt(10000, 8))
print(t_pdf)
print(t_cdf)
print(t_quantile)
print(t_random)
n <- 50
k <- seq(0,1,by=1/n)
nt_pdf <- microbenchmark(pdf<-dt(k, 10,1, log = FALSE))
nt_cdf <- microbenchmark(cdf<-pt(k, 10,1, log = FALSE))
nt_quantile <- microbenchmark(quantile<-qt(cdf, 10,1, log = FALSE))
nt_random <- microbenchmark(random<-rt(10000, 10,1))
print(nt_pdf)
print(nt_cdf)
print(nt_quantile)
print(nt_random)
Resultado:
R version 3.2.5 (2016-04-14) -- "Very, Very Secure Dishes" Copyright (C) 2016 The R Foundation for Statistical Computing Platform: x86_64-w64-mingw32/x64 (64-bit) R is free software and comes with ABSOLUTELY NO WARRANTY. You are welcome to redistribute it under certain conditions. Type 'license()' or 'licence()' for distribution details. R is a collaborative project with many contributors. Type 'contributors()' for more information and 'citation()' on how to cite R or R packages in publications. Type 'demo()' for some demos, 'help()' for on-line help, or 'help.start()' for an HTML browser interface to help. Type 'q()' to quit R. [Workspace loaded from ~/Test/111/.RData] > library(microbenchmark) > n <- 50 > k <- seq(0,n,by=1) > binomial_pdf <- microbenchmark(pdf<-dbinom(k, 50, 0.6, log = FALSE)) > binomial_cdf <- microbenchmark(cdf<-pbinom(k, 50, 0.6, log = FALSE)) > binomial_quantile <- microbenchmark(quantile<-qbinom(cdf, 50, 0.6, log = FALSE)) > binomial_random <- microbenchmark(random<-rbinom(10000, 50, 0.6)) > print(binomial_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dbinom(k, 50, 0.6, log = FALSE) 11.663 11.948 13.37888 12.233 12.233 47.503 100 > print(binomial_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pbinom(k, 50, 0.6, log = FALSE) 25.316 25.602 29.63195 25.886 35.557 93.868 100 > print(binomial_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qbinom(cdf, 50, 0.6, log = FALSE) 66.845 67.13 72.09098 67.699 73.672 130.276 100 > print(binomial_random) Unit: milliseconds expr min lq mean median uq max neval random <- rbinom(10000, 50, 0.6) 1.816463 1.89056 1.948185 1.929814 1.989262 2.308835 100 > > > n <- 50 > k <- seq(0,1,by=1/n) > beta_pdf <- microbenchmark(pdf<-dbeta(k, 2, 4, log = FALSE)) > beta_cdf <- microbenchmark(cdf<-pbeta(k, 2, 4, log = FALSE)) > beta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2, 4, log = FALSE)) > beta_random <- microbenchmark(random<-rbeta(10000, 2, 4,)) > print(beta_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dbeta(k, 2, 4, log = FALSE) 17.352 17.637 19.99512 17.638 18.206 109.797 100 > print(beta_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pbeta(k, 2, 4, log = FALSE) 15.076 15.361 16.83489 15.646 15.9295 75.379 100 > print(beta_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qbeta(cdf, 2, 4, log = FALSE) 129.992 130.277 140.8325 131.4145 143.93 201.672 100 > print(beta_random) Unit: milliseconds expr min lq mean median uq max neval random <- rbeta(10000, 2, 4, ) 1.72345 1.794132 1.862292 1.836515 1.901226 2.823963 100 > > n <- 50 > k <- seq(0,1,by=1/n) > gamma_pdf <- microbenchmark(pdf<-dgamma(k, 1,1, log = FALSE)) > gamma_cdf <- microbenchmark(cdf<-pgamma(k, 1,1, log = FALSE)) > gamma_quantile <- microbenchmark(quantile<-qgamma(cdf, 1, 1, log = FALSE)) > gamma_random <- microbenchmark(random<-rgamma(10000, 1,1)) > print(gamma_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dgamma(k, 1, 1, log = FALSE) 8.251 8.8195 10.92684 9.104 9.389 122.312 100 > print(gamma_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pgamma(k, 1, 1, log = FALSE) 14.792 15.646 20.43306 20.055 21.334 106.099 100 > print(gamma_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qgamma(cdf, 1, 1, log = FALSE) 64.286 64.854 70.09419 65.139 67.13 162.988 100 > print(gamma_random) Unit: milliseconds expr min lq mean median uq max neval random <- rgamma(10000, 1, 1) 1.281707 1.330347 1.410961 1.362631 1.421226 2.322204 100 > > n <- 50 > k <- seq(0,1,by=1/n) > cauchy_pdf <- microbenchmark(pdf<-dcauchy(k, 2,1, log = FALSE)) > cauchy_cdf <- microbenchmark(cdf<-pgamma(k, 2,1, log = FALSE)) > cauchy_quantile <- microbenchmark(quantile<-qcauchy(cdf, 2, 1, log = FALSE)) > cauchy_random <- microbenchmark(random<-rcauchy(10000, 2, 1)) > print(cauchy_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dcauchy(k, 2, 1, log = FALSE) 1.423 1.708 2.8431 1.709 2.278 67.415 100 > print(cauchy_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pgamma(k, 2, 1, log = FALSE) 15.078 15.646 16.51914 15.93 16.215 33.281 100 > print(cauchy_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qcauchy(cdf, 2, 1, log = FALSE) 2.845 3.13 3.8044 3.131 3.415 56.606 100 > print(cauchy_random) Unit: microseconds expr min lq mean median uq max neval random <- rcauchy(10000, 2, 1) 588.517 615.823 663.8658 637.7255 674.845 1520.356 100 > > n <- 50 > k <- seq(0,1,by=1/n) > exponential_pdf <- microbenchmark(pdf<-dexp(k, 2, log = FALSE)) > exponential_cdf <- microbenchmark(cdf<-pexp(k, 2, log = FALSE)) > exponential_quantile <- microbenchmark(quantile<-qexp(cdf, 2, log = FALSE)) > exponential_random <- microbenchmark(random<-rexp(10000, 2)) > print(exponential_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dexp(k, 2, log = FALSE) 3.13 3.414 4.08887 3.415 3.415 67.699 100 > print(exponential_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pexp(k, 2, log = FALSE) 2.845 3.13 4.38756 3.414 3.5565 58.597 100 > print(exponential_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qexp(cdf, 2, log = FALSE) 2.276 2.561 3.80729 2.5615 2.846 44.659 100 > print(exponential_random) Unit: microseconds expr min lq mean median uq max neval random <- rexp(10000, 2) 389.406 408.8895 440.9583 418.4185 444.8715 1371.875 100 > > > n <- 50 > k <- seq(0,1,by=1/n) > uniform_pdf <- microbenchmark(pdf<-dunif(k, 0, 10, log = FALSE)) > uniform_cdf <- microbenchmark(cdf<-punif(k, 0, 10, log = FALSE)) > uniform_quantile <- microbenchmark(quantile<-qunif(cdf, 0, 10, log = FALSE)) > uniform_random <- microbenchmark(random<-runif(10000, 0, 10)) > print(uniform_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dunif(k, 0, 10, log = FALSE) 2.561 2.846 3.78734 3.13 3.131 66.277 100 > print(uniform_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- punif(k, 0, 10, log = FALSE) 1.423 1.708 2.41635 1.992 1.993 53.477 100 > print(uniform_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qunif(cdf, 0, 10, log = FALSE) 2.846 3.131 5.13561 3.415 3.6995 82.774 100 > print(uniform_random) Unit: microseconds expr min lq mean median uq max neval random <- runif(10000, 0, 10) 247.467 258.7035 317.1567 279.6095 357.2635 1267.769 100 > > > n <- 50 > k <- seq(0,n,by=1) > geometric_pdf <- microbenchmark(pdf<-dgeom(k, 0.3, log = FALSE)) > geometric_cdf <- microbenchmark(cdf<-pgeom(k, 0.3, log = FALSE)) > geometric_quantile <- microbenchmark(quantile<-qgeom(cdf, 0.3, log = FALSE)) > geometric_random <- microbenchmark(random<-rgeom(10000, 0.3)) > print(geometric_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dgeom(k, 0.3, log = FALSE) 5.121 5.122 6.14258 5.406 5.406 60.304 100 > print(geometric_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pgeom(k, 0.3, log = FALSE) 4.552 4.836 5.50548 4.837 5.1215 46.081 100 > print(geometric_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qgeom(cdf, 0.3, log = FALSE) 5.407 5.974 7.12107 5.975 6.259 71.681 100 > print(geometric_random) Unit: milliseconds expr min lq mean median uq max neval random <- rgeom(10000, 0.3) 1.078045 1.127681 1.192608 1.156125 1.199361 1.604267 100 > > n <- 50 > k <- seq(0,n,by=1) > hypergeometric_pdf <- microbenchmark(pdf<-dhyper(k, 12,38,11, log = FALSE)) > hypergeometric_cdf <- microbenchmark(cdf<-phyper(k, 12,38,11, log = FALSE)) > hypergeometric_quantile <- microbenchmark(quantile<-qhyper(cdf, 12,38,11, log = FALSE)) > hypergeometric_random <- microbenchmark(random<-rhyper(10000, 12,38,11)) > print(hypergeometric_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dhyper(k, 12, 38, 11, log = FALSE) 11.095 13.939 17.07667 14.224 14.935 101.548 100 > print(hypergeometric_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- phyper(k, 12, 38, 11, log = FALSE) 8.819 9.387 12.60515 9.672 12.517 62.01 100 > print(hypergeometric_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qhyper(cdf, 12, 38, 11, log = FALSE) 9.957 10.3835 13.00618 10.81 11.948 64.286 100 > print(hypergeometric_random) Unit: microseconds expr min lq mean median uq max neval random <- rhyper(10000, 12, 38, 11) 880.356 938.9515 993.8324 963.9835 996.8365 1375.289 100 > > n <- 50 > k <- seq(0,1,by=1/n) > logistic_pdf <- microbenchmark(pdf<-dlogis(k, 1,2, log = FALSE)) > logistic_cdf <- microbenchmark(cdf<-plogis(k, 1,2, log = FALSE)) > logistic_quantile <- microbenchmark(quantile<-qlogis(cdf, 1,2, log = FALSE)) > logistic_random <- microbenchmark(random<-rlogis(10000, 1,2)) > print(logistic_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dlogis(k, 1, 2, log = FALSE) 4.267 4.552 5.94354 4.553 4.837 53.477 100 > print(logistic_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- plogis(k, 1, 2, log = FALSE) 4.267 4.552 5.96056 4.837 4.837 96.428 100 > print(logistic_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qlogis(cdf, 1, 2, log = FALSE) 3.13 3.415 4.1742 3.415 3.699 56.036 100 > print(logistic_random) Unit: microseconds expr min lq mean median uq max neval random <- rlogis(10000, 1, 2) 626.632 649.956 696.2128 675.2725 715.805 1589.191 100 > > n <- 50 > k <- seq(0,1,by=1/n) > weibull_pdf <- microbenchmark(pdf<-dweibull(k, 5,1, log = FALSE)) > weibull_cdf <- microbenchmark(cdf<-pweibull(k, 5,1, log = FALSE)) > weibull_quantile <- microbenchmark(quantile<-qweibull(cdf, 5,1, log = FALSE)) > weibull_random <- microbenchmark(random<-rweibull(10000, 5,1)) > print(weibull_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dweibull(k, 5, 1, log = FALSE) 5.69 5.974 7.21775 5.975 6.259 85.619 100 > print(weibull_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pweibull(k, 5, 1, log = FALSE) 4.268 4.552 7.83782 4.8365 7.966 90.455 100 > print(weibull_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qweibull(cdf, 5, 1, log = FALSE) 6.828 7.112 7.96587 7.113 7.397 48.641 100 > print(weibull_random) Unit: milliseconds expr min lq mean median uq max neval random <- rweibull(10000, 5, 1) 1.558472 1.59744 1.659753 1.632853 1.679502 2.616603 100 > > n <- 50 > k <- seq(0,n,by=1) > poisson_pdf <- microbenchmark(pdf<-dpois(k, 1, log = FALSE)) > poisson_cdf <- microbenchmark(cdf<-ppois(k, 1, log = FALSE)) > poisson_quantile <- microbenchmark(quantile<-qpois(cdf, 1, log = FALSE)) > poisson_random <- microbenchmark(random<-rpois(10000, 1)) > print(poisson_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dpois(k, 1, log = FALSE) 5.974 6.543 7.30316 6.544 6.828 54.046 100 > print(poisson_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- ppois(k, 1, log = FALSE) 8.534 8.819 10.25846 9.104 9.388 64.286 100 > print(poisson_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qpois(cdf, 1, log = FALSE) 13.085 13.086 14.37438 13.37 13.654 61.157 100 > print(poisson_random) Unit: microseconds expr min lq mean median uq max neval random <- rpois(10000, 1) 303.219 314.8815 327.5787 324.552 341.335 373.477 100 > > n <- 50 > k <- seq(0,1,by=1/n) > f_pdf <- microbenchmark(pdf<-df(k, 10,20, log = FALSE)) > f_cdf <- microbenchmark(cdf<-pf(k, 10,20, log = FALSE)) > f_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,log = FALSE)) > f_random <- microbenchmark(random<-rf(10000, 10,20)) > print(f_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- df(k, 10, 20, log = FALSE) 10.241 10.81 12.43159 10.811 11.095 71.112 100 > print(f_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pf(k, 10, 20, log = FALSE) 22.472 22.757 25.66972 23.041 23.3265 86.189 100 > print(f_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qf(cdf, 10, 20, log = FALSE) 135.396 136.25 166.7057 157.7255 186.171 255.717 100 > print(f_random) Unit: milliseconds expr min lq mean median uq max neval random <- rf(10000, 10, 20) 1.801955 1.889706 1.947645 1.929528 1.98272 2.725546 100 > > n <- 50 > k <- seq(0,1,by=1/n) > chisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,log = FALSE)) > chisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2, log = FALSE)) > chisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2, log = FALSE)) > chisquare_random <- microbenchmark(random<-rchisq(10000, 2)) > print(chisquare_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dchisq(k, 2, log = FALSE) 5.974 6.259 7.06416 6.4015 6.544 52.339 100 > print(chisquare_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pchisq(k, 2, log = FALSE) 13.37 13.655 15.46392 13.655 13.94 99.841 100 > print(chisquare_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qchisq(cdf, 2, log = FALSE) 61.725 62.2945 68.40176 62.7215 72.25 132.553 100 > print(chisquare_random) Unit: milliseconds expr min lq mean median uq max neval random <- rchisq(10000, 2) 1.235059 1.29408 1.38993 1.333903 1.401743 2.205582 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nchisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,1, log = FALSE)) > nchisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2,1,log = FALSE)) > nchisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2,1, log = FALSE)) > nchisquare_random <- microbenchmark(random<-rchisq(10000, 2,1)) > print(nchisquare_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dchisq(k, 2, 1, log = FALSE) 14.223 14.509 17.3866 14.793 15.6455 37.548 100 > print(nchisquare_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pchisq(k, 2, 1, log = FALSE) 209.068 210.49 231.6357 223.1475 240.499 309.193 100 > print(nchisquare_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qchisq(cdf, 2, 1, log = FALSE) 10.34296 10.65955 10.90239 10.83733 11.02563 12.31558 100 > print(nchisquare_random) Unit: milliseconds expr min lq mean median uq max neval random <- rchisq(10000, 2, 1) 1.997653 2.073457 2.187417 2.114845 2.183111 3.134576 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nf_pdf <- microbenchmark(pdf<-df(k, 10,20,2, log = FALSE)) > nf_cdf <- microbenchmark(cdf<-pf(k, 10,20,2, log = FALSE)) > nf_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,2, log = FALSE)) > nf_random <- microbenchmark(random<-rf(10000, 10,20,2)) > print(nf_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- df(k, 10, 20, 2, log = FALSE) 28.446 30.153 34.12338 30.438 31.291 68.836 100 > print(nf_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pf(k, 10, 20, 2, log = FALSE) 46.935 61.8685 64.53899 63.433 65.708 106.953 100 > print(nf_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qf(cdf, 10, 20, 2, log = FALSE) 2.561991 2.640355 2.719223 2.68999 2.744461 3.737598 100 > print(nf_random) Unit: milliseconds expr min lq mean median uq max neval random <- rf(10000, 10, 20, 2) 2.912141 2.989225 3.100073 3.035163 3.110825 4.062433 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nbeta_pdf <- microbenchmark(pdf<-dbeta(k, 2,4,1, log = FALSE)) > nbeta_cdf <- microbenchmark(cdf<-pbeta(k, 2,4,1, log = FALSE)) > nbeta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2,4,1, log = FALSE)) > nbeta_random <- microbenchmark(random<-rbeta(10000, 2,4,1)) > print(nbeta_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dbeta(k, 2, 4, 1, log = FALSE) 26.739 27.308 31.31301 27.592 30.5795 56.891 100 > print(nbeta_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pbeta(k, 2, 4, 1, log = FALSE) 43.237 43.806 55.11814 56.321 57.7435 167.255 100 > print(nbeta_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qbeta(cdf, 2, 4, 1, log = FALSE) 2.290915 2.375111 2.440959 2.431146 2.49927 2.644764 100 > print(nbeta_random) Unit: milliseconds expr min lq mean median uq max neval random <- rbeta(10000, 2, 4, 1) 2.839893 3.002737 3.143906 3.073848 3.150932 4.302789 100 > > n <- 50 > k <- seq(0,n,by=1) > nbinom_pdf <- microbenchmark(pdf<-dnbinom(k, 2, 0.5, log = FALSE)) > nbinom_cdf <- microbenchmark(cdf<-pnbinom(k, 2, 0.5, log = FALSE)) > nbinom_quantile <- microbenchmark(quantile<-qnbinom(cdf, 2, 0.5, log = FALSE)) > nbinom_random <- microbenchmark(random<-rnbinom(10000, 2, 0.5)) > print(nbinom_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dnbinom(k, 2, 0.5, log = FALSE) 11.094 11.379 13.37031 11.664 11.948 78.508 100 > print(nbinom_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pnbinom(k, 2, 0.5, log = FALSE) 19.627 19.913 22.94469 20.197 20.482 130.277 100 > print(nbinom_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qnbinom(cdf, 2, 0.5, log = FALSE) 60.019 60.588 69.73866 61.442 74.099 122.028 100 > print(nbinom_random) Unit: milliseconds expr min lq mean median uq max neval random <- rnbinom(10000, 2, 0.5) 1.936498 2.029226 2.086237 2.072035 2.125084 2.354061 100 > > n <- 50 > k <- seq(0,1,by=1/n) > normal_pdf <- microbenchmark(pdf<-dnorm(k, 1, 1, log = FALSE)) > normal_cdf <- microbenchmark(cdf<-pnorm(k, 1, 1, log = FALSE)) > normal_quantile <- microbenchmark(quantile<-qnorm(cdf, 1,1, log = FALSE)) > normal_random <- microbenchmark(random<-rnorm(10000, 1,1)) > print(normal_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dnorm(k, 1, 1, log = FALSE) 4.267 4.552 5.7927 4.553 4.837 75.663 100 > print(normal_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pnorm(k, 1, 1, log = FALSE) 3.983 4.269 5.94911 4.553 4.979 50.632 100 > print(normal_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qnorm(cdf, 1, 1, log = FALSE) 2.277 2.561 3.42042 2.845 2.846 45.227 100 > print(normal_random) Unit: microseconds expr min lq mean median uq max neval random <- rnorm(10000, 1, 1) 696.321 728.747 779.1994 749.7965 778.3835 1541.12 100 > > n <- 50 > k <- seq(0,1,by=1/n) > lognormal_pdf <- microbenchmark(pdf<-dlnorm(k, 0.5,0.6, log = FALSE)) > lognormal_cdf <- microbenchmark(cdf<-plnorm(k, 0.5,0.6, log = FALSE)) > lognormal_quantile <- microbenchmark(quantile<-qlnorm(cdf, 0.5,0.6, log = FALSE)) > lognormal_random <- microbenchmark(random<-rlnorm(10000, 0.5,0.6)) > print(lognormal_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dlnorm(k, 0.5, 0.6, log = FALSE) 5.406 5.69 6.89638 5.975 6.259 50.917 100 > print(lognormal_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- plnorm(k, 0.5, 0.6, log = FALSE) 8.819 9.387 12.3463 9.3885 12.6595 71.681 100 > print(lognormal_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qlnorm(cdf, 0.5, 0.6, log = FALSE) 6.259 6.544 7.38277 6.544 6.828 58.881 100 > print(lognormal_random) Unit: milliseconds expr min lq mean median uq max neval random <- rlnorm(10000, 0.5, 0.6) 1.269761 1.329209 1.380386 1.362632 1.401743 2.247395 100 > > n <- 50 > k <- seq(0,1,by=1/n) > t_pdf <- microbenchmark(pdf<-dt(k, 8, log = FALSE)) > t_cdf <- microbenchmark(cdf<-pt(k, 8, log = FALSE)) > t_quantile <- microbenchmark(quantile<-qt(cdf, 8, log = FALSE)) > t_random <- microbenchmark(random<-rt(10000, 8)) > print(t_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dt(k, 8, log = FALSE) 11.663 12.233 15.71413 12.517 16.0725 76.517 100 > print(t_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pt(k, 8, log = FALSE) 19.059 20.6235 23.23485 21.05 21.619 127.717 100 > print(t_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qt(cdf, 8, log = FALSE) 58.596 58.882 64.84339 59.166 62.01 151.611 100 > print(t_random) Unit: milliseconds expr min lq mean median uq max neval random <- rt(10000, 8) 1.42592 1.480676 1.553132 1.51424 1.569565 2.44679 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nt_pdf <- microbenchmark(pdf<-dt(k, 10,1, log = FALSE)) > nt_cdf <- microbenchmark(cdf<-pt(k, 10,1, log = FALSE)) > nt_quantile <- microbenchmark(quantile<-qt(cdf, 10,1, log = FALSE)) > nt_random <- microbenchmark(random<-rt(10000, 10,1)) > print(nt_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dt(k, 10, 1, log = FALSE) 86.757 88.037 92.88671 89.317 91.4505 130.276 100 > print(nt_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pt(k, 10, 1, log = FALSE) 39.823 40.2505 44.51695 40.6765 49.352 70.829 100 > print(nt_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qt(cdf, 10, 1, log = FALSE) 1.930524 1.981866 2.038755 2.0224 2.079715 2.594987 100 > print(nt_random) Unit: milliseconds expr min lq mean median uq max neval random <- rt(10000, 10, 1) 1.69984 1.764693 1.867469 1.814044 1.893263 2.856959 100
Resultados de la ejecución del script TestStatBenchmark.mq5:
PP 0 13:06:15.252 TestStatBenchmark (EURUSD,H1)
KJ 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): pdf_mean=4.39, pdf_median=4.00, pdf_min=3.00, pdf_max=40.00, pdf_stddev=2.21, pdf_avgdev=0.95
MS 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): cdf_mean=13.65, cdf_median=12.00, cdf_min=11.00, cdf_max=54.00, cdf_stddev=4.09, cdf_avgdev=2.37
GF 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): quantile_mean=50.18, quantile_median=45.00, quantile_min=43.00, quantile_max=108.00, quantile_stddev=9.97, quantile_avgdev=7.41
QO 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): random_mean=318.73, random_median=312.00, random_min=284.00, random_max=478.00, random_stddev=28.74, random_avgdev=22.22
LP 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): pdf_mean=1.74, pdf_median=2.00, pdf_min=1.00, pdf_max=18.00, pdf_stddev=1.07, pdf_avgdev=0.53
EI 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): cdf_mean=4.76, cdf_median=4.00, cdf_min=3.00, cdf_max=68.00, cdf_stddev=3.07, cdf_avgdev=1.19
LM 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): quantile_mean=48.72, quantile_median=44.00, quantile_min=43.00, quantile_max=111.00, quantile_stddev=10.21, quantile_avgdev=6.96
QG 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): random_mean=688.81, random_median=680.00, random_min=625.00, random_max=976.00, random_stddev=43.92, random_avgdev=31.81
HE 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): pdf_mean=1.31, pdf_median=1.00, pdf_min=1.00, pdf_max=13.00, pdf_stddev=0.82, pdf_avgdev=0.47
GL 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): cdf_mean=8.09, cdf_median=7.00, cdf_min=7.00, cdf_max=92.00, cdf_stddev=3.67, cdf_avgdev=1.40
CF 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): quantile_mean=50.83, quantile_median=46.00, quantile_min=45.00, quantile_max=106.00, quantile_stddev=9.27, quantile_avgdev=6.72
GR 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): random_mean=142.84, random_median=132.00, random_min=128.00, random_max=260.00, random_stddev=19.73, random_avgdev=15.32
QD 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): pdf_mean=0.45, pdf_median=0.00, pdf_min=0.00, pdf_max=11.00, pdf_stddev=0.85, pdf_avgdev=0.54
QK 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): cdf_mean=1.33, cdf_median=1.00, cdf_min=1.00, cdf_max=12.00, cdf_stddev=0.81, cdf_avgdev=0.48
MR 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): quantile_mean=1.37, quantile_median=1.00, quantile_min=1.00, quantile_max=14.00, quantile_stddev=0.89, quantile_avgdev=0.51
IK 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): random_mean=224.19, random_median=215.00, random_min=200.00, random_max=352.00, random_stddev=26.86, random_avgdev=20.34
PQ 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): pdf_mean=0.85, pdf_median=1.00, pdf_min=0.00, pdf_max=18.00, pdf_stddev=1.40, pdf_avgdev=0.54
GK 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): cdf_mean=0.77, cdf_median=1.00, cdf_min=0.00, cdf_max=16.00, cdf_stddev=0.94, cdf_avgdev=0.47
HE 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): quantile_mean=0.53, quantile_median=0.00, quantile_min=0.00, quantile_max=10.00, quantile_stddev=0.78, quantile_avgdev=0.54
HL 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): random_mean=143.18, random_median=130.00, random_min=128.00, random_max=272.00, random_stddev=21.58, random_avgdev=16.98
LK 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): pdf_mean=0.42, pdf_median=0.00, pdf_min=0.00, pdf_max=12.00, pdf_stddev=0.82, pdf_avgdev=0.52
CE 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): cdf_mean=0.45, cdf_median=0.00, cdf_min=0.00, cdf_max=16.00, cdf_stddev=0.96, cdf_avgdev=0.55
LO 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): quantile_mean=0.18, quantile_median=0.00, quantile_min=0.00, quantile_max=1.00, quantile_stddev=0.38, quantile_avgdev=0.29
GE 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): random_mean=40.30, random_median=36.00, random_min=35.00, random_max=83.00, random_stddev=7.61, random_avgdev=5.41
OP 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): pdf_mean=2.30, pdf_median=2.00, pdf_min=1.00, pdf_max=14.00, pdf_stddev=1.30, pdf_avgdev=0.52
DK 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): cdf_mean=2.12, cdf_median=2.00, cdf_min=1.00, cdf_max=18.00, cdf_stddev=1.69, cdf_avgdev=0.53
NE 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): quantile_mean=0.81, quantile_median=1.00, quantile_min=0.00, quantile_max=10.00, quantile_stddev=0.68, quantile_avgdev=0.39
IL 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): random_mean=278.00, random_median=271.00, random_min=251.00, random_max=429.00, random_stddev=28.23, random_avgdev=21.62
PG 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): pdf_mean=1.85, pdf_median=2.00, pdf_min=1.00, pdf_max=15.00, pdf_stddev=1.07, pdf_avgdev=0.48
CM 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): cdf_mean=0.90, cdf_median=1.00, cdf_min=0.00, cdf_max=17.00, cdf_stddev=0.85, cdf_avgdev=0.32
NP 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): quantile_mean=0.75, quantile_median=1.00, quantile_min=0.00, quantile_max=12.00, quantile_stddev=0.96, quantile_avgdev=0.48
FE 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): random_mean=302.55, random_median=295.00, random_min=272.00, random_max=466.00, random_stddev=30.20, random_avgdev=22.99
ML 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): pdf_mean=1.27, pdf_median=1.00, pdf_min=0.00, pdf_max=91.00, pdf_stddev=3.04, pdf_avgdev=0.56
DR 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): cdf_mean=1.11, cdf_median=1.00, cdf_min=0.00, cdf_max=17.00, cdf_stddev=1.34, cdf_avgdev=0.40
IH 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): quantile_mean=0.71, quantile_median=1.00, quantile_min=0.00, quantile_max=12.00, quantile_stddev=0.79, quantile_avgdev=0.47
GL 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): random_mean=178.65, random_median=164.00, random_min=162.00, random_max=309.00, random_stddev=24.09, random_avgdev=17.94
MJ 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): pdf_mean=2.99, pdf_median=3.00, pdf_min=2.00, pdf_max=17.00, pdf_stddev=1.63, pdf_avgdev=0.57
GD 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): cdf_mean=2.74, cdf_median=3.00, cdf_min=2.00, cdf_max=19.00, cdf_stddev=1.23, cdf_avgdev=0.58
FO 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): quantile_mean=2.64, quantile_median=2.00, quantile_min=2.00, quantile_max=19.00, quantile_stddev=1.64, quantile_avgdev=0.76
DJ 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): random_mean=536.37, random_median=526.00, random_min=483.00, random_max=759.00, random_stddev=46.99, random_avgdev=34.40
HR 0 13:06:18.485 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): pdf_mean=2.91, pdf_median=3.00, pdf_min=2.00, pdf_max=15.00, pdf_stddev=1.40, pdf_avgdev=0.58
IL 0 13:06:18.486 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): cdf_mean=6.26, cdf_median=6.00, cdf_min=5.00, cdf_max=23.00, cdf_stddev=2.38, cdf_avgdev=1.07
HE 0 13:06:18.486 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): quantile_mean=3.43, quantile_median=3.00, quantile_min=2.00, quantile_max=20.00, quantile_stddev=1.48, quantile_avgdev=0.68
DL 0 13:06:18.486 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): random_mean=153.59, random_median=144.00, random_min=138.00, random_max=265.00, random_stddev=18.57, random_avgdev=13.99
IH 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): pdf_mean=3.86, pdf_median=4.00, pdf_min=3.00, pdf_max=21.00, pdf_stddev=1.78, pdf_avgdev=0.76
GS 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): cdf_mean=9.94, cdf_median=9.00, cdf_min=7.00, cdf_max=36.00, cdf_stddev=3.82, cdf_avgdev=2.15
OI 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): quantile_mean=65.47, quantile_median=59.00, quantile_min=57.00, quantile_max=147.00, quantile_stddev=12.99, quantile_avgdev=9.64
DE 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): random_mean=1249.22, random_median=1213.00, random_min=1127.00, random_max=1968.00, random_stddev=117.69, random_avgdev=72.17
EL 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): pdf_mean=2.47, pdf_median=2.00, pdf_min=2.00, pdf_max=13.00, pdf_stddev=1.32, pdf_avgdev=0.65
JK 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): cdf_mean=7.71, cdf_median=7.00, cdf_min=7.00, cdf_max=23.00, cdf_stddev=1.91, cdf_avgdev=0.88
KQ 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): quantile_mean=44.11, quantile_median=41.00, quantile_min=40.00, quantile_max=120.00, quantile_stddev=8.17, quantile_avgdev=5.38
CL 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): random_mean=210.24, random_median=196.00, random_min=190.00, random_max=437.00, random_stddev=29.14, random_avgdev=21.00
HD 0 13:06:21.098 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): pdf_mean=8.05, pdf_median=8.00, pdf_min=7.00, pdf_max=24.00, pdf_stddev=2.41, pdf_avgdev=1.09
MR 0 13:06:21.098 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): cdf_mean=45.61, cdf_median=42.00, cdf_min=41.00, cdf_max=97.00, cdf_stddev=8.25, cdf_avgdev=5.70
FN 0 13:06:21.098 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): quantile_mean=220.66, quantile_median=211.50, quantile_min=196.00, quantile_max=362.00, quantile_stddev=24.71, quantile_avgdev=19.45
LI 0 13:06:21.099 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): random_mean=744.45, random_median=728.00, random_min=672.00, random_max=1082.00, random_stddev=62.42, random_avgdev=43.24
RE 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): pdf_mean=19.10, pdf_median=18.00, pdf_min=16.00, pdf_max=50.00, pdf_stddev=4.67, pdf_avgdev=2.64
FS 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): cdf_mean=14.67, cdf_median=13.00, cdf_min=12.00, cdf_max=39.00, cdf_stddev=3.94, cdf_avgdev=2.44
EN 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): quantile_mean=212.21, quantile_median=203.00, quantile_min=189.00, quantile_max=347.00, quantile_stddev=24.37, quantile_avgdev=19.30
EF 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): random_mean=1848.90, random_median=1819.00, random_min=1704.00, random_max=2556.00, random_stddev=118.75, random_avgdev=78.66
EN 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): pdf_mean=16.30, pdf_median=15.00, pdf_min=14.00, pdf_max=43.00, pdf_stddev=4.32, pdf_avgdev=2.43
EP 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): cdf_mean=10.48, cdf_median=10.00, cdf_min=8.00, cdf_max=32.00, cdf_stddev=3.02, cdf_avgdev=1.72
ME 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): quantile_mean=153.66, quantile_median=141.00, quantile_min=135.00, quantile_max=283.00, quantile_stddev=20.83, quantile_avgdev=16.16
QJ 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): random_mean=2686.82, random_median=2649.00, random_min=2457.00, random_max=3753.00, random_stddev=150.32, random_avgdev=98.23
OO 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): pdf_mean=6.13, pdf_median=6.00, pdf_min=5.00, pdf_max=24.00, pdf_stddev=2.38, pdf_avgdev=1.22
DG 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): cdf_mean=12.21, cdf_median=11.00, cdf_min=11.00, cdf_max=33.00, cdf_stddev=3.07, cdf_avgdev=1.58
LJ 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): quantile_mean=14.05, quantile_median=13.00, quantile_min=12.00, quantile_max=82.00, quantile_stddev=4.81, quantile_avgdev=2.28
EM 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): random_mean=1130.39, random_median=1108.00, random_min=1039.00, random_max=1454.00, random_stddev=69.41, random_avgdev=51.70
GP 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): pdf_mean=1.15, pdf_median=1.00, pdf_min=0.00, pdf_max=19.00, pdf_stddev=1.34, pdf_avgdev=0.45
OI 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): cdf_mean=0.81, cdf_median=1.00, cdf_min=0.00, cdf_max=17.00, cdf_stddev=1.16, cdf_avgdev=0.49
CN 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): quantile_mean=0.70, quantile_median=1.00, quantile_min=0.00, quantile_max=13.00, quantile_stddev=0.82, quantile_avgdev=0.49
EG 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): random_mean=293.70, random_median=281.00, random_min=256.00, random_max=537.00, random_stddev=43.28, random_avgdev=31.62
FD 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): pdf_mean=1.99, pdf_median=2.00, pdf_min=1.00, pdf_max=18.00, pdf_stddev=1.48, pdf_avgdev=0.48
PN 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): cdf_mean=3.19, cdf_median=3.00, cdf_min=2.00, cdf_max=17.00, cdf_stddev=1.61, cdf_avgdev=0.64
DH 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): quantile_mean=3.18, quantile_median=3.00, quantile_min=2.00, quantile_max=19.00, quantile_stddev=1.77, quantile_avgdev=0.64
NR 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): random_mean=479.75, random_median=468.00, random_min=428.00, random_max=754.00, random_stddev=48.26, random_avgdev=34.30
FL 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): pdf_mean=2.32, pdf_median=2.00, pdf_min=1.00, pdf_max=15.00, pdf_stddev=1.29, pdf_avgdev=0.54
QE 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): cdf_mean=8.01, cdf_median=7.00, cdf_min=6.00, cdf_max=39.00, cdf_stddev=3.13, cdf_avgdev=1.73
MM 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): quantile_mean=50.23, quantile_median=45.00, quantile_min=44.00, quantile_max=113.00, quantile_stddev=10.28, quantile_avgdev=7.73
KG 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): random_mean=951.58, random_median=931.00, random_min=859.00, random_max=1439.00, random_stddev=78.14, random_avgdev=49.72
CQ 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): pdf_mean=38.47, pdf_median=35.00, pdf_min=32.00, pdf_max=164.00, pdf_stddev=9.66, pdf_avgdev=6.38
OO 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): cdf_mean=27.75, cdf_median=25.00, cdf_min=24.00, cdf_max=80.00, cdf_stddev=7.02, cdf_avgdev=4.63
PF 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): quantile_mean=1339.51, quantile_median=1306.00, quantile_min=1206.00, quantile_max=2262.00, quantile_stddev=128.18, quantile_avgdev=74.83
OR 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): random_mean=1550.27, random_median=1520.00, random_min=1418.00, random_max=2317.00, random_stddev=112.08, random_avgdev=73.74
LQ 0 13:06:31.979 TestStatBenchmark (EURUSD,H1)
GH 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) 21 of 21 passed
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/2742
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
 Interfaces gráficas X: Actualizaciones para la librería Easy And Fast (build 3)
Interfaces gráficas X: Actualizaciones para la librería Easy And Fast (build 3)
 Comparando MQL5 y QLUA - ¿Por qué las operaciones comerciales en MQL5 son hasta 28 veces más rápidas?
Comparando MQL5 y QLUA - ¿Por qué las operaciones comerciales en MQL5 son hasta 28 veces más rápidas?
 Interfaces gráficas X: Control "Gráfico estándar" (build 4)
Interfaces gráficas X: Control "Gráfico estándar" (build 4)
 Valoración rápida de señales: actividad comercial, gráficos de reducción/carga y distribuciones MFE/MAE
Valoración rápida de señales: actividad comercial, gráficos de reducción/carga y distribuciones MFE/MAE
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Fórmula en Documentación:
Es el análogo en Wikipedia:
Mirado el código.
La función MathRandomNoncentralBeta() tiene líneas como esta:
La misma Wikipedia tiene esto:
The noncentral beta distribution (Type I) is the distribution of the ratio
donde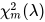 es unavariable aleatoria chi-cuadrado no centralcon grados de libertad m y parámetro de no centralidad 𝜆 , y 𝜒 𝑛 2 es unavariable aleatoria chi-cuadrado centralcon grados de libertad n , independiente de 𝜒 𝑚 2 ( 𝜆 ) .
es unavariable aleatoria chi-cuadrado no centralcon grados de libertad m y parámetro de no centralidad 𝜆 , y 𝜒 𝑛 2 es unavariable aleatoria chi-cuadrado centralcon grados de libertad n , independiente de 𝜒 𝑚 2 ( 𝜆 ) .
Es decir, se toman dos variables aleatorias, donde la primera es de una distribución chi-cuadrado no central y la segunda es de una central. Probablemente el código pueda corregirse en este sentido:
Los gráficos modificados del ejemplo serán los siguientes.
Estos son los resultados.
Tampoco son muy buenos... En general, trabajar con una distribución beta no central pertenece más bien a la clase de tareas no triviales. Nos las arreglamos para ver Boost desde el código fuente abierto. Y será más complicado que el que tenemos ahora en SB.
La misma Wikipedia lo tiene:
Es decir, se toman dos variables aleatorias, donde la primera es de una distribución chi-cuadrado no central y la segunda es de una distribución central. Probablemente el código se pueda corregir a esto:
Los gráficos modificados del ejemplo serán los siguientes.
Gracias, tienes razón, hay que calcular a través de esta fórmula, sin embargo había otro error, el parámetro de no centralidad lambda debería ser sin multiplicador 2.
Script de prueba:
Resultado:
También he comprobado la función CFD para la distribución beta no central.
Algunos resultados cuestionables:
Fuentes alternativas utilizan el algoritmo ASA310:
Por ejemplo algunos de los resultados en Wolfram Mathematica:
Que es más o menos similar a la verdad...