Pon "Me gusta" y sigue las noticias
Deje un enlace a él, ¡qué los demás también lo valoren!
Evalúe su trabajo en el terminal MetaTrader 5
- Publicado por:
- MetaQuotes
- Visualizaciones:
- 2497
- Ranking:
- Publicado:
- Actualizado:
-
¿Necesita un robot o indicador basado en este código? Solicítelo en la bolsa freelance Pasar a la bolsa
Autor real
Dmitry Kalyuzhny. Página del proyecto FuzzyNet - http://sourceforge.net/projects/fuzzynet/
Para que funcione, es necesario el archivo en la carpeta catálogo_de_datos_del_terminal.
Los códigos de la biblioteca se colocan en la carpeta: <catálogo_de_datos_del_terminal>\MQL5\Include\Math\FuzzyNet\
Es posible encontrar ejemplos de scripts de prueba en la carpeta: <catálogo_de_datos_del_terminal>\MQL5\Scripts\FuzzyNet\
FuzzyNet es una de la bibliotecas matemáticas más populares para crear modelos difusos
Fuzzy Logic Library Microsoft.Net (FuzzyNet) es una biblioteca de lógica difusa fácil de usar, en la que están implementados los sistemas de deducción de lógica difusa Mamdani y Sugeno.
FuzzyNet incluye:
- 5 funciones de pertenencia.
- Forma flexible de escritura de normas para los sistemas difusos.
- Sistema de deducción de lógica difusa Mamdani.
- Sistema de deducción de lógica difusa Sugeno.
- 1 método de defusificación para los sistemas del tipo Mamdani.
- Cantidad ilimitada de variables de entrada y salida.
Al pasar la biblioteca a MQL5 se ha añadido a la biblioteca de manera adicional:
- 8 nuevas funciones de pertenencia.
- 4 nuevos métodos de defusificación para los sistemas del tipo Mamdani.
Orden de trabajo con la biblioteca
- Dependiendo de la tarea a resolver, se crea un sistema difuso vacío del tipo Mamdani o Sugeno.
- A continuación, creamos las variables de entrada y salida difusas.
- A cada variable difusa se le añaden sus términos. Antes de ello, al término se le asigna un nombre y una función de pertenencia de término a su variable difusa.
- Las variables se añaden al sistema.
- Se crea una base de normas.
- Las normas se añaden al sistema.
- Se envían al sistema los datos de entrada.
- Se llama a la función de cálculo del sistema.
Advertencia: Es posible producir los ajustes del sistema de deducción lógica del tipo Mamdani en cualquier etapa después de su creación y hasta la llamada de la función de cálculo del sistema. Si después de crear el sistema sus parámetros no han cambiado, entonces el sistema funcionará con los parámetros por defecto. Que serían, precisamente:
- Implicación material, sucederá utilizando el operador Min, es decir, la abreviatura de la multiplicidad deductiva difusa.
- Agregación, sucederá utilizando el operador Max, es decir, obteniendo los valores máximos de las funciones deductivas de pertenencia, obtenidas después de la implicación material.
- La defusificación tendrá lugar según el método del centro de gravedad.
Aquí presentamos la conversión de la biblioteca FuzzyNet de la versión 1.2.0.
Para trabajar con con la biblioteca, es imprescindible conectar los archivos MamdaniFuzzySystem.mqh o SugenoFuzzySystem.mqh, dependiendo del sistema creado.
Más información sobre los paquetes de la biblioteca portada FuzzyNet:| Paquetes |
Descripción |
|---|---|
| Dictionary.mqh |
El paquete incluye las clases auxiliares necesarias para otros paquetes. |
| FuzzyRule.mqh |
Clases para la creación de normas difusas:
El paquete también contiene las clases auxiliares para la implementación de las normas difusas. |
| FuzzyTerm.mqh | Paquete para la creación de términos difusos. |
| FuzzyVariable.mqh | Paquete para la creación de variables difusas |
| GenericFuzzySystem.mqh | Clase que realiza la parte funcional general para los sistemas Mamdani y Sugeno. |
| Helper.mqh | El paquete incluye las clases auxiliares necesarias para otros paquetes. |
| InferenceMethod.mqh | El paquete incluye las clases auxiliares necesarias para otros paquetes. |
| MamdaniFuzzySystem.mqh | Clase para la creación de un sistema difuso del tipo Mamdani. |
| MembershipFunction.mqh | Clases de las funciones de pertenencia:
|
| RuleParser.mqh | Clase para el análisis de normas difusas. |
| SugenoFuzzySystem.mqh | Clase para la creación de un sistema difuso del tipo Sugeno. |
| SugenoVariable.mqh | El paquete contiene las clases:
Las variables difusas del tipo Sugeno se usan al escribir las normas para un sistema del tipo Sugeno. |
Régimen de trabajo con la biblioteca FuzzyNet en MQL5
Antes de escribir un sistema difuso, es necesario presentarlo de forma detallada. Que serían, precisamente:
- Cantidad de valores de entrada y salida que se presentarán mediante variables difusas.
- Cantidad de términos y sus funciones de pertenencia para cada variable difusa.
- Elegir el tipo de sistema difuso, dependiendo de la tarea a resolver.
- Cantidad y contenido de las normas difusas correspondientes al sistema elegido.
- Parámetros individuales y peculiaridades del sistema.
Proceso de creación del sistema y su cálculo:
- Crear un sistema vacío.
Para el sistema del tipo Mamdani:
MamdaniFuzzySystem *fuzzy_system=new MamdaniFuzzySystem();
Para el sistema del tipo Sugeno:SugenoFuzzySystem *fuzzy_system=new SugenoFuzzySystem();
- Separadamente del sistema se crean todos los parámetros difusos de entrada, estableciendo para ellos en calidad de parámetros el nombre de la variable, sus valores máximo y mínimo:
FuzzyVariable *fuzzy_variable=new FuzzyVariable(const string name,const double min,const double max);
- Crear las funciones de los términos difusos, crear los propios términos difusos, como parámetros se les transmiten sus nombres y funciones de pertenencia, después se añaden estos términos a las variables correspondientes. Para reducir el código de programación, este proceso se puede describir de esta forma:
fuzzy_variable.Terms().Add(new FuzzyTerm(const string name,new IMembershipFunction());
- A continuación se introducen los parámetros de entrada en el sistema:
fuzzy_system.Input().Add(FuzzyVariable fuzzy_variable);
- Creamos las variables de entrada. Al crearlas, es importante prestar atención al tipo que tiene el sistema de usted. Para los sistemas del tipo Mamdani, su proceso de creación es idéntico a los puntos 2 y 3. En el caso de los modelos del tipo Sugeno, es necesario crear variables difusas especiales. Como parámetros, adoptan solo el nombre de la variable:
SugenoVariable *sugeno_variable=new SugenoVariable(const string name);
En lugar de los términos difusos, a la variable difusa del tipo Sugeno se añaden funciones lineales que interpretan la combinación lineal de los valores de entrada. Los parámetros de la función lineal serán su nombre y la matriz de los coeficientes. En base a esta matriz se creará una ecuación lineal, por eso es importante respetar el orden de los elementos en la matriz. La longitud de la matriz de los coeficientes deberá ser igual o superior en una unidad a la cantidad de valores de entrada. Si las longitudes son iguales, entonces el miembro libre de la ecuación será igual a cero. Si la longitud de la matriz es superior en una unidad, entonces el miembro libre será igual al valor del último elemento. A todos los demás elementos de la matriz, comenzando por el primero, se les da de la forma correspondiente una variable de entrada difusa, de acuerdo con el orden en el que se introdujeron en el sistema.sugeno_varriable.Functions().Add(fuzzy_sytem.CreateSugenoFunction(const string name, const double &coeffs[]));
- Por analogía con el punto 4, los valores de entrada deben ser igualmente añadidos al sistema:
Para el sistema del tipo Mamdani:
fuzzy_system.Output().Add(FuzzyVariable fuzzy_variable);
Para el sistema del tipo Sugeno:
fuzzy_system.Output().Add(FuzzyVariable fuzzy_variable);
- De acuerdo con el sistema, confeccionamos una base de normas. Las normas se establecen en forma de línea corriente, y se analizan de forma automática a partir de palabras clave. Las palabras clave son: "if", "then", "is", "and", "or", "not", "(" , ")", "slightly", "somewhat", "very", "extremely", así como todos los nombres de las variables, términos y funciones que estén en su sistema.
Para el sistema del tipo Mamdani:
MamdaniFuzzyRule *fuzzy_rule = fuzzy_system.ParseRule(const string rule_text);
Para el sistema del tipo Sugeno:
SugenoFuzzyRule *fuzzy_rule = fuzzy_system.ParseRule(const string rule_text);
- Introducir todas las normas en el sistema:
Para el sistema del tipo Mamdani:
fuzzy_system.Rules().Add(MamdaniFuzzyRule fuzzy_rule);
Para el sistema del tipo Sugeno:
fuzzy_system.Rules().Add(SugenoFuzzyRule fuzzy_rule);
- Suministrar al sistema los valores de entrada de las variables para el cálculo. Para ello es imprescindible formular. En su entrada, el sistema recibe la lista de valores, uno de cuyos elementos será un objeto de la clase Dictionary_Obj_Double. Esta clase está descrita en el archivo Dictionary.mqh.
Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double;
Esta clase realiza en sí mismo el método SetAll(CObject *key, const double value), que adopta dos parámetros: una variable difusa y un valor numérico. Este elemento es el que supone el valor de entrada del sistema.p_od_in.SetAll(FuzzyVariable fuzzy_variable,const double value);
Según esta misma tecnología, rellenamos el resto de los valores de entrada. Creamos una lista y los introducimos todos en ella:CList *in=new CList; in.Add(p_od_in);
- Asimismo, establecemos los valores de entrada:
Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double; CList *out=new CList;
- Llamamos a la función Calculate(CList *&list) para nuestro sistema, esta nos devolverá la lista de resultados de los cálculos del sistema:
out=fuzzy_system.Calculate(in);
Después de esto, en la lista out se guardarán todos los valores de salida calculados en el mismo orden en el que se introdujeron en el sistema. Lo único que nos queda es obtener estos valores:p_od_out=out.GetNodeAtIndex(int index); double result=p_od_out.Value();
Ahora, en la varible result se guardará el resultado del cálculo del sistema para el valor de entrada introducido en el sistema, con el número que se haya indicado en index.
Tips Sample (Mamdani)
El script de prueba Tips_Sample_Mamdani.mq5 calcula el tanto por ciento de propina que hay que dejar en un establecimiento, partiendo de la calidad del servicio y la comida.
Introducimos los parámetros de entrada:
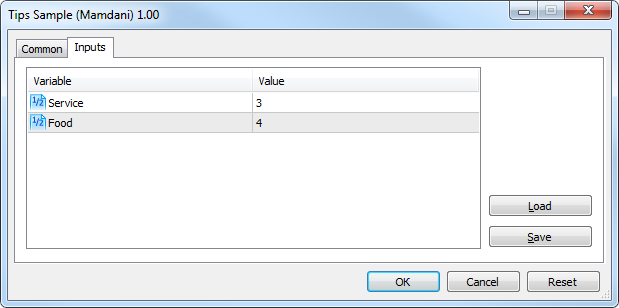
El resultado del cálculo será:
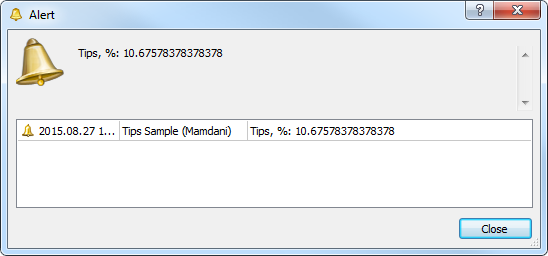
Cruise Control Sample (Sugeno)
El script de prueba Cruise_Control_Sample_Sugeno.mq5 es un ejemplo de un regulador difuso. Representa el sistema de cruise-control de un automóvil que calcula la aceleración necesaria para el automóvil, para que este salga a la velocidad establecida, apoyándose en los datos sobre la desviación y velocidad actual de cambio de esta desviación.
Introducimos los parámetros de entrada:
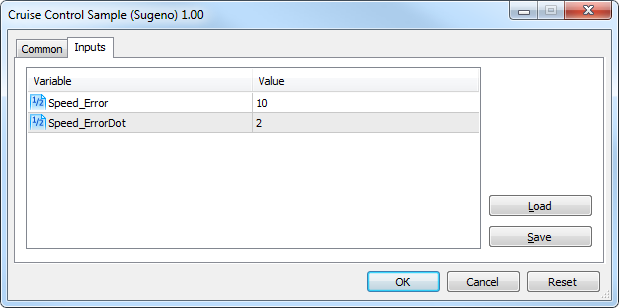
El resultado del cálculo será:
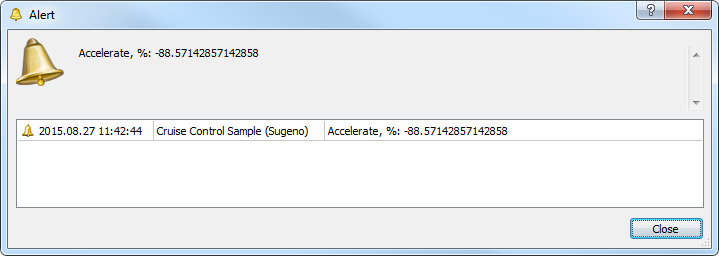
Traducción del ruso realizada por MetaQuotes Ltd
Artículo original: https://www.mql5.com/ru/code/13697
 ColorSchaffMomentumTrendCycle_HTF
ColorSchaffMomentumTrendCycle_HTF
Indicador ColorSchaffMomentumTrendCycle con posibilidad de cambiar el marco temporal del indicador en los parámetros de entrada.
 ColorSchaffMFITrendCycle_HTF
ColorSchaffMFITrendCycle_HTF
Indicador ColorSchaffMFITrendCycle con posibilidad de cambiar el marco temporal del indicador en los parámetros de entrada.
 ColorSchaffRSITrendCycle_HTF
ColorSchaffRSITrendCycle_HTF
Indicador ColorSchaffRSITrendCycle con posibilidad de cambiar el marco temporal del indicador en los parámetros de entrada.
 ColorSchaffRVITrendCycle_HTF
ColorSchaffRVITrendCycle_HTF
Indicador ColorSchaffRVITrendCycle con posibilidad de cambiar el marco temporal del indicador en los parámetros de entrada.
