
Utilizar Mapas con Función de Auto-Organización (Mapas Kohonen) en MetaTrader 5
Introducción
Un Mapa con Función de Auto-Organización (SOM, por sus siglas en inglés) es un tipo de red neuronal artificial que se forma usando aprendizaje no supervisado para producir una representacion discretizada bidimensional del espacio de entrada de las muestras de formación, llamada mapa.
Estos mapas son útiles para la clasificación y muestra de visualizaciones de baja dimensión de datos de alta dimensión, similar al ajuste multidimensional. El modelo se describió por primera vez como una red neuronal artificial por el profesor finlandés Teuvo Kohonen, y en ocasiones se conoce como Mapa Kohonen.
Hay muchos algoritmos disponibles. Nosotros seguiremos el código presentado en http://www.ai-junkie.com. Para visualizar los datos en el Terminal de Cliente MetaTrader 5, usaremos cIntBMP E- una biblioteca de imágenes BMP. En este artículo consideraremos varias aplicaciones sencillas de los mapas Kohonen.
1. Mapas con Función de Auto-Organización
Los Mapas con Función de Auto-Organización se describieron por primera vez por Teuvo Kohonen en 1982. En contraste con otras redes neuronales, no necesita una correspondencia exacta entre los datos objetivo de entrada y salida. Esta red neuronal se forma usando aprendizaje no supervisado.
El SOM se puede describir formalmente como mapas no lineales, ordenados y suavizados de datos de entrada de alta dimensión en los elementos de un array regular, de dimensión baja. En su forma más básica, produce un mapa de similitud de datos de entrada.
El SOM convierte las relaciones estadísticas no lineales entre datos de dimensión alta en relaciones geométricas simples de sus puntos de imagen en una cuadrícula de nodos regular bidimensional. Los mapas SOM se pueden usar para la clasificación y visualización de datos de alta dimensión.
1.1. Arquitectura de Red
Puede ver un mapa Kohonen simple como una cuadrícula de 16 nodos (4x4 cada uno de ellos conectado con un vector de entrada tridimensional) en la Fig. 1.
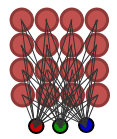
Figura 1. Mapa Kohonen simple (16 nodos)
Cada nodo tiene coordenadas (x,y) en enrejado y vector de pesos con componentes definidos en base al vector de entrada.
1.2. Algoritmo de Aprendizaje
A diferencia de muchas otras redes neuronales, el SOM no necesita una salida objetivo especificada. En lugar de ello, el área del enrejado donde los pesos de nodo coinciden con el vector de entrada se optimiza selectivamente para parecerse más a los datos para la clase de la que el vector de entrada es miembro.
Para una distribución inicial de pesos aleatorios, y por con muchas iteraciones, el SOM eventualmente llega a ser un mapa de zonas estables. Cada zona es una herramienta clasificadora, de modo que puede considerar la salida de datos gráfica como un tipo de herramienta de mapa del espacio de entrada.
La formación se da en varios pasos y con muchas iteraciones:
- Los pesos de cada nodo se inicializan con valores aleatorios.
- Un vector se elige de forma aleatoria del conjunto de datos de formación.
- Cada nodo se examina para calcular los pesos de cuál de ellos tienen más similitudes con el vector de entrada. El nodo ganador se conoce comúnmente como la Unidad de Mayor Coincidencia, o Best Matching Unit (BMU).
- Se calcula el radio de la sección del BMU. Inicialmente, este valor se configura al radio del enrejado, pero se reduce con cada paso.
- Para cualquier nodo que se encuentre dentro del radio del BMU, los pesos del nodo se ajustan para hacerlos más similares al vector de entrada. Cuanto más cercano esté un nodo al BMU, más alertas recibirán sus pesos.
- Repita el paso 2 para N iteraciones.
Los detalles se pueden encontrar en http://www.ai-junkie.com.
2. Estudios de casos
2.1. Ejemplo 1. "Hello World!" en SOM
El ejemplo clásico de un mapa Kohonen es un problema de agrupación de colores.
Supongamos que tenemos un conjunto de 8 colores, y cada uno de ellos se representa como un vector tridimensional en un modelo de colores RGB.
-
 Rojo: (255,0,0);
Rojo: (255,0,0);  Verde: (0,128,0);
Verde: (0,128,0); Azul: (0,0,255);
Azul: (0,0,255); Verde Oscuro: (0,100,0);
Verde Oscuro: (0,100,0); Azul Oscuro: (0,0,139);
Azul Oscuro: (0,0,139); Amarillo: (255,255,0);
Amarillo: (255,255,0); Naranja: (255,165,0);
Naranja: (255,165,0); Morado: (128,0,128).
Morado: (128,0,128).
Al trabajar con mapas Kohonen en el lenguaje MQL5, seguiremos el paradigma de orientación al objeto.
Necesitaremos dos clases: la clase CSOMNode para un nodo de cuadrícula regulas, y la clase CSOM, que es una clase de red neuronal.
//+------------------------------------------------------------------+ //| CSOMNode class | //+------------------------------------------------------------------+ class CSOMNode { protected: int m_x1; int m_y1; int m_x2; int m_y2; double m_x; double m_y; double m_weights[]; public: //--- class constructor CSOMNode(); //--- class destructor ~CSOMNode(); //--- node initialization void InitNode(int x1,int y1,int x2,int y2); //--- return coordinates of the node's center double X() const { return(m_x);} double Y() const { return(m_y);} //--- returns the node coordinates void GetCoordinates(int &x1,int &y1,int &x2,int &y2); //--- returns the value of weight_index component of weight's vector double GetWeight(int weight_index); //--- returns the squared distance between the node weights and specified vector double CalculateDistance(double &vector[]); //--- adjust weights of the node void AdjustWeights(double &vector[],double learning_rate,double influence); };
La implementación de métodos de clase se pueden encontrar en som_ex1.mq5. El código tiene muchos comentarios, nos centraremos en la idea.
La descripción de la clase CSOM tiene el siguiente aspecto:
//+------------------------------------------------------------------+ //| CSOM class | //+------------------------------------------------------------------+ class CSOM { protected: //--- class for using of bmp images cIntBMP m_bmp; //--- grid mode int m_gridmode; //--- bmp image size int m_xsize; int m_ysize; //--- number of nodes int m_xcells; int m_ycells; //--- array with nodes CSOMNode m_som_nodes[]; //--- total items in training set int m_total_training_sets; //--- training set array double m_training_sets_array[]; protected: //--- radius of the neighbourhood (used for training) double m_map_radius; //--- time constant (used for training) double m_time_constant; //--- initial learning rate (used for training) double m_initial_learning_rate; //--- iterations (used for training) int m_iterations; public: //--- class constructor CSOM(); //--- class destructor ~CSOM(); //--- net initialization void InitParameters(int iterations,int xcells,int ycells,int bmpwidth,int bmpheight); //--- finds the best matching node, closest to the specified vector int BestMatchingNode(double &vector[]); //--- train method void Train(); //--- render method void Render(); //--- shows the bmp image on the chart void ShowBMP(bool back); //--- adds a vector to training set void AddVectorToTrainingSet(double &vector[]); //--- shows the pattern title void ShowPattern(double c1,double c2,double c3,string name); //--- adds a pattern to training set void AddTrainPattern(double c1,double c2,double c3); //--- returns the RGB components of the color void ColToRGB(int col,int &r,int &g,int &b); //--- returns the color by RGB components int RGB256(int r,int g,int b) const {return(r+256*g+65536*b); } //--- deletes image from the chart void NetDeinit(); };
El uso de la clase CSOM es simple:
CSOM KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ void OnInit() { MathSrand(200); //--- initialize net, 10000 iterations will be used for training //--- the net contains 15x20 nodes, bmp image size 400x400 KohonenMap.InitParameters(10000,15,20,400,400); //-- add RGB-components of each color from training set KohonenMap.AddTrainPattern(255, 0, 0); // Red KohonenMap.AddTrainPattern( 0,128, 0); // Green KohonenMap.AddTrainPattern( 0, 0,255); // Blue KohonenMap.AddTrainPattern( 0,100, 0); // Dark green KohonenMap.AddTrainPattern( 0, 0,139); // Dark blue KohonenMap.AddTrainPattern(255,255, 0); // Yellow KohonenMap.AddTrainPattern(255,165, 0); // Orange KohonenMap.AddTrainPattern(128, 0,128); // Purple //--- train net KohonenMap.Train(); //--- render map to bmp KohonenMap.Render(); //--- show patterns and titles for each color KohonenMap.ShowPattern(255, 0, 0,"Red"); KohonenMap.ShowPattern( 0,128, 0,"Green"); KohonenMap.ShowPattern( 0, 0,255,"Blue"); KohonenMap.ShowPattern( 0,100, 0,"Dark green"); KohonenMap.ShowPattern( 0, 0,139,"Dark blue"); KohonenMap.ShowPattern(255,255, 0,"Yellow"); KohonenMap.ShowPattern(255,165, 0,"Orange"); KohonenMap.ShowPattern(128, 0,128,"Purple"); //--- show bmp image on the chart KohonenMap.ShowBMP(false); //--- }
El resultado se presenta en la Fig. 2.
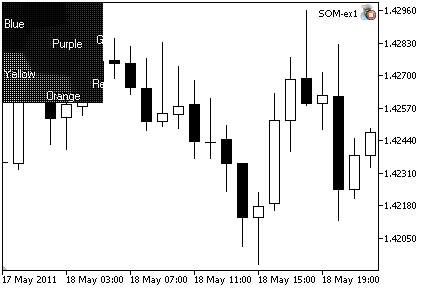
Figura 2. Datos de salida del Asesor Experto SOM_ex1.mq5
La dinámica del aprendizaje de un mapa Kohonen se presenta en la Fig. 3 (vea los pasos debajo de la imagen):
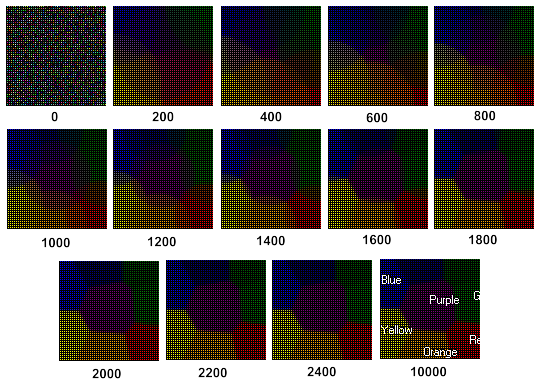
Figura 3. La dinámica del aprendizaje de un mapa Kohonen
Como puede observar en la Fig. 3, el mapa Kohonen se forma tras 2.400 pasos.
Si creamos un enrejado de 300 nodos y especificamos el tamaño de imagen como 400x400:
//--- lattice of 15x20 nodes, image size 400x400 KohonenMap.InitParameters(10000,15,20,400,400);
obtendremos la imagen presentada en la Fig. 4:
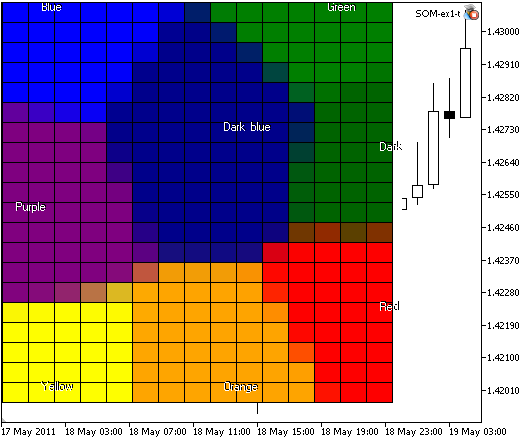
Figura 4. El mapa Kohonen con 300 nodos, tamaño de imagen 400x400
Si lee el libro Visual Explorations in Finance: with Self-Organizing Maps (Exploraciones Visuales en Finanzas: Mapas de Auto-Organización) escrito por Guido Deboeck y Teuvo Kohonen, recordará que los nodos del enrejado también se pueden representar como celdas hexagonales. Modificando el código del Asesor Experto (EA, por sus siglas en inglés) podemos implementar otra visualización.
El resultado de SOM-ex1-hex.mq5 se presenta en la Fig. 5:
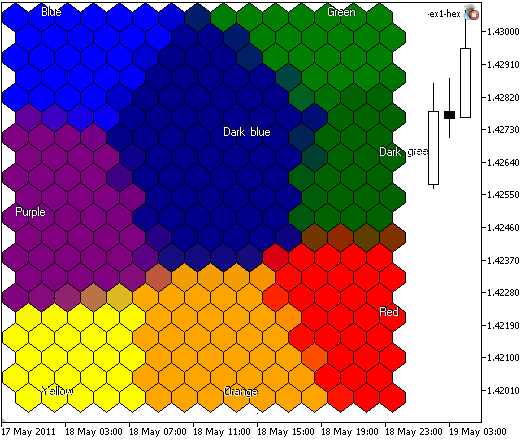
Figura 5. Mapa Kohonen con 300 nodos, tamaño de imagen 400x400. Los nodos del enrejado se representan como celdas hexagonales.
En esta versión, podemos definir la visualización de bordes de celda usando los parámetros de entrada:
// input parameter, used to show hexagonal cells input bool HexagonalCell=true; // input parameter, used to show borders input bool ShowBorders=true;
En algunos casos no necesitamos mostrar los bordes de celda. Si especifica ShowBorders=false, obtendrá la siguiente imagen (vea Fig. 6):
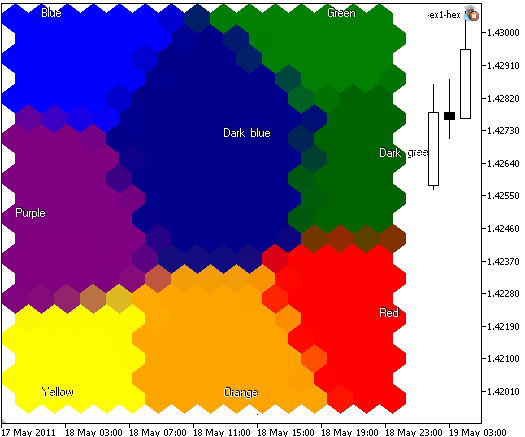
Fig. 6. Mapa Kohonen con 300 nodos, tamaño de imagen 400x400, nodos representados como celdas hexagonales, bordes de celda desactivados.
En el primer ejemplo hemos usado 8 colores en el conjunto de formación con componentes de color especificados. Podemos extender el conjunto de formación y simplificar la especificación de componentes de color añadiendo dos métodos a la clase CSOM.
Note que en este caso, los mapas Kohonen son simples porque solo hay unos pocos colores separados en el espacio de color. Como resultado, obtenemos los grupos localizados.
El problema aparece si usamos más colores con componentes de color más juntos.
2.2. Ejemplo 2. Usar colores web como muestras de formación
En el lenguaje MQL5, los colores web con constantes predefinidas.
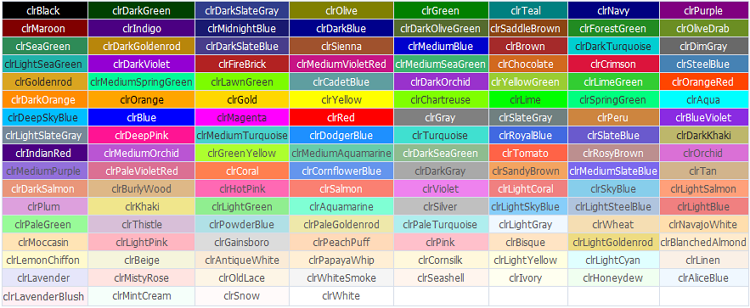
Figura 7. Colores web
¿Qué pasaría si aplicamos el algoritmo Kohonen a un conjunto de vectores con componentes similares?
Podemos crear una clase CSOMWeb derivada de la clase CSOM:
//+------------------------------------------------------------------+ //| CSOMWeb class | //+------------------------------------------------------------------+ class CSOMWeb : public CSOM { public: //--- adds a color to training set (used for colors, instead of AddTrainPattern) void AddTrainColor(int col); //--- method of showing of title of the pattern (used for colors, instead of ShowPattern) void ShowColor(int col,string name); };
Como puede ver, para simplificar el trabajo con colores hemos añadido dos nuevos métodos. La especificación explícita de componentes de color no es necesaria ahora.
La implementación de métodos de clase tiene el siguiente aspecto:
//+------------------------------------------------------------------+ //| Adds a color to training set | //| (used for colors, instead of AddTrainPattern) | //+------------------------------------------------------------------+ void CSOMWeb::AddTrainColor(int col) { double vector[]; ArrayResize(vector,3); int r=0; int g=0; int b=0; ColToRGB(col,r,g,b); vector[0]=r; vector[1]=g; vector[2]=b; AddVectorToTrainingSet(vector); ArrayResize(vector,0); } //+------------------------------------------------------------------+ //| Method of showing of title of the pattern | //| (used for colors, instead of ShowPattern) | //+------------------------------------------------------------------+ void CSOMWeb::ShowColor(int col,string name) { int r=0; int g=0; int b=0; ColToRGB(col,r,g,b); ShowPattern(r,g,b,name); }
Todos los colores web se pueden combinar en el array web_colors[]:
//--- web colors array color web_colors[132]= { clrBlack, clrDarkGreen, clrDarkSlateGray, clrOlive, clrGreen, clrTeal, clrNavy, clrPurple, clrMaroon, clrIndigo, clrMidnightBlue, clrDarkBlue, clrDarkOliveGreen, clrSaddleBrown, clrForestGreen, clrOliveDrab, clrSeaGreen, clrDarkGoldenrod, clrDarkSlateBlue, clrSienna, clrMediumBlue, clrBrown, clrDarkTurquoise, clrDimGray, clrLightSeaGreen, clrDarkViolet, clrFireBrick, clrMediumVioletRed, clrMediumSeaGreen, clrChocolate, clrCrimson, clrSteelBlue, clrGoldenrod, clrMediumSpringGreen, clrLawnGreen, clrCadetBlue, clrDarkOrchid, clrYellowGreen, clrLimeGreen, clrOrangeRed, clrDarkOrange, clrOrange, clrGold, clrYellow, clrChartreuse, clrLime, clrSpringGreen, clrAqua, clrDeepSkyBlue, clrBlue, clrMagenta, clrRed, clrGray, clrSlateGray, clrPeru, clrBlueViolet, clrLightSlateGray, clrDeepPink, clrMediumTurquoise, clrDodgerBlue, clrTurquoise, clrRoyalBlue, clrSlateBlue, clrDarkKhaki, clrIndianRed, clrMediumOrchid, clrGreenYellow, clrMediumAquamarine, clrDarkSeaGreen, clrTomato, clrRosyBrown, clrOrchid, clrMediumPurple, clrPaleVioletRed, clrCoral, clrCornflowerBlue, clrDarkGray, clrSandyBrown, clrMediumSlateBlue, clrTan, clrDarkSalmon, clrBurlyWood, clrHotPink, clrSalmon, clrViolet, clrLightCoral, clrSkyBlue, clrLightSalmon, clrPlum, clrKhaki, clrLightGreen, clrAquamarine, clrSilver, clrLightSkyBlue, clrLightSteelBlue, clrLightBlue, clrPaleGreen, clrThistle, clrPowderBlue, clrPaleGoldenrod, clrPaleTurquoise, clrLightGray, clrWheat, clrNavajoWhite, clrMoccasin, clrLightPink, clrGainsboro, clrPeachPuff, clrPink, clrBisque, clrLightGoldenrod, clrBlanchedAlmond, clrLemonChiffon, clrBeige, clrAntiqueWhite, clrPapayaWhip, clrCornsilk, clrLightYellow, clrLightCyan, clrLinen, clrLavender, clrMistyRose, clrOldLace, clrWhiteSmoke, clrSeashell, clrIvory, clrHoneydew, clrAliceBlue, clrLavenderBlush, clrMintCream, clrSnow, clrWhite };
La función OnInit() tiene una forma simple:
CSOMWeb KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ void OnInit() { MathSrand(200); int total_web_colors=ArraySize(web_colors); //--- initialize net, 10000 iterations will be used for training //--- the net contains 15x20 nodes, bmp image size 400x400 KohonenMap.InitParameters(10000,50,50,500,500); //-- add all web colors to training set for(int i=0; i<total_web_colors; i++) { KohonenMap.AddTrainColor(web_colors[i]); } //--- train net KohonenMap.Train(); //--- render map to bmp KohonenMap.Render(); //--- show patterns and titles for each color for(int i=0; i<total_web_colors; i++) { KohonenMap.ShowColor(web_colors[i],ColorToString(web_colors[i],true)); } //--- show bmp image on the chart KohonenMap.ShowBMP(false); }
Si ejecutamos som-ex2-hex.mq5, obtendremos la imagen presentada en la Fig. 8.
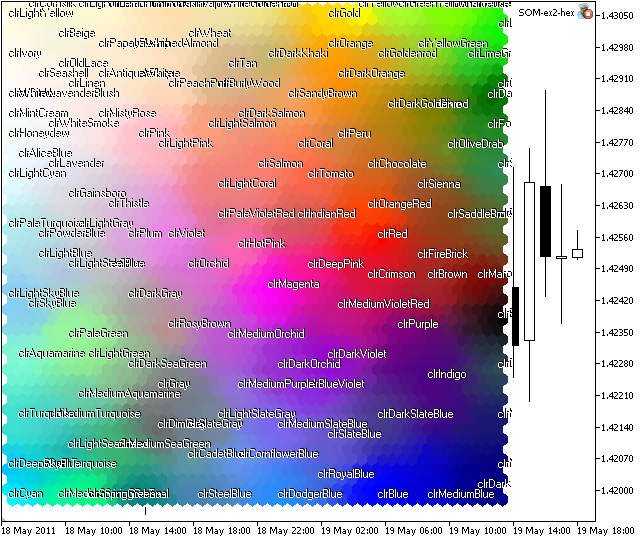
Figura 8. Mapa Kohonen de colores web
Como puede ver, hay algunos grupos, pero algunos colores (como el xxxBlue) se colocan en diferentes regiones.
Esto se debe a la estructura del conjunto de formación: hay muchos vectores con componentes cercanos.
2.3. Ejemplo 3. Agrupación de productos
A continuación consideraremos un ejemplo simple que intentará agrupar veinticinco alimentos en regiones de similitud, basándonos en tres parámetros: proteína, carbohidratos y grasa.
| Alimento |
Proteína | Carbohidratos | Grasa |
|
|---|---|---|---|---|
| 1 | Manzanas |
0.4 |
11.8 |
0.1 |
| 2 | Aguacate |
1.9 |
1.9 |
19.5 |
| 3 | Plátanos |
1.2 |
23.2 |
0.3 |
| 4 | Filete de ternera |
20.9 |
0 |
7.9 |
| 5 | Hamburguesa Big Mac |
13 |
19 |
11 |
| 6 | Nueces de Brasil |
15.5 |
2.9 |
68.3 |
| 7 | Pan |
10.5 |
37 |
3.2 |
| 8 | Mantequilla |
1 |
0 |
81 |
| 9 | Queso |
25 |
0.1 |
34.4 |
| 10 | Tarta de queso |
6.4 |
28.2 |
22.7 |
| 11 | Galletas |
5.7 |
58.7 |
29.3 |
| 12 | Copos de maíz |
7 |
84 |
0.9 |
| 13 | Huevos |
12.5 |
0 |
10.8 |
| 14 | Pollo frito |
17 |
7 |
20 |
| 15 | Patatas fritas |
3 |
36 |
13 |
| 16 | Chocolate caliente |
3.8 |
19.4 |
10.2 |
| 17 | Pepperoni |
20.9 |
5.1 |
38.3 |
| 18 | Pizza |
12.5 |
30 |
11 |
| 19 | Pastel de carne porcina (Pork Pie) |
10.1 |
27.3 |
24.2 |
| 20 | Patatas |
1.7 |
16.1 |
0.3 |
| 21 | Arroz |
6.9 |
74 |
2.8 |
| 22 | Pollo asado |
26.1 |
0.3 |
5.8 |
| 23 | Azúcar |
0 |
95.1 |
0 |
| 24 | Filete de atún |
25.6 |
0 |
0.5 |
| 25 | Agua |
0 |
0 |
0 |
Tabla 1. Proteína, carbohidratos y grasa para 25 alimentos.
El problema es interesante porque los vectores de entrada tienen diferentes valores, y cada componente tiene su propio abanico de valores. Es importante para la visualización, porque usamos el modelo de colores RGB con componentes que oscilan entre 0 y 255.
Afortunadamente, en este caso los vectores de entrada son también tridimensionales, y podemos usar el modelo de color RGB para la visualización del mapa Kohonen.
//+------------------------------------------------------------------+ //| CSOMFood class | //+------------------------------------------------------------------+ class CSOMFood : public CSOM { protected: double m_max_values[]; double m_min_values[]; public: void Train(); void Render(); void ShowPattern(double c1,double c2,double c3,string name); };
Como puede ver, hemos añadido los arrays m_max_values[] y m_min_values[] para el almacenamiento de valores máximos y mínimos de conjunto de formación. Para la visualización en modelo de color RGB se necesita el "ajuste", de modo que hemos sobrecargado los métodos Train(), Render() y ShowPattern().
La búsqueda de los valores máximo y mínimo se implementa en el método Train().
//--- find minimal and maximal values of the training set ArrayResize(m_max_values,3); ArrayResize(m_min_values,3); for(int j=0; j<3; j++) { double maxv=m_training_sets_array[3+j]; double minv=m_training_sets_array[3+j]; for(int i=1; i<m_total_training_sets; i++) { double v=m_training_sets_array[3*i+j]; if(v>maxv) {maxv=v;} if(v<minv) {minv=v;} } m_max_values[j]=maxv; m_min_values[j]=minv; Print(j,"m_min_value=",m_min_values[j],"m_max_value=",m_max_values[j]); }
Para mostrar los componentes en modelo de color RGB debemos modificar el método Render():
// int r = int(m_som_nodes[ind].GetWeight(0)); // int g = int(m_som_nodes[ind].GetWeight(1)); // int b = int(m_som_nodes[ind].GetWeight(2)); int r=int ((255*(m_som_nodes[ind].GetWeight(0)-m_min_values[0])/(m_max_values[0]-m_min_values[0]))); int g=int ((255*(m_som_nodes[ind].GetWeight(1)-m_min_values[1])/(m_max_values[1]-m_min_values[1]))); int b=int ((255*(m_som_nodes[ind].GetWeight(2)-m_min_values[2])/(m_max_values[2]-m_min_values[2])));
El resultado de som_ex3.mq5 se presenta en la Fig. 9.
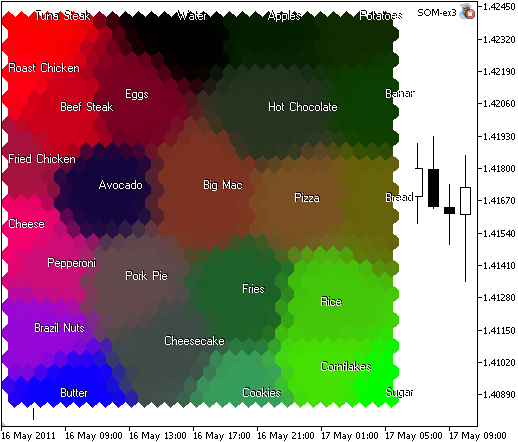
Figura 9. Mapa de alimentos agrupados en regiones de similitud basándonos en proteína, carbohidratos y grasa
Análisis de componente. Se puede ver en el mapa que el azúcar, el arroz y los copos de maíz se dibujan en color verde a causa de los carbohidratos (2º componente). La mantequilla se encuentra en la zona verde, tiene mucha grasa (3er componente). Los filetes de ternera y atún y el pollo asado contienen muchas proteínas (1er componente).
Puede extender el conjunto de formación añadiendo nuevos alimentos de las Tablas de Composición de Alimentos (tabla alternativa).
Como puede ver, el problema está resuelto para direcciones R,G,B "puras". ¿Pero qué pasa con alimentos que tienen varios componentes en igual medida, o casi igual? Seguiremos considerando los Planes de Componentes. Resulta muy útil, especialmente para casos en los que los vectores de entrada tienen una dimensión mayor de 3.
2.4. Ejemplo 4. Un caso cuatridimensional. Conjunto de datos de Iris de Fisher. CMYK
Para los vectores tridimensionales no hay problema con la visualización. Los resultados quedan claros a causa del modelo de colores RGB, usado para visualizar componentes de color.
Al trabajar con datos con dimensión alta, debemos encontrar la forma de visualizarlos. La solución más simple es esbozar un mapa de gradiente (por ejemplo, Black/White, o Blanco/Negro) con colores, proporcional a la longitud del vector. La otra manera es usar otros espacios de color. En este ejemplo consideraremos el modelo de color CMYK para el conjunto de datos de Iris de Fisher. Hay una solución mejor, pero la trataremos después.
El conjunto de datos florales de Iris, o el conjunto de datos de Iris de Fisher, es un conjunto de datos multivariados presentado por R. Fisher (1936) como ejemplo de un análisis discriminado. El conjunto de datos consta de 50 muestras de cada una de tres especies de flores Iris (Iris setosa, Iris virginica e Iris versicolor).
Se midieron cuatro cualidades de cada muestra: longitud y anchura del sépalo y el pétalo en centímetros.

Figura 10. Flor Iris
Cada muestra tiene 4 características:
- Longitud del sépalo;
- Anchura del sépalo;
- Longitud del pétalo;
- Anchura del pétalo.
El conjunto de datos de las flores Iris se puede encontrar en SOM_ex4.mq5.
En este ejemplo usaremos el espacio intermedio de color CMYK para dibujar, es decir, consideraremos los pesos del nodo como vectores en el espacio CMYK. Para visualizar los resultados se usó la conversión CMYK->RGB. Se añade un nuevo método int CSOM::CMYK2Col(uchar c,uchar m,uchar y,uchar k) a la clase CSOM, se usa en el método CSOM::Render(). También hemos modificado las clases para soportar vectores cuatridimensionales.
El resultado se presenta en la Fig. 11.
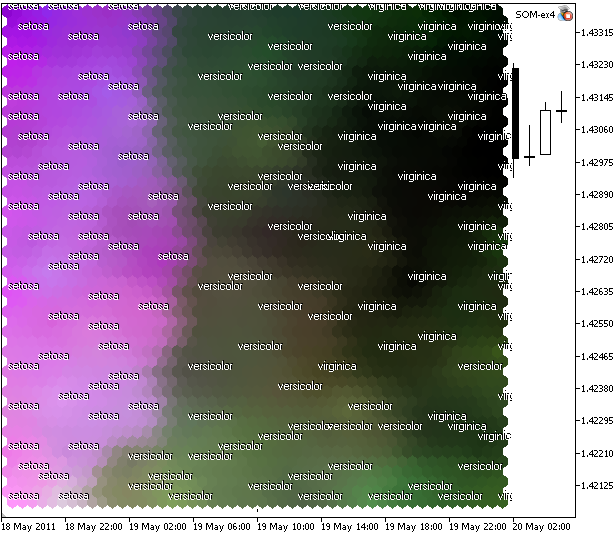
Figura 11. Mapa Kohonen para el conjunto de datos de flores dibujado en el modelo de color CMYK
¿Qué vemos? No hemos obtenido la agrupación completa (a causa de las cualidades del problema), pero se puede ver la separación lineal de la iris setosa.
La razón de esta separación lineal de la setosa es un gran componente "Magenta" (2º) en el espacio CMYK.
2.6. Análisis de Plano de Componente
En los ejemplos anteriores (agrupación de datos sobre alimentos y flores iris) se puede ver que hay un problema con la visualización de datos.
Por ejemplo, para el problema de los alimentos analizamos el mapa Kohonen usando la información en determinados colore (rojo, verde, azul). Además de los grupos básicos, había algunos alimentos con varios componentes. Además, el análisis se volvía difícil si los componentes eran prácticamente iguales.
Los planos de componentes dacilitan la posibilidad de ver la intensidad relativa para cada uno de los alimentos.
Debemos añadir las instancias de clase CIntBMP (el array m_bmp[]) en la clase CSOM y modificar los métodos de interpretación correspondientes. Asimismo, necesitaremos un mapa de gradiente para visualizar la intensidad de cada componente (los valores más bajos en color azul, los valores más altos en color rojo):
![]()
Figura 12. Paleta de gradiente
Añadimos el array Palette[768] y los métodos GetPalColor() y Blend(). El dibujo de un nodo se coloca en el método RenderCell().
El Conjunto de Datos de Flores Iris
Los resultados de som-ex4-cpr.mq5 se presentan en la Fig. 13.
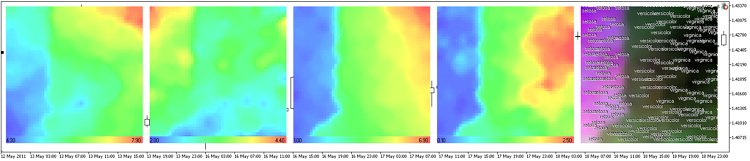
Figura 13. Representación de los planos de componente del conjunto de datos de flores Iris
En este caso usamos la cuadrícula con 30x30 nodos, tamaño de imagen 300x300.
Los planos de componente juegan un papel importante en la detección de correlación: comparando estos planos, incluso las variables parcialmente correlativas se pueden detectar con una inspección visual. Esto es más fácil si los planos de componente se reorganizan para que los correlativos estén cerca los unos de los otros. De esta forma, es fácil seleccionar combinaciones de componente interesantes para próximas investigaciones.
Consideremos los planos de componente (Fig. 14).
Los valores de componentes máximos y mínimos se muestran en la tabla de gradiente.
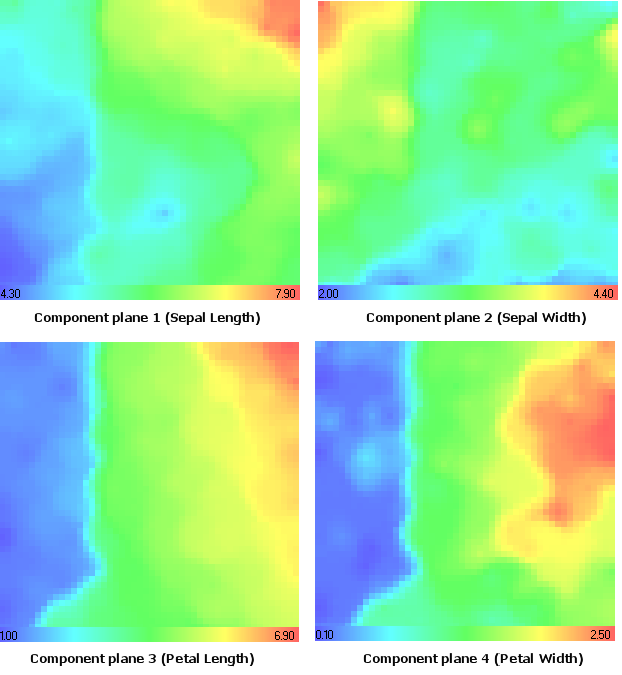
Figura 14. Conjunto de datos de flores Iris. Planos de componente
Todos estos planos de componente representados en el modelo de color CMYK se muestran en la Fig. 15.

Figura 15. Conjunto de datos de flores Iris. Mapa Kohonen en modelo de color CMYK
Recordemos el tipo de iris setosa. Usando el análisis de plano de componente (Fig. 14) se puede ver que tiene valores mínimos en los siguientes planos de componente: 1º (Longitud de sépalo), 3º (Longitud de pétalo) y 4º (Anchura de pétalo) planos de componente.
Es destacable que tiene los valores máximos en el 2º plano de componente (Anchura de sépalo), el mismo resultado que obtuvimos en el modelo de color CMYK (componente Magenta, Fig. 15).
Agrupación de Alimentos
Ahora consideremos el problema de la agrupación de alimentos usando el análisis de plano de componente (som-ex3-cpr.mq5).
El resultado se presenta en la Fig. 16 (30x30 nodos, tamaño de imagen 300x300, celdas hexagonales sin bordes).
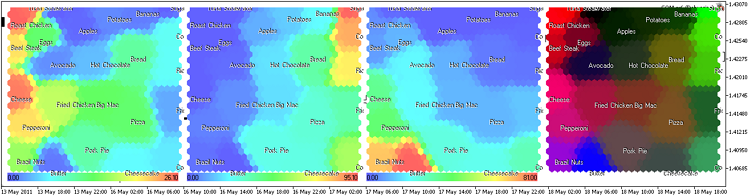
Figura 16. Mapa Kohonen de alimentos, representación de plano de componente
Hemos añadido la opción de visualización de títulos en el método ShowPattern() de la clase CSOM (parámetro de entrada ShowTitles=true).
Los planos de componente (proteína, carbohidratos, grasa) tienen el siguiente aspecto:
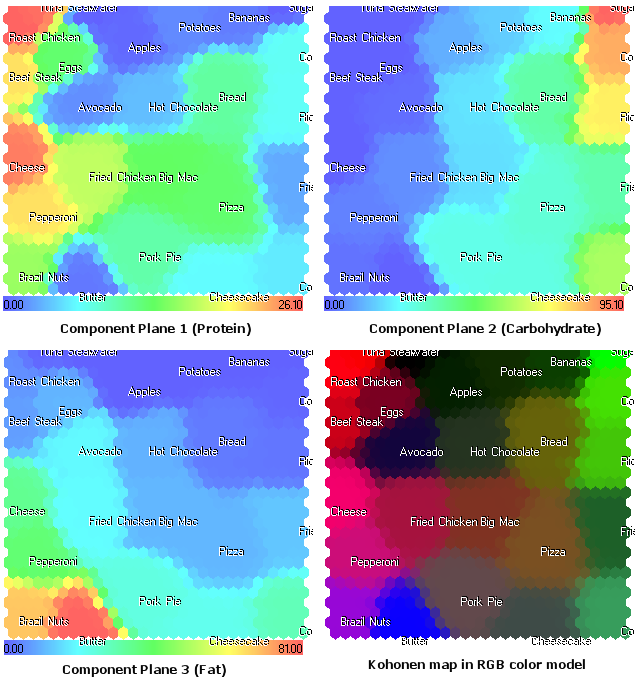
Figura 17. Mapa Kohonen de alimentos. Planos de componente y modelo de color RGB
La representación de plano de componente que se muestra en la Fig. 17 abre una nueva visualización de la estructura de componentes de alimentos. Además, facilita información adicional que no se puede ver en el modelo de color RGB, presentado en la Fig. 9.
Por ejemplo, ahora vemos el Queso en el 1er plano de componente (proteína). En el modelo de color RGB se muestra con un color cercano al magenta a causa de la grasa (2º componente).
2.5. Implementación de Planos de Componente para un Caso de Dimensión Arbitraria
Los ejemplos que hemos considerado tienen algunas cualidades específicas, la dimensión estaba fijada y el algoritmo de visualización era diferente en las distintas representaciones (modelos de color RGB y CMYK).
Ahora podemos generalizar el algoritmo para dimensiones arbitrarias, pero en este caso visualizaremos solo los planos de componente. El programa debe ser capaz de cargar los datos arbitrarios de un archivo CSV.
Por ejemplo, food.csv tiene el siguiente aspecto:
Protein;Carbohydrate;Fat;Title 0.4;11.8;0.1;Apples 1.9;1.9;19.5;Avocado 1.2;23.2;0.3;Bananas 20.9;0.0;7.9;Beef Steak 13.0;19.0;11.0;Big Mac 15.5;2.9;68.3;Brazil Nuts 10.5;37.0;3.2;Bread 1.0;0.0;81.0;Butter 25.0;0.1;34.4;Cheese 6.4;28.2;22.7;Cheesecake 5.7;58.7;29.3;Cookies 7.0;84.0;0.9;Cornflakes 12.5;0.0;10.8;Eggs 17.0;7.0;20.0;Fried Chicken 3.0;36.0;13.0;Fries 3.8;19.4;10.2;Hot Chocolate 20.9;5.1;38.3;Pepperoni 12.5;30.0;11.0;Pizza 10.1;27.3;24.2;Pork Pie 1.7;16.1;0.3;Potatoes 6.9;74.0;2.8;Rice 26.1;0.3;5.8;Roast Chicken 0.0;95.1;0.0;Sugar 25.6;0.0;0.5;Tuna Steak 0.0;0.0;0.0;Water
La primera línea del archivo contiene los nombres (títulos) del vector de datos de entrada. Los títulos son necesarios para distinguir entre los planos de componente; imprimiremos sus nombres en el panel de gradiente.
El nombre del patrón se encuentra en la última columna, en nuestro caso es el nombre del alimento.
El código de SOM.mq5 (OnInit function) se simplifica:
CSOM KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { MathSrand(200); //--- load patterns from file if(!KohonenMap.LoadTrainDataFromFile(DataFileName)) { Print("Error in loading data for training."); return(1); } //--- train net KohonenMap.Train(); //--- render map KohonenMap.Render(); //--- show patterns from training set KohonenMap.ShowTrainPatterns(); //--- show bmp on the chart KohonenMap.ShowBMP(false); return(0); }
En nombre del archivo con patrones de formación se especifica en el parámetro de entrada DataFileName, en nuestro caso "food.csv".
El resultado se muestra en la Fig. 18.

Figura 18. Mapa Kohonen de alimentos en esquema de gradiente de color en blanco y negro
Also we added the ColorScheme input parameter for gradient scheme selection.
Actualmente hay 4 esquemas de color disponibles (ColorScheme=0,1,2,4=Black-White (Negro-Blanco), DarkBlue-Blue-Green-Yellow-Red (Azul Oscuro-Azul-Verde-Amarillo-Rojo), Red-Black-Green (Rojo-Negro-Verde), Red-White-Green (Rojo-Blanco-Verde)).

Usted puede añadir
fácilmente su propio esquema agregando el gradiente en el método CSOM::InitParameters().
El esquema de colores se puede seleccionar de los parámetros de entrada del Asesor Experto:
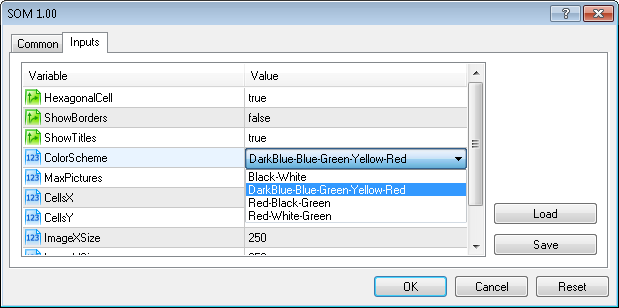
Similarmente, podemos preparar el conjunto de datos de la flor Iris flower (iris-fisher.csv):
Sepal length;Sepal width;Petal length;Petal width;Title 5.1;3.5;1.4;0.2;setosa 4.9;3.0;1.4;0.2;setosa 4.7;3.2;1.3;0.2;setosa 4.6;3.1;1.5;0.2;setosa 5.0;3.6;1.4;0.2;setosa 5.4;3.9;1.7;0.4;setosa 4.6;3.4;1.4;0.3;setosa 5.0;3.4;1.5;0.2;setosa 4.4;2.9;1.4;0.2;setosa 4.9;3.1;1.5;0.1;setosa 5.4;3.7;1.5;0.2;setosa 4.8;3.4;1.6;0.2;setosa 4.8;3.0;1.4;0.1;setosa 4.3;3.0;1.1;0.1;setosa 5.8;4.0;1.2;0.2;setosa 5.7;4.4;1.5;0.4;setosa 5.4;3.9;1.3;0.4;setosa 5.1;3.5;1.4;0.3;setosa 5.7;3.8;1.7;0.3;setosa 5.1;3.8;1.5;0.3;setosa 5.4;3.4;1.7;0.2;setosa 5.1;3.7;1.5;0.4;setosa 4.6;3.6;1.0;0.2;setosa 5.1;3.3;1.7;0.5;setosa 4.8;3.4;1.9;0.2;setosa 5.0;3.0;1.6;0.2;setosa 5.0;3.4;1.6;0.4;setosa 5.2;3.5;1.5;0.2;setosa 5.2;3.4;1.4;0.2;setosa 4.7;3.2;1.6;0.2;setosa 4.8;3.1;1.6;0.2;setosa 5.4;3.4;1.5;0.4;setosa 5.2;4.1;1.5;0.1;setosa 5.5;4.2;1.4;0.2;setosa 4.9;3.1;1.5;0.2;setosa 5.0;3.2;1.2;0.2;setosa 5.5;3.5;1.3;0.2;setosa 4.9;3.6;1.4;0.1;setosa 4.4;3.0;1.3;0.2;setosa 5.1;3.4;1.5;0.2;setosa 5.0;3.5;1.3;0.3;setosa 4.5;2.3;1.3;0.3;setosa 4.4;3.2;1.3;0.2;setosa 5.0;3.5;1.6;0.6;setosa 5.1;3.8;1.9;0.4;setosa 4.8;3.0;1.4;0.3;setosa 5.1;3.8;1.6;0.2;setosa 4.6;3.2;1.4;0.2;setosa 5.3;3.7;1.5;0.2;setosa 5.0;3.3;1.4;0.2;setosa 7.0;3.2;4.7;1.4;versicolor 6.4;3.2;4.5;1.5;versicolor 6.9;3.1;4.9;1.5;versicolor 5.5;2.3;4.0;1.3;versicolor 6.5;2.8;4.6;1.5;versicolor 5.7;2.8;4.5;1.3;versicolor 6.3;3.3;4.7;1.6;versicolor 4.9;2.4;3.3;1.0;versicolor 6.6;2.9;4.6;1.3;versicolor 5.2;2.7;3.9;1.4;versicolor 5.0;2.0;3.5;1.0;versicolor 5.9;3.0;4.2;1.5;versicolor 6.0;2.2;4.0;1.0;versicolor 6.1;2.9;4.7;1.4;versicolor 5.6;2.9;3.6;1.3;versicolor 6.7;3.1;4.4;1.4;versicolor 5.6;3.0;4.5;1.5;versicolor 5.8;2.7;4.1;1.0;versicolor 6.2;2.2;4.5;1.5;versicolor 5.6;2.5;3.9;1.1;versicolor 5.9;3.2;4.8;1.8;versicolor 6.1;2.8;4.0;1.3;versicolor 6.3;2.5;4.9;1.5;versicolor 6.1;2.8;4.7;1.2;versicolor 6.4;2.9;4.3;1.3;versicolor 6.6;3.0;4.4;1.4;versicolor 6.8;2.8;4.8;1.4;versicolor 6.7;3.0;5.0;1.7;versicolor 6.0;2.9;4.5;1.5;versicolor 5.7;2.6;3.5;1.0;versicolor 5.5;2.4;3.8;1.1;versicolor 5.5;2.4;3.7;1.0;versicolor 5.8;2.7;3.9;1.2;versicolor 6.0;2.7;5.1;1.6;versicolor 5.4;3.0;4.5;1.5;versicolor 6.0;3.4;4.5;1.6;versicolor 6.7;3.1;4.7;1.5;versicolor 6.3;2.3;4.4;1.3;versicolor 5.6;3.0;4.1;1.3;versicolor 5.5;2.5;4.0;1.3;versicolor 5.5;2.6;4.4;1.2;versicolor 6.1;3.0;4.6;1.4;versicolor 5.8;2.6;4.0;1.2;versicolor 5.0;2.3;3.3;1.0;versicolor 5.6;2.7;4.2;1.3;versicolor 5.7;3.0;4.2;1.2;versicolor 5.7;2.9;4.2;1.3;versicolor 6.2;2.9;4.3;1.3;versicolor 5.1;2.5;3.0;1.1;versicolor 5.7;2.8;4.1;1.3;versicolor 6.3;3.3;6.0;2.5;virginica 5.8;2.7;5.1;1.9;virginica 7.1;3.0;5.9;2.1;virginica 6.3;2.9;5.6;1.8;virginica 6.5;3.0;5.8;2.2;virginica 7.6;3.0;6.6;2.1;virginica 4.9;2.5;4.5;1.7;virginica 7.3;2.9;6.3;1.8;virginica 6.7;2.5;5.8;1.8;virginica 7.2;3.6;6.1;2.5;virginica 6.5;3.2;5.1;2.0;virginica 6.4;2.7;5.3;1.9;virginica 6.8;3.0;5.5;2.1;virginica 5.7;2.5;5.0;2.0;virginica 5.8;2.8;5.1;2.4;virginica 6.4;3.2;5.3;2.3;virginica 6.5;3.0;5.5;1.8;virginica 7.7;3.8;6.7;2.2;virginica 7.7;2.6;6.9;2.3;virginica 6.0;2.2;5.0;1.5;virginica 6.9;3.2;5.7;2.3;virginica 5.6;2.8;4.9;2.0;virginica 7.7;2.8;6.7;2.0;virginica 6.3;2.7;4.9;1.8;virginica 6.7;3.3;5.7;2.1;virginica 7.2;3.2;6.0;1.8;virginica 6.2;2.8;4.8;1.8;virginica 6.1;3.0;4.9;1.8;virginica 6.4;2.8;5.6;2.1;virginica 7.2;3.0;5.8;1.6;virginica 7.4;2.8;6.1;1.9;virginica 7.9;3.8;6.4;2.0;virginica 6.4;2.8;5.6;2.2;virginica 6.3;2.8;5.1;1.5;virginica 6.1;2.6;5.6;1.4;virginica 7.7;3.0;6.1;2.3;virginica 6.3;3.4;5.6;2.4;virginica 6.4;3.1;5.5;1.8;virginica 6.0;3.0;4.8;1.8;virginica 6.9;3.1;5.4;2.1;virginica 6.7;3.1;5.6;2.4;virginica 6.9;3.1;5.1;2.3;virginica 5.8;2.7;5.1;1.9;virginica 6.8;3.2;5.9;2.3;virginica 6.7;3.3;5.7;2.5;virginica 6.7;3.0;5.2;2.3;virginica 6.3;2.5;5.0;1.9;virginica 6.5;3.0;5.2;2.0;virginica 6.2;3.4;5.4;2.3;virginica 5.9;3.0;5.1;1.8;virginica
El resultado se muestra
en la Fig. 19.

Figura 19. Conjunto de datos de flores Iris. Planos de componente en esquema de color Rojo-Negro-Verde
Ahora ya tenemos una herramienta para las aplicaciones reales.
2.6. Ejemplo 5. Mapas de temperatura de mercado
Los Mapas con Función De Auto-Organización se pueden usar para los mapas de movimiento de mercado. A veces, es necesario tener una imagen global del mercado, y para ello, una herramienta muy útil son los mapas de temperatura de mercado. Las acciones se combinan según los sectores económicos.
El color actual de la acción depende del ritmo de crecimiento actual (en %):

Figura 20. Mapa de temperatura de mercado para acciones de S&P500.
El mapa de temperatura de mercado semanal de las acciones de S&P (http://finviz.com) se muestra en la Fig. 20. El color depende del ritmo de crecimiento (en %):
![]()
El tamaño del rectángulo de la acción depende de la capitalización del mercado. El mismo análisis se puede realizar en el Terminal de Cliente MetaTrader 5 usando los Mapas Kohonen.
La idea es usar los ritmos de crecimiento (en %) en diferentes intervalos cronológicos. Ya tenemos la herramienta para trabajar con Mapas Kohonen, de modo que lo único que necesitamos es el script, que guardar los datos en el archivo .csv.
Los datos de precio en los precios CDF de los mercados bursátiles americanos (#AA, #AIG, #AXP, #BA, #BAC, #C, #CAT, #CVX, #DD, #DIS, #EK, #GE, #HD, #HON, #HPQ, #IBM, #INTC, #IP, #JNJ, #JPM, #KFT, #KO, #MCD, #MMM, #MO, #MRK, #MSFT, #PFE, #PG, #T, #TRV, #UTX, #VZ, #WMT и #XOM) se pueden encontrar en el servidor de MetaQuotes Demo.
El script que prepara el archivo dj.csv es muy sencillo:
//+------------------------------------------------------------------+ //| DJ.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" string s_cfd[35]= { "#AA","#AIG","#AXP","#BA","#BAC","#C","#CAT","#CVX","#DD","#DIS","#EK","#GE", "#HD","#HON","#HPQ","#IBM","#INTC","#IP","#JNJ","#JPM","#KFT","#KO","#MCD","#MMM", "#MO","#MRK","#MSFT","#PFE","#PG","#T","#TRV","#UTX","#VZ","#WMT","#XOM" }; //+------------------------------------------------------------------+ //| Returns price change in percents | //+------------------------------------------------------------------+ double PercentChange(double Open,double Close) { return(100.0*(Close-Open)/Close); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { ResetLastError(); int filehandle=FileOpen("dj.csv",FILE_WRITE|FILE_ANSI); if(filehandle==INVALID_HANDLE) { Alert("Error opening file"); return; } //--- MqlRates MyRates[]; ArraySetAsSeries(MyRates,true); string t="M30;M60;M90;M120;M150;M180;M210;M240;Title"; FileWrite(filehandle,t); Print(t); int total_symbols=ArraySize(s_cfd); for(int i=0; i<total_symbols; i++) { string cursymbol=s_cfd[i]; int copied1=CopyRates(cursymbol,PERIOD_M30,0,8,MyRates); if(copied1>0) { string s=""; s=s+DoubleToString(PercentChange(MyRates[1].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[2].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[3].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[4].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[5].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[6].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[7].open,MyRates[0].close),3)+";"; s=s+cursymbol; Print(s); FileWrite(filehandle,s); } else { Print("Error in request of historical data on symbol ",cursymbol); return; } } Alert("OK"); FileClose(filehandle); } //+------------------------------------------------------------------+
Los datos del historial
se deben descargar, lo puede hacer automáticamente usando el script DownloadHistory.
Como resultado del script dj.mq5, obtendremos el archivo dj.csv con los siguientes datos:
M30;M60;M90;M120;M150;M180;M210;M240;Title 0.063;-0.564;-0.188;0.376;0.251;0.313;0.627;0.439;#AA -0.033;0.033;0.067;-0.033;0.067;-0.133;0.266;0.533;#AIG -0.176;0.039;0.039;0.274;0.196;0.215;0.430;0.646;#AXP -0.052;-0.328;-0.118;0.315;0.223;0.367;0.288;0.328;#BA -0.263;-0.351;-0.263;0.000;-0.088;0.088;0.000;-0.088;#BAC -0.224;-0.274;-0.374;-0.100;-0.274;-0.224;-0.324;-0.598;#C -0.069;-0.550;-0.079;0.766;0.727;0.638;0.736;0.589;#CAT -0.049;-0.168;0.099;0.247;0.187;0.049;0.355;0.266;#CVX 0.019;-0.058;0.058;0.446;0.174;0.349;0.136;-0.329;#DD -0.073;-0.219;-0.146;0.267;0.170;0.292;0.170;0.267;#DIS -1.099;-1.923;-1.099;0.275;0.275;0.275;-0.549;-1.374;#EK -0.052;-0.310;-0.103;0.362;0.258;0.362;0.465;0.258;#GE -0.081;-0.244;-0.326;-0.136;0.081;0.326;0.489;0.489;#HD -0.137;-0.427;-0.171;0.427;0.445;0.342;0.325;0.359;#HON -0.335;-0.363;-0.112;0.112;0.168;0.307;0.475;0.251;#HPQ 0.030;-0.095;0.065;0.190;0.071;0.214;0.279;0.327;#IBM 0.000;-0.131;-0.044;-0.088;-0.044;0.000;0.000;0.044;#INTC -0.100;-0.200;-0.166;0.100;-0.067;0.033;-0.532;-0.798;#IP -0.076;0.076;0.259;0.473;0.427;0.336;0.336;-0.076;#JNJ -0.376;-0.353;-0.494;-0.259;-0.423;-0.329;-0.259;-0.541;#JPM -0.057;-0.086;-0.029;0.086;0.114;0.057;0.257;-0.114;#KFT 0.059;-0.030;0.119;0.282;0.119;0.193;0.208;-0.119;#KO -0.109;-0.182;0.206;0.352;0.279;0.473;0.521;0.194;#MCD -0.043;-0.195;-0.151;0.216;0.270;0.227;0.411;0.206;#MMM -0.036;-0.072;0.072;0.144;-0.072;-0.108;0.108;0.072;#MO 0.081;-0.081;0.027;0.081;-0.054;0.027;-0.027;-0.108;#MRK 0.083;0.083;0.041;0.331;0.083;0.248;0.166;0.041;#MSFT 0.049;0.000;0.243;0.680;0.194;0.243;0.340;0.097;#PFE -0.045;0.060;0.104;0.015;-0.179;-0.149;-0.224;-0.224;#PG 0.097;-0.032;0.000;0.129;0.129;0.064;0.097;0.064;#T -0.277;-0.440;-0.326;-0.358;-0.537;-0.619;-0.570;-0.733;#TRV -0.081;-0.209;0.035;0.325;0.198;0.093;0.128;-0.035;#UTX 0.054;0.000;0.054;0.190;0.136;0.326;0.380;0.353;#VZ -0.091;-0.091;-0.036;0.036;-0.072;0.000;0.145;-0.127;#WMT -0.062;-0.211;0.087;0.198;0.186;0.050;0.347;0.508;#XOM
Tras ejecutar el archivo som.mq5(ColorScheme=3, CellsX=30,CellsY=30, ImageXSize=200, ImageXSize=200, DataFileName="dj.csv"), obtendremos 8 imágenes. Cada una de ellas se corresponderá con los intervalos cronológicos de 30, 60, 90, 120, 150, 180, 210 y 240 minutos.
En la Fig. 21 se presentan los mapas Kohonen de datos sobre el ritmo de crecimiento del mercado (en los mercados bursátiles americanos) de las últimas 4 horas de la sesión de trading del 23 de mayo de 2011.
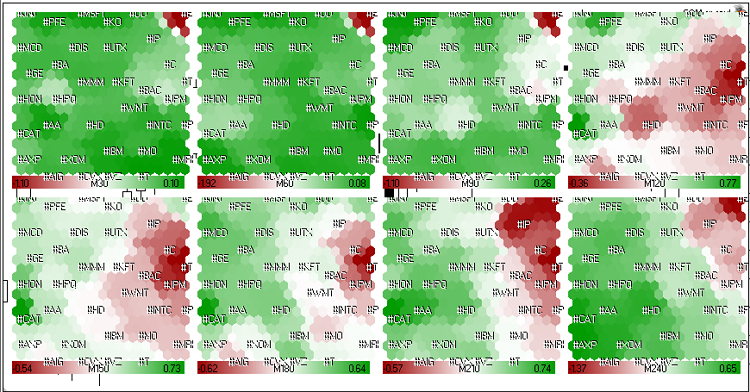
Figura 21. Mapas Kohonen de los mercados bursátiles americanos (últimas 4 horas de la sesión de trading del 23 de mayo de 2011).
Como puede observar en la Fig. 21, la dinámica de #C (Citigroup Inc.), #T (AT&T Inc.), #JPM (JPMorgan Chase & Co) y #BAC (Banco de América) es similar. Han formado un grupo rojo a largo plazo.
Durante la última hora y media (M30, M60, M90) su dinámica se volvió verde, pero generalmente (M240) las acciones permanecían en la zona roja.
Usando mapas Kohonen podemos visualizar la dinámica de los mercados bursátiles, encontrar líderes y perdedores y aprender sobre su entorno. Los elementos con datos similares forman grupos.
Como podemos ver en la Fig. 21a, el precio de las acciones de Citigroup Inc fue el líder de la caída. Generalmente, todas las acciones de compañías financieras se encontraban en la zona roja.
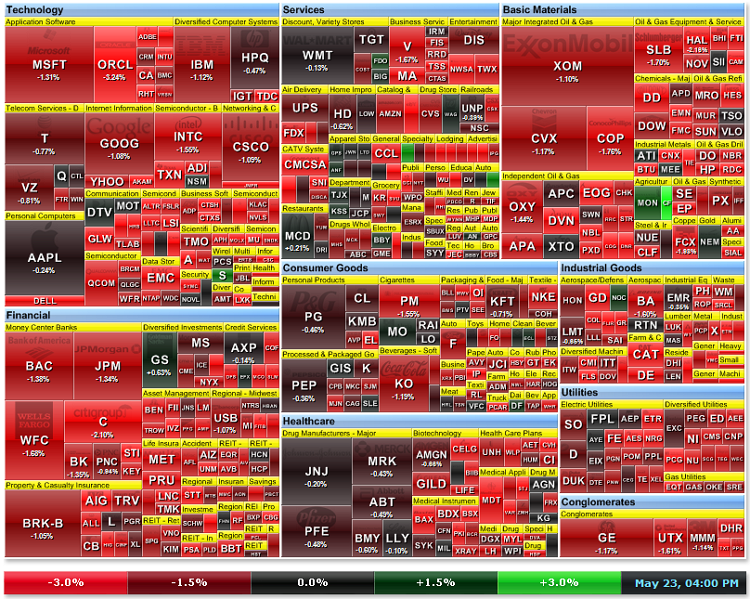
Figure 21a. Mapa de temperatura de mercado del 23 de mayo de 2011 (Fuente: http://finviz.com).
Similarmente, podemos
calcular los mapas Kohonen del mercado FOREX (Fig. 22):
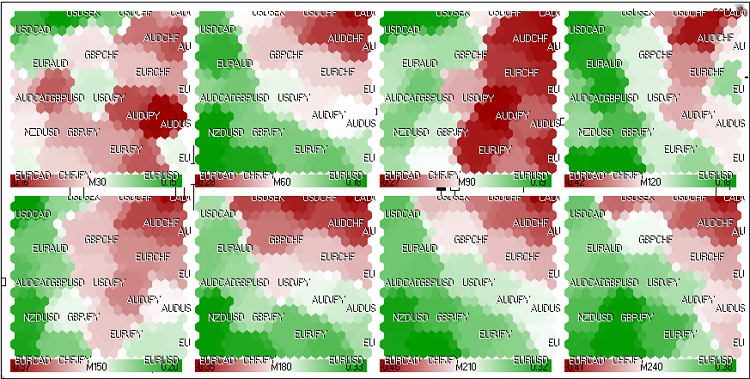
Figura 22. Mapa Kohonen del mercado FOREX (24 de mayo de 2011, sesión europea).
Se usaron los siguientes pares: EURUSD, GBPUSD, USDCHF, USDJPY, USDCAD, AUDUSD, NZDUSD, USDSEK, AUDNZD, AUDCAD, AUDCHF, AUDJPY, CHFJPY, EURGBP, EURAUD, EURCHF, EURJPY, EURNZD, EURCAD, GBPCHF, GBPJPY, CADCHF.
Los ritmos de crecimiento se exportan a fx.csv usando el script fx.mq5.
M30;M60;M90;M120;M150;M180;M210;M240;Title 0.058;-0.145;0.045;-0.113;-0.038;-0.063;0.180;0.067;EURUSD 0.046;-0.100;0.078;0.094;0.167;0.048;0.123;0.160;GBPUSD -0.048;0.109;-0.142;-0.097;-0.219;-0.143;-0.277;-0.236;USDCHF 0.042;0.097;0.043;-0.024;-0.009;-0.067;0.024;0.103;USDJPY -0.045;0.162;0.155;0.239;0.217;0.246;0.157;0.227;USDCAD 0.095;-0.126;-0.018;-0.141;-0.113;-0.062;0.081;-0.005;AUDUSD 0.131;-0.028;0.167;0.096;-0.013;0.147;0.314;0.279;NZDUSD -0.047;0.189;-0.016;0.107;0.084;0.076;-0.213;-0.133;USDSEK -0.034;-0.067;-0.188;-0.227;-0.102;-0.225;-0.234;-0.291;AUDNZD 0.046;0.039;0.117;0.102;0.097;0.170;0.234;0.216;AUDCAD 0.057;-0.016;-0.158;-0.226;-0.328;-0.215;-0.180;-0.237;AUDCHF 0.134;-0.020;0.024;-0.139;-0.124;-0.127;0.107;0.098;AUDJPY 0.083;-0.009;0.184;0.084;0.208;0.082;0.311;0.340;CHFJPY 0.025;-0.036;-0.030;-0.200;-0.185;-0.072;0.058;-0.096;EURGBP -0.036;-0.028;0.061;0.010;0.074;-0.006;0.088;0.070;EURAUD 0.008;-0.049;-0.098;-0.219;-0.259;-0.217;-0.094;-0.169;EURCHF 0.096;-0.043;0.085;-0.124;-0.049;-0.128;0.206;0.157;EURJPY -0.073;-0.086;-0.119;-0.211;-0.016;-0.213;-0.128;-0.213;EURNZD 0.002;0.009;0.181;0.119;0.182;0.171;0.327;0.284;EURCAD -0.008;0.004;-0.077;-0.015;-0.054;-0.127;-0.164;-0.080;GBPCHF 0.079;-0.005;0.115;0.079;0.148;-0.008;0.144;0.253;GBPJPY 0.013;-0.060;-0.294;-0.335;-0.432;-0.376;-0.356;-0.465;CADCHF
Además de los precios, puede usar los valores de los indicadores en diferentes intervalos cronológicos.
2.6. Ejemplo 6. Análisis de Resultados de Resultados de Optimización
El Probador de Estrategias del Terminal de Cliente MetaTrader 5 ofrece la oportunidad para explorar la estructura del espacio de parámetros y encontrar el mejor conjunto de parámetros de estrategia. Asimismo, puede exportar los resultados de la optimización usando la opción "Export to XML (MS Office Excel)" (“Exportar a XML (MS Office Excel)") del menú de contexto de la pestaña "Optimization Results" ("Resultados de Optimización").
Las Estadísticas del Probador también se incluyen en los resultados de optimización (41 columnas):
- Result (Resultado)
- Profit (Beneficio)
- Gross Profit (Beneficio bruto)
- Gross Loss (Pérdida bruta)
- Withdrawal (Reducción)
- Expected Payoff (Pago esperado)
- Profit Factor (Factor de beneficio)
- Recovery Factor (Factor de recuperación)
- Sharpe Ratio (Proporción Sharpe)
- Margin Level (Nivel de margen)
- Custom (Personalización)
- Minimal Balance (Saldo mínimo)
- Balance DD Maximal (Saldo máximo DD)
- Balance DD Maximal (%) (Saldo relativo DD (%))
- Balance DD Relative (Saldo relativo DD)
- Balance DD Relative (%) (Saldo relativo DD (%))
- Minimal Equity (Beneficio mínimo)
- Equity DD Maximal (Beneficio máximo DD)
- Equity DD Maximal (%) (Beneficio máximo DD (%))
- Equity DD Relative (Beneficio relativo DD)
- Equity DD Relative (%) (Beneficio relativo DD (%))
- Trades (Operaciones de trading)
- Deals (Transacciones)
- Short Trades (Operaciones cortas)
- Profit Short Trades (Operaciones cortas rentables)
- Long Trades (Operaciones largas)
- Profit Long Trades (Operaciones largas rentables)
- Profit Trades (Operaciones rentables)
- Loss Trades (Operaciones no rentables)
- Max profit trade (Máxima operación rentable)
- Max loss trade (Máxima operación no rentable)
- Max consecutive wins (Ganancias consecutivas máximas)
- Max consecutive wins ($) (Ganancias consecutivas máximas)
- Max consecutive profit (Beneficio consecutivo máximo)
- Max consecutive profit count (Cuenta de beneficio consecutivo máximo)
- Max consecutive losses (Pérdidas consecutivas máximas)
- Max consecutive losses ($) (Pérdidas consecutivas máximas ($))
- Max consecutive loss (Pérdida consecutiva máxima)
- Max consecutive loss count (Cuenta de pérdida consecutiva máxima)
- Avg consecutive wins (Media de ganancias consecutivas)
- Avg consecutive losses (Media de pérdidas consecutivas)
El uso de estadísticas del probador nos ayuda a analizar el espacio de parámetros. Es destacable que muchos parámetros de la estadística están estrechamente relacionados y dependen de los resultados del rendimiento de las operaciones de trading.
Por ejemplo, los mejores resultados de trading tiene los mayores valores de los parámetros Profit, Profit Factor, Recovery Factor y Sharpe Ratio. Esto nos permite usar los en el análisis de resultados.
Resultados de la Optimización del Asesor Experto MovingAverage.mq5
En este capítulo consideraremos el análisis de los resultados de la optimización del Asesor Experto MovingAverage.mq5, incluido en el paquete estándar del Terminal de Cliente MetaTrader 5. Este Asesor Experto se basa en el cruce de precios y el indicador de media móvil. Tiene dos parámetros de entrada: MovingPeriod y MovingShift. Es decir, tendremos el archivo XML con 43 columnas como resultado.
No tendremos en cuenta el espacio de 43 dimensiones de los parámetros, los más interesantes son:
- Profit;
- Profit Factor;
- Recovery Factor;
- Sharpe Ratio;
- Trades;
- ProfitTrades(%);
- MovingPeriod;
- MovingShift;
Note que hemos añadido el parámetro ProfitTrades (%), que estaba ausente en los resultados. Se trata del porcentaje de transacciones rentables y calculadas como resultado de la división de ProfitTrades (28) entre Trades (22), multiplicado por 100.
Preparemos el archivo optim.csv con 9 columnas para 400 conjuntos de parámetros de entrada en el Probador de Estrategias de MetaTrader 5.
Profit;Profit Factor;Recovery Factor;Sharpe Ratio;Trades;ProfitTrades(%);MovingPeriod;MovingShift;Title -372.3;0.83;-0.51;-0.05;71;28.16901408;43;6;43 -345.79;0.84;-0.37;-0.05;66;27.27272727;50;6;50 ...
Note que hemos usado el valor de MovingPeriod como la columna Title ("Título"); se usará para “marcar” los patrones en los mapas Kohonen.
Hemos optimizado los valores de MovingPeriod y MovingShift en el Probador de Estrategias con los siguientes parámetros:
- Symbol (Símbolo) - EURUSD,
- Period (Período) - H1,
- Tick generation mode (Modo de generación de ticks) - "1 Minute OHLC" ("1 MInuto OHLC"),
- Testing interval (Intervalo de simulación) - 2011.01.01-2011.05.24,
- Optimization (Optimización) - Fast (genetic algorithm) (Rápida (algoritmo genético),
- Optimization - Balance max. (Saldo máximo)
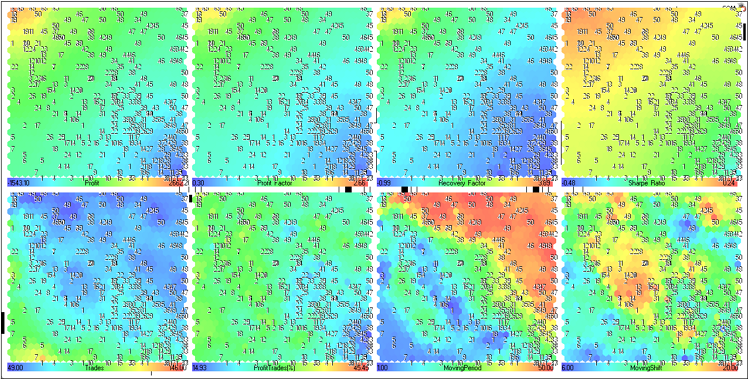
Figure 23. Mapa Kohonen de los resultados de optimización del Asesor Experto MovingAverage (Media Móvil) (representación de plano de componentes)
Consideremos los planos de componente de la fila superior (Profit, Profit Factor, Recovery Factor y Sharpe Ratio).
Se combinan en la Fig. 24.
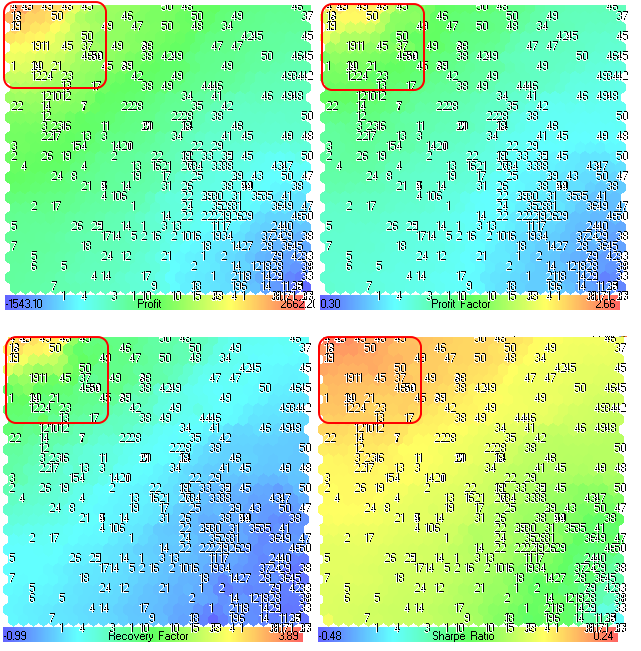
Figura 24. Planos de componente para los parámetros Profit, Profit Factor, Recovery Factor y Sharpe Ratio
Lo primero que necesitamos es encontrar las regiones con los mejores resultados de optimización.
Se puede observar en la Fig. 24 que las regiones con los valores máximos se encuentran en la esquina superior izquierda. Los números se corresponden con el período medio del indicador Media Móvil (el parámetro MovingPeriod, que usamos como título). La localización de los números es la misma para todos los planos de componente. Puesto que cada plano de componente tiene su propio intervalo de valores, los valores se muestran en el panel de gradiente.
Los mejores resultados de optimización tienen los mayores valores de Profit, Profit Factor, Recovery Factor y Sharpe Ratio, de modo que tenemos información sobre la región es en el mapa (señalada en la Fig. 24).
Los planos de componentes para Trades, ProfitTrades(%), MovingPeriod y MovingShift se muestran en la Fig. 25.
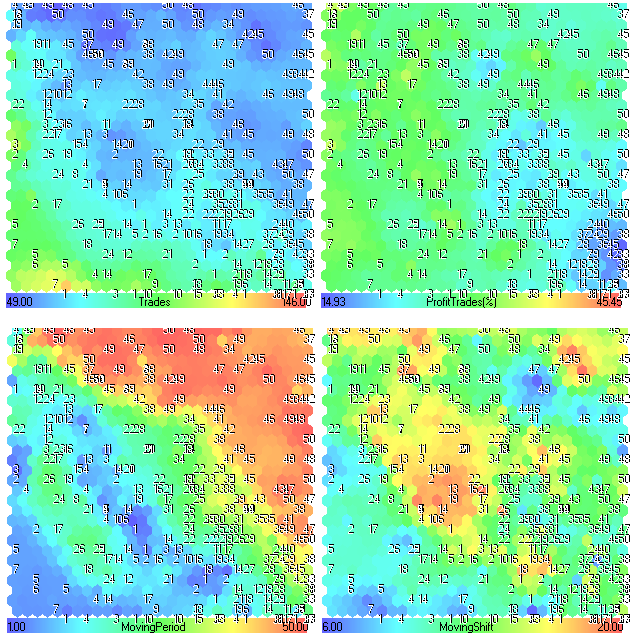
Figura 25. Planos de componente para los parámetros Trades, ProfitTrades(%), MovingPeriod y MovingShift
Análisis de Plano de Componente
A primera vista, no hay ninguna información interesante. Los primeros 4 planos de componente (Profit, Profit Factor, Recovery Factor y Sharpe Ratio) tienen un aspecto similar, porque dependen directamente del rendimiento o del sistema de trading.
Tal y como se puede ver en la Fig. 24, la región superior izquierda es muy interesante (por ejemplo, se pueden conseguir los mejores resultados si configuramos MovingPeriod entre 45 y 50).
El Asesor Experto se simuló en un intervalo de una hora en EURUSD, y su estrategia se basó en la tendencia; podemos considerar estos valores como una memoria de “tendencia de mercado”. Si es cierta, la memoria la tendencia de mercado para la primera mitad de 2011 es igual a 2 días.
Consideremos otros planos de componente.
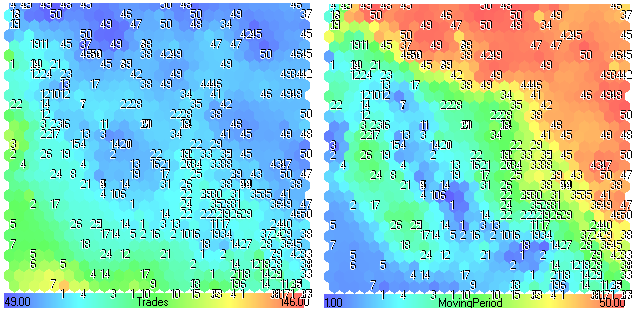
Figure 26. Planos de componente Trades-MovingPeriod
Si observamos la Fig. 26, podemos ver que los valores más bajos de MovingPeriod (las regiones azules) llevan a los valores más grandes de Trades (la regiones amarillas-rojas). Si el período de media móvil es bajo, habrá muchos cruces (operaciones de trading).
Asimismo, podemos ver este hecho en el plano de componente Trades (regiones verdes con números por debajo de 20).
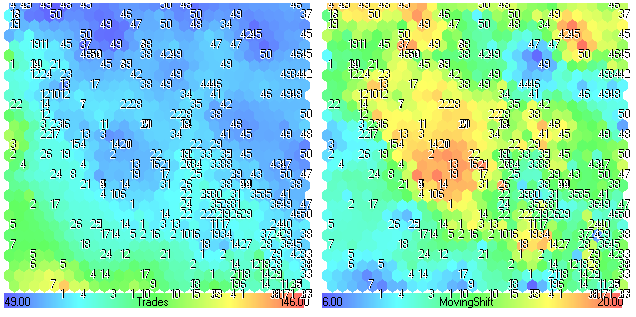
Figure 27. Planos de componente Trades-MovingShift
El número de operaciones se reduce (regiones azules) con el incremento de MovingShift (regiones amarillas-rojas). Comparando los planos de componente de MovingShift y la Fig.24, podemos ver que el parámetro MovingShift no es muy importante para el rendimiento de esta estrategia de trading.
El porcentaje de operaciones rentables ProfitTrades(%) no depende directamente de MovingPeriod o MovingShift, se trata de una característica integral del sistema de trading. En otras palabras, el análisis de su correlación con los parámetros de entrada no tiene significado alguno.
Otras estrategias de trading más complejas se pueden analizar de la misma manera. Debe encontrar los parámetros más importantes de su sistema de trading y usarlos como título.
Conclusión
La principal ventaja de los Mapas con Función de Auto-Organización es que dan la oportunidad de producir una representación bidimensional discretizada de datos de altas dimensiones. Los datos con características similares forman grupos, lo que simplifica el análisis de correlación.
Los detalles y otras aplicaciones se pueden encontrar en el excelente libro Visual Explorations in Finance: with Self-Organizing Maps (Exploraciones Visuales en Finanzas: Mapas de Auto-Organización), de Guido Deboeck y Teuvo Kohonen.
Appendix
Tras la publicación de la versión rusa, Alex Sergeev ha propuesto la versión mejorada de clases (SOM_Alex-Sergeev_en.zip).
Lista de cambios:
1. La visualización de imágenes ha cambiado: cIntBMP::Show(int aX, int aY, string aBMPFileName, string aObjectName, bool aFromImages=true)
2. Se ha añadido la posibilidad de abrir carpetas con imágenes:
#import "shell32.dll" int ShellExecuteW(int hwnd, string oper, string prog, string param, string dir, int show); #import input bool OpenAfterAnaliz=true; // open folder with maps after finish
Cambios en la clase CSOM:
- Se ha añadido un método CSOM::HideChart - oculta el gráfico.
- Se han añadido los miembros de clase m_chart, m_wnd, m_x0, m_y0 - (gráfico, ventana y coordenadas para mostrar imágenes).
+ Se ha añadido m_sID - prefijo de nombres de objeto. El prefijo usa el nombre del archivo, y por defecto se usa el prefijo"SOM".
- Todos los mapas se guardan en la carpeta con el nombre m_sID.
- Los archivos bmp se nombran según el nombre de columna de los patrones.
- Se ha modificado el método CSOM::ShowBMP (los mapas se guardan en la carpeta \Files en lugar de \Images, funciona mucho más rápido).
- CSOM::NetDeinit ha cambiado a CSOM::HideBMP.
- Se ha modificado el método CSOM::ReadCSVData, la primera columna contiene títulos.
- Se ha añadido una flag para mostrar mapas intermedios en CSOM::Train(bool bShowProgress).
- La visualización de mapas intermedios en CSOM::Train se lleva a cabo cada 2 segundos (en lugar de iteración), el progreso se muestra en el gráfico usando el Comentario.
- Se han optimizado los nombres de algunas variables, y los métodos de clase se ordenan por categoría.
El proceso de dibujo de bmp es muy lento. Si no lo necesita realmente, no lo realice en cada ocasión.
Los ejemplos de imágenes SOM con resultados optimizados están incluidos en el archivo.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/283
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
 Crear Criterios Personalizados de Optimización de Asesores Expertos
Crear Criterios Personalizados de Optimización de Asesores Expertos
 Cálculos Estadísticos
Cálculos Estadísticos
 MQL5 Wizard para "Dummies"
MQL5 Wizard para "Dummies"
 Rastreo, Depuración y Análisis Estructural de Código Fuente
Rastreo, Depuración y Análisis Estructural de Código Fuente
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Siempre miro la raíz, sabía que nadie la llamaría red neuronal si los mapas de Kohonen no podían predecir.
no pueden, el entrenamiento está ahí para desplegar vectores de pesos NS sobre conjuntos de entrenamiento - el resultado es agrupar los datos, pero la respuesta de la red en sí está ausente a otros datos - o más bien será, pero producirá valores aleatorios.
sobre la raíz... el nombre no es red de Kohonen, es como Self Organising Maps (SOM).
UPD: No veo el punto de continuar la discusión, la segunda vez que la discusión se reduce a lo que está escrito en Wiki, y ahora a lo que un cierto "Citando a S. Osovsky" escribió. Estoy de acuerdo en permanecer en el cautiverio de mi razonamiento, que no se apoya en la frase "SOM Kohonen" puede predecir, y lo contrario - no pueden
no saben cómo hacerlo, existe un entrenamiento para desplegar vectores de pesos NS sobre conjuntos de entrenamiento - el resultado es agrupar los datos, pero la respuesta de la propia red está ausente en otros datos - o más bien lo estará, pero producirá valores aleatorios.
sobre la raíz... el nombre no es red de Kohonen, sino mapas autoorganizados (SOM).
UPD: No veo el punto de continuar la discusión, la segunda vez que la discusión se reduce a lo que está escrito en Wiki, y ahora a lo que está escrito por alguien "Citando a S. Osovsky". Estoy de acuerdo en permanecer en el cautiverio de mi razonamiento, que no se apoya en la frase "SOM Kohonen" puede predecir, y lo contrario - no pueden
Uno siempre ve lo que quiere ver.
eso es exactamente lo que confirmaste con el post anterior - no tengo ganas de discutir en absoluto sobre la traducción correcta de "mapas autoorganizativos de Kohonen" - si había lugar en esa traducción:
Siempre miro la raíz, sabía que nadie lo llamaría red neuronal si los mapas de Kohonen no pudieran predecir.
Del mismo modo que no hay absolutamente ningún interés en discutir "citas de S. Osovsky", como demuestra la práctica - reimpresiones de obras de los recursos ingleses prevalecen en runet, no estoy seguro de que Osovsky escribió su propia obra, y discuto con los miembros del foro, no con el escritor?
en el enlace que mostré mis búsquedas sobre este tema en runet, en la autorizada, en mi opinión, sitio BaseGroup Labs también no hay confirmación.....
.... ok, he terminado - No quiero repetirme, sólo predecir )))).
Los mapas de Kohonen son adecuados para clasificar grandes cantidades de datos diferentes. Por ejemplo, 100 animales diferentes. En este caso, habrá que clasificar por un parámetro: el color del pelaje. Las matemáticas de este enfoque no permiten reunir diferentes parámetros.
Este enfoque es lo más estúpido posible para las decisiones de Forex. Imagínese, la clasificación por un parámetro se reduce a tomar una decisión "comprar" o "no comprar". Entonces se pueden hacer 2 nodos en el mapa de Kohonen y será bastante divertido. Por supuesto, hay mastadontos que harán 10 mil nodos y mirarán este mapa con lujuria, diciendo, ah, cómo está bellamente coloreado.
He aquí un ejemplo con el periodo y el desplazamiento de un Asesor Experto estándar de MT5 - un mapa de Kohonen separado (¿red?) para el periodo de suavizado y otro separado para el desplazamiento. Siéntese y piense qué hacer con él.
Un perseptrón multicapa es una caja negra, para la que, si todo se hace correctamente, es necesario introducir diferentes parámetros y en la salida se puede obtener una respuesta inequívoca - más que el umbral (respuesta "sí") o menos que el umbral (respuesta "no"). Esto es lo que más me conviene.
Después de leer varios libros sobre el tema del aprendizaje automático, me di cuenta de una idea que siempre se repite: no existe una plantilla única para crear una red neuronal. Cada tarea requiere un estudio extremadamente individual de los datos, su preparación, encontrar la estructura de la red y afinar esa red. En otras palabras, hay opciones que no sirven para Forex y para tomar una decisión de "comprar" o "no comprar". Creo que los mapas de Kohonen no son adecuados para esto.
Aunque las personas con talento nos equivocamos a menudo, ya que los errores son la principal fuerza del talento.
Aunque las personas con talento nos equivocamos a menudo, ya que los errores son la principal fuerza del talento.
Casi vomito
Los mapas de Kohonen son adecuados para clasificar un gran número de datos diferentes. Por ejemplo, 100 animales diferentes. En este caso, habrá que clasificar por un parámetro: el color del pelaje. Las matemáticas de este enfoque no permiten reunir diferentes parámetros.
Este enfoque es lo más estúpido posible para las decisiones de Forex. Imagínese, la clasificación por un parámetro se reduce a tomar una decisión "comprar" o "no comprar". Entonces se pueden hacer 2 nodos en el mapa de Kohonen y será bastante divertido. Por supuesto, hay mastadones que harán 10 mil nodos y mirarán este mapa con lujuria, diciendo, ah, cómo está bellamente coloreado.
He aquí un ejemplo con el periodo y el desplazamiento de un Asesor Experto estándar de MT5 - un mapa de Kohonen separado (¿red?) para el periodo de suavizado y otro separado para el desplazamiento. Te sientas y piensas qué hacer con ello.
Creo que los mapas de Kohonen no son adecuados para esto.
Simplemente no lo entiendes.
Un mapa no tiene por qué responder a la pregunta "¿hacia dónde?".
Puede resaltar patrones similares en el historial, de forma que no tengas que sentarte manualmente durante medio año a buscarlos.
Cuando a un mono se le da una herramienta, existe la posibilidad de que empiece a clavar clavos con una regla.