Asesores Expertos Auto-Optimizables con MQL5 y Python (Parte VI): Cómo aprovechar el doble descenso profundo

El sobreajuste en el aprendizaje automático puede adoptar muchas formas diferentes. Lo más común es que esto ocurra cuando un modelo de IA aprende demasiado del ruido en los datos y no logra hacer generalizaciones útiles. Esto da como resultado un desempeño pésimo cuando evaluamos el modelo con datos que no ha visto antes. Se han desarrollado muchas técnicas para mitigar el sobreajuste, pero dichos métodos a menudo pueden resultar difíciles de implementar, especialmente cuando recién estás comenzando tu viaje. Sin embargo, un artículo reciente, publicado por un grupo de diligentes ex alumnos de Harvard, sugiere que en ciertas tareas, el sobreajuste puede ser un problema del pasado. Este artículo lo guiará a través del documento de investigación y le demostrará cómo puede construir modelos de IA de primer nivel, en línea con la investigación líder a nivel mundial.

Descripción general de la metodología

Existen muchas técnicas que se utilizan para detectar el sobreajuste al desarrollar modelos de IA. El método más confiable es examinar las gráficas de error de prueba y entrenamiento del modelo. Al principio, ambas tramas pueden caer juntas, lo que es una buena señal. A medida que continuamos entrenando nuestro modelo, alcanzaremos un nivel de error óptimo y, una vez que lo superemos, nuestro error de entrenamiento seguirá disminuyendo, pero nuestro error de prueba solo empeorará. Se han desarrollado muchas técnicas para remediar este problema, como por ejemplo la parada anticipada. La detención anticipada finaliza el procedimiento de entrenamiento si el error de validación del modelo no cambia significativamente o se deteriora continuamente. Posteriormente se restauran los mejores pesos y se asume que se ha localizado el mejor modelo, como en la figura 1 a continuación.

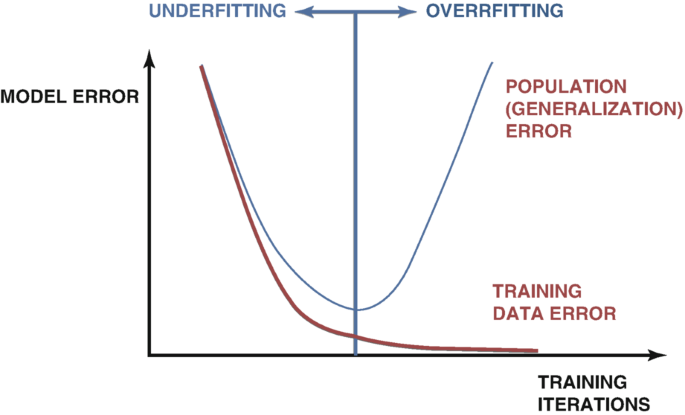
Figura 1: Un gráfico generalizado que demuestra el sobreajuste en la práctica.

Estas ideas se han visto sacudidas hasta sus cimientos por un artículo de investigación de 2019 titulado «Deep Double Descent» (Doble descenso profundo), cuyo enlace se proporciona aquí. El artículo no intenta explicar el fenómeno que demuestra, sino que solo describe las características observadas al momento de su redacción. En esencia, el artículo demuestra que, en ciertos problemas, el error de prueba del modelo disminuirá inicialmente, antes de comenzar a aumentar y luego disminuirá drásticamente una segunda vez, alcanzando nuevos mínimos antes de que el modelo finalmente converja, como se muestra en la figura 2 a continuación.

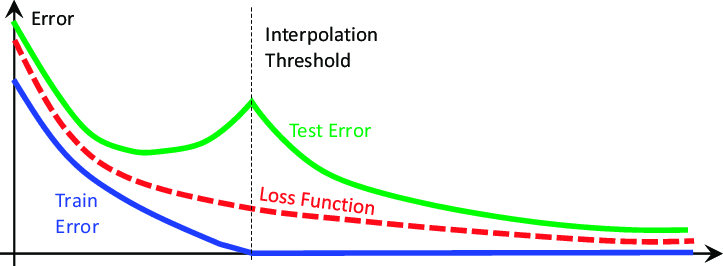
Figura 2: Visualización del fenómeno del doble descenso profundo.

El artículo demuestra que este fenómeno puede conceptualizarse como una función de:

1. Los parámetros en el modelo.
2. El número máximo de iteraciones de entrenamiento.

Es decir, si entrenamos continuamente modelos cada vez más grandes en el mismo conjunto de datos, observaremos que nuestro error de prueba primero caerá antes de empezar a aumentar, y si continuamos entrenando modelos más grandes, observaremos que nuestro error de prueba caer una segunda vez, a nuevos mínimos, creando un gráfico de error similar a la figura 2 anterior. Sin embargo, entrenar progresivamente modelos cada vez más grandes no siempre es factible debido al costo computacional. Para nuestra discusión, exploraremos el fenómeno del doble descenso profundo en función del número máximo de iteraciones que permitimos.

La idea es que, a medida que permitimos que nuestro modelo realice más iteraciones de entrenamiento, su error de validación siempre aumentará, antes de caer a nuevos mínimos. La cantidad de tiempo que tarda el modelo en alcanzar sus niveles máximos de error y comenzar a caer varía según diversos factores, como la cantidad de ruido en el conjunto de datos y el tipo de modelo que se está entrenando.

No existen explicaciones ampliamente aceptadas para el fenómeno, pero hasta ahora, la forma más fácil de comprenderlo es cuando imaginamos el doble descenso en función de los parámetros del modelo.

Imaginemos que empezamos con una red neuronal simple: lo más probable es que el modelo no se ajuste a nuestros datos. Es decir, su rendimiento podría mejorar añadiendo más complejidad al modelo. A medida que aumentamos la complejidad de nuestra red neuronal, nos acercamos lentamente a un punto en el que nuestro modelo se ajusta con precisión a nuestros datos. En el aprendizaje automático tradicional, se nos enseña que el error de entrenamiento del modelo siempre disminuirá si lo hacemos más complejo. Esto es cierto. Sin embargo, no es la verdad completa.

Una vez que nuestro modelo es lo suficientemente complejo para ajustarse perfectamente a nuestros datos, en este punto el error de entrenamiento suele ser una cantidad muy cercana a 0, y deja de disminuir a medida que hacemos nuestro modelo más complejo. Este es el primer golpe a las ideologías tradicionales del aprendizaje automático. Este punto se conoce comúnmente como el umbral de interpolación. Si continuamos aumentando la complejidad del modelo más allá de este umbral, observaremos una caída notable en la precisión de la prueba. Y en la mayoría de los casos, los índices de error del modelo caerán a nuevos mínimos y se estabilizarán allí.

Los algoritmos diseñados para mitigar el sobreajuste, como la detención temprana, parecen habernos estado frenando involuntariamente. Estos algoritmos siempre finalizarán el procedimiento de entrenamiento antes de que observemos el segundo descenso. Recreemos el fenómeno del doble descenso para observarlo por nosotros mismos de forma independiente.

Empezando

Primero necesitaremos extraer nuestros datos de nuestra plataforma MetaTrader 5 usando un script que creamos en MQL5.

//+------------------------------------------------------------------+
//|                                                      ProjectName |
//|                                      Copyright 2020, CompanyName |
//|                                       http://www.companyname.net |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//+------------------------------------------------------------------+
//| Script Inputs                                                    |
//+------------------------------------------------------------------+
input int size = 100000; //How much data should we fetch?

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//| On start function                                                |
//+------------------------------------------------------------------+
void OnStart()
  {

//--- File name
   string file_name = "Market Data " + Symbol()+  ".csv";

//--- Write to file
   int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");

   for(int i= size;i>=0;i--)
     {
      if(i == size)
        {
         FileWrite(file_handle,"Time","Open","High","Low","Close");
        }

      else
        {
         FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i),
                   iOpen(Symbol(),PERIOD_CURRENT,i),
                   iHigh(Symbol(),PERIOD_CURRENT,i),
                   iLow(Symbol(),PERIOD_CURRENT,i),
                   iClose(Symbol(),PERIOD_CURRENT,i)
                  );
        }
     }
//--- Close the file
   FileClose(file_handle);
  }
//+------------------------------------------------------------------+

Para comenzar, primero importemos las bibliotecas que necesitamos.

#Standard libraries
import pandas                  as     pd
import numpy                   as     np
import seaborn                 as     sns
import matplotlib.pyplot       as     plt
from   mpl_toolkits.mplot3d    import Axes3D
from   sklearn.linear_model    import LinearRegression
from   sklearn.neural_network  import MLPRegressor
from   sklearn.metrics         import mean_squared_error
from   sklearn.model_selection import cross_val_score,TimeSeriesSplit

Ahora, lea los datos.

#Read in the data
data = pd.read_csv('GBPUSD_Daily_20160103_20240131.csv',sep='\t')

Limpiemos nuestros datos.

#Clean up the data
data.rename(columns={'<OPEN>':'Open','<HIGH>':'High','<LOW>':'Low','<CLOSE>':'Close'},inplace=True)

Elimina las columnas innecesarias.

#Drop columns we don't need
data = data.drop(['<DATE>','<VOL>','<SPREAD>','<TICKVOL>'],axis=1)
data

Visualizando los datos.

#Plot the close price
plt.plot(data["Close"])
plt.xlabel("Time")
plt.ylabel("Close Price")
plt.title("GBPUSD Daily Close")

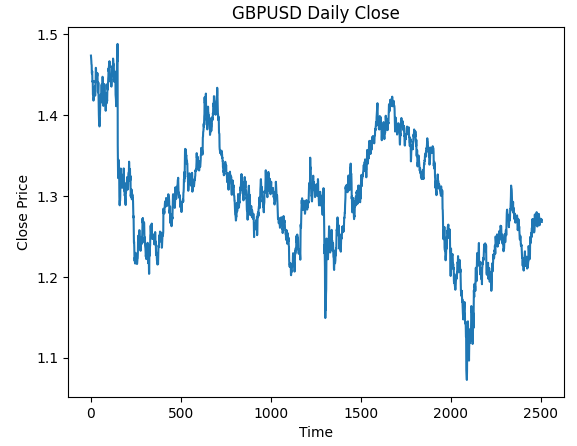
Figura 3: Los datos OHLC diarios del GBPUSD con los que trabajaremos.

Queremos entrenar un modelo que pronostique los retornos diarios del GBPUSD. Sin embargo, hay 2 variables que debemos elegir:

1. ¿Con qué frecuencia debemos calcular los rendimientos?
2. ¿Hasta dónde en el futuro debemos pronosticar?

Normalmente pronosticamos 1 paso hacia el futuro y calculamos los rendimientos como la diferencia entre 2 días consecutivos. Pero ¿es esto realmente óptimo? ¿Es esto lo mejor que podemos hacer en todo momento? No responderemos a esta pregunta, los datos mismos la responderán por nosotros.

Realicemos una búsqueda en cuadrícula de los parámetros para nuestros retornos y nuestro horizonte de pronóstico. Primero, necesitamos definir un eje uniforme para ambos parámetros.

#Define the input range
x_min , x_max = 2,100 #Look ahead
y_min , y_max = 2,100 #Period

Ahora, defina los ejes 'x' e 'y'.

#Sample input range uniformly
x_axis = np.arange(x_min,x_max,4) #Look ahead
y_axis = np.arange(y_min,y_max,4) #Period

Necesitamos crear una malla cuadriculada. La cuadrícula de malla consta de dos matrices individuales, bidimensionales, que pueden usarse juntas para mapear todas las posibles combinaciones de entrada que queremos evaluar.

#Create a meshgrid
x , y = np.meshgrid(x_axis,y_axis)

Esta función se utilizará para limpiar el conjunto de datos antes de probar la precisión de nuestro modelo con las nuevas configuraciones que nos gustaría evaluar.

#This function will create and return a clean dataframe according to our specifications
def clean_data(look_ahead,period):
    #Create a copy of the data
    temp = pd.read_csv('GBPUSD_Daily_20160103_20240131.csv',sep='\t')
    #Clean up the data
    temp.rename(columns={'<OPEN>':'Open','<HIGH>':'High','<LOW>':'Low','<CLOSE>':'Close'},inplace=True)
    temp = temp.drop(['<DATE>','<VOL>','<SPREAD>','<TICKVOL>'],axis=1)
    #Define our target
    temp["Target"] = temp["Close"].shift(-look_ahead)
    #Apply the differencing
    temp["Close"] = temp["Close"].diff(period)
    temp["Open"] = temp["Open"].diff(period)
    temp["High"] = temp["High"].diff(period)
    temp["Low"] = temp["Low"].diff(period)
    temp = temp.dropna()
    temp = temp.reset_index(drop=True)
    return(temp)

Nuestra próxima función validará de forma cruzada nuestro modelo bajo las configuraciones que pasemos y devolverá su error de validación cruzada.

#Evaluate the objective function
def evaluate(look_ahead,period):
    #Define the model
    model = LinearRegression()
    #Define our time series split
    tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)
    temp = clean_data(look_ahead,period)
    score = np.mean(cross_val_score(model,temp.loc[:,["Open","High","Low","Close"]],temp["Target"],cv=tscv))
    return(score)

Por último, necesitamos una función que registre nuestros resultados en una matriz que tenga la misma forma que cualquiera de nuestras cuadrículas de malla.

#Define the objective
def objective(x,y):
    #Define the output matrix
    results = np.zeros([x.shape[0],y.shape[0]])
    #Fill in the output matrix
    for i in np.arange(0,x.shape[0]):
        #Select the rows
        look_ahead = x[i]
        period     = y[i]
        for j in np.arange(0,y.shape[0]):
            results[i,j] = evaluate(look_ahead[j],period[j])
    return(results)

Hasta ahora, hemos implementado las funciones que necesitamos para ver cómo cambian los niveles de error de nuestro modelo a medida que cambiamos el intervalo con el que calculamos nuestros retornos y qué tan lejos en el futuro deseamos pronosticar. Observemos primero cómo se comporta un modelo simple a medida que cambiamos estos parámetros, antes de comenzar a trabajar con redes neuronales más complejas y profundas.

linear_reg_res = objective(x,y)
linear_reg_res = np.abs(linear_reg_res)

Un gráfico de contorno se utiliza comúnmente en geografía para mostrar cambios en las altitudes sobre un terreno. Podemos utilizar estos gráficos de superficie para encontrar qué par de parámetros produce los niveles de error más bajos en nuestro modelo de regresión lineal simple. Las regiones azules son combinaciones que produjeron un error bajo, mientras que las regiones rojas son combinaciones insatisfactorias. El punto blanco, en la región azul más oscura de nuestro gráfico de contorno, representa la mejor configuración de pronóstico para nuestro modelo de regresión lineal.

Como podemos ver en el gráfico a continuación, nuestro modelo de IA lineal simple habría superado fácilmente a cualquier operador en el mercado que usara el período de retorno clásico de 1 y pronosticara 1 paso en el futuro.

plt.contourf(x,y,linear_reg_res,100,cmap="jet")
plt.plot(x_axis[linear_reg_res.min(axis=0).argmin()],y_axis[linear_reg_res.min(axis=1).argmin()],'.',color='white')
plt.ylabel("Differencing Period")
plt.xlabel("Forecast Horizon")
plt.title("Linear Regression Accuracy Forecasting GBPUSD Daily Close")

Figura 4: Nuestro gráfico de contorno de la precisión de nuestra regresión lineal pronosticando el GBPUSD diario.

Visualizar los resultados en 3D genera una superficie que nos permite visualizar la relación de nuestro modelo con el mercado GBPUSD. El gráfico nos muestra que, a medida que hacemos pronósticos más a futuro, nuestros índices de error disminuyen hasta un nivel óptimo y comienzan a aumentar a medida que seguimos mirando hacia el futuro. Sin embargo, la conclusión más importante es que, para nuestro modelo lineal, la figura 5 a continuación muestra claramente que nuestras mejores entradas de modelo están en el rango de 20 a 40, tanto para nuestro horizonte de pronóstico como para el período de retorno.

#Create a surface plot
fig , ax = plt.subplots(subplot_kw={"projection":"3d"})
fig.set_size_inches(8,8)
ax.plot_surface(x,y,linear_reg_res,cmap="jet")

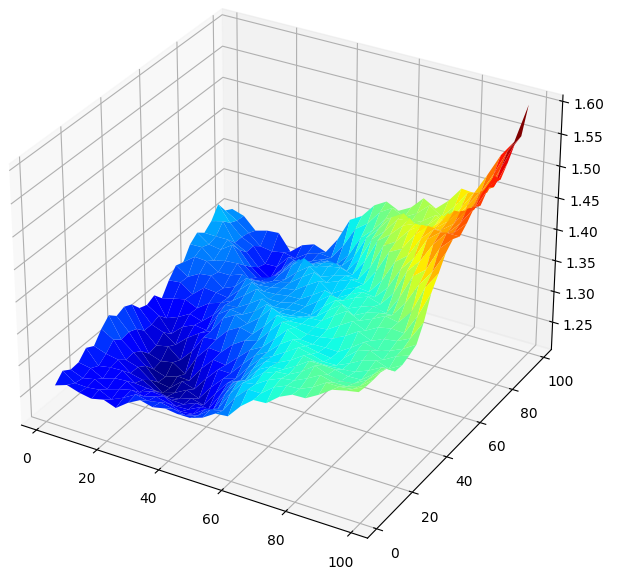
Figura 5: Visualización del error de nuestro modelo lineal al pronosticar los retornos diarios del GBPUSD.

Ahora que estamos familiarizados con los gráficos de contorno y de superficie, observemos cómo funciona nuestra red neuronal profunda cuando la usamos para buscar en el mismo espacio de parámetros.

res = objective(x,y)
res = np.abs(res)

Nuestro gráfico de superficie de redes neuronales es exponencialmente más complejo de visualizar. Las zonas azules son deseables porque representan combinaciones que produjeron niveles bajos de error. Sin embargo, observe que observamos zonas rojas que aparecen abruptamente en medio de combinaciones óptimas. Esto es bastante interesante, ¿no?

¿Cómo pueden dos combinaciones estar tan próximas entre sí y, sin embargo, tener niveles de error tan diferentes? Esto se debe en parte a la naturaleza de los algoritmos de optimización utilizados para entrenar redes neuronales. Si entrenáramos este modelo una segunda vez, obtendríamos un gráfico completamente diferente, con un punto óptimo diferente.

plt.contourf(x,y,res,100,cmap="jet")
plt.plot(x_axis[res.min(axis=0).argmin()],y_axis[res.min(axis=1).argmin()],'.',color='white')
plt.ylabel("Differencing Period")
plt.xlabel("Forecast Horizon")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")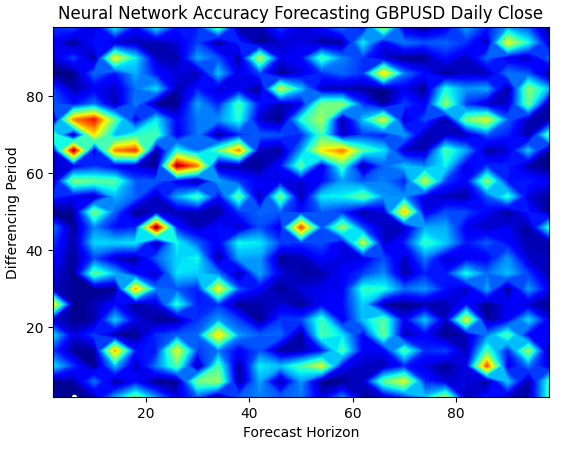

Figura 6: Las redes neuronales son muy sensibles a las entradas que tenemos.

Cuando visualizamos el rendimiento del modelo en 3D, podemos ver cuán inestables pueden ser las redes neuronales. ¿Podemos decir con seguridad que la red neuronal ha aprendido efectivamente alguna relación útil? ¿Qué modelo está funcionando mejor hasta ahora? Si abordamos el problema desde la escuela de pensamiento tradicional, seleccionaremos el modelo lineal simple porque crea gráficos de error más suaves, lo que puede ser una señal de que tiene más habilidad y las tasas de error volátiles de la red neuronal podrían verse como una señal de que está sobreajustando los datos.

Sin embargo, ese es un enfoque clásico del aprendizaje automático; desde la escuela de pensamiento contemporánea, vemos los gráficos de error de la red neuronal como una indicación de que el modelo aún no ha convergido verdaderamente, no como una indicación de que está sobreajustado. En otras palabras, según el artículo sobre el doble descenso, aún es demasiado pronto para comparar la red neuronal. Intentemos demostrarlo nosotros mismos de forma independiente, en lugar de confiar ciegamente en los artículos de investigación debido a la acreditación de los autores.

#Create a surface plot
fig , ax = plt.subplots(subplot_kw={"projection":"3d"})
fig.set_size_inches(8,8)
ax.plot_surface(x,y,res,cmap="jet")

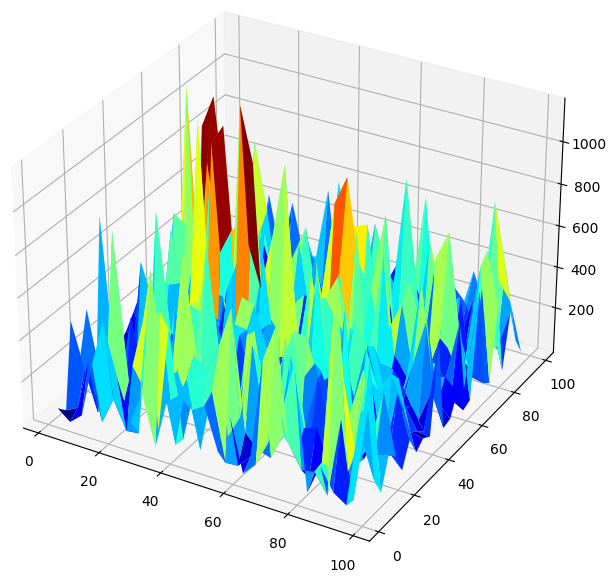
Figura 7: Nuestros niveles de error de redes neuronales pronostican el rendimiento diario del GBPUSD.

Comprobación de doble descendencia

Primero aplicaremos los mejores parámetros que hemos encontrado para calcular los retornos y hasta qué punto en el futuro deberíamos realizar pronósticos.

#The best settings we have found so far
look_ahead = x_axis[res.min(axis=0).argmin()]
difference_period = y_axis[res.min(axis=1).argmin()]
data["Target"] = data["Close"].shift(-look_ahead)
#Apply the differencing
data["Close"] = data["Close"].diff(difference_period)
data["Open"] = data["Open"].diff(difference_period)
data["High"] = data["High"].diff(difference_period)
data["Low"] = data["Low"].diff(difference_period)
data.dropna(inplace=True)
data.reset_index(drop=True,inplace=True)
data

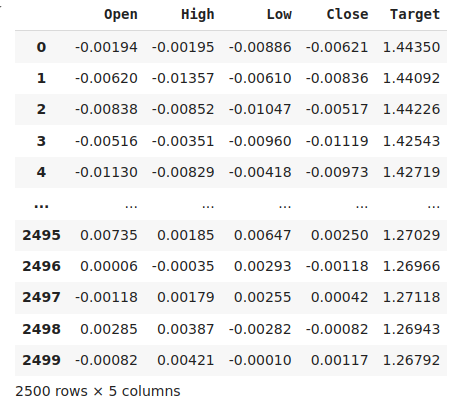
Figura 8: Nuestros datos en su forma actual.

Importando las librerías que necesitamos.

from sklearn.model_selection import train_test_split,TimeSeriesSplit
from sklearn.metrics         import mean_squared_error

Define el número máximo de épocas. Recuerde que el doble descenso es una función de la complejidad del modelo o del número máximo de iteraciones de entrenamiento. Probaremos esto con una red neuronal simple y variaremos el número máximo de iteraciones. Nuestro número máximo de iteraciones de entrenamiento serán potencias progresivas de 2.

max_epoch = 50

Creando un marco de datos para almacenar nuestros niveles de error.

err_rates = pd.DataFrame(columns = np.arange(0,max_epoch),index=["Train","Validation","Test"])

Necesitamos configurar nuestro objeto de división de series de tiempo.

tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)

Ahora realice una división de prueba de entrenamiento.

train , test = train_test_split(data,shuffle=False,test_size=0.5)

Validamos de forma cruzada nuestro modelo a medida que aumentamos el número máximo de iteraciones como potencias uniformes de 2.

for j in np.arange(0,max_epoch):
  #Define our model and measure its error
  current_train_err = []
  current_val_err = []
  model = MLPRegressor(hidden_layer_sizes=(6,5),max_iter=(2 ** j))

  for i,(train_index,test_index) in enumerate(tscv.split(train)):
    #Assess the model
    model.fit(train.loc[train_index,["Open","High","Low","Close"]],train.loc[train_index,'Target'])
    current_train_err.append(mean_squared_error(train.loc[train_index,'Target'],model.predict(train.loc[train_index,["Open","High","Low","Close"]])))
    current_val_err.append(mean_squared_error(train.loc[test_index,'Target'],model.predict(train.loc[test_index,["Open","High","Low","Close"]])))

  #Record our observations
  err_rates.loc["Train",j]      = np.mean(current_train_err)
  err_rates.loc["Validation",j] = np.mean(current_val_err)
  err_rates.loc["Test",j]       = mean_squared_error(test['Target'],model.predict(test.loc[:,["Open","High","Low","Close"]]))

Nuestras primeras 6 iteraciones muestran cómo cambiaron las tasas de error de nuestros modelos a medida que pasamos de 1 a 32 iteraciones de entrenamiento. Como podemos ver en el gráfico a continuación, nuestro error de prueba comenzó a caer, luego comenzó a aumentar, antes de alcanzar un mínimo más alto. Nuestras tasas de error de entrenamiento y validación comenzaron aumentando antes de caer a un mínimo levemente más alto y volver a aumentar. Sin embargo, 32 iteraciones solo representan un pequeño intervalo del procedimiento de entrenamiento, observemos cómo se desarrolla el resto del procedimiento de entrenamiento.

plt.plot(err_rates.iloc[0,0:5])
plt.plot(err_rates.iloc[1,0:5])
plt.plot(err_rates.iloc[2,0:5])
plt.legend(["Train Error","Validation Error","Test Error"])
plt.ylabel("RMSE")
plt.xlabel("Epochs: Our Epochs Are Indices of 2")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")

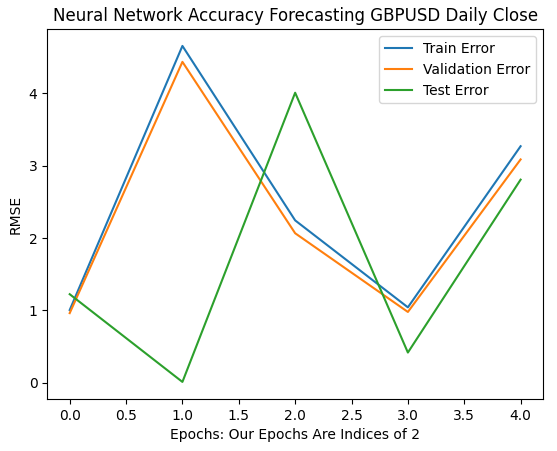
Figura 9: Nuestra precisión de validación a medida que pasamos de 1 a 32 iteraciones.

A medida que avanzamos, ahora vemos cómo evolucionan las tasas de error de nuestro modelo en el intervalo de 64 a 256. Parece que después de cierta divergencia, nuestros índices de error finalmente están convergiendo hacia un mínimo. Sin embargo, según el documento, todavía queda un largo camino por recorrer.

El lector debe tener en cuenta que, de manera predeterminada, scikit-learn crea redes neuronales que realizan solo 200 iteraciones. Este es un número ligeramente menor que 2 elevado a 8. Y con algoritmos como la parada temprana, habríamos quedado atrapados en óptimos locales engañosos, en algún lugar entre las colinas y los valles de la superficie irregular que observamos en la figura 7 anterior. 

plt.plot(err_rates.iloc[0,0:9])
plt.plot(err_rates.iloc[1,0:9])
plt.plot(err_rates.iloc[2,0:9])
plt.legend(["Train Error","Validation Error","Test Error"])
plt.ylabel("RMSE")
plt.xlabel("Epochs: Our Epochs Are Indices of 2")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")

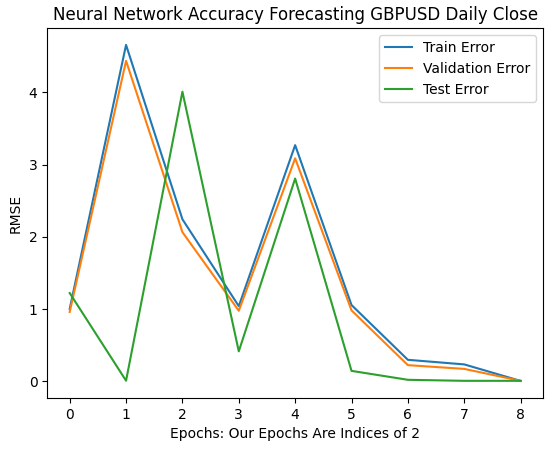
Figura 10: Las tasas de error de nuestro modelo están comenzando a converger.

¡Nuestras tasas de error óptimas se produjeron cuando se permitió que nuestro modelo realizara más de mil millones de iteraciones! El número exacto es 2 elevado a 30. Este punto está marcado por la línea vertical roja en la figura 11 a continuación. Normalmente realizamos fracciones del número óptimo de iteraciones, por miedo a sobreajustar los datos, dejándonos atrapados en niveles de error subóptimos a la izquierda de la línea roja.

plt.plot(err_rates.iloc[0,:])
plt.plot(err_rates.iloc[1,:])
plt.plot(err_rates.iloc[2,:])
plt.axvline(err_rates.loc["Test",:].argmin(),color='red')
plt.legend(["Train Error","Validation Error","Test Error","Double Descent Error"])
plt.ylabel("RMSE")
plt.xlabel("Epochs: Our Epochs Are Indices of 2")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")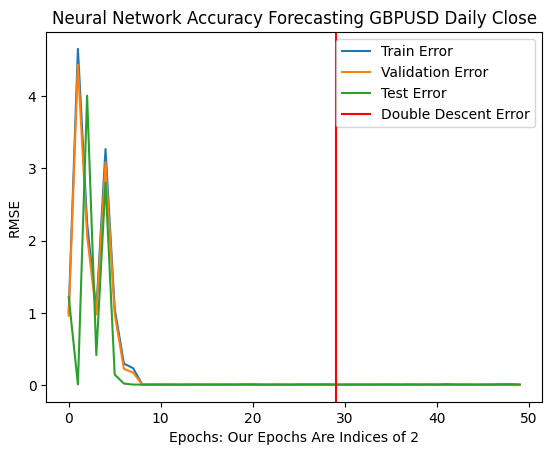

Figura 11: Nuestros niveles de error de doble descenso están marcados por la línea vertical roja, y a la izquierda podemos observar el dominio clásico del aprendizaje automático tradicional.

Optimizando nuestra red neuronal

Está claro que el artículo tiene cierto mérito. En circunstancias normales, ni siquiera consideraríamos remotamente permitir numerosas iteraciones, por temor al sobreajuste. Ahora podemos optimizar nuestro modelo con confianza sin temor a sobreajustarlo a los datos de entrenamiento.

from sklearn.model_selection import RandomizedSearchCV

Inicializar el modelo.

#Reinitialize the model
model = MLPRegressor(max_iter=(err_rates.loc["Test",:].argmin()))

Definamos los parámetros que queremos buscar.

#Define the tuner
tuner = RandomizedSearchCV(
        model,
        {
        "activation" : ["relu","logistic","tanh","identity"],
        "solver":["adam","sgd","lbfgs"],
        "alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
        "tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "learning_rate":['constant','adaptive','invscaling'],
        "learning_rate_init":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "hidden_layer_sizes":[(1,4),(5,8,10),(5,10,20),(10,50,10),(20,5),(1,5),(20,10)],
        "early_stopping":[True,False],
        "warm_start":[True,False],
        "shuffle": [True,False]
        },
        n_iter=2**9,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

Por último, ajuste el objeto sintonizador.

tuner.fit(train.loc[:,["Open","High","Low","Close"]],train.loc[:,"Target"])

Los mejores parámetros que encontramos.

tuner.best_params_

{'warm_start': True,
 'tol': 0.1,
 'solver': 'lbfgs',
 'shuffle': False,
 'learning_rate_init': 1e-06,
 'learning_rate': 'adaptive',
 'hidden_layer_sizes': (5, 8, 10),
 'early_stopping': False,
 'alpha': 1e-05,
 'activation': 'relu'}

Conversión a ONNX

Ahora que hemos creado nuestro modelo, podemos convertirlo al formato ONNX. ONNX significa Open Neural Network Exchange y es un protocolo de código abierto que nos permite crear e implementar modelos de IA en cualquier lenguaje de programación que amplíe el soporte a la especificación API de ONNX. MQL5 nos permite importar nuestros modelos de IA e implementarlos directamente en nuestras terminales. Primero, importaremos las bibliotecas que necesitamos.

import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType

Entonces, ajustemos nuestro modelo a todos los datos que tenemos.

model = tuner.best_estimator_.fit(train.loc[:,["Open","High","Low","Close"]],train.loc[:,"Target"])

Especifique la forma de entrada de su modelo.

#Define the input shape of 1,4
initial_type = [('float_input', FloatTensorType([1, 4]))]
#Specify the input shape
onnx_model = convert_sklearn(model, initial_types=initial_type)

Guarde el modelo ONNX.

#Save the onnx model
onnx.save(onnx_model,"GBPUSD DAILY.onnx")

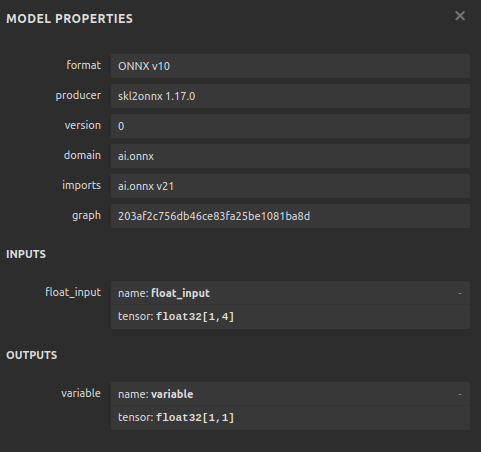
Figura 12: Parámetros de entrada y salida de nuestro modelo ONNX.

 

Implementación en MQL5

Ahora podemos comenzar a implementar nuestra estrategia comercial en MQL5. Nuestra estrategia se basará en el marco temporal diario. Utilizaremos una combinación de Bandas de Bollinger y promedios móviles para determinar la tendencia predominante del mercado.

Las Bandas de Bollinger se utilizan comúnmente para identificar valores que están sobrecomprados o sobrevendidos. Comúnmente, cuando los niveles de precios alcanzan la banda superior, el valor en observación se considera sobrecomprado. Normalmente, cuando los niveles de precios están sobrecomprados, los operadores esperan que los niveles de precios futuros caigan y vuelvan al nivel de precios promedio. En lugar de ello, utilizaremos la Banda de Bollinger con el fin de seguir la tendencia.

Cuando los niveles de precios cruzan por encima de la línea media de las Bandas, consideraremos que es una fuerte señal alcista, y lo contrario es cierto cuando los niveles de precios caen por debajo de la banda media, lo tomaremos como una fuerte señal de venta. Es probable que unas reglas comerciales tan simples generen demasiadas señales, lo que no siempre es ideal. En su lugar, filtraremos las fluctuaciones de precios teniendo en cuenta los valores medios móviles en lugar de la propia evolución de los precios.

Aplicaremos 2 medias móviles, una en el precio alto y otra en el precio bajo, para crear un canal de media móvil. Nuestras señales de entrada se generarán cuando ambas medias móviles crucen la línea media de la banda de Bollinger y nuestra señal de IA pronostique que el precio se moverá efectivamente en esa dirección. 

Por último, nuestras posiciones se cerrarán cuando los canales de media móvil crucen la línea media de la banda de Bollinger, o si el canal de media móvil vuelve a caer dentro de las Bandas de Bollinger tras romperlas, lo que ocurra primero.

Comencemos cargando primero nuestro modelo ONNX.

//+------------------------------------------------------------------+
//|                                                    GBPUSD AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Load our ONNX file                                               |
//+------------------------------------------------------------------+
#resource  "\\Files\\GBPUSD DAILY.onnx" as const uchar onnx_buffer[];

A continuación, debemos cargar la biblioteca de comercio 'Trade' para obtener ayuda para administrar nuestras posiciones.

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include <Trade\Trade.mqh>
CTrade Trade;

También necesitamos algunas variables globales para los datos que compartiremos en diferentes partes de nuestra aplicación.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
bool   patience = true;
long   onnx_model;
int    bb_handler,ma_h_handler,ma_l_handler;
double ma_h_buffer[],ma_l_buffer[];
double bb_h_buffer[],bb_m_buffer[],bb_l_buffer[];
int    state;
double bid,ask;
vectorf model_forecast = vectorf::Zeros(1);

Nuestros indicadores técnicos tienen parámetros de período que queremos que nuestro usuario final pueda ajustar a medida que cambian las condiciones del mercado.

//+------------------------------------------------------------------+
//| User Inputs                                                      |
//+------------------------------------------------------------------+
input group "Technical Indicators"
input int bb_period = 60;
input int ma_period = 14;

La primera vez que se carga nuestra aplicación, primero cargaremos nuestros indicadores técnicos antes de cargar nuestro modelo ONNX. Utilizaremos el buffer ONNX que definimos al comienzo de nuestro programa para crear un modelo ONNX a partir de ese buffer. A partir de ahí, validaremos que nuestro modelo ONNX sea sólido y que nuestros parámetros de entrada y salida estén en línea con nuestras especificaciones.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Setup technical indicators
   bb_handler   = iBands(Symbol(),PERIOD_D1,bb_period,0,1,PRICE_CLOSE);
   ma_h_handler = iMA(Symbol(),PERIOD_D1,ma_period,0,MODE_SMA,PRICE_HIGH);
   ma_l_handler = iMA(Symbol(),PERIOD_D1,ma_period,0,MODE_SMA,PRICE_LOW);
//--- Define our ONNX model
   ulong input_shape [] = {1,4};
   ulong output_shape [] = {1,1};
//--- Create the model
   onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT);

   if(onnx_model == INVALID_HANDLE)
     {
      Comment("[ERROR] Failed to load AI module correctly");
      return(INIT_FAILED);
     }

//--- Validate I/O
   if(!OnnxSetInputShape(onnx_model,0,input_shape))
     {
      Comment("[ERROR] Failed to set input shape correctly: ",GetLastError()," Actual shape: ",OnnxGetInputCount(onnx_model));
      return(INIT_FAILED);
     }

   if(!OnnxSetOutputShape(onnx_model,0,output_shape))
     {
      Comment("[ERROR] Failed to load AI module correctly: ",GetLastError()," Actual shape: ",OnnxGetOutputCount(onnx_model));
      return(INIT_FAILED);
     }


//--- Everything was okay
   return(INIT_SUCCEEDED);
  }

Si nuestra aplicación comercial ya no está en uso, liberaremos los recursos que ya no utilizamos.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   OnnxRelease(onnx_model);
   IndicatorRelease(bb_handler);
   IndicatorRelease(ma_h_handler);
   IndicatorRelease(ma_l_handler);
  }

Finalmente, cada vez que recibamos nuevas cotizaciones de precios, actualizaremos nuestras variables globales. A partir de ahí, nuestro siguiente paso a dar dependerá del número de posiciones que tengamos abiertas. Si no hay ninguna, buscaremos una señal de entrada. De lo contrario, comprobaremos si hay señales de salida.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Update technical data
   update();

   if(PositionsTotal() == 0)
     {
      patience = true;
      check_setup();
     }

   if(PositionsTotal() > 0)
     {
      string direction = model_forecast[0] > iClose(Symbol(),PERIOD_D1,0) ? "UP" : "DOWN";
      Comment("Model Forecast: ",model_forecast[0]," ",direction);
      close_setup();
     }
  }

La siguiente función obtendrá un pronóstico de nuestro modelo.

//+------------------------------------------------------------------+
//| Get a prediction from our model                                  |
//+------------------------------------------------------------------+
void model_predict(void)
  {
   double o,h,l,c;
   vector op,hi,lo,cl;
   op.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_OPEN,0,3);
   hi.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_HIGH,0,3);
   lo.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_LOW,0,3);
   cl.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_CLOSE,0,3);

   o =  op[2]  - op[0];
   h =  hi[2]  - hi[0];
   l =  lo[2]  - lo[0];
   c =  cl[2]  - cl[0];

   vectorf model_inputs = vectorf::Zeros(4);
   model_inputs[0] = o;
   model_inputs[1] = h;
   model_inputs[2] = l;
   model_inputs[3] = c;

   OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_forecast);
  }

Ahora definiremos cómo nuestra aplicación debe cerrar sus posiciones. El booleano de paciencia se utiliza para controlar cuándo la aplicación debe cerrar nuestras posiciones. Si el canal de media móvil no ha roto las bandas de Bollinger cuando se abrieron inicialmente nuestras posiciones, la variable de paciencia se establecerá en verdadera. El valor seguirá siendo verdadero hasta que el canal de media móvil salga de las bandas. En ese punto, la bandera de paciencia se establece en falsa, y si el canal vuelve a caer dentro de las bandas, nuestras posiciones se cerrarán.

//+------------------------------------------------------------------+
//| Close our open positions                                         |
//+------------------------------------------------------------------+
void close_setup(void)
  {
   if(patience)
     {
      if(state == 1)
        {
         if(ma_l_buffer[0] > bb_h_buffer[0])
           {
            patience = false;
           }


         if((ma_h_buffer[0] < bb_m_buffer[0]) && (ma_l_buffer[0] < bb_m_buffer[0]))
           {
            Trade.PositionClose(Symbol());
           }
        }

      else
         if(state == -1)
           {
            if(ma_h_buffer[0] < bb_l_buffer[0])
              {
               patience = false;
              }

            if((ma_h_buffer[0] > bb_m_buffer[0]) && (ma_l_buffer[0] > bb_m_buffer[0]))
              {
               Trade.PositionClose(Symbol());
              }
           }
     }

   else
     {
      if((state == -1) && (ma_l_buffer[0] > bb_l_buffer[0]))
        {
         Trade.PositionClose(Symbol());
        }

      if((state == 1) && (ma_h_buffer[0] < bb_h_buffer[0]))
        {
         Trade.PositionClose(Symbol());
        }
     }

  }

Para que consideremos válida la configuración, queremos que el canal de media móvil esté completamente en un lado de la banda media y que nuestro pronóstico de IA concuerde con la acción del precio. De lo contrario, simplemente esperaremos en lugar de perseguir fluctuaciones fugaces en los precios.

//+------------------------------------------------------------------+
//| Check for valid trade setups                                     |
//+------------------------------------------------------------------+
void check_setup(void)
  {

   if((ma_h_buffer[0] < bb_m_buffer[0]) && (ma_l_buffer[0] < bb_m_buffer[0]))
     {
      model_predict();
      if((model_forecast[0] < iClose(Symbol(),PERIOD_CURRENT,0)))
        {
         if(ma_h_buffer[0] < bb_l_buffer[0])
            patience = false;

         Trade.Sell(0.3,Symbol(),bid,0,0,"GBPUSD AI");
         state = -1;
        }
     }

   if((ma_h_buffer[0] > bb_m_buffer[0]) && (ma_l_buffer[0] > bb_m_buffer[0]))
     {
      model_predict();
      if(model_forecast[0] > iClose(Symbol(),PERIOD_CURRENT,0))
        {
         if(ma_l_buffer[0] > bb_h_buffer[0])
            patience = false;

         Trade.Buy(0.3,Symbol(),ask,0,0,"GBPUSD AI");
         state = 1;
        }
     }
  }

Por último, necesitamos una función responsable de actualizar nuestras variables globales.

//+------------------------------------------------------------------+
//| Update our market data                                           |
//+------------------------------------------------------------------+
void update(void)
  {
   CopyBuffer(bb_handler,0,0,1,bb_m_buffer);
   CopyBuffer(bb_handler,1,0,1,bb_h_buffer);
   CopyBuffer(bb_handler,2,0,1,bb_l_buffer);
   CopyBuffer(ma_h_handler,0,0,1,ma_h_buffer);
   CopyBuffer(ma_l_handler,0,0,1,ma_l_buffer);
  }
//+------------------------------------------------------------------+

Ahora podemos volver a probar nuestra estrategia comercial. Utilizamos el Probador de estrategias para evaluar nuestra aplicación durante aproximadamente 3 años de datos diarios del mercado GBPUSD. Tenga en cuenta que cuando construimos nuestro modelo de IA, utilizamos datos diarios del mercado desde 2016 hasta 2024. Por lo tanto, la prueba retrospectiva que mostramos a continuación prueba efectivamente nuestra estrategia de IA con datos que el modelo ya ha visto. Tenga en cuenta que, si bien nuestro modelo estuvo expuesto a los datos y entrenado bien, el saldo de nuestra cuenta fue muy volátil a lo largo del tiempo.

Esto demuestra que, aunque hemos entrenado bien nuestro modelo, los modelos de IA no "recuerdan" lo que "aprendieron" en el sentido en que lo hace un humano. Intenta crear una fórmula que se generalice bien a los datos. Lo que significa que aún puede cometer errores en los datos con los que ya fue entrenado.

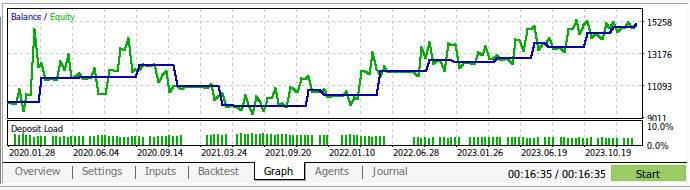
Figura 13: Realizamos pruebas retrospectivas de nuestra aplicación durante aproximadamente 3 años de datos diarios del mercado GBPUSD.

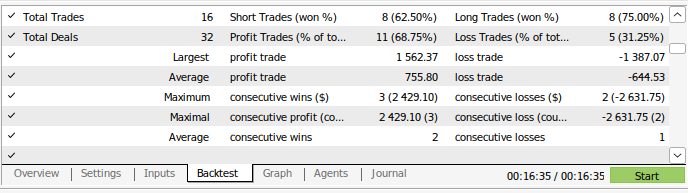
Figura 14: Detalles del rendimiento comercial de nuestro modelo.

Conclusión

Para recapitular, hemos demostrado que la apariencia de "sobreajuste" en algunas circunstancias puede ser sólo un llamado a un mayor esfuerzo. La ideología clásica de sobreajustar los modelos de IA nos ha mantenido, hasta cierto punto, estancados en niveles de error subóptimos. Sin embargo, estamos seguros de que después de leer este artículo, usted podrá hacer un mejor uso de sus modelos. Que el lector recuerde que también teníamos la opción de simplemente aumentar el número de capas ocultas en el modelo, o simplemente entrenar un modelo con una capa y aumentar el ancho de la capa del modelo. Sin embargo, entrenar modelos tan masivos requerirá un enfoque completamente diferente, que requerirá habilidades en computación paralela.

Este artículo le ha proporcionado un enfoque computacionalmente económico para entrenar un modelo básico de tamaño fijo y usar datos diarios debido a la pequeña cantidad de filas que tendremos que procesar en ese período de tiempo. Sin embargo, para que nuestros resultados sean concluyentes y sólidos, es posible que necesitemos reducir nuestro conjunto de entrenamiento a la mitad de su tamaño para que nuestro modelo se entrene de 2016 a 2020 y todos los datos de 2020 a 2024 no estén expuestos a nuestro modelo durante el entrenamiento.