Redes neuronales en el trading: Análisis de nubes de puntos (PointNet)

Introducción

Las nubes de puntos son estructuras sencillas y unificadas que evitan las heterogeneidades combinatorias y las complejidades en las redes. Como las nubes de puntos no tienen un formato convencional, la mayoría de los investigadores suelen convertir estos conjuntos de datos en mallas de vóxeles 3D convencionales o conjuntos de imágenes antes de pasarlos a la arquitectura de las redes profundas. No obstante, dicha transformación hace que los datos resultantes sean innecesariamente voluminosos, y también puede introducir artefactos de cuantificación que a menudo ocultan la invarianza natural de los datos.

Por esta razón, algunos investigadores han recurrido a una representación de datos diferente para la geometría 3D, utilizando simplemente una nube de puntos. Los modelos que trabajan con esa representación de los datos de origen deben considera el hecho de que una nube de puntos es simplemente un conjunto de puntos y resulta invariable a las permutaciones de sus miembros. Esto requiere una cierta simetría en los cálculos del modelo.

Una de estas soluciones se describe en el artículo "PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation". El modelo presentado, denominado PointNet, es una solución arquitectónica unificada que toma directamente una nube de puntos como datos de entrada y retorna etiquetas de clase para todo el conjunto de datos de origen o etiquetas de segmentos (partes) para cada punto de los datos de origen.

La arquitectura básica del modelo es notablemente sencilla. En las fases iniciales, cada punto se procesa de forma idéntica e independiente. En la configuración básica, cada punto está representado por solo tres de sus coordenadas (x, y, z). Es posible añadir dimensiones adicionales calculando las normales y otros objetos locales o globales.

La clave del enfoque PointNet reside en el uso de una única función simétrica, MaxPooling. En esencia, la red aprende un conjunto de funciones de optimización que seleccionan objetos interesantes o informativos en una nube de puntos y codifican la razón de su selección, mientras que las capas totalmente conectadas en la salida del modelo agregan estos valores óptimos aprendidos en un descriptor global para toda la forma.

Resulta sencillo aplicar transformaciones rígidas o afines al formato de datos de origen especificado porque cada punto se transforma de forma independiente. Por ello, los autores del método añaden un modelo de transformación espacial dependiente de los datos que intenta canonizar los datos antes de procesarlos en PointNet, lo que mejora aún más la eficacia de la solución.

1. El algoritmo PointNet

Los autores del método PointNet han desarrollado un marco de aprendizaje profundo que utiliza directamente conjuntos de puntos desordenados como datos de entrada. Una nube de puntos se representa como un conjunto de puntos 3D {Pi|i=1,…,n}, donde cada punto Pi constituye su vector de coordinadas (x, y, z) más canales de características adicionales como el color, etc.

Las entradas del modelo son un subconjunto de puntos del espacio euclidiano que poseen tres propiedades básicas:

• Desorden. A diferencia de los arrays de píxeles de las imágenes, una nube de puntos supone una colección de elementos sin un orden determinado. En otras palabras, un modelo que consuma un conjunto de N puntos 3D deberá ser invariable a N! permutaciones en el orden en que se suministra el conjunto de datos original.
• Interacciones entre puntos. Los puntos se toman de un espacio con una métrica de distancia. Esto significa que los puntos no están aislados, sino que los puntos vecinos forman un subconjunto significativo. Por lo tanto, el modelo deberá ser capaz de captar las estructuras locales de los puntos cercanos, así como las interacciones combinatorias entre las estructuras locales.
• Invarianza bajo transformaciones. Como objeto geométrico, la representación aprendida de un conjunto de puntos deberá ser invariante ante determinadas transformaciones. Por ejemplo, la rotación y desplazamiento simultáneos de puntos no debería cambiar la categorización global de la nube de puntos ni su segmentación.

La arquitectura PointNet está diseñada de tal manera que los modelos de clasificación y segmentación de datos comparten la mayoría de las estructuras comunes. Asimismo, contiene tres módulos clave:

• la capa de agrupación máxima como función simétrica para agregar la información de todos los puntos,
• la estructura de combinación de datos locales y globales,
• dos redes de alineación conjunta que alinean tanto los puntos de origen como los objetos puntuales.

Para que el modelo resulte invariable a las permutaciones de los datos de entrada, existen tres estrategias:

1. clasificar los datos iniciales en orden canónico;
2. usar los datos de origen como secuencia para el entrenamiento de la RNN, pero complementando obligatoriamente la muestra de entrenamiento con todos los tipos posibles de permutaciones;
3. utilizar una simple función simétrica para agregar la información de cada punto. Cuando una función simétrica toma n vectores como entradas y ofrece como salida un nuevo vector que es invariante respecto al orden de entrada.

la clasificación de los datos de origen parece una solución sencilla. Pero de hecho no existe ninguna ordenación en el espacio multidimensional que resulte estable bajo perturbaciones puntuales en el sentido general. Por lo tanto, la clasificación no resolverá completamente el problema de ordenación, así que resulta difícil que un modelo aprenda una correspondencia coherente entre entradas y salidas. En sus experimentos, los autores del método han descubierto que aplicar MLP directamente a un conjunto clasificado de puntos ofrece un rendimiento pobre, aunque ligeramente superior al procesamiento directo de datos de origen sin clasificar.

Aunque la RNN posee una robustez relativamente buena frente al orden de las fuentes para secuencias de pequeña longitud (decenas), resulta difícil de escalar a miles de elementos fuente. El artículo del autor también demuestra empíricamente que el modelo basado en RNN no obtiene peores resultados que el algoritmo PointNet propuesto.

La idea básica de PointNet consiste en aproximar una función general definida sobre un conjunto de puntos aplicando una función simétrica a los elementos transformados del conjunto:

El módulo básico propuesto empíricamente por los autores del método es muy sencillo: en primer lugar, se estiman aproximadamente h mediante un MLP y g usando una composición de una función de variable única y una función de agrupación máxima. La eficacia de este planteamiento se ha confirmado en experimentos. A través de la colección h, se puede conocer un número f para captar diferentes propiedades del conjunto de datos de origen.

A pesar de la simplicidad del módulo clave, este tiene propiedades interesantes y puede alcanzar un alto rendimiento en varias aplicaciones diferentes.

La salida del módulo de claves propuesto genera un vector [f1,…,fK], que supone la firma global del conjunto de datos original. A continuación, se puede entrenar fácilmente un clasificador SVM o MLP como características globales para la clasificación. No obstante, la segmentación de puntos requiere una combinación de conocimientos locales y globales. Esto puede lograrse de forma sencilla pero muy eficaz.

Tras calcular el vector de características de la nube de puntos global, los autores de PointNet proponen devolverlo a cada objeto puntual concatenando el objeto global con cada uno de ellos. A continuación, se extraen nuevas características puntuales basadas en los objetos puntuales fusionados; esta vez, la característica de flujo considerarán tanto la información local como la global.

Con esta modificación, PointNet puede predecir el número de puntos por punto, basado tanto en la geometría local como en la semántica global. Por ejemplo, podemos predecir con exactitud las normales de cada punto confirmando que el modelo es capaz de resumir la información de la vecindad local de un punto. Los resultados experimentales presentados, realizados por los autores del método, demuestran que el modelo propuesto puede alcanzar resultados de vanguardia en la segmentación de partes de formas y en la segmentación de escenas.

El etiquetado semántico de una nube de puntos debe ser invariable si la nube de puntos sufre determinadas transformaciones geométricas, como transformaciones rígidas. Por consiguiente, los autores del método esperan que la representación aprendida sobre el conjunto de puntos sea invariante a estas transformaciones.

Una solución natural sería alinear todo el conjunto de fuentes con el espacio canónico antes de extraer las características. El formulario de introducción de nubes de puntos logra este objetivo de forma simple. Basta con predecir la matriz de transformación afín usando una minirred (T-net) y aplicando directamente esta transformación a las coordenadas de los puntos fuente. La minirred en sí misma es similar a una red grande y consta de módulos básicos de extracción de características independientes del punto, agrupación máxima y capas totalmente conectadas.

Esta idea puede ampliarse a la alineación del espacio de características. Podemos insertar otra red de alineación en objetos puntuales y predecir una matriz de transformación de características para alinear objetos partiendo de diferentes datos de entrada de nubes de puntos. No obstante, la matriz de transformación del espacio de características posee una dimensionalidad mucho mayor que la matriz de transformación espacial, lo cual aumenta enormemente la complejidad de la optimización. Por ello, los autores del método añaden al error de entrenamiento SoftMax un término de regularización. Para ello, limitamos la matriz de transformación de características para que se aproxime a una matriz ortogonal:

donde A será la matriz de alineación de características predicha por la minirred.

La transformación ortogonal no supondrá una pérdida de información en la entrada, por lo que resulta deseable. Los autores de PointNet han descubierto que cuando se añade un término de regularización, la optimización se vuelve más estable y el modelo logra un mejor rendimiento.

A continuación le presentamos la visualización del método PointNet por parte del autor.

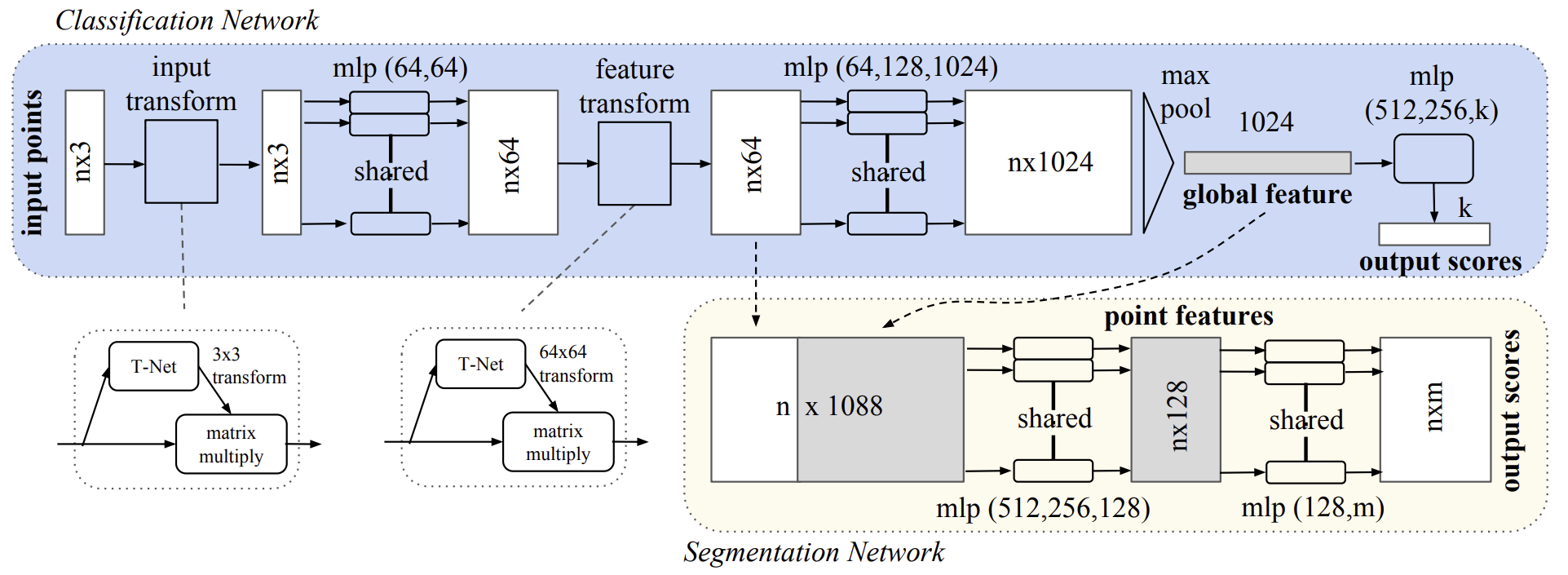
2. Implementación con MQL5

En la sección anterior nos hemos familiarizado con la descripción teórica de los enfoques propuestos por los autores del método PointNet. Ahora es el momento de pasar a la parte práctica de nuestro artículo, donde implementaremos nuestra propia visión de los enfoques propuestos utilizando los recursos de MQL5.

2.1 Creando la clase PointNet

Para implementar los algoritmos PointNet en código, crearemos una nueva clase CNeuronPointNetOCL con herencia de la funcionalidad básica de la capa CNeuronBaseOCL completamente conectada. A continuación, le mostraremos la estructura de la nueva clase,

class CNeuronPointNetOCL   :  public CNeuronBaseOCL
  {
protected:
   CNeuronPointNetOCL   *cTNet1;
   CNeuronBaseOCL       *cTurned1;
   CNeuronConvOCL       cPreNet[2];
   CNeuronBatchNormOCL  cPreNetNorm[2];
   CNeuronPointNetOCL   *cTNet2;
   CNeuronBaseOCL       *cTurned2;
   CNeuronConvOCL       cFeatureNet[3];
   CNeuronBatchNormOCL  cFeatureNetNorm[3];
   CNeuronTransposeOCL  cTranspose;
   CNeuronProofOCL      cMaxPool;
   CNeuronBaseOCL       cFinalMLP[2];
   //---
   virtual bool         OrthoganalLoss(CNeuronBaseOCL *NeuronOCL, bool add = false);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override ;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronPointNetOCL(void) {};
                    ~CNeuronPointNetOCL(void);
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint output, bool use_tnets,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronPointNetOCL; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Ya es habitual observar un gran número de objetos anidados en la estructura de clases. pero en este caso, existen matices. En primer lugar, junto a los objetos estáticos, se observan varios objetos dinámicos. Y en el destructor de la clase deberemos eliminarlos de la memoria del dispositivo.

CNeuronPointNetOCL::~CNeuronPointNetOCL(void)
  {
   if(!!cTNet1)
      delete cTNet1;
   if(!!cTNet2)
      delete cTNet2;
   if(!!cTurned1)
      delete cTurned1;
   if(!!cTurned2)
      delete cTurned2;
  }

Sin embargo, no estamos creando los objetos especificados en el constructor de la clase, lo cual nos permite dejarla vacía.

El segundo matiz es que dos de los objetos dinámicos anidados son instancias de la clase CNeuronPointNetOCL que estamos creando. Sería una especie de "matrioshka dentro de otra matrioshka".

Y ambos matices se relacionan con el planteamiento de alinear los datos y características originales con algún espacio canónico propuesto por los autores del método. Hablaremos más sobre esto durante la implementación de los métodos de nuestra clase.

Como viene siendo habitual, la inicialización de una nueva instancia de un objeto de clase se realizará en el método Init. En los parámetros de este método obtendremos las constantes principales que definirán la arquitectura del objeto a crear.

Aquí cabe señalar que, en este estudio de caso, hemos tomado la decisión de construir un algoritmo de clasificación de nubes de puntos. La idea general consiste en construir un Codificador de estados del entorno utilizando enfoques PointNet que retorne alguna distribución de probabilidad de atribución del estado del entorno actual a un tipo u otro. La política del Actor, entre tanto, consistirá en hacer corresponder un determinado tipo de condición del entorno con algún conjunto de parámetros de transacción que potencialmente produzcan el máximo rendimiento en la condición del entorno analizada. De ahí los principales parámetros de la arquitectura de clases que hay que crear:

• window — tamaño de la ventana de parámetros de un punto de la nube analizada;
• units_count — número de puntos en la nube;
• output — tamaño del tensor de resultados;
• use_tnets — necesidad de crear modelos de proyección de los datos y características de origen en el espacio canónico.

Aquí deberá considerarse que el parámetro output especificará el tamaño completo del búfer de resultados. Y no deberá confundirse con el parámetro de la ventana de resultados que hemos utilizado antes. Al fin y al cabo, en este caso esperamos obtener como salida un descriptor del estado analizado del entorno. Y el tamaño del tensor resultante podrá compararse lógicamente con el número de tipos posibles de clasificación de los estados del entorno. 

bool CNeuronPointNetOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                              uint window, uint units_count, uint output, bool use_tnets,
                              ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, output, optimization_type, batch))
      return false;

En el cuerpo del método, como es habitual, primero llamaremos al método homónimo de la clase padre, en el que ya se han implementado el control mínimo necesario de los parámetros recibidos y la inicialización de los objetos heredados. Al mismo tiempo, no nos olvidaremos comprobar el resultado de las operaciones del método que realiza la llamada.

A continuación, procederemos a inicializar los objetos anidados. Y primero comprobaremos la necesidad de crear los modelos de proyección interna de los datos y las características originales en el espacio canónico.

//--- Init T-Nets
   if(use_tnets)
     {
      if(!cTNet1)
        {
         cTNet1 = new CNeuronPointNetOCL();
         if(!cTNet1)
            return false;
        }
      if(!cTNet1.Init(0, 0, OpenCL, window, units_count, window * window, false, optimization, iBatch))
         return false;

Cuando necesitemos crear modelos de proyección, primero comprobaremos la relevancia del puntero del objeto de modelo y, si es necesario, crearemos un nuevo objeto de la clase CNeuronPointNetOCL. Después lo inicializaremos.

Note que el tamaño de los datos de origen del objeto de generación de la matriz de proyección se corresponde con el tamaño de los datos de origen recibidos por la clase principal desde el programa externo. Pero el tamaño del búfer de resultados será igual al cuadrado de la ventana de datos de origen. Después de todo, en la salida de este modelo, esperamos obtener una matriz cuadrada para proyectar los datos de origen en el espacio canónico. Asimismo, especificaremos el valor false en el parámetro de necesidad de las crear matrices de proyección de los datos y características originales. Después de todo, no queremos la creación incontrolada de objetos recursivos. Además, la creación de modelos de transformación de datos de origen anidados dentro de un modelo de transformación de datos de origen suena ilógico. 

Aquí comprobaremos el puntero al objeto de registro de datos corregido y, de ser necesario, crearemos una nueva instancia del objeto.

      if(!cTurned1)
        {
         cTurned1 = new CNeuronBaseOCL();
         if(!cTurned1)
            return false;
        }
      if(!cTurned1.Init(0, 1, OpenCL, window * units_count, optimization, iBatch))
         return false;

E inicializaremos esta capa interna. Su tamaño se corresponderá con el tensor de los datos de origen.

Realizaremos operaciones similares para el modelo de proyección de características. La única diferencia estribará en las dimensionalidades de las capas interiores.

      if(!cTNet2)
        {
         cTNet2 = new CNeuronPointNetOCL();
         if(!cTNet2)
            return false;
        }
      if(!cTNet2.Init(0, 2, OpenCL, 64, units_count, 64 * 64, false, optimization, iBatch))
         return false;
      if(!cTurned2)
        {
         cTurned2 = new CNeuronBaseOCL();
         if(!cTurned2)
            return false;
        }
      if(!cTurned2.Init(0, 3, OpenCL, 64 * units_count, optimization, iBatch))
         return false;
     }

A continuación, formaremos el MLP para la extracción primaria de características de los puntos. Como en esta fase los autores de PointNet proponen una extracción independiente de las características de los puntos, sustituiremos las capas totalmente conectadas por capas convolucionales con un tamaño de paso igual al tamaño de la ventana de los datos analizados. En nuestro caso, serán iguales al tamaño de un vector de descripción de un punto.

//--- Init PreNet
   if(!cPreNet[0].Init(0, 0, OpenCL, window, window, 64, units_count, optimization, iBatch))
      return false;
   cPreNet[0].SetActivationFunction(None);
   if(!cPreNetNorm[0].Init(0, 1, OpenCL, 64 * units_count, iBatch, optimization))
      return false;
   cPreNetNorm[0].SetActivationFunction(LReLU);
   if(!cPreNet[1].Init(0, 2, OpenCL, 64, 64, 64, units_count, optimization, iBatch))
      return false;
   cPreNet[1].SetActivationFunction(None);
   if(!cPreNetNorm[1].Init(0, 3, OpenCL, 64 * units_count, iBatch, optimization))
      return false;
   cPreNetNorm[1].SetActivationFunction(None);

Insertaremos las capas de normalización por lotes entre las capas de convolución y les aplicaremos la función de activación. En este caso, utilizaremos 2 capas de cada tipo con la dimensionalidad propuesta por los autores del método.

Y de forma similar añadiremos un perceptrón de tres capas de extracción de características de orden superior.

//--- Init Feature Net
   if(!cFeatureNet[0].Init(0, 4, OpenCL, 64, 64, 64, units_count, optimization, iBatch))
      return false;
   cFeatureNet[0].SetActivationFunction(None);
   if(!cFeatureNetNorm[0].Init(0, 5, OpenCL, 64 * units_count, iBatch, optimization))
      return false;
   cFeatureNet[0].SetActivationFunction(LReLU);
   if(!cFeatureNet[1].Init(0, 6, OpenCL, 64, 64, 128, units_count, optimization, iBatch))
      return false;
   cFeatureNet[1].SetActivationFunction(None);
   if(!cFeatureNetNorm[1].Init(0, 7, OpenCL, 128 * units_count, iBatch, optimization))
      return false;
   cFeatureNetNorm[1].SetActivationFunction(LReLU);
   if(!cFeatureNet[2].Init(0, 8, OpenCL, 128, 128, 512, units_count, optimization, iBatch))
      return false;
   cFeatureNet[2].SetActivationFunction(None);
   if(!cFeatureNetNorm[2].Init(0, 9, OpenCL, 512 * units_count, iBatch, optimization))
      return false;
   cFeatureNetNorm[2].SetActivationFunction(None);

En esencia, la arquitectura de los dos últimos bloques será idéntica. La única diferencia residirá en el número de capas y su tamaño. Y, lógicamente, podrán combinarse en una sola unidad. En este caso, solo se separarán para permitir la inserción de un bloque de transformación de características en el espacio canónico entre ellos.

En el siguiente paso, tras extraer las características puntuales, el algoritmo PointNet pronosticará la aplicación de la función MaxPooling, que deberá seleccionar el valor máximo para cada elemento del vector de características puntuales de toda la nube analizada. Así, se supone que una nube de puntos se caracteriza por un vector de características que contiene los valores máximos de los elementos correspondientes de todos los puntos de la nube analizada.

Ya tenemos una clase CNeuronProofOCL en nuestro arsenal que realiza una funcionalidad parecida, pero en una dimensión diferente. Por consiguiente, primero transpondremos la matriz de características de puntos obtenida.

   if(!cTranspose.Init(0, 10, OpenCL, units_count, 512, optimization, iBatch))
      return false;

Y luego generaremos un vector de valores máximos.

   if(!cMaxPool.Init(512, 11, OpenCL, units_count, units_count, 512, optimization, iBatch))
      return false;

El descriptor resultante de la nube de puntos analizada se procesará mediante un MLP de tres capas. Sin embargo, en este caso hemos decidido recurrir a un pequeño truco: declararemos solo 2 capas internas totalmente conectadas. Como tercera, hemos decidido utilizar el propio objeto creado, ya que heredará toda la funcionalidad necesaria de la clase padre.

//--- Init Final MLP
   if(!cFinalMLP[0].Init(256, 12, OpenCL, 512, optimization, iBatch))
      return false;
   cFinalMLP[0].SetActivationFunction(LReLU);
   if(!cFinalMLP[1].Init(output, 13, OpenCL, 256, optimization, iBatch))
      return false;
   cFinalMLP[1].SetActivationFunction(LReLU);

Al final del método de inicialización del objeto de clase, indicaremos explícitamente la función de activación y devolveremos el resultado lógico de las operaciones al programa que realiza la llamada.

   SetActivationFunction(None);
//---
   return true;
  }

Tras completar la implementación del método de inicialización de nuestra nueva clase, pasaremos a construir los algoritmos de pasada directa de PointNet en el método feedForward. Como antes, obtendremos un puntero al objeto de datos de origen en los parámetros de este método.

bool CNeuronPointNetOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- PreNet
   if(!cTNet1)
     {
      if(!cPreNet[0].FeedForward(NeuronOCL))
         return false;
     }

Y en el cuerpo del método nos esperará de inmediato la ramificación del algoritmo según si es o no necesario realizar la proyección de los datos iniciales en el espacio canónico. Cabe señalar aquí que al inicializar el objeto, almacenaremos en variables internas la bandera sobre la necesidad de realizar la proyección de datos. Sin embargo, podemos usar la comprobación de la relevancia de los punteros a los objetos correspondientes para comprobar si la proyección de datos es necesaria. Al fin y al cabo, los modelos de proyección solo se crearán cuando sea necesario. Por defecto, estarán ausentes.

Por consiguiente, cuando no exista un puntero real al objeto de modelo para generar la matriz de proyección de los datos de origen, simplemente transmitiremos el puntero obtenido (al objeto de datos de origen) al método de pasada directa de la primera capa de convolución del bloque de extracción previa de características.

En caso de que necesitemos proyectar los datos en el espacio canónico, transmitiremos los datos obtenidos al método de pasada directa del modelo para generar la matriz de transformación de datos.

   else
     {
      if(!cTurned1)
         return false;
      if(!cTNet1.FeedForward(NeuronOCL))
         return false;

En la salida del modelo de proyección, obtendremos una matriz cuadrada de transformación de datos. En consecuencia, podremos determinar la dimensionalidad de la ventana de datos según el tamaño del tensor de resultados.

      int window = (int)MathSqrt(cTNet1.Neurons());

A continuación, utilizaremos la operación de multiplicación de matrices para obtener la proyección de la nube de puntos original en el espacio canónico.

      if(IsStopped() ||
         !MatMul(NeuronOCL.getOutput(), cTNet1.getOutput(), cTurned1.getOutput(), NeuronOCL.Neurons() / window,
                                                                                                window, window))
         return false;

Y ya la proyección de los puntos iniciales en el espacio canónico la transmitiremos a la entrada de la primera capa del bloque de extracción primaria de características.

      if(!cPreNet[0].FeedForward(cTurned1.AsObject()))
         return false;
     }

En esta fase, independientemente de la necesidad de proyectar los datos de origen en el espacio canónico, ya hemos realizado una pasada directa de la primera capa del bloque primario de extracción de características. Y luego haremos una llamada secuencial a los métodos de pasada directa de todas las capas del bloque especificado.

   if(!cPreNetNorm[0].FeedForward(cPreNet[0].AsObject()))
      return false;
   if(!cPreNet[1].FeedForward(cPreNetNorm[0].AsObject()))
      return false;
   if(!cPreNetNorm[1].FeedForward(cPreNet[1].AsObject()))
      return false;

Entonces nos enfrentaremos a la cuestión de la necesidad de proyectar las características de los puntos en el espacio canónico. Aquí el algoritmo será el mismo que para la proyección de los puntos de origen.

//--- Feature Net
   if(!cTNet2)
     {
      if(!cFeatureNet[0].FeedForward(cPreNetNorm[1].AsObject()))
         return false;
     }
   else
     {
      if(!cTurned2)
         return false;
      if(!cTNet2.FeedForward(cPreNetNorm[1].AsObject()))
         return false;
      int window = (int)MathSqrt(cTNet2.Neurons());
      if(IsStopped() ||
         !MatMul(cPreNetNorm[1].getOutput(), cTNet2.getOutput(), cTurned2.getOutput(),
                                     cPreNetNorm[1].Neurons() / window, window, window))
         return false;
      if(!cFeatureNet[0].FeedForward(cTurned2.AsObject()))
         return false;
     }

A continuación, finalizaremos las operaciones de extracción de características de los puntos de la nube de datos de origen analizada.

   if(!cFeatureNetNorm[0].FeedForward(cFeatureNet[0].AsObject()))
      return false;
   uint total = cFeatureNet.Size();
   for(uint i = 1; i < total; i++)
     {
      if(!cFeatureNet[i].FeedForward(cFeatureNetNorm[i - 1].AsObject()))
         return false;
      if(!cFeatureNetNorm[i].FeedForward(cFeatureNet[i].AsObject()))
         return false;
     }

En el siguiente paso, transpondremos el tensor de características obtenido. Y formaremos el vector descriptor de la nube analizada.

   if(!cTranspose.FeedForward(cFeatureNetNorm[total - 1].AsObject()))
      return false;
   if(!cMaxPool.FeedForward(cTranspose.AsObject()))
      return false;

Y además, según el algoritmo de clasificación PointNet, se realizará el procesamiento de lo que se haya recibido en un MLP. Aquí realizaremos las operaciones de pasada directa de las 2 capas internas completamente conectadas.

   if(!cFinalMLP[0].FeedForward(cMaxPool.AsObject()))
      return false;
   if(!cFinalMLP[1].FeedForward(cFinalMLP[0].AsObject()))
      return false;

Y luego llamaremos al método similar de la clase padre, pasándole un puntero a la capa interna.

   if(!CNeuronBaseOCL::feedForward(cFinalMLP[1].AsObject()))
      return false;
//---
   return true;
  }

Recordemos que en este caso la clase padre será una capa totalmente conectada. En consecuencia, llamando al método de pasada directa de la clase padre realizaremos un pasada directa de la capa totalmente conectada. Solo que esta vez utilizaremos los objetos heredados de la clase padre para realizar las operaciones, en lugar de objetos de capa anidados.

Una vez ejecutadas con éxito todas las operaciones de nuestro método de pasada directa, retornaremos el valor lógico de las operaciones ejecutadas al programa que realiza la llamada.

Aquí podemos dar por finalizado el trabajo con el método de pasada directa; ahora comenzaremos a trabajar en los métodos pasada inversa, que se dividen en 2 bloques: la distribución del gradiente de error y el ajuste de los parámetros del modelo entrenado.

Ya hemos dicho muchas veces que la distribución del gradiente de error repite al completo el algoritmo de pasada directa, solo que el flujo de información se hace en orden inverso. Sin embargo, hay un matiz en este caso. Para las matrices de proyección de datos, los autores del método PointNet han introducido una regularización que hace que la matriz de proyección de datos sea lo más ortogonal posible. Las operaciones de regularización no se reflejan en el algoritmo de pasada directa y solo intervienen en el proceso de optimización de los parámetros. Además, para efectuar estas operaciones, necesitaremos realizar trabajo adicional por parte del programa OpenCL.

En primer lugar, echaremos un vistazo a la fórmula de regularización propuesta.

Obviamente, en este caso los autores del método explotan la propiedad que dice que al multiplicar una matriz ortogonal por su copia transpuesta se obtiene una matriz unitaria.

Si profundizamos en este aspecto, veremos que la multiplicación de una matriz por su copia transpuesta en cada elemento de la matriz resultante devuelve el producto de las dos filas correspondientes. Así, para una matriz ortogonal, la multiplicación vectorial de una fila por su copia deberá dar "1". En todos los demás casos, la multiplicación vectorial de dos filas de una matriz dará "0".

No obstante, cabe señalar que se trata de una regularización dentro de la pasada inversa. Y esto significa que no solo tendremos que calcular el error, sino también el gradiente de error para cada elemento.

Para implementar este algoritmo en el lado del programa OpenCL, crearemos el kernel OrthoganalLoss. En los parámetros de este kernel obtendremos los punteros a dos búferes de datos. Uno de ellos contendrá la matriz original, mientras que el otro registrará los gradientes de error correspondientes. Aquí también añadiremos una bandera para indicar que el gradiente de error se sobrescribe o se añade a los valores ya guardados.

__kernel void OrthoganalLoss(__global const float *data,
                             __global float *grad,
                             const int add
                            )
  {
   const size_t r = get_global_id(0);
   const size_t c = get_local_id(1);
   const size_t cols = get_local_size(1);

Al hacerlo, no especificaremos las dimensiones de las matrices. Pero aquí resultará bastante sencillo. Planeamos ejecutar el kernel en un espacio de tareas bidimensional según el número de filas y columnas de la matriz.

En el cuerpo del kernel, identificaremos inmediatamente el flujo actual en ambas dimensiones del espacio de tareas.

También conviene recordar que se trata de una matriz cuadrada. Por consiguiente, para comprender el tamaño completo de la matriz, solo tendremos que determinar el número de flujos en una de las dimensiones.

Para distribuir las operaciones de multiplicación de vectores entre varios flujos, crearemos grupos de trabajo locales dentro de las filas de la matriz original. Y para organizar el proceso de intercambio de datos entre flujos, utilizaremos un array en la memoria local del contexto OpenCL.

   __local float Temp[LOCAL_ARRAY_SIZE];
   uint ls = min((uint)cols, (uint)LOCAL_ARRAY_SIZE);

A continuación, definiremos las constantes de desplazamiento a los objetos necesarios en el búfer de datos de origen.

   const int shift1 = r * cols + c;
   const int shift2 = c * cols + r;

Y cargaremos los valores de los elementos correspondientes desde el búfer de datos.

   float value1 = data[shift1];
   float value2 = (shift1==shift2 ? value1 : data[shift2]);

Obsérvese que, para minimizar las operaciones de acceso global a la memoria, excluiremos la relectura de los elementos diagonales.

Aquí comprobaremos inmediatamente la validez de los valores obtenidos sustituyendo los números no válidos por valores cero.

   if(isinf(value1) || isnan(value1))
      value1 = 0;
   if(isinf(value2) || isnan(value2))
      value2 = 0;

Después calcularemos su producto con la comprobación obligatoria de la validez del resultado.

   float v2 = value1 * value2;
   if(isinf(v2) || isnan(v2))
      v2 = 0;

A continuación organizaremos un ciclo de suma paralela de los valores obtenidos en elementos separados del array local con sincronización obligatoria de los flujos del grupo de trabajo.

   for(int i = 0; i < cols; i += ls)
     {
      //---
      if(i <= c && (i + ls) > c)
         Temp[c - i] = (i == 0 ? 0 : Temp[c - i]) + v2;
      barrier(CLK_LOCAL_MEM_FENCE);
     }

Y a continuación organizaremos un ciclo de suma de los valores obtenidos de los elementos del array local.

   uint count = min(ls, (uint)cols);
   do
     {
      count = (count + 1) / 2;
      if(c < ls)
         Temp[c] += (c < count && (c + count) < cols ? Temp[c + count] : 0);
      if(c + count < ls)
         Temp[c + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

También prestaremos especial atención a la sincronización de los flujos de los grupos de trabajo.

Como resultado de las operaciones realizadas en el primer elemento del la array local obtendremos el valor del producto de las dos filas analizadas del array. Y ahora podremos calcular el valor del error.

   const float sum = Temp[0];
   float loss = -pow((float)(r == c) - sum, 2.0f);

Sin embargo, esto será solo una parte del trabajo. A continuación, tendremos que determinar el gradiente de error para cada elemento de la matriz original. Consideraremos en primer lugar el gradiente de error a nivel del producto de vectores.

   float g = (2 * (sum - (float)(r == c))) * loss;

Y luego llevaremos el gradiente de error hasta el primer elemento en el producto de los valores del flujo actual.

   g = value2 * g;

Deberemos comprobar obligatoriamente la validez del valor del gradiente de error obtenido.

   if(isinf(g) || isnan(g))
      g = 0;

A continuación, lo almacenaremos en el elemento correspondiente del búfer del gradiente de error global.

   if(add == 1)
      grad[shift1] += g;
   else
      grad[shift1] = g;
  }

Aquí comprobaremos necesariamente la bandera de adición o sobrescritura del valor del gradiente de error y realizaremos la operación correspondiente.

Nótese que en el marco del kernel, calcularemos el gradiente de error para solo uno de los elementos del trabajo. El gradiente del error para el segundo elemento del producto se calculará en un flujo separado, en el que se invertirán la fila y la columna de la matriz.

La colocación de este kernel en la cola de ejecución se realizará en el método CNeuronPointNetOCL::OrthoganalLoss. Su algoritmo se construirá en total conformidad con los principios básicos de colocación de kernels de los programas OpenCL en la cola de ejecución que ya hemos discutido muchas veces en artículos anteriores. Así que le sugiero que estudie por su cuenta el código del método anterior. Su código completo figura en el archivo adjunto.

También le sugiero que se familiarice con el algoritmo del método de distribución del gradiente de error calcInputGradients. En los parámetros de este método, al igual que antes, obtendremos el puntero al objeto de la capa anterior, que en este caso será el receptor del gradiente de error en el nivel de datos de origen.

bool CNeuronPointNetOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

En el cuerpo del método comprobaremos directamente la relevancia del puntero recibido. De lo contrario, se perderá el sentido de las operaciones posteriores.

A continuación, ejecutaremos el gradiente de error a través de una interpretación de perceptrón del descriptor de la nube de puntos.

   if(!CNeuronBaseOCL::calcInputGradients(cFinalMLP[1].AsObject()))
      return false;
   if(!cFinalMLP[0].calcHiddenGradients(cFinalMLP[1].AsObject()))
      return false;

A través de la capa MaxPooling y la posterior transposición llevaremos el gradiente de error a las características de los puntos correspondientes.

   if(!cMaxPool.calcHiddenGradients(cFinalMLP[0].AsObject()))
      return false;
   if(!cTranspose.calcHiddenGradients(cMaxPool.AsObject()))
      return false;

Y haremos descender el gradiente de error a través de las capas de extracción de características puntuales, en orden inverso, por supuesto.

   uint total = cFeatureNet.Size();
   for(uint i = total - 1; i > 0; i--)
     {
      if(!cFeatureNet[i].calcHiddenGradients(cFeatureNetNorm[i].AsObject()))
         return false;
      if(!cFeatureNetNorm[i - 1].calcHiddenGradients(cFeatureNet[i].AsObject()))
         return false;
     }
   if(!cFeatureNet[0].calcHiddenGradients(cFeatureNetNorm[0].AsObject()))
      return false;

Hasta aquí, todo sigue igual. Pero ahora hemos llegado al nivel de la proyección de características puntuales en el espacio canónico. Obviamente, si esto no es necesario, simplemente transmitiremos el gradiente de error al bloque primario de extracción de características.

   if(!cTNet2)
     {
      if(!cPreNetNorm[1].calcHiddenGradients(cFeatureNet[0].AsObject()))
         return false;
     }

Pero en el segundo caso, el algoritmo resultará más complicado. Primero haremos descender el gradiente de error hasta el nivel de la proyección de datos.

   else
     {
      if(!cTurned2)
         return false;
      if(!cTurned2.calcHiddenGradients(cFeatureNet[0].AsObject()))
         return false;

Luego distribuiremos el gradiente de error entre las características puntuales y la matriz de proyección. Y aquí, si miramos un par de pasos por delante, podremos ver que también haremos descender el gradiente de error hasta el nivel de la característica puntual a través del modelo de generación de la matriz de proyección. Por lo tanto, para no sobrescribir los datos necesarios más adelante, en esta fase transmitiremos el gradiente de error a la penúltima capa del bloque de extracción de características en lugar de a la última capa del bloque de extracción de características.

Recordemos que la última capa del bloque de extracción previa de características será la capa de normalización por lotes. Y delante vendrá una capa convolucional de extracción de características independientes de puntos individuales. Ambas capas tendrán la misma dimensionalidad de los búferes de gradiente de error, lo que nos permitirá realizar la sustitución de búferes sin temor a sobrepasar los límites de los mismos.

      int window = (int)MathSqrt(cTNet2.Neurons());
      if(IsStopped() ||
         !MatMulGrad(cPreNetNorm[1].getOutput(), cPreNet[1].getGradient(), cTNet2.getOutput(), 
                     cTNet2.getGradient(), cTurned2.getGradient(), cPreNetNorm[1].Neurons() / window,
                                                                                       window, window))
         return false;

Y después de dividir el gradiente de error en los dos flujos de datos, añadiremos el gradiente de error de regularización al nivel de la matriz de proyección.

      if(!OrthoganalLoss(cTNet2.AsObject(), true))
         return false;

A continuación, pasaremos el gradiente de error por el bloque de formación de la matriz de proyección.

      if(!cPreNetNorm[1].calcHiddenGradients((CObject*)cTNet2))
         return false;

Y sumaremos el gradiente de error a partir de los dos flujos de información.

      if(!SumAndNormilize(cPreNetNorm[1].getGradient(), cPreNet[1].getGradient(), cPreNetNorm[1].getGradient(),
                                                                                         1, false, 0, 0, 0, 1))
         return false;
     }

Y entonces podemos pasar con seguridad el gradiente de error a través del bloque primario de extracción de características al nivel de proyección de los datos de origen.

   if(!cPreNet[1].calcHiddenGradients(cPreNetNorm[1].AsObject()))
      return false;
   if(!cPreNetNorm[0].calcHiddenGradients(cPreNet[1].AsObject()))
      return false;
   if(!cPreNet[0].calcHiddenGradients(cPreNetNorm[0].AsObject()))
      return false;

Aquí aplicaremos un algoritmo similar a la distribución del gradiente de error mediante la proyección de características. La variante más sencilla del algoritmo se observará cuando no existe una matriz de proyección de datos. Simplemente pasaremos el gradiente de error al búfer de la capa anterior.

   if(!cTNet1)
     {
      if(!NeuronOCL.calcHiddenGradients(cPreNet[0].AsObject()))
         return false;
     }

Pero en caso de que necesitemos proyectar los datos, primero haremos descender el gradiente de error al nivel de proyección.

      if(!cTurned1)
         return false;
      if(!cTurned1.calcHiddenGradients(cPreNet[0].AsObject()))
         return false;

Y distribuiremos el gradiente de error entre los dos flujos según su influencia en el resultado.

      int window = (int)MathSqrt(cTNet1.Neurons());
      if(IsStopped() ||
         !MatMulGrad(NeuronOCL.getOutput(), NeuronOCL.getGradient(), cTNet1.getOutput(), cTNet1.getGradient(),
                     cTurned1.getGradient(), NeuronOCL.Neurons() / window, window, window))
         return false;

Y añadiremos el valor de regularización al gradiente de error obtenido.

      if(!OrthoganalLoss(cTNet1, true))
         return false;

Y aquí nos encontraremos con el problema de sobrescribir el gradiente de error. En esta fase no tendremos búferes libres en los que escribir datos. Y al distribuiremos el gradiente de error a lo largo de las 2 direcciones, y escribiremos inmediatamente el gradiente de error en el búfer de la capa precedente. Y ahora tendremos que pasar el gradiente de error por el bloque de generación de la matriz de proyección de los datos de origen, cuyas operaciones sobrescribirán los valores del gradiente de error con la pérdida de los datos almacenados anteriormente. Para evitar la pérdida de datos, deberemos copiarlos en un búfer de datos adecuado. Pero, ¿de dónde sacaremos ese búfer? Al inicializar la clase, no hemos creado un búfer de almacenamiento de datos intermedios. Y entonces nuestra mirada se posa en la capa de registro de proyección de datos. Su tamaño es similar al tamaño del tensor de datos original. En cuanto al gradiente de error almacenado en él, ya lo hemos distribuido en dos flujos y no se utilizará en operaciones posteriores.

Al mismo tiempo, la igualdad de tamaños de los búferes nos sugiere que la transferencia directa de datos es viable. ¿Y si, en lugar de copiar los datos directamente, realizáramos un intercambio de punteros en los búferes de datos? Después de todo, la operación de copiado de punteros resulta mucho menos costosa que el copiado de datos del búfer completo y no depende del tamaño del búfer.

      CBufferFloat *temp = NeuronOCL.getGradient();
      NeuronOCL.SetGradient(cTurned1.getGradient(), false);
      cTurned1.SetGradient(temp, false);

Y después de redistribuir los punteros por los búferes de datos, podremos pasar con seguridad el gradiente de error de la matriz de proyección de datos al nivel de la capa anterior.

      if(!NeuronOCL.calcHiddenGradients(cTNet1.AsObject()))
         return false;
      if(!SumAndNormilize(NeuronOCL.getGradient(), cTurned1.getGradient(), NeuronOCL.getGradient(),
                                                                            1, false, 0, 0, 0, 1))
         return false; 
     }
//---
   return true;
  }

Una vez finalizadas las operaciones del método, sumaremos el gradiente de error de los dos flujos de información y retornaremos el resultado lógico de las operaciones del método al programa que realiza la llamada.

Los parámetros del modelo entrenado se actualizarán en el método updateInputWeights. El algoritmo de este método suele ser sencillo: bastará con llamar alternativamente a los métodos de los objetos internos que contienen los parámetros a entrenar. Al mismo tiempo, no nos olvidaremos de llamar al método similar de la clase padre, ya que hemos usado su funcionalidad como la tercera capa de evaluación MLP del descriptor de la nube de puntos. En el marco de este artículo no nos detendremos en el código de este método. Le propongo familiarizarse con él en los archivos adjuntos al artículo.

Y aquí concluimos el análisis de algoritmos para construir los métodos de la clase CNeuronPointNetOCL. En el archivo adjunto a este artículo encontrará el código completo de esta clase y todos sus métodos.

2.2 Arquitectura del modelo

Tras implementar los enfoques propuestos por los autores del método PointNet usando MQL5, procederemos a implementar el nuevo objeto en la arquitectura de nuestros modelos. Como hemos mencionado antes, añadiremos nuestra nueva clase CNeuronPointNetOCL a la arquitectura del modelo del Codificador del estado del entorno, que se representa en el método CreateEncoderDescriptions.

Aquí cabe destacar que hemos implementado casi por completo todo el algoritmo en un solo bloque. Y esto nos permite crear un modelo con una arquitectura de alto nivel bastante concisa y escueta. Ya hemos hecho especial hincapié en que este método presenta una "arquitectura de alto nivel". Al fin y al cabo, bajo el nombre abreviado de bloque CNeuronPointNetOCL se esconde una arquitectura de red neuronal bastante compleja y multicapa.

Como de costumbre, introduciremos en el modelo datos "brutos" sin procesar, que se llevarán a un formato comparable mediante la capa de normalización de datos por lotes.

bool CreateEncoderDescriptions(CArrayObj *&encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación, los transferiremos inmediatamente a nuestra nueva unidad PointNet.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPointNetOCL;
   descr.window = BarDescr;                        // Variables
   descr.count = HistoryBars;                      // Units
   descr.window_out = LatentCount;                 // Output Dimension
   descr.step = int(true);                         // Use input and feature transformation
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Cabe señalar aquí que no hemos especificado una función de activación en la salida de nuestro bloque CNeuronPointNetOCL. Este movimiento se ha hecho intencionadamente para ofrecer al usuario la posibilidad de ampliar la arquitectura de la unidad de identificación de nubes de puntos. Sin embargo, en lo que respecta a este experimento, solo añadiremos una capa SoftMax para trasladar los resultados obtenidos al dominio de la probabilidad.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = LatentCount;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Con esto damos por concluida la arquitectura de nuestro nuevo modelo de Codificador del estado del entorno.

También hemos simplificado la arquitectura de los modelos del Actor y el Crítico. En ellos, sustituiremos el bloque multicabeza de atención cruzada por una simple capa de concatenación de datos. Para mayor seguridad, le sugiero revisar estas ediciones puntuales por su cuenta en el archivo adjunto.

También debemos decir unas palabras sobre los programas de entrenamiento de modelos. El cambio en la arquitectura del modelo no ha afectado a la estructura de los datos de entrada y salida, lo cual nos ha permitido utilizar programas de interacción con el entorno creados previamente, así como los datos que recogían para el aprendizaje offline. Sin embargo, las etiquetas de clase de los estados del entorno seleccionados faltan en el conjunto de datos que hemos recogido anteriormente. Y el trabajo para crearlos supondrá costes adicionales. No obstante, hemos decidido tomar un camino diferente y entrenar al Codificador del estado del entorno durante el entrenamiento de la política del Actor. Por lo tanto, hemos excluido el EA de entrenamiento aparte del Codificador del estado del entorno "StudyEncoder.mq5". Y en el programa de entrenamiento de modelo del Actor y el Crítico "Study.mq5" hemos introducido ciertas correcciones para entrenar el Codificador del estado del entorno, que le sugiero que lea por su cuenta.

Le recuerdo que en el archivo adjunto encontrará el código completo de la clase presentada en este artículo y todos sus métodos, así como los algoritmos de todos los programas utilizados para preparar el artículo. Ahora pasaremos a la fase final de nuestro trabajo: probar y evaluar los resultados de nuestro trabajo.

3. Simulación

En este artículo, nos hemos familiarizado con un nuevo método de procesamiento de los datos iniciales en forma de nube de puntos PointNet y hemos implementado nuestra visión de los enfoques propuestos por los autores del método utilizando herramientas MQL5. Y ahora es el momento de probar la eficacia de los enfoques propuestos para resolver nuestros problemas. Para ello, entrenaremos los modelos presentados en este artículo con los datos históricos reales del instrumento EURUSD. En nuestro experimento, utilizaremos los datos históricos del año 2023 como muestra de entrenamiento para entrenar los modelos. Y probaremos los modelos entrenados con los datos de enero de 2024. En ambos casos utilizaremos el marco temporal H1 y los parámetros por defecto para todos los indicadores analizados.

Básicamente, llevamos varios artículos usando los parámetros de entrenamiento y prueba del modelo sin cambios. Por consiguiente, el entrenamiento inicial se realizará con los datos de las muestras recogidas previamente.

Al mismo tiempo, el entrenamiento del modelo del codificador del estado del entorno se realizará simultáneamente con el entrenamiento de la política del actor, mientras que el entrenamiento de esta última, como usted sabe, se realizará de forma iterativa, con una actualización periódica de los datos de la muestra de entrenamiento. Este enfoque mantendrá la muestra de entrenamiento actualizada y relevante para el ámbito de la política actual del Actor. Esto, a su vez, permitirá un ajuste más fino de la política entrenada.

Tras varias iteraciones de entrenamiento de los modelos, hemos logrado obtener una política del Actor capaz de generar beneficios en las muestras de entrenamiento y de prueba. Ahora le presentamos los resultados de las mismas.

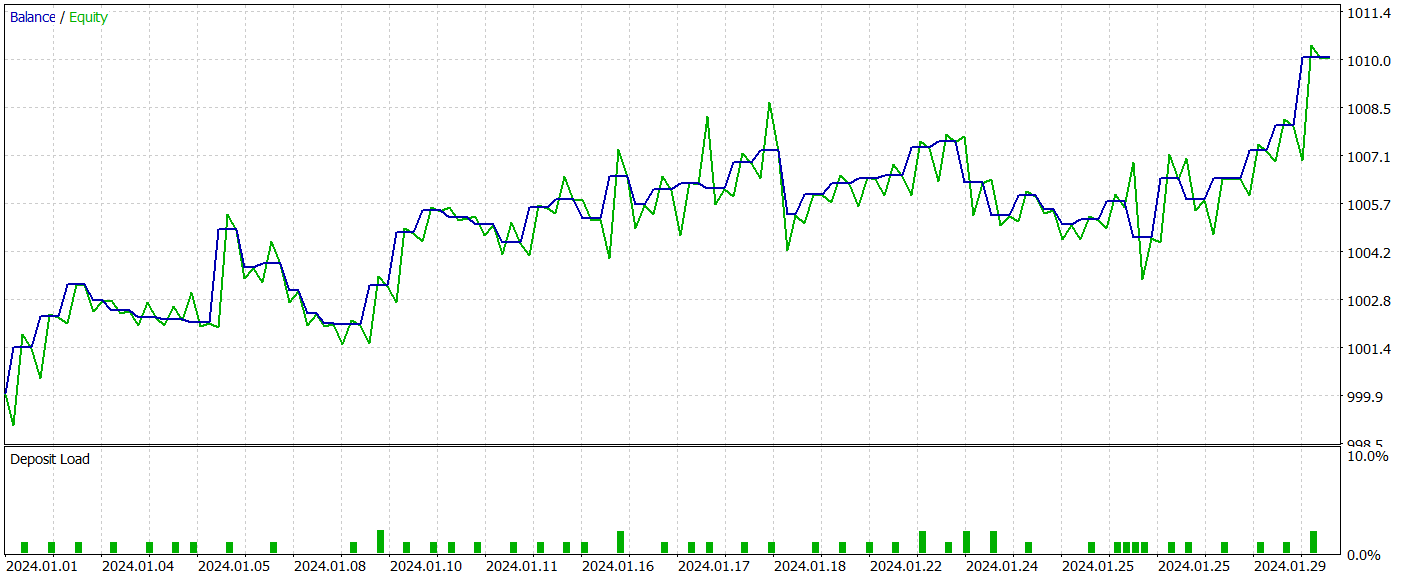
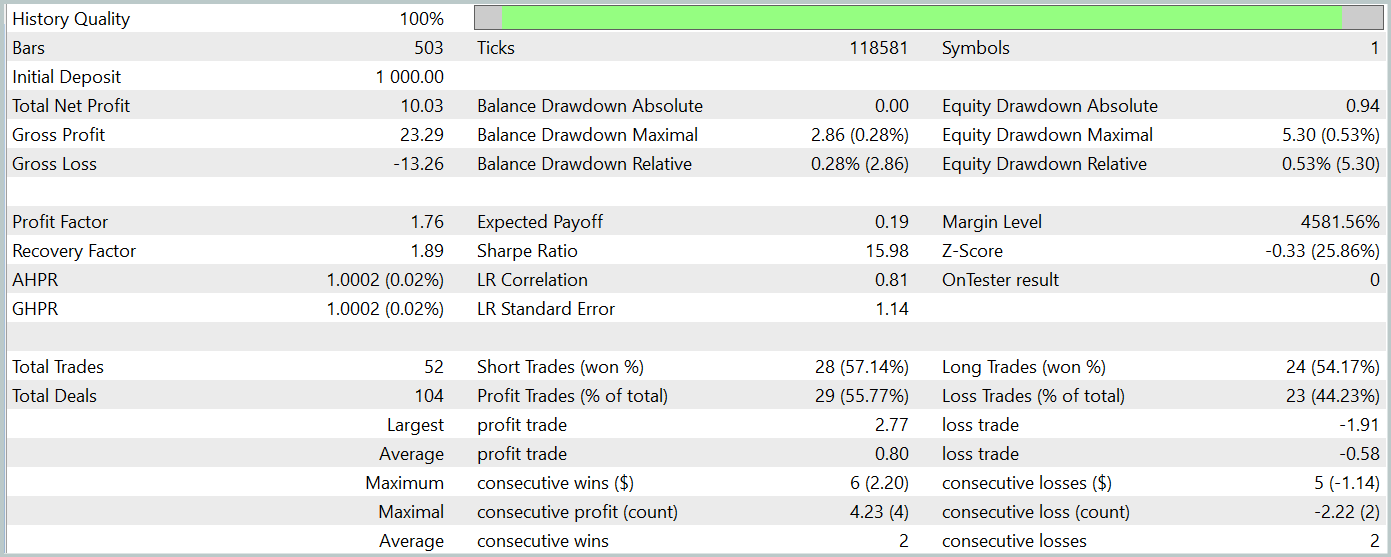
Durante el periodo de prueba, el modelo ha realizado 52 transacciones comerciales, de las cuales el 55,77% se han cerrado con beneficio. Cabe destacar que tenemos una práctica paridad de posiciones largas y cortas (24 frente a 28, respectivamente). Al mismo tiempo, tanto las transacciones rentables máximas como las medias superan las mismas métricas de las posiciones perdedoras. Eso ha permitido fijar el factor de beneficio al nivel de 1,76. El gráfico del balance tiene una clara tendencia al alza. Sin embargo, el breve periodo de prueba y el reducido número de transacciones realizadas no nos permiten hablar de una eventual estabilidad del rendimiento de la política aprendida a lo largo de un intervalo de tiempo prolongado.

En general, los enfoques aplicados son dignos de mención, pero requieren pruebas adicionales.

Conclusión

En este artículo, nos hemos familiarizado con el nuevo método PointNet, una solución arquitectónica unificada que adopta directamente la nube de puntos como datos de entrada. La aplicación de PointNet en el ámbito comercial permite analizar eficazmente datos multidimensionales complejos, como los patrones de precios, sin necesidad de convertirlos a otros formatos. Y esto descubre nuevas oportunidades para predecir con mayor precisión las tendencias del mercado y mejorar los algoritmos de toma de decisiones. Así, podemos mejorar potencialmente la eficacia de las estrategias comerciales en los mercados financieros.

En la parte práctica del artículo, hemos implementado nuestra propia visión de los enfoques propuestos utilizando herramientas MQL5, hemos entrenado los modelos con datos históricos reales y hemos probado el asesor experto utilizando la política aprendida en el simulador de estrategias de MetaTrader 5. Según los resultados de nuestras pruebas, hemos obtenido resultados prometedores. No obstante, conviene recordar que todos los programas presentados en este artículo son de carácter introductorio y se han creado únicamente para demostrar las capacidades de los enfoques propuestos. Antes de usar los programas en mercados financieros reales, será necesario perfeccionarlos, proceso que también incluirá el entrenamiento adicional y la prueba exhaustivas de los modelos presentados.

Enlaces

PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation

Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL