
Population optimization algorithms: ElectroMagnetism-like algorithm (ЕМ)
Contents:
1. Introduction
2. Algorithm
3. Test results
1. Introduction
Over the past few decades, researchers around the world have come up with many metaheuristic search methods to solve complex global optimization problems and ways to improve them.
The ElectroMagnetism-like (ЕМ) algorithm is a relatively new metaheuristic search algorithm based on the simulation of the behavior of electromagnetic particles in physical space, first introduced by I. Birbil and S.С. Fang in 2003. It is described as an evolutionary algorithm with random noise and a population based on the electromagnetic force of the interaction between charged particles.
This algorithm is inspired by the mechanism of attraction and repulsion of charges in the theory of electromagnetism for solving non-linear optimization problems without restrictions in a continuous domain. Due to its ability to solve complex global optimization problems, EM is widely used as an optimization tool in many areas.
Interesting facts about electromagnetism and electric charges:
- There are two types of electric charges: positive and negative. All charges are either positive or negative.
- The electromagnetic field can be used to transmit information in the form of radio waves. We use this feature every day when we listen to the radio or watch TV.
- We have the Earth's magnetic field, which protects us from the solar wind and cosmic rays.
- There are various materials that can be magnetized, and this makes it possible to create electromagnets. Electromagnets are used in various applications such as power generators.
- There are many applications based on electromagnetism. For example, computers, mobile phones and other devices use electromagnetic technology.
- All luminous objects (for example, light bulbs and car lights) emit electromagnetic radiation.
- Electromagnetism also plays an important role in medicine. Medical devices such as MRI and CT use an electromagnetic field to create images inside the body.
- Some animals, such as sharks and electric eels, can use electromagnetism to navigate in water.
- Electromagnetism is one of the four fundamental forces of nature, along with the gravitational, weak and strong forces.
2. Algorithm
Guided by the theory of electromagnetism, EM simulates the mechanism of attraction-repulsion of charges to achieve a global optimal solution using limited variables. In the algorithm, all solutions are considered as charged particles in the search space, and the charge of each particle is associated with the value of the target function. Particles with better objective output will apply attractive forces, while particles with worse objective values will apply repulsive forces to other particles. The better the value of the objective function, the higher will be the amount of attraction or repulsion between particles.
The principle of the algorithm is that at the initial stage a population of random solutions is formed and each solution is represented by a vector of coordinates corresponding to charges on electromagnetic particles. Further, at each iteration of the algorithm, the motion of these charges in space is simulated under the action of electromagnetic forces. While moving, each charge interacts with other charges leading to a change in the direction of movement and speed. As a result, there is a gradual convergence of solutions to the optimal value of the objective function.
The main components of the EM algorithm are:
- Formation of the initial population of solutions (charges), where each charge is represented by a coordinate vector and corresponds to a certain solution of the optimization problem.
- Calculation of the electromagnetic force of interaction between charges. The calculation is performed at each iteration of the algorithm and depends on the distance between the charges (solutions).
- Movement of charges in space under the influence of electromagnetic forces of interaction.
- Updating the solution population at each iteration by the objective function (the objective function can be, for example, the loss function in machine learning problems).
- Determining the condition for stopping the algorithm, for example, reaching a certain value of the objective function.
Particles interact with each other, attracting or repelling depending on the charge and the distance between them. The algorithm is executed in several iterations, at each of which the coordinates and charges of the particles are updated, as well as the new values of the fitness function are calculated.
The logical unit of the EM optimization algorithm is a particle. It can be described by the S_Particle structure, which is an agent in the search space. Each particle has c [] coordinates, which determine its position in the search space, as well as the C charge, which affects the interaction with other particles. For each particle, the value of the fitness function f is calculated, which evaluates the quality of the solution corresponding to the given coordinate. In addition, for each particle, distances R to other particles and force vectors F are calculated, which determine the direction of particle motion in the search space.
//—————————————————————————————————————————————————————————————————————————————— struct S_Particle { double c []; //coordinates double C; //charge double f; //fitness double R []; //euclidean distance to other particles double F []; //force vector }; //——————————————————————————————————————————————————————————————————————————————
The C_AO_EM class is an implementation of the electromagnetic optimization algorithm. It is used to find the optimal values of a function given on some set of real numbers. The algorithm is based on simulating the processes of interaction between magnetic and electrical particles in a physical system.
The class contains the following fields:
- S_Particle p[] - array of particles representing potential solutions to the optimization problem.
- double rangeMax[] — array of maximum search range values for each coordinate.
- double rangeMin[] — array of minimum search range values for each coordinate.
- double rangeStep[] - array of search steps for each coordinate.
- double cB[] — array of coordinates of the best solution.
- double fB - value of the best solution function.
The class contains the following methods:
- void Init() initializes the algorithm, setting the number of coordinates, the number of particles, the environment constant and the movement step.
- void Moving(int iter) iterates the algorithm moving particles in accordance with the rules for the interaction of magnetic and electric fields.
- void Revision() performs a revision of the particles checking them for going beyond the search range and adjusting their position if necessary.
The class also contains private fields:
- int coordinatesNumber — number of coordinates.
- int particlesNumber — number of particles.
- double envConstant — environment constant.
- double movConstant — movement step.
- double exponent — distance exponent.
- double vect[] — array of vectors.
- bool revision — flag indicating the need for a particle revision.
The class contains private methods:
- double SeInDiSp(double In, double InMin, double InMax, double Step) distributes points on a uniform grid.
- double RNDfromCI(double min, double max) generates a random number in the given range.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_EM { //---------------------------------------------------------------------------- public: S_Particle p []; //particles public: double rangeMax []; //maximum search range public: double rangeMin []; //minimum search range public: double rangeStep []; //step search public: double cB []; //best coordinates public: double fB; //FF of the best coordinates public: void Init (const int coordinatesNumberP, //coordinates number const int particlesNumberP, //particles number const double envConstantP, //environmental constant const double movConstantP, //movement step const double exponentP); //exponent public: void Moving (); public: void Revision (); //---------------------------------------------------------------------------- private: int coordinatesNumber; //coordinates number private: int particlesNumber; //particles number private: double envConstant; //environmental constant private: double movConstant; //movement step private: double exponent; //exponent private: double vect []; //vector private: bool revision; private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double min, double max); }; //——————————————————————————————————————————————————————————————————————————————
The "electromagnetic algorithm" optimization algorithm initialization method begins with resetting the random number generator and setting initial values for some variables. Then the method takes several parameters as inputs: the number of coordinates, the number of particles, the value of the environment and the movement step. Next, the method creates several arrays of the required sizes and fills them with initial values.
The arrays store the maximum and minimum values of the range for each coordinate, the step of changing the coordinate, the vector and the current position of each particle. The method then creates an array of particles and, for each particle, creates arrays to store its coordinates, the matrix of distances to other particles, the force vector and the current best value of the function. At the end, the method creates an array to store the best coordinates of all the particles. Thus, the method initializes all the necessary variables and arrays for the "electromagnetic algorithm" optimization algorithm to work.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_EM::Init (const int coordinatesNumberP, //coordinates number const int particlesNumberP, //particles number const double envConstantP, //environmental constant const double movConstantP, //movement step const double exponentP) //exponent { MathSrand ((int)GetMicrosecondCount ()); // reset of the generator fB = -DBL_MAX; revision = false; coordinatesNumber = coordinatesNumberP; particlesNumber = particlesNumberP; envConstant = envConstantP; movConstant = movConstantP; exponent = exponentP; ArrayResize (rangeMax, coordinatesNumber); ArrayResize (rangeMin, coordinatesNumber); ArrayResize (rangeStep, coordinatesNumber); ArrayResize (vect, coordinatesNumber); ArrayResize (p, particlesNumber); for (int i = 0; i < particlesNumber; i++) { ArrayResize (p [i].c, coordinatesNumber); ArrayResize (p [i].R, particlesNumber); ArrayResize (p [i].F, coordinatesNumber); p [i].f = -DBL_MAX; } ArrayResize (cB, coordinatesNumber); } //——————————————————————————————————————————————————————————————————————————————
The Moving() method is the first one that must be executed on each iteration. It is responsible for the movement of particles in the solution search space. First, the method checks if the particles have already been initialized. If not, then each particle receives random coordinates within the given limits and resets its current estimate and charge to zero. The vector of differences vect [] between the maximum and minimum values in each dimension of the search space is also calculated.
//---------------------------------------------------------------------------- if (!revision) { fB = -DBL_MAX; for (int obj = 0; obj < particlesNumber; obj++) { for (int c = 0; c < coordinatesNumber; c++) { p [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); p [obj].C = 0.0; p [obj].f = -DBL_MAX; } } for (int c = 0; c < coordinatesNumber; c++) { vect [c] = rangeMax [c] - rangeMin [c]; } revision = true; }
If the initialization has already been carried out, then the method calculates the charge of each particle based on its deviation from the global maximum normalized to the sum of the deviations from the global maximum of all particles. Calculate the sum of the differences as follows:
//calculate the sum of the differences of the fitness of the particles with the global value for (int obj = 0; obj < particlesNumber; obj++) { sumDiff += fB - p [obj].f; }
The particle charge is calculated by the equation:
p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff));As you can see, the value of the charge in the equation is positive. The sign of the charge will be taken into account later in the algorithm. If the sum of the differences in deviations from the global maximum is zero, then the charge of the particle is assumed to be zero. The calculated charge of the particle will determine the amplitude of the force acting from the particle on other relevant particles during the force calculation step. The code for calculating the charge of a particle will look like this://calculating the charge of particles======================================= for (int obj = 0; obj < particlesNumber; obj++) { if (sumDiff == 0.0) { p [obj].C = 0.0; } else { p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff)); } }
Before we start calculating the distances between particles, it is necessary to reset the array of distances from the particle to other particles and also reset the vector of forces acting on the particle:
//calculation of Euclidean distances between all particles================== for (int obj = 0; obj < particlesNumber; obj++) { ArrayInitialize (p [obj].R, 0.0); ArrayInitialize (p [obj].F, 0.0); }
Then the distances between all pairs of particles and the forces acting between them are calculated. It uses a formula based on Coulomb's law, which describes the interaction between charged particles. The forces acting on each particle are calculated as the vector sum of all the forces acting on it from other particles.
According to the electromagnetic theory, the force of action of one particle on another is inversely proportional to the distance between the two particles and directly proportional to the product of their charges. A particle with a lower target value applies a repulsive force to a particle with a relatively higher target value. Similarly, it pushes a good particle away from a region with a bad target value. On the other hand, a particle with a higher target value exerts attraction on particles with relatively lower values.
Taking into account all relevant forces generated by all other particles, the total force vector for the particle is calculated. This combined force vector determines the direction, in which the particle will move during the particle motion phase. The authors of the algorithm recommend normalizing the force vector of the particle to the vector of forces between all particles. My experiments have shown that without normalization the results are better and the code is presented without normalization.
Depending on which particle has the greater value of the objective function, we set the direction of the force (imitation of the sign of the charge).
for (int obj = 0; obj < particlesNumber; obj++) { for (int obj2 = 0; obj2 < particlesNumber; obj2++) { if (obj != obj2) { if (p [obj].R [obj2] == 0.0) { for (int c = 0; c < coordinatesNumber; c++) { diffDist = p [obj].c [c] - p [obj2].c [c]; p [obj].R [obj2] += diffDist * diffDist; } p [obj].R [obj2] = sqrt (p [obj].R [obj2]); p [obj2].R [obj] = p [obj].R [obj2]; //calculation of the force------------------------------------------ Fp = p [obj].C * p [obj2].C / (4.0 * M_PI * envConstant * pow (p [obj].R [obj2], exponent)); for (int c = 0; c < coordinatesNumber; c++) { if (p [obj].f > p [obj2].f) { p [obj ].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp; p [obj2].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp; } else { p [obj ].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp; p [obj2].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp; } } } } } }
Finally, new coordinates are calculated for each particle based on its current position and the force acting on it. The particles have no mass, which means there is no acceleration. In contrast to the GSA gravitational search algorithm, the particles move to a new location instantly. Movement coordinates are limited by search range and change step.
The commented out code returns the particle on the opposite side of the range at a distance from the corresponding coordinate in case the particle is out of range.
//calculation of particle motions=========================================== for (int obj = 0; obj < particlesNumber; obj++) { for (int c = 0; c < coordinatesNumber; c++) { r = RNDfromCI (0.0, 1.0); p [obj].c [c] = p [obj].c [c] + r * p [obj].F [c] * vect [c] * movConstant; //if (p [obj].c [c] > rangeMax [c]) p [obj].c [c] = rangeMin [c] + (p [obj].c [c] - rangeMax [c]); //if (p [obj].c [c] < rangeMin [c]) p [obj].c [c] = rangeMax [c] - (rangeMin [c] - p [obj].c [c]); p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } }
The Revision() method, the second one that must be executed at each iteration, in the EM optimization algorithm, is responsible for checking the best position of the particle at the current iteration. Inside the method, it loops through all the particles and compares the value of their fitness function with the current best value of fB. If the value of the fitness function of the current particle is greater than fB, then fB is updated and the position of the particle is copied to the cB array.
Thus, the Revision() method allows tracking the best position of the particle at each iteration of the algorithm and store it in the cB array. This helps optimizing the process of finding the optimal solution and increases the efficiency of the algorithm.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_EM::Revision () { for (int s = 0; s < particlesNumber; s++) { if (p [s].f > fB) { fB = p [s].f; ArrayCopy (cB, p [s].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
The SeInDiSp() method in the "electromagnetic algorithm" optimization algorithm is used to limit the values of the In variable within a given range [InMin, InMax] with a Step. If In is less than or equal to InMin, then the method returns InMin. If In is greater than or equal to InMax, then the method returns InMax. If the step is zero, then the method returns the original In value. Otherwise, the method calculates a new In value using the equation: InMin + Step * (In - InMin) / Step, where MathRound() is the method for rounding a number to the nearest integer.
Thus, the SeInDiSp() method allows controlling the change in the value of the In variable within the specified limits and with a specified step, which helps to optimize the function more efficiently and quickly.
//—————————————————————————————————————————————————————————————————————————————— // Choice in discrete space double C_AO_EM::SeInDiSp (double In, double InMin, double InMax, double Step) { if (In <= InMin) return (InMin); if (In >= InMax) return (InMax); if (Step == 0.0) return (In); else return (InMin + Step * (double)MathRound ((In - InMin) / Step)); } //——————————————————————————————————————————————————————————————————————————————
3. Test results
ME algorithm test stand results:
2023.03.26 18:27:39.259 C_AO_EM:50;0.1;0.8
2023.03.26 18:27:39.259 =============================
2023.03.26 18:27:43.215 5 Rastrigin's; Func runs 10000 result: 59.939529106561224
2023.03.26 18:27:43.215 Score: 0.74268
2023.03.26 18:27:52.960 25 Rastrigin's; Func runs 10000 result: 59.780143424645416
2023.03.26 18:27:52.960 Score: 0.74071
2023.03.26 18:29:22.856 500 Rastrigin's; Func runs 10000 result: 63.94951378068386
2023.03.26 18:29:22.856 Score: 0.79237
2023.03.26 18:29:22.856 =============================
2023.03.26 18:29:28.901 5 Forest's; Func runs 10000 result: 0.28698617113254693
2023.03.26 18:29:28.901 Score: 0.16233
2023.03.26 18:29:38.103 25 Forest's; Func runs 10000 result: 0.1571444033424823
2023.03.26 18:29:38.103 Score: 0.08889
2023.03.26 18:30:53.341 500 Forest's; Func runs 10000 result: 0.11734383105881332
2023.03.26 18:30:53.341 Score: 0.06638
2023.03.26 18:30:53.341 =============================
2023.03.26 18:30:58.108 5 Megacity's; Func runs 10000 result: 1.3599999999999999
2023.03.26 18:30:58.108 Score: 0.11333
2023.03.26 18:31:08.897 25 Megacity's; Func runs 10000 result: 0.776
2023.03.26 18:31:08.897 Score: 0.06467
2023.03.26 18:32:23.199 500 Megacity's; Func runs 10000 result: 0.34320000000000006
2023.03.26 18:32:23.199 Score: 0.02860
2023.03.26 18:32:23.199 =============================
2023.03.26 18:32:23.199 All score: 2.79996
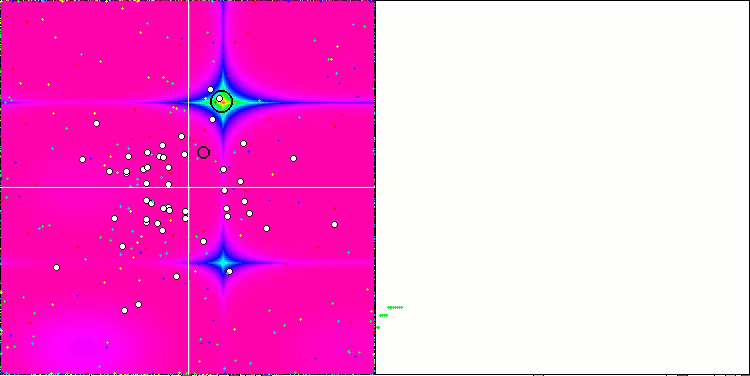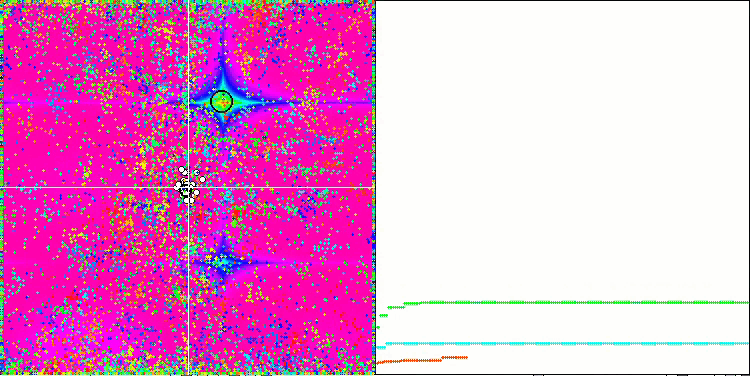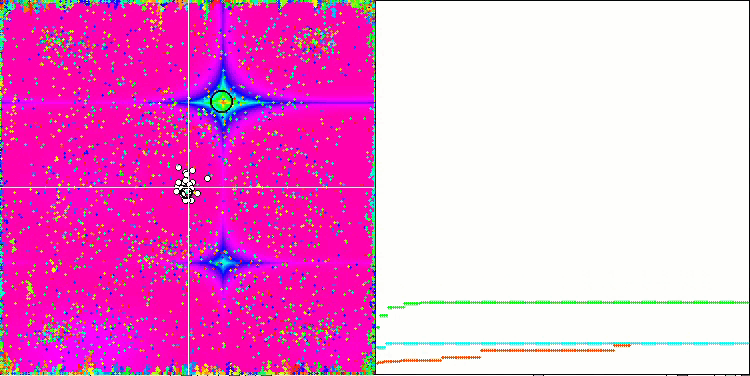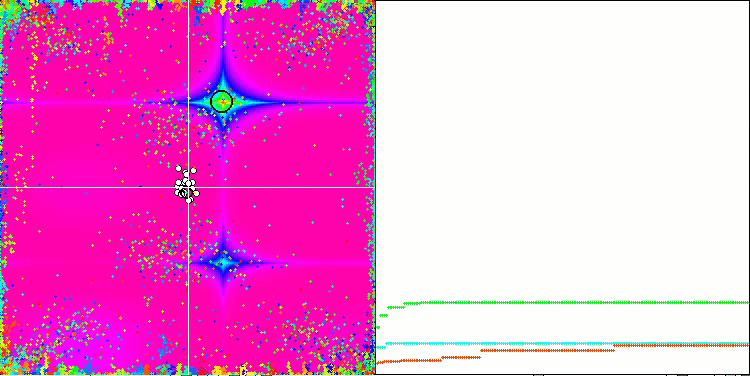
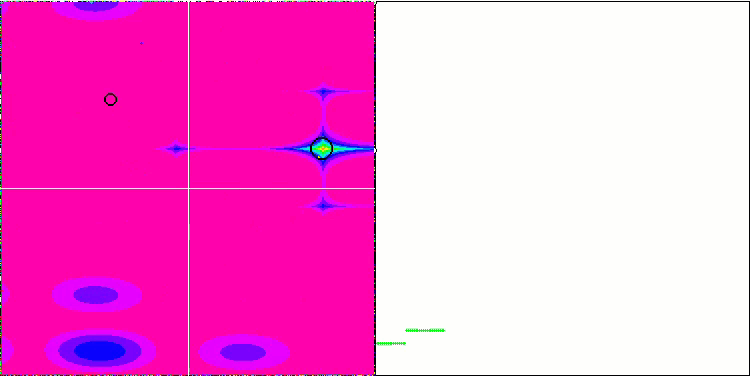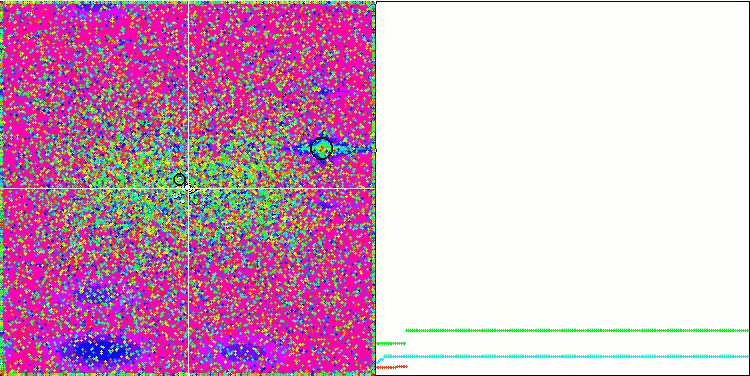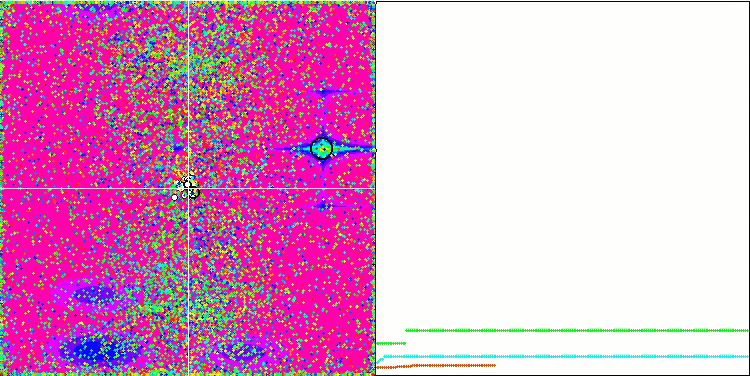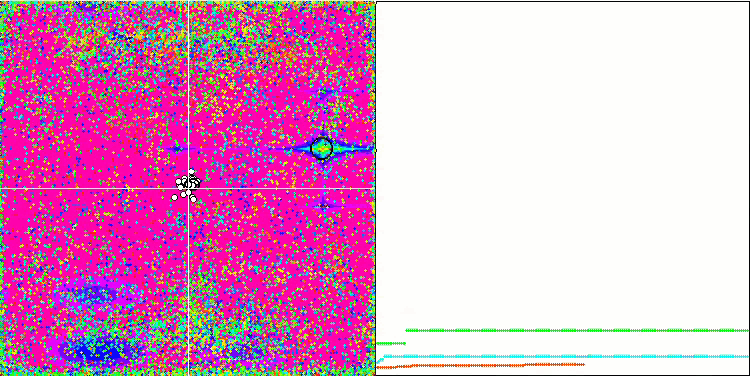
Paying attention to the animation of the ME algorithm on test functions, we can imagine some kind of "electrification" of the search space field. Particles form groups of high charges following the features of the surface of the test function. Unfortunately, the quality of convergence is noticeably low but the image is undeniably beautiful.
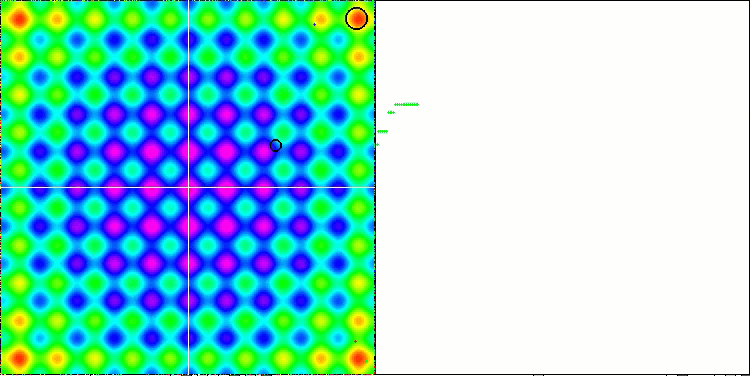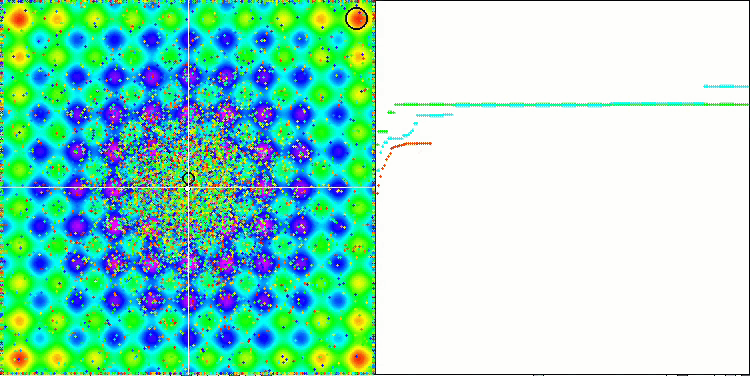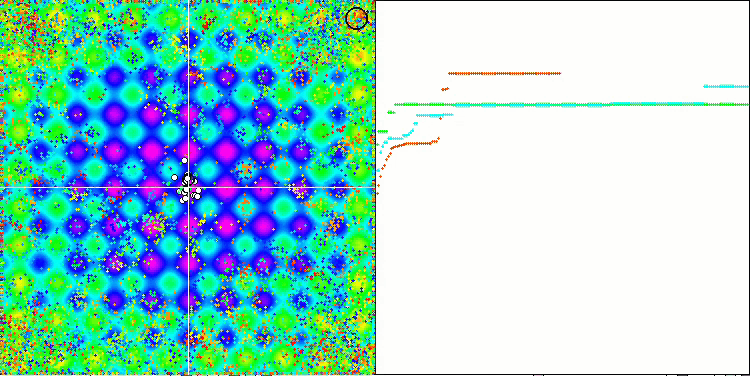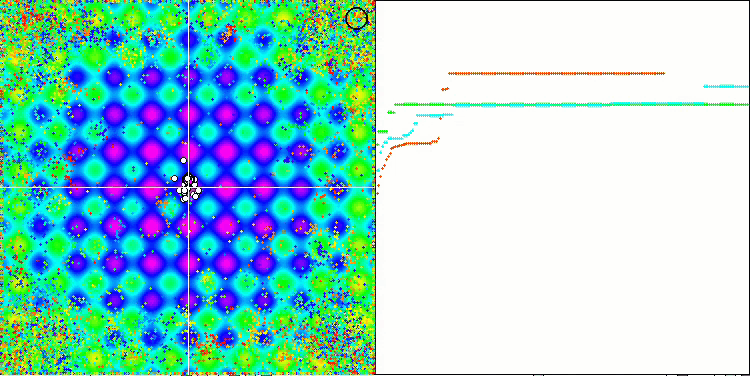
EM on the Rastrigin test function.
EM on the Forest test function.
EM on the Megacity test function.
Let's move on to the test results of the EM optimization algorithm. EM performed below average with a final score of 22. The algorithm showed poor results in almost all tests. The exception is the Rastrigin function test with 1000 parameters, in which EM turned out to be better than such powerful algorithms as SSG and BA. Moreover, the absolute values of the function at 1000 parameters turned out to be higher than in tests with 10 and 50 parameters!
This is the first time when the search results improve with an increase in the number of optimized parameters. Most likely, this phenomenon is associated with the peculiarities of the EM search strategy itself. It is necessary to note the sensitivity of EM to the presence of a gradient and differentiability over the entire area of the studied function definition.
| AO | Description | Rastrigin | Rastrigin final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | ||||||
| 10 params (5 F) | 50 params (25 F) | 1000 params (500 F) | 10 params (5 F) | 50 params (25 F) | 1000 params (500 F) | 10 params (5 F) | 50 params (25 F) | 1000 params (500 F) | ||||||
| SSG | saplings sowing and growing | 1.00000 | 1.00000 | 0.55665 | 2.55665 | 0.72740 | 0.94522 | 1.00000 | 2.67262 | 0.76364 | 0.85977 | 1.00000 | 2.62340 | 100.000 |
| HS | harmony search | 0.99676 | 0.95282 | 0.48178 | 2.43136 | 1.00000 | 0.98931 | 0.44806 | 2.43736 | 1.00000 | 1.00000 | 0.41537 | 2.41537 | 92.329 |
| ACOm | ant colony optimization M | 0.34611 | 0.17985 | 0.17044 | 0.69640 | 0.86888 | 1.00000 | 0.77362 | 2.64249 | 1.00000 | 0.88930 | 0.05606 | 1.94536 | 65.347 |
| IWO | invasive weed optimization | 0.95828 | 0.67083 | 0.29807 | 1.92719 | 0.70773 | 0.46349 | 0.31773 | 1.48896 | 0.80000 | 0.42067 | 0.33289 | 1.55356 | 61.104 |
| COAm | cuckoo optimization algorithm M | 0.92400 | 0.46794 | 0.26004 | 1.65199 | 0.58378 | 0.34034 | 0.16526 | 1.08939 | 0.72727 | 0.33025 | 0.17083 | 1.22835 | 47.612 |
| FAm | firefly algorithm M | 0.59825 | 0.33980 | 0.17135 | 1.10941 | 0.51073 | 0.42299 | 0.49790 | 1.43161 | 0.34545 | 0.28044 | 0.35258 | 0.97847 | 41.537 |
| ABC | artificial bee colony | 0.78170 | 0.32715 | 0.20822 | 1.31707 | 0.53837 | 0.21455 | 0.13344 | 0.88636 | 0.56364 | 0.26569 | 0.13926 | 0.96858 | 36.849 |
| GSA | gravitational search algorithm | 0.70167 | 0.45217 | 0.00000 | 1.15384 | 0.31660 | 0.36416 | 0.33204 | 1.01280 | 0.59395 | 0.35054 | 0.00000 | 0.94448 | 36.028 |
| BA | bat algorithm | 0.40526 | 0.63761 | 0.84451 | 1.88738 | 0.20841 | 0.17477 | 0.25989 | 0.64308 | 0.29698 | 0.09963 | 0.17371 | 0.57032 | 35.888 |
| BFO | bacterial foraging optimization | 0.67203 | 0.30963 | 0.11813 | 1.09979 | 0.39702 | 0.26623 | 0.20652 | 0.86976 | 0.52122 | 0.33211 | 0.18932 | 1.04264 | 34.693 |
| EM | electroMagnetism-like algorithm | 0.12235 | 0.46278 | 1.00000 | 1.58513 | 0.00000 | 0.03498 | 0.34880 | 0.38377 | 0.00000 | 0.00000 | 0.10924 | 0.10924 | 22.091 |
| MA | monkey algorithm | 0.33192 | 0.33451 | 0.14644 | 0.81287 | 0.10012 | 0.07891 | 0.08932 | 0.26836 | 0.21818 | 0.04243 | 0.10720 | 0.36781 | 13.603 |
| FSS | fish school search | 0.46812 | 0.25337 | 0.11302 | 0.83451 | 0.12840 | 0.05013 | 0.06516 | 0.24369 | 0.16971 | 0.04796 | 0.08283 | 0.30050 | 12.655 |
| PSO | particle swarm optimisation | 0.20449 | 0.08200 | 0.07160 | 0.35809 | 0.18895 | 0.10486 | 0.21738 | 0.51119 | 0.23636 | 0.05903 | 0.01957 | 0.31496 | 10.031 |
| RND | random | 0.16826 | 0.09743 | 0.08019 | 0.34589 | 0.13496 | 0.04810 | 0.04715 | 0.23021 | 0.16971 | 0.03875 | 0.04922 | 0.25767 | 5.302 |
| GWO | grey wolf optimizer | 0.00000 | 0.00000 | 0.02256 | 0.02256 | 0.06570 | 0.00000 | 0.00000 | 0.06570 | 0.32727 | 0.07378 | 0.02557 | 0.42663 | 1.000 |
Summary
- The EM algorithm is an efficient optimization method capable of solving various optimization problems, especially those associated with processing large amounts of data and high dimensionality on smooth functions.
- The algorithm is based on simulating the behavior of electromagnetic particles in physical space, which allows it to achieve high accuracy of the result when working with complex multidimensional functions.
- The EM algorithm does not require gradient calculations, which makes it more versatile and easier to apply to various problems, but it is sensitive to the presence of a gradient in the function being optimized.
- The algorithm can be modified and customized depending on the specific optimization problem, which makes it a flexible tool for optimizing various functions.
- There are various modifications of the EM algorithm that can be improved over the basic version and adapted to specific optimization problems.
- The EM algorithm can be used in various fields such as machine learning, artificial intelligence, financial market optimization and others.
The main advantage of the electromagnetic algorithm is the ability to solve optimization problems in multidimensional spaces and large dimensions, while maintaining high accuracy of the result.
Thus, the EM algorithm is an effective tool for optimizing various functions and can be used in a wide range of optimization problems, especially when processing a large amount of data and/or high dimensionality.
This rating can be useful for choosing the most suitable algorithm for solving a particular optimization problem. However, the efficiency of the algorithm depends on many factors, such as the size of the problem, the type of function, the number of variables, etc. Therefore, the choice of an algorithm should be based on a thorough analysis of a particular problem.
Figure 1 shows the test results of the algorithms
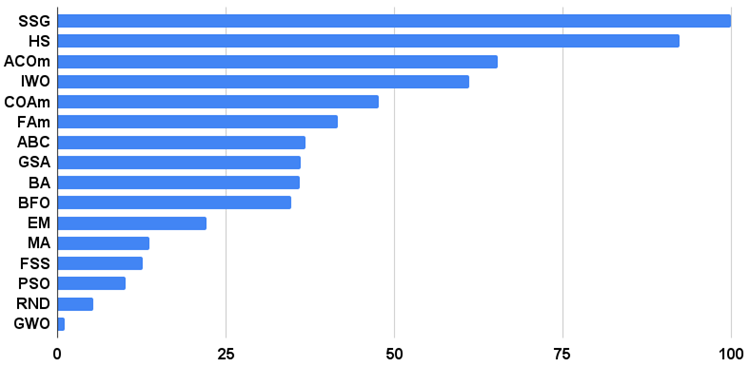
Figure 1. Histogram of the test results of the algorithms
Pros and cons of the electromagnetic algorithm (EM):
1. Easy implementation.
2. Impressive scalability on smooth functions.
3. Small number of external parameters.
Cons:
1. High computational complexity.
2. Poor results on discrete functions.
3. Getting stuck on functions with flat horizontal "platforms".
Each article features an archive that contains updated current versions of the algorithm codes for all previous articles. The article is based on the accumulated experience of the author and represents his personal opinion. The conclusions and judgments are based on the experiments.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/12352
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use