群体算法的基类作为高效优化的支柱

目录

1.介绍 - 继承群体算法基类的前景和机遇
2.实现群体算法的基类
3.后代算法的代码
4.所有算法的统一测试代码
5.添加常用测试函数
6.构建 3D 测试函数
7.结论

1.介绍 - 继承群体算法基类的前景和机遇

在现代计算和人工智能领域，旨在将优化算法集成到最终软件解决方案中的基类是为开发人员开辟无限技术可能性的关键要素。在群体算法的背景下，继承这个基类不仅为开发新的优化方法提供了便利和效率，而且为创建能够适应各种问题的混合算法拓展了前景。

在基类中组合优化算法为创建结合不同方法的最佳特性的创新解决方案打开了大门。通过这种方法产生的混合算法能够有效地克服单一方法的局限性，在解决复杂的优化问题上达到新的高度。

此外，群体算法的基类确保了在标准测试函数集上易于使用和测试所开发的算法。这使得研究人员和开发人员能够通过将新优化方法的性能与现有解决方案进行比较来快速评估新优化方法的效率。

让我们想象一下，优化和寻找解决方案的世界就像令人惊叹的烹饪世界，其中每种优化方法都是独特的成分，为菜肴赋予其独特的味道。这里所说的混合就像是巧妙地将不同的食材组合在一起，创造出新的、更美味、更有趣的菜肴。

您有各种不同的优化方法 - 遗传算法、进化策略、蚂蚁算法、粒子群优化等等。它们各自都有自己的优势和能力，但也有其局限性。

这就是混合的用武之地！您可以像经验丰富的厨师一样，从每种方法中汲取最佳优势，将它们组合成独特的组合。通过这种方式，混合优化方法可以结合不同方法的优势，弥补各自的弱点，创造出更高效、更强大的寻找最优解决方案的工具。

想象一下遗传算法与局部搜索的结合，就好比一道菜中辣椒和甜蜂蜜的完美结合，赋予其浓郁的味道。同样，群体算法的混合允许创建创新方法，可以在各个领域快速准确地找到最佳解决方案，无论是工程问题、金融分析还是人工智能。

因此，优化中的混合不仅仅是混合方法，它还是创造新方法的艺术，可以最大限度地发挥每种方法的潜力并取得优异的结果。最终，通过混合，我们可以创建更高效、创新和强大的优化方法，解决最复杂的问题，并带来各个领域的新发现和进步。

此外，统一的基类允许将每种算法的各个元素集成到定制解决方案中，以用于设计新的、独特和强大的优化方法。

2.实现群体算法的基类

在关于从群体算法的基类继承并创建混合优化方法的文章中，我们可以考虑几个有趣的组合作为示例：

• 增强局部搜索的遗传算法。在这种组合中，遗传算法用于全局搜索最优解，而局部搜索用于优化邻域内找到的解。这样可以结合全局和局部搜索的优点，提高算法收敛的准确性和速度。

• 采用蚂蚁算法的进化策略。这里，可以采用进化策略来改变模型参数，而采用蚂蚁算法来在参数空间中寻找最优路径。这种组合可以有效地优化需要找到最佳参数组合的复杂问题。

• 利用遗传编程来聚集粒子。在这种组合中，可以使用群体粒子来探索解空间，并使用遗传编程来进化解决优化问题的程序结构。这使得能够有效地探索参数空间和解决方案结构。

• 利用遗传算法进行模拟退火搜索。这里，可以使用模拟退火来探索考虑温度状况的解空间，并且可以使用遗传算法在给定空间中寻找最优解。这种组合可以提供更深入的解空间探索，并提高算法的收敛性。

我们还可以考虑将群体算法的功能组合到一个基类中来使用，具体方法如下：

• 组合元启发式方法。该方法可以将遗传算法、蚂蚁算法、粒子群优化算法、模拟退火等几种不同的元启发式算法结合起来。这些算法可以并行或按顺序工作，交换信息并结合其优势，更有效地找到最佳解决方案。

• 具有自适应控制搜索策略的混合方法。在这种方法中，可以使用自适应控制机制根据问题特点动态地组合不同的优化策略。例如，我们可以根据每个方法在当前优化阶段的表现来改变其权重或参数。

• 与人工神经网络的混合方法。在该方法中，可以使用人工神经网络来自适应地控制群体算法的参数和优化策略。神经网络可以动态学习，适应搜索空间的变化，并为每种优化方法提出最佳参数。

• 联合优化与强化学习方法。该方法可以将群体算法与强化学习技术相结合，创建一个可以有效探索和优化复杂解决方案空间的混合系统。强化学习代理可以从群体算法的结果中学习，反之亦然，从而在不同的优化方法之间建立相互作用。

各个优化算法中外部参数的数量不同，会造成继承和统一应用的问题。为了解决这个问题，根据大量测试的结果，决定在构造函数中指定默认算法的外部参数。同时，在初始化算法之前仍然可以改变这些参数。因此，每个算法的对象将代表可供使用的最终解决方案。以前，算法及其参数是独立的实体。

因此，让我们从算法参数开始。使用包含参数名称和值的 S_AlgoParam 结构来描述每个参数很方便。因此，该结构的对象数组将代表一组算法的外部参数。

struct S_AlgoParam
{
    double val;
    string name;
};

每一个优化算法都有一个搜索代理 - 这是搜索策略中的一个基本单元和不可缺少的参与者 - 萤火虫算法中的一只萤火虫，蜜蜂算法中的一只勤奋的蜜蜂，蚂蚁算法中的一只勤奋的蚂蚁等等。它们是最优化迷宫中独一无二的艺术家，展现出寻找和发现成功最佳路径的艺术的光辉。它们的努力和抱负犹如魔法，将数据的混乱转化为解决方案的和谐，照亮了通往理想优化新视野的道路。

因此，每个代理代表优化问题的一个特定解决方案，并具有两个强制性属性：搜索空间中的坐标（优化参数）和解决方案质量（适应度函数）。为了能够扩展功能和能力并实现算法的特定属性，我们将以 C_AO_Agent 类的形式将代理形式化，随后我们可以继承它。

class C_AO_Agent
{
  public:
  ~C_AO_Agent () { }

  double c []; //coordinates
  double f;    //fitness
};

优化算法中的大多数逻辑操作都是重复的，并且可以单独设计为 C_AO_Utilities 类的一组函数，而该类的对象又可以在算法类和代理中使用。

C_AO_Utilities 类包含以下方法：

• Scale:重载方法，将“In”输入从 [InMIN, InMAX] 范围缩放到 [OutMIN, OutMAX] 范围。如果“revers”参数设置为“true”，也可以执行反向缩放。
• RNDfromCI:生成指定 [min，max] 范围内的随机实数。
• RNDintInRange：生成指定 [min，max] 范围内的随机整数。
• RNDbool:生成一个随机布尔值（true/false）。
• RNDprobab:生成一个随机概率（0 到 1 之间的实数）。
• SeInDiSp：考虑 [InMin, InMax] 范围内指定的“Step”来计算值。
• “DecimalToGray”、“IntegerToBinary”、“GrayToDecimal”、“BinaryToInteger”和“GetMaxDecimalFromGray”方法：执行十进制数、二进制数和格雷码之间的转换。
• "GaussDistribution" 和 "PowerDistribution" 方法：分别对正态分布和功率分布进行计算。
• ”Sorting”方法（模板方法）：对“T”类型的“p”数组按降序排序。
• “S_Roulette”结构：包含“start”和“end”字段来表示范围。
• “PreCalcRoulette” 和 “SpinRoulette” 方法：“PreCalcRoulette” 计算“T”类型对象的范围并将其保存在“roulette”数组中。“SpinRoulette” 根据“aPopSize” 群体规模进行轮盘“spin”。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_Utilities
{
  public: //--------------------------------------------------------------------
  double Scale                 (double In, double InMIN, double InMAX, double OutMIN, double OutMAX);
  double Scale                 (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
  double RNDfromCI             (double min, double max);
  int    RNDintInRange         (int min, int max);
  bool   RNDbool               ();
  double RNDprobab             ();
  double SeInDiSp              (double In, double InMin, double InMax, double Step);
  void   DecimalToGray         (ulong decimalNumber, char &array []);
  void   IntegerToBinary       (ulong number, char &array []);
  ulong  GrayToDecimal         (const char &grayCode [], int startInd, int endInd);
  ulong  BinaryToInteger       (const char &binaryStr [], const int startInd, const int endInd);
  ulong  GetMaxDecimalFromGray (int digitsInGrayCode);
  double GaussDistribution     (const double In, const double outMin, const double outMax, const double sigma);
  double PowerDistribution     (const double In, const double outMin, const double outMax, const double p);

  //----------------------------------------------------------------------------
  template<typename T>
  void Sorting (T &p [], T &pTemp [], int size)
  {
    int    cnt = 1;
    int    t0  = 0;
    double t1  = 0.0;
    int    ind [];
    double val [];

    ArrayResize (ind, size);
    ArrayResize (val, size);

    for (int i = 0; i < size; i++)
    {
      ind [i] = i;
      val [i] = p [i].f;
    }

    while (cnt > 0)
    {
      cnt = 0;
      for (int i = 0; i < size - 1; i++)
      {
        if (val [i] < val [i + 1])
        {
          t0 = ind [i + 1];
          t1 = val [i + 1];
          ind [i + 1] = ind [i];
          val [i + 1] = val [i];
          ind [i] = t0;
          val [i] = t1;
          cnt++;
        }
      }
    }

    for (int u = 0; u < size; u++) pTemp [u] = p [ind [u]];
    for (int u = 0; u < size; u++) p [u] = pTemp [u];
  }

  //----------------------------------------------------------------------------
  struct S_Roulette
  {
      double start;
      double end;
  };
  S_Roulette roulette [];

  template<typename T>
  void PreCalcRoulette (T &agents [])
  {
    int aPopSize = ArraySize (agents);
    roulette [0].start = agents [0].f;
    roulette [0].end   = roulette [0].start + (agents [0].f - agents [aPopSize - 1].f);

    for (int s = 1; s < aPopSize; s++)
    {
      if (s != aPopSize - 1)
      {
        roulette [s].start = roulette [s - 1].end;
        roulette [s].end   = roulette [s].start + (agents [s].f - agents [aPopSize - 1].f);
      }
      else
      {
        roulette [s].start = roulette [s - 1].end;
        roulette [s].end   = roulette [s].start + (agents [s - 1].f - agents [s].f) * 0.1;
      }
    }
  }
  int  SpinRoulette (int aPopSize);
};
//——————————————————————————————————————————————————————————————————————————————

由于随机优化算法基于生成随机数，因此可以执行数百甚至数千次此操作以获得每个解决方案。因此，建议通过分离特定任务来优化随机数的生成。鉴于标准生成器创建的是整数，因此有可能加快这一过程。

我们已经了解了“RNDfromCI”方法，它在给定的[“min”，“max”]范围内生成一个随机实数：

double C_AO_Utilities ::RNDfromCI (double min, double max)
{
  if (min == max) return min;
  if (min > max)
  {
    double temp = min;
    min = max;
    max = temp;
  }
  return min + ((max - min) * rand () / 32767.0);
}

我们经常需要生成一个随机整数，例如在群体中随机选择一个代理。“RNDintInRange”方法将帮助我们实现这一点。

int C_AO_Utilities :: RNDintInRange (int min, int max)
{
  if (min == max) return min;
  if (min > max)
  {
    int temp = min;
    min = max;
    max = temp;
  }
  return min + rand () % (max - min + 1);
}

与上述两种方法相比，使用“RNDbool”方法可以非常快速地获得随机布尔变量，这就是为什么根据任务将随机变量分成单独的方法是有意义的。

bool C_AO_Utilities :: RNDbool ()
{
  return rand () % 2 == 0;
}

还有另一种方法“RNDprobab”，它允许我们获取 [0.0, 1.0] 范围内的随机实数。它非常适合执行某些操作的概率，例如遗传算法中的交叉的概率。此类操作也经常进行。

double C_AO_Utilities :: RNDprobab ()
{
  return (double)rand () / 32767;
}

现在我们看一下群体优化算法的“C_AO”基类。此类描述了所有群体算法所需的属性，例如：

• “C_AO”类的方法和属性：

- SetParams：用于设置算法参数的虚拟方法。
- Init：虚拟方法初始化算法，传递最小和最大搜索范围、步长和世代数。
- Moving：执行算法步骤的虚拟方法。
- Revision：用于对算法进行修订的虚拟方法。
- GetName：获取算法名称的方法。
- GetDesc：用于获取算法描述的方法。
- GetParams：用于以字符串形式获取算法参数的方法。

• “C_AO”类的受保护属性：

- ao_name：算法名称。
- ao_desc：算法描述。
- rangeMin、rangeMax、rangeStep：用于存储最小和最大搜索范围以及步长的数组。
- coords：坐标数量。
- popSize：群体规模。
- revision：修订标志。
- u：用于执行辅助函数的“C_AO_Utilities”类对象。

#include "#C_AO_Utilities.mqh"

//——————————————————————————————————————————————————————————————————————————————
class C_AO
{
  public: //--------------------------------------------------------------------
  C_AO () { }
  ~C_AO () { for (int i = 0; i < ArraySize (a); i++) delete a [i];}

  double      cB     []; //best coordinates
  double      fB;        //FF of the best coordinates
  C_AO_Agent *a      []; //agents
  S_AlgoParam params []; //algorithm parameters

  virtual void SetParams () { }
  virtual bool Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
  { return false;}

  virtual void Moving   () { }
  virtual void Revision () { }

  string GetName   () { return ao_name;}
  string GetDesc   () { return ao_desc;}
  string GetParams ()
  {
    string str = "";
    for (int i = 0; i < ArraySize (params); i++)
    {
      str += (string)params [i].val + "|";
    }
    return str;
  }


  protected: //-----------------------------------------------------------------
  string ao_name;      //ao name;
  string ao_desc;      //ao description

  double rangeMin  []; //minimum search range
  double rangeMax  []; //maximum search range
  double rangeStep []; //step search

  int    coords;       //coordinates number
  int    popSize;      //population size
  bool   revision;

  C_AO_Utilities u;     //auxiliary functions

  bool StandardInit (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP []) //step search
  {
    MathSrand ((int)GetMicrosecondCount ()); //reset of the generator
    fB       = -DBL_MAX;
    revision = false;

    coords  = ArraySize (rangeMinP);
    if (coords == 0 || coords != ArraySize (rangeMaxP) || coords != ArraySize (rangeStepP)) return false;

    ArrayResize (rangeMin,  coords);
    ArrayResize (rangeMax,  coords);
    ArrayResize (rangeStep, coords);
    ArrayResize (cB,        coords);

    ArrayCopy (rangeMin,  rangeMinP,  0, 0, WHOLE_ARRAY);
    ArrayCopy (rangeMax,  rangeMaxP,  0, 0, WHOLE_ARRAY);
    ArrayCopy (rangeStep, rangeStepP, 0, 0, WHOLE_ARRAY);

    return true;
  }
};
//——————————————————————————————————————————————————————————————————————————————

此外，在同一个文件中，除了基类之外，还有“E_AO”枚举，其中包含优化算法的 ID 和 SelectAO 函数，这使我们能够创建相应算法的实例并获取其指针。

#include "AO_BGA_Binary_Genetic_Algorithm.mqh"
#include "AO_(P_O)ES_Evolution_Strategies.mqh"
#include "AO_DE_Differential_Evolution.mqh"
#include "AO_SDSm_Stochastic_Diffusion_Search.mqh"
#include "AO_ESG_Evolution_of_Social_Groups.mqh";

//——————————————————————————————————————————————————————————————————————————————
enum E_AO
{
  AO_BGA,
  AO_P_O_ES,
  AO_SDSm,
  AO_ESG,
  AO_DE,
  AO_NONE
};
C_AO *SelectAO (E_AO a)
{
  C_AO *ao;
  switch (a)
  {
    case  AO_BGA:
      ao = new C_AO_BGA (); return (GetPointer (ao));
    case  AO_P_O_ES:
      ao = new C_AO_P_O_ES (); return (GetPointer (ao));
    case  AO_SDSm:
      ao = new C_AO_SDSm (); return (GetPointer (ao));
    case  AO_ESG:
      ao = new C_AO_ESG (); return (GetPointer (ao));
    case  AO_DE:
      ao = new C_AO_DE (); return (GetPointer (ao));

    default:
      ao = NULL; return NULL;
  }
}
//——————————————————————————————————————————————————————————————————————————————

3.后代算法的代码

我们将随机扩散搜索算法（SDSm）作为从基类继承的一个例子。我们将从基础“C_AO_Agent”继承该算法的“C_SDS_Agent”。请注意，代理初始化方法包含“c”坐标和“f”适应度，但它们未在“C_SDS_Agent”类中声明。这是有道理的，因为这些属性是所有优化算法代理都需要的，并且是从基础算法继承的，所以不需要再次声明它们。

//——————————————————————————————————————————————————————————————————————————————
class C_SDS_Agent : public C_AO_Agent
{
  public: //--------------------------------------------------------------------
  ~C_SDS_Agent () { }

  int    raddr     []; //restaurant address
  int    raddrPrev []; //previous restaurant address
  double cPrev     []; //previous coordinates (dishes)
  double fPrev;        //previous fitness

  void Init (int coords)
  {
    ArrayResize (c,         coords);
    ArrayResize (cPrev,     coords);
    ArrayResize (raddr,     coords);
    ArrayResize (raddrPrev, coords);
    f        = -DBL_MAX;
    fPrev    = -DBL_MAX;
  }
};
//——————————————————————————————————————————————————————————————————————————————

SDSm 算法的“C_AO_SDSm”类源自“C_AO”类。在构造函数中声明类对象时，我们将初始化算法的外部参数，随后用户可以根据需要更改这些参数。参数将以数组的形式提供，这样我们就不必担心与测试台的兼容性。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SDSm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_SDSm () { }
  C_AO_SDSm ()
  {
    ao_name = "SDSm";
    ao_desc = "Stochastic Diffusion Search";

    popSize    = 100; //population size

    restNumb   = 100;  //restaurants number
    probabRest = 0.05; //probability restaurant choosing

    ArrayResize (params, 3);

    params [0].name = "popSize";    params [0].val  = popSize;

    params [1].name = "restNumb";   params [1].val  = restNumb;
    params [2].name = "probabRest"; params [2].val  = probabRest;
  }

  void SetParams ()
  {
    popSize    = (int)params [0].val;

    restNumb   = (int)params [1].val;
    probabRest = params      [2].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    restNumb;          //restaurants number
  double probabRest;        //probability restaurant choosing

  C_SDS_Agent *agent []; //candidates

  private: //-------------------------------------------------------------------
  struct S_Riverbed //river bed
  {
      double coordOnSector []; //coordinate on the sector (number of cells: number of sectors on the coordinate, cell value: specific coordinate on the sector)
  };

  double restSpace [];      //restaurants space
  S_Riverbed    rb [];      //riverbed

  void Research  (const double  ko,
                  const int     raddr,
                  const double  restSpace,
                  const double  rangeMin,
                  const double  rangeStep,
                  const double  pitOld,
                  double       &pitNew);
};
//——————————————————————————————————————————————————————————————————————————————

接下来，我们应该特别考虑“C_AO_SDSm”类的“Init”初始化方法。该方法执行以下操作：

1.从一开始，我们需要调用基类方法“StandardInit”，并将“rangeMinP”、“rangeMaxP”、“rangeStepP”传递给它。如果该方法返回“false”，则“Init”函数也返回“false”，表示算法初始化失败。
2.使用“delete”删除代理。重用算法对象时这是必要的。
3.然后我们将SDSm算法的“agent”数组和基类的“a”的大小更改为“popSize”并执行类型转换。
4.接下来，我们执行与 有关 SDSm 的文章中描述的算法类似的操作。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_SDSm::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  for (int i = 0; i < ArraySize (agent); i++) delete agent [i];

  ArrayResize (agent, popSize);
  ArrayResize (a,     popSize);

  for (int i = 0; i < popSize; i++)
  {
    a     [i] = new C_SDS_Agent ();
    agent [i] = (C_SDS_Agent *)a [i];

    agent [i].Init (coords);
  }

  ArrayResize (restSpace, coords);
  ArrayResize (rb,        coords);
  for (int i = 0; i < coords; i++)
  {
    ArrayResize     (rb [i].coordOnSector, restNumb);
    ArrayInitialize (rb [i].coordOnSector, -DBL_MAX);
  }

  for (int i = 0; i < coords; i++)
  {
    restSpace [i] = (rangeMax [i] - rangeMin [i]) / restNumb;
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

4.所有算法的统一测试代码

虽然目前还不需要“增加”测试台，但我们仍然会把测试台的所有功能转移到“C_TestStand”类中。这将使我们能够方便地封装测试台功能。由于测试台功能没有发生重大变化，因此我就不详细描述了。我们简单看一下它的当前状态：

#include <Canvas\Canvas.mqh>
#include <\Math\Functions.mqh>

//——————————————————————————————————————————————————————————————————————————————
class C_TestStand
{
  public: void Init (int width, int height)
  {
    W = width;  //750;
    H = height; //375;

    WscrFunc = H - 2;
    HscrFunc = H - 2;

    //creating a table ---------------------------------------------------------
    string canvasName = "AO_Test_Func_Canvas";

    if (!Canvas.CreateBitmapLabel (canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW))
    {
      Print ("Error creating Canvas: ", GetLastError ());
      return;
    }

    ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false);
    ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true);

    ArrayResize (FunctScrin, HscrFunc);

    for (int i = 0; i < HscrFunc; i++) ArrayResize (FunctScrin [i].clr, HscrFunc);

  }

  struct S_CLR
  {
    color clr [];
  };

  //----------------------------------------------------------------------------
  public: void CanvasErase ()
  {
    Canvas.Erase (XRGB (0, 0, 0));
    Canvas.FillRectangle (1,     1, H - 2, H - 2, COLOR2RGB (clrWhite));
    Canvas.FillRectangle (H + 1, 1, W - 2, H - 2, COLOR2RGB (clrWhite));
  }

  //----------------------------------------------------------------------------
  public: void MaxMinDr (C_Function & f)
  {
    //draw Max global-------------------------------------------------------------
    int x = (int)Scale(f.GetMaxFuncX(), f.GetMinRangeX(), f.GetMaxRangeX(), 1, W/2 - 1, false);
    int y = (int)Scale(f.GetMaxFuncY(), f.GetMinRangeY(), f.GetMaxRangeY(), 1, H   - 1, true);

    Canvas.Circle(x, y, 12, COLOR2RGB(clrBlack));
    Canvas.Circle(x, y, 13, COLOR2RGB(clrBlack));
    Canvas.Circle(x, y, 14, COLOR2RGB(clrBlack));
    Canvas.Circle(x, y, 15, COLOR2RGB(clrBlack));

    //draw Min global-------------------------------------------------------------
    x = (int)Scale(f.GetMinFuncX(), f.GetMinRangeX(), f.GetMaxRangeX(), 0, W/2 - 1, false);
    y = (int)Scale(f.GetMinFuncY(), f.GetMinRangeY(), f.GetMaxRangeY(), 0, H - 1, true);

    Canvas.Circle(x, y, 12, COLOR2RGB(clrBlack));
    Canvas.Circle(x, y, 13, COLOR2RGB(clrBlack));
  }

  //----------------------------------------------------------------------------
  public: void PointDr (double &args [], C_Function & f, int shiftX, int shiftY, int count, bool main)
  {
    double x = 0.0;
    double y = 0.0;

    double xAve = 0.0;
    double yAve = 0.0;

    int width  = 0;
    int height = 0;

    color clrF = clrNONE;

    for(int i = 0; i < count; i++)
    {
      xAve += args [i * 2];
      yAve += args [i * 2 + 1];

      x = args [i * 2];
      y = args [i * 2 + 1];

      width  = (int)Scale(x, f.GetMinRangeX(), f.GetMaxRangeX(), 0, WscrFunc - 1, false);
      height = (int)Scale(y, f.GetMinRangeY(), f.GetMaxRangeY(), 0, HscrFunc - 1, true);

      clrF = DoubleToColor(i, 0, count - 1, 0, 270);
      Canvas.FillCircle(width + shiftX, height + shiftY, 1, COLOR2RGB(clrF));
    }

    xAve /=(double)count;
    yAve /=(double)count;

    width  = (int)Scale(xAve, f.GetMinRangeX(), f.GetMaxRangeX(), 0, WscrFunc - 1, false);
    height = (int)Scale(yAve, f.GetMinRangeY(), f.GetMaxRangeY(), 0, HscrFunc - 1, true);

    if(!main)
    {
      Canvas.FillCircle(width + shiftX, height + shiftY, 3, COLOR2RGB(clrBlack));
      Canvas.FillCircle(width + shiftX, height + shiftY, 2, COLOR2RGB(clrWhite));
    }
    else
    {
      Canvas.Circle (width + shiftX, height + shiftY, 5, COLOR2RGB (clrBlack));
      Canvas.Circle (width + shiftX, height + shiftY, 6, COLOR2RGB (clrBlack));
    }
  }

  //----------------------------------------------------------------------------
  public: void SendGraphToCanvas ()
  {
    for (int w = 0; w < HscrFunc; w++)
    {
      for (int h = 0; h < HscrFunc; h++)
      {
        Canvas.PixelSet (w + 1, h + 1, COLOR2RGB (FunctScrin [w].clr [h]));
      }
    }
  }

  //----------------------------------------------------------------------------
  public: void DrawFunctionGraph (C_Function & f)
  {
    double ar [2];
    double fV;

    for (int w = 0; w < HscrFunc; w++)
    {
      ar [0] = Scale (w, 0, H, f.GetMinRangeX (), f.GetMaxRangeX (), false);
      for (int h = 0; h < HscrFunc; h++)
      {
        ar [1] = Scale (h, 0, H, f.GetMinRangeY (), f.GetMaxRangeY (), true);
        fV = f.CalcFunc (ar, 1);
        FunctScrin [w].clr [h] = DoubleToColor (fV, f.GetMinFunValue (), f.GetMaxFunValue (), 0, 270);
      }
    }
  }

  //----------------------------------------------------------------------------
  public: void Update ()
  {
    Canvas.Update ();
  }

  //----------------------------------------------------------------------------
  //Scaling a number from a range to a specified range
  public: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers = false)
  {
    if (OutMIN == OutMAX) return (OutMIN);
    if (InMIN == InMAX) return ((OutMIN + OutMAX) / 2.0);
    else
    {
      if (Revers)
      {
        if (In < InMIN) return (OutMAX);
        if (In > InMAX) return (OutMIN);
        return (((InMAX - In) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
      }
      else
      {
        if (In < InMIN) return (OutMIN);
        if (In > InMAX) return (OutMAX);
        return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
      }
    }
  }

  //----------------------------------------------------------------------------
  private: color DoubleToColor (const double In,    //input value
                                const double inMin, //minimum of input values
                                const double inMax, //maximum of input values
                                const int    loH,   //lower bound of HSL range values
                                const int    upH)   //upper bound of HSL range values
  {
    int h = (int) Scale (In, inMin, inMax, loH, upH, true);
    return HSLtoRGB (h, 1.0, 0.5);
  }

  //----------------------------------------------------------------------------
  private: color HSLtoRGB (const int    h, //0   ... 360
                           const double s, //0.0 ... 1.0
                           const double l) //0.0 ... 1.0
  {
    int r;
    int g;
    int b;
    if (s == 0.0)
    {
      r = g = b = (unsigned char)(l * 255);
      return StringToColor ((string) r + "," + (string) g + "," + (string) b);
    }
    else
    {
      double v1, v2;
      double hue = (double) h / 360.0;
      v2 = (l < 0.5) ? (l * (1.0 + s)) : ((l + s) - (l * s));
      v1 = 2.0 * l - v2;
      r = (unsigned char)(255 * HueToRGB (v1, v2, hue + (1.0 / 3.0)));
      g = (unsigned char)(255 * HueToRGB (v1, v2, hue));
      b = (unsigned char)(255 * HueToRGB (v1, v2, hue - (1.0 / 3.0)));
      return StringToColor ((string) r + "," + (string) g + "," + (string) b);
    }
  }

  //----------------------------------------------------------------------------
  private: double HueToRGB (double v1, double v2, double vH)
  {
    if (vH < 0) vH += 1;
    if (vH > 1) vH -= 1;
    if ((6 * vH) < 1) return (v1 + (v2 - v1) * 6 * vH);
    if ((2 * vH) < 1) return v2;
    if ((3 * vH) < 2) return (v1 + (v2 - v1) * ((2.0f / 3) - vH) * 6);
    return v1;
  }

  //----------------------------------------------------------------------------
  public: int W; //monitor screen width
  public: int H; //monitor screen height

  private: int WscrFunc; //test function screen width
  private: int HscrFunc; //test function screen height

  public:  CCanvas Canvas;      //drawing table
  private: S_CLR FunctScrin []; //two-dimensional matrix of colors
};
//——————————————————————————————————————————————————————————————————————————————

现在让我们看一下测试台代码本身。当研究标准输入参数时，很明显我们现在能够在设置中选择优化算法和测试函数。这使得我们可以创建独特的测试函数集来测试算法。现在我们只能对平滑函数或离散函数进行测试。此外，现在可以选择最适合用户需求的任意测试函数组合。

#include "PAO\#C_TestStandFunctions.mqh"
#include "PAO\#C_AO.mqh"

//——————————————————————————————————————————————————————————————————————————————
input string AOparam            = "----------------"; //AO parameters-----------
input E_AO   AOexactly_P        = AO_NONE;

input string TestStand_1        = "----------------"; //Test stand--------------
input double ArgumentStep_P     = 0.0;   //Argument Step

input string TestStand_2        = "----------------"; //------------------------
input int    Test1FuncRuns_P    = 5;     //Test #1: Number of functions in the test
input int    Test2FuncRuns_P    = 25;    //Test #2: Number of functions in the test
input int    Test3FuncRuns_P    = 500;   //Test #3: Number of functions in the test

input string TestStand_3        = "----------------"; //------------------------
input EFunc  Function1          = Hilly;
input EFunc  Function2          = Forest;
input EFunc  Function3          = Megacity;

input string TestStand_4        = "----------------"; //------------------------
input int    NumbTestFuncRuns_P = 10000; //Number of test function runs
input int    NumberRepetTest_P  = 10;    //Test repets number

input string TestStand_5        = "----------------"; //------------------------
input bool   Video_P            = true;  //Show video
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  C_AO *AO = SelectAO (AOexactly_P);
  if (AO == NULL)
  {
    Print ("AO is not selected...");
    return;
  }

  Print (AO.GetName (), "|", AO.GetDesc (), "|", AO.GetParams ());

  //============================================================================
  C_TestStand ST; //stand
  ST.Init (750, 375);

  double allScore = 0.0;
  double allTests = 0.0;

  C_Function *F1 = SelectFunction (Function1);
  C_Function *F2 = SelectFunction (Function2);
  C_Function *F3 = SelectFunction (Function3);

  if (F1 != NULL)
  {
    Print ("=============================");
    ST.CanvasErase ();

    FuncTests (AO, ST, F1, Test1FuncRuns_P, clrLime,      allScore, allTests);
    FuncTests (AO, ST, F1, Test2FuncRuns_P, clrAqua,      allScore, allTests);
    FuncTests (AO, ST, F1, Test3FuncRuns_P, clrOrangeRed, allScore, allTests);
    delete F1;
  }

  if (F2 != NULL)
  {
    Print ("=============================");
    ST.CanvasErase ();
    FuncTests (AO, ST, F2, Test1FuncRuns_P, clrLime,      allScore, allTests);
    FuncTests (AO, ST, F2, Test2FuncRuns_P, clrAqua,      allScore, allTests);
    FuncTests (AO, ST, F2, Test3FuncRuns_P, clrOrangeRed, allScore, allTests);
    delete F2;
  }

  if (F3 != NULL)
  {
    Print ("=============================");
    ST.CanvasErase ();
    FuncTests (AO, ST, F3, Test1FuncRuns_P, clrLime,      allScore, allTests);
    FuncTests (AO, ST, F3, Test2FuncRuns_P, clrAqua,      allScore, allTests);
    FuncTests (AO, ST, F3, Test3FuncRuns_P, clrOrangeRed, allScore, allTests);
    delete F3;
  }

  Print ("=============================");
  if (allTests > 0.0) Print ("All score: ", DoubleToString (allScore, 5), " (", DoubleToString (allScore * 100 / allTests, 2), "%)");
  delete AO;
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void FuncTests (C_AO          &ao,
                C_TestStand   &st,
                C_Function    &f,
                const  int     funcCount,
                const  color   clrConv,
                double        &allScore,
                double        &allTests)
{
  if (funcCount <= 0) return;

  allTests++;

  if (Video_P)
  {
    st.DrawFunctionGraph (f);
    st.SendGraphToCanvas ();
    st.MaxMinDr          (f);
    st.Update            ();
  }

  int    xConv      = 0.0;
  int    yConv      = 0.0;
  double aveResult  = 0.0;
  int    params     = funcCount * 2;
  int    epochCount = NumbTestFuncRuns_P / (int)ao.params [0].val;

  //----------------------------------------------------------------------------
  double rangeMin  [], rangeMax  [], rangeStep [];
  ArrayResize (rangeMin,  params);
  ArrayResize (rangeMax,  params);
  ArrayResize (rangeStep, params);

  for (int i = 0; i < funcCount; i++)
  {
    rangeMax  [i * 2] = f.GetMaxRangeX ();
    rangeMin  [i * 2] = f.GetMinRangeX ();
    rangeStep [i * 2] = ArgumentStep_P;

    rangeMax  [i * 2 + 1] = f.GetMaxRangeY ();
    rangeMin  [i * 2 + 1] = f.GetMinRangeY ();
    rangeStep [i * 2 + 1] = ArgumentStep_P;
  }

  for (int test = 0; test < NumberRepetTest_P; test++)
  {
    //--------------------------------------------------------------------------
    if (!ao.Init (rangeMin, rangeMax, rangeStep)) break;

    // Optimization-------------------------------------------------------------
    for (int epochCNT = 1; epochCNT <= epochCount && !IsStopped (); epochCNT++)
    {
      ao.Moving ();

      for (int set = 0; set < ArraySize (ao.a); set++)
      {
        ao.a [set].f = f.CalcFunc (ao.a [set].c, funcCount);
      }

      ao.Revision  ();

      if (Video_P)
      {
        //drawing a population--------------------------------------------------
        st.SendGraphToCanvas  ();

        for (int i = 0; i < ArraySize (ao.a); i++)
        {
          st.PointDr (ao.a [i].c, f, 1, 1, funcCount, false);
        }
        st.PointDr (ao.cB, f, 1, 1, funcCount, true);

        st.MaxMinDr (f);

        //drawing a convergence graph---------------------------------------------
        xConv = (int)st.Scale (epochCNT, 1, epochCount, st.H + 2, st.W - 3, false);
        yConv = (int)st.Scale (ao.fB, f.GetMinFunValue (), f.GetMaxFunValue (), 2, st.H - 2, true);
        st.Canvas.FillCircle (xConv, yConv, 1, COLOR2RGB (clrConv));

        st.Update ();
      }
    }

    aveResult += ao.fB;
  }

  aveResult /= (double)NumberRepetTest_P;

  double score = aveResult;

  Print (funcCount, " ", f.GetFuncName (), "'s; Func runs: ", NumbTestFuncRuns_P, "; result: ", aveResult);
  allScore += score;
}
//——————————————————————————————————————————————————————————————————————————————

5.让我们添加流行的测试函数

有时我会被问到为什么我没有将这些流行且积极使用的优化算法纳入研究和开发测试函数集中。原因在于，按照我的分类，它们都属于“简单”测试函数类别。它们超过一半的表面集中在全局极端附近，这使得它们太“可预测”而无法进行适当的测试。但尽管如此，人们还是习惯于信任它们，并倾向于在这些函数上测试它们的算法。所以我决定将 Ackley、Goldstein-Price 和 Shaffer #2 纳入到这个系列中。这将有助于平衡用户测试函数的选择，提供更全面、更可靠的优化算法测试，为研究人员开辟新的视野，并有助于更深入地了解其效率。

Ackley 方程：

f(x, y) = -(-20 * exp(-0.2 * sqrt(0.5 * (x^2 + y^2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20)

其中：
- x, y - 函数输入参数，
- e - 欧拉数（约 2.71828），
- π - 圆周率（约为 3.14159）。

函数代码：

double Core (double x, double y)
{
  double res1 = -20.0 * MathExp (-0.2 * MathSqrt (0.5 * (x * x + y * y)));
  double res2 = -MathExp (0.5 * (MathCos (2.0 * M_PI * x) + MathCos (2.0 * M_PI * y)));
  double res3 = -(res1 + res2 + M_E + 20.0);

  return Scale (res3, -14.302667500265278, 0.0, 0.0, 1.0);
}

Goldstein-Price 方程：

f(x, y) = -([1 + (x + y + 1)^2 * (19 - 14x + 3x^2 - 14y + 6xy + 3y^2)] * [30 + (2x - 3y)^2 * (18 - 32x + 12x^2 + 48y - 36xy + 27y^2)])

函数代码：

double Core (double x, double y)
{
  double part1 = 1 + MathPow ((x + y + 1), 2) * (19 - 14 * x + 3 * x * x - 14 * y + 6 * x * y + 3 * y * y);
  double part2 = 30 + MathPow ((2 * x - 3 * y), 2) * (18 - 32 * x + 12 * x * x + 48 * y - 36 * x * y + 27 * y * y);

  return Scale (-part1 * part2, -1015690.2717980597, -3.0, 0.0, 1.0);
}

Shaffer #2 方程：

f(x, y) = -(0.5 + ((sin(x^2 - y^2)^2 - 0.5) / (1 + 0.001 * (x^2 + y^2))^2))

函数代码：

double Core (double x, double y)
{
  double numerator   = MathPow (MathSin (x * x - y * y), 2) - 0.5;
  double denominator = MathPow (1 + 0.001 * (x * x + y * y), 2);
    
  return Scale (-(0.5 + numerator / denominator), -0.9984331449753265, 0, 0, 1.0);
}

注意：测试函数值标准化为[0.0,1.0]。

6.构建 3D 测试函数

有时，不仅需要从数字和方程式中抽象出来，还需要直观地看待它们，以便更深入地理解测试函数及其解法。因此我决定利用 MetaTrader 5 平台中利用 DirectX 构建 3D 场景的功能。我受到标准发行版中包含的开发人员提供的“...\MQL5\Experts\Examples\Math 3D Morpher\Math 3D Morpher.mq5”文件的启发，并将我之前开发的函数可视化（我计划将其添加到测试台的函数列表中）。所以我决定创建一个用于测试函数的可视化工具。

为此，我必须扩展 Functions.mqh 文件，该文件存储了用于测试优化算法的测试函数类。我添加的附加函数不仅可以让您在需要时直观地研究函数的变化，还可以更深入地探索它们的属性和特性。

这不仅使我的研究更加有趣和直观，而且还帮助我更全面地理解测试函数的行为。最终，3D 可视化不仅可以帮助我在屏幕上看到数字，还可以直接与函数的形状和结构进行交互，这在修改它们和分析属性时非常重要。

用于构建 3D 场景模型的附加函数代码：

//——————————————————————————————————————————————————————————————————————————————
//GenerateFunctionDataFixedSize
bool GenerateFunctionDataFixedSize (int x_size, int y_size, double &data [], double x_min, double x_max, double y_min, double y_max, C_Function &function)
{
  if (x_size < 2 || y_size < 2)
  {
    PrintFormat ("Error in data sizes: x_size=%d,y_size=%d", x_size, y_size);
    return (false);
  }

  double dx = (x_max - x_min) / (x_size - 1);
  double dy = (y_max - y_min) / (y_size - 1);

  ArrayResize (data, x_size * y_size);

  //---
  for (int j = 0; j < y_size; j++)
  {
    for (int i = 0; i < x_size; i++)
    {
      double x = x_min + i * dx;
      double y = y_min + j * dy;

      data [j * x_size + i] = function.Core (x, y);
    }
  }
  return (true);
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//GenerateDataFixedSize
bool GenerateDataFixedSize (int x_size, int y_size, C_Function &function, double &data [])
{
  if (x_size < 2 || y_size < 2)
  {
    PrintFormat ("Error in data sizes: x_size=%d,y_size=%d", x_size, y_size);
    return (false);
  }

  return GenerateFunctionDataFixedSize (x_size, y_size, data,
                                        function.GetMinRangeX (),
                                        function.GetMaxRangeX (),
                                        function.GetMinRangeY (),
                                        function.GetMaxRangeY (),
                                        function);
}
//——————————————————————————————————————————————————————————————————————————————

此外，我还添加了已经熟悉的函数的离散变体 - SkinDiscrete 和 HillyDiscrete。

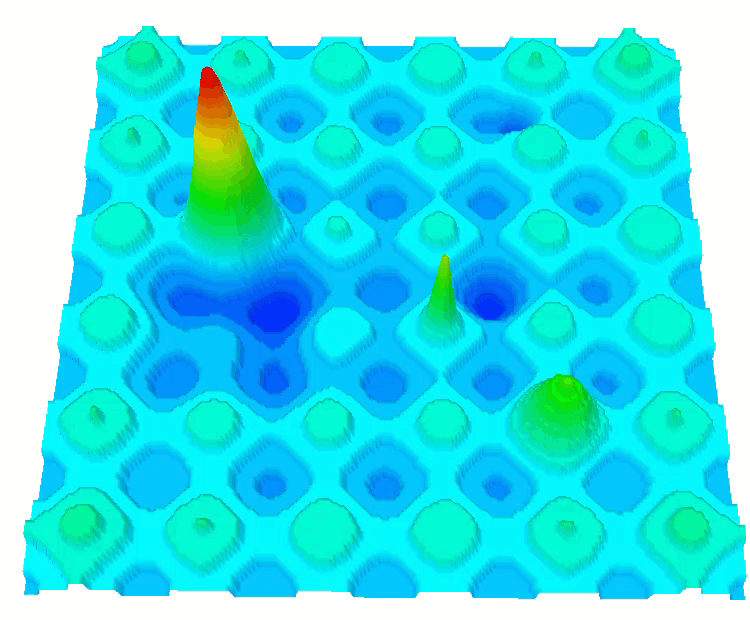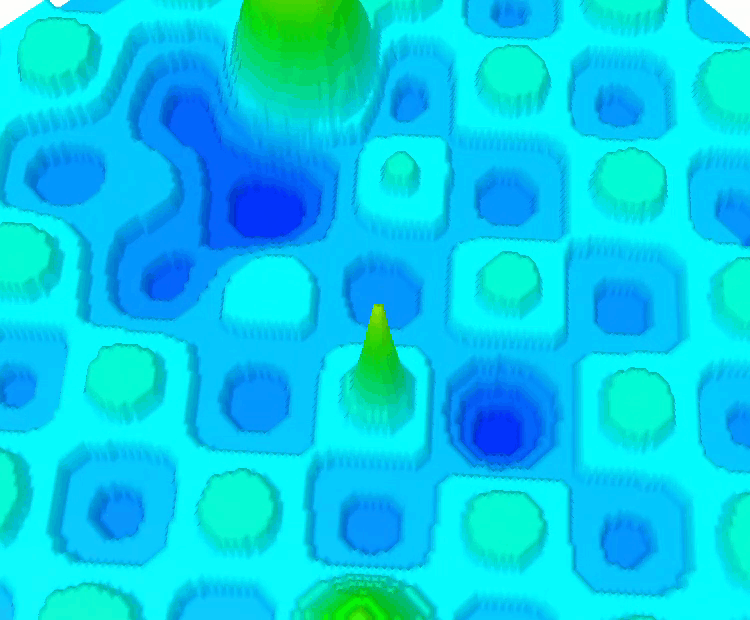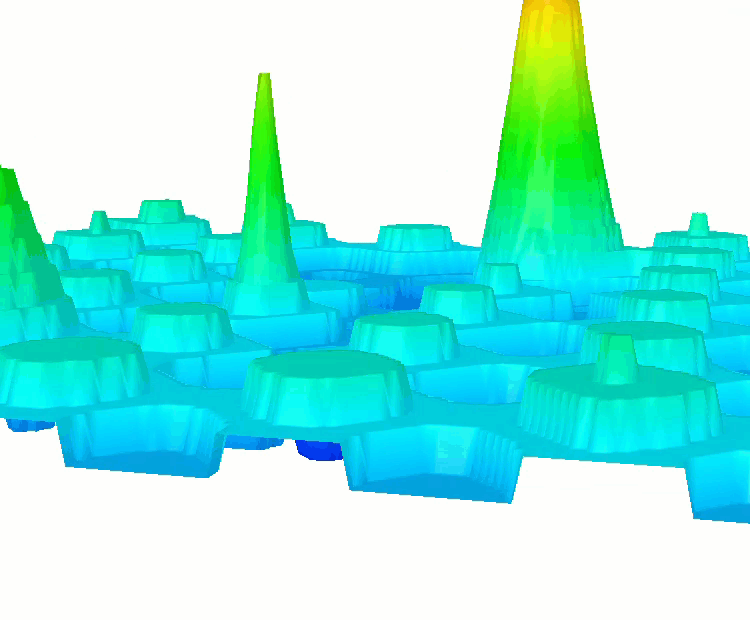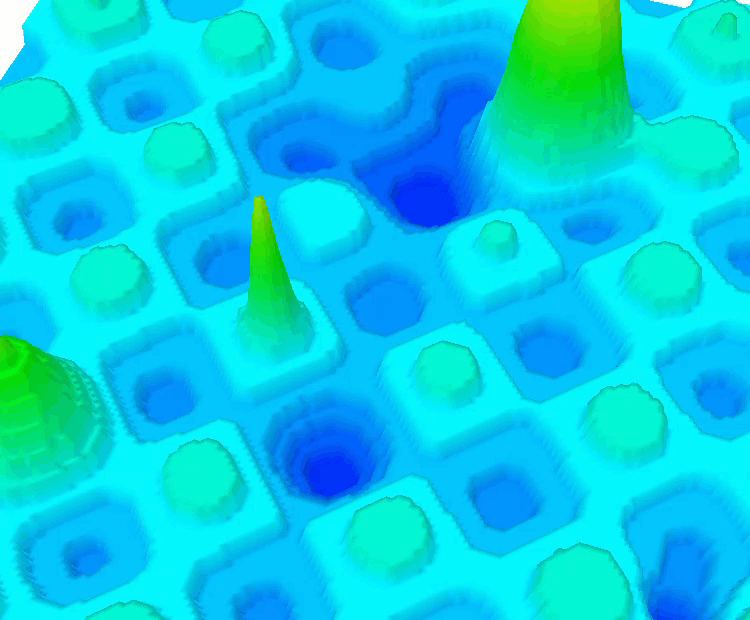
HillyDiscrete 函数

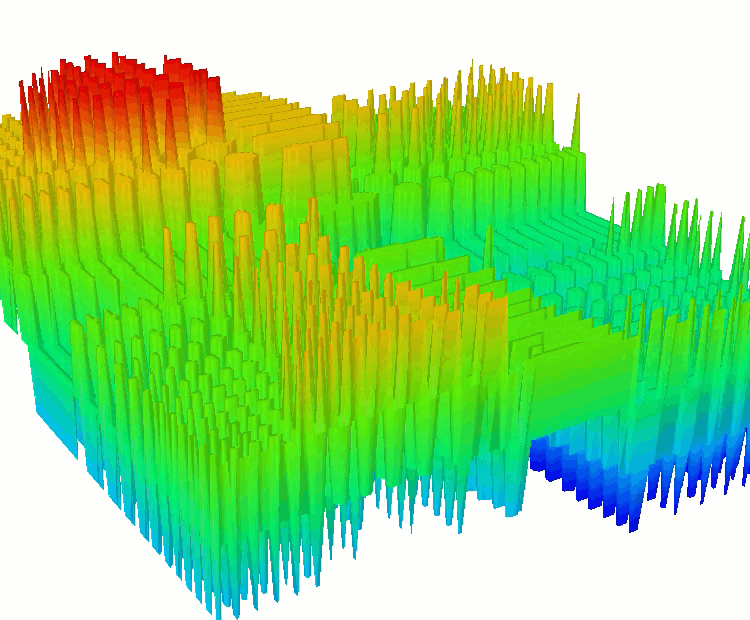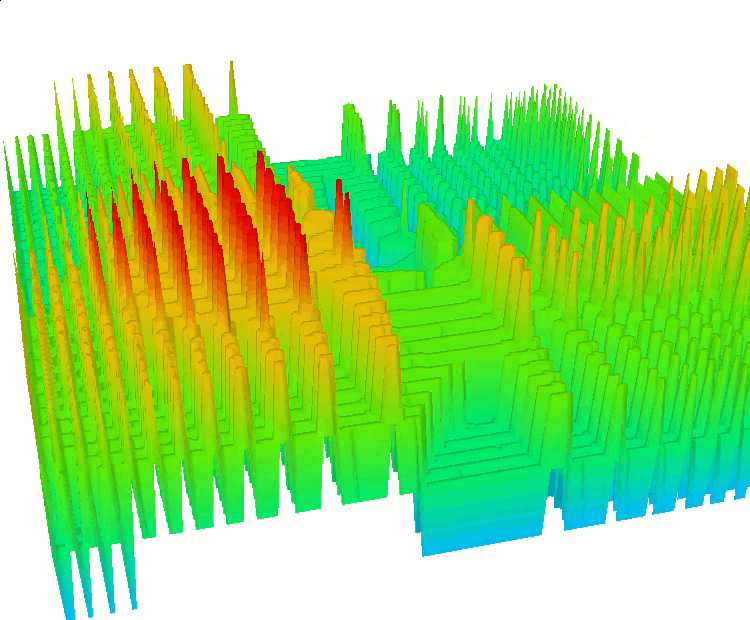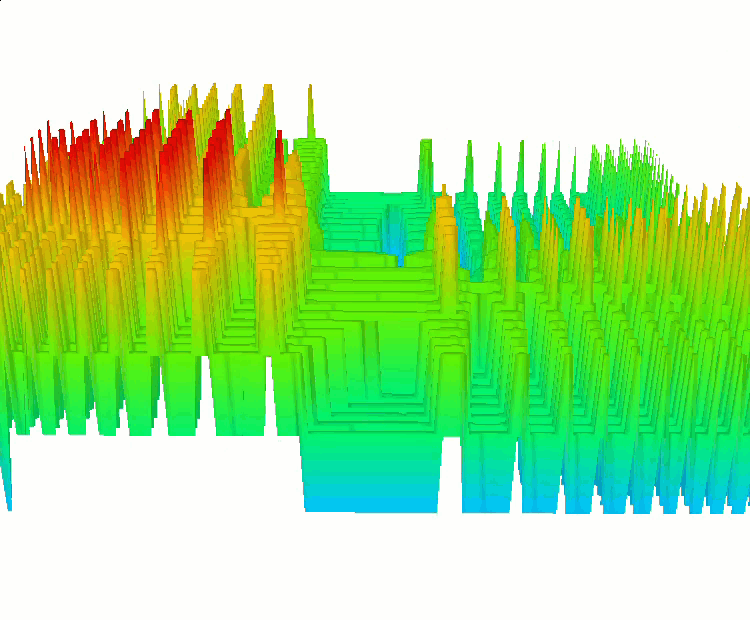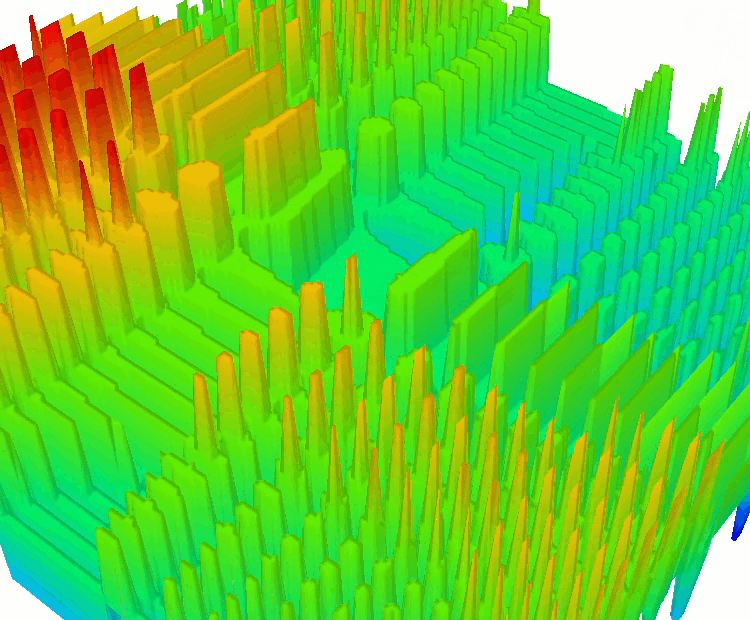
SkinDiscrete 函数

Shaffer #2 函数

7.总结

我们将继续使用 Hilly、Forest 和 Megacity 测试函数，这些函数已经被誉为优化算法的真正测试，有助于创建可靠的排名表。然而，我们不应该仅仅局限于这些函数 - 毕竟，测试函数列表已经成功扩展！因此，您可以自由选择：实验、探索、发现新视野，因为这就是科学研究的美妙之处。

在我们通过基类继承对混合优化方法进行烹饪探索结束时，我们发现建立这样的起点为无尽的研究可能性打开了大门。将各种群体算法合并为一类，不仅可以提高寻找最优解的准确性和速度，还可以创建一个通用的研究工具。

创建一个结合各种测试函数（离散、平滑、尖锐、不可微）的单一测试台，为测试和比较不同的优化方法开辟了新的机会。这种方法不仅允许研究人员使用标准函数集，还可以创建适合特定任务和要求的自己的测试台。

因此，将群体算法组合成一个类并创建一个通用的测试台为我们开辟了一条令人兴奋的道路，可以创建优化方法的新“美食”组合，让我们能够在寻找最优解决方案的世界中发现新的风味。让我们继续这场烹饪实验，在优化领域的卓越和创新的道路上创造出新的杰作！