Otimização de nuvens atmosféricas — Atmosphere Clouds Model Optimization (ACMO): Teoria

Conteúdo

1. Introdução
2. Implementação do algoritmo

Introdução

No mundo das tecnologias modernas, a busca pelas melhores soluções tornou-se uma tarefa cada vez mais relevante para algoritmos de otimização. Uma das abordagens mais interessantes para esse problema é o algoritmo meta-heurístico Atmosphere Clouds Model Optimization (ACMO), que, apesar de sua complexidade matemática, pode ser explicado de maneira simples e intuitiva. 

Imagine um céu virtual infinito, onde nuvens se formam e se movem como na atmosfera real. O clima aqui não é apenas um conjunto de condições, mas um sistema dinâmico, no qual umidade e pressão atmosférica influenciam cada decisão. Inspirado por fenômenos naturais, o algoritmo ACMO utiliza os princípios da formação de nuvens para explorar o espaço de soluções, da mesma forma que as nuvens se formam, se dispersam e desaparecem nos vastos céus, buscando os caminhos mais otimizados. O algoritmo foi proposto pelos autores Yan e outros, e publicado em 2013.

Neste artigo, examinaremos detalhadamente cada etapa do algoritmo ACMO, começando pela preparação do "céu", onde as nuvens nascem como potenciais soluções. Acompanharemos seu movimento pelo espaço atmosférico virtual, observando como se adaptam e se transformam de acordo com as condições climáticas. Mergulhando nesse fascinante processo, você verá como as nuvens, semelhantes a grupos exploratórios, buscam encontrar soluções ótimas no labirinto de possibilidades. Vamos juntos desvendar os segredos desse algoritmo e entender seu funcionamento, passo a passo.

A ideia principal do algoritmo Atmosphere Clouds Model Optimization (ACMO) é modelar o comportamento das nuvens na natureza para resolver problemas de otimização. O algoritmo utiliza três aspectos fundamentais do comportamento das nuvens:

• Geração. As nuvens se formam em áreas de alta umidade, permitindo ao algoritmo explorar a vizinhança das soluções ótimas atuais.
• Movimento. As nuvens se deslocam pelo espaço de soluções, promovendo a disseminação da população e aumentando sua diversidade. Isso ajuda a evitar que o algoritmo fique preso em ótimos locais.
• Dispersão. As nuvens se espalham por todo o espaço de busca, permitindo ao algoritmo cobrir uma faixa mais ampla de soluções possíveis e melhorar as chances de encontrar o ótimo global.

Implementação do algoritmo

Como o conceito do algoritmo ACMO é bastante complexo, avançaremos do simples para o mais elaborado. Vamos descrever de forma simples e concisa a ideia principal do algoritmo.

1. Preparação do "céu". Imagine que estamos criando um céu virtual. Esse céu é dividido em várias regiões. Cada região possui sua própria umidade (qualidade das soluções) e pressão atmosférica (experiência acumulada na busca).

2. Nascimento das nuvens. As nuvens aparecem apenas nas regiões mais "úmidas". Cada nuvem é composta por inúmeras gotas, e cada gota representa uma possível solução para nosso problema.

3. Movimento das nuvens. As nuvens praticamente nunca ficam paradas. Elas se movem das regiões de alta pressão para regiões de baixa pressão. Isso é semelhante ao vento soprando de uma área de alta pressão para uma de baixa pressão na atmosfera real.

4. Mudança na forma das nuvens. Enquanto as nuvens se movem, elas aumentam de tamanho. O grau de crescimento das nuvens depende da diferença de pressão entre as regiões.

5. Evaporação. A cada iteração, as nuvens perdem algumas de suas gotas e, ao perder umidade, sua densidade diminui. Se a nuvem perder umidade demais, ela desaparece completamente.

6. Atualização do "clima". Após cada movimento das nuvens, a umidade e a pressão de cada região são reavaliadas. Se uma nuvem encontrou uma boa solução, a umidade naquela região aumenta.

7. Repetição. Os passos 2 a 6 são repetidos. A cada repetição, as nuvens exploram novas áreas do céu virtual em busca da melhor solução possível.

8. Conclusão. Após atingir um número predefinido de repetições ou encontrar uma solução suficientemente boa, o algoritmo para.

Esse algoritmo pode ser comparado ao envio de várias equipes exploratórias (nuvens) para encontrar um tesouro (solução ótima) em um enorme labirinto (espaço de busca). Cada equipe busca de sua própria maneira, compartilhando informações com outras por meio das mudanças no "clima" das regiões. Aos poucos, juntas, elas encontram o melhor caminho.

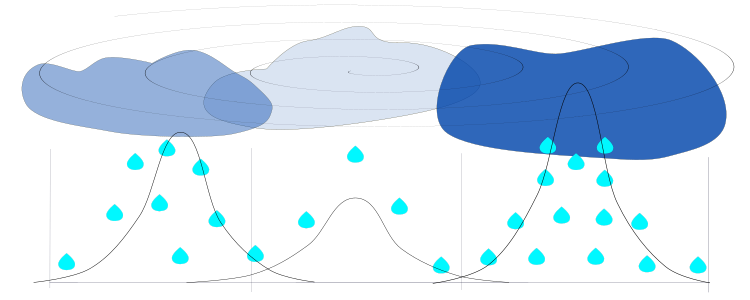
Figura 1. Nuvens de diferentes densidades, umidades e tamanhos sobre as regiões. A precipitação das gotas segue uma distribuição normal.

Agora, vamos nos familiarizar com os parâmetros externos do ACMO e seus propósitos por meio da tabela abaixo.

Parâmetro	Finalidade do parâmetro
popSize - tamanho da população	Tamanho da população de gotas. A população tem um tamanho fixo, e as gotas são distribuídas entre as nuvens.
cloudsNumber - número de nuvens	Quantidade de nuvens
regionsNumber - número de regiões	Cada parâmetro a ser otimizado é dividido em um número igual de regiões.
dMin - quantidade mínima de gotas	Quantidade mínima de gotas em relação à quantidade média de gotas nas nuvens. Valor limite abaixo do qual a nuvem é considerada evaporada.
λ - fator de limite	Fator de limite da umidade de uma região, que define onde pode ser formada uma nuvem com geração de chuva (gotas).
γ - coeficiente de evaporação	Coeficiente de evaporação que reduz a quantidade de umidade nas nuvens a cada iteração.
EnM0 - entropia inicial	Entropia inicial, representando a largura da nuvem no momento de sua formação.
HeM0 - hiperentropia inicial	Hiperentropia, densidade da nuvem ao ser formada, regulando a forma da distribuição normal.

Agora, vamos examinar as etapas do algoritmo ACMO.

1. Inicialização:

• Divisão do espaço de busca U em MD regiões Ui.
• Inicialização dos valores de umidade HUi e pressão atmosférica PUi para cada região.
• Configuração dos parâmetros do algoritmo: fator de limite λ, coeficiente de evaporação γ, entropia inicial EnM0, hiperentropia inicial HeM0, entre outros.

2. Geração das nuvens:

• Identificação do conjunto de regiões S onde a umidade HUi ultrapassa o limite dinâmico calculado Ht.
• Para cada região Ui em S:
• Cálculo do centro da nuvem CenterCk usando a fórmula CenterCk = Center (Ui).
• Cálculo da entropia EnCk e da hiperentropia HeCk com base na entropia inicial EnM0, hiperentropia inicial HeM0 e no coeficiente de contração ζ.
• Geração da nuvem Ck com centro CenterCk, entropia EnCk e hiperentropia HeCk.

3. Atualização da umidade e da pressão:

• Atualização dos valores de umidade HUi e pressão atmosférica PUi para cada região Ui.

4. Fase de movimento das nuvens:

• Para cada nuvem Ck:
• Determinação da direção do movimento com base na diferença de pressão atmosférica entre a região atual e uma região vizinha selecionada.
• Deslocamento da nuvem Ck em direção à região com menor pressão atmosférica.

5. Fase de dispersão das nuvens:

• Para cada nuvem Ck:
• Determinação das gotas da nuvem que se espalham para outras regiões com base na diferença de pressão atmosférica.
• Dispersão das gotas da nuvem Ck para regiões vizinhas com menor pressão atmosférica.

6. Atualização da umidade e da pressão:

• Atualização dos valores de umidade HUi e pressão atmosférica PUi para cada região Ui após o movimento e a dispersão das nuvens.

7. Verificação da condição de término:

• Incremento do contador de iterações t.
• Se t < tmax, retornar ao passo 2 (geração das nuvens).
• Se t >= tmax, o algoritmo é finalizado.

Pontos-chave:

• As regiões Ui formam o espaço de busca, e cada uma é caracterizada por sua umidade HUi e pressão atmosférica PUi.
• As nuvens Ck só são geradas em regiões com umidade suficiente (HUi > Ht).
• O movimento e a dispersão das nuvens ocorrem com base na diferença de pressão atmosférica entre as regiões.
• Os valores de umidade e pressão são atualizados após cada ciclo de movimentação e dispersão das nuvens.

Agora, vamos nos aprofundar nas principais operações das nuvens.

1. A operação Cloudmove (C) é responsável pelo deslocamento das nuvens.

1.1 Para cada nuvem Ck:

• Uma região-alvo F é escolhida aleatoriamente dentro do espaço de busca U.
• Calcula-se a diferença de pressão ΔP entre a região atual E, onde a nuvem está localizada, e a região-alvo F.
• Se a pressão em F for menor do que em E (ΔP > 0), então a nuvem Ck será movida em direção à região com menor pressão.
• A velocidade do deslocamento da nuvem Vk é calculada com base na diferença de pressão e na entropia da nuvem.
• O centro da nuvem Ck é deslocado em uma distância Vk.
• A quantidade de umidade na nuvem Ck diminui em γ * 100% devido à evaporação.
• Se o número de gotas nk cair abaixo do valor limite dN, a nuvem Ck é removida do conjunto de nuvens C (na prática, a nuvem não é eliminada, mas sim realocada para regiões com umidade acima do valor limite, restabelecendo os valores iniciais de entropia e hiperentropia, ajustados para a iteração atual).

Dessa forma, as nuvens se movem em direção a áreas de menor pressão, enquanto sua energia (quantidade de umidade) diminui gradualmente. Esse mecanismo de deslocamento reflete o comportamento físico das nuvens na natureza.

2. A operação Cloudspread (C) é responsável pela dispersão das nuvens.

2.1 Para cada nuvem Ck:

• Identificar a região atual E onde está localizado o centro da nuvem.
• Identificar a região G para onde o centro da nuvem será movido após a fase de deslocamento.
• Calcular a diferença de pressão ΔP = PE - PG entre a região atual e a nova.
• Se as regiões E e G forem diferentes, calcular o fator de dispersão α = ΔP / ΔPmax.
• Se as regiões E e G forem iguais, definir α = 0.3 (velocidade básica de dispersão).
• Calcular a nova entropia da nuvem EnCk = EnCk × (1 + α), onde α é o fator de dispersão.
• Calcular a nova hiperentropia da nuvem HeCk = HeCk × (1 + α), aumentando proporcionalmente ao fator de dispersão.
• Se a entropia da nuvem Ck for maior que 5 × EnM0 ou se a quantidade de umidade nela for menor do que o limite dN, a nuvem Ck é "removida" do conjunto C.

Ideias principais das operações 1 e 2:

• Quanto maior a diferença de pressão entre as regiões, mais rapidamente as nuvens se movem.
• A entropia aumenta para expandir a área do espaço de busca.
  
• A hiperentropia da nuvem cresce para permitir uma exploração mais detalhada do espaço.
• Critérios para a dissipação das nuvens: entropia maior que 5 × EnM0 ou quantidade de umidade menor que dN.

Na descrição do algoritmo, os autores não especificam restrições sobre o número de regiões que uma única nuvem pode abranger. O algoritmo considera apenas duas regiões: a região atual E, onde está localizado o centro da nuvem Ck, e a nova região G (o novo centro após o deslocamento). No entanto, as nuvens aumentam de tamanho a cada iteração, englobando regiões vizinhas, o que leva ao aumento da umidade e da pressão nas áreas onde as gotas precipitam. Dessa forma, uma nuvem pode se mover sequencialmente de uma região para outra, mas, em cada momento específico, o algoritmo trabalha apenas com duas regiões – a atual e a nova. Isso significa que os processos de deslocamento das nuvens e de precipitação de gotas nas regiões são tratados separadamente. As nuvens e as gotas não estão diretamente vinculadas e representam entidades distintas dentro do algoritmo.

O algoritmo atualiza a posição da nuvem, recalcula sua entropia e hiperentropia e verifica se a nuvem atende aos critérios de dissipação, mas não impõe restrições explícitas ao número de regiões que ela pode abranger.

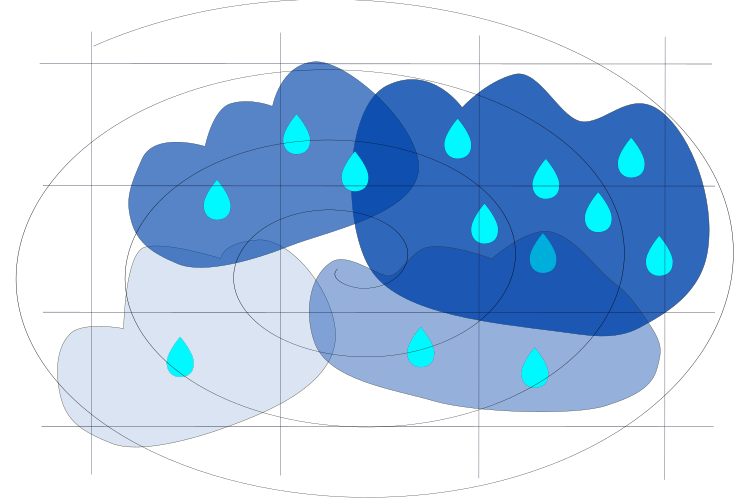
Figura 2. Movimento das nuvens entre as regiões em direção a áreas de menor pressão.

A descrição do algoritmo indica que a região, e não a nuvem, possui uma "função de aptidão", representada pela umidade da região. O papel da nuvem nesse algoritmo é mais como um indicador, determinando quantas gotas cairão em uma determinada região. Pontos-chave:

1. Cada região possui sua própria pressão P, que determina a velocidade de dispersão das nuvens.
2. A nuvem Ck não "possui" gotas; ela apenas indica quantas gotas precipitarão na região atual E e na nova região G.
3. O deslocamento da nuvem da região E para a região G é definido pelo gradiente de pressão ΔP = PE - PG.
4. As gotas não pertencem a uma nuvem específica; elas precipitam nas regiões onde as nuvens estão localizadas.

Dessa forma, a principal entidade que define a dinâmica do "clima" dentro do sistema é a região, e não a nuvem. Isso diferencia esse algoritmo dos algoritmos multipopulacionais tradicionais.

A pressão é uma característica fundamental de cada região dentro do espaço de busca e é usada para determinar a direção do movimento das nuvens. Ou seja, as nuvens se deslocam de áreas de alta pressão para áreas de baixa pressão. Conceitualmente, a pressão em uma região aumenta toda vez que ela é avaliada (quando o valor da função objetivo é calculado para um ponto naquela região). Isso reflete a ideia de que, quanto mais uma determinada área é explorada, maior a "pressão" naquela região, incentivando o algoritmo a explorar outras áreas menos investigadas.

De acordo com a proposta dos autores, a mudança na forma das nuvens ocorre com base na diferença de pressão atmosférica entre a região atual, onde a nuvem está localizada, e a nova região para onde a nuvem se move. Isso acontece da seguinte forma:

• Se a diferença de pressão ΔP = PE - PG for grande, significa que a nuvem está se movendo entre regiões com pressões muito diferentes, resultando em uma maior velocidade de deslocamento.
• Se a diferença de pressão ΔP for pequena, significa que a nuvem está se movendo para uma região com pressão semelhante, resultando em uma velocidade menor.

Além disso, de acordo com a descrição do algoritmo, os valores de entropia e hiperentropia na primeira iteração são definidos da seguinte maneira:

1. A entropia inicial EnM0 é dada por Ij / A, onde:

• A é definido como 6.
• Ij representa o comprimento da região na dimensão j.

2. A hiperentropia inicial HeM0 é fixada em 0.5.

A entropia no algoritmo determina a extensão da dispersão da nuvem (tamanho). Na primeira iteração, a nuvem deve cobrir pelo menos uma região completa do espaço de busca.

A hiperentropia define a "espessura" da nuvem e regula a forma da distribuição normal, ou seja, determina o quão densamente as gotas estão distribuídas dentro da nuvem. O valor inicial 0.5 foi determinado experimentalmente como um equilíbrio entre uma nuvem muito dispersa e uma muito densa.

1. A entropia aumenta a cada iteração. Isso significa que as nuvens gradualmente "se expandem", abrangendo áreas cada vez maiores do espaço de busca, ajudando a evitar que o algoritmo fique preso em ótimos locais.
2. A hiperentropia, por outro lado, aumenta a densidade no centro da nuvem. Isso faz com que a nuvem refine a solução dentro da região mais promissora.

Esse método permite que o algoritmo expanda a área de busca ao mesmo tempo que refina soluções, sem perder a capacidade de "escapar" de ótimos locais.

Em um espaço multidimensional, a definição do índice da região para a nuvem torna-se um pouco mais complexa, mas o princípio permanece o mesmo. Veja como funciona:

• O espaço de busca é dividido em regiões ao longo de todas as dimensões. Se tivermos D dimensões e cada dimensão for dividida em M intervalos, então o número total de regiões será M×D.
• O índice da região, nesse caso, não é apenas um número, mas um conjunto de coordenadas que indica a posição da região em cada dimensão. Para determinar o índice da região para uma nuvem, o algoritmo verifica em quais intervalos de cada dimensão o centro da nuvem está localizado.

Por exemplo, em um espaço tridimensional (D = 3), dividido em 10 intervalos por dimensão (M = 10), o índice da região pode ser representado como (3, 7, 2), indicando o 3º intervalo na primeira dimensão, o 7º na segunda e o 2º na terceira.

É importante destacar que o centro da nuvem não é necessariamente a melhor gota da nuvem. Aqui estão alguns pontos essenciais:

• O centro da nuvem é definido como uma espécie de "ponto médio" da área onde a nuvem foi gerada.
• A melhor gota da nuvem é aquela que fornece o melhor valor da função objetivo (o valor mais alto de aptidão).
• No algoritmo, há um conceito chamado "valor de umidade da região" (UiH), que representa o melhor valor de aptidão encontrado naquela região. Esse valor está associado à melhor gota, não ao centro da nuvem.
• O centro da nuvem é usado para determinar sua posição no espaço de busca e para calcular seu deslocamento, mas ele não representa necessariamente a melhor solução.

Portanto, centro da nuvem e melhor gota são conceitos distintos dentro desse algoritmo. O centro da nuvem serve para a navegação dentro do espaço de busca, enquanto a melhor gota representa a solução mais otimizada encontrada na região até aquele momento.

Essa abordagem permite que o algoritmo explore eficientemente o espaço de busca (usando o centro da nuvem para movimentação), ao mesmo tempo que rastreia e preserva as melhores soluções descobertas nas regiões (melhores gotas precipitadas nas regiões).

No ACMO, há alguns cenários nos quais ocorre a dissipação ou "dissolução" das nuvens. Vamos analisá-los:

1. Quantidade insuficiente de umidade:

• Cada nuvem contém uma certa quantidade de umidade.
• Se essa quantidade cair abaixo do limite dN, a nuvem é considerada seca demais e desaparece.
• Isso é semelhante ao que ocorre na natureza, onde pequenas nuvens acabam se dissipando.

2. Entropia excessiva:

• A entropia da nuvem indica o quão amplamente dispersa ela está.
• Se a entropia ultrapassar 5 vezes a entropia inicial (5 × EnM0), a nuvem é considerada dispersa demais e desaparece.

Isso pode ser comparado a uma nuvem que se expandiu tanto que simplesmente se dissolveu no ar.

3. Evaporação natural:

• Após cada deslocamento, a quantidade de umidade da nuvem diminui em uma determinada porcentagem (γ * 100%).
• Se, após essa redução, a umidade cair abaixo do limite dN, a nuvem desaparece.

Isso se assemelha ao processo natural de evaporação das nuvens.

4. Fusão de nuvens:

• Embora esse aspecto não seja explicitamente descrito no algoritmo original, algumas variações do ACMO permitem a fusão de nuvens.
• Durante esse processo, uma das nuvens (geralmente a menor) pode ser considerada dissolvida ao se tornar parte de uma nuvem maior.

Todos esses mecanismos de dissipação das nuvens ajudam o algoritmo a "limpar" o espaço de busca de soluções não promissoras e a se concentrar nas áreas mais promissoras. 

Um pesquisador atento pode questionar: o que acontece se todas as nuvens se moverem para regiões de baixa pressão e se agruparem nos mesmos locais? Primeiramente, as regiões de baixa pressão não representam necessariamente as piores soluções no espaço de busca; elas são simplesmente áreas que ainda foram pouco exploradas. Mesmo que todas as nuvens se concentrem nessas regiões, elas gradualmente aumentarão a pressão nesses locais. Em determinado momento, isso criará novas regiões com menor pressão, forçando as nuvens a se deslocarem novamente.

Assim, as nuvens nunca permanecem paradas por muito tempo e transitam tanto por áreas de boas soluções quanto por regiões menos promissoras. Além disso, os mecanismos de evaporação e expansão contínua das nuvens, seguidos por sua dissipação, possibilitam a criação de novas nuvens em regiões favoráveis. Isso inicia um novo ciclo de refinamento das áreas promissoras dentro do espaço de busca.

Definição do centro de uma nova nuvem Ck. Se o valor da umidade em uma região ultrapassar o limite, ela pode gerar uma nova nuvem. O valor limite de umidade Ht é calculado dinamicamente pela equação:

Ht = Hmin + λ * (Hmax - Hmin), onde:

• Hmin e Hmax são os valores mínimos e máximos de umidade em toda a área de busca.
• λ é o fator de limite, definido experimentalmente como 0.7.

Cálculo da entropia e da hiperentropia. O valor da entropia para novas nuvens EnM diminui ao longo da busca e é determinado pela equação:

EnMt = ζ * EnM0, onde ζ é o coeficiente de contração, calculado por:

ζ = 1 / (1 + e^(- (8 - 16 * (t / tmax)))).

A hiperentropia das novas nuvens aumenta a cada iteração:

HeMt = ζ * HeM0, onde ζ atua como um coeficiente de expansão, calculado por:

ζ = 1 / (1 + e^(8 - 16 * (t / tmax))), onde:

• EnM0j é a entropia inicial, igual a 0.2.
  
• HeM0 é a hiperentropia inicial, igual a 0.5.
• t é a iteração atual.
• tmax é o número máximo de iterações.

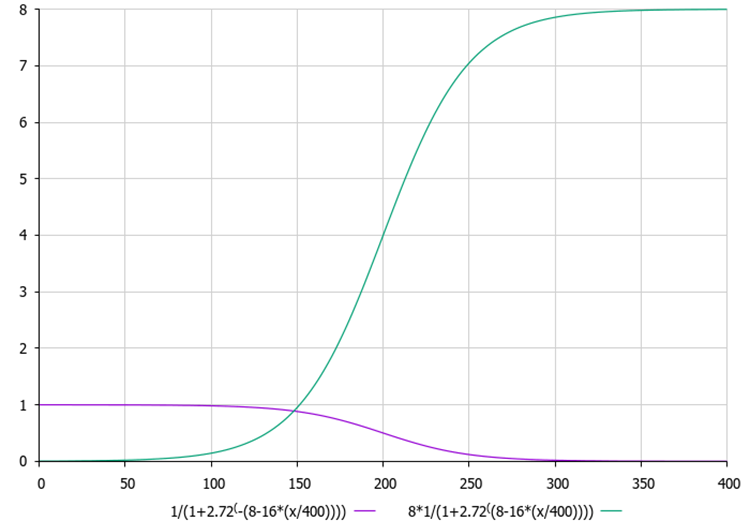
Figura 3. Gráficos da entropia e da hiperentropia para novas nuvens em função da época atual.

A velocidade de deslocamento da nuvem obedece à seguinte equação:

Vk = β * EnCk, onde β é definido pela equação:

β = (PCk - PF) / (PMax - PMin), onde:

• β é o fator de pressão atmosférica.
• PMax e PMin são a pressão atmosférica máxima e mínima no espaço de busca.
  
• PCk e PF representam a pressão na região atual e na região-alvo.
• EnCk é a entropia atual da nuvem.
  

Agora que entendemos toda a teoria do modelo meteorológico de deslocamento das nuvens no ACMO, vamos escrever o código do algoritmo.

Vamos descrever a estrutura "S_ACMO_Region", usada para representar uma região com características meteorológicas. A estrutura "S_ACMO_Region" contém diversos campos, cada um armazenando informações sobre a região:

Campos da estrutura:

• humidity - nível de umidade na região.
• pressure - pressão atmosférica na região.
• centre - centro da região representado por um vetor de coordenadas, indicando o ponto central.
• x - indica o ponto de maior pressão na região.

Init() - método de inicialização que define os valores iniciais dos campos da estrutura.

• humidity é inicializado com "-DBL_MAX", indicando um nível de umidade extremamente baixo.
• pressure é inicializado como zero, pois a pressão ainda não foi medida.

A estrutura "S_ACMO_Region" é usada no modelo meteorológico para armazenar e processar informações sobre diferentes regiões, levando em conta suas condições climáticas. O método "Init ()" garante que a estrutura seja corretamente inicializada antes de seu uso. 

//——————————————————————————————————————————————————————————————————————————————
// Region structure
struct S_ACMO_Region
{
    double humidity; //humidity in the region
    double pressure; //pressure in the region
    double centre;   //the center of the region
    double x;        //point of highest pressure in the region

    void Init ()
    {
      humidity = -DBL_MAX;
      pressure = 0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Agora, vamos descrever duas estruturas: "S_ACMO_Area" e "S_ACMO_Cloud" e analisá-las detalhadamente.

 1. A estrutura "S_ACMO_Area" representa uma área composta por um conjunto de regiões, descritas pela estrutura "S_ACMO_Region". Ela contém informações sobre vários locais dentro de uma determinada área.

 2. A estrutura "S_ACMO_Cloud" representa uma nuvem e suas características. Campos da estrutura:

• center [] - vetor que armazena as coordenadas do centro da nuvem.
• entropy [] - vetor contendo os valores de entropia da nuvem em cada coordenada.
  
• entropyStart [] - vetor dos valores iniciais de entropia.
• hyperEntropy - valor da hiperentropia.
  
• regionIndex [] - vetor de índices das regiões associadas às nuvens.
• droplets - quantidade de gotas na nuvem (um conceito abstrato que representa a umidade da nuvem).

Método "Init (int coords)" - inicializa os vetores da estrutura, ajustando seu tamanho com base no parâmetro passado "coords".

Ambas as estruturas são usadas no modelo meteorológico para representar e analisar regiões e nuvens. A estrutura "S_ACMO_Area" é utilizada para agrupar regiões, enquanto "S_ACMO_Cloud" descreve as características das nuvens.

//——————————————————————————————————————————————————————————————————————————————
struct S_ACMO_Area
{
    S_ACMO_Region regions [];
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Cloud structure
struct S_ACMO_Cloud
{
    double center       [];    // cloud center
    double entropy      [];    // entropy
    double entropyStart [];    // initial entropy
    double hyperEntropy;       // hyperEntropy
    int    regionIndex  [];    // index of regions
    double droplets;           // droplets

    void Init (int coords)
    {
      ArrayResize (center,       coords);
      ArrayResize (entropy,      coords);
      ArrayResize (entropyStart, coords);
      ArrayResize (regionIndex,  coords);
      droplets = 0.0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Agora, vamos analisar a classe "C_AO_ACMO", que herda da classe "C_AO". Estrutura geral da classe:

1. Parâmetros da classe, que desempenham o papel de parâmetros externos do algoritmo:

• popSize - tamanho da população.
• cloudsNumber - número de nuvens.
• regionsNumber - número de regiões por dimensão.
• dMin - quantidade mínima de gotas em relação ao número médio de gotas nas nuvens.
• EnM0 e HeM0 - valores iniciais de entropia e hiperentropia.
• λ - fator de limite para determinar regiões chuvosas.
• γ - taxa de dissipação.

2. Matriz de parâmetros:

• params - matriz de estruturas, onde cada elemento contém o nome e o valor do parâmetro.

3.  Métodos:

• SetParams () - define os parâmetros do modelo a partir da matriz "params".
• Init () - inicializa o modelo com limites de busca definidos, passo e número de épocas.
• Moving () - método responsável pelo deslocamento das nuvens.
• Revision () - método que revisa o estado do modelo.
• MoveClouds () - método responsável pelo movimento das nuvens.
• GetRegionIndex () - método para obter o índice da região a partir de um ponto específico.
• RainProcess() - método responsável pelo processo de chuva.
• DropletsDistribution () - método para distribuir gotas nas nuvens.
• UpdateRegionProperties () - método para atualizar as propriedades das regiões.
• GenerateClouds () - método para gerar nuvens.
• CalculateHumidityThreshold () - método para calcular o limite de umidade.
• CalculateNewEntropy () - método para calcular a nova entropia da nuvem.

4. Membros da classe:

   S_ACMO_Area areas [] - matriz de áreas contendo informações sobre diversas regiões.

   S_ACMO_Cloud clouds [] - matriz de nuvens contendo informações sobre suas características.

   Variáveis privadas, como "epochs", "epochNow", "dTotal", "entropy []" e "minGp", são usadas para monitorar o estado do modelo e realizar cálculos.

A classe "C_AO_ACMO" é projetada para modelar e controlar o movimento das nuvens na atmosfera. Ela inclui diversos parâmetros e métodos que permitem gerenciar o estado das nuvens, seu deslocamento e sua interação com as regiões.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACMO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ACMO () { }
  C_AO_ACMO ()
  {
    ao_name = "ACMO";
    ao_desc = "Atmospheric Cloud Model Optimization";
    ao_link = "https://www.mql5.com/ru/articles/15849";

    popSize       = 50;    //population size

    cloudsNumber  = 5;     // Number of clouds
    regionsNumber = 10;    // Number of regions per dimension  (M)
    dMin          = 0.2;   // Minimum number of drops relative to the average number of drops in the clouds (dN)
    EnM0          = 1.0;   // Initial value of entropy
    HeM0          = 0.5;   // Initial value of hyperentropy
    λ             = 0.7;   // Threshold factor (threshold of the rainiest regions)
    γ             = 0.2;   // Weaken rate

    ArrayResize (params, 8);

    params [0].name = "popSize";       params [0].val = popSize;

    params [1].name = "cloudsNumber";  params [1].val = cloudsNumber;
    params [2].name = "regionsNumber"; params [2].val = regionsNumber;
    params [3].name = "dMin";          params [3].val = dMin;
    params [4].name = "EnM0";          params [4].val = EnM0;
    params [5].name = "HeM0";          params [5].val = HeM0;
    params [6].name = "λ";             params [6].val = λ;
    params [7].name = "γ";             params [7].val = γ;
  }

  void SetParams ()
  {
    popSize       = (int)params [0].val;

    cloudsNumber  = (int)params [1].val;
    regionsNumber = (int)params [2].val;
    dMin          = params      [3].val;
    EnM0          = params      [4].val;
    HeM0          = params      [5].val;
    λ             = params      [6].val;
    γ             = params      [7].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    cloudsNumber;  // Number of clouds
  int    regionsNumber; // Number of regions per dimension (M)
  double dMin;          // Minimum number of drops relative to the average number of drops in the clouds (dN)
  double EnM0;          // Initial value of entropy
  double HeM0;          // Initial value of hyperentropy
  double λ;             // Threshold factor
  double γ;             // Weaken rate


  S_ACMO_Area   areas  [];
  S_ACMO_Cloud  clouds [];

  private: //-------------------------------------------------------------------
  int    epochs;
  int    epochNow;
  int    dTotal;         // Maximum total number of droplets (N)
  double entropy [];     // Entropy
  double minGp;          // Minimum global pressure


  void   MoveClouds                 (bool &rev);
  int    GetRegionIndex             (double point, int ind);
  void   RainProcess                (bool &rev);
  void   DropletsDistribution       (double &clouds [], int &droplets []);

  void   UpdateRegionProperties     ();

  void   GenerateClouds             ();
  double CalculateHumidityThreshold ();
  void   CalculateNewEntropy        (S_ACMO_Cloud &cl, int t);
};
//——————————————————————————————————————————————————————————————————————————————

Agora, vamos analisar o método "Init" da classe "C_AO_ACMO", que é responsável pela inicialização dos parâmetros do modelo de nuvens.

1. O método recebe três matrizes: "rangeMinP", "rangeMaxP" e "rangeStepP", que definem os limites e os passos dos parâmetros do modelo. O quarto parâmetro é "epochsP", que, por padrão, é 0 e indica o número de épocas.

2. O método "StandardInit" é chamado para executar a inicialização básica. Se a inicialização falhar, o método retorna "false".

3. Inicialização de variáveis: O método define o número total de épocas e redefine a época atual para 0.

4. Configuração dos parâmetros:

• dTotal é definido como o tamanho da população.
• dMin é recalculado considerando a relação entre o tamanho da população e o número de nuvens.

5. Alocação de memória para matrizes: O método ajusta o tamanho das matrizes "entropy" e "areas" de acordo com o número de coordenadas.

6. Inicialização da entropia e das regiões:

• Para cada coordenada "c", o valor da entropia é calculado.
• Para cada região "r", o método "Init ()" é chamado para inicializar a região.
• O centro da região é calculado como o valor médio entre os limites mínimo e máximo, multiplicado pelo número de regiões.
• Em seguida, o centro passa pelo método "SeInDiSp", que normaliza os valores dentro do intervalo especificado.
• A coordenada "x" é definida para a região (representando o ponto com o maior valor de umidade, que por padrão está localizado no centro da região).
  

7. Inicialização das nuvens:

• O tamanho da matriz "clouds" é ajustado de acordo com o número de nuvens.
• Para cada nuvem, o método "Init" é chamado para inicializar seus parâmetros.

O método "Init" realiza a configuração principal e a inicialização do modelo de nuvens, definindo os parâmetros essenciais, os tamanhos das matrizes e os valores necessários para a simulação. Ele é estruturado para, primeiro, executar a inicialização padrão da classe-mãe e, em seguida, configurar os parâmetros específicos relacionados às coordenadas, regiões e nuvens.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ACMO::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  //----------------------------------------------------------------------------
  dTotal       = popSize;
  dMin         = dMin * (popSize / (double)cloudsNumber);

  ArrayResize (entropy, coords);
  ArrayResize (areas,   coords);

  for (int c = 0; c < coords; c++)
  {
    entropy [c] = (rangeMax [c] - rangeMin [c]) / regionsNumber;

    ArrayResize (areas [c].regions, regionsNumber);

    for (int r = 0; r < regionsNumber; r++)
    {
      areas [c].regions [r].Init ();
      areas [c].regions [r].centre = rangeMin [c] + entropy [c] * (r + 0.5);
      areas [c].regions [r].centre = u.SeInDiSp (areas [c].regions [r].centre, rangeMin [c], rangeMax [c], rangeStep [c]);
      areas [c].regions [r].x      = areas [c].regions [r].centre;
    }
  }

  ArrayResize (clouds, cloudsNumber);
  for (int i = 0; i < cloudsNumber; i++) clouds [i].Init (coords);

  minGp = DBL_MAX;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Considerações finais

Neste artigo, exploramos o fascinante e inovador algoritmo ACMO, que se baseia em um modelo meteorológico atmosférico para resolver problemas de otimização multidimensionais. À primeira vista, o ACMO pode parecer um algoritmo multipopulacional, mas uma análise mais profunda revela sua originalidade e singularidade.

A estrutura do modelo é composta por três elementos fundamentais: nuvens, regiões e gotas. Cada um desses componentes opera de forma independente, mas sua interação cria um sistema harmonioso e eficiente, no qual cada parte desempenha um papel essencial. As nuvens representam a diversidade de soluções, as regiões formam o espaço de busca e as gotas são os elementos que promovem transições entre diferentes soluções. Essa combinação faz do ACMO um algoritmo não apenas inovador, mas também uma poderosa ferramenta para otimização.

Na segunda parte deste estudo, daremos um passo da teoria para a prática. Testaremos o algoritmo em diversas funções de teste para avaliar sua eficácia e identificar seus pontos fortes. Ao final, faremos uma análise dos resultados e, possivelmente, abriremos novos horizontes para a aplicação desse modelo inovador em problemas reais.