
Redes neurais em trading: Explorando a estrutura local dos dados
Introdução
A tarefa de detectar objetos em nuvens de pontos tem atraído cada vez mais atenção. A eficácia na resolução dessa tarefa depende fortemente das informações sobre a estrutura das regiões locais. No entanto, a natureza esparsa e irregular das nuvens de pontos frequentemente torna a estrutura local incompleta e imprecisa.
A detecção tradicional de objetos baseada em convolução é construída com o uso de núcleos fixos, e todos os pontos vizinhos são processados da mesma forma. Por isso, pontos não relacionados ou ruidosos de outros objetos acabam sendo inevitavelmente considerados.
O Transformer demonstrou sua eficácia na solução de diversas tarefas. Em comparação com a convolução, o mecanismo Self-Attention é capaz de excluir de forma adaptativa pontos irrelevantes ou ruidosos. No entanto, o Transformer tradicional usa uma única função para transformar todos os elementos da sequência. Esse processamento isotrópico ignora as informações sobre a estrutura local nas relações espaciais e não considera a direção nem a distância entre o ponto central e seus vizinhos. Se trocarmos as posições dos pontos, o resultado do Transformer permanecerá o mesmo. Isso cria problemas para o reconhecimento da orientação dos objetos, o que é importante para a detecção de padrões de preços.
Os autores do artigo "SEFormer: Structure Embedding Transformer for 3D Object Detection" buscaram unir o melhor de ambas as abordagens e desenvolveram um novo Transformer de codificação de estrutura (Structure-Embedding transFormer — SEFormer), capaz de codificar a estrutura local levando em conta direção e distância. O SEFormer proposto explora diferentes transformações nos Value dos pontos provenientes de várias direções e distâncias. Dessa maneira, a mudança na estrutura espacial local pode ser codificada nos resultados da operação do modelo, o que proporciona a chave para o reconhecimento preciso das direções dos objetos.
Com base no módulo SEFormer proposto, o trabalho mencionado apresenta uma rede multiescalar para a detecção de objetos 3D.
1. Algoritmo SEFormer
A localidade e a invariância espacial da convolução se adaptam bem ao viés indutivo presente em imagens. Outra vantagem importante da convolução é sua capacidade de codificar informações estruturais dos dados. Os autores do método SEFormer decompuseram a convolução em um operador de duas etapas: transformação e agregação. Durante a transformação, cada ponto é multiplicado pelo núcleo wδ correspondente. Em seguida, esses valores são simplesmente somados com um coeficiente de agregação fixo, α = 1. Na convolução, os núcleos são treinados de maneira diferente, dependendo de suas direções e distâncias em relação ao centro do núcleo. Dessa forma, a convolução pode codificar a estrutura espacial local. No entanto, na convolução, todos os pontos vizinhos no processo de agregação são tratados igualmente (α = 1). O operador principal de convolução utiliza um núcleo estático e rígido, mas a nuvem de pontos frequentemente é irregular e até incompleta. Consequentemente, a convolução inevitavelmente inclui pontos irrelevantes ou ruidosos no resultado.
Comparado à convolução, o mecanismo Self-Attention no Transformer oferece um método mais eficaz para preservar formas irregulares e fronteiras de objetos na nuvem de pontos. Para uma nuvem de pontos com N elementos 𝒑=[p1,…, pN], o Transformer calcula a resposta de cada ponto da seguinte forma:
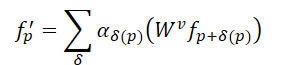
Aqui, αδ representa os coeficientes de autoatenção entre os pontos na área vizinha, enquanto 𝑾v indica a transformação Value. Em comparação com o coeficiente estático α=1 da convolução, os coeficientes de autoatenção permitem a seleção adaptativa de pontos para agregação e a exclusão do impacto de pontos não relacionados. No entanto, a mesma transformação para Value é aplicada a todos os pontos no Transformer, o que significa que a capacidade de codificação estrutural presente na convolução se perde.
Diante disso, os autores do SEFormer descobriram que a convolução possui a capacidade de codificar a estrutura dos dados, enquanto o Transformer é eficiente em preservá-la. Assim, a ideia principal foi desenvolver um novo operador que combinasse as vantagens da convolução e do Transformer. Portanto, eles propuseram o SEFormer, que pode ser formulado da seguinte maneira:
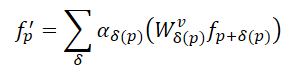
A maior diferença entre o SEFormer e o Transformer tradicional está na função de transformação para os pontos Value, treinada com base na posição relativa entre os pontos.
Considerando a irregularidade da nuvem de pontos, os autores do SEFormer seguiram a abordagem do Point Transformer para amostrar independentemente os pontos vizinhos ao redor de cada ponto Query antes de sua entrada no Transformer. Neste caso, os autores decidiram usar a interpolação em grade para gerar pontos-chave. Vários pontos virtuais são gerados em uma distribuição em grade ao redor do ponto analisado. A distância entre dois elementos da grade é predefinida como d.
Em seguida, os pontos virtuais são interpolados com os elementos vizinhos mais próximos da nuvem de pontos analisada. Em comparação com a amostragem tradicional, como o KNN, a vantagem da amostragem em grade está na capacidade de selecionar pontos de diferentes direções de maneira controlada. A interpolação em grade permite uma descrição mais precisa da estrutura local. No entanto, como essa interpolação utiliza uma distância fixa d, os autores do método aplicaram uma estratégia com múltiplos raios para aumentar a flexibilidade da amostragem.
O SEFormer constrói um pool de memória contendo múltiplas matrizes de transformação para os Value (𝑾v). Os pontos-chave interpolados procuram as matrizes 𝑾v correspondentes com base em suas coordenadas relativas ao ponto original. Assim, suas características são transformadas de maneira distinta. Dessa forma, o SEFormer adquire a capacidade de codificar a estrutura, uma funcionalidade ausente no Transformer tradicional.
No modelo de detecção de objetos proposto pelos autores, primeiro é construída uma espinha dorsal baseada em convolução 3D para a extração de características voxel multiescalares e a geração de propostas primárias. A espinha dorsal de convolução transforma os dados brutos em uma série de características voxel com reduções de discretização de 1×, 2×, 4× e 8×. Esses objetos de diferentes tamanhos apresentam diferentes camadas de profundidade. Após a extração das características, o volume dos elementos 3D é comprimido ao longo do eixo Z e transformado em um mapa de características 2D, como uma "vista aérea". Com base nesses mapas, é feito o primeiro prognóstico dos objetos candidatos.
Em seguida, a estrutura espacial proposta pelo módulo agrega os objetos multiescalares [𝑭1, 𝑭2, 𝑭3, 𝑭4] em vários embeddings em nível de pontos 𝑬. A partir de 𝑬init, são interpolados pontos-chave para cada elemento analisado, baseados nas características do menor nível de escala 𝑭1. Os autores adotaram m diferentes distâncias de grade d para criar conjuntos de características-chave multiescalares na forma de 𝑭1,1, 𝑭2,1,…, 𝑭m,1. Essa estratégia de múltiplos raios permite lidar melhor com a distribuição esparsa e irregular da nuvem de pontos. São aplicados m blocos paralelos do SEFormer, que geram m embeddings atualizados 𝑬1,1, 𝑬2,1,…, 𝑬m,1. Os embeddings resultantes são concatenados e transformados em um embedding final 𝑬1 por meio do Transformer tradicional. Em seguida, 𝑬1 repete o processo descrito anteriormente e agrega[𝑭2, 𝑭3, 𝑭4] no embedding 𝑬final. Em comparação com as características voxel originais 𝑭, o embedding 𝑬final contém uma descrição estrutural mais detalhada da área local.
Com base nos embeddings obtidos no nível de pontos 𝑬final, a cabeça do modelo proposta pelos autores os agrega em vários embeddings de objetos para gerar as propostas finais. Mais precisamente, cada proposta da primeira etapa é dividida em várias sub-regiões cúbicas, e cada sub-região é interpolada com os embeddings dos objetos circundantes no nível de pontos. Devido à esparsidade da nuvem de pontos, algumas regiões frequentemente ficam vazias. A abordagem tradicional consiste em simplesmente somar as características das regiões não vazias. Em contraste, o SEFormer proposto é capaz de utilizar informações tanto das regiões preenchidas quanto das vazias. As capacidades ampliadas de incorporação estrutural do SEFormer proporcionam uma descrição mais precisa da estrutura no nível do objeto, resultando em propostas mais precisas.
A visualização do método proposto pelos autores é apresentada abaixo.

2. Implementação com MQL5
Após analisar os aspectos teóricos do método SEFormer proposto, passamos para a parte prática do nosso artigo, na qual implementamos nossa visão dos métodos sugeridos. Vamos, então, refletir sobre a arquitetura do nosso futuro modelo.
Para a extração inicial de características, os autores sugerem o uso de convolução 3D em voxel. No entanto, no nosso caso, o vetor de características de uma única barra pode conter um número significativamente maior de atributos, tornando essa abordagem menos eficiente. Por isso, proponho adotar o método anteriormente utilizado, que consiste na agregação de características por meio de um bloco de atenção esparsa com diferentes níveis de concentração.
Outro ponto importante a considerar é a construção da grade ao redor do ponto analisado. No contexto da detecção de objetos 3D, os autores conseguem comprimir os dados em altura e analisar os objetos em mapas planos. No entanto, em nosso caso de representação multidimensional dos dados, cada dimensão pode exercer uma influência crucial em diferentes momentos. Não podemos, portanto, nos permitir comprimir os dados em qualquer dimensão. Além disso, a construção de uma "grade" em um espaço multidimensional pode se revelar uma tarefa complexa, pois o número de elementos cresce em progressão geométrica conforme aumenta o número de características analisadas. Nessa situação, considero mais eficiente treinar o modelo para aprender os pontos centroides mais ideais no espaço multidimensional.
Levando em conta o exposto, proponho construir nosso novo objeto herdando as funcionalidades principais da classe CNeuronPointNet2OCL. A estrutura geral da nova classe CNeuronSEFormer é apresentada a seguir.
class CNeuronSEFormer : public CNeuronPointNet2OCL { protected: uint iUnits; uint iPoints; //--- CLayer cQuery; CLayer cKey; CLayer cValue; CLayer cKeyValue; CArrayInt cScores; CLayer cMHAttentionOut; CLayer cAttentionOut; CLayer cResidual; CLayer cFeedForward; CLayer cCenterPoints; CLayer cFinalAttention; CNeuronMLCrossAttentionMLKV SEOut; CBufferFloat cbTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, int scores, CBufferFloat *out); virtual bool AttentionInsideGradients(CBufferFloat *q, CBufferFloat *q_g, CBufferFloat *kv, CBufferFloat *kv_g, int scores, CBufferFloat *gradient); //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronSEFormer(void) {}; ~CNeuronSEFormer(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint output, bool use_tnets, uint center_points, uint center_window, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronSEFormer; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Na estrutura apresentada acima, é possível notar a presença do conjunto de métodos sobrescritos já conhecido, bem como uma série de objetos aninhados. O nome de alguns desses objetos pode lembrar a arquitetura do Transformer, o que não é por acaso, pois os autores do SEFormer buscaram aprimorar o algoritmo do Transformer tradicional. Vamos por partes.
Todos os objetos internos da nossa classe foram declarados como estáticos, o que nos permite manter os métodos de construtor e destrutor da classe vazios. A inicialização dos objetos declarados e herdados ocorre no método Init, cujos parâmetros, como você sabe, recebem as constantes básicas que definem a arquitetura do objeto em construção.
bool CNeuronSEFormer::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint output, bool use_tnets, uint center_points, uint center_window, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronPointNet2OCL::Init(numOutputs, myIndex, open_cl, window, units_count, output, use_tnets, optimization_type, batch)) return false;
Além dos parâmetros já conhecidos, aqui incluímos a quantidade de centroides treináveis e o tamanho do vetor que descreve seu estado.
Vale destacar que a arquitetura do nosso bloco foi projetada de forma que o tamanho do vetor de descrição do centroide possa ser diferente do número de características que descrevem uma barra analisada.
No corpo do método, como de costume, chamamos imediatamente o método homônimo da classe pai, que já implementa os mecanismos de controle dos parâmetros recebidos e a inicialização dos objetos herdados. Apenas verificamos o resultado lógico das operações realizadas pelo método da classe pai.
Em seguida, armazenamos alguns parâmetros da arquitetura em construção que serão necessários durante a execução das operações do algoritmo implementado.
iUnits = units_count; iPoints = MathMax(center_points, 9);
Como conjunto de objetos internos, utilizei objetos da classe CLayer. Para seu funcionamento correto, passamos um ponteiro para o objeto do contexto OpenCL.
cQuery.SetOpenCL(OpenCL); cKey.SetOpenCL(OpenCL); cValue.SetOpenCL(OpenCL); cKeyValue.SetOpenCL(OpenCL); cMHAttentionOut.SetOpenCL(OpenCL); cAttentionOut.SetOpenCL(OpenCL); cResidual.SetOpenCL(OpenCL); cFeedForward.SetOpenCL(OpenCL); cCenterPoints.SetOpenCL(OpenCL); cFinalAttention.SetOpenCL(OpenCL);
Para o treinamento das representações dos centroides, criamos uma pequena MLP composta por dois camadas densamente conectadas.
//--- Init center points CNeuronBaseOCL *base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(iPoints * center_window * 2, 0, OpenCL, 1, optimization, iBatch)) return false; CBufferFloat *buf = base.getOutput(); if(!buf || !buf.BufferInit(1, 1) || !buf.BufferWrite()) return false; if(!cCenterPoints.Add(base)) return false; base = new CNeuronBaseOCL(); if(!base.Init(0, 1, OpenCL, iPoints * center_window * 2, optimization, iBatch)) return false; if(!cCenterPoints.Add(base)) return false;
Observe que criamos o dobro da quantidade especificada de centroides. Dessa forma, geramos dois conjuntos de centroides, simulando a construção de uma grade em diferentes escalas.
Em seguida, criamos um laço para inicializar os objetos internos de acordo com o número de camadas de escalonamento das características.
Lembro que, na classe pai, agregamos os dados brutos com dois coeficientes de concentração de atenção. Consequentemente, nosso laço conterá duas iterações.
//--- Inside layers for(int i = 0; i < 2; i++) { //--- Interpolation CNeuronMVCrossAttentionMLKV *cross = new CNeuronMVCrossAttentionMLKV(); if(!cross || !cross.Init(0, i * 12 + 2, OpenCL, center_window, 32, 4, 64, 2, iPoints, iUnits, 2, 2, 2, 1, optimization, iBatch)) return false; if(!cCenterPoints.Add(cross)) return false;
Para a interpolação dos centroides, utilizamos um bloco de cross-attention, no qual associamos a representação atual dos centroides ao conjunto de dados brutos analisados. A ideia principal desse processo é encontrar o conjunto de centroides que divida os dados de entrada em regiões locais de forma mais precisa e eficiente, permitindo, assim, o aprendizado da estrutura dos dados brutos.
Em seguida, inicializamos os objetos do bloco SEFormer proposto pelos autores. Nesse bloco, o objetivo é enriquecer os embeddings dos pontos analisados com informações estruturais da nuvem de pontos. Tecnicamente, utilizaremos o algoritmo de cross-attention entre os pontos analisados e os centroides, enriquecidos com os dados estruturais da nuvem de pontos.
Aqui, usamos uma camada convolucional para gerar a entidade Query com base nos embeddings dos pontos analisados.
//--- Query CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, i * 12 + 3, OpenCL, 64, 64, 64, iUnits, optimization, iBatch)) return false; if(!cQuery.Add(conv)) return false;
Da mesma forma, geramos as entidades Key, mas agora a partir da representação dos centroides.
//--- Key conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, i * 12 + 4, OpenCL, center_window, center_window, 32, iPoints, 2, optimization, iBatch)) return false; if(!cKey.Add(conv)) return false;
Já para a geração da entidade Value, os autores do SEFormer propõem o uso de uma matriz de transformação individual para cada elemento da sequência. Por isso, utilizamos uma camada convolucional semelhante, mas definimos o número de elementos na sequência como 1, transferindo toda a quantidade de centroides para o parâmetro das variáveis analisadas. Essa abordagem nos permite alcançar o resultado desejado.
//--- Value conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, i * 12 + 5, OpenCL, center_window, center_window, 32, 1, iPoints * 2, optimization, iBatch)) return false; if(!cValue.Add(conv)) return false;
Vale lembrar, no entanto, que todos os nossos kernels do algoritmo de cross-attention foram criados para operar com um tensor concatenado das entidades Key-Value. Para evitar alterações no programa OpenCL, simplesmente adicionamos a concatenação desses tensores.
//--- Key-Value base = new CNeuronBaseOCL(); if(!base || !base.Init(0, i * 12 + 6, OpenCL, iPoints * 2 * 32 * 2, optimization, iBatch)) return false; if(!cKeyValue.Add(base)) return false;
A matriz de coeficientes de dependência é utilizada exclusivamente no contexto OpenCL e é recalculada a cada propagação para frente. Portanto, a criação desse buffer na memória principal não é necessária. Assim, criamos esse buffer apenas na memória do contexto OpenCL.
//--- Score int s = int(iUnits * iPoints * 4); s = OpenCL.AddBuffer(sizeof(float) * s, CL_MEM_READ_WRITE); if(s < 0 || !cScores.Add(s)) return false;
Neste ponto, também criamos uma camada para registrar os dados da atenção multi-head
//--- MH Attention Out base = new CNeuronBaseOCL(); if(!base || !base.Init(0, i * 12 + 7, OpenCL, iUnits * 64, optimization, iBatch)) return false; if(!cMHAttentionOut.Add(base)) return false;
Em seguida, adicionamos uma camada convolucional para escalonar os resultados obtidos.
//--- Attention Out conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, i * 12 + 8, OpenCL, 64, 64, 64, iUnits, 1, optimization, iBatch)) return false; if(!cAttentionOut.Add(conv)) return false;
De acordo com o algoritmo Transformer, os resultados do Self-Attention são somados aos dados originais e normalizados.
//--- Residual base = new CNeuronBaseOCL(); if(!base || !base.Init(0, i * 12 + 9, OpenCL, iUnits * 64, optimization, iBatch)) return false; if(!cResidual.Add(base)) return false;
Após isso, adicionamos duas camadas do bloco FeedForward.
//--- Feed Forward conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, i * 12 + 10, OpenCL, 64, 64, 256, iUnits, 1, optimization, iBatch)) return false; conv.SetActivationFunction(LReLU); if(!cFeedForward.Add(conv)) return false; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, i * 12 + 11, OpenCL, 256, 64, 64, iUnits, 1, optimization, iBatch)) return false; if(!cFeedForward.Add(conv)) return false;
Também criamos um objeto para facilitar a conexão residual.
//--- Residual base = new CNeuronBaseOCL(); if(!base || !base.Init(0, i * 12 + 12, OpenCL, iUnits * 64, optimization, iBatch)) return false; if(!base.SetGradient(conv.getGradient(), true)) return false; if(!cResidual.Add(base)) return false;
Vale destacar que, neste caso, realizamos a substituição do buffer do gradiente de erro na camada de criação da conexão residual. Essa substituição nos permite evitar a operação de cópia dos dados de gradiente de erro da camada de conexão residual para a última camada do bloco de propagação para frente.
Na finalização do módulo SEFormer, os autores sugerem o uso do Transformer tradicional. No entanto, decidi adotar uma arquitetura mais complexa, inserindo um módulo de atenção condicionado ao contexto.
//--- Final Attention CNeuronMLMHSceneConditionAttention *att = new CNeuronMLMHSceneConditionAttention(); if(!att || !att.Init(0, i * 12 + 13, OpenCL, 64, 16, 4, 2, iUnits, 2, 1, optimization, iBatch)) return false; if(!cFinalAttention.Add(att)) return false; }
Neste estágio, já inicializamos todos os objetos de uma camada interna e seguimos para a próxima iteração do ciclo.
Após a conclusão de todas as iterações do ciclo de inicialização dos objetos das camadas internas, é importante observar que não utilizamos os resultados de cada camada interna diretamente. Seria lógico concatenar esses resultados em um único tensor e, em seguida, passá-lo para a geração do embedding global da nuvem de pontos, utilizando os recursos da classe pai. No entanto, essa abordagem exigiria escalonar previamente o tensor obtido para o tamanho desejado. Em vez disso, optei por um caminho alternativo: utilizamos o bloco de cross-attention para enriquecer os dados em menor escala com informações provenientes das camadas de maior escala.
if(!SEOut.Init(0, 26, OpenCL, 64, 64, 4, 16, 4, iUnits, iUnits, 4, 1, optimization, iBatch)) return false;
Para finalizar o método, inicializamos um buffer auxiliar para o armazenamento temporário de dados.
if(!cbTemp.BufferInit(buf_size, 0) || !cbTemp.BufferCreate(OpenCL)) return false; //--- return true; }
Em seguida, retornamos um valor lógico indicando o resultado bem-sucedido das operações do método.
Nesse estágio, concluímos o trabalho no método de inicialização do objeto da classe. Agora avançamos para a construção do algoritmo de propagação para frente no método feedForward. Como você sabe, os parâmetros desse método incluem um ponteiro para o objeto de dados brutos.
bool CNeuronSEFormer::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- CNeuronBaseOCL *neuron = NULL, *q = NULL, *k = NULL, *v = NULL, *kv = NULL;
No corpo do método, primeiramente declaramos algumas variáveis locais para o armazenamento temporário de ponteiros dos objetos internos. Em seguida, geramos a representação dos centroides.
//--- Init Points if(bTrain) { neuron = cCenterPoints[1]; if(!neuron || !neuron.FeedForward(cCenterPoints[0])) return false; }
É importante ressaltar que a representação dos centroides é gerada apenas durante o treinamento do modelo. Durante a fase de execução, os pontos dos centroides permanecem estáticos, eliminando a necessidade de gerá-los a cada passagem.
Em seguida, criamos um laço para iterar sobre as camadas internas.
//--- Inside Layers for(int l = 0; l < 2; l++) { //--- Segmentation Inputs if(l > 0 || !cTNetG) { if(!caLocalPointNet[l].FeedForward((l == 0 ? NeuronOCL : GetPointer(caLocalPointNet[l - 1])))) return false; } else { if(!cTurnedG) return false; if(!cTNetG.FeedForward(NeuronOCL)) return false; int window = (int)MathSqrt(cTNetG.Neurons()); if(IsStopped() || !MatMul(NeuronOCL.getOutput(), cTNetG.getOutput(), cTurnedG.getOutput(), NeuronOCL.Neurons() / window, window, window)) return false; if(!caLocalPointNet[0].FeedForward(cTurnedG.AsObject())) return false; }
Dentro desse laço, segmentamos os dados brutos — um algoritmo herdado da classe pai — e, logo após, enriquecemos os centroides com os dados obtidos.
//--- Interpolate center points neuron = cCenterPoints[l + 2]; if(!neuron || !neuron.FeedForward(cCenterPoints[l + 1], caLocalPointNet[l].getOutput())) return false;
Na sequência, passamos ao módulo de atenção com codificação estrutural dos dados. Primeiro, extraímos dos arrays as camadas internas correspondentes.
//--- Structure-Embedding Attention
q = cQuery[l];
k = cKey[l];
v = cValue[l];
kv = cKeyValue[l];
Depois, geramos sequencialmente todas as entidades necessárias.
//--- Query if(!q || !q.FeedForward(GetPointer(caLocalPointNet[l]))) return false; //--- Key if(!k || !k.FeedForward(cCenterPoints[l + 2])) return false; //--- Value if(!v || !v.FeedForward(cCenterPoints[l + 2])) return false;
Os resultados das entidades Key e Value são concatenados em um único tensor.
if(!kv || !Concat(k.getOutput(), v.getOutput(), kv.getOutput(), 32 * 2, 32 * 2, iPoints)) return false;
Com isso, podemos utilizar os métodos clássicos de Multi-Head Self-Attention.
//--- Multi-Head Attention neuron = cMHAttentionOut[l]; if(!neuron || !AttentionOut(q.getOutput(), kv.getOutput(), cScores[l], neuron.getOutput())) return false;
Os dados obtidos são escalonados para o tamanho dos dados brutos.
//--- Scale neuron = cAttentionOut[l]; if(!neuron || !neuron.FeedForward(cMHAttentionOut[l])) return false;
Em seguida, somamos os dois fluxos de informações e normalizamos os dados resultantes.
//--- Residual q = cResidual[l * 2]; if(!q || !SumAndNormilize(caLocalPointNet[l].getOutput(), neuron.getOutput(), q.getOutput(), 64, true, 0, 0, 0, 1)) return false;
De forma semelhante ao codificador do Transformer tradicional, utilizamos o bloco FeedForward com conexão residual e normalização dos dados.
//--- Feed Forward neuron = cFeedForward[l * 2]; if(!neuron || !neuron.FeedForward(q)) return false; neuron = cFeedForward[l * 2 + 1]; if(!neuron || !neuron.FeedForward(cFeedForward[l * 2])) return false; //--- Residual k = cResidual[l * 2 + 1]; if(!k || !SumAndNormilize(q.getOutput(), neuron.getOutput(), k.getOutput(), 64, true, 0, 0, 0, 1)) return false;
Os resultados obtidos passam então pelo bloco de atenção condicionado ao contexto. E seguimos para a próxima iteração do ciclo.
//--- Final Attention neuron = cFinalAttention[l]; if(!neuron || !neuron.FeedForward(k)) return false; }
Após a execução bem-sucedida de todas as operações nas camadas internas, enriquecemos os embeddings dos pontos em menor escala com as informações em maior escala.
//--- Cross scale attention if(!SEOut.FeedForward(cFinalAttention[0], neuron.getOutput())) return false;
Finalmente, passamos o resultado obtido para a formação do embedding global da nuvem de pontos analisada.
//--- Global Point Cloud Embedding if(!CNeuronPointNetOCL::feedForward(SEOut.AsObject())) return false; //--- result return true; }
Ao final da execução do método de propagação para frente, retornamos um valor lógico indicando o resultado das operações para o programa chamador.
Como podemos observar, durante a implementação do algoritmo de propagação para frente, criamos uma estrutura complexa de fluxo de informações, longe de ser linear. Aqui, encontramos conexões residuais, com alguns objetos utilizando duas fontes de dados. Além disso, certos fluxos de informação se entrelaçam. Naturalmente, isso impactou o algoritmo de propagação reversa, implementado no método calcInputGradients.
bool CNeuronSEFormer::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Nos parâmetros desse método, recebemos um ponteiro para o objeto da camada anterior. Durante a propagação para frente, ele fornecia os dados brutos. Agora, precisamos transmitir a ele o gradiente de erro, correspondente ao impacto dos dados brutos no resultado final do modelo.
Dentro do método, verificamos imediatamente a validade do ponteiro recebido, pois, caso contrário, todas as operações subsequentes seriam inválidas.
Também declaramos várias variáveis locais para o armazenamento temporário de ponteiros dos objetos internos.
CNeuronBaseOCL *neuron = NULL, *q = NULL, *k = NULL, *v = NULL, *kv = NULL; CBufferFloat *buf = NULL;
Após isso, propagamos o gradiente de erro do embedding global da nuvem de pontos para as camadas internas.
//--- Global Point Cloud Embedding if(!CNeuronPointNetOCL::calcInputGradients(SEOut.AsObject())) return false;
Vale lembrar que, durante a propagação para frente, o resultado final foi obtido por meio do método da classe pai. Portanto, para calcular o gradiente de erro, também precisamos utilizar o método correspondente da classe pai.
Em seguida, distribuímos o gradiente de erro entre os fluxos de diferentes escalas.
//--- Cross scale attention neuron = cFinalAttention[0]; q = cFinalAttention[1]; if(!neuron.calcHiddenGradients(SEOut.AsObject(), q.getOutput(), q.getGradient(), ( ENUM_ACTIVATION)q.Activation())) return false;
Elaboramos, então, um ciclo para a retropropagação nas camadas internas.
for(int l = 1; l >= 0; l--) { //--- Final Attention neuron = cResidual[l * 2 + 1]; if(!neuron || !neuron.calcHiddenGradients(cFinalAttention[l])) return false;
Nesse ciclo, primeiro propagamos o gradiente de erro até o nível da camada de conexão residual.
Lembro que, ao inicializar os objetos internos, substituímos o buffer de gradientes de erro da camada de conexão residual pelo buffer correspondente da camada do bloco FeedForward. Isso nos permite evitar a operação desnecessária de cópia de dados e transmitir diretamente o gradiente de erro para o próximo nível.
//--- Feed Forward neuron = cFeedForward[l * 2]; if(!neuron || !neuron.calcHiddenGradients(cFeedForward[l * 2 + 1])) return false;
Depois, propagamos o gradiente de erro até a camada de conexão residual do bloco de atenção.
neuron = cResidual[l * 2]; if(!neuron || !neuron.calcHiddenGradients(cFeedForward[l * 2])) return false;
Nesse estágio, somamos os gradientes de erro provenientes dos dois fluxos de informação e transmitimos o valor resultante ao bloco de atenção.
//--- Residual q = cResidual[l * 2 + 1]; k = neuron; neuron = cAttentionOut[l]; if(!neuron || !SumAndNormilize(q.getGradient(), k.getGradient(), neuron.getGradient(), 64, false, 0, 0, 0, 1)) return false;
Em seguida, distribuímos o gradiente de erro pelas cabeças de atenção.
//--- Scale neuron = cMHAttentionOut[l]; if(!neuron || !neuron.calcHiddenGradients(cAttentionOut[l])) return false;
Por meio dos algoritmos do Transformer tradicional, propagamos o gradiente de erro até o nível das entidades Query, Key e Value.
//--- MH Attention q = cQuery[l]; kv = cKeyValue[l]; k = cKey[l]; v = cValue[l]; if(!AttentionInsideGradients(q.getOutput(), q.getGradient(), kv.getOutput(), kv.getGradient(), cScores[l], neuron.getGradient())) return false;
Como resultado dessa operação, obtemos dois tensores de gradientes de erro: um no nível da Query e outro no tensor concatenado de Key-Value. Distribuímos os gradientes de erro de Key e Value nos buffers das respectivas camadas internas.
if(!DeConcat(k.getGradient(), v.getGradient(), kv.getGradient(), 32 * 2, 32 * 2, iPoints)) return false;
Em seguida, propagamos o gradiente de erro do tensor Query até o nível de segmentação dos dados brutos. No entanto, há um detalhe importante. Para a última camada, essa operação não é significativamente complexa. Já para a primeira camada, o buffer de gradientes já conterá informações sobre o erro provenientes da segmentação subsequente, e precisamos preservá-las. Por isso, verificamos o índice da camada atual e, quando necessário, substituímos os ponteiros dos buffers de dados.
if(l == 0) { buf = caLocalPointNet[l].getGradient(); if(!caLocalPointNet[l].SetGradient(GetPointer(cbTemp), false)) return false; }
Depois disso, propagamos o gradiente de erro.
if(!caLocalPointNet[l].calcHiddenGradients(q, NULL)) return false;
Se necessário, somamos os dados dos dois fluxos de informação, retornando em seguida o ponteiro extraído para o buffer de dados.
if(l == 0) { if(!SumAndNormilize(buf, GetPointer(cbTemp), buf, 64, false, 0, 0, 0, 1)) return false; if(!caLocalPointNet[l].SetGradient(buf, false)) return false; }
Nesse ponto, também incluímos o gradiente de erro das conexões residuais do bloco de atenção.
neuron = cAttentionOut[l]; //--- Residual if(!SumAndNormilize(caLocalPointNet[l].getGradient(), neuron.getGradient(), caLocalPointNet[l].getGradient(), 64, false, 0, 0, 0, 1)) return false;
O próximo passo é distribuir o gradiente de erro até o nível dos centroides. Aqui, precisamos propagar o gradiente tanto da entidade Key quanto da entidade Value, utilizando novamente a substituição de ponteiros dos buffers de dados.
//--- Interpolate Center points neuron = cCenterPoints[l + 2]; if(!neuron) return false; buf = neuron.getGradient(); if(!neuron.SetGradient(GetPointer(cbTemp), false)) return false;
Em seguida, propagamos o primeiro gradiente de erro proveniente da entidade Key.
if(!neuron.calcHiddenGradients(k, NULL)) return false;
Contudo, ele será o primeiro apenas para a última camada. Já para a primeira camada, o buffer já conterá informações sobre o gradiente de erro decorrente da influência da camada subsequente. Portanto, verificamos o índice da camada interna em análise e, se necessário, somamos os dados provenientes dos dois fluxos de informação.
if(l == 0) { if(!SumAndNormilize(buf, GetPointer(cbTemp), buf, 1, false, 0, 0, 0, 1)) return false; } else { if(!SumAndNormilize(GetPointer(cbTemp), GetPointer(cbTemp), buf, 1, false, 0, 0, 0, 0.5f)) return false; }
Da mesma forma, propagamos o gradiente de erro da entidade Value, somando os dados dos dois fluxos de informação.
if(!neuron.calcHiddenGradients(v, NULL)) return false; if(!SumAndNormilize(buf, GetPointer(cbTemp), buf, 1, false, 0, 0, 0, 1)) return false;
Após isso, retornamos o ponteiro anteriormente extraído para o buffer de gradientes de erro.
if(!neuron.SetGradient(buf, false)) return false;
Em seguida, distribuímos o gradiente de erro entre o nível anterior dos centroides e os dados segmentados da camada atual.
neuron = cCenterPoints[l + 1]; if(!neuron.calcHiddenGradients(cCenterPoints[l + 2], caLocalPointNet[l].getOutput(), GetPointer(cbTemp), (ENUM_ACTIVATION)caLocalPointNet[l].Activation())) return false;
Para preservar esse gradiente de erro específico, substituímos os buffers na camada de centroides. Além disso, vale destacar que o buffer de gradiente de erro da camada de segmentação já contém a maior parte das informações necessárias. Portanto, nesse estágio, gravamos o gradiente de erro em um buffer temporário de dados e, em seguida, somamos os dados dos dois fluxos de informação.
if(!SumAndNormilize(caLocalPointNet[l].getGradient(), GetPointer(cbTemp), caLocalPointNet[l].getGradient(), 64, false, 0, 0, 0, 1)) return false;
Neste ponto, distribuímos o gradiente de erro entre todos os objetos internos recém-declarados. No entanto, ainda precisamos propagá-lo pelas camadas de segmentação dos dados. Esse algoritmo é totalmente herdado do método da classe pai.
//--- Local Net neuron = (l > 0 ? GetPointer(caLocalPointNet[l - 1]) : NeuronOCL); if(l > 0 || !cTNetG) { if(!neuron.calcHiddenGradients(caLocalPointNet[l].AsObject())) return false; } else { if(!cTurnedG) return false; if(!cTurnedG.calcHiddenGradients(caLocalPointNet[l].AsObject())) return false; int window = (int)MathSqrt(cTNetG.Neurons()); if(IsStopped() || !MatMulGrad(neuron.getOutput(), neuron.getGradient(), cTNetG.getOutput(), cTNetG.getGradient(), cTurnedG.getGradient(), neuron.Neurons() / window, window, window)) return false; if(!OrthoganalLoss(cTNetG, true)) return false; //--- CBufferFloat *temp = neuron.getGradient(); neuron.SetGradient(cTurnedG.getGradient(), false); cTurnedG.SetGradient(temp, false); //--- if(!neuron.calcHiddenGradients(cTNetG.AsObject())) return false; if(!SumAndNormilize(neuron.getGradient(), cTurnedG.getGradient(), neuron.getGradient(), 1, false, 0, 0, 0, 1)) return false; } } //--- return true; }
Após a conclusão de todas as iterações do ciclo de retropropagação nas camadas internas, retornamos um valor lógico para o programa chamador, indicando o resultado das operações do método.
Acabamos de implementar os algoritmos de propagação para frente e de distribuição do gradiente de erro através dos objetos internos da nova classe. Agora, resta implementar o método updateInputWeights para a atualização dos parâmetros treináveis da classe. Nesse caso, todos os parâmetros treináveis estão contidos nos objetos aninhados. Assim, para atualizar os parâmetros da nossa classe, basta chamar, de forma sequencial, os métodos homônimos dos objetos internos. Esse algoritmo é bastante direto, e sugiro deixá-lo para estudo independente.
Lembro que o código completo da nova classe CNeuronSEFormer e de todos os seus métodos pode ser encontrado no anexo. Lá, você também encontrará o código dos métodos que dão suporte a essa classe, os quais foram mencionados anteriormente para sobrescrição.
Também é importante destacar que a arquitetura das redes foi praticamente toda aproveitada do artigo anterior. Apenas substituímos uma camada no Codificador do estado do ambiente.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSEFormer; { int temp[] = {BarDescr, 8}; // Variables, Center embedding if(ArrayCopy(descr.windows, temp) < (int)temp.Size()) return false; } { int temp[] = {HistoryBars, 27}; // Units, Centers if(ArrayCopy(descr.units, temp) < (int)temp.Size()) return false; } descr.window_out = LatentCount; // Output Dimension descr.step = int(true); // Use input and feature transformation descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Isso também se aplica a todos os programas de interação com o ambiente e ao treinamento das redes, que foram integralmente reaproveitados do artigo anterior. Por esse motivo, não entraremos em detalhes sobre eles. O código completo de todos os programas utilizados na preparação deste artigo está disponível no anexo.
3. Testes
Após concluir um trabalho considerável, chegamos à etapa final — e, talvez, a mais empolgante —, que consiste no treinamento das redes e na avaliação da política aprendida pelo ator com base em dados históricos reais.
Assim como anteriormente, utilizamos dados históricos reais do par EURUSD ao longo de todo o ano de 2023, no timeframe H1, para o treinamento das redes. Os parâmetros de todos os indicadores analisados foram mantidos em suas configurações padrão.
O algoritmo de treinamento das redes foi reaproveitado dos artigos anteriores, juntamente com os programas usados para o treinamento e teste das redes.
Para testar a política aprendida pelo ator, utilizamos dados históricos reais de janeiro de 2024, mantendo todos os outros parâmetros inalterados. Os resultados dos testes são apresentados a seguir.
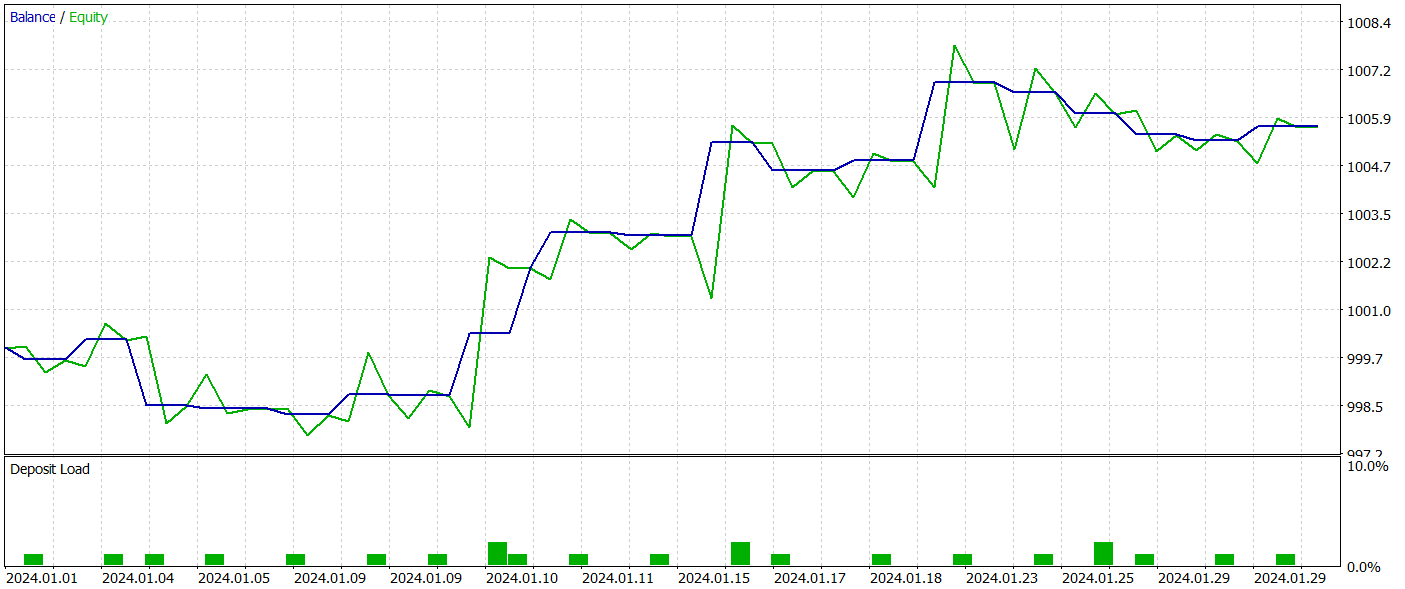
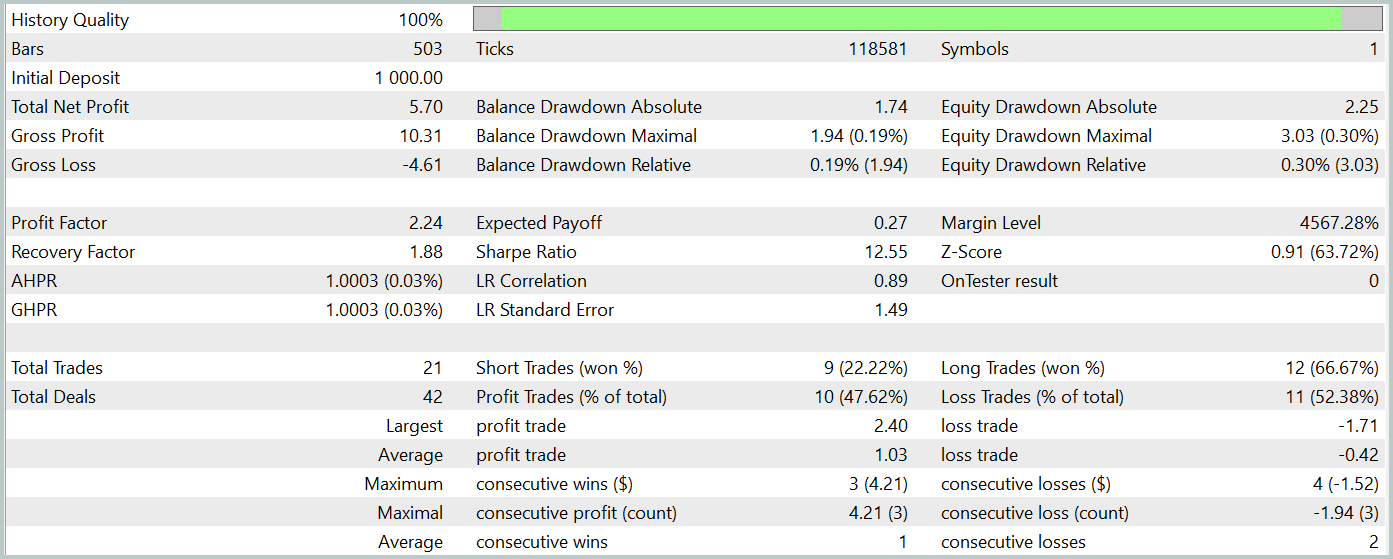
Durante o período de teste, o modelo realizou 21 operações, das quais mais de 47% foram encerradas com lucro. É interessante notar que as operações longas apresentaram uma rentabilidade significativamente maior (66% contra 22%). Isso sugere a necessidade de um treinamento adicional da rede. No entanto, a operação média lucrativa foi 2,5 vezes maior do que a operação média com prejuízo, o que garantiu um resultado geral positivo no teste.
Na minha opinião, a rede ficou relativamente pesada, provavelmente devido ao uso do algoritmo de atenção condicionado ao contexto. No entanto, a aplicação dessa abordagem no método HyperDet3D permitiu alcançar resultados superiores com menor custo computacional.
Ainda assim, o número reduzido de operações e o curto período de teste impedem conclusões definitivas sobre a eficácia dos métodos em prazos mais longos.
Considerações finais
O método SEFormer foi adaptado para a análise de nuvens de pontos, permitindo identificar dependências locais em ambientes ruidosos com eficácia, um fator essencial para previsões precisas. Essa abordagem possibilita previsões mais confiáveis dos movimentos do mercado e a melhoria das estratégias de tomada de decisão.
Na parte prática deste artigo, implementamos nossa visão dos métodos propostos utilizando MQL5. Treinamos e testamos o modelo com dados históricos reais. Os resultados obtidos demonstraram o potencial do método proposto. No entanto, antes de aplicar o modelo em condições reais de negociação, é necessário um treinamento adicional com um histórico mais extenso, seguido de uma testagem abrangente da política treinada.
Referências
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA para coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA para coleta de exemplos pelo método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA para treinamento de Modelos |
| 4 | Test.mq5 | Expert Advisor | EA para teste do modelo |
| 5 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema |
| 6 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criar uma rede neural |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código do programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15882
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Construindo um Modelo de Restrição de Tendência de Candlestick (Parte 7): Refinando nosso modelo para o desenvolvimento de EA
Construindo um Modelo de Restrição de Tendência de Candlestick (Parte 7): Refinando nosso modelo para o desenvolvimento de EA
 Optimização por nuvens atmosféricas — Atmosphere Clouds Model Optimization (ACMO): Prática
Optimização por nuvens atmosféricas — Atmosphere Clouds Model Optimization (ACMO): Prática
 Análise causal de séries temporais usando entropia de transferência
Análise causal de séries temporais usando entropia de transferência
 Simulação de mercado (Parte 09): Sockets (III)
Simulação de mercado (Parte 09): Sockets (III)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Belo artigo
Obrigado.