Algoritmos de otimização populacional: Algoritmo Boids, ou algoritmo de comportamento de enxame (Boids Algorithm, Boids)

Conteúdo:

1. Introdução
2. Descrição do algoritmo
3. Resultados dos testes

1. Introdução

Ao observar o comportamento de enxame de animais na natureza, inevitavelmente nos maravilhamos com a coordenação harmoniosa e eficiente que eles apresentam. Como se estivessem sob o comando de uma força invisível, eles se reestruturam de forma sincronizada, como um único organismo, superando obstáculos e encontrando os caminhos mais otimizados. Essa harmonia hipnotizante de movimentos, baseada em regras simples de interação, inspirou a criação de muitos algoritmos de otimização metaheurísticos.

Ao estudar as complexas rotas migratórias de bandos de pássaros, os cientistas descobriram que eles seguem princípios semelhantes aos algoritmos de inteligência de enxame. Assim, cardumes de peixes, como células vivas, formam estruturas pulsantes que lembram métodos de otimização baseados em autômatos celulares. O comportamento gregário de animais ungulados, suas reações coordenadas ao perigo, e o voo sincronizado de grupos de estorninhos representam capacidades incríveis dos animais para ações conjuntas coordenadas.

Esses exemplos fascinantes do mundo natural serviram de inspiração para a criação de poderosas ferramentas de otimização, capazes de resolver problemas complexos, desde o planejamento de rotas logísticas até o desenvolvimento de sistemas de gestão eficientes.

O algoritmo Boids (do inglês "boid" - abreviação de "bird-pássaro" e "oid" - semelhança) é um algoritmo computacional criado por Craig Reynolds em 1986, que modela o comportamento de enxames de animais, particularmente pássaros. Este algoritmo foi desenvolvido com o objetivo de imitar o comportamento natural de enxames, onde cada indivíduo se move de acordo com regras simples, resultando em um comportamento coletivo. Ele é baseado nas três regras a seguir:

1. Separação (Separation). Cada objeto (ou "boid") tenta minimizar a possibilidade de colisão com objetos próximos.
2. Alinhamento (Alignment). Cada objeto busca alinhar sua direção de movimento com a direção média dos objetos próximos.
3. Coesão (Cohesion). Cada objeto tenta se posicionar próximo à posição média dos objetos próximos.

Essas três regras simples permitem modelar o comportamento complexo de um bando de pássaros ou de um enxame de insetos. O algoritmo Boids é amplamente utilizado em gráficos de computador para criar animações de bandos de pássaros, enxames de insetos ou cardumes de peixes.

Inicialmente, a criação do algoritmo Boids tinha vários objetivos e aplicações:

1. Criação de animações realistas. O algoritmo Boids permite criar animações realistas de enxames de animais, o que se tornou um importante campo de desenvolvimento em gráficos de computador e animação.
2. Modelagem de Comportamento. O Boids permite modelar comportamentos coletivos complexos com base em regras simples para cada indivíduo. Isso encontra aplicação em diversas áreas, como estudos de comportamento animal, robótica, gerenciamento de tráfego e outras.

Um fato interessante é que o algoritmo Boids serviu de inspiração para o desenvolvimento de outros algoritmos: por exemplo, o de enxame de partículas (PSO) e algoritmos de modelagem de comportamento de multidões.

O algoritmo Boids continua a ser uma ferramenta popular para modelar comportamento coletivo e permanece como objeto de pesquisa e desenvolvimento em diversas áreas da ciência e tecnologia.

Na animação abaixo, pode-se observar o comportamento dos boids, que podem se agrupar em formações compactas, dispersar-se e sincronizar a velocidade em relação aos seus vizinhos. Durante a gravação da animação, as configurações do algoritmo foram alteradas "ao vivo", permitindo visualizar o impacto dessas mudanças no comportamento dos boids.

Visualização do funcionamento do algoritmo Boids.

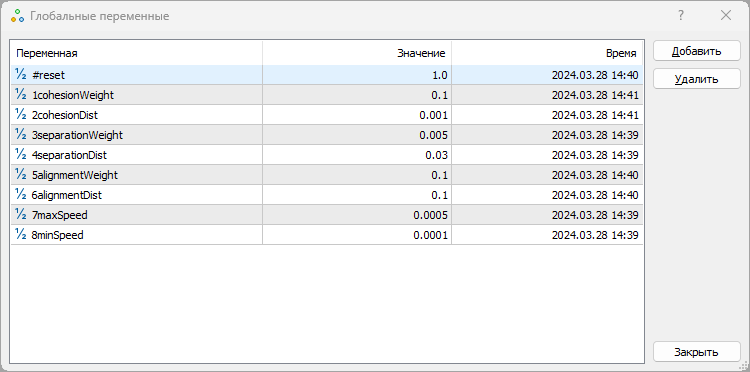
Janela de configuração do algoritmo Boids, acessada pela tecla F3. O parâmetro "#reset" permite reiniciar o algoritmo aplicando o valor "1".

2. Descrição do algoritmo

O algoritmo Boids, desenvolvido por Craig Reynolds, foi inicialmente projetado para modelar qualquer comportamento de enxame de animais, como bandos de pássaros, enxames de insetos e outros. No entanto, devido à sua flexibilidade e adaptabilidade, esse algoritmo encontrou aplicações em várias áreas, incluindo otimização e busca. No contexto de otimização e busca, o algoritmo Boids pode ser utilizado para resolver problemas relacionados ao comportamento coordenado de um grupo de agentes. Por exemplo, ele pode ser usado para modelar o comportamento de um enxame que explora um território desconhecido.

No entanto, é importante notar que o algoritmo Boids, por si só, não é um algoritmo de busca no sentido tradicional do termo. Ele não é projetado para encontrar a solução ótima em um espaço de soluções possíveis, como fazem, por exemplo, os algoritmos de descida de gradiente ou algoritmos genéticos. Em vez disso, o algoritmo Boids modela o comportamento de um grupo de agentes com base em um conjunto de regras simples, permitindo modelar um comportamento complexo e coordenado ao nível de grupo.

O algoritmo Boids pode ser adaptado para a busca distribuída do extremo de uma função. Nesse contexto, cada "boid" representa um agente de busca que se move pelo espaço de soluções possíveis. Em vez de simplesmente seguir outros "boids", cada agente pode usar o valor da função em sua posição atual para ajustar seu movimento ou considerar a adaptibilidade de outros boids na população.

O trabalho de Craig Reynolds no algoritmo Boids, que modela o comportamento de enxames, inspirou a criação da concepção de inteligência de enxame. A inteligência de enxame descreve o comportamento coletivo de um sistema descentralizado e auto-organizado, ao qual pertence o algoritmo PSO.

Os sistemas de inteligência de enxame geralmente consistem em muitos agentes (boids) que interagem localmente entre si e com o ambiente. As ideias de comportamento são geralmente inspiradas na natureza, especialmente em sistemas biológicos. Cada boid segue regras muito simples e, embora não exista um sistema de controle centralizado que dite o que cada um deve fazer, as interações locais e, em certa medida, aleatórias levam ao surgimento de um comportamento coletivo inteligente, não controlado pelos boids individualmente.

O algoritmo Boids possui uma variedade de parâmetros externos, e cada um deles afeta significativamente o comportamento dos boids. Vejamos esses parâmetros:

1. cohesionWeight - peso da coesão, que determina a força de atração entre os membros do enxame.
2. cohesionDist - distância de coesão, que define a distância entre os membros do enxame a partir da qual eles começam a se atrair.
3. separationWeight - peso de separação, que determina quão fortemente os membros do enxame se repelem.
4. separationDist - distância de separação, que define a distância entre os membros do enxame a partir da qual eles começam a se repelir.
5. alignmentWeight - peso de alinhamento, que determina quão fortemente os membros do enxame alinham sua direção de movimento com a dos outros.
6. alignmentDist - distância de alinhamento, que define a distância entre os membros do enxame a partir da qual eles começam a alinhar sua direção de movimento com a dos outros.
   
7. minSpeed - velocidade mínima, um parâmetro necessário para evitar que os boids parem de se mover.
   
8. maxSpeed - velocidade máxima com a qual um boid pode se mover.
   

É importante realizar uma série de experimentos para ajustar esses parâmetros e obter o comportamento desejado do enxame. Você pode começar com os valores sugeridos e ajustá-los gradualmente para observar como eles influenciam o comportamento do enxame. Lembre-se de que não existem valores "corretos" ou "melhores" para os parâmetros do algoritmo Boids em termos absolutos, tudo depende da tarefa específica e do cenário em questão.

Vamos começar a escrever o código do algoritmo Boids. Para descrever cada agente, definimos a estrutura "S_Boids_Agent". Vamos entender o que está acontecendo aqui:

1. A estrutura contém os seguintes campos:

• x[] - array para armazenar as coordenadas atuais do agente.
• dx[] - array das velocidades atuais do agente.
• m - massa do agente.
  

2. Init - método da estrutura "S_Boids_Agent", que inicializa os campos da estrutura. Ele recebe um argumento inteiro "coords", usado para redimensionar os arrays "x" e "dx" usando a função "ArrayResize".

Esse código representa a estrutura de dados básica para os agentes no algoritmo Boids e inicializa seus campos ao criar um novo agente. Isso permite que cada agente tenha suas próprias coordenadas e velocidades, o que é um aspecto fundamental do algoritmo Boids. O campo "m" foi adicionado por minha iniciativa para considerar a superfície da função de adaptabilidade durante o movimento dos boids, onde a massa representa o valor da adaptabilidade.

//——————————————————————————————————————————————————————————————————————————————
struct S_Boids_Agent
{
    double x  [];
    double dx [];
    double m;

    void Init (int coords)
    {
      ArrayResize (x,  coords);
      ArrayResize (dx, coords);
    }
};
//——————————————————————————————————————————————————————————————————————————————

Vamos definir a classe "C_AO_Boids" do algoritmo Boids, que é herdeira da classe básica de algoritmos populacionais "C_AO" e contém os seguintes campos e métodos:

1. Públicos:

• ao_name - nome do algoritmo de otimização.
• ao_desc - descrição do algoritmo de otimização.
• popSize - tamanho da população.
• params - array de parâmetros do algoritmo.
• cohesionWeight - peso da coesão.
• cohesionDist - distância de coesão.
• separationWeight - peso da separação.
• separationDist - distância de separação.
• alignmentWeight - peso do alinhamento.
• alignmentDist - distância de alinhamento.
• maxSpeed - velocidade máxima.
• minSpeed - velocidade mínima.
• agent - vetor de agentes.

2. Métodos:

• C_AO_Boids - construtor da classe, inicializando os campos da classe.
• SetParams - método para definir os parâmetros do algoritmo.
• Init - método para inicializar o algoritmo. Aceita os intervalos mínimo e máximo de busca, o passo de busca e o número de épocas.
• Moving - método para mover os agentes.
• Revision - método para revisar os agentes.

3. Campos Privados:

• distanceMax - distância euclidiana máxima possível no espaço de busca.
• speedMax - velocidade máxima.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_Boids : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_Boids () { }
  C_AO_Boids ()
  {
    ao_name = "Boids";
    ao_desc = "Boids Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/14576";

    popSize          = 50;   //population size

    cohesionWeight   = 0.6;
    cohesionDist     = 0.001;

    separationWeight = 0.005;
    separationDist   = 0.03;

    alignmentWeight  = 0.1;
    alignmentDist    = 0.1;

    maxSpeed         = 0.001;
    minSpeed         = 0.0001;

    ArrayResize (params, 9);

    params [0].name = "popSize";          params [0].val = popSize;

    params [1].name = "cohesionWeight";   params [1].val = cohesionWeight;
    params [2].name = "cohesionDist";     params [2].val = cohesionDist;


    params [3].name = "separationWeight"; params [3].val = separationWeight;
    params [4].name = "separationDist";   params [4].val = separationDist;

    params [5].name = "alignmentWeight";  params [5].val = alignmentWeight;
    params [6].name = "alignmentDist";    params [6].val = alignmentDist;

    params [7].name = "maxSpeed";         params [7].val = maxSpeed;
    params [8].name = "minSpeed";         params [8].val = minSpeed;
  }

  void SetParams ()
  {
    popSize          = (int)params [0].val;

    cohesionWeight   = params [1].val;
    cohesionDist     = params [2].val;

    separationWeight = params [3].val;
    separationDist   = params [4].val;

    alignmentWeight  = params [5].val;
    alignmentDist    = params [6].val;

    maxSpeed         = params [7].val;
    minSpeed         = params [8].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  double cohesionWeight;   //cohesion weight
  double cohesionDist;     //cohesion distance

  double separationWeight; //separation weight
  double separationDist;   //separation distance

  double alignmentWeight;  //alignment weight
  double alignmentDist;    //alignment distance

  double minSpeed;         //minimum velocity
  double maxSpeed;         //maximum velocity

  S_Boids_Agent agent [];

  private: //-------------------------------------------------------------------
  double distanceMax;
  double speedMax [];

  void   CalculateMass    ();
  void   Cohesion         (S_Boids_Agent &boid, int pos);
  void   Separation       (S_Boids_Agent &boid, int pos);
  void   Alignment        (S_Boids_Agent &boid, int pos);
  void   LimitSpeed       (S_Boids_Agent &boid);
  void   KeepWithinBounds (S_Boids_Agent &boid);
  double Distance         (S_Boids_Agent &boid1, S_Boids_Agent &boid2);
};
//——————————————————————————————————————————————————————————————————————————————

O método "Init" da classe "C_AO_Boids" é utilizado para inicializar as variáveis da classe com base nos parâmetros fornecidos. Esse método realiza a inicialização padrão utilizando o método "StandardInit", que aceita os intervalos mínimo e máximo de busca, além do passo de busca.

Se a inicialização padrão for bem-sucedida, o método altera o tamanho do array "agent" para o tamanho "popSize". Para cada elemento em "agent", o método "Init" é chamado com o parâmetro "coords".

Em seguida, o método calcula a distância máxima e a velocidade máxima, que são utilizadas no algoritmo Boids para determinar o movimento dos agentes.

Depois disso, o método define variáveis globais para vários parâmetros do algoritmo Boids, como peso da coesão, distância de coesão, peso da separação, distância de separação, peso do alinhamento, distância de alinhamento, velocidade máxima e velocidade mínima.

O método retorna "true" se a inicialização for bem-sucedida, e "false" caso contrário.

Esse método realiza a configuração inicial do algoritmo de otimização Boids com os parâmetros especificados e o prepara para executar a otimização.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_Boids::Init (const double &rangeMinP  [], //minimum search range
                       const double &rangeMaxP  [], //maximum search range
                       const double &rangeStepP [], //step search
                       const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  distanceMax = 0;
  ArrayResize (speedMax, coords);

  for (int c = 0; c < coords; c++)
  {
    speedMax [c] = rangeMax [c] - rangeMin [c];
    distanceMax += pow (speedMax [c], 2);
  }

  distanceMax = sqrt (distanceMax);

  GlobalVariableSet ("#reset", 1.0);

  GlobalVariableSet ("1cohesionWeight",   params [1].val);
  GlobalVariableSet ("2cohesionDist",     params [2].val);

  GlobalVariableSet ("3separationWeight", params [3].val);
  GlobalVariableSet ("4separationDist",   params [4].val);

  GlobalVariableSet ("5alignmentWeight",  params [5].val);
  GlobalVariableSet ("6alignmentDist",    params [6].val);

  GlobalVariableSet ("7maxSpeed",         params [7].val);
  GlobalVariableSet ("8minSpeed",         params [8].val);


  return true;
}
//——————————————————————————————————————————————————————————————————————————————

O método "Moving" da classe "C_AO_Boids" é utilizado para mover os agentes durante o processo de otimização. O método executa as seguintes ações:

1. Verifica o valor da variável global "reset". Se for igual a 1.0, a flag "revision" é definida como "false", o valor da variável global "reset" é definido como 0.0, e o método encerra sua execução.
2. Os valores dos parâmetros do algoritmo são extraídos das variáveis globais.
3. Se a flag "revision" for "false", a inicialização das coordenadas e velocidades dos agentes ocorre com valores aleatórios dentro dos intervalos especificados. Em seguida, a flag "revision" é definida como "true", e o método encerra sua execução.
4. Se a flag "revision" não for "false", para cada agente são realizadas as seguintes ações:

• Os métodos "CalculateMass", "Cohesion", "Separation", "Alignment", "LimitSpeed" e "KeepWithinBounds" são chamados para atualizar as velocidades do agente.
• As coordenadas do agente são atualizadas com base em suas velocidades.
• As coordenadas do agente são copiadas para o elemento correspondente do array "a".

/——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Moving ()
{
  double reset = GlobalVariableGet ("#reset");
  if (reset == 1.0)
  {
    revision = false;
    GlobalVariableSet ("#reset", 0.0);
  }

  cohesionWeight   = GlobalVariableGet ("1cohesionWeight");
  cohesionDist     = GlobalVariableGet ("2cohesionDist");

  separationWeight = GlobalVariableGet ("3separationWeight");
  separationDist   = GlobalVariableGet ("4separationDist");

  alignmentWeight  = GlobalVariableGet ("5alignmentWeight");
  alignmentDist    = GlobalVariableGet ("6alignmentDist");

  maxSpeed         = GlobalVariableGet ("7maxSpeed");
  minSpeed         = GlobalVariableGet ("8minSpeed");

  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        agent [i].x [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        agent [i].dx [c] = (rangeMax [c] - rangeMin [c]) * u.RNDfromCI (-1.0, 1.0) * 0.001;

        a [i].c [c] = u.SeInDiSp  (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    CalculateMass    ();
    Cohesion         (agent [i], i);
    Separation       (agent [i], i);
    Alignment        (agent [i], i);
    LimitSpeed       (agent [i]);
    KeepWithinBounds (agent [i]);

    for (int c = 0; c < coords; c++)
    {
      agent [i].x [c] += agent [i].dx [c];
      a [i].c [c] = u.SeInDiSp  (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "CalculateMass" da classe "C_AO_Boids" é utilizado para calcular a "massa" de cada agente no algoritmo Boids. Aqui está o que acontece nesse método:

1. As variáveis "maxMass" e "minMass" são inicializadas para armazenar os valores máximo e mínimo da função de adaptabilidade entre todos os agentes.
2. Para cada agente na população, verifica-se se a função de adaptabilidade "a[i].f" do agente excede o valor máximo atual "maxMass" e se é menor que o valor mínimo atual "minMass". Se for o caso, os valores máximos e mínimos correspondentes são atualizados.
3. Depois que todos os agentes foram verificados, a "massa" de cada agente é calculada como um valor escalonado da sua função de adaptabilidade em relação aos valores mínimos e máximos.

Este método garante o cálculo da "massa" de cada agente no algoritmo Boids, algo que não está presente na lógica original do algoritmo Boids, mas que permite considerar a "superfície" do terreno sobre o qual os boids se movem.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::CalculateMass ()
{
  double maxMass = -DBL_MAX;
  double minMass =  DBL_MAX;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > maxMass) maxMass = a [i].f;
    if (a [i].f < minMass) minMass = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    agent [i].m = u.Scale (a [i].f, minMass, maxMass, 0.0, 1.0);
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "Cohesion" da classe "C_AO_Boids" é utilizado para implementar o comportamento de "coesão" no algoritmo Boids. Este comportamento faz com que os agentes se movam em direção ao "centro de massa" dos seus vizinhos. O método realiza as seguintes ações:

1. Um array "centerX" é inicializado para armazenar as coordenadas do centro de massa e uma variável "numNeighbors" para contar o número de vizinhos.
2. Para cada agente na população, verifica-se se ele não é ele mesmo (pois o agente não deve considerar a si próprio como um vizinho) e se ele está dentro de uma certa distância (definida como "distanceMax * cohesionDist"). Se ambas as condições forem atendidas, as coordenadas do agente são adicionadas a "centerX" e "numNeighbors" é incrementado em 1.
3. Se pelo menos um vizinho foi encontrado, as coordenadas de "centerX" são divididas pelo número de vizinhos para obter as coordenadas do centro de massa dos vizinhos. Em seguida, a velocidade do agente "boid.dx" é ajustada na direção do centro de massa, considerando o peso da coesão "cohesionWeight".

Este método garante a implementação do comportamento de "coesão" no algoritmo Boids, o que ajuda os agentes a se moverem juntos como um grupo.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Cohesion (S_Boids_Agent &boid, int pos)
{
  double centerX [];
  ArrayResize     (centerX, coords);
  ArrayInitialize (centerX, 0.0);

  int    numNeighbors = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * cohesionDist)
      {
        for (int c = 0; c < coords; c++)
        {
          centerX [c] += agent [i].x [c];
        }

        numNeighbors++;
      }
    }
  }

  for (int c = 0; c < coords; c++)
  {
    centerX [c] /= numNeighbors;
    boid.dx [c] += (centerX [c] - boid.x [c]) * cohesionWeight;
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "Separation" da classe "C_AO_Boids" é utilizado para implementar o comportamento de "separação" no algoritmo Boids. Esse comportamento faz com que os agentes se movam na direção oposta aos vizinhos que estão muito próximos, a fim de evitar colisões. Aqui está o que acontece nesse método:

1. Um array "moveX" é inicializado para armazenar as mudanças nas coordenadas do agente.
2. Para cada agente na população, verifica-se se ele não é ele mesmo (pois o agente não deve considerar a si próprio como um vizinho) e se ele está dentro de uma certa distância (definida como "distanceMax * separationDist"). Se ambas as condições forem atendidas, a diferença entre as coordenadas do agente atual e do vizinho é adicionada a "moveX".
3. Depois que todos os vizinhos foram verificados, a velocidade do agente "boid.dx" é ajustada na direção oposta a "moveX", considerando o peso da separação "separationWeight".

Este método garante a execução do comportamento de "separação" no algoritmo Boids, o que ajuda os agentes a evitar colisões entre si.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Separation (S_Boids_Agent &boid, int pos)
{
  double moveX [];
  ArrayResize     (moveX, coords);
  ArrayInitialize (moveX, 0.0);

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * separationDist)
      {
        for (int c = 0; c < coords; c++)
        {
          moveX [c] += boid.x [c] - agent [i].x [c];
        }
      }
    }
  }

  for (int c = 0; c < coords; c++)
  {
    boid.dx [c] += moveX [c] * separationWeight;
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "Alignment" da classe "C_AO_Boids" é utilizado para implementar o comportamento de "alinhamento" no algoritmo Boids. Esse comportamento faz com que os agentes se movam na mesma direção que seus vizinhos. Neste método:

1. Um array "avgDX" é inicializado para armazenar a velocidade média dos vizinhos e uma variável "numNeighbors" para contar o número de vizinhos.
2. Para cada agente na população, verifica-se se ele não é ele mesmo (pois o agente não deve considerar a si próprio como um vizinho) e se ele está dentro de uma certa distância (definida como "distanceMax * alignmentDist"). Se ambas as condições forem atendidas, a velocidade do vizinho é adicionada a "avgDX" e "numNeighbors" é incrementado em 1.
3. Se pelo menos um vizinho foi encontrado, as velocidades de "avgDX" são divididas pelo número de vizinhos para obter a velocidade média. Em seguida, a velocidade do agente "boid.dx" é ajustada na direção da velocidade média, considerando o peso do alinhamento "alignmentWeight".

Este método garante a execução do comportamento de "alinhamento" no algoritmo Boids, o que ajuda os agentes a se moverem juntos na mesma direção.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Alignment (S_Boids_Agent &boid, int pos)
{
  double avgDX [];
  ArrayResize     (avgDX, coords);
  ArrayInitialize (avgDX, 0.0);

  int numNeighbors = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * alignmentDist)
      {
        for (int c = 0; c < coords; c++)
        {
          avgDX [c] += agent [i].dx [c];
        }

        numNeighbors++;
      }
    }
  }

    for (int c = 0; c < coords; c++)
    {
      avgDX   [c] /= numNeighbors;
      boid.dx [c] += (avgDX [c] - boid.dx [c]) * alignmentWeight;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "LimitSpeed" da classe "C_AO_Boids" é utilizado para limitar a velocidade dos agentes no algoritmo Boids. Esse comportamento evita o aumento infinito da velocidade dos agentes, o que seria antinatural para animais reais. Neste método, ocorre o seguinte:

1. Uma variável "speed" é inicializada para armazenar a velocidade atual do agente e uma variável "d" para armazenar temporariamente os dados.
2. A velocidade atual do agente é calculada com base em suas velocidades em cada coordenada.
3. Para cada coordenada do agente, são realizadas as seguintes ações:

• Calcula-se "d" como a diferença entre os valores máximos e mínimos do intervalo, multiplicada pelo coeficiente da velocidade mínima. 
• A velocidade do agente "boid.dx" é ajustada consoante a velocidade máxima possível "speedMax" e o coeficiente da velocidade máxima "maxSpeed".
• Se o valor absoluto da velocidade do agente for menor que "d", então a velocidade do agente é definida como "d" (mantendo o sinal).

Este método garante a execução do comportamento de "limitação de velocidade" no algoritmo Boids, o que ajuda a controlar a velocidade de movimento dos agentes e impede que os boids parem de se mover.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::LimitSpeed (S_Boids_Agent &boid)
{
  double speed = 0;

  for (int c = 0; c < coords; c++)
  {
    speed += boid.dx [c] * boid.dx [c];
  }

  speed = sqrt (speed);

  double d = 0;

  for (int c = 0; c < coords; c++)
  {
    d = (rangeMax [c] - rangeMin [c]) * minSpeed;

    boid.dx [c] = (boid.dx [c] / speed) * speedMax [c] * maxSpeed;

    if (fabs (boid.dx [c]) < d)
    {
      if (boid.dx [c] < 0.0) boid.dx [c] = -d;
      else                   boid.dx [c] =  d;
    }

  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "KeepWithinBounds" da classe "C_AO_Boids" é utilizado para restringir o movimento dos agentes dentro de limites especificados no algoritmo Boids. Esse comportamento evita que os agentes ultrapassem os limites estabelecidos.

1. Para cada coordenada do agente, verifica-se se ela está fora dos limites especificados (definidos como "rangeMin" e "rangeMax").
2. Se a coordenada do agente for menor que "rangeMin", ela é definida como "rangeMax", movendo o agente para o lado oposto do limite.
3. Se a coordenada do agente for maior que "rangeMax", ela é definida como "rangeMin", movendo o agente para o lado oposto do limite.

Este método garante a execução da "limitação de fronteiras" no algoritmo Boids, o que ajuda os agentes a permanecerem dentro dos limites estabelecidos.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::KeepWithinBounds (S_Boids_Agent &boid)
{
  for (int c = 0; c < coords; c++)
  {
    double margin     = 0; //(rangeMax [c] - rangeMin [c])* 0.00001;
    double turnFactor = (rangeMax [c] - rangeMin [c]) * 0.0001;

    /*
    if (boid.x [c] < rangeMin [c] + margin)
    {
      boid.dx [c] += turnFactor;
    }
    if (boid.x [c] > rangeMax [c] - margin)
    {
      boid.dx [c] -= turnFactor;
    }
    */
    if (boid.x [c] < rangeMin [c]) 
    {
      //boid.x [c] = rangeMax [c];
      boid.dx [c] *= -1;
      
    }
    if (boid.x [c] > rangeMax [c])
    {
      //boid.x [c] = rangeMin [c];
      boid.dx [c] *= -1;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "Distance" da classe "C_AO_Boids" é utilizado para calcular a distância euclidiana entre dois agentes no algoritmo Boids.

1. Inicializa-se uma variável "dist" para armazenar a distância.
2. Para cada coordenada dos agentes, é calculado o quadrado da diferença entre suas coordenadas, que é então adicionado a "dist".
3. No final, o método retorna a raiz quadrada de "dist", o que corresponde à distância euclidiana entre os agentes.

Este método garante o cálculo da distância entre os agentes no algoritmo Boids, o que é utilizado para determinar sua interação mútua.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_Boids::Distance (S_Boids_Agent &boid1, S_Boids_Agent &boid2)
{
  double dist = 0;

  for (int c = 0; c < coords; c++)
  {
    dist += pow (boid1.x [c] - boid1.x [c], 2);
  }

  return sqrt (dist);
}
//——————————————————————————————————————————————————————————————————————————————

O método "Revision" da classe "C_AO_Boids" é utilizado para atualizar a melhor solução no algoritmo Boids.

1. Inicializa-se uma variável "ind" com o valor -1. Esta variável será utilizada para armazenar o índice do agente com a melhor solução.
2. Para cada agente na população, verifica-se se a função de adaptabilidade "a[i].f" do agente excede a melhor solução atual "fB". Se for o caso, "ind" é definido como o índice desse agente.
3. Se um agente com a melhor solução for encontrado (ou seja, se "ind" não for igual a -1), a melhor solução "fB" e as melhores coordenadas "cB" são atualizadas com os valores desse agente.

Este método garante a atualização da melhor solução no algoritmo Boids, o que ajuda o algoritmo a se concentrar nas áreas mais promissoras do espaço de soluções.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = a [ind].f;
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Resultados dos testes

Gostaria de abordar em mais detalhes os resultados do algoritmo Boids em vários conjuntos de funções. A pontuação geral do Boids em todas as funções de teste foi 2.22889, o que corresponde a 24,77% do resultado máximo possível. Este resultado indica a baixa eficácia do algoritmo. Com base nisso, pode-se concluir que o algoritmo Boids possui um potencial limitado para resolver problemas de otimização em várias funções.

Boids|50.0|0.05|0.002|0.01|0.01|0.0001|0.01|0.001|0.0001|
=============================
5 Hilly's; Func runs: 100000; result: 0.43339505349362384
25 Hilly's; Func runs: 100000; result: 0.3058074706767012
500 Hilly's; Func runs: 100000; result: 0.2542539219446322
=============================
5 Forest's; Func runs: 100000; result: 0.35717696198531945
25 Forest's; Func runs: 100000; result: 0.20160005990319796
500 Forest's; Func runs: 100000; result: 0.15708435238635948
=============================
5 Megacity's; Func runs: 100000; result: 0.2784615384615384
25 Megacity's; Func runs: 100000; result: 0.14276923076923081
500 Megacity's; Func runs: 100000; result: 0.09833846153846236
=============================
All score: 2.22889 (24.77%)

O algoritmo Boids ficou em 28º lugar na tabela de classificação, próximo ao seu "parente" dos sistemas de inteligência de enxame, o algoritmo PSO.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	BGA	binary genetic algorithm	0,99992	0,99484	0,50483	2,49959	1,00000	0,99975	0,32054	2,32029	0,90667	0,96400	0,23035	2,10102	6,921	76,90
2	(P+O)ES	(P+O) evolution strategies	0,99934	0,91895	0,56297	2,48127	1,00000	0,93522	0,39179	2,32701	0,83167	0,64433	0,21155	1,68755	6,496	72,18
3	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
4	ESG	evolution of social groups	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
5	SIA	simulated isotropic annealing	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
6	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
7	BSA	bird swarm algorithm	0,90857	0,73661	0,25767	1,90285	0,90437	0,81619	0,16401	1,88457	0,61692	0,54154	0,10951	1,26797	5,055	56,17
8	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
9	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
10	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
11	WOAm	whale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
12	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
13	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
14	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
15	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
16	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
17	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
18	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
19	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
20	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
21	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
22	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
23	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
24	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
25	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
26	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06
27	PSO	particle swarm optimisation	0,59726	0,36923	0,29928	1,26577	0,37237	0,16324	0,07010	0,60572	0,25667	0,08000	0,02157	0,35823	2,230	24,77
28	Boids	boids algorithm	0,43340	0,30581	0,25425	0,99346	0,35718	0,20160	0,15708	0,71586	0,27846	0,14277	0,09834	0,51957	2,229	24,77
29	MA	monkey algorithm	0,59107	0,42681	0,31816	1,33604	0,31138	0,14069	0,06612	0,51819	0,22833	0,08567	0,02790	0,34190	2,196	24,40
30	SFL	shuffled frog-leaping	0,53925	0,35816	0,29809	1,19551	0,37141	0,11427	0,04051	0,52618	0,27167	0,08667	0,02402	0,38235	2,104	23,38
31	FSS	fish school search	0,55669	0,39992	0,31172	1,26833	0,31009	0,11889	0,04569	0,47467	0,21167	0,07633	0,02488	0,31288	2,056	22,84
32	RND	random	0,52033	0,36068	0,30133	1,18234	0,31335	0,11787	0,04354	0,47476	0,25333	0,07933	0,02382	0,35648	2,014	22,37
33	GWO	grey wolf optimizer	0,59169	0,36561	0,29595	1,25326	0,24499	0,09047	0,03612	0,37158	0,27667	0,08567	0,02170	0,38403	2,009	22,32
34	CSS	charged system search	0,44252	0,35454	0,35201	1,14907	0,24140	0,11345	0,06814	0,42299	0,18333	0,06300	0,02322	0,26955	1,842	20,46
35	EM	electroMagnetism-like algorithm	0,46250	0,34594	0,32285	1,13129	0,21245	0,09783	0,10057	0,41085	0,15667	0,06033	0,02712	0,24412	1,786	19,85

Considerações finais

Apesar dos resultados fracos nas funções de teste, vale destacar que nas funções Forest e Megacity com 1000 variáveis, os resultados foram bastante satisfatórios e comparáveis aos dos algoritmos na metade superior da tabela. Isso pode indicar que o algoritmo Boids pode ser mais eficaz ao trabalhar com um grande número de variáveis. No geral, esses resultados mostram que seria difícil esperar um maior potencial do algoritmo Boids.

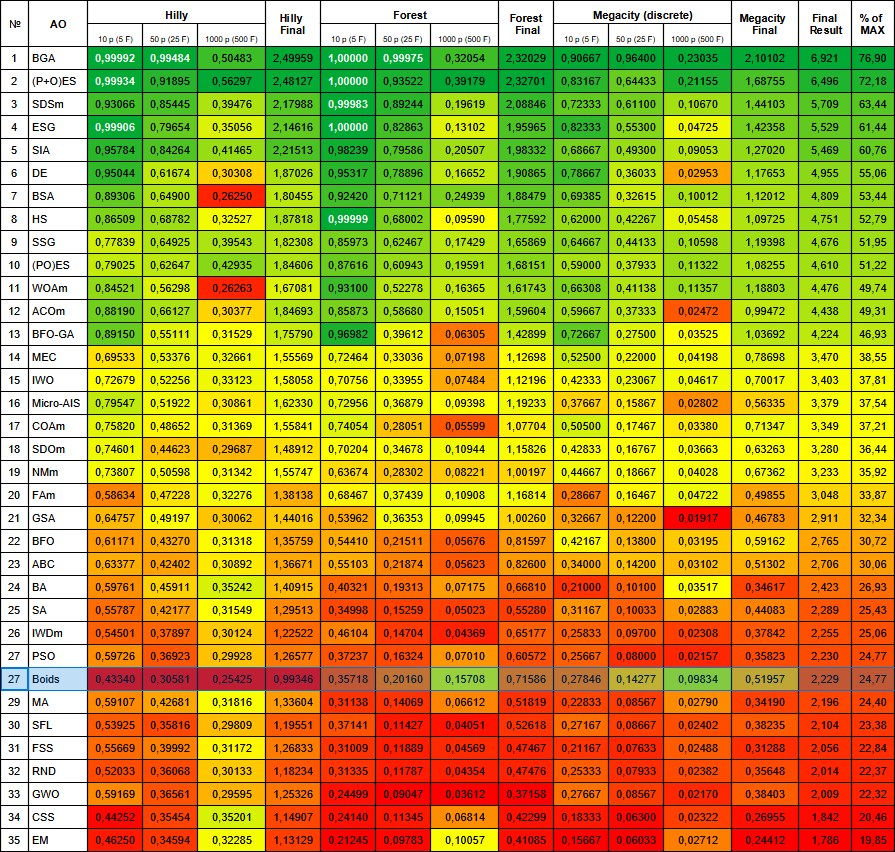
Figura 1. Graduação de cores dos algoritmos nos respectivos testes. Os resultados maiores ou iguais a 0,99 são destacados em branco.

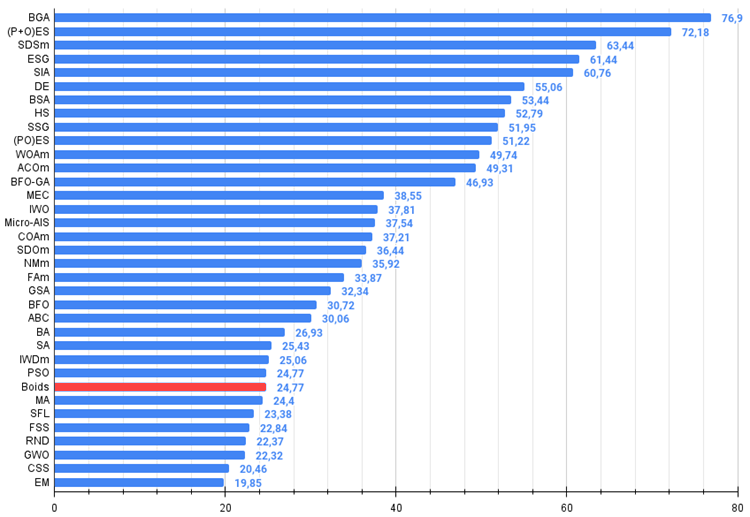
Figura 2. Histograma dos resultados dos testes dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor,

onde 100 é o resultado teórico máximo possível, no arquivo há um script para calcular a tabela de classificação).

Prós e contras do algoritmo de comportamento de enxame (Boids):

Prós:

1. Modelagem realista do comportamento de enxame.
   

Contras:

1. Baixa convergência.
2. Alta complexidade computacional.
   
3. Baixa escalabilidade em funções suaves, como Hilly (problemas com tarefas de alta dimensionalidade).

O artigo inclui um arquivo com as versões atualizadas dos códigos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e opiniões apresentadas nos artigos são baseadas nos resultados dos experimentos realizados.