
Ciência de Dados e ML (Parte 27): Redes Neurais Convolucionais (CNNs) em Bots de Trading no MetaTrader 5 — Vale a Pena?
A operação de pooling usada em redes neurais convolucionais é um grande erro, e o fato de que ela funciona tão bem é um desastre.
Geoffrey Hinton
Conteúdo
- O que são Redes Neurais Convolucionais (CNNs)?
- Camadas Convolucionais
- Funções de Ativação
- Camadas de Pooling
- Camadas Totalmente Conectadas
- Camadas Dropout - Por que usar Redes Neurais Convolucionais (CNNs) para Análise Financeira e Aplicações de Trading?
- Criando uma Rede Neural Convolucional (CNN) em Python
- Criando um Robô de Trading baseado em Rede Neural Convolucional (CNN)
- A linha de fundo
Um entendimento básico da linguagem de programação Python, Redes Neurais Artificiais, Aprendizado de Máquina e ONNX no MQL5 é necessário para compreender totalmente o conteúdo deste artigo.
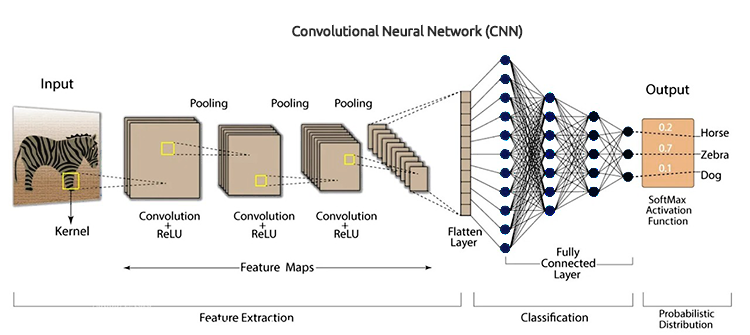
O que são Redes Neurais Convolucionais (CNNs)?
As Redes Neurais Convolucionais (CNNs) são uma classe de algoritmos de aprendizado profundo projetados especificamente para processar dados estruturados em grade, como imagens, espectrogramas de áudio e séries temporais. Elas são particularmente adequadas para tarefas envolvendo dados visuais, pois podem aprender automaticamente e de forma adaptativa hierarquias espaciais de características a partir dos dados de entrada.
As CNNs são uma versão estendida das redes neurais artificiais (ANN). Elas são predominantemente usadas para extrair características de conjuntos de dados em formato de grade. Por exemplo, conjuntos de dados visuais como imagens ou vídeos, onde os padrões de dados desempenham um papel fundamental.
As redes neurais convolucionais possuem vários componentes-chave, como camadas convolucionais, funções de ativação, camadas de pooling, camadas totalmente conectadas e camadas dropout. Para entender as CNNs em profundidade, vamos dissecar cada componente e ver do que se trata.
Camadas Convolucionais
Essas são as estruturas centrais das CNNs, onde ocorre a maior parte dos cálculos. As camadas convolucionais são responsáveis por detectar padrões locais nos dados de entrada, como bordas em imagens. Isso é alcançado por meio do uso de filtros (ou kernels) que percorrem os dados de entrada para produzir mapas de características.
Uma camada convolucional é uma camada oculta que contém várias unidades convolucionais em uma rede neural convolucional, sendo utilizada para a extração de características.
from tensorflow.keras.layers import Conv1D
model = Sequential()
model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(window_size, X_train.shape[2]))) Filters/Kernels
Filtros (ou kernels) são pequenas matrizes quadradas treináveis (geralmente de tamanho 3x3, 5x5, etc.) que percorrem os dados de entrada para detectar padrões locais.
Como eles funcionam?
Eles operam movendo-se através dos dados de entrada e realizando uma multiplicação elemento a elemento entre os valores do filtro e os valores de entrada dentro do campo receptivo atual do filtro, seguida da soma dos resultados. Essa operação é chamada de convolução.
Durante o treinamento, a rede aprende os valores ideais dos filtros. Nas camadas iniciais, os filtros geralmente aprendem a detectar características simples, como bordas e texturas, enquanto nas camadas mais profundas, os filtros podem detectar padrões mais complexos, como formas e objetos.
Considere um filtro simples de 3x3 e uma imagem de entrada de 5x5. O filtro percorre a imagem, computando a operação de convolução para produzir um mapa de características.
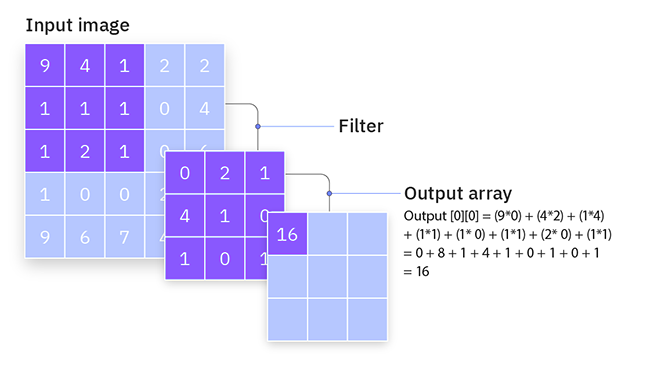
Stride
Este é outro recurso encontrado na camada de convolução. O stride é o tamanho do passo pelo qual o filtro se move sobre os dados de entrada. Ele determina o quanto o filtro se desloca a cada etapa durante o processo de convolução.
Como eles funcionam?
Stride de 1: O filtro se move um único pixel por vez, resultando em um mapa de características altamente sobreposto e detalhado. Isso gera um mapa de características de saída maior.
Stride de 2 ou mais: O filtro pula unidades, resultando em um mapa de características de saída menos detalhado, mas menor. Isso reduz as dimensões espaciais da saída, efetivamente diminuindo a resolução da entrada.
Por exemplo, se você tiver um filtro de 3x3 e uma imagem de entrada de 5x5 com um stride de 1, o filtro se moverá um pixel por vez, produzindo um mapa de características de saída de 3x3. Com um stride de 2, o filtro se moverá dois pixels por vez, produzindo um mapa de características de saída de 2x2.
Preenchimento
O preenchimento envolve adicionar pixels extras (geralmente zeros) ao redor da borda dos dados de entrada. Isso garante que o filtro se encaixe corretamente e controle as dimensões espaciais do mapa de características de saída.
Tipos de preenchimento
De acordo com Keras, existem três tipos de preenchimento. (sensível a maiúsculas e minúsculas)
- valid - nenhum preenchimento será aplicado.
- same - adiciona preenchimento à entrada para que o tamanho da saída corresponda ao tamanho da entrada quando strides=1.
- causal - usado para dados temporais para garantir que a saída no instante de tempo 𝑡 não dependa de entradas futuras.
O preenchimento ajuda a preservar as dimensões espaciais dos dados de entrada. Sem preenchimento, o mapa de características de saída diminui a cada camada convolucional, o que pode resultar na perda de informações importantes nas bordas.
Ao adicionar preenchimento, a rede pode aprender melhor as características das bordas e manter a resolução espacial da entrada.
Considere um filtro de 3x3 e uma imagem de entrada de 5x5. Com preenchimento válido (sem preenchimento), o mapa de características de saída será 3x3. Com o preenchimento "same", você pode adicionar uma borda de zeros ao redor da entrada, tornando-a 7x7. O mapa de características de saída será então 5x5, preservando as dimensões da entrada.
Abaixo está o código para uma camada de convolução em Python.
from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Conv1D model = Sequential() model.add(Conv1D(filters=64, kernel_size=3, activation='relu', strides=2, padding='causal', input_shape=(window_size, X_train.shape[2]) ) )
Funções de Ativação
Conforme discutido no artigo Redes Neurais Desmistificadas, uma função de ativação é uma função matemática que recebe uma entrada e processa uma saída.
A função de ativação é aplicada elemento a elemento para introduzir não-linearidade no modelo. As funções de ativação mais utilizadas em CNNs incluem ReLU (Rectified Linear Unit), Sigmoid e TanH.
Camadas de Pooling
Também conhecidas como camadas de amostragem, essas camadas são uma parte essencial das CNNs, pois são responsáveis por reduzir a dimensão espacial dos dados de entrada em termos de largura e altura, enquanto retêm as informações mais importantes.
Como eles funcionam?
Primeiramente, elas dividem os dados de entrada em regiões ou janelas sobrepostas e, em seguida, aplicam uma função de agregação, como Max pooling ou Average pooling, em cada janela para obter um único valor.
Max pooling seleciona o valor máximo de um conjunto de valores dentro da região do filtro. Isso reduz as dimensões espaciais dos dados, o que ajuda a diminuir a carga computacional e o número de parâmetros.
Python
from tensorflow.keras.layers import Conv1D, MaxPooling1D model = Sequential() model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(window_size, X_train.shape[2]))) model.add(MaxPooling1D(pool_size=2))
MaxPooling1D(pool_size=2) Esta camada seleciona o valor máximo de cada janela de 2 elementos.
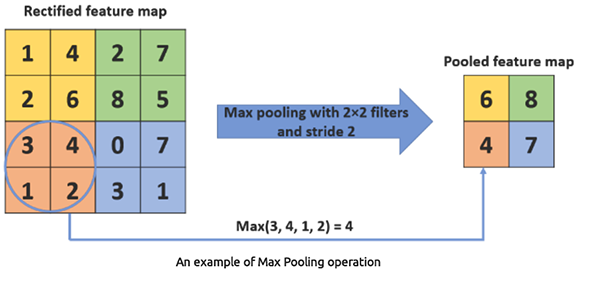
Average pooling calcula a média dos valores dentro da região do filtro. É menos utilizado do que o max pooling.
Python
from tensorflow.keras.layers import Conv1D, AveragePooling1D model = Sequential() model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(window_size, X_train.shape[2]))) model.add(AveragePooling1D(pool_size=2))
AveragePooling1D(pool_size=2) Esta camada calcula a média de cada janela de 2 elementos.
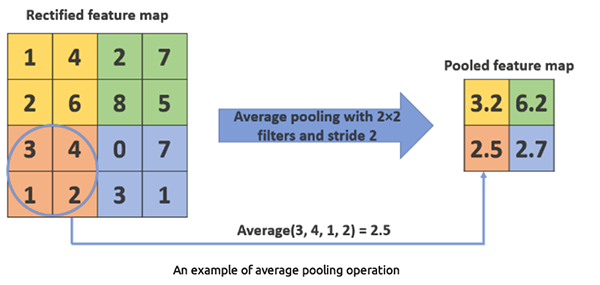
Por que usar uma Camada Convolucional 1D?
Existem camadas Conv1D, Conv2D e Conv3D para CNNs. A camada de convolução 1D é a mais adequada para esse tipo de problema, pois é projetada para dados unidimensionais, tornando-a apropriada para dados sequenciais ou séries temporais. Outras camadas convolucionais, como Conv2D e Conv3D, são muito complexas para esse tipo de problema.
Camadas Totalmente Conectadas
Os neurônios em uma camada totalmente conectada têm conexões com todas as ativações da camada anterior. Essas camadas são normalmente utilizadas no final da rede para realizar classificação ou regressão com base nas características extraídas pelas camadas convolucionais e de pooling.
from tensorflow.keras.layers import Conv1D, MaxPooling1D, Flatten, Dense, Dropout
model = Sequential()
model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(window_size, X_train.shape[2])))
model.add(MaxPooling1D(pool_size=2))
model.add(Flatten())
model.add(Dense(100, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=len(np.unique(y)), activation='sigmoid')) # For binary classification (e.g., buy/sell signal)
model.summary() A Camada Flatten converte o mapa de características agrupado 1D em um vetor 1D, para que possa ser alimentado nas camadas totalmente conectadas (densas).
As Camadas Densas (Dense) são camadas totalmente conectadas usadas para tomar decisões finais com base nas características extraídas pelas camadas de convolução e pooling. As camadas densas são essencialmente o componente central das redes neurais artificiais (ANNs) tradicionais.
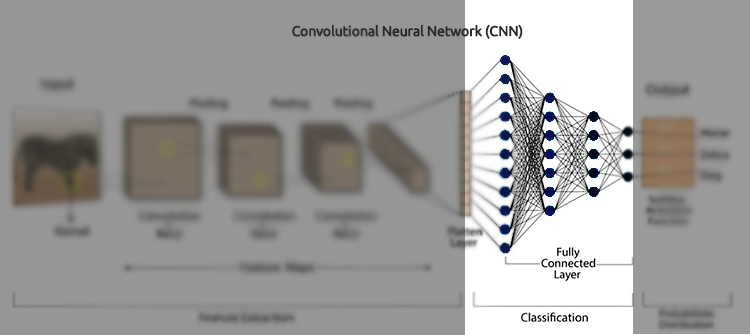
Camadas Dropout
A camada Dropout age como uma máscara, eliminando a contribuição de alguns neurônios para a camada subsequente, enquanto mantém a funcionalidade de todos os outros neurônios. Se aplicarmos uma camada Dropout ao vetor de entrada, algumas de suas características são eliminadas. No entanto, se a aplicarmos a uma camada oculta, alguns neurônios ocultos serão eliminados.
Como as camadas Dropout evitam o overfitting dos dados de treinamento, elas são cruciais no treinamento de CNNs. Se estiverem ausentes, o primeiro conjunto de amostras de treinamento tem um impacto excessivo no aprendizado. Como resultado, características que aparecem apenas em amostras ou lotes posteriores não seriam aprendidas.
from tensorflow.keras.layers import Conv1D, MaxPooling1D, Flatten, Dense, Dropout
model = Sequential()
model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(window_size, X_train.shape[2])))
model.add(MaxPooling1D(pool_size=2))
model.add(Flatten())
model.add(Dense(100, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=len(np.unique(y)), activation='sigmoid')) # For binary classification (e.g., buy/sell signal)
model.summary() Por que usar Redes Neurais Convolucionais (CNNs) para Análise Financeira e Aplicações de Trading?
As CNNs são amplamente utilizadas em aplicações de processamento de imagens e vídeos, pois foram projetadas para isso. Se você observar as explicações acima, poderá perceber que me refiro ao uso de CNNs para classificação de imagens e outros tipos de dados visuais.
Usar Redes Neurais Convolucionais (CNNs) para dados tabulares, como análise financeira, pode parecer incomum em comparação com outros tipos de redes neurais, como Redes Neurais Feed Forward (FFNN), Redes Neurais Recorrentes (RNNs), Long Short-Term Memory (LSTMs) e Gated Recurrent Units (GRUs). No entanto, existem várias razões e benefícios potenciais destacados abaixo para o uso de CNNs nesse contexto.
01. CNNs são excelentes para extrair padrões locais automaticamente dos dados.
03. Elas são robustas contra ruídos e características redundantes.
04. CNNs lidam bem com séries temporais multivariadas.
Agora que temos razões válidas para usar CNNs em aplicações de trading, vamos criar uma e treiná-la. Em seguida, veremos como podemos usar uma CNN em um Expert Advisor (EA) no MetaTrader 5.
Criando uma Rede Neural Convolucional (CNN) em Python
Isso envolve várias etapas, que são:
- Coletando os dados
- Preparando os dados para um modelo de CNN
- Treinando um modelo de CNN
- Salvando um modelo de CNN no formato ONNX
01: Coletando os dados
Usando o conjunto de dados para previsão de séries temporais que utilizamos nos artigos anteriores.
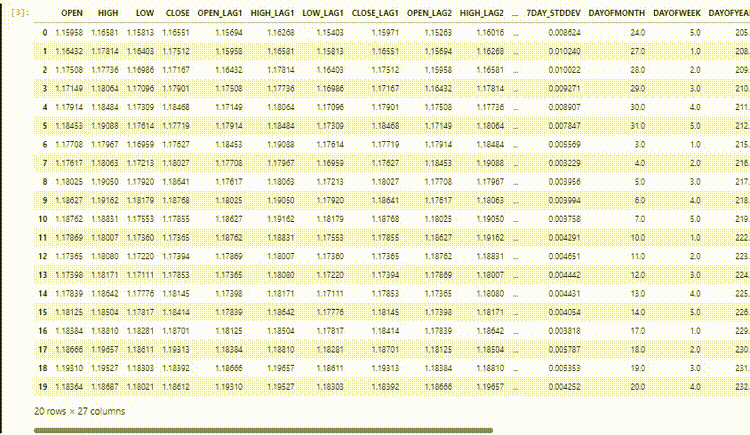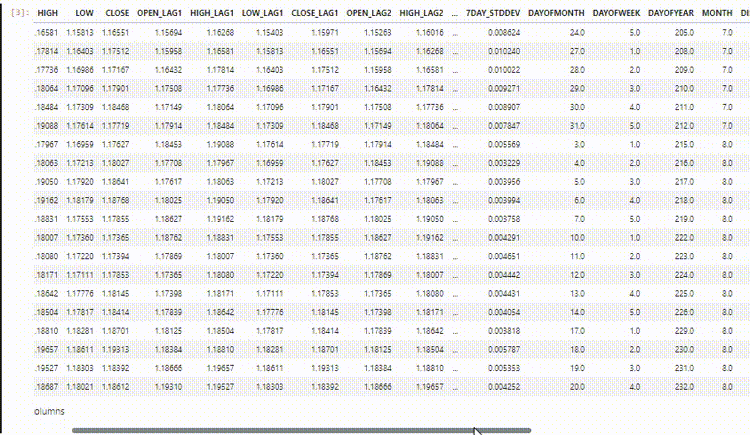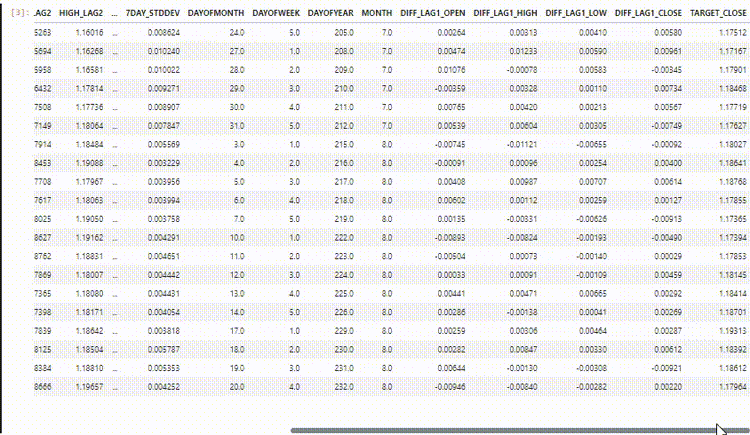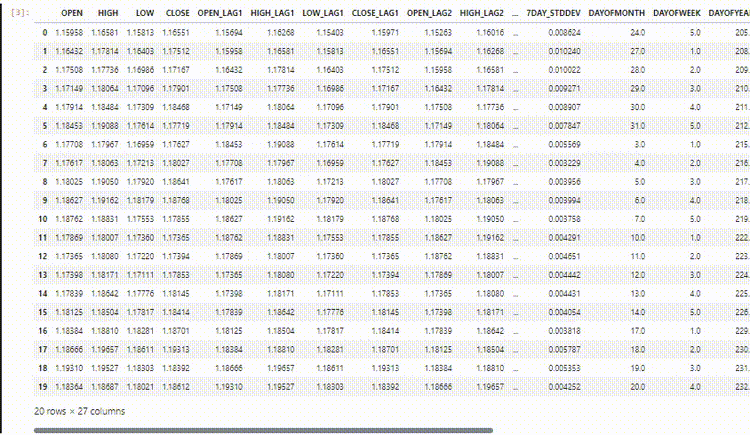
Agora que sabemos que as Redes Neurais Convolucionais (CNNs) são boas em detectar padrões dentro de dados de alta dimensão, podemos escolher algumas características que acredito conter muitos padrões que o modelo de CNN pode detectar.
Código Python
open_price = df['TARGET_OPEN'] close_price = df['TARGET_CLOSE'] # making the target variable target_var = [] for i in range(len(open_price)): if close_price[i] > open_price[i]: # if the price closed above where it opened target_var.append(1) # bullish signal else: target_var.append(0) # bearish signal new_df = pd.DataFrame({ 'OPEN': df['OPEN'], 'HIGH': df['HIGH'], 'LOW': df['LOW'], 'CLOSE': df['CLOSE'], 'TARGET_VAR': target_var }) print(new_df.shape)
Logo após preparar a variável alvo com base em TARGET_OPEN e TARGET_CLOSE, que são respectivamente os valores de abertura e fechamento coletados um período à frente. Criamos uma versão reduzida do conjunto de dados chamada new_df, que continha apenas 4 variáveis independentes: valores de OPEN, HIGH e LOW, além de uma variável dependente chamada TARGET_VAR.
02: Preparando Dados para um Modelo de CNN
Primeiramente, precisamos pré-processar os dados de entrada, reorganizando e alinhando-os em janelas. Isso é extremamente importante ao trabalhar com dados tabulares em CNNs, e aqui está o porquê.
Como os dados de trading são sequenciais, os padrões geralmente surgem ao longo de uma série de etapas temporais, em vez de um único ponto no tempo. Ao criar janelas sobrepostas de dados, podemos capturar dependências temporais e fornecer contexto ao modelo de CNN.
Além disso, as CNNs esperam que os dados de entrada estejam em um formato específico. Para camadas convolucionais 1D, o formato de entrada normalmente precisa ser (número de janelas, tamanho da janela, número de características). Esse formato se assemelha ao que usamos na análise de séries temporais utilizando Redes Neurais Recorrentes (RNNs) no artigo anterior. O procedimento de pré-processamento que faremos agora garante que os dados estejam nesse formato, tornando-os adequados para serem usados como entrada de um modelo de CNN.
# Example data preprocessing function def preprocess_data(df, window_size): X, y = [], [] for i in range(len(df) - window_size): X.append(df.iloc[i:i+window_size, :-1].values) y.append(df.iloc[i+window_size, -1]) return np.array(X), np.array(y) window_size = 10 X, y = preprocess_data(new_df, window_size) print(f"x_shape = {X.shape}\ny_shape = {y.shape}")
Saídas:
x_shape = (990, 10, 4) y_shape = (990,)
Como nossos dados foram coletados em uma escala de tempo diária, o tamanho da janela de 10 indica que estaremos treinando o modelo de CNN para entender padrões dentro de um período de 10 dias.
Em seguida, precisamos dividir os dados em amostras de treinamento e teste.
# Split data into training and testing sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=False) # Standardize the data scaler = StandardScaler() X_train = scaler.fit_transform(X_train.reshape(-1, X_train.shape[-1])).reshape(X_train.shape) X_test = scaler.transform(X_test.reshape(-1, X_test.shape[-1])).reshape(X_test.shape) print(f"x_train\n{X_train.shape}\nx_test\n{X_test.shape}\n\ny_train {y_train.shape} y_test {y_test.shape}")
Saídas:
x_train (792, 10, 4) x_test (198, 10, 4) y_train (792,) y_test (198,)
Por fim, precisamos aplicar one-hot encoding à variável alvo para esta tarefa de classificação.
from tensorflow.keras.utils import to_categorical
y_train_encoded = to_categorical(y_train)
y_test_encoded = to_categorical(y_test)
print(f"One hot encoded\n\ny_train {y_train_encoded.shape}\ny_test {y_test_encoded.shape}") Saídas:
One hot encoded y_train (792, 2) y_test (198, 2)
03: Treinando um Modelo de CNN
Aqui é onde a maior parte do trabalho acontece.
# Defining the CNN model model = Sequential() model.add(Conv1D(filters=64, kernel_size=3, activation='relu', strides=2, padding='causal', input_shape=(window_size, X_train.shape[2]) ) ) model.add(MaxPooling1D(pool_size=2)) model.add(Flatten()) model.add(Dense(100, activation='relu')) model.add(Dropout(0.5)) model.add(Dense(units=len(np.unique(y)), activation='softmax')) # For binary classification (buy/sell signal) model.summary() # Compiling the model optimizer = Adam(learning_rate=0.001) model.compile(optimizer=optimizer, loss='categorical_crossentropy', metrics=['accuracy']) # Training the model early_stopping = EarlyStopping(monitor='val_loss', patience=10, restore_best_weights=True) history = model.fit(X_train, y_train_encoded, epochs=100, batch_size=16, validation_split=0.2, callbacks=[early_stopping]) plt.figure(figsize=(7.5, 6)) plt.plot(history.history['loss'], label='Training Loss') plt.plot(history.history['val_loss'], label='Validation Loss') plt.xlabel('Epochs') plt.ylabel('Loss') plt.title('Training Loss Curve') plt.legend() plt.savefig("training loss cuver-cnn-clf.png") plt.show()
Saídas:
Model: "sequential_2" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ conv1d_2 (Conv1D) │ (None, 5, 64) │ 832 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ max_pooling1d_2 (MaxPooling1D) │ (None, 2, 64) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ flatten_2 (Flatten) │ (None, 128) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_4 (Dense) │ (None, 100) │ 12,900 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dropout_2 (Dropout) │ (None, 100) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_5 (Dense) │ (None, 2) │ 202 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
O treinamento parou na 34ª época.
40/40 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.5105 - loss: 0.6875 - val_accuracy: 0.4843 - val_loss: 0.6955 Epoch 32/100 40/40 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.5099 - loss: 0.6888 - val_accuracy: 0.5283 - val_loss: 0.6933 Epoch 33/100 40/40 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.4636 - loss: 0.6933 - val_accuracy: 0.5283 - val_loss: 0.6926 Epoch 34/100 40/40 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.5070 - loss: 0.6876 - val_accuracy: 0.5346 - val_loss: 0.6963
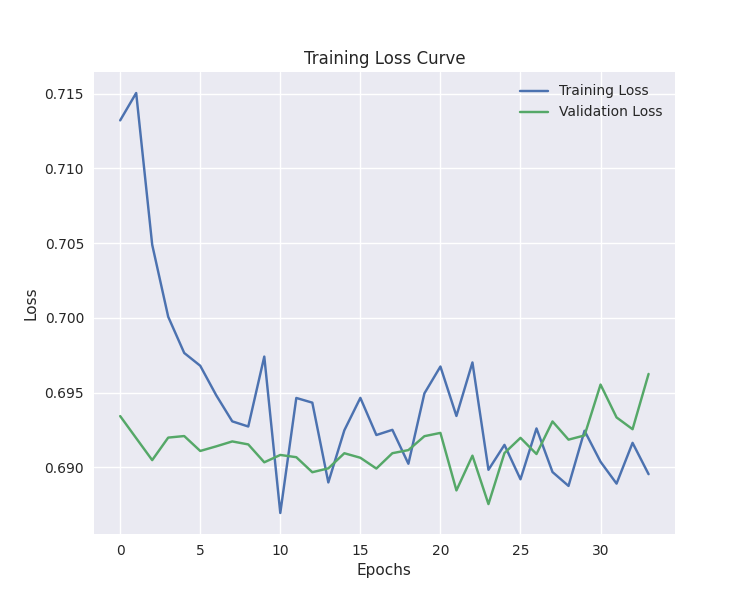
O modelo foi aproximadamente 57% preciso nas previsões fora da amostra.
y_pred = model.predict(X_test)
classes_in_y = np.unique(y)
y_pred_binary = classes_in_y[np.argmax(y_pred, axis=1)]
# Confusion Matrix
cm = confusion_matrix(y_test, y_pred_binary)
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
plt.xlabel("Predicted Label")
plt.ylabel("True Label")
plt.title("Confusion Matrix")
plt.savefig("confusion-matrix CNN") # Display the heatmap
print("Classification Report\n",
classification_report(y_test, y_pred_binary)) Saídas:
7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step Classification Report precision recall f1-score support 0 0.53 0.24 0.33 88 1 0.58 0.83 0.68 110 accuracy 0.57 198 macro avg 0.55 0.53 0.50 198 weighted avg 0.55 0.57 0.52 198
Nosso modelo de CNN é suficientemente bom para um Expert Advisor. Mas, antes de começarmos a codificar um EA, precisamos salvar o modelo de CNN treinado no formato ONNX.
04: Salvando um modelo de CNN no formato ONNX
O processo é bastante simples. Precisamos salvar o modelo da CNN no formato .onnx e os parâmetros da técnica de normalização em arquivos binários.
import tf2onnx
onnx_file_name = "cnn.EURUSD.D1.onnx"
spec = (tf.TensorSpec((None, window_size, X_train.shape[2]), tf.float16, name="input"),)
model.output_names = ['outputs']
onnx_model, _ = tf2onnx.convert.from_keras(model, input_signature=spec, opset=13)
# Save the ONNX model to a file
with open(onnx_file_name, "wb") as f:
f.write(onnx_model.SerializeToString())
# Save the mean and scale parameters to binary files
scaler.mean_.tofile(f"{onnx_file_name.replace('.onnx','')}.standard_scaler_mean.bin")
scaler.scale_.tofile(f"{onnx_file_name.replace('.onnx','')}.standard_scaler_scale.bin") Criando um Robô de Trading baseado em Rede Neural Convolucional (CNN)
Dentro de um Expert Advisor, a primeira coisa que precisamos fazer é incluir o modelo no formato ONNX e os arquivos binários do Standard Scaler como recursos.
MQL5 | ConvNet EA.mq5
#resource "\\Files\\cnn.EURUSD.D1.onnx" as uchar onnx_model[] #resource "\\Files\\cnn.EURUSD.D1.standard_scaler_scale.bin" as double scaler_stddev[] #resource "\\Files\\cnn.EURUSD.D1.standard_scaler_mean.bin" as double scaler_mean[]
Precisamos inicializar tanto o scaler quanto o modelo ONNX.
#include <MALE5\Convolutioal Neural Networks(CNNs)\Convnet.mqh> #include <MALE5\preprocessing.mqh> CConvNet cnn; StandardizationScaler scaler; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ input group "cnn"; input uint cnn_data_window = 10; //this value must be the same as the one used during training in a python script vector classes_in_y = {0,1}; //we have to assign the classes manually | it is essential that their order is preserved as they can be seen in python code, HINT: They are usually in ascending order //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- if (!cnn.Init(onnx_model)) //Initialize the ONNX model return INIT_FAILED; //--- Initializing the scaler with values loaded from binary files scaler = new StandardizationScaler(scaler_mean, scaler_stddev); //load the scaler return(INIT_SUCCEEDED); }
Isso é o suficiente para fazer o modelo funcionar. Agora, vamos criar a função para extrair os dados de forma semelhante à usada durante o treinamento. Usamos quatro variáveis OHLC dos últimos 10 períodos anteriores, que representam o tamanho da janela. O período de tempo deve ser mantido (gráfico diário).
input group "cnn"; input uint cnn_data_window = 10; //this value must be the same as the one used during training in a python script input ENUM_TIMEFRAMES timeframe = PERIOD_D1; input int magic_number = 1945; input int slippage = 50;
matrix GetXVars(int bars, int start_bar=1) { vector open(bars), high(bars), low(bars), close(bars); //--- Getting OHLC values open.CopyRates(Symbol(), timeframe, COPY_RATES_OPEN, start_bar, bars); high.CopyRates(Symbol(), timeframe, COPY_RATES_HIGH, start_bar, bars); low.CopyRates(Symbol(), timeframe, COPY_RATES_LOW, start_bar, bars); close.CopyRates(Symbol(), timeframe, COPY_RATES_CLOSE, start_bar, bars); //--- matrix data(bars, 4); //we have 10 inputs from cnn | this value is fixed //--- adding the features into a data matrix data.Col(open, 0); data.Col(high, 1); data.Col(low, 2); data.Col(close, 3); return data; }
Agora que temos uma função para coletar as variáveis independentes, podemos finalizar nossa estratégia de trading.
void OnTick() { //--- if (NewBar()) //Trade at the opening of a new candle { matrix input_data_matrix = GetXVars(cnn_data_window); //get data for the past 10 days(default) input_data_matrix = scaler.transform(input_data_matrix); //applying StandardSCaler to the input data int signal = cnn.predict_bin(input_data_matrix, classes_in_y); //getting trade signal from the RNN model Comment("Signal==",signal); //--- MqlTick ticks; SymbolInfoTick(Symbol(), ticks); if (signal==1) //if the signal is bullish { if (!PosExists(POSITION_TYPE_BUY)) //There are no buy positions { if (!m_trade.Buy(lotsize, Symbol(), ticks.ask, 0, 0)) //Open a buy trade printf("Failed to open a buy position err=%d",GetLastError()); ClosePosition(POSITION_TYPE_SELL); //close opposite trade } } else if (signal==0) //Bearish signal { if (!PosExists(POSITION_TYPE_SELL)) //There are no Sell positions if (!m_trade.Sell(lotsize, Symbol(), ticks.bid, 0, 0)) //open a sell trade printf("Failed to open a sell position err=%d",GetLastError()); ClosePosition(POSITION_TYPE_BUY); } else //There was an error return; } }
A estratégia é simples. Ao receber um determinado sinal, como um sinal de compra, abrimos uma posição de compra sem definir stop loss ou take profit e fechamos a posição oposta. O mesmo vale para sinais de venda.
Testei essa estratégia no símbolo para o qual foi treinada, EURUSD, por dez anos. De 01/01/2014 a 27/05/2024 em um gráfico de 4 horas usando preços de abertura de cada barra.
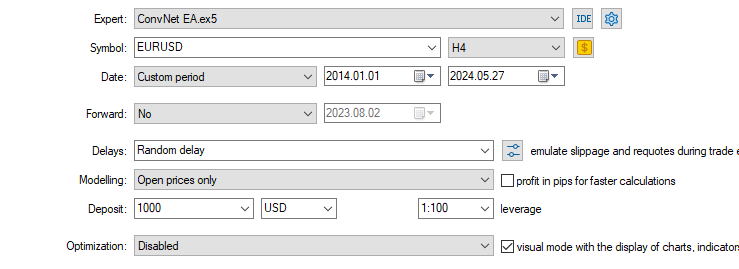
Os resultados obtidos no testador de estratégia foram excelentes.
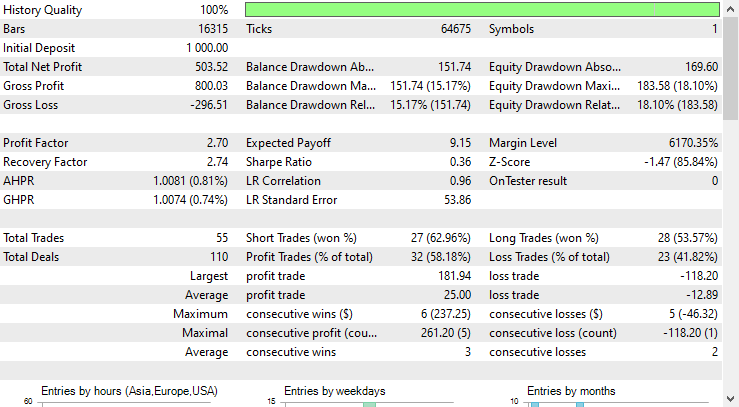
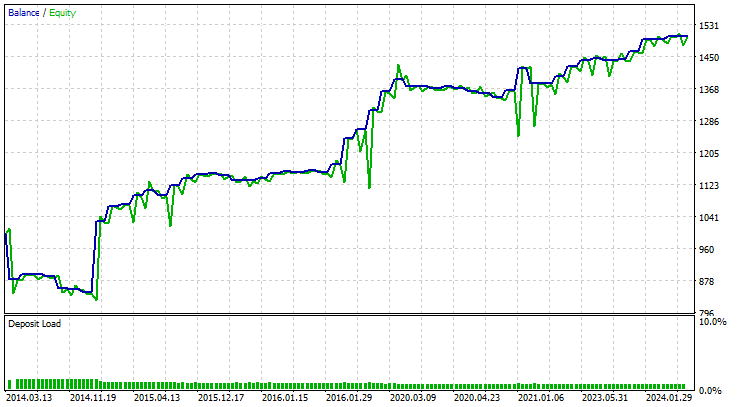
O EA fez previsões precisas 58% do tempo, resultando em um lucro líquido de $503.
A linha de fundo
Apesar de terem sido projetadas especificamente para o processamento de imagens e vídeos, quando adaptadas para lidar com dados tabulares, como os dados do mercado forex que utilizamos, As Redes Neurais Convolucionais (CNNs) podem desempenhar um bom papel na detecção de padrões e no uso desses padrões para fazer previsões no mercado forex.
Conforme pode ser visto no relatório do testador de estratégia, O EA baseado em CNN fez previsões razoavelmente precisas. Aposto que muitos modelos tradicionais projetados para dados tabulares, como Regressão Linear, Support Vector Machine e Naive Bayes, não conseguiriam alcançar essa precisão preditiva, considerando que o modelo de CNN foi treinado com apenas 4 variáveis independentes (OHLC). Na minha experiência, poucos modelos conseguem alcançar esse desempenho com um número tão reduzido de variáveis.
Atenciosamente.
Acompanhe o desenvolvimento de modelos de machine learning e muito mais discutido nesta série de artigos no repositório do GitHub.
Tabela de Anexos
| Nome do Arquivo | Tipo de Arquivo | Descrição|Uso |
|---|---|---|
| ConvNet EA.mq5 | Consultor Especialista | Robô de trading para carregar o modelo CNN no formato ONNX e testar a estratégia final de negociação no MetaTrader 5. |
| cnn.EURUSD.D1.onnx | ONNX | CNN model in ONNX format. |
| cnn.EURUSD.D1.standard_scaler_mean.bin cnn.EURUSD.D1.standard_scaler_scale.bin | Arquivos Binários | Arquivos binários para o Scaler de Padronização |
| preprocessing.mqh | Um arquivo de inclusão | Uma biblioteca que consiste no Scaler de Padronização |
| ConvNet.mqh | Um arquivo de inclusão | Uma biblioteca para carregar e implantar um modelo CNN no formato ONNX. |
| cnn-for-trading-applications-tutorial.ipynb | r | Consiste em todo o código Python discutido neste artigo |
Fontes e Referências:
- Uma nova estratégia de acompanhamento de tendência profunda baseada em Redes Neurais Convolucionais para negociação no mercado de ações(https://ceur-ws.org/Vol-3052/paper2.pdf)
- O que são Redes Neurais Convolucionais (CNNs)? (https://youtu.be/QzY57FaENXg)
- Convertendo dados tabulares em imagens para aprendizado profundo com redes neurais convolucionais(https://www.nature.com/articles/s41598-021-90923-y)
- Kernels de imagem(https://setosa.io/ev/image-kernels/)
- Métodos de Pooling em Redes Neurais Profundas: uma revisão(https://arxiv.org/pdf/2009.07485)
Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/15259
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Redes neurais em trading: Transformer vetorial hierárquico (HiVT)
Redes neurais em trading: Transformer vetorial hierárquico (HiVT)
 Combine Estratégias de Análise Fundamental e Técnica no MQL5 Para Iniciantes
Combine Estratégias de Análise Fundamental e Técnica no MQL5 Para Iniciantes
 Técnicas do MQL5 Wizard que você deve conhecer (Parte 28): GANs revisitados com uma introdução às taxas de aprendizado
Técnicas do MQL5 Wizard que você deve conhecer (Parte 28): GANs revisitados com uma introdução às taxas de aprendizado
 Otimização por Quimiotaxia Bacteriana (BCO)
Otimização por Quimiotaxia Bacteriana (BCO)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Artigo publicado Aprendizado de máquina e ciência de dados (Parte 27): Redes neurais convolucionais (CNNs) em robôs de negociação para o MetaTrader 5:
Autor: Omega J Msigwa
5,5 negociações por ano no H4 não são suficientes. Muito pouco.
Esta é a explicação mais concisa da CNN aplicada à negociação que já vi e, em sua maior parte, em linguagem simples e diagramas. Em seguida, ela é reduzida para o código MQL5. Observe que o código não está limitado ao período de tempo H4.
Muito bem, senhor!👍